Mathematik f¨ ur Naturwissenschaftler I WS 2020/21
Prof. Andreas Dreuw
Ubungsblatt 3¨ Ausgabe: Do 19.11.2020
Abgabe: Fr 27.11.2020 10:00
1 2 3 4 Σ
/ 21 P
Basiswissen
Polynome, trigonometrische Funktionen, Definitionsbereich einer Funktion, Definiti- onsl¨ucken
Neue Themen
Komplex konjugierte Nullstellen, Polynomdi- vision, Additionstheoreme, harmonischer Os- zillator, Singularit¨at
Aufgabe 3.1 (6 P). Nullstellen von Polynomen und Definitionsl¨ucken
Viele Modelle und Formeln in der Chemie und Physik besitzen ganz oder teilweise die Form reeller oder komplexer Polynome. Die F¨ahigkeit mit ihnen rechnen zu k¨onnen und ihre Eigenschaften zu verstehen ist wichtig f¨ur die Planung und Auswertung vieler Experimente.
Im Folgenden finden Sie ein paar Aufgaben um das Rechnen mit Polynomen zu ¨uben, damit wir sp¨ater tiefer in die Analyse solcher Funktionen einsteigen k¨onnen.
(a) Berechnen Sie die Nullstellen von
x2+ 6x+ 5 (1)
(1 P) (b) Berechnen Sie die Nullstellen von
x2+ 6x+ 13 (2)
Vergleichen Sie das Ergebnis mit dem von Aufgabenteil a). Was f¨allt auf? (1 P) (c) Berechnen Sie die Nullstellen von
x4−x3+ 10x2−16x−96 (3)
mithilfe der Polynomdivision und ihrem Wissen bez¨uglich der Eigenschaften von Null- stellen. Hinweis: Eine Nullstelle des Polynoms liegt bei x= 4i. (2 P) (d) Geben Sie den jeweiligen Definitionsbereich der folgenden reellwertigen Funktionen an:
f(x) =x2−25
x−5 , g(x) = x−5
x2−25 (4)
Vereinfachen Sie nun beide Ausdr¨ucke. Wie sieht nun der Definitionsbereich aus?(2 P) Aufgabe 3.2 (4 P). Polynomdivision
Betrachten Sie folgende Polynome
3x7−7x5−14x3+ 10x= (3x2+ 5)·p(x) (5) und
x4−4x3+ 3x2−2x+ 1
x2+ 1 =q(x). (6)
Berechnen Sie mithilfe der Polynomdivision
1
(a) das Polynomp(x). (2 P)
(b) das Polynomq(x). (2 P)
Aufgabe 3.3 (5 P). Trigonometrische Funktionen
Im wissenschaftlichen Alltag vorkommende trigonometrische Funktionen, etwa in Formeln oder als gefittete Kurven bei Messungen, sind h¨aufig kompliziert. Additionstheoreme sind mathematische Zusammenh¨ange, die es einem oft erlauben mit geschickten Umformungen kompliziertere Funktionen auf einfachere Strukturen zu reduzieren.
Zwei dieser Additionstheoreme f¨ur Sinus und Cosinus lauten
sin(a+b) = sin(a) cos(b) + cos(a) sin(b) (7) und
cos(a+b) = cos(a) cos(b)−sin(a) sin(b). (8) Außerdem gilt folgender Zusammenhang
sin2(x) + cos2(x) = 1. (9)
(a) Benutzen Sie die oben aufgelisteten Identit¨aten, um folgende Gleichung zu beweisen:
cos(3x) + 3 cos(x) = 4 cos3(x) (10) (2 P) (b) Berechenen Sie alle reellen Zahlenx, f¨ur die gilt:
1−cos2(x) = 1
2 sin(x) sin(2x) (11)
(3 P) Aufgabe 3.4 (6 P). Harmonischer Oszillator
Der harmonische Oszillator findet Anwendung als Grundmodell f¨ur ideale Schwingungen.
Schwingungen (etwa von Elektronen oder ganzen Atomen) sind in der Chemie und Physik allgegenw¨artig, zum Beispiel beim Aufnehmen elektromagnetischer Spektren, der thermi- schen Bewegung von Teilchen oder als theoretisches Modell f¨ur die Beschreibung von Wel- lenfunktionen.
Die Bewegung des harmonischen Oszillators wird durch die allgemeine Gleichung
x(t) =A·cos(ωt+φ) (12)
beschrieben. Hierbei ist:
x(t) die Auslenkung vom Ruhepunkt, Adie maximale Auslenkung oder Amplitude, φdie Phasenverschiebung undωdie Kreisfrequenz.
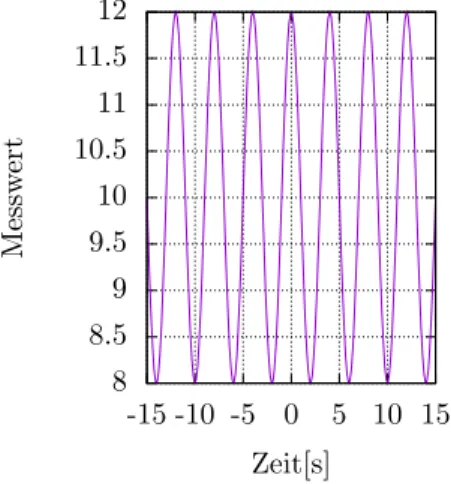
(a) Es soll gelten: x(0) = A. Was bedeutet dies f¨ur die Phase φ? Was bedeutet das an- schaulich f¨ur den Messversuch des schwingenden (idealen) Pendels? (2 P) (b) Ihre Messung im Labor liefert Ihnen den Graph 1. F¨ur Ihre Auswertung ben¨otigen Sie allerdings die der Schwingung zu Grunde liegende Amplitude, Kreisfrequenz und die Phasenverschiebung. Schlagen Sie hierf¨ur eine passende Funktion auf Basis des
harmonischen Oszillators vor. (2 P)
(c) Neben der Kreisfrequenz ω existieren noch zwei weitere Gr¨oßen (T, f), um das pe- riodische Zeitintervall zu beschreiben. Geben Sie die Namen beider Gr¨oßen mitsamt ihrer Umrechnung und den zugeh¨origen SI Einheiten an. (2 P)
2
8 8.5 9 9.5 10 10.5 11 11.5 12
-15 -10 -5 0 5 10 15
Messwert
Zeit[s]
Abbildung 1: Ein gemessenes Spektrum.
3