Mathematik f¨ ur Naturwissenschaftler I WS 2020/21
Prof. Andreas Dreuw
Ubungsblatt 3¨ Ausgabe: Do 19.11.2020
Abgabe: Fr 27.11.2020 10:00
1 2 3 4 Σ
/ 21 P
Basiswissen
Polynome, trigonometrische Funktionen, Definitionsbereich einer Funktion, Definiti- onsl¨ucken
Neue Themen
Komplex konjugierte Nullstellen, Polynomdi- vision, Additionstheoreme, harmonischer Os- zillator, Singularit¨at
Aufgabe 3.1 (6 P). Nullstellen von Polynomen und Definitionsl¨ucken
Viele Modelle und Formeln in der Chemie und Physik besitzen ganz oder teilweise die Form reeller oder komplexer Polynome. Die F¨ahigkeit mit ihnen rechnen zu k¨onnen und ihre Eigenschaften zu verstehen ist wichtig f¨ur die Planung und Auswertung vieler Experimente.
Im Folgenden finden Sie ein paar Aufgaben um das Rechnen mit Polynomen zu ¨uben, damit wir sp¨ater tiefer in die Analyse solcher Funktionen einsteigen k¨onnen.
(a) Berechnen Sie die Nullstellen von
x2+ 6x+ 5 (1)
(1 P) (b) Berechnen Sie die Nullstellen von
x2+ 6x+ 13 (2)
Vergleichen Sie das Ergebnis mit dem von Aufgabenteil a). Was f¨allt auf? (1 P) (c) Berechnen Sie die Nullstellen von
x4−x3+ 10x2−16x−96 (3)
mithilfe der Polynomdivision und ihrem Wissen bez¨uglich der Eigenschaften von Null- stellen. Hinweis: Eine Nullstelle des Polynoms liegt bei x= 4i. (2 P) (d) Geben Sie den jeweiligen Definitionsbereich der folgenden reellwertigen Funktionen an:
f(x) =x2−25
x−5 , g(x) = x−5
x2−25 (4)
Vereinfachen Sie nun beide Ausdr¨ucke. Wie sieht nun der Definitionsbereich aus?(2 P)
L¨osung 3.1.
(b) x1=−3−2i, x2=−3 + 2i
Ebenfalls mit pq- oder abc-Formel. Die Diskriminante hat in beiden F¨allen densel- ben Betrag, jedoch ist sie in b) negativ, wodurch sich zwei komlexe (und zueinander konjugiert) Nullstellen ergeben.
(c) Die erste Nullstelle ist gegeben mit x1 = 4i. Bei Polynomen impliziert dies sofort die dazu komplex konjugierte als weitere Nullstelle, alsox2=−4i. Anstatt nun nachein- ander erst durch den Linearfaktor (x−4i) und dann (x+ 4i) zu teilen, kann man sofort durch das Produkt dieser beiden Linearfaktoren, also (x2−16) teilen:
x4−x3+ 10x2−16x−96
: x2+ 16
=x2−x−6
−x4 −16x2
−x3 −6x2−16x
x3 + 16x
−6x2 −96
6x2 + 96
0
Die beiden verbleibenden Nullstellen sind somit 3 und −2. Diese k¨onnen wieder mit einer L¨osungsformel der Wahl gefunden werden.
(d) Df =R\5, Dg=R\ {−5,5}
Vereinfachen liefert:
f(x) =(x+ 5)(x−5)
x−5 (5)
⇒f(x) =x+ 5 (6)
g(x) = x−5
(x+ 5)(x−5) (7)
⇒g(x) = 1
x+ 5. (8)
Nun sind die Definitionsbereiche gegeben als:
Df =R, Dg=R\ −5
Es handelt sich also in beiden F¨allen bei dem Wert 5 um eine hebbare Singularit¨at.
Aufgabe 3.2 (4 P). Polynomdivision Betrachten Sie folgende Polynome
3x7−7x5−14x3+ 10x= (3x2+ 5)·p(x) (9) und
x4−4x3+ 3x2−2x+ 1
x2+ 1 =q(x). (10)
Berechnen Sie mithilfe der Polynomdivision
(a) das Polynomp(x). (2 P)
(b) das Polynomq(x). (2 P)
L¨osung 3.2.
(a) 3x7 −7x5−14x3+ 10x
: 3x2+ 5
=x5−4x3+ 2x
−3x7 −5x5
−12x5−14x3 12x5+ 20x3
6x3+ 10x
−6x3−10x 0 (b) x4−4x3+ 3x2−2x+ 1
: x2+ 1
=x2−4x+ 2 +2x−1 x2+ 1
−x4 −x2
−4x3+ 2x2−2x
4x3 + 4x
2x2+ 2x+ 1
−2x2 −2 2x−1
Aufgabe 3.3 (5 P). Trigonometrische Funktionen
Im wissenschaftlichen Alltag vorkommende trigonometrische Funktionen, etwa in Formeln oder als gefittete Kurven bei Messungen, sind h¨aufig kompliziert. Additionstheoreme sind mathematische Zusammenh¨ange, die es einem oft erlauben mit geschickten Umformungen kompliziertere Funktionen auf einfachere Strukturen zu reduzieren.
Zwei dieser Additionstheoreme f¨ur Sinus und Cosinus lauten
sin(a+b) = sin(a) cos(b) + cos(a) sin(b) (11) und
cos(a+b) = cos(a) cos(b)−sin(a) sin(b). (12) Außerdem gilt folgender Zusammenhang
sin2(x) + cos2(x) = 1. (13)
(a) Benutzen Sie die oben aufgelisteten Identit¨aten, um folgende Gleichung zu beweisen:
cos(3x) + 3 cos(x) = 4 cos3(x) (14) (2 P) (b) Berechenen Sie alle reellen Zahlenx, f¨ur die gilt:
1−cos2(x) = 1
2 sin(x) sin(2x) (15)
(3 P) L¨osung 3.3.
(a)
cos(3x) + 3 cos(x) = cos(2x) cos(x)−sin(2x) sin(x) + 3 cos(x) (16)
= cos2(x)−sin2(x)
cos(x)−2 sin2(x) cos(x) + 3 cos(x) (17)
= cos3(x)−3 sin2(x) cos(x) + 3 cos(x) (18)
(b)
1−cos2(x) = 1
2 sin(x) sin(2x) (21)
⇒sin2(x) = sin2(x) cos(x) (22)
⇒sin2(x) [1−cos(x)] = 0 (23)
(24) Es muss also entweder sin2(x) = 0 oder cos(x) = 1 gelten. sin2(x) besitzt genau wie sin(x) Nullstellen beix=nπ, n∈Z. cos(x) = 1 gilt f¨ur allex= 2nπ, n∈Z, somit gilt der Gesamtausdruck f¨ur allenπ, n∈Z.
Aufgabe 3.4 (6 P). Harmonischer Oszillator
Der harmonische Oszillator findet Anwendung als Grundmodell f¨ur ideale Schwingungen.
Schwingungen (etwa von Elektronen oder ganzen Atomen) sind in der Chemie und Physik allgegenw¨artig, zum Beispiel beim Aufnehmen elektromagnetischer Spektren, der thermi- schen Bewegung von Teilchen oder als theoretisches Modell f¨ur die Beschreibung von Wel- lenfunktionen.
Die Bewegung des harmonischen Oszillators wird durch die allgemeine Gleichung
x(t) =A·cos(ωt+φ) (25)
beschrieben. Hierbei ist:
x(t) die Auslenkung vom Ruhepunkt, Adie maximale Auslenkung oder Amplitude, φdie Phasenverschiebung undωdie Kreisfrequenz.
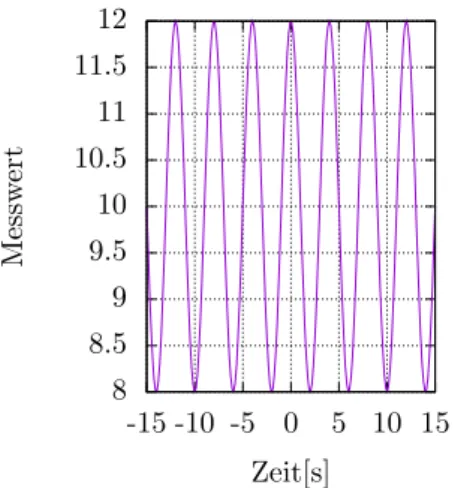
(a) Es soll gelten: x(0) = A. Was bedeutet dies f¨ur die Phase φ? Was bedeutet das an- schaulich f¨ur den Messversuch des schwingenden (idealen) Pendels? (2 P) (b) Ihre Messung im Labor liefert Ihnen den Graph 1. F¨ur Ihre Auswertung ben¨otigen Sie allerdings die der Schwingung zu Grunde liegende Amplitude, Kreisfrequenz und die Phasenverschiebung. Schlagen Sie hierf¨ur eine passende Funktion auf Basis des
harmonischen Oszillators vor. (2 P)
(c) Neben der Kreisfrequenz ω existieren noch zwei weitere Gr¨oßen (T, f), um das pe- riodische Zeitintervall zu beschreiben. Geben Sie die Namen beider Gr¨oßen mitsamt ihrer Umrechnung und den zugeh¨origen SI Einheiten an. (2 P)
L¨osung 3.4.
(a) Damit cos(0 +φ) = 1 gilt, mussφ= 0 gelten. Bei einem Pendel w¨urde das bedeuten, dass man die Messung in dem Moment (t= 0) beginnt, wo der Ausschlag maximal ist.
(b) A = 2, ω = π2 und φ = 0 (wenn cosinus angenommen wird, ansonsten ist der sinus Phasenverschoben).
(c) Schwingungsdauer T,T =2πω[s]; Frequenzf,f =T−1[1s].
8 8.5 9 9.5 10 10.5 11 11.5 12
-15 -10 -5 0 5 10 15
Messwert
Zeit[s]
Abbildung 1: Ein gemessenes Spektrum.