Mathematik f¨ur Naturwissenschaftler I WS 2020/21 Prof. Andreas Dreuw
Volltext
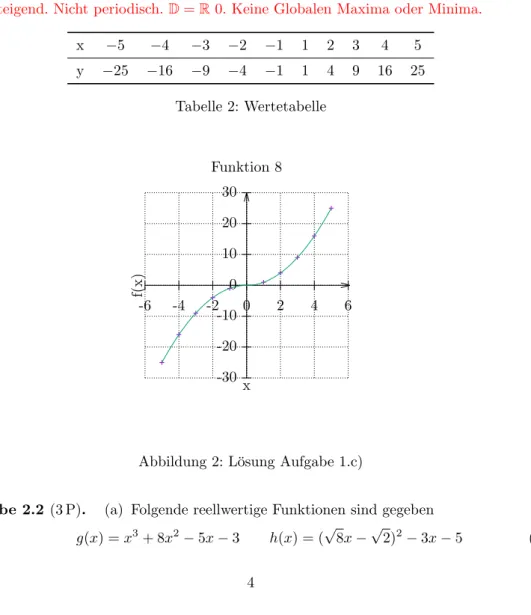
Abbildung


ÄHNLICHE DOKUMENTE
Diese DGL ist implizit, da vor der h¨ ochsten Ableitung ein x dranmultipliziert wurde (xy 000 (x)), gew¨ ohnlich, weil wir nur Ableitungen zu einer unabh¨ angige Gr¨ oße (x)
Mathematik f¨ ur Naturwissenschaftler I WS
(a) Geben Sie die drei elementare Operationen f¨ ur das Rechnen mit Mengen an und ver- anschaulichen Sie diese grafisch.. (b) Gegeben seien folgende Ungleichungen mit x ∈ R : 2x − 3
Funktionstheorie, Polynome n-ten Grades, Komplexe Polynome n-ten Grades, Defini- tionsbereich, Wertebereich, Monotonie, Be- tragsfunktion, Komposition von Funktionen,
Schwingungen (etwa von Elektronen oder ganzen Atomen) sind in der Chemie und Physik allgegenw¨ artig, zum Beispiel beim Aufnehmen elektromagnetischer Spektren, der thermi-
Da die Chemie zu großen Teilen eine empirische Wissenschaft ist, verwendet man h¨ aufig Methoden aus Statistik und Stochastik, um die Verteilung von einzelnen Messungen um
Als Schwebung wird in der Physik eine ¨ Uberlagerung (Superposition) von zwei Schwingungen
Welche physikalischen Gr¨ oßen (mit Einheit) stecken jeweils hinter den einfach, zweifach und dreifach nach der Zeit?.