Festk¨orperphysik II

Festk¨ orperphysik II

Studienjahr 2009/2010 Vorl.-Nr. 138.024

Silke B¨uhler-Paschen, Institut f¨ur Festk¨orperphysik Peter Mohn, Institut f¨ur Allgemeine Physik

• 810 Technische Physik (2002U), 3. Abschnitt, 7. Semester, 6.0 ECTS

• 066 461 Master Technische Physik (2006U), Master 1. Semester, 4.0 ECTS

• 066 434 Master Materialwissenschaften (2006U), 3.0 ECTS

• 860 Technische Mathematik (2002U), 3.2 ECTS

• 864 Mathematik i.d. Naturwissenschaften (Stzw, 2002U), 3. Abschnitt, 3.2 ECTS

• 866 Wirtschaftsmathematik (Stzw, 2002U), 3. Abschnitt, 3.2 ECTS

• 867 Statistik (Stzw, 2002U), 3. Abschnitt, 3.2 ECTS

• 869 Mathematik i.d. Computerwissenschaften(Stzw, 2002U), 3. Ab- schnitt, 3.2

• 873 Finanz- u. Versicherungsmathematik (Stzw, 2002U), 3. Abschnitt, 3.2 ECTS

• 066 400-405 Master Mathematik und Varianten (2006U), 3.0 ECTS

Kapitel 1 Einleitung

Das Ihnen vorliegende Skriptum Festk¨orperphysik II baut auf den Inhalten der Vorlesun- gen Materialwissenschaften und Festk¨orperphysik I auf. Weiters sind zum Verst¨andnis des abgehandelten Stoffes Grundkenntnisse der Quantenmechanik und der Statistischen Physik von Nutzen. Ziel der Vorlesung ist es, von diesem Grundstock ausgehend eine Br¨ucke zur aktuellen Festk¨orperforschung zu schlagen und Ihnen damit einen Einstieg in eigene Forschungsaktivit¨aten zu erleichtern.

Aufgrund der kleinen Abst¨ande der Atome im Festk¨orper (im Vergleich zur Fl¨ussigkeit oder zum Gas) spielen Wechselwirkungen eine zentrale Rolle und sind daher auch das Kernst¨uck der Vorlesung. Als Beispiel sei die Bewegung eines Atoms im Festk¨orper genannt.

Sie ist keinesfalls unabh¨angig von der aller anderer Atome. Die Auslenkung eines einzelnen Atoms aus seiner Ruhelage zieht auf Grund der starken Wechselwirkung der Atome miteinan- der eine Bewegung der anderen Atome im Festk¨orper nach sich. Man spricht von einer kollek- tiven Anregung (Phonon). Dass das Modell des freien Elektronengases (Sommerfeld-Theorie, Festk¨orperphysik I), das Wechselwirkungen zwischen den Elektronen v¨ollig vernachl¨assigt, viele Eigenschaften einfacher Metalle relativ gut beschreibt ist eigentlich ein Wunder, denn die Wechselwirkungen zwischen den Elektronen sind keinesfalls klein. Dieses

”Wunder“ kann mit der Landau’schen Theorie der Fermifl¨ussigkeit (s.u.) verstanden werden. Auch magneti- sche Momente im Festk¨orper, die auf die Spins der Elektronen zur¨uckgehen, sind nicht un- abh¨angig voneinander. So beruht z.B. das Ph¨anomen der magnetischen Ordnung eben gerade auf der Wechselwirkung zwischen den Momenten. Wechselwirkungen zwischen verschiedenen

”Teilchenarten“ f¨uhren zu einer Vielzahl von interessanten Effekten wie z.B. der konventio- nellen Supraleitung (Elektron-Phonon-Wechselwirkung), der unkonventionellen Supraleitung (Elektron-Paramagnon-Wechselwirkung) oder dem Schwere-Fermionen-Verhalten (Elektron- Spin-Wechselwirkung). Derartige Wechselwirkungseffekte werden meist erst bei tiefen Tem- peraturen beobachtet, da die thermische Energie, die jeder Art von Ordnung entgegenwirkt, hier reduziert ist. Moderne experimentelle Festk¨orperphysik ist daher oft Tieftemperatur- physik. Die theoretische Beschreibung eines Ensembles wechselwirkender Teilchen, die sog.

Vielteilchenphysik, stellt eine der bedeutendsten Herausforderungen der modernen Physik dar. Da die Anzahl der zu beschreibenden

”Teilchen“ im Festk¨orper gigantisch ist (von der Gr¨oßenordnung der AvogadrozahlN_A≈6×10²³mol⁻¹), ist eine exakte quantenmechanische

iii

Behandlung des Festk¨orpers ausgeschlossen. Man ist auf N¨aherungsmethoden oder auf Mo- dellrechnungen, in denen nur die wesentlichsten Wechselwirkungsterme behandelt werden, angewiesen.

In Kap. 2 wird ein ¨Uberblick ¨uber Materialien der aktuellen Festk¨orperforschung gege- ben. Bei der Auswahl wurde jenen Systemen der Vorzug gegeben, in denen eine bestimmte Wechselwirkungen dominiert und somit gut

”greifbar“ ist. In Kap. 3 wird eines der bedeu- tendsten Konzepte der modernen Festk¨orperphysik, das Quasiteilchenkonzept eingef¨uhrt und dessen Bedeutung f¨ur die Entwicklung der

”Standardtheorie der Metalle“, der Landau’schen Theorie der Fermifl¨ussigkeit, erl¨autert. Bevor wir uns den Wechselwirkungen (Kap. 5) zuwen- den k¨onnen, m¨ussen wir genau definieren, welche

”Teilchen“ wir miteinander wechselwirken lassen wollen. Dies geschieht im Kapitel ¨uber elementare Anregungen (Kap. 4). W¨ahrend in Kap. 4 und 5 einige Modell-Hamiltonoperatoren besprochen werden, sindab initio-Methoden Thema in Kap. 6.

Zur Erstellung des Skriptums wurden verschiedene Literaturquellen herangezogen. Ori- ginalliteratur wird stets im Text zitiert. Informationen, die aus Lehrb¨uchern stammen und somit als

”Allgemeingut“ gelten, werden nicht im Text zitiert, jedoch unten angef¨uhrt. Sie k¨onnen auch zur weiterf¨uhrenden Lekt¨ure herangezogen werden.

• A Quantum Approach to Condensed Matter Physics, Philip L. Taylor & Olle Heinonen (Cambridge University Press, Cambridge, 2002, ISBN 0-521-77827-1)

• Condensed Matter Physics, Michael P. Marder (John Wiley & Sons, Inc., New York, 2000, ISBN 0-471-17779-2)

• Einf¨uhrung in die Festk¨orperphysik, Charles Kittel (Oldenbourg Verlag, M¨unchen, 1983, ISBN 3-486-32766-6)

• Festk¨orperphysik, N. W. Ashcroft/N. D. Mermin (Oldenbourg Verlag, M¨unchen, 2001, ISBN 3-486-24834-0)

• Festk¨orpertheorie I/II, Otfried Madelung (Springer Verlag, Berlin, 1972, ISBN 0-387- 05731-5/0-387-05866-4)

• Introduction to Condensed Matter Physics, Feng Duan, Jin Guojun (World Scientific, New Jersey, 2005, ISBN 981-256-070-X)

• Quantum Theory of the Solid State, Joseph Callaway (Academic Press, Inc., Boston, 1991, ISBN 0-12-1555203-9)

Silke B¨uhler-Paschen und Peter Mohn, Oktober 2009

Inhaltsverzeichnis

1 Einleitung iii

2 Materialien der aktuellen Forschung 3

2.1 Schwere-Fermionen-Verbindungen . . . 3

2.2 Quantenkritische Systeme . . . 8

2.2.1 Quanten-Ising-Systeme . . . 9

2.2.2 Quantenkritische Schwere-Fermionen-Systeme . . . 10

2.2.3 Systeme mit quantenkritischem Endpunkt . . . 14

2.3 Unkonventionelle Supraleiter . . . 16

2.3.1 Hochtemperatur-Supraleiter . . . 16

2.3.2 Schwere-Fermionen-Supraleiter . . . 19

2.4 Quasi-eindimensionale Systeme . . . 20

2.4.1 Das Kuprat SrCuO2 . . . 21

2.4.2 Kohlenstoff-Nanor¨ohrchen . . . 22

2.5 Invar-Materialien . . . 24

2.5.1 Fe-Ni-Legierungen . . . 25

2.5.2 Die Verbindung YbGaGe . . . 26

3 Landau’sche Theorie der Fermifl¨ussigkeit 29 3.1 Das Konzept der Quasiteilchen . . . 29

3.2 Spezifische W¨arme und Paulisuszeptibilit¨at . . . 31

3.2.1 Statistische Thermodynamik der Quasiteilchen . . . 32

3.2.2 Spezifische W¨arme der Quasiteilchen . . . 34

3.2.3 Effektive Masse . . . 36

3.2.4 Fermifl¨ussigkeitsparameter . . . 38

3.2.5 Magnetische Suszeptibilit¨at . . . 40

3.3 Transporteigenschaften . . . 42

3.4 Kollektive Anregungen . . . 43

3.5 Eigenschaften der wechselwirkenden Elektronen . . . 44

4 Elementare Anregungen 47 4.1 Uberblick . . . .¨ 48

4.1.1 Elektronisches Quasiteilchen . . . 48

4.1.2 Phonon . . . 49 v

4.1.3 Soliton . . . 51

4.1.4 Magnon . . . 54

4.1.5 Paramagnon . . . 57

4.1.6 Domain-wall- und Flipped-spin-Quasiteilchen . . . 58

4.1.7 Spinon und Holon . . . 60

4.1.8 Gebrochene valence bonds instripes . . . 61

4.2 Beispiele . . . 64

4.2.1 Phononen . . . 64

4.2.2 Magnonen . . . 67

5 Wechselwirkungen 79 5.1 Elektron-Phonon-Wechselwirkung . . . 79

5.1.1 Auswirkung auf die Dispersionsrelation der Phononen . . . 83

5.1.2 Der Peierls- ¨Ubergang . . . 85

5.1.3 Der Jahn-Teller- ¨Ubergang . . . 87

5.1.4 Auswirkungen auf die Elektronen . . . 92

5.2 Elektron-Spin-Wechselwirkung . . . 93

5.2.1 Anderson-Modell . . . 94

5.2.2 Von der Verunreinigung zum lokalen Moment . . . 97

5.2.3 Skalentheorie . . . 99

5.3 Elektron-Photon-Wechselwirkung . . . 103

6 Materialspezifische Methoden der Festk¨orperphysik 121 6.1 Elektronen im Kristall . . . 121

6.1.1 Die tight-binding-N¨aherung . . . 121

6.1.2 Hartree und Hartree-Fock-Methode . . . 126

6.2 Dichtefunktional-Theorie . . . 138

6.2.1 Das Hohenberg-Kohn-Sham-Theorem . . . 138

6.2.2 Lokale Dichtefunktional-N¨aherung (LDA) . . . 140

6.3 Starke elektronische Korrelationen . . . 141

6.3.1 Hubbard-Model . . . 142

6.3.2 Korrelationskorrekturen in der LDA . . . 144

6.3.3 Dynamische Molekularfeld-Theorie (DMFT) . . . 146

A Das freie Fermigas 147 A.1 Quantenstatistik der Fermionen . . . 147

A.2 Die Freie Energie des Fermigases . . . 150

A.3 Zustandsdichte . . . 157

Kapitel 2

Materialien der aktuellen Forschung

Ein Großteil der aktuellen Festk¨orperforschung besch¨aftigt sich mit Materialien, die mit den bisher beschriebenen Modellen (Skripten Materialwissenschaften und Festk¨orperphysik I) nicht oder nur sehr unzureichen beschrieben werden k¨onnen. Einige dieser Materialien sollen hier beispielhaft vorgestellt werden.

2.1 Schwere-Fermionen-Verbindungen

1975 wurde mit CeAl3 die erste Schwere-Fermionen-Verbindung entdeckt. Diese f¨ur das For- schungsgebiet der elektronisch hochkorrelierten Systeme wesentliche Entdeckung wurde bei der im Juli 2005 an der TU Wien abgehaltenen Konferenz

”The International Conference on Strongly Correlated Electron Systems“ im Rahmen der Plenarsitzung

”30 Years of Heavy Fermion Physics“ gefeiert.

Das paramagnetische Metall CeAl3 kristallisiert in der hexagonalen Ni3Sn-Struktur.

Bei hohen Temperaturen zeigt die magnetische Suszeptibilit¨at Curie-Weiss-Verhalten [χ = C/(T − Θp)], mit einem f¨ur Ce³⁺ charakteristischen effektiven magnetischen Moment.

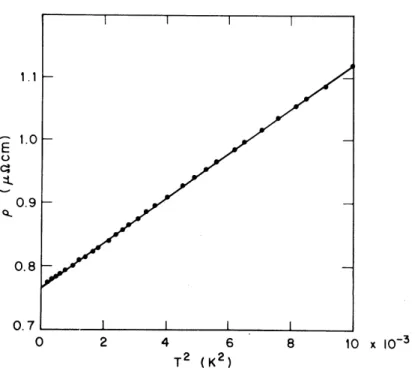
Die wichtigsten experimentellen Ergebnisse der Originalver¨offentlichung von 1975 sind in Abb. 2.1, 2.2 und 2.3 dargestellt. Die spezifische W¨armeC(Abb. 2.1) steigt bei Temperaturen unterhalb von 150 mK linear mit der TemperaturT an:C =γT. Der Proportionalit¨atsfaktor γ betr¨agt 1620 mJ/(mol K²). Die magnetische Suszeptibilit¨at (Abb. 2.2) ist bei tiefen Tem- peraturen nur schwach temperaturabh¨angig und s¨attigt unterhalb von 100 mK bei einem Wert von 0,036 emu/mol (SI: 4,52·10⁻⁷ m³/mol). Der spezifische elektrische Widerstand (Abb. 2.3) variiert unterhalb von 100 mK quadratisch mit der Temperatur: ρ = ρ0 +AT². Der Proportionalit¨atsfaktor A betr¨agt 35 µΩcm/K².

Die spezifische W¨arme von einfachen Metallen ist bei Temperaturen weit unterhalb der Debyetemperatur durch C = γT +βT³ gegeben. Der erste Term ist der elektronische, der zweite der phononische Beitrag. γ wird auch als der Sommerfeld-Koeffizient der spezifischen W¨arme bezeichnet. Einfache Metalle habenγ-Werte von der Gr¨oßenordnung 1 mJ/(mol K²), was im Einklang mit der Sommerfeld-Theorie freier Elektronen ist: γ = (π²N k_B²)/(2EF) (N ist die Anzahl der Leitungselektronen pro Mol, kB die Boltzmannkonstante und EF

die Fermienergie). Beispiel Au: N = N_A, E_F = 5,53 eV =⇒ γ_theor = 0.63 mJ/(mol K²);

3

Abbildung 2.1: Spezifische W¨arme von CeAl3 als Funktion der Temperatur im Nullfeld (•,

△) und bei 10 kOe (¤) [Andres et al., Phys. Rev. Lett. 35 (1975) 1779].

T [K]

Abbildung 2.2: Magnetische Suszeptibilit¨at von CeAl3 als Funktion der Temperatur in ver- schiedenen Magnetfeldern [Andres et al., Phys. Rev. Lett. 35 (1975) 1779].

γexp = 0.67 mJ/(mol K²) (Ashcroft/Mermin).

Die Pauli-Suszeptibilit¨at der Leitungselektronen ist in einfachen Metallen bei Temperatu- ren weit unterhalb der Fermitemperatur konstant und von der Gr¨oßenordnung 10⁻¹⁰m³/mol, wiederum in ¨Ubereinstimmung mit der Sommerfeld-Theorie freier Elektronen: χ_Pauli =

Abbildung 2.3: Elektrischer Widerstand von CeAl3 als Funktion des Quadrats der Tempe- ratur [Andres et al., Phys. Rev. Lett. 35 (1975) 1779].

(3µ0µ²_BN)/(2EF) (µ0ist die Induktionskonstante,µBdas Bohr’sches Magneton). Beispiel Na:

N =NA,EF = 3,24 eV =⇒χPauli,theor = 1,88·10⁻¹⁰m³/mol;χPauli,exp = 2,0·10⁻¹⁰ m³/mol (Kittel).

Der elektrische Widerstand folgt in einfachen Metallen (Edelmetalle, Alkalimetalle) bei Temperaturen wesentlich unterhalb der Debyetemperatur einemT⁵-Gesetz:ρ=ρ₀+aT⁵.ρ₀ ist der durch elastische Streuung an Verunreinigungen bedingte Restwiderstand, der Term aT⁵ ist durch Streuung an Phononen bedingt. In ¨Ubergangsmetallen wird hingegen wie in CeAl₃ eine T²-Abh¨angigkeit beobachtet, die durch Elektron-Elektron-Streuung bedingt ist.

Ein Vergleich des Verhaltens von CeAl₃ mit dem einfacher Metalle zeigt also, dassγ und χPauli in CeAl3 um drei Gr¨oßenordnungen erh¨oht sind. Mit Hilfe der obigen Beziehungen der Sommerfeld-Theorie freier Elektronen kann das auf eine um drei Gr¨oßenordnungen reduzier- te (”renormalisierte“) Fermienergie zur¨uckgef¨uhrt werden. Andererseits entspricht es wegen EF =~²k_F²/(2m) (h = 2π~ ist die Plank’sche Konstante,kF der Fermi-Wellenvektor) einer Erh¨ohung der Elektronenmasse mum drei Gr¨oßenordnungen, was der Ursprung des Begriffs

”Schwere Fermionen“ ist. Der normale T⁵-Term im elektrischen Widerstand ist in CeAl₃ durch eine wesentlich st¨arkere T²-Abh¨angigkeit ¨uberdeckt. Der Proportionalit¨atsfaktor A dieses Terms ¨ubertrifft den in ¨Ubergangsmetallen gefundenen um sechs Gr¨oßenordnungen.

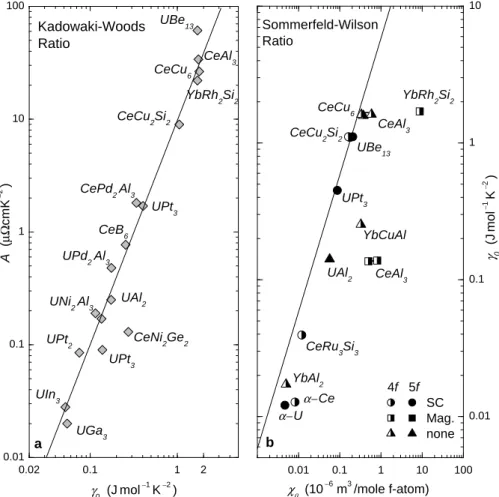
Ahnliche Eingeschaften wie in CeAl¨ 3 wurden bis heute an einer Vielzahl verschie- denster bin¨aren und tern¨arer Verbindungen gefunden. Eine interessante Beobachtung ist, dass die Verh¨altnisse A/γ (Kadowaki-Woods-Verh¨altnis) undγ/χPauli (Sommerfeld-Wilson- Verh¨altnis) f¨ur viele dieser Verbindungen ann¨ahernd konstant sind, obwohl die A-, γ- und χ_Pauli-Werte selbst um Gr¨oßenordnungen variieren (Abb. 2.4). Das ist ein starker Hinweis

daf¨ur, dass die Renormalisierung aller drei Parameter eine gemeinsame Ursache hat. Wie wir in Kapitel 3 sehen werden, entspricht das Tieftemperatur-Verhalten

C/T = const (2.1)

χ= const (2.2)

ρ=ρ0+AT² (2.3)

genau den Vorhersagen der Landau’schen Theorie der Fermifl¨ussigkeit.

0.01 0.1 1 10 100

0.01 0.1 1 10

0.02 0.1 1 2

0.01 0.1 1 10 100

YbRh₂Si₂

a b

CePd₂Al₃

UBe₁₃

CeAl₃ CeCu₆

CeCu₂Si₂

UPt₃

UPd₂Al₃ CeB₆

UNi₂Al₃

CeNi₂Ge₂ UAl₂

UPt₂

UPt₃ UIn₃

χ₀ (10 ⁻⁶m³/mole f-atom)

γ0(Jmol −1 K −2 )

UGa₃ Kadowaki-Woods Ratio

A(µΩcmK−2 )

γ₀ (J mol ⁻¹K ⁻²)

4f 5f SC Mag.

none Sommerfeld-Wilson

Ratio

YbRh₂Si₂ CeAl₃ CeCu₆

CeCu₂Si₂ UBe₁₃

UPt₃ YbCuAl

CeAl₃ UAl₂

CeRu₃Si₃

α−U α−Ce YbAl₂

Abbildung 2.4: Charakteristische Parameter A, γ und χPauli f¨ur verschiedene Schwere- Fermionen-Verbindungen. Die Linien entsprechen A/γ² = 10 µΩcm(mol K/J)² und R = χPauli/γ·π²k_B²/µ²_eff = 1 [J. Custers, Dissertation, TU Dresden, 2004].

Eine mikroskopische Theorie f¨ur Schwere-Fermionen-Systeme gibt es bis heute nicht.

Die Ingredienzien f¨ur eine solche Theorie k¨onnen wir aber leicht zusammenstellen. Schwere- Fermionen-Systeme sind Metalle. Daher wird man die Leitungselektronen ber¨ucksichtigen m¨ussen. Weiters besetzt in all diesen Verbindungen ein Element der Seltenen Erden oder der Aktiniden einen der Gitterpl¨atze. Diese Elemente haben unvollst¨andig gef¨ullte innere Schalen (4f oder 5f) und somit lokale magnetische Momente. Ein Gitter aus magnetischen

Momenten muss also in der Theorie ber¨ucksichtigt werden. Es ist naheliegend anzunehmen, dass das unkonventionelle Verhalten von Schwere-Fermionen-Systemen durch die Wechsel- wirkung dieser beiden Untersysteme bedingt ist. In Kapitel 5 werden wir einen Hamiltonope- rator kennenlernen (Anderson-Hamiltonoperator), der h¨aufig zur theoretischen Formulierung des Problems verwendet wird. Eine exakte L¨osung dieses komplexen Vielteilchenproblems ist allerdings nicht m¨oglich.

Viel zum derzeitigen Verst¨andnis dieser Materialklasse haben Analogien zu Metallen mit sehr wenigen magnetischen Verunreinigungen beigetragen (z.B. Au mit 0.01% Fe, LaB6 mit 0.5% Ce): Auch hier werden bei tiefen Temperaturen stark renormalisierte Werte f¨urγ und χPauli und ein anomales Widerstandsverhalten beobachtet. Die theoretische Beschreibung von diesen sog. Kondo-Systemen ist wesentlich einfacher als die von Schwere-Fermionen- Systemen, sodass erstere heute als

”verstanden“ gelten. 1964 erkl¨arte Kondo das in Kondo- Systemen beobachtete Minimum im elektrischen Widerstand theoretisch. Es r¨uhrt von der Streuung der Leitungselektronen an den magnetischen Momenten der Verunreinigungen her.

Dieser Prozess f¨uhrt bei nicht zu tiefen Temperaturen zu einem −ln(T)-Term im elektri- schen Widerstand. In Kombination mit dem normalen ρ = ρ0 +aT⁵-Verhalten ergibt sich das beobachtete Widerstandsminimum (Abschnitt 5.2). Das bei den tiefsten Temperaturen beobachtete ρ=ρ0 −AT²-Verhalten wird auf die Ausbildung eines kollektiven gebundenen Zustandes zwischen dem lokalen Spin der magnetischen Verunreinigung und den Leitungs- elektronen zur¨uckgef¨uhrt (Kondo-Effekt). Der lokale Spin wird dabei vom Kollektiv der Spins der Leitungselektronen kompensiert. Ein solcher Zustand entspricht in der elektroni- schen Zustandsdichte einer Resonanz am Ferminiveau (Kondo-Resonanz). Das experimen- tell beobachtete Tieftemperaturverhalten l¨asst sich mit dieser ver¨anderten Zustandsdichte erkl¨aren.

In Schwere-Fermionen-Systemen sind die Abst¨ande zwischen den lokalen Momenten we- sentlich kleiner als in Kondo-Systemen. Daher kann die Wechselwirkung zwischen ihnen hier nicht vernachl¨assigt werden. Zwar kommt es wegen der stark lokalisierten Wellenfunktio- nen der f-Elektronen nicht zu einem direkten Austausch, doch spielt der indirekte Aus- tausch ¨uber die Polarisierung der Leitungselektronen (RKKY-Wechselwirkung) eine wesent- liche Rolle. W¨ahrend die RKKY-Wechselwirkung magnetische Ordnung der lokalen Momente beg¨unstigt, favorisiert die Kondo-Wechselwirkung die Kompensierung der lokalen Momente und einen unmagnetischen Grundzustand. Tats¨achlich gibt es sowohl Schwere-Fermionen- Systeme mit magnetisch geordnetem (meist antiferromagnetischem) als auch mit paramagne- tischem Grundzustand. Einen großen Fortschritt f¨ur das Gebiet bedeutete die Entdeckung, dass man gewisse Schwere-Fermionen-Verbindungen durch Variation eines nicht-thermischen Parameters wie Druck oder Magnetfeld kontinuierlich vom magnetisch geordneten in den pa- ramagnetischen Zustand ¨uberf¨uhren kann. Solche Verbindungen werden in 2.2 vorgestellt.

2.2 Quantenkritische Systeme

In diesem Abschnitt werden wir verschiedene Materialklassen kennenlernen, in denen Quan- tenphasen¨uberg¨ange auftreten.

Im Gegensatz zu klassischen Phasen¨uberg¨angen wie dem Schmelzen von Eis bei 0^◦C oder dem ferromagnetischen ¨Ubergang von Eisen bei 770^◦C verlaufen Quantenphasen¨uberg¨ange am absoluten Temperaturnullpunkt als Funktion eines nicht-thermischen Parameters wie Druck, chemische Zusammensetzung oder Magnetfeld. Abbildung 2.5 zeigt ein schematisches Phasendiagramm in der Umgebung eines quantenkritischen Punktes. Die dicke durchgezo-

| | |

|

Magnetfeldes, auftritt, ist die thermische Energie immer exakt Null,und die Quantenfluktuationen dominieren selbst den Übergangspunkt. Daher die Bezeichnung Quanten- phasenübergang.

Der aufmerksame Leser wird jetzt sicher fragen:Warum sind Quantenphasenübergänge mehr als ein akademisches Problem? Der absolute Temperaturnullpunkt ist unerreich- bar.Jedes Experiment wird bei einer endlichen Temperatur durchgeführt,bei der,wie gerade erklärt,das asymptotische kritische Verhalten klassisch ist. Um dies zu beantworten, wollen wir noch einmal zu der Bedingung (4) zurückkom- men: Falls die Übergangstemperatur sehr klein ist, ist auch die thermische Energieskala sehr klein,und deshalb werden Quantenfluktuationen bis zu sehr kleinen Abständen vom kritischen Punkt wichtig bleiben. Nur in einer sehr schmalen Umgebung des kritischen Punktes werden die klassischen Fluktuationen dominieren. Während also das asymptotische kritische Verhalten bei jeder endlichen Temperatur klassisch ist,wird der Bereich,in dem es gültig ist,mit sinkender Temperatur immer kleiner.Bei genügend tiefer Temperatur kann der klassische Bereich so schmal werden,dass er im Experiment nicht zugänglich ist.

Die Konkurrenz zwischen thermischen und Quanten- fluktuationen in der Nähe eines quantenkritischen Punktes führt zu einer sehr reichen Struktur des Phasendiagramms.

Dabei muss man prinzipiell zwei Fälle unterscheiden, je nachdem,ob eine geordnete Phase auch bei endlichen Tem- peraturen existiert.Ein schematisches Phasendiagramm der Umgebung des quantenkritischen Punktes für den einfa- cheren Fall,bei dem makroskopische Ordnung nur am Tem- peraturnullpunkt existiert,ist in Abbildung 3 gezeigt.Dabei steht

für den Parameter,der den Quantenphasenübergang steuert (Magnetfeld,Druck,chemische Zusammensetzung).

In einem fiktiven Experiment, in dem

am Temperatur-

nullpunkt variert wird, würde man am quantenkritischen Punkt bei

=

einen Quantenphasenübergang von der geordneten in die (durch Quantenfluktuationen) ungeord- nete Phase beobachten. In jedem realen Experiment bei von Null verschiedener Temperatur,wie beispielsweise ent- lang Pfad (a), kann man dagegen keinen wirklichen Pha- senübergang beobachten, weil sich das System immer in der ungeordneten Phase befindet. Die ungeordnete Phase zerfällt jedoch in drei Regionen mit sehr verschiedenen physikalischen Eigenschaften,je nachdem,ob Quanten- oder thermische Fluktuationen dominieren und je nachdem, in welcher Phase sich der zugehörige Grundzustand befindet.

Diese drei Regionen sind nicht durch scharfe Phasenüber- gänge,sondern durch allmähliche „Crossover“ bei

|

–

|

getrennt (in der Abbildung 3 durch die gestri- chelten Linien gekennzeichnet). In der quantenmechnisch ungeordneten Region dominieren die Quantenfluktuatio- nen,und thermische Effekte sind unwichtig.Das System be- sitzt im wesentlichen die Eigenschaften des ungeordneten Grundzustandes. Die Eigenschaften der thermisch unge- ordneten Region sind bestimmt durch thermische Fluktua- tionen um den geordneten Grundzustand.Zwischen diesen beiden Regionen befindet sich die quantenkritische Region.

Der Name der Region erscheint zunächst etwas irreführend, denn der Charakter der Fluktuationen ist wegen

>

thermisch.Die Eigenschaften des Systems in dieser Region werden jedoch durch den quantenkritischen Grundzustand im Zusammenhang mit der Temperatur bestimmt.In einem Experiment entlang Pfad b beobachtet man die Divergenz der Fluktuationen des Ordnungsparameters mit der Tem- peratur und erhält folglich Aussagen über das Skalenver- halten mit der Temperatur am quantenkritischen Punkt.

Falls das System nicht nur am Temperaturnullpunkt ma- kroskopische Ordnung aufweist, sondern auch bei endli- chen Temperaturen, wird das Phasendiagramm noch rei- cher.Ein derartiges Phasendiagramm,gültig etwa für unser

|

klassisch kritisch

quantenmech.

ungeordnet a

b quantenkritisch

kT - បω_c T

0

B_c

QCP

B geordnet

thermisch ungeordnet

|

~

Abbildung 2.5: Schematisches Phasendiagramm in der Umgebung eines quantenkritischen Punktes (QCP), f¨ur den Fall, dass makroskopische Ordnung bei endliche Temperaturen existiert [Vojta, Physik in unserer Zeit32 (2001) 38].

gene Linie stellt die Phasengrenze zwischen einer geordneten und einer ungeordneten Phase dar. Die Phasenumwandlung zwischen diesen beiden Phasen verlaufe kontinuierlich (Pha- sen¨ubergang 2. Ordnung). B steht f¨ur den Parameter, der den Quantenphasen¨ubergang steuert. Mit steigendem B wird die Temperatur des ¨Ubergangs in die geordnete Phase kontinuierlich reduziert und schließlich beim kritischen Wert Bc g¨anzlich unterdr¨uckt. Ein kontinuierlicher Phasen¨ubergang kann ¨ublicherweise durch einen Ordnungsparameter (z.B.

Magnetisierung im Falle eines ferromagnetischen ¨Ubergangs) charakterisiert werden. Der Ordnungsparameter ist eine thermodynamische Gr¨oße, deren thermodynamischer Mittel- wert in der ungeordneten Phase verschwindet, w¨ahrend dieser in der geordneten Phase von Null verschieden ist. Die Abweichungen vom Mittelwert bezeichnet man als Fluktuationen des Ordnungsparameters. Es gibt klassische thermische Fluktuationen mit der typischen Energie k_BT und Quantenfluktuationen mit der Frequenz ω und Energie ~ω. Ein einfa- ches Beispiel f¨ur eine thermische Fluktuation ist die ¨Uberquerung eines Potentialbergs. Das Durchtunneln dieses Bergs entspricht einer Quantenfluktuation. Am Temperaturnullpunkt gibt es keine thermischen Fluktuationen. Daher wird ein Phasen¨ubergang hier durch Quan-

tenfluktuationen getrieben. Im hell schraffierten Bereich in Abb. 2.5 dominieren thermische Fluktuationen um den geordneten Grundzustand, im hellen Bereich dominieren Quantenf- luktuationen. Im quantenkritischen Bereich werden die Eigenschaften des Systems durch den quantenkritischen Grundzustand in Zusammenhang mit der Temperatur bestimmt. Experi- mente werden ¨ublicherweise entweder bei konstanter (endlicher!) Temperatur als Funktion eines Kontrollparameters B gemacht (Weg a in Abb. 2.5) oder bei konstantem Kontrollpa- rameter als Funktion der Temperatur (Weg b in Abb. 2.5).

2.2.1 Quanten-Ising-Systeme

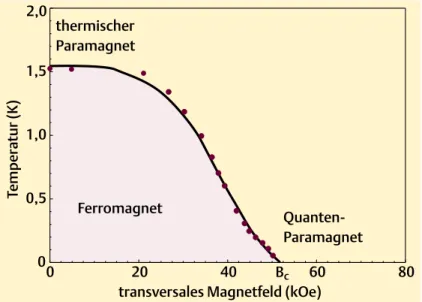
Als Quanten-Ising-Systeme bezeichnet man Materialien, in denen sich magnetische Momente nur entlang einer bestimmten Achse im Raum ausrichten k¨onnen. Ein solches System ist der Isolator LiHoF4. Das Selten-Erd-Element Holmium tr¨agt einen Spin, der sich nur parallel oder antiparallel zur c-Achse des Kristalls ausrichten kann. Ohne Magnetfeld ordnet das System unterhalb der Curie-Temperatur T_C = 1,53 K ferromagnetisch (Abb. 2.6). Dabei

| | |

|

voll polarisierter Ferromagnet.Theoretisch lässt sich ein solches System durch das Ising-Modell beschreiben (Abbil- dung 1,siehe „Ising-Modell im transversalen Magnetfeld“).

Im Jahre 1996 untersuchten Bitko, Rosenbaum und Aeppli [1] die magnetischen Eigenschaften von LiHoF

als Funktion der Temperatur und eines äußeren Magnetfeldes, das im rechten Winkel zur Achse der Spins zeigte. Abbildung 2 zeigt das experimentell bestimmte Phasendiagramm. Am Temperaturnullpunkt und ohne Magnetfeld ist das System, wie bereits erwähnt, ein voll polarisierter Ferromagnet.

Erhöht man die Temperatur, werden zunächst einige Spins umklappen.Mit weiter steigender Temperatur nehmen die thermischen Fluktuationen zu. Die Bereiche mit umge- klappten Spins werden immer größer bis die gleiche Anzahl von „auf“- und „ab“-Spins erreicht ist. An diesem Punkt verschwindet die spontane Magnetisierung. Dies ist ein konventioneller kontinuierlicher Phasenübergang von einem Ferromagneten zu einem thermischen Paramagne- ten, getrieben ausschließlich durch thermische Fluktua- tionen.

Wie das Phasendiagramm in Abbildung 2 zeigt, kann man die ferromagnetische Ordnung in LiHoF

aber auch auf ganz andere Weise zerstören.Ein Magnetfeld senkrecht zur Achse der Spins induziert quantenmechanisches Tunneln zwischen den „auf“- und „ab“-Zuständen der Spins.

Erreicht die Feldstärke einen kritischen Wert,werden diese Quantenfluktuationen so stark, dass sie die ferromag- netische Ordnung sogar am Temperaturnullpunkt zerstören.

Das System durchläuft einen Quantenphasenübergang von einem Ferromagneten zu einem Quantenparamagneten, getrieben ausschließlich durch Quantenfluktuationen.

Die Eigenschaften eines solchen Quantenparamagneten sind qualitativ sehr verschieden von denen des thermischen Paramagneten. Im Falle des thermischen Paramagneten

fluktuieren die Spins mit der Zeit zwischen „auf“ und „ab“, so dass der Mittelwert der Magnetisierung verschwindet.Im Falle des Quantenparamagneten gibt es dagegen eine eindeutige quantenmechanische Wellenfunktion.Sie ist eine Superposition aus „auf“- und „ab“-Zuständen und führt deshalb zu einer verschwindenden Magnetisierung,präzise:

zu einem verschwindenden quantenmechnischen Erwar- tungswert.

Um Gemeinsamkeiten und Unterschiede zwischen thermischen und Quantenphasenübergängen besser zu verstehen,wollen wir zunächst einige grundlegende Fakten zusammentragen [2].Ein kontinuierlicher Phasenübergang kann üblicherweise durch einen Ordnungsparameter charakterisiert werden, ein Konzept, das von Landau eingeführt wurde. Ein Ordnungsparameter ist eine thermodynamische Größe, die in der ungeordneten Phase verschwindet, während sie in der geordneten Phase von Null verschieden ist. Sehr häufig ist die Wahl eines Ordnungsparameters für einen bestimmten Phasenüber- gang offensichtlich, wie im Falle des ferromagnetischen Überganges, bei dem die Magnetisierung ein Ordnungs- parameter ist.Manchmal kann es aber auch schwierig sein, einen geeigneten Ordnungsparameter zu finden, wie für den unordnungsinduzierten Metall-Isolator-Übergang in dotierten Halbleitern.

In der ungeordneten Phase verschwindet der thermo- dynamische Mittelwert des Ordnungsparameters,aber seine Fluktuationen – die Abweichungen vom Mittelwert an

thermischer Paramagnet

Ferromagnet

Quanten- Paramagnet

0 20 40 60 80

transversales Magnetfeld (kOe) 0

0,5 1,0 1,5 2,0

Temperatur (K)

B_c

| |

Abbildung 2.6: Phasendiagramm von LiHoF4 in der Temperatur-Magnetfeld-Ebene [Bitko et al., Phys. Rev. Lett. 77 (1996) 940].

zeigen alle Spins in die gleiche Richtung, entweder

”auf“ oder

”ab“ (parallel oder antiparallel zur c-Achse). Der klassische Phasen¨ubergang bei der endlichen Temperatur TC (bei B = 0) ist ein Phasen¨ubergang 2. Ordnung. Ein solcher ¨Ubergang ist durch eine bei T_C divergie- rende Korrelationsl¨ange und -zeit charakterisiert. Die Korrelationsl¨ange gibt die Gr¨oße der w¨ahrend der Korrelationszeit bestehenden ferromagnetisch geordneten Clustern an. Bei der Ann¨aherung (von hohen Temperaturen her kommend) an T_C wachsen diese Cluster an und bleiben f¨ur l¨angere Zeit bestehen, d.h., Korrelationsl¨ange und -zeit wachsen an. BeiTC diver- gieren Korrelationsl¨ange und -zeit und ein Cluster erstreckt sich ¨uber die ganze Probe. Die Magentisierung (der Ordnungsparameter) nimmt dann einen von Null verschiedenen Wert

an. Die magnetische Suszeptibilit¨at divergiert bei TC, was einer extremen Empfindlichkeit des Systems auf ein externes Magnetfeld entspricht.

Wird nun ein Magnetfeld senkrecht zur c-Achse angelegt, so wird die ferromagnetische Ordnung sukzessive geschw¨acht und beim kritischen Wert des Magnetfelds H_c = 49,3 kOe g¨anzlich unterdr¨uckt, wie in Abb. 2.6 gezeigt. Die Phasengrenze wurde mit Messungen der magnetischen Suszeptibilit¨at als Funktion der Temperatur und des Magnetfelds bestimmt.

Mittels dieser Daten wurde auch das kritische Verhalten sowohl im klassischen Grenzfall (H = 0, T ≥Tc) als auch im Quanten-Grenzfall (T = 100 mK,H ≥Hc) untersucht. In bei- den F¨allen variiert der Realteil der Suszeptibilit¨atχ^′ als Funktion des normierten Abstandes vom kritischen Punkt t = (T −T_c)/T_c bzw. h = (H−H_c)/H_c mit einem einfachen Potenz- gesetz: χ^′ ∼ t^−γ (bzw. χ^′ ∼ h^−γ), wie dies f¨ur kritisches Verhalten typisch ist. γ wird als kritischer Exponent bezeichnet. Die Tatsache, dass eine Vielzahl ganz unterschiedlicher Ma- terialien das selbe kritische Verhalten (den gleichen kritischen Exponenten) zeigen, wird als Universalit¨at bezeichnet. In LiHoF4 ist γ ≈1. Dieses Verhalten entspricht den Vorhersagen der Molekularfeldtheorie. Die auf den beiden Seiten des Quantenphasen¨ubergangs relevanten elementaren Anregungen werden wir in Abschnitt 4.1.6 behandeln.

Die Situation wird komplizierter, wenn zus¨atzlich zu lokalisierten magnetischen Momen- ten Ladungstr¨ager vorhanden sind. Derartige Systeme werden im Folgenden behandelt.

2.2.2 Quantenkritische Schwere-Fermionen-Systeme

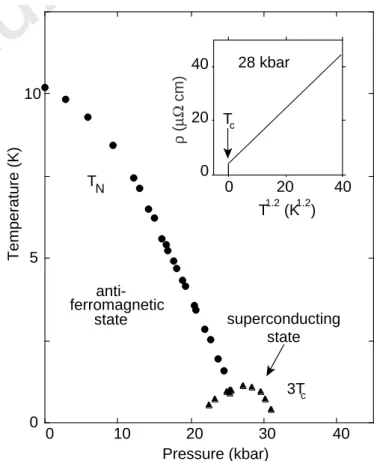
Wie bereits in Abschnitt 2.1 erw¨ahnt, tritt quantenkritisches Verhalten in vielen Schwere- Fermionen-Systemen auf. Ein prototypisches Beispiel ist CePd2Si2, das unterhalb der N´eel- Temperatur TN ≈ 10 K antiferromagnetisch ordnet (Abb. 2.7). Unter Druck wird die N´eel- Temperatur reduziert. Mit einer linearen Extrapolation von T_N(p) wird der kritische Wert des Drucks, bei dem TN verschwindet, zu 28 kbar (2,8 GPa) bestimmt. In einem kleinen Bereich um diesen kritischen Druck tritt Supraleitung unterhalb der kritischen Temperatur T_c auf. Auf diese werden wir in Abschnitt 2.3 noch weiter eingehen. Das Teilbild in Abb. 2.7 zeigt, dass der elektrische Widerstand beim kritischen Druck oberhalb Tc nicht dem T²- Gesetz einer Landau’schen Fermifl¨ussigkeit folgt, sondern ann¨ahernd proportional zu T^1.2 ansteigt, also der Beziehung

ρ=ρ0+AT^α (2.4)

mit α= 1.2 gehorcht.

Ahnliches Verhalten wird auch in anderen Schwere-Fermionen-Systemen beobachtet. In¨ Abb. 2.8 sieht man am Fall von YbRh2Si2, dass die Abweichungen vom T²-Gesetz nur im quantenkritischen Bereich des Phasendiagramms (Abb. 2.5) auftreten. Der gem¨aß Glg. (2.4) bestimmte Exponent α ist in Abb. 2.8 als Helligkeit (bzw. F¨arbung) dargestellt. Im Null- feld ordnet YbRh2Si2 unterhalb von 70 mK antiferromagnetisch. Die N´eel-Temperatur wird mit steigendem Magnetfeld reduziert und verschwindet beim kritischen Feld von 0.7 T. Bei diesem Feld wird bis zu den tiefsten Temperaturen ein in T linearer Widerstand (α = 1) beobachtet.

Neben dem elektrischen Widerstand haben auch anderen Messgr¨oßen im quantenkri- tischen Bereich einen ungew¨ohnlichen, vom Verhalten einer Landau’schen Fermifl¨ussigkeit

0 5 10

0 10 20 30 40

Temperature (K)

Pressure (kbar) T_N

3T_c anti-

ferromagnetic

state superconducting state 0

20 40

0 20 40

T^1.2 (K^1.2) 28 kbar

T_c

ρ (µΩ cm)

Abbildung 2.7: Phasendiagramm von CePd2Si2 in der Temperatur-Druck-Ebene. Teilbild:

Elektrischer Widerstand als Funktion von T^1.2 [Mathur et al., Nature 394 (1998) 39].

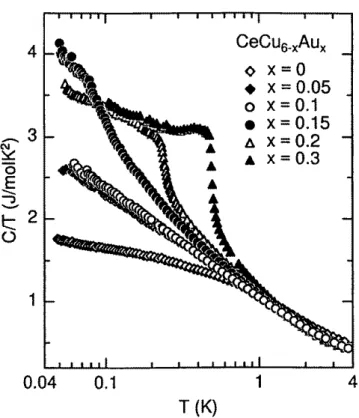
(Glgn. (2.1-2.3)) abweichenden Temperaturverlauf. Der Koeffizient aus spezifischer W¨arme und Temperatur bleibt im quantenkritischen Bereich temperaturabh¨angig. Dies ist am Bei- spiel von CeCu6−xAux, das bei der Dotierung xc = 0.1 quantenkritisch ist (Abb. 2.9), in Abb. 2.10 gezeigt. Bei x = 0.1 (und bis zu den hier gemessenen Temperaturen auch bei x= 0.05) wird das Verhalten

C/T ∼ −lnT (2.5)

beobachtet. Beix= 0 wirdC/T bei tiefen Temperaturen sehr flach, was dem ¨Ubergang zum Fermifl¨ussigkeitsverhalten nach Glg. (2.1) entspricht. Beix= 0.05 wird ein solcher ¨Ubergang bei tieferen Temperaturen erwartet. Die Schultern f¨ur die Verbindungen mitx≥0.15 r¨uhren vom antiferromagnetischen Phasen¨ubergang her, das Abflachen der Kurven bei tieferen Tem- peraturen ist wiederum Zeichen f¨ur Fermifl¨ussigkeitsverhalten in der antiferromagnetischen Phase.

Die Ursache f¨ur das im quantenkritischen Bereich auftretende sog. Nicht- Fermifl¨ussigkeitsverhalten ist noch nicht gekl¨art. Ein Erkl¨arungsansatz geht davon aus, dass Quantenfluktuationen die Ursache sind. In Schwere-Fermionen-Systemen mit antiferroma- gnetischem Ordnungsparameter dominieren meist antiferromagnetische Spinfluktuationen (auch Paramagnonen genannt, vgl. Abschnitt 4.1.5). Ihre Anwesenheit macht sich dadurch

B (T)

Abbildung 2.8: Phasendiagramm von YbRh2Si2 in der Temperatur-Magnetfeld-Ebene in Form des Widerstand-Exponenten α (hier mit ǫ bezeichnet) [Custers et al., Nature 424 (2003) 524].

Abbildung 2.9: Phasendiagramm von CeCu6−xAux in der Temperatur-Dotierungs-Ebene [v.

L¨ohneysen et al., J. Phys. Condens. Matter 8(1996) 9689].

Abbildung 2.10: Temperaturabh¨angigkeit des Quotienten aus spezifischer W¨arme und Tem- peratur von CeCu6−xAux [von L¨ohneysen et al., J. Phys. Condens. Matter8 (1996) 9689].

bemerkbar, dass nahe am quantenkritischen Punkt dauernd kleinere und gr¨oßere antifer- romagnetische Bereiche entstehen und wieder verschwinden. Mit abnehmender Temperatur w¨achst die typische Gr¨oße dieser Bereiche und damit auch die Wechselwirkung zwischen den Elektronen, die durch den Austausch von Spinfluktuationen bedingt ist. Dies w¨urde das anomale Widerstandsverhalten qualitativ erkl¨aren. Andererseits beeinflussen die ma- gnetischen Fluktuationen, die als Quasiteilchen aufgefasst werden k¨onnen, nat¨urlich auch die Energiebilanz und damit die spezifische W¨arme. Der Anstieg von C/T mit abnehmen- der Temperatur bedeutet in diesem Bild, dass mit abnehmender Temperatur immer mehr Spinfluktuationen erzeugt werden. Verschiedene experimentelle Beobachtungen insbes. an CeCu6−xAux und YbRh2Si2 deuten aber darauf hin, dass zumindest nicht alle quantenkriti- schen Schwere-Fermionen-Systeme auf diese Art verstanden werden k¨onnen. G¨anzlich neue Ans¨atze ziehen in Betracht, dass es die Quasiteilchen der Fermifl¨ussigkeit beim quantenkriti- schen Punkt ¨uberhaupt nicht mehr gibt, sondern dass sie am quantenkritischen Punkt

”aus- einanderbrechen“. Auf der paramagnetischen Seite w¨are ein Komposit-Teilchen aus lokalem magnetischem Moment und einer das Moment abschirmenden Elektronenwolke ein plausibles Quasiteilchen. Dieses w¨urde am quantenkritischen Punkt in ein von den Leitungselektronen unabh¨angiges lokales magnetisches Moment und einfache elektronische Quasiteilchen aufbre- chen.

2.2.3 Systeme mit quantenkritischem Endpunkt

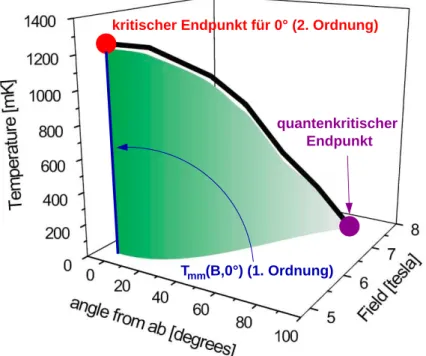
In Abb. 2.5 ist der Fall dargestellt, wo am quantenkritischen Punkt eine geordnete Phase gerade unterdr¨uckt wird. Es gibt aber auch quantenkritische Punkte, an denen kein Symme- triebruch auftritt. Ein Beispiel daf¨ur ist das Ruthenat Sr3Ru2O7, das das typische Verhalten eines itineranten Metamagneten zeigt: Als Funktion des Magnetfeldes nimmt die Magnetisie- rung in einem schmalen Feldbereich sehr rasch zu. Das Magnetfeld, bei dem der metamagne- tische ¨Ubergang in Sr3Ru2O7 auftritt, h¨angt einerseits von der Temperatur ab, andererseits vom Winkel zwischen Magnetfeld und kristallographischerab-Ebene (Abb. 2.11). Der schat-

kritischer Endpunkt für 0° (2. Ordnung)

T (B,0°) (1. Ordnung)_mm

quantenkritischer Endpunkt

Abbildung 2.11: Dreidimensionales Phasendiagramm von Sr3Ru2O7 erstellt aus Messungen der komplexen Suszeptibilit¨at χ = χ^′ + iχ^′′. Bei den ¨Uberg¨angen erster Ordnung treten Hysteresiseffekte und ein nichtverschwindendesχ^′′auf [Grigera et al., Phys. Rev. B67(2003) 214427].

tierte Bereich stellt die Fl¨ache metamagnetischer Phasen¨uberg¨ange erster Ordnung dar. Sie wird zu hohen Temperaturen hin von einer Linie kritischer Temperaturen (kritischer End- punkte) begrenzt. Jeder kritische Endpunkt stellt einen Phasen¨ubergang zweiter Ordnung dar. Der quantenkritische Punkt tritt auf, wo die Linie kritischer Endpunkte die T = 0- Ebene schneidet, also in Abb. 2.11 bei ca. 90^◦ und 7.8 T. Dies wird etwas anschaulicher, wenn wir einen Schnitt durch das dreidimensionale Phasendiagramm, z.B. die Ebene zum Winkel 0^◦, betrachten. Hier wird die Abh¨angigkeit der kritischen Temperatur des metama- gnetischen ¨UbergangsT_mm als Funktion des Magnetfeldes dargestellt. Bei einem Magnetfeld von ca. 5 T ist Tmm zu Null unterdr¨uckt. Mit steigendem Feld steigt Tmm steil an. Die Pha- sen¨ubergangslinie erster Ordnung Tmm(B) endet schließlich in einem kritischen Endpunkt zweiter Ordnung. In der entsprechenden Ebene zum Winkel 90^◦ befindet sich nur noch dieser

kritische Endpunkt, und zwar eben bei einem Feld von ca. 7.8 T bei T = 0. Da hier also ein Phasen¨ubergang zweiter Ordnung beiT = 0 passiert, handelt es sich um einen quantenkriti- schen Punkt, eben einen sog. quantenkritischen Endpunkt. Wie bei den Schwere-Fermionen- Systemen zeigen verschiedene physikalische Eigenschaften in der Umgebung dieses quan- tenkritischen Punktes Abweichungen vom Fermifl¨ussigkeitsverhalten. Abbildung 2.12 zeigt den gem¨aß Glg. (2.4) bestimmten Exponenten α. Auch hier tritt ein großer quantenkriti-

Abbildung 2.12: Widerstandsexponent α von Sr₃Ru₂O₇ in der Temperatur-Magnetfeld- Ebene, f¨ur einen Winkel zwischen Magnetfeld und ab-Ebene von 90^◦ [Grigera et al., Science 294 (2001) 330].

scher Bereich mit α≈1 auf. Genaue Untersuchungen an hochreinen Proben haben gezeigt, dass unterhalb von 1 K in einem schmalen Feldbereich um das kritische Magnetfeld eine neue Phase bisher unbekannter Natur existiert, auf die wir hier aber nicht weiter eingehen m¨ochten.

Ahnliches, wenn auch noch wesentlich komplizierteres Verhalten wird f¨ur URu¨ 2Si₂ be- obachtet, wo die Bildung von gleich drei Phasen mit der Existenz eines metamagnetischen quantenkritischen Punktes zusammenzuh¨angen scheint. Eine weitere, supraleitende Tieftem- peraturphase, die in unmittelbarer Umgebung eines quantenkritischen Punktes auftritt, ha- ben wir bereits am Beispiel von CePd2Si2 in Abschnitt 2.2.2 kennengelernt. Auch wenn ein kausaler Zusammenhang zwischen diesen Tieftemperaturphasen und einem quantenkriti- schen Punkt noch nicht bewiesen werden konnte, so scheint die Annahme, dass die Vielzahl niederenergetischer Anregungen in der Umgebung eines quantenkritischen Punktes die Ent- stehung neuer Phasen beg¨unstigt, zumindest plausibel.

Es gibt noch etliche weitere Materialklassen, die derzeit im Zusammenhang mit Quan- tenkritikalit¨at diskutiert werden, so z.B. die Manganate, Kobaltate, Kondoisolatoren, Spingl¨aser, organische Ladungstransfer-Komplexe und auch die Hochtemperatur-Supraleiter.

Und es gibt sogar Hinweise darauf, dass Quantenkritikalit¨at auch ausserhalb der traditio-

nellen Festk¨orperphysik von Bedeutung ist, z.B. in Quanten-Punkt-Systemen oder in Multi- lagen aus He³-Atomen. Faszinierend – wenn auch noch etwas spekulativ – ist die derzeitige Diskussion ¨uber Parallelen mit der Physik Schwarzer L¨ocher.

2.3 Unkonventionelle Supraleiter

Supraleitung ist ein makroskopisches Quantenph¨anomen, bei dem die beweglichen Elektro- nen eines Metalls unterhalb einer kritischen Temperatur sog. Cooper-Paare bilden und in einen gemeinsamen Grundzustand

”kondensieren“. Die Paarbildung ist erforderlich, da nur Teilchen mit ganzzahligem Spin (Bosonen) den gleichen Zustand einnehmen k¨onnen, w¨ahrend dies f¨ur Teilchen mit halbzahligem Spin (Fermionen) wie Elektronen nach dem Pauliprinzip verboten ist. F¨ur konventionelle Supraleiter basiert der Paarungsmechanismus auf der Wech- selwirkung mit den Gitterschwingungen (Phononen), wie sie die BCS-Theorie beschreibt. Es gibt aber auch Materialien, in denen dieser Paarungsmechanismus unwahrscheinlich ist. Ei- nige solche Systeme wollen wir im Folgenden behandeln.

2.3.1 Hochtemperatur-Supraleiter

Seit der Entdeckung der Hochtemperatur-Supraleitung in der Familie der Kuprate im Jahre 1986 durch Bednorz und M¨uller bleibt trotz einer F¨ulle an experimentellen Ergebnissen der zu Grunde liegende mikroskopische Mechanismus unklar. Ein auch nur halbwegs vollst¨andiger Uberblick ¨uber den Stand der Forschung an Hochtemperatur-Supraleitern w¨urde eine ganze¨ Vorlesung f¨ullen. Hier wurde daher eine Auswahl nur weniger Aspekte getroffen.

In Abb. 2.13 ist die Struktur des typischen Hochtemperatur-Supraleiters La2−xSrxCuO4

zu sehen. Charakteristisch sind die CuO₂-Ebenen, die f¨ur die Supraleitung in den Kupra- ten eine entscheidende Rolle spielen. Die bisher h¨ochste kritische Temperatur von 133.5 K wurde in dem System HgBa2Ca2Cu3O8+x gefunden, in dem gleich drei CuO2-Ebenen pro Einheitszelle vorhanden sind. Die Schichtstruktur f¨uhrt zu extrem anisotropem Verhalten im normalleitenden Zustand. Der elektrische Widerstand senkrecht zu den CuO2-Ebenen kann bis zu tausend Mal gr¨oßer sein als der entlang der Ebenen.

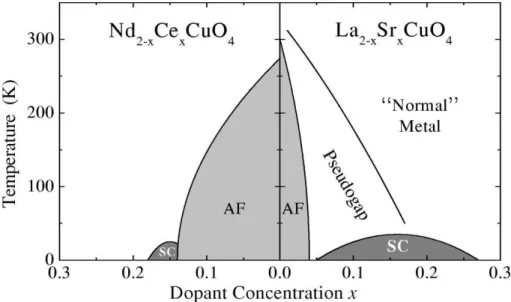
Das ph¨anomenologische Phasendiagram der Elektron- und Loch-dotierten (n- und p- Typ) Hochtemperatur-Supraleiter ist in Abb. 2.14 am Beispiel von Nd2−xCexCuO4 und La2−xSrxCuO4 gezeigt. Ohne Dotierung (x = 0) sind beide Verbindungen antiferroma- gnetische Isolatoren. Bereits dieser Zustand ist ungew¨ohnlich, da die Systeme gem¨aß Bandstrukturrechnungen Metalle sein sollten. Er r¨uhrt von starken Elektron-Elektron- Wechselwirkungen her und wird als Mott-Isolator bezeichnet. (In einem Mott-Isolator ist jeder Gitterplatz mit einem Elektron besetzt. F¨ur eine Bewegung der Elektronen m¨usste ein Gitterplatz zeitweise doppelt besetzt werden. Dieser Prozess w¨urde wegen der starken Coulomb-Abstoßung zwischen den Elektronen zu viel Energie kosten und findet daher nicht statt.) Mit zunehmender Dotierung wird die antiferromagnetische Phase unterdr¨uckt und schliesslich eine supraleitende Phase stabilisiert. Der supraleitende Ordnungsparameter (die Energiel¨ucke) hat nicht wie bei konventionellen Supraleitern s-Wellen-Symmetrie, sondern d-Wellen-Symmetrie. Das heißt, dass die Energiel¨ucke an bestimmten Orten der Fermifl¨ache

Abbildung 2.13: Tetragonale Hochtemperatur-Struktur von La2−xSrxCuO4 [Damascelli et al., Rev. Mod. Phys. 75 (2003) 474].

Abbildung 2.14: Ph¨anomenologisches Phasendiagramm der Hochtemperatur-Supraleiter am Beispiel von Nd_2−xCe_xCuO₄ und La_2−xSr_xCuO₄ [Damascelli et al., Rev. Mod. Phys. 75 (2003) 473].

verschwindet. Hier sind elektronische Anregungen beliebig kleiner Energie m¨oglich. Pro- ben mit maximaler Sprungtemperatur werden als

”optimal dotiert“ (optimally doped) be-

zeichnet, solche mit kleinerer bzw. gr¨oßerer Dotierung als

”unterdotiert“ (underdoped) bzw.

”uberdotiert“ (overdoped). Im wesentlich genauer untersuchen Loch-dotierten Fall gibt es¨ eine weitere Linie im Phasendiagramm. Unterhalb dieser oft mitT^∗ bezeichneten charakteri- stischen Temperatur verschwinden niederenergetische Spin-Fluktuationen mit abnehmender Temperatur, was auf eine (Pseudo-)Energiel¨ucke (pseudogap) der Breite kBT^∗ im elektro- nischen Anregungsspektrum zur¨uckgef¨uhrt wird. Innerhalb diesem pseudogap-Bereich kann es je nach Material und Probenqualit¨at weitere Phasen mit lokaler oder inkommensura- bler (nicht gitterperiodischer) magnetischer Ordnung geben, z.B. einen Spin-Glas-Zustand oder einen als

”Streifen“ (stripes) bezeichneten Zustand mit inhomogener Spin- und La- dungsordnung, der statisch oder zeitlich fluktuierend sein kann (vgl. Abschnitt 4.14). In

¨uberdotierten Proben scheinen magnetische Korrelationen hingegen vernachl¨assigbar zu sein. Damit dr¨angt sich ein Vergleich mit Schwere-Fermionen-Supraleitern wie dem in Ab- schnitt 2.2.2 besprochenen CePd2Si2 auf. Die Rolle der N´eel-Temperatur spielt im Fall der Hochtemperatur-Supraleiter die pseudogap-Temperatur T^∗. Es wird spekuliert, dass es einen quantenkritischen Punkt gibt, an dem T^∗ verschwindet und dass die Cooper-Paare durch den Austausch kritischer Spinfluktuationen gebildet werden. Tats¨achlich wird auch in Hochtemperatur-Supraleitern in der Umgebung dieses hypothetischen quantenkritischen Punktes Nicht-Fermifl¨ussigkeitsverhalten beobachtet (Abb. 2.15), so z.B. ein mit der Tempe- ratur linear ansteigender elektrischer Widerstand (Abb. 2.16). Es muss aber betont werden, dass es f¨ur diese Erkl¨arung derzeit keinen breiten Konsens gibt, ebensowenig wie f¨ur irgend einen anderen Erkl¨arungsansatz.

Abbildung 2.15: Schematisches Phasendiagramm der Hochtemperatur-Supraleiter [Orenstein und Millis, Science 288 (2000) 468].

Abbildung 2.16: Elektrischer Widerstand von La1.85Sr0.15CuO4, gemessen entlang den CuO2- Ebenen, als Funktion der Temperatur [Takagi et al., Phys. Rev. Lett.69 (1992) 2975].

2.3.2 Schwere-Fermionen-Supraleiter

In einigen Schwere-Fermionen-Verbindungen (z.B. CeIn3, CeRh2Si2, CeNi2Ge2) wird wie f¨ur CePd2Si2 (Abschnitt 2.2.2) in der unmittelbaren Umgebung des quantenkritischen Punktes Supraleitung beobachtet. Die kritische Temperatur ist niedrig (ca. 0.4 K f¨ur CePd2Si2). Zu- dem tritt Supraleitung nur in sehr reinen Proben (Proben mit niedrigem Restwiderstand) auf. Es wird davon ausgegangen, dass diese Supraleitung nicht wie in konventionellen Supra- leitern durch den Austausch von Phononen bedingt ist, sondern durch den Austausch von Spinfluktuationen (vgl. Abschnitt 2.2.2 und 4.1.5). Theoretische Modelle, die den quantenkri- tischen Punkt als Spindichtewellen-Instabilit¨at beschreiben, sagen tats¨achlich Supraleitung mit obigen Eigenschaften vorher. Dies ist auch mit der Beobachtung konsistent, dass in Schwere-Fermionen-Verbindungen wie YbRh2Si2 oder CeCu6−xAux, in denen die magneti- sche Orndung auf lokalisierte magnetische Momente zur¨uckgef¨uhrt wird (und nicht auf eine Spindichtewelle der Leitungselektronen), bisher keine Supraleitung gefunden wurde.

Auf die Existenz eines weiteren, neuen Paarungsmechanismus scheinen Ergebnisse an der Verbindung CeCu2Si2 hinzuweisen. In Abb. 2.17 ist das Phasendiagramm f¨ur CeCu2(Si1−xGex)2 dargestellt. Mit zunehmender Unordnung durch Dotierung wird die Su- praleitung, die sich in reinem CeCu₂Si₂ (punktierte und strichpunktierte Kurven) und CeCu2Ge2 (dunkle durchgezogene Kurve) ¨uber das ganze Phasendiagramm erstreckt, ge- schw¨acht und zerf¨allt bei x = 0.1 (dunkle Bereiche) in zwei voneinander getrennte supra- leitende Phasen: Eine Phase in der Umgebung des quantenkritischen Punktes, bei dem die N´eel-Temperatur verschwindet und die mit Spinfluktuationen erkl¨art wird und eine zweite Phase mit maximalem Tc bei 4 GPa. Verschiedene Experimente deuten darauf hin, dass bei diesem Druck ein Valenz¨ubergang des Ce auftritt (ein Teil des lokalisierten f-Elektrons des

Abbildung 2.17: Phasendiagramm von CeCu2(Si1−xGex)2 in der Temperatur-Druck-Ebene [Yuan et al., Science 302 (2003) 2104].

Ce wird itinerant). Damit Supraleitung durch den Austausch kritischer Valenzfluktuatio- nen als Paarungsmechanismus in Frage kommt, m¨usste der Valenz¨ubergang bei T = 0 ein quantenkritischer Punkt und somit ein kontinuierlicher ¨Ubergang sein. Im Allgemeinen sind Valenz¨uberg¨ange allerdings Phasen¨uberg¨ange erster Ordnung. Daher m¨usste es sich hier um einen quantenkritischen Endpunkt (vgl. Abschnitt 2.2.3) handeln.

Unkonventionelle Supraleitung tritt noch in weiteren Materialklassen, wie z.B. in Einfach- Lagen-Perovskit-Ruthenaten (z.B. Sr2RuO4) und in quasi-zweidimensionalen organischen Leitern (z.B. BEDT-TTF) auf. Es handelt sich also um ein relativ weit verbreitetes Ph¨anomen.

2.4 Quasi-eindimensionale Systeme

In dreidimensionalen Leitern wird abgesehen von der Umgebung von Quantenpha- sen¨uberg¨angen im Allgemeinen Fermifl¨ussigkeitsverhalten beobachtet. Dies liegt daran, dass hier die freien Elektronen im Zusammenspiel mit den positiv geladenen Ionen des Kristall- gitters f¨ur eine effektive Abschirmung der langreichweitigen Coulomb-Felder sorgen. In re- duzierten Dimensionen wird diese Abschirmung weniger effizient. Im Grenzfall eindimen- sionaler Leiter ist die Abschirmung so schwach, dass das Bild der Fermifl¨ussigkeit g¨anzlich zusammenbricht. Das experimentell beobachtete Verhalten ist vielmehr im Einklang mit den theoretischen Vorhersagen f¨ur eine sog. Luttinger-Fl¨ussigkeit. Zwei charakteristische Eigen- schaften, n¨amlich das Ph¨anomen der Spin-Ladungs-Separation und das des Verschwindens

der elektronischen Zustandsdichte in Tunnelexperimenten, werden im Folgenden anhand von Beispielen vorgestellt.

2.4.1 Das Kuprat SrCuO

Die Struktur von SrCuO2 ist in Abb. 2.18 dargestellt. Jedes Cu-Atom ist von vier in ei- ner Ebene liegenden O-Atomen umgeben. Diese sog. CuO4-Plaketten sind ¨uber gemeinsame Kanten so angeordnet, dass sich entlang der c-Achse zickzackf¨ormige CuO2-Ketten erge- ben. Die Wechselwirkung zwischen Cu²⁺-Ionen entlang dieser Ketten ist wesentlich st¨arker als jene zwischen den Ketten, was zu quasi-eindimensionalem Verhalten f¨uhrt. Die Spins der Cu²⁺-Ionen ordnen in einem weiten Temperaturbereich antiferromagnetisch. Ein stark vereinfachtes Modell f¨ur SrCuO2 ist ein System aus voneinander unabh¨angigen antiferroma- gnetischen Ketten aus Elektronen mit Spin 1/2. Wenn ein Elektron aus einer solchen Kette entfernt wird, werden gem¨aß der Luttinger-Theorie zwei Anregungen erzeugt, ein Holon (tr¨agt die Ladung des Elektrons bzw. Lochs) und ein Spinon (tr¨agt den Spin des Elektrons bzw. Lochs) (vgl. Abschnitt 4.1.7).

Abbildung 2.18: Schematische Kristallstruktur von SrCuO₂. Schraffiert: Sr, schwarz: Cu, weiss: O [Motoyama et al., Phys. Rev. Lett.76 (1996) 3212].

Experimentell k¨onnen Anregungen, bei denen ein Elektron entfernt wird, mit Photo- emissionsspektroskopie untersucht werden. In Abb. 2.19 sind ARPES (angle-resolved photo- emission spectroscopy)-Spektren f¨ur verschienede k-Positionen entlang der Kettenrichtung von SrCuO2 gezeigt. Mit Hilfe von Modellrechnungen im Rahmen des sog.t−J-Modells (t steht f¨ur einen sog. hopping-Term, J f¨ur die Austausch-Wechselwirkung) konnte der Peak, der zwischenk=π/2 undπauftritt (rechtes Teilbild) als Holon identifiziert werden, der Peak

zwischenk = 0 undπ/2 (linkes Teilbild) als Gemisch aus Spinon- und Holon-Anregung. Die starke Dispersion (k-Abh¨angigkeit der Peak-Position) ist typisch f¨ur quasi-eindimensionale Anregungen.

Abbildung 2.19: ARPES-Spektren von SrCuO2[Kim et al., Phys. Rev. Lett.77(1996) 4054].

2.4.2 Kohlenstoff-Nanor¨ ohrchen

Kohlenstoff-Nanor¨ohrchen kann man sich wie eine zu einem Zylinder aufgerollte und naht- los verschweißte Graphitschicht vorstellen. Je nach der Richtung, um die die Graphitschicht gekr¨ummt ist, entstehen unterschiedliche Strukturen (Abb. 2.20). R¨ohrchen vom Armsessel- Typ (schr¨ager Pfeil in Abb. 2.20) sind metallisch, solche vom Zickzack-Typ (waagerechter Pfeil in Abb. 2.20) sind ¨uberwiegend halbleitend. Chirale R¨ohrchen, die entlang einer belie- bigen anderen Richtung aufgerollt sind, k¨onnen metallisch oder halbleitend sein. Diese Un- terschiede k¨onnen mit Bandstrukturrechnungen erkl¨art werden. Neben diesen einwandigen Nanor¨ohrchen gibt es auch mehrwandige Nanor¨ohrchen. Diese scheinen aber nicht

”eindi- mensional genug“ zu sein, um mit der Theorie der Luttinger-Fl¨ussigkeit beschrieben werden zu k¨onnen. Bisher konnten noch keine Messungen an einzelnen einwandigen Nanor¨ohrchen gemacht werden. Es k¨onnen aber B¨undel von einwandigen Nanor¨ohrchen hergestellt werden, in denen der elektronische Transport durch eine einzige metallische Nanor¨ohre dominiert wird.

Zickzack- struktur

Chirale Struktur Armsessel-

struktur

Abbildung 2.20: Graphit und verschiedene Arten von Kohlenstoff-Nanor¨ohrchen [C. Strunk, Physik in unserer Zeit 36 (2005) 176; nach Chemie in unserer Zeit39 (2005) 17 ].

Abbildung 2.21 zeigt die Ergebnisse eines Tunnelexperiments an einem solchen B¨undel, das auf zwei Metallkontakte gelegt wurde (Skizze in Abb. 2.21). Die differentielle Leitf¨ahigkeit dI/dV wurde bei verschiedenen Temperaturen als Funktion der Spannung zwischen den Kon- takten gemessen. Bei kleinen Spannungen istdI/dV konstant. Dieses ohmsche Verhalten wird in Tunnelexperimenten zwischen zwei normalen Metallen beobachtet. Wie das lineare Verhal- ten in doppelt-logarithmischer Darstellung zeigt, steigt bei h¨oheren SpannungendI/dV aber nach einem Potenzgesetz dI/dV ∼ V^α an. Zudem fallen die Messkurven bei verschiedenen Temperaturen in einer Auftragung (dI/dV)/T^α gegen eV /(k_BT) auf eine universelle Kurve (Hauptteil von Abb. 2.21). Beides ist im Einklang mit der Theorie der Luttinger-Fl¨ussigkeit.

In einer Luttinger-Fl¨ussigkeit zieht die Bewegung eines Elektrons eine wellenf¨ormige Anre- gung des gesamten Elektronensystems, eine sog. Plasmaschwingung nach sich. Die Quanten dieser Schwingung sind die Plasmonen. W¨ahrend eine Tunnelbarriere von einzelnen Elektro- nen passiert (durchtunnelt) werden kann, ist sie f¨ur Plasmonen undurchl¨assig. Die Injektion eines einzelnen Elektrons in eine Luttinger-Fl¨ussigkeit kostet Energie, da das zus¨atzliche Elektron in der Luttinger-Fl¨ussigkeit nicht stabil ist und in Plasmonen zerfallen muss. Die Energie, die zur Anregung dieser Plasmonen n¨otig ist, wird von der Spannungsquelle geliefert und f¨uhrt zu dem experimentell beobachteten Potenzgesetz.

Abbildung 2.21: Differentielle Leitf¨ahigkeit dI/dV eines Metall/B¨undel einwandiger Kohlenstoff-Nanor¨ohrchen/Metall-Tunnelkontakts (Skizze). Die Rohdaten des Teilbildes sind im Hauptbild skaliert dargestellt [Bockrath et al., Nature 397 (1999) 598].

2.5 Invar-Materialien

Die (normale) thermische Ausdehnung eines Festk¨orpers (Isolators, elektronische Beitr¨age werden hier nicht betrachtet) ist eine Folge der Anharmonizit¨at der Bindungsenergie. Ein unsymmetrischer Verlauf des Potentials zwischen benachbarten Atomen f¨uhrt dazu, dass mit steigender Temperatur nicht nur die Amplitude der Schwingungen der Atome w¨achst, son- dern auch der mittlere Atomabstand; das Material dehnt sich aus. Dieses normale Verhalten wird durch das Gr¨uneisen-Gesetz beschrieben, gem¨aß dem der thermische Ausdehnungskoef- fizient ann¨ahernd proportional zur spezifischen W¨arme ist. Diese folgt der Debye-Funktion, die mit steigender Temperatur S-f¨ormig zunimmt und bei hohen Temperaturen in S¨attigung geht.

2.5.1 Fe-Ni-Legierungen

Bereits im Jahr 1897 entdeckte Ch. E. Guillaume (Comp. Rend. Acad. Sci. Paris125 (1897) 235), dass eine Legierung der Zusammensetzung Fe₆₅Ni₃₅ in einem Temperaturbereich rund um Raumtemperatur einen verschwindend kleinen thermischen Ausdehnungskoeffizienten hat (Abb. 2.22). 1920 erhielt er f¨ur diese Entdeckung den Physiknobelpreis. Dieses anomale

Abbildung 2.22: Oben: Thermischer Ausdehnungskoeffizient von Fe-Ni-Invar im Vergleich zu normalem Stahl. F¨ur hohe Temperaturen folgt der Ausdehnungskoeffizient wieder dem Gr¨uneisengesetz. Unten: Thermischer Ausdehnungskoeffizient von Fe-Ni-Invar bei 300 K als Funktion der Ni-Konzentration.

Verhalten wird als Invar-Effekt bezeichnet. Dieser Effekt ist von praktischem Interesse, da Materialien mit sehr geringem Ausdehnungskoeffizienten durch Temperaturschocks mecha- nisch kaum beansprucht werden. Heute kennt man auch Materialien mit besonders großem Ausdehnungskoeffizienten (z.B. fcc Eisen); in diesem Fall spricht man vom anti-Invar-Effekt.

Der Invar-Effekt tritt auf, wenn der normale positive Beitrag zur thermischen Ausdehnung, der von den thermischen Anregungen der Gitterschwingungen (Phononen) herr¨uhrt, gera-

de duch einen negativen Beitrag kompensiert wird. Da alle Invar-Materialien magnetisch sind, liegt es nahe, dass die magnetische Ordnung an diesem Effekt beteiligt ist. Dies um- somehr, als es oberhalb der Curie-Temperatur keinen Invar-Effekt gibt. Da der Invar-Effekt kein isoliertes Ph¨anomen ist, sondern in einer großen Anzahl von Legierungen, jedoch immer bei bestimmter Zusammensetzung, gefunden wird, muß der entsprechende Machanismus ein fundamentaler sein. Invar-Verhalten tritt sowohl in Systemen mit itineranten magnetischen Momenten (z.B. Fe und seinen Legierungen), als auch in solchen mit lokalisierten Momen- ten (Legierungen, die Selten-Erd-Atome enthalten) auf. Als m¨ogliche Anregungen werden derzeit Magnonen und Spinfluktuationen (Abschnitte 4.1.4/4.2.2 und 4.1.5) diskutiert. Man kann zeigen, dass diese Anregungen unter bestimmten Umst¨anden stark an das Volumen koppeln und somit die Temperaturabh¨angigkeit der Magnetostriktion (Volumen¨anderung im Magnetfeld) steuern.

2.5.2 Die Verbindung YbGaGe

F¨ur das Invar-Verhalten der Verbindung YbGaGe wird ein anderer Mechanismus verantwort- lich gemacht. Messungen der magnetischen Suszeptibilit¨at zeigen (Abb. 2.23), dass das effek- tive magnetische Moment mit steigender Temperatur zunimmt. Dies wird so interpretiert, dass mit steigender Temperatur mehr und mehr Yb-Atome vom diamagnetischen Valenz- zustand Yb²⁺ in den paramagnetischen Valenzzustand Yb³⁺ ¨ubergehen (effektives Moment von freiem Yb³⁺-Ion: 4,54µB). Da das Volumen von Yb³⁺ wesentlich kleiner ist als jenes von Yb²⁺ bedingt dieser Effekt eine Volumenverkleinerung mit steigender Temperatur (negati- ve thermische Ausdehnung). Kombiniert mit der normalen (Phononen-bedingten) positiven thermischen Ausdehnung ergibt sich insgesamt der experimentell beobachtete Invar-Effekt (Abb. 2.24). Die elementaren Anregungen dieses Valenz¨ubergangs sind Valenzfluktuationen.

Temperature (K)

Abbildung 2.23: Magnetische Suszeptibilit¨at (links) und ihr Inverses (rechts) als Funktion der Temperatur von YbGaGe [Salvador et al., Nature 425 (2003) 702].

Temperature (K)

Abbildung 2.24: Temperaturabh¨angigkeit des Einheitszellenvolumens von zwei leicht unstoi- chiometrischen YbGaGe Verbindungen YbGa1+δGe1−δ (oben) und YbGa1−δGe1+δ (unten) [Salvador et al., Nature425 (2003) 702].

Kapitel 3

Landau’sche Theorie der Fermifl¨ ussigkeit

Die Landau’sche Theorie der Fermifl¨ussigkeit wurde 1956 von Laudau entwickelt, um die Eigenschaften von ³He zu erkl¨aren. Ihre Bedeutung geht aber weit ¨uber diesen Spezial- fall hinaus: grunds¨atzlich kann sie zur Beschreibung aller fermionischen Systeme verwendet werden. Die Landau’sche Theorie der Fermifl¨ussigkeit gilt heute als eine der bedeutendsten Theorien der Festk¨orperphysik und ist derzeit das

”Standardmodell“ der Metalle. Sie erkl¨art, warum sich ein System aus stark wechselwirkenden Teilchen ann¨ahernd wie ein System freier Teilchen verhalten kann und gibt an, wie man die ¨Anderungen, die die Wechselwirkungen hervorrufen, quantifizieren kann.

3.1 Das Konzept der Quasiteilchen

Dass einfache Metalle sehr gut mit der Sommerfeld-Theorie freier Elektronen beschrieben werden k¨onnen (vgl. Abschnitt 2.1, spezifische W¨arme von Au und Paulisuszeptibilit¨at von Na) ist eigentlich ¨uberaus erstaunlich, denn die Coulomb-Wechselwirkung zwischen den Elek- tronen ist trotz Abschirmung keineswegs vernachl¨assigbar klein. Sie ist in Metallen von der gleichen Gr¨oßenordnung wie die kinetische Energie der Elektronen. Warum kann eine Theo- rie, die die Coulomb-Wechselwirkung g¨anzlich außer Acht l¨asst, dann so gut funktionieren?

Die Antwort liegt in Landau’s Konzept der Quasiteilchen.

Tats¨achlich haben wir mit den Beziehungen freier Elektronen n¨amlich nicht die freien Elektronen selbst beschrieben, sondern den Elektronen ¨ahnliche (Landau’sche) Quasiteil- chen. Obwohl sich der Grundzustand des wechselwirkenden Systems erheblich von dem des nichtwechselwirkenden Systems unterscheiden kann, haben die elementaren Anregungen des wechselwirkenden Systems (die Quasiteilchen) praktisch die gleichen Eigenschaften wie die urspr¨unglichen Elektronen: sie haben die gleiche Ladung, den gleichen Spin und den gleichen maximalen Impuls p_F. Nur ihre effektive Masse m^∗ und damit auch ihre Energie p²/(2m^∗) kann sich erheblich von der freier Elektronen unterscheiden. Zudem ist die Gesamtenergie mehrerer Quasiteilchen ann¨ahernd gleich der Summe ihrer Einzelenergien. Man kann damit komplizierte angeregte Zust¨ande einfach als Summe von vielen Quasiteilchen beschreiben.

29