1.1 Mathematische Sprache

Inhaltsverzeichnis

1 Grundlagen 3

1.1 Mathematische Sprache . . . 3

1.2 Beweistechniken . . . 5

1.3 Mengen . . . 7

1.4 Abbildungen . . . 12

1.5 Natürliche ZahlenN und vollständige Induktion . . . 15

2 Zahlen 21 2.1 Die Gruppe der ganzen ZahlenZ . . . 23

2.2 Der Körper der rationalen ZahlenQ . . . 25

2.3 Der Körper der reellen Zahlen R . . . 28

2.4 Mächtigkeit von Mengen und Abzählbarkeit . . . 35

2.5 Rechnerarithmetik . . . 38

2.6 Der Körper der komplexen Zahlen C . . . 42

3 Konvergenz, Folgen und Reihen 47 3.1 Konvergenz . . . 47

3.2 Bestimmung von Konvergenz und Grenzwerten . . . 50

3.3 Häufungspunkte und Teilfolgen . . . 53

3.4 Reihen . . . 54

3.5 Konvergenzkriterien für Reihen . . . 57

3.6 Potenzreihen . . . 59

4 Stetigkeit 61 4.1 Intervalle . . . 61

4.2 Folgenstetigkeit . . . 62

4.3 -δ-Stetigkeit . . . 65

4.4 Rechenregeln für stetige Funktionen . . . 67

4.5 Zwischenwertsatz . . . 70

5 Differentiation 73 5.1 Ableitung von Funktionen . . . 74

5.2 Ableitung als lineare Approximation . . . 76

5.3 Ableitungsregeln . . . 78

5.4 Extrema und Mittelwertsatz . . . 81

5.5 Taylorreihe . . . 84

5.6 Newton-Verfahren . . . 89

6 Integration 95 6.1 Zerlegungen und Flächeninhalte . . . 95

6.2 Riemann-Integral . . . 97

6.3 Hauptsatz der Differential- und Integralrechnung . . . 104

6.4 Integrationsregeln . . . 105

6.4.1 Partielle Integration . . . 106

6.4.2 Substitutionsregeln . . . 106

6.5 Quadraturformeln . . . 107

7 Vektorräume 113 7.1 Der n-dimensionale reelle Raum Rⁿ . . . 113

7.2 Raum von Folgen und Funktionen . . . 117

7.3 Allgemeine Definition von Vektorräumen . . . 120

7.4 Linearkombination, Span und lineare Unabhängigkeit . . . 122

7.5 Basis und Dimension . . . 126

1 Grundlagen

1.1 Mathematische Sprache

Möchte man mathematische Sachverhalte ausdrücken, so verwendet man dafür eine Spra- che, die präziser in seiner Aussagekraft ist als dies zum Beispiel in der Alltagssprache üblich ist. Dadurch sollen mathematische Zusammenhänge übersichtlich und kompakt darstellbar sein und vor allem sollen mathematische Aussagen beweisbar werden. Es hat sich dazu ein gebräuchlicher Zeichenvorrat entwickelt, der neben weiteren grundlegenden Begriffen im Folgenden vorgestellt werden soll.

Mathematische Aussagen

Eine mathematische Aussage ist ein Satz, der wahr oder falsch sein kann. So ist zum Beispiel der Satz

„Die Summe einer ganzen Zahl mit sich selbst ergibt eine gerade Zahl.“

eine Aussage, die wahr ist. Zwei Dinge sind bei der Betrachtung von Aussagen wichtig:

(i) Eine Aussage ist immer ein ganzer Satz. Aussagen der Form „x² + 3“ sind nur Terme, deren Wahrheitsgehalt sich nicht ermitteln lässt.

(ii) Eine Aussage ist immer entweder wahr oder falsch („Tertium non datur“; Prinzip des ausgeschlossenen Dritten). Dabei ist durchaus möglich, dass noch nicht bekannt ist, ob eine Aussage wahr oder falsch ist (z.B. da noch kein Beweis gefunden ist).

Aussagen werden gewöhlich mit lateinischen Großbuchstaben bezeichnet. Man verwendet bei der Angabe dasDefinitionssymbol :=(„ist definiert durch“). Zudem können Aussagen auch von Variablen abhängen. Durch Einsetzen eines konkreten Wertes für die Variable kann dann der Wahrheitsgehalt der so entstandenen Aussage ermittelt werden. Dadurch lassen sich ganze Klassen von Aussagen kompakt angeben.

Beispiele 1.1

(i) A:=„Die Summe einer ganzen Zahl mit sich selbst ergibt eine gerade Zahl.“

(ii) B(n) := „n+n ist eine gerade Zahl.“

(iii) C(n) := „n²+ 2n= 8“ (iv) D:=„2 = 3“

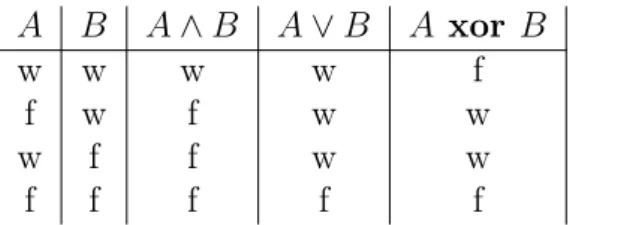
A B A∧B A∨B A xor B

w w w w f

f w f w w

w f f w w

f f f f f

A ¬A

w f

f w

Tabelle 1.1: Wahrheitstafeln (w: wahr; f: falsch)

Hierbei ist sowohlA als auch B(n) für alle natürlichen Zahlen eine wahre Aussage. Die Gültigkeit von C(n) hängt vom gewählten n ab und D ist falsch.

Kombination und Folgerung von Aussagen

In der Alltagssprache ist es üblich Aussagen zu verneinen oder durch die Wörter „und“,

„oder“, etc. zu neuen Aussagen zusammenzusetzen. Dies wird auch bei mathematischen Aussagen gemacht. Die dabei entstehenden zusammengesetzten Aussagen sind wiederum Aussagen, die wahr oder falsch sein können. Die Verknüpfungen werden mathematisch präzise über Wahrheitstafeln definiert.

Seien A, B Aussagen, dann schreibt man:

(i) A∧B: „Aund B sind wahr“ (Konjunktion) (ii) A∨B: „Aoder B ist wahr“ (Disjunktion) (iii) ¬A: „A ist falsch / A gilt nicht“ (Negation)

(iv) A xor B: „Entweder A oder B ist wahr“ (Kontravalenz)

Je nach Wahrheitsbelegung der ursprünglichen Aussagen besitzt die zusammengesetzte Aussage einen Wahrheitswert gemäß Tabelle 1.1. Wesentlich sind die Punkte:

(i) A∧B ist genau nur dann wahr, wenn beide Aussagen A und B wahr sind.

(ii) A∨B ist wahr, sobald mindestens eine der AussagenA oderB wahr ist. Es dürfen dabei auch beide Aussagen wahr sein (inklusive oder).

(iii) A xor B ist wahr, wenn genau nur eine der Aussagen A oder B wahr ist. Sind A und B wahr, dann wird die Zusammensetzung falsch (exklusives oder).

Folgt ausA die Gültigkeit der AussageB („WennA gilt, dann gilt auch B“ (Implika- tion)), so schreibt man dies als

A⇒B.

In diesem Fall bezeichnet man die Aussage A alshinreichend für die Gültigkeit von B. Verliert die Aussage B immer ihre Gültigkeit, sobaldA nicht gültig ist (¬A⇒ ¬B), so bezeichnet man A alsnotwendig für B.

1.2 Beweistechniken Man beachte, dass es bei der Folgerung A⇒B jedoch zwei Möglichkeiten gibt:

- A ist wahr, B ist wahr - das ist der übliche, gewünschte Fall der Schlussfolgerung.

- A ist falsch, B ist wahr oder falsch - d.h., aus einer falschen Aussage lässt sich alles schlussfolgern.

Um auszudrücken, dass zwei Aussagen A, B gleichwertig sind („A gilt genau dann, wenn B gilt“ (Äquivalenz)), schreibt man

A⇔B.

Quantoren

Oftmals möchte man Aussagen tätigen, die von äußeren Parametern abhängen. Dabei stellt sich dann zum Beispiel die Frage, ob die Aussage für alle möglichen Parameter gültig ist oder ob überhaupt ein Parameter existiert, für den diese Aussage gültig wird.

Dies lässt sich über sogenannte Quantoren ausdrücken, die sich wie folgt lesen:

(i) ∀: „für alle“

(ii) ∃: „es existiert (mindestens) ein“

(iii) ∃!: „es existiert genau ein“

(iv) @: „es existiert kein“

Beispiel 1.2

Sei B(n) := „n+n ist eine gerade Zahl.“ und C(n) := „n²+ 2n = 8“.

(i) D:=„∀n:B(n)“ (ii) E :=„∃n:C(n)“ (iii) F :=„∀n :C(n)“

Die beiden Aussagen D, E sind beide wahr. Hingegen ist die Aussage F falsch.

1.2 Beweistechniken

In der Mathematik geht man davon aus, dass es gewissse Aussagen gibt, die gültig sind.

Diese nennt man Axiome. Ausgehend von diesen Grundwahrheiten werden dann alle weiteren Aussagen gefolgert. Für die Schlussfolgerungen gibt es ein paar grundlegende Techniken, die sich oft anwenden lassen.

Direkter Beweis

Die einfachste Form des Beweises ist die direkte Schlussfolgerung. Dabei wird ausgehend von als wahr bekannten (bzw. als Axiom vorausgesetzen) Aussagen eine weitere wahre Aussage gefolgert. Dazu ein Beispiel:

Satz 1.3 (Quadratzahlen von geraden Zahlen sind gerade)

Sei n eine gerade natürliche Zahl. Dann ist auch n² eine gerade natürliche Zahl.

Beweis. Sei A := „n eine gerade natürliche Zahl“. Daraus wird nun gezeigt, dass sich durch eine Kette von Implikationen die Aussage B := „n² eine gerade natürliche Zahl“

folgern lässt.

n gerade⇒Es gibt eine natürliche Zahl m mit n = 2·m

⇒n² = (2·m)² = 4·m² = 2·(2·m²)

⇒n² gerade.

Äquivalenzbeweis

EinÄquivalenzbeweis dient dazu die Gleichheit zweier Aussagen zu zeigen:A⇔B. Dies wird dadurch bewiesen, dass man einen direkten Beweis in beide Richtungen ausführt:

Man zeigt sowohl A ⇒ B als auch B ⇒ A. Hieraus sieht man die Gleichheit der Aussagen.

Beweis durch Kontraposition

Möchte man A ⇒ B zeigen, so kann man stattdessen auch die äquivalente Aussage

¬B ⇒ ¬A zeigen, denn es gilt:

(A⇒B)⇔(¬B ⇒ ¬A).

Dazu ein Beispiel:

Satz 1.4

Sei n² eine gerade natürliche Zahl. Dann ist auchn eine gerade natürliche Zahl.

Beweis. Sei A:= „n² eine gerade natürliche Zahl“ undB :=„n eine gerade natürliche Zahl“. AnstattA ⇒B zu folgern, wird nun ¬B ⇒ ¬A gezeigt.

¬B =n ist eine ungerade natürliche Zahl

⇒Es gibt eine natürliche Zahl m mit n = 2·m+ 1

⇒n² = (2·m+ 1)² = 4·m²+ 4·m+ 1 = 2·(2·m²+ 2·m) + 1

⇒n² ist eine ungerade natürliche Zahl=¬A

1.3 Mengen

Widerspruchsbeweis (indirekter Schluss)

Hier nimmt man an, dass die AussageA⇒B, die man eigentlich beweisen möchte, nicht gilt. Die Negation von A⇒B lautetA∧ ¬B. Hieraus leitet man nun einen Widerspruch her, d.h. dass damit dann gleichzeitig auch eine Aussage C und dessen Gegenteil ¬C gelten muss. Da dies nicht sein kann, muss die Annahme der Nagation falsch gewesen sein und somit die zu beweisende Aussage gelten.

Satz 1.5 (Euklid)

Es gibt unendlich viele Primzahlen.

Beweis. Der Beweis wird durch einen Widerspruch geführt. Angenommen, es gäbe nur endlich viele Primzahlen. Dann lassen sich diese als p₁, p₂, . . . , p_n auflisten und daraus eine neue ZahlM :=p1·p2·. . .·pnbilden. DaM durch jede der Primzahlen teilbar ist, ist jedochM+1durch keine der Primzahlen teilbar und somit selbst eine Primzahl. Die Zahl M + 1 ist somit eine weitere Primzahl, die nicht in p₁, . . . , p_n vorkommt - Widerspruch.

Somit muss die Annahme, dass es nur endlich viele Primzahlen gibt, falsch gewesen sein.

Eine weitere, sehr wichtige Beiweistechnik ist derInduktionsbeweis, mit dem man Aussa- gen beweisen kann, die von den natürlichen Zahlen abhängen. Auf Grund der Wichtigkeit der Induktion wird diese im weiteren Verlauf gesondert behandelt.

1.3 Mengen

Einer der grundlegenden Begriffe der Mathematik ist die Menge. Die folgende intuitive Beschreibung stammt von G. Cantor.

Definition 1.6 (Menge (Cantor, 1885))

Eine Menge ist eine wohldefinierte Zusammenfassung verschiedener Objekte zu einem Ganzen.

Die Objekte in einer Menge werden Elemente genannt. Gemäß der Definition sind alle Elemente einer Menge von einander unterschiedlich. Üblicherweise werden Mengen durch lateinische Großbuchstaben A, B, C, . . . bezeichnet.

Ist ein Objekt a Element einer Menge A, so schreibt man dies als a ∈A (∈:„ist Element von“), andernfalls schreibt man

a /∈A (∈/:„ist nicht Element von“).

Beispiele 1.7

Beispiele für Mengen sind:

(i) Die Menge der Studierenden an der Universität Frankfurt.

(ii) Die Menge der Gemüse G:={ Tomate, Gurke, Paprika, . . .}.

(iii) Die Menge N:={0,1,2,3, . . .} der natürlichen Zahlen.

(iv) Die MengeN⁺ :={1,2,3, . . .} der positiven natürlichen Zahlen.

(v) Die MengeZ:={. . . ,−3,−2,−1,0,1,2,3, . . .} der ganzen Zahlen.

Mengen werden durch die explizite Angabe ihrer Elemente beschrieben, A:={a, b, c, . . .},

oder man gibt die charakterisierende Eigenschaft ihrer Elemente an A:={ a| {z }∈O

Obermenge

| a| hat die Eigenschaft XY{z }

Bedingung

}.

Beispiele 1.8

(i) Die Menge P

P :={2,3,5,7,11, ..}, oder P :={n∈N⁺ |n ist Primzahl }

beschreibt die Menge der Primzahlen, d.h. derjenigen natürlichen Zahlen, die nur durch 1und sich selbst teilbar sind.

(ii) Die Menge der positiven, geraden Zahlen

{2,4,6, . . .}, oder {n∈N⁺ | ∃m∈N:n= 2·m}. (iii) Die Menge der Zahlen, die durch b ∈N teilbar sind:

{b,2b,3b, . . .}, oder {n ∈N⁺| ∃m ∈N:n =b·m}. (iv) Die MengeQ:={_n^z |z ∈Z, n∈N⁺}.

Definition 1.9

Seien A und B Mengen.

(a) Aheißt Teilmenge von B, falls jedes Element von A auch inB enthalten ist. Man schreibt dies alsA⊂B.

(b) GiltA⊂B und B ⊂A, so sind die Mengen gleich:A=B.

(c) Die leere Menge ∅ enthält kein Element und ist in jeder Menge enthalten.

1.3 Mengen (d) Der Durchschnitt A∩B besteht aus allen Elementen, die sowohl in A als auch in

B enthalten sind:

A∩B :={x|x∈A und x∈B}.

(e) Die Vereinigung A∪B besteht aus allen Elementen, die in A oder inB enthalten sind:

A∪B :={x|x∈A oderx∈B}.

(f) DerDifferenz A\B besteht aus den Elementen, die inAaber nicht inB enthalten sind:

A\B :={x|x∈A und x /∈B}.

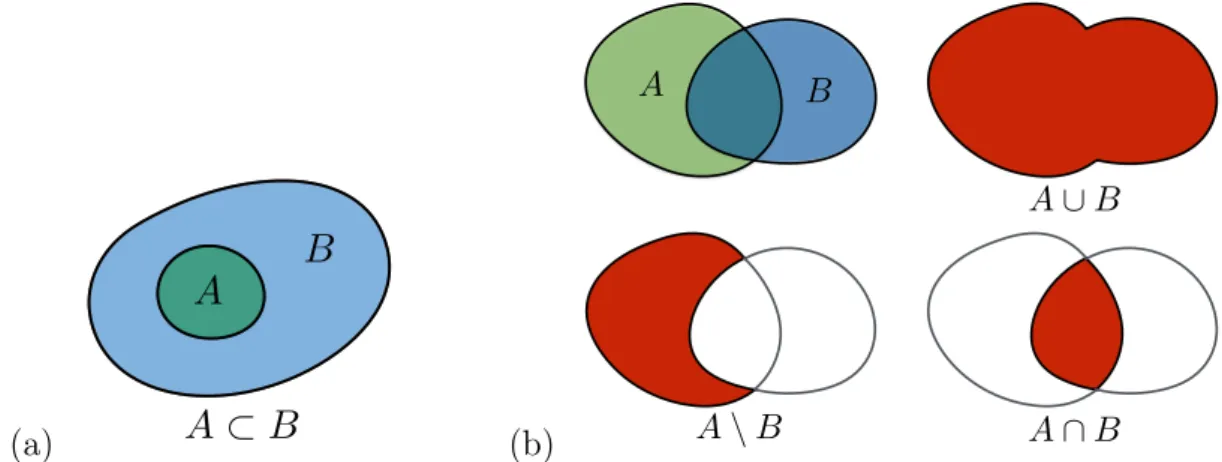
(a)

A

B

A ⇢ B

A B

A\B A[B

A\B

Abbildung 1.1: (a) Teilmenge (b) verschiedene Mengenoperationen

Bemerkung 1.10 (Exklusives und inklusives „oder“)

Mit „oder“ ist das inklusive oder gemeint, d.h. A∪B enthält auch die Elemente, die sowohl in A als auch in B liegen. (Die Alternative ist das exklusive oder, bei dem ein Element entweder in A oder in B liegen muss, jedoch nicht in beiden gleichzeitig.) Für Vereinigung und Durchschnitt von Mengen gelten die folgenden Regeln:

(a) Das Kommutativgesetz (es kommt nicht auf die Reihenfolge an):

A∪B =B ∪A, A∩B =B∩A

(b) Das Assoziativgesetz (bei Mehrfachverkettung ist die Reihenfolge egal):

(A∪B)∪C =A∪(B∪C), (A∩B)∩C=A∩(B∩C)

(c) Das Distributivgesetz:

A∪(B∩C) = (A∪B)∩(A∪C), A∩(B∪C) = (A∩B)∪(A∩C) Beweis. Möchte man zeigen, dass zwei MengenX =Y identisch sind, dann bietet sich an zunächst einzeln sowohlX ⊂Y als auchY ⊂X zu zeigen. Daraus folgt dannX =Y. Um die Aussage X ⊂Y zu zeigen, wählt man ein beliebiges Element der Menge x∈X und zeigt dann, dass auch x ∈ Y gilt. Da das Element beliebig war, ist somit jedes Element aus X auch in Y enthalten und dies zeigt X ⊂Y.

Nach diesem Muster sei exemplarisch die Aussage

A∪(B∩C) = (A∪B)∩(A∪C) bewiesen.

„A∪(B∩C)⊂(A∪B)∩(A∪C)“: Sei ein x∈A∪(B∩C)beliebig gewählt. Somit gilt x∈A oderx∈B∩C. Die beiden Fälle lassen sich getrennt betrachten:

1. Fall: Giltx∈A, dann istx∈A∪B undx∈A∪Cund somit auchx∈(A∪B)∩(A∪C). 2. Fall: Gilt x ∈ B ∩C, dann gilt x ∈ B und x ∈ C. Somit gilt auch x ∈ A∪B und x∈A∪C. Darauf folgt ebenfalls x∈(A∪B)∩(A∪C).

„A∪(B∩C)⊃(A∪B)∩(A∪C)“: Sei einx∈(A∪B)∩(A∪C)beliebig gewählt. Somit gilt x∈A∪B und x∈A∪C. Es lassen sich erneut zwei Fälle getrennt betrachten:

1. Fall: Gilt x∈A, dann ist x∈A∪(B∩C).

2. Fall: Giltx /∈A, dann mussx∈B undx∈C gelten. Somit gilt auchx∈A∪(B∩C).

Hat man mehrere Mengen, so lassen sich aus diesen die „Produktmenge“ bilden.

Definition 1.11 (Kartesisches Produkt)

Seien A, B zwei Mengen. Das kartesische Produkt von A und B ist die Menge A×B :={(a, b)|a∈A, b∈B}.

Die Elemente (a, b) sind geordnete Paare und werdenTupel genannt.

Analog lassen sich auch kartesische Produkte A₁ × A₂ ×. . .× A_n definieren, die als Elemente n-Tupel (a1, a2, . . . , an) besitzen.

Zu einer gegebenen Menge lässt sich zudem die „Menge aller Teilmengen“ bilden.

Definition 1.12 (Potenzmenge)

Zu einer Menge A ist die Potenzmenge P gegeben durch die Menge aller Teilmengen, d.h.

P(A) := {B |B ⊂A}. (1.1)

1.3 Mengen

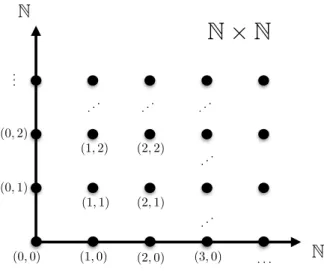
(0,0) (1,0) (2,0)

(2,1) (2,2) (1,2)

(1,1) (0,1)

(0,2)

(3,0) . . . ...

...

...

...

... ...

N

N

N ⇥ N

Abbildung 1.2: Kartesisches Produkt N² :=N×N

Beispiel 1.13 (i) P({1}) = n

∅,{1}o . (ii) P({1,2}) =n

∅,{1},{2},{1,2}o . (iii) P({1,2,3}) =n

∅,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}o . Bemerkung 1.14 (Russellsche Antinomie)

Der Mathematiker B. Russell hat durch ein Paradoxon gezeigt, dass beim Umgang von Konstrukten gemäß „Menge aller Mengen mit gewisser Eigenschaft“ Vorsicht geboten ist.

Dazu konstruiert er die „Menge aller Mengen, die sich nicht selbst als Element enthalten“, d.h. formal

R :={M |M /∈M}. (1.2)

Man denke zum Beispiel an ein Buch, das alle Bücher auflistet, in denen nicht auf sich selbst verwiesen wird.

Die Frage ist nun, ob diese Menge in sich selbst enthalten ist, d.h ob gilt R ∈ R oder R /∈ R. Enthält sich die Menge R nicht selbst, so muss sie sich aber gemäß Definition enthalten. Enthält R sich selbst, dann darf sie sich gemäß Definition nicht enthalten. Es gilt also der Widerspruch

R∈R ⇔R /∈R. (1.3)

Diese Problematik kann durch einen axiomatischen Ansatz der Mengenlehre umgangen werden. Für den Rahmen dieser Vorlesung soll der einfache Ansatz zur Mengenlehre aber genügen, auf widersprüchliche Definitionen wird verzichtet.

1.4 Abbildungen

Definition 1.15 (Abbildung)

Eine Abbildung (auch Funktion) f von einer Menge A auf eine Menge B ist eine Vor- schrift, die jedem Element a∈A genau ein Element b ∈B zuordnet. Man schreibt:

f :A→B, a7→f(a) oder auch kurz

f :A →B, A3a7→f(a)∈B.

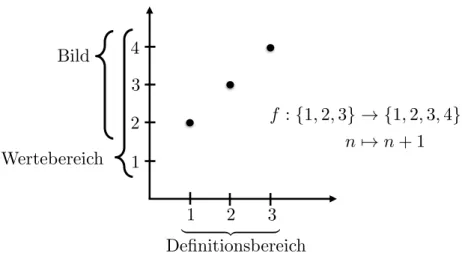
Die Menge A heißt Definitionsbereich von f. Die Menge B heißt Wertebereich von f.

Die Menge f(A) := {f(a)|a∈A} ⊂B heißt Bild von f. Beispiele 1.16

Beispiele für Abbildungen zwischen Mengen:

(a) f :{1,2,3} → {1,2,3,4}, n7→n+ 1: Abbildung auf nächste Zahl

(b) g :N→N, n 7→n²: Abbildung der natürlichen Zahlen auf die Quadratzahlen (c) h:Z→Z, n 7→n²: Abbildung der ganzen Zahlen auf die Quadratzahlen

Abbildungen zwischen Mengen lassen sich durch Wertetabellen angeben. Dies ist zum Beispiel die übliche Angabe einer Abbildung zwischen zwei Mengen, wenn es sich um experimentelle Messwerte handelt. Dann wird eine Abbildug zwischen der Menge der Messpunkte MP und der Menge der Messwerte MW aufgezeichnet:

Messung:MP→MW. x∈MP f(x)∈MW

3 9

1 8

5 16

Tabelle 1.2: Illustration der Wertetabelle zu einer Messung Alternativ lässt sich eine Abbildung gut durch ihrenGraph veranschaulichen.

Definition 1.17 (Graph)

Zu einer Abbildungf :A→B heißt die Menge

G:={(a, b)∈A×B |b=f(a)} der Graph der Abbildung.

1.4 Abbildungen

1 1

2 2

3 4

| {z 3}

Definitionsbereich Wertebereich

Bild

f :{1,2,3} ! {1,2,3,4}, n7!n+ 1

Abbildung 1.3: Graph, Definitonsbereich, Wertebereich und Bild einer Funktion

Definition 1.18 (Injektiv, surjektiv und bijektiv) Sei f :A→B eine Abbildung. Die Abbildung heißt

(a) injektiv, falls jedes Element aus B höchstens ein Urbild hat, d.h. wenn gilt

∀a1, a2 ∈A:f(a1) = f(a2)⇒a1 =a2,

(b) surjektiv, falls auf jedes Element aus B abgebildet wird, d.h. wenn gilt f(A) =B,

(c) bijektiv (oder auch one-to-one), falls sie injektiv und surjektiv ist.

Ist eine Abbildung f :A→B bijektiv, dann existiert zu jedem Elementb ∈B im Wer- tebereich mindestens ein Elementa∈Aim Definitionsbereich, das aufb =f(a)abbildet (surjektiv). Gleichzeitig gibt es aber höchstens ein Elementa∈Aim Definitionsbereich, das auf b =f(a) abbildet (injektiv). Somit gibt es genau ein solches Element.

Bijektive Abbildungen lassen sich eindeutig umkehren.

Definition 1.19 (Umkehrabbildung)

Zu einer bijektiven Abbildung f :A→B ist die Umkehrabbildung gegeben durch f⁻¹ :B →A, a=f⁻¹(b) :⇔b=f(a).

Umkehrabbildungen sind wieder bijektiv.

Manchmal möchte man auch mehrere Abbildungen hintereinander ausführen. Dies geht dann, wenn der Bildbereich der einen Abbildung im Definitionsbereich der zweiten liegt.

A B

a3

a₂ a1

a₀

b₀ b1

b₂ b₃

A:={a0, a1, a2, a3} B:={b0, b1, b2, b3}

f : A!B

A ^B

a2

a₁ a0

b0

b₁

b₂ b₃

B:={b₀, b₁, b₂, b₃}

f : A!B

A B

a3

a2

a₁ a₀

b₀ b₁

b₂

A:={a0, a1, a2, a3}

f : A!B

B:={b0, b1, b2} A:={a₀, a₁, a₂}

(a)

(b)

(c)

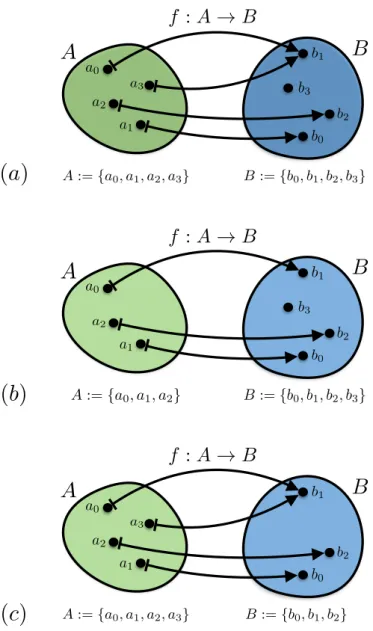
Abbildung 1.4: Beispiele für eine Funktionf :A→B: (a) nicht injektiv, nicht surjektiv (b) injektiv, nicht surjektiv, (b) nicht injektiv, surjektiv

A B

a3

a2

a1

a0

b₀ b1

b₂ b₃

f :A!B

A B

a3

a2

a1

a0

b₀ b₁

b₂ b3

f ¹ :B!A

Abbildung 1.5: Bijektive Funktion f :A→B und Umkehrfunktion f⁻¹ :B →A

1.5 Natürliche ZahlenN und vollständige Induktion Definition 1.20 (Verkettung von Abbildungen)

Seien f :A→B und g :C →Dmit f(A)⊂C. Dann heißt die Abbildung g◦f :A→D,

a7→g(f(a)), die Verkettung der Abbildungen f und g.

Man liest dies als „g nachf“, denn die Abbildung f wird zuerst ausgeführt.

1.5 Natürliche Zahlen N und vollständige Induktion

Die Menge der natürlichen Zahlen

N:={0,1,2,3, . . .}

wird intuitiv verstanden und - wie der Name schon sagt - als „natürlich“ gegeben ange- sehen. Was aber genau die natürlichen Zahlen sind und wie diese mathematisch präzise zu verstehen sind, wurde immer wieder diskutiert. Heute werden die natürlichen Zahlen üblicherweise über ein Axiomensystem eingeführt.

Definition 1.21 (G. Peano, 1889)

(P1) Es gibt ein ausgezeichnetes (kleinstes) Element: 0∈N.

(P2) Zu jeder natürlichen Zahl n ∈Ngibt es einen Nachfolger ν(n)∈N.

(P3) Die Zahl 0∈N ist nicht Nachfolger einer natürlichen Zahl.

(P4) Die Nachfolger unterschiedlicher Zahlen sind unterschiedlich:

n₁ 6=n₂ ⇒ν(n₁)6=ν(n₂).

(P5) Enthält eine MengeM ⊂Ndie Zahl0 und mit jedemn ∈M auch den Nachfolger ν(n)∈M, dann ist M =N.

Die arithmetischen Grundoperationen lassen sich ausgehend von diesen Axiomen wie folgt definieren:

n+ 0 :=n, n+ν(m) :=ν(n+m), n·0 := 0, n·ν(m) :=n·m+n.

Man erhält so die üblichen Zahlen, wenn man definiert:

0 := 0, 1 := ν(0),

2 := ν(ν(0)) =ν(1),

3 := ν(ν(ν(0))) =ν(ν(1)) =ν(2), ...

Vollständige Induktion

Eine wichtige Beweismethode ist die vollständige Induktion. Diese dient dazu Aussagen der Form A(n) zu beweisen, die von den natürlichen Zahlen abhängen. Man ist daran interessiert, dass man die Aussage für alle natürlichen Zahlen beweist. Dies sind jedoch unendlich viele AussagenA(0), A(1), A(2), A(3), . . .und man kann diese nicht alle einzeln beweisen. Stattdessen zieht man sich auf das folgende Beweisprinzip zurück.

Satz 1.22 (Induktionsprinzip)

Sei A(n)eine Aussage, die von den natürlichen Zahlen n ∈N abhängt. Falls gilt:

(IA) Induktionsanfang:A(0) ist wahr,

(IS) Induktionsschritt: Wenn A(n) wahr ist, dann ist auchA(n+ 1) wahr, dann ist die AussageA(n) für alle n∈N wahr.

Beweis. Das Induktionsprinzip folgt direkt aus dem 5. Peanoschen Axiom. Dies sieht man wie folgt: Sei eine Teilmenge M ⊂N definiert durch

M :={n ∈N|A(n) ist wahr }.

Durch den Induktionsanfang gilt0∈M. Die Induktionsannahme besagt, dass ausn ∈M auchn+ 1∈M folgt. Somit gilt mit dem 5. Peanoschen AxiomM =N.

Bemerkung 1.23

Der Induktionsanfang muss nicht immer bei0gewählt werden. Gilt eine Aussage erst ab einemn0 ≥1, so zeigt man die Gültigkeit vonA(n0)und ebenfalls den Induktionsschritt.

Also Folgerung gilt dann A(n) für alle n∈N, n ≥n0, jedoch nicht für n < n0.

Mittels der Induktion lassen sich viele Aussagen über Summen beweisen. Dazu sei zu- nächst eine vereinfachende Notation für Summen und Produkte definiert.

Definition 1.24 (Summe, Produkt)

Seien {am, am+1, . . . , an} ⊂ A Elemente einer Menge A, für die Summe als auch Pro- duktbildung definiert ist. Fürm, n∈Z, m≤n schreibt man

am+am+1+. . .+an=:

Xn i=m

ai.

1.5 Natürliche ZahlenN und vollständige Induktion Für m > n definiert man die leere Summe

Xn i=m

ai := 0, (m > n).

Analog schreibt man für die Multiplikation am·am+1·. . .·an =:

Yn i=m

ai, (m≤n), und

Yn i=m

ai := 1, (m > n).

Ein paar Beispiele sollen den Beiweis durch Induktion verdeutlichen.

Satz 1.25 (C. F. Gauß) Für alle n ∈N gilt:

Xn k=1

k = n(n+ 1)

2 .

Beweis.

Sei A(n) die Aussage: „Pⁿ

k=1

k = ⁿ⁽ⁿ⁺¹⁾₂ ist wahr“.

Induktionsanfang (n= 0):

Für n = 0 ist P⁰

k=1

k= 0 und ⁰⁽⁰⁺¹⁾₂ = 0. Somit istA(0) wahr.

Für n = 1 ist P¹

k=1

k= 1 und ¹⁽¹⁺¹⁾₂ = 1. Somit istA(1) wahr.

Induktionsschritt:

Angenommen A(n) ist wahr (Induktionsvoraussetzung, IV), d.h. es gelte Pⁿ

k=1

k =

n(n+1) 2 .

Daraus schließt man auf die Gültigkeit von A(n+ 1) wie folgt:

Xn+1 k=1

k = Xn k=1

k+ (n+ 1)^(IV)= n(n+ 1)

2 + (n+ 1)

= n(n+ 1) + 2(n+ 1)

2 = (n+ 2)(n+ 1) 2

= (n+ 1)((n+ 1) + 1)

2 .

Somit folgt aus der Gültigkeit von A(n)auch die Gültigkeit von A(n+ 1).

Satz 1.26 (Anzahl der Elemente der Potenzmenge)

Sei M eine Menge mit n ∈ N Elementen. Dann hat die Potenzmenge P(M) genau 2ⁿ Elemente.

Beweis.

SeiA(n)die Aussage: „Die Potenzmenge einer Menge mitnElementen hat2ⁿElemente“.

Induktionsanfang(n = 1):

Für M ={m}ist P({m}) =

∅,{m} und hat 2 = 2¹ Elemente. Somit ist A(1) wahr.

Induktionsschritt:

AngenommenA(n)ist wahr (Induktionsannahme), d.h. die Potenzmenge einer Menge mit n Elementen hat 2ⁿ Elemente. Nun muss gezeigt werden, wie viele Elemente die Potenzmenge einer Menge mit n+ 1 Elementen hat.

Sei M eine Menge mit n+ 1 Elementen und sei ein m ∈ M willkürlich gewählt. Dann lässt sich M schreiben als

M =N ∪ {m}, mit N :=M \ {m}, und N hat n Elemente.

Es gibt nun zwei Arten von Teilmengen vonM:

(a) Jene Teilmengen, die m nicht enthalten, d.h. die Teilmengen von N := M \ {m}.

Nach Induktionsvoraussetzung sind dies 2ⁿ.

(b) Jene Teilmengen, die m enthalten, d.h. alle Teilmengen der Form B ∪ {m} mit B ⊂N. Nach Induktionsvoraussetzung sind dies 2ⁿ.

Somit hat M genau 2ⁿ+ 2ⁿ= 2·2ⁿ = 2ⁿ⁺¹ Elemente. Somit giltA(n+ 1). Rekursive Definition

Umgekehrt kann das Induktionsprinzip auch genutzt werden, um rekursive Definitionen D(n) vorzunehmen. Dazu definiert man zunächst fürD(0) und gibt dann die Definition D(n)für alle weiterenn ∈N, n≥1durch D(n) := F(D(0), D(1), . . . , D(n−1))als eine Vorschrift an, die von den vorhergehenden Definitionen abhängen kann.

Definition 1.27 (Potenz)

Sei a∈N. Die n-te Potenz von a ist rekursiv definiert durch aⁿ:=

(1, n= 0, a·aⁿ⁻¹, n≥1.

Definition 1.28 (Fakultät)

Die n-Fakultät ist rekursiv definiert durch n! :=

(1, n = 0, n·(n−1)!, n ≥1.

1.5 Natürliche ZahlenN und vollständige Induktion Solche rekursiven Definitionen lassen sich auch verwenden, um biologische Populationen zu beschreiben. So hat Leonardo da Pisa (genannt Fibonacci) bereits 1220 die Anzahl an Kaninchenpaaren berechnet. Er nahm dabei an, dass jedes Paar an Kaninchen ab dem zweiten Lebensmonat jeden Monat ein weiteres Paar als Nachwuchs bekommt und Kaninchen unsterblich sind. Beginnt man mit einer Population von einem neu geborenen Kaninchenpaar in Monat eins, F1 = 1, so bleibt es bei einem in Monat zwei, F2 = 1, und in Monat drei bekommt dieses Paar den ersten Nachwuchs, F3 = 2. Im Monat vier bekommt weiterhin nur das erste Paar Nachwuchs, F₄ = 3, ab Monat fünf dann auch das Paar aus Monat 3, F5 = 5, usw. In jedem Monat gibt es folglich immer die Anzahl Paare, die im Vormonat vorhanden waren, plus der Nachwuchs der Paare die bereits vor zwei Monaten lebten, d.h. F_n+1 =F_n+F_n−1.

Definition 1.29 (Fibonacci-Folge)

Die Fibonacci-Zahlen Fn, n∈N⁺, sind definiert durch

Fn:=







1, n = 1,

1, n = 2,

Fn−1+Fn−2, n ≥3.

2 Zahlen

Betrachtet man die Menge der natürlichen Zahlen N = {0,1,2,3, . . .}, so lassen sich in gewissen Fällen die elementaren arithmetischen Operationen „a+b“ (Addition) und

„a·b“ (Multiplikation) umkehren, die dann als „b−a“ (Subtraktion) und „^a_b“ (Divisi- on) bezeichnet werden. Allerdings lassen sich Addition und Division nicht für beliebige Zahlen aus N definieren - so ist z.B. die Subtraktion für „b−a“ zunächst nur für Paare (b, a)natürlicher Zahlen sinnvoll, für die b > a gilt. Dies zeigt: Während die Addition

+ :N×N→N, (a, b)7→a+b für alle Paare natürliche Zahlen definiert ist, so ist die Subtraktion

−:N×N→N, (a, b)7→a−b

nicht immer erklärt - man spricht davon, dass die Menge der natürlichen Zahlen bezüglich der Subtraktion „unvollständig“ ist. Man möchte daher den Zahlenraum dahingehend erweitern, dass die Operationen der Subtraktion und Division immer erklärt sind - dies führt auf die größeren Zahlenmengen der ganzen Zahlen Zund der rationalen ZahlenQ.

Um diesen Erweiterungsprozess mathematisch beschreiben zu können, wird die Äquiva- lenzrelation verwendet.

Definition 2.1 (Relation)

EineRelation zwischen zwei MengenA, B ist eine TeilmengeR⊂A×B des kartesischen Produkts der Mengen.

Zu einer Relation R lässt sich immer entscheiden, ob ein Paar (a, b) ∈ A×B in der Relation vorhanden ist oder nicht. Ist es Teil der Relation, d.h. (a, b) ∈ R, so schreibt man dies als a ∼^R b oder auch kurz a ∼ b, wenn aus dem Kontext hervorgeht, welche Relation gemeint ist.

Eine sehr häufige Verwendung der Relation dient zur Beschreibung von Äquivalenzen innerhalb einer Menge.

Definition 2.2 (Äquivalenzrelation)

Eine Äquivalenzrelation auf einer Menge Aist eine Relation R ⊂A×A mit den Eigen- schaften

(i) Reflexivität: a∼a für alle a∈A, (ii) Symmetriegesetz: a∼b ⇒b ∼a,

1 2 3 4

t

t

t

5 6

y₁ y₁

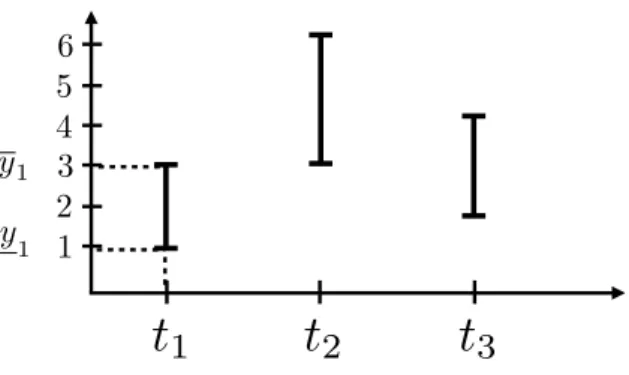
Abbildung 2.1: Beispiel einer Relation: Eine Messreihe an den Zeitpunkten t1, t2, t3, . . . zeichnet im Fehlerbalkendiagramm als „Messwert“ den Fehlerbereich zu jedem t_i als die Teilmenge {y|y

i ≤≤y_i} auf (iii) Transitivität: a∼b, b∼c⇒a∼c.

Die Bedeutung von Äquivalenzrelationen liegt darin, dass sich dadurch Mengen in Teil- mengen („Klassen“) einteilen lassen, die eine gröbere Beschreibung der Menge sind, je- doch gewünschte „wesentliche“ Aspekte hervorheben.

Beispiel 2.3

Als Blutgruppen von Menschen werden die Zuordnungen A, B, AB und 0 verwendet.

Durch diese Zuordnung lässt sich auf der Menge der Menschen eine Relation definitieren gemäß

x∼y:⇔x, y haben diesselbe Blutgruppe

Dabei bezeichnet man die Äquivalenzklassen durch die folgende Schreibweise [a] :={b∈A|b ∼a}.

Das (zufällig gewählte) erzeugene Elementa wirdRepräsentant der Äquivalenzklasse[a]

genannt.

Beispiel 2.4

Die natürlichen ZahlenNlassen sich gerade und ungerade Zahlen aufteilen. Diese unter- scheiden sich dadurch, ob sie durch 2 teilbar sind oder nicht, d.h. ob bei Division durch 2 ein Rest bleibt oder nicht:

a∼b:⇔a, bhaben bei Division durch 2 denselben Rest Dadurch entstehen die Restklassen

[1] :={a∈N|@c∈N:a= 2c}={1,3,5,7, . . .}, [2] :={a∈N| ∃c∈N:a= 2c}={0,2,4,6, . . .}.

2.1 Die Gruppe der ganzen ZahlenZ Beispiel 2.5

Der Menge Z×N⁺ lassen sich die rationalen Zahlen als Brüche zuordnen:

a

b mit (a, b)∈Z×N⁺.

Hier sind jedoch gewisse Brüche äquivalent. So sind z.B. ¹₂,²₄,³₆, . . . alle mit derselben rationalen Zahl assoziiert. Dafür lässt sich die Äquivalenzrelation

(a, b)∼(a⁰, b⁰) :⇔ab⁰ =a⁰b (d.h. gedacht a b = a⁰

b⁰).

Die Menge der rationalen Zahlen kann man dann auffassen als die Menge der Äquiva- lenzklassen

Q:={[(a, b)]|(a, b)∈Z×N⁺}.

Das letzte Beispiel motiviert nun die folgende Erweiterung des Zahlenbereichs N zu Z und Zzu Q.

2.1 Die Gruppe der ganzen Zahlen Z

Die Menge der natürlichen Zahlen ist unter der Subtraktion nicht vollständig. Für Paare a, b∈N ist die Gleichung

a+x=b

nicht immer durch ein x ∈ N lösbar. Formal lässt sich dies für den Fall a > b immer durch die Einführung einer negativen Zahl x:=b−a erreichen. Allerdings gibt es hier eine Mehrdeutigkeit: Es gibt unendlich vielen Differenzen b−a= (b+ 1)−(a+ 1) = (b+ 2)−(a+ 2) =. . ., die diese Gleichung formal lösen. Abhilfe schafft hier die Betrachtung der folgenden Äquivalenzrelation auf N×N:

(a, b)∼(a⁰, b⁰) :⇔a+b⁰ =a⁰+b.

Dass es sich hier um eine Äquivalenzrelation handelt, zeigt sich folgendermaßen:

(i) Reflexivität: für alle a, b∈N gilt a+b=a+b⇒(a, b)∼(a, b).

(ii) Symmetrie: (a, b)∼(a⁰, b⁰)⇔a+b⁰ =a⁰+b⇔a⁰ +b =a+b⁰ ⇔(a⁰, b⁰)∼(a, b).

(iii) Transitivität: Mit (a, b) ∼ (a⁰, b⁰) und (a⁰, b⁰) ∼ (a⁰⁰, b⁰⁰) gilt a+b⁰ = a⁰ +b und a⁰+b⁰⁰ =a⁰⁰+b⁰. Somit

a+b⁰⁰+b⁰ = (a+b⁰) +b⁰⁰ = (a⁰+b) +b⁰⁰ = (a⁰+b⁰⁰) +b = (a⁰⁰+b⁰) +b=a⁰⁰+b+b⁰ und somit a+b⁰⁰ =a⁰⁰+b bzw. (a, b)∼(a⁰⁰, b⁰⁰).

Die zugehörigen Äquivalenzklassen[(a, b)]werden von den Paaren der natürlichen Zahlen gebildet, die dieselbe Differenz aufweisen. Damit lässt sich die Äquivalenzklasse [(a, b)]

dann interpretieren als

(i) für a > b als natürliche Zahl a−b ∈N, (ii) für a=b als neutrale Zahl 0,

(iii) für a < b als negative Zahl a−b.

Die Menge der ganzen Zahlen lässt sich entsprechend als Menge von Äquivalenzklassen definieren:

Z: ={[(n,0)]|n ∈N} ∪

[(0, n)]|n∈N⁺ .

Die natürlichen Zahlen sind diesen Äquivalenzklassen zuordbar, indem man den folgen- den Repräsentanten wählt

N3n 7→[(n,0)]∈Z.

Die Äquivalenzklassen[(0, n)]∈Z notiert man entsprechend mit0−n oder einfach−n.

Mittels dieser Erweiterung von N nach Z ist nun der Zahlenbereich bezüglich der Sub- traktion abgeschlossen, d.h. formal: jede Gleichung der Forma+x=b mit a, b∈Zhat eine Lösung x ∈ Z. Das mathematische Konstrukt der ganzen Zahlen ist prototypisch für viele andere Gebilde der Mathematik. Die elementaren Eigenschaften werden in der folgenden Definition zusammengefasst.

Definition 2.6 (Gruppe)

Eine Menge G mit einer Verknüpfung

◦: G×G→G (a, b)7→a◦b

wird alsGruppe (G,◦) bezeichnet, falls die folgenden Eigenschaften gelten:

(a) Die Verknüpfung istassoziativ, d.h. es gilt

(a◦b)◦c=a◦(b◦c) für alle a, b, c∈G.

(b) Es existiert ein neutrales Element e∈G, so dass

a◦e=e◦a=a für alle a∈G.

(c) Es existiert ein inverses Element a⁻¹ ∈G, so dass

a◦a⁻¹ =a⁻¹◦a=e für alle a∈G.

Eine Gruppe (G,◦) heißt kommutativ (oder abelsch), falls für alle a, b ∈ G zusätzlich das Kommutativgesetz

a◦b =b◦a erfüllt ist.

2.2 Der Körper der rationalen Zahlen Q Eine Gruppe ist dadurch gekennzeichnet, dass sich Gleichungen der Forma◦x=b lösen lassen. Denn für jede Gleichung a◦x=b mit a, b∈Gfolgt allein aus der Gruppendefi- nition, dass x=a⁻¹◦b eine Lösung ist, da gilt

a◦(a⁻¹◦b) = (a◦a⁻¹)◦b=e◦b =b.

Die ganzen Zahlen mit der Addition bilden folglich eine Gruppe (Z,+). Das neutrale Element ist die Null (e = 0) und das inverse Element zu einer Zahl a ∈ Z ist die Zahl

−a ∈ Z. Die natürlichen Zahlen (N,+) hingegen bilden noch keine Gruppe, da das inverse Element nicht zu jedem Element existiert.

2.2 Der Körper der rationalen Zahlen Q

Für die Menge Z hat nun die Gleichung a+x =b die Lösung x =b−a und ist somit bezüglich der Subtraktion abgeschlossen. Jedoch lässt sich die Gleichung

a·x=b

nicht immer durch ein x ∈ Z lösen. Der Zahlenbereich muss folglich ein weiteres mal erweitert werden, diesmal zur Menge der rationalen Zahlen Q.

Man betrachte für a, a⁰ ∈Z,b, b⁰ ∈N⁺ zunächst die Äquivalenzrelation (a, b)∼(a⁰, b⁰) :⇔ab⁰ =a⁰b.

Zu a∈Z, b∈N⁺ sei die zugehörige Äquivalenzklasse[(a, b)]dann mit a

b := [(a, b)] ={a⁰ ∈Z, b⁰ ∈N⁺ |ab⁰ =a⁰b} bezeichnet.

Dies führt auf die Menge der rationalen Zahlen als Menge von Äquivalenzklassen Q:=na

b |a∈Z\ {0}, b ∈N⁺, a, b teilerfremdo

∪ 0

1

.

Als Repräsentant der jeweiligen Äquivalenzklasse wird also der Bruch in seiner vollstän- dig gekürzten Fassung gewählt, bzw. ⁰₁ als Repräsentant der 0.

In der Menge Q hat nun sowohl die Gleichung a+x =b als auch a·x =b immer eine Lösung. Sie ist somit sowohl bezüglich der Subtraktion als auch bezüglich der Divisi- on abgeschlossen. Dieses mathematische Gebilde ist wiederum sehr prototypisch. Seine Eigenschaften werden unter der Bezeichnung Körper abstrakt zusammengefasst.

Definition 2.7 (Körper)

Eine Menge K mit zwei Verknüpfungen

+ :K×K→K, (a, b)7→a+b, (Addition)

·:K×K→K, (a, b)7→a·b, (M ultiplikation) heißt Körper, falls gilt:

(K1) Addition und Multiplikation sind kommutativ, d.h. für alle a, b∈Kgilt:

a+b =b+a, a·b=b·a.

(K2) Addition und Multiplikation sind assoziativ, d.h. für alle a, b, c∈K gilt:

(a+b) +c=a+ (b+c), (a·b)·c=a·(b·c).

(K3) Es gilt das Distributivgesetz, d.h. für alle a, b, c∈K gilt:

a·(b+c) =a·b+a·c.

(K4) Die folgenden Gleichungen haben für alle a, b∈K ein Lösung x∈K:

a+x=b, a·x=b sofern a 6= 0.

Aus den Eigenschaften (K4) folgen direkt wichtige Eigenschaften eines Körpers.

Satz 2.8

In einem Körper gibt es bzgl. der Addition ein neutrales Element0und zu jedem Element a ein Inverses −a. Ebenso gibt es bzgl. der Multiplikation ein neutrales Element 1 und zu jedem Elementa 6= 0 ein Inverses a⁻¹.

Beweis. Nach (K4) ist im Speziellen die Gleichung a +x = a für alle a lösbar. Die Lösung ist das verlangte neutrale Element 0. Dieses ist eindeutig, denn gäbe es ein weiteres Element 0⁰ mit a+ 0⁰ =a, so folgt mit a+ 0⁰ =a =a+ 0 durch Kürzen von a immer0⁰ = 0. Ebenso folgt aus (K4), dass die Lösung vona+x= 0existiert und gerade das inverse Element−a darstellt.

Für die Multiplikation argumentiert man analog.

Der vorangeganene Satz zeigt, dass man einen Körper auch alternativ folgendermaßen definieren kann:

Bemerkung 2.9 (Körper – alternative Definition)

Ein Körper (K,+,·) ist eine Menge K mit zwei Verknüpfungen + („Addition“) und · (Multiplikation) mit den Eigenschaften

(i) (K,+) ist eine kommutative Gruppe mit neutralem Element 0, (ii) (K\ {0},·)ist eine kommutative Gruppe mit neutralem Element 1, (iii) Multiplikation und Addition sind distributiv: a·(b+c) =a·b+a·c.

2.2 Der Körper der rationalen Zahlen Q

Anordnung von Q

Auf der Menge der rationalen ZahlenQlassen sich gewisse Zahlen alspositiv auszeichnen, indem man die Teilmenge

Q⁺ :={a∈Q|a= z

n, z, n∈N⁺}

auszeichnet. Dadurch lässt sich für Paare (a, b)∈Q×Q die Ordnungsrelation a > b:⇔a−b ∈Q⁺

definieren. Analog definiert man

a < b :⇔b > a,

a≤b :⇔a < b odera=b, a≥b :⇔b≤a,

und erhält die gewohnten kleiner und größer Beziehungen.

Auf Qlässt sich der Absolutbetrag definieren durch

|a|:=







a, a >0,

0, a= 0,

−a, a <0.

Satz 2.10 (Eigenschaften des Betrags)

Für beliebige Zahlen a, b ∈ Q besitzt der Betrag die folgenden drei charakteristischen Eigenschaften:

(i) Definitheit:|a|= 0 ⇒a= 0. (ii) Multiplikativität: |a·b|=|a| · |b|.

(iii) Dreiecksungleichung: |a+b| ≤ |a|+|b| (auch Subadditivität).

Zudem gilt:

(iv) ||a| − |b|| ≤ |a+b|.

(v) ||a| − |b|| ≤ |a−b|.

Beweis. Exemplarisch wird (v) gezeigt:

|a|=|a−b+b| ≤ |a−b|+|b| und |b|=|b−a+a| ≤ |b−a|+|a|

⇒ |a| − |b| ≤ |a−b| und |b| − |a| ≤ |a−b|. Somit folgt insgesamt:

||a| − |b|| ≤ |a−b|.

2.3 Der Körper der reellen Zahlen R

In den vorangegenenen Abschnitten wurde der Zahlenbereich der natürlichen Zahlen N schrittweise zunächst zu den ganzen Zahlen Z und dann zu den rationalen Zahlen Q erweitert, so dass man immer größere Zahlenräume N⊂ Z⊂ Q erhalten hat. Bei jeder Erweiterung stand die Fragestellung im Raum, ob sich gewisse Gleichungen lösen lassen.

Im Körper Q schließlich lassen sich nun lineare Gleichungen bzgl. der Addition und der Multiplikation stets lösen.

Konsequenter Weise lässt sich fragen, ob nun allgemeine quadratische Gleichungen der Form

a+b·x+c·x² =d für a, b, c, d∈Q

eine Lösungx∈Q besitzen. Wieder stellt man fest, dass sich nicht jede Gleichung in Q lösen lässt.

Satz 2.11 (Irrationalität der Quadratwurzel) Die quadratische Gleichung

x² = 2 besitzt keine Lösung in Q.

Beweis. Widerspruchsbeweis: Angenommen, es gäbe die Lösung x = _n^z mit Zahlen r∈Z, n ∈N⁺, so dass x² = 2. Es sei dann die vollständig gekürzte Fassung des Bruchs gewählt. Insbesondere seien Nenner und Zähler nicht gleichzeitig durch 2 teilbar. Nun ist aber r² = 2·n² und somit r durch 2 teilbar. Wählt man r = 2·s, so ist aber wegen

2·s² =n² auchn durch 2 teilbar. Widerspruch.

1

1 p2

Abbildung 2.2: Geometrische Interpretation der Lösung von x² = 1²+ 1² = 2.

Erneut möchte man den Zahlenbereich erweitern, damit solche Gleichungen eine Lösung bekommen. Anschaulich entspricht die Lösung x² = 2 zum Beispiel der Diagonalen im

2.3 Der Körper der reellen Zahlen R Einheitsquadrat und solche Längen möchte man mit dem Zahlenraum ebenfalls abdecken können.

Die Idee ist nun, nach und nach eine Folge von rationalen Zahlen zu konstruieren, die die Lösung der Gleichung x² = 2 immer besser annähern. Man gewinnt so eine Appro- ximation, d.h. eine Näherungslösung, der gesuchten Lösung. Dazu seien zunächst einige Begrifflichkeiten genauer geklärt:

Definition 2.12 (Folge)

Unter einerFolge(an)_n∈N= (a0, a1, a2, ...)in einer MengeAversteht man eine Abbildung N→A. Jeder natürlichen Zahl n ∈N wird dabei einFolgenlied an∈A zugeordnet.

Beispiele 2.13

(a) Mit an =n ∀n∈N erhält man die Folge (an)_n∈N = (0,1,2,3, ...) = (n)_n∈N. (b) Mit an = _n+1¹ ∀n∈N erhält man die Folge (an)n∈N = (1,¹₂,¹₃, ...) = (_n+1¹ )n∈N.

(c) (_n+1ⁿ )n∈N= (0,¹₂,²₃,³₄, ...).

Nützlich ist im Folgenden auch die Darstellung von Zahlen als Dezimalzahlen.

Definition 2.14 (Dezimalbruchdarstellung) Die Dezimalbruchdarstellung einer Zahl

a=± a0+ Xk

j=1

dj ·10^−j

!

=±

a0+ d1

10 + d2

10² + d3

10³ +...+ dk

10^k

mit a0, k∈N, d1, ..., dk∈ {0,1,2, ...,9},sei im Folgenden gegeben durch a=±(a0, d1...dk).

Ein mögliches Verfahren zur Approximation der Lösung von x² = 2 besteht nun darin, die Lösung x durch eine Folge von Zahlen aus Q sowohl von unten als auch von oben einzugrenzen.

Dazu betrachte man die Foglen

an =an−1+ d^a_n

10ⁿ, für n>0, a0 = 1, und

bn=b_n−1− d^b_n

10ⁿ, für n>0, b0 = 2, mit d^a_n, d^b_n ∈ {0,1,2, ...,9} ∀n∈N⁺,wobei für alle n ∈N gelte:

bn−an = 10⁻ⁿ, a²_n <2< b²_n.

Um diese Folge zu konstruieren beginnt man also mit denjenigen ganzen Zahlen, die am nächsten unterhalb bzw. oberhalb der gesuchten Lösung liegen (a₀ = 1 und b₀ = 2).

Diese erfüllen die geforderten Bedingungen:

b0−a0 = 2−1 = 1 = 10⁻⁰, a²₀ = 1<2<4 =b²₀.

Die nächste Annäherung an die Lösung erhält man nun, indem man diejenigen Zehntel

d^a₁

10 und ^d₁₀^b1 addiert bzw. abzieht, so dass die oben geforderten Bedingungen erfüllt sind.

Dazu zählt mand^a₁ von 0aus so lange hoch bis gilt:

a₀+ ^d₁₀^a12

<2<

a₀+^da1₁₀⁺¹2

Dies ist gerade für d^a₁ = 4 der Fall. Man wähle dann d^b₁ = 9−d^a₁, womit sich ergibt:

b₁−a₁ = 1,5−1,4 = 0,1 = 10⁻¹, a²₁ = 1,96<2<2,25 =b²₁.

Dieses Vorgehen lässt sich beliebig lang fortführen. In den ersten 10 Schritten erhält man so die folgenden Werte für a_n und b_n:

n a_n b_n

0: 1 2

1: 1,4 1,5

2: 1,41 1,42

3: 1,414 1,415

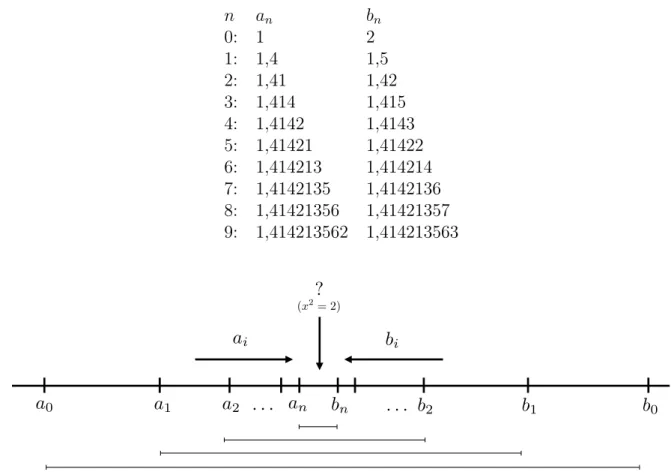
4: 1,4142 1,4143 5: 1,41421 1,41422 6: 1,414213 1,414214 7: 1,4142135 1,4142136 8: 1,41421356 1,41421357 9: 1,414213562 1,414213563

a0 a1 a2 b2 b1 b0

bi

ai

?

(x²= 2)

. . . an bn . . .

Abbildung 2.3: Approximation der Lösung von x² = 2 durch zwei Folgen.

Nach Konstruktion liegen folglich die Zahlenanstets unterhalb, die Zahlenbnstets über- halb der gesuchten Lösung. Zusätzlich jedoch verringert sich der Abstand zwischen den

2.3 Der Körper der reellen Zahlen R Zahlen immer mehr, so dass für dasn-te Folgenglied beider Folgen gilt, dass der Abstand zur tatsächlichen Lösung kleiner10⁻ⁿist, die Lösung also immer besser angenähert (ap- proximiert) wird. Die Lösung der Gleichung x² = 2 lässt sich also über Folgen beliebig genau eingrenzen. Man ist deshalb bestrebt den Zahlenraum um die Grenzwerte dieser Folgen zu erweitern.

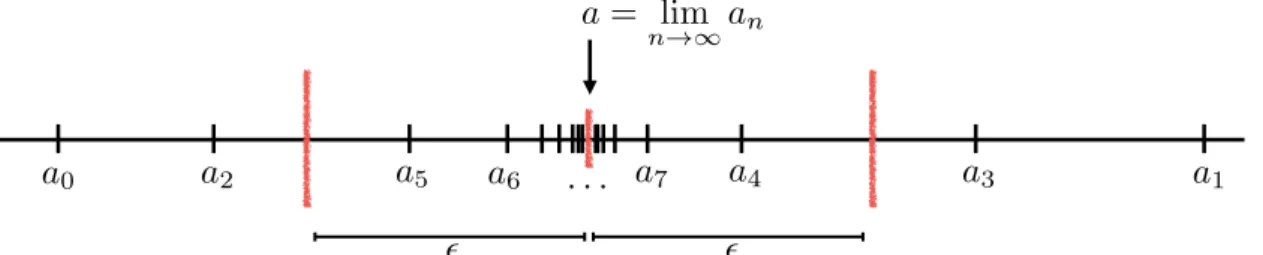
Mit dem Grenzwert a zur Folge (an)_n∈N = (a0, a1, a2, . . .) ist dabei derjenige Wert ge- meint, dem die Folgenglieder mit fortschreitendemnimmer näher kommen. Der Abstand zwischen den Folgengliedernanund dem Grenzwertawird also immer kleiner. Dies wird durch das folgende Kriterium formalisiert.

Definition 2.15 (Cauchy Konvergenzkriterium)

Eine Folge (a_n)_n∈N heißt konvergent gegen einen Grenzwert (Limes)a, falls es zu jedem (beliebig kleinen) >0ein n ∈N gibt, so dass gilt:

|a_n−a|< für n≥n. Dies wird notiert als

|an−a| →0 (n→0) oder lim

n→∞an =a.

Man beachte dabei, dass das zu wählende n vom gewählten abhängt. Im Allgemeinen wird man n desto größer wählen müssen je kleiner man wählt.

a0 a2 a5 a6 . . . a7 a4 a3 a1

✏

✏

a= lim

n!1an

Abbildung 2.4: Illustration des Konvergenzkriterium für die Folge (an)n∈N mit a = limn→∞an. Für jedes > 0 liegen die Folgenglieder ab einem n ∈ N alle höchstens vom Grenzwert a entfernt.

Problematisch ist diese Definition, wenn der Grenzwert einer Folge nicht im gleichen Raum wie die Folgenglieder selbst liegen. Dies ist aber gerade bei der oben konstruierten Folge in Q der Fall, da der Grenzwert√

2 selbst nicht in Q liegt.

Dies lässt sich umgehen, indem man die Konvergenz einer Folge ausdrückt, ohne den Grenzwert explizit zu verwenden:

Definition 2.16 (Cauchy-Folge)

Eine Folge (an)n∈N heißt Cauchy-Folge, wenn es zu jedem (beliebig kleinen) > 0 eine natürliche Zahl n ∈N gibt, so dass gilt:

|an−am|< für alle n, m≥n.

Anschaulich bedeutet dies, dass sich die Folgenglieder einer Cauchy-Folge ab einer ge- wissen Stelle nicht mehr als einen vorgegebenen Abstand voneinander unterscheiden und dass dieser Abstand beliebig klein gewählt werden kann.

Analog zur Konstruktion der ganzen und rationalen Zahlen wird zur Konstruktion der reellen Zahlen eine Äquivalenzrelation verwendet. Für die Menge der Cauchy-Folgen in den rationalen Zahlen ist durch

(an)n∈N∼(a⁰n)n∈N:⇔ |an−a⁰n| →0 (n→ ∞)

eine Äquivalenzrelation gegeben. Die reellen Zahlen lassen sich dann als Menge der Äquivalenzklassen bezüglich dieser Relation auffassen:

R:={[(a_n)_n∈N]|(a_n)_n∈N ist Cauchy-Folge in Q}.

Die rationalen Zahlen lassen sich in die Menge der reellen Zahlen in natürlicher Weise einbetten, indem man diese als konstante Cauchy-Folgen auffasst:

Für a∈Q: (an)n∈N mit an=a für alle n

Identifiziert man jede Äquivalenzklasse von Cauchy-Folgen mit dem gemeinsamen Grenz- wert der jeweils enthaltenen Folgen, so wird die Idee hinter der Konstruktion der reellen Zahlen als Menge aller Grenzwerte von Cauchy-Folgen in Qklarer.

Der folgende Satz hilft dabei eine konkretere Vorstellung der reellen Zahlen zu entwickeln:

Satz 2.17

Jeder Äquivalenzklasse [(an)n∈N]∈R entspricht genau ein (gegebenenfalls unendlicher) Dezimalbruch.

a:={±(a₀, d₁d₂d₃...)|a₀ ∈N, d_k ∈ {0,1, ...,9} ∀k >0}.

Umgekehrt entspricht jedem solchen Dezimalbruch genau eine Äquivalenzklasse in R.

R lässt sich dementsprechend auch als Menge von (gegebenenfalls unendlichen) Dezi- malbrüchen auffassen.

Beweis. (Skizze) Fasst man einen unendlichen Dezimalbruch als Folge von endlichen Dezimalbrüchen auf, so lässt sich zeigen, dass es sich dabei um eine Cauchy-Folge han- delt. Damit repräsentiert der Dezimalbruch ein Element aus R. Schließt man Periode 9 bei der Dezimalbruchdarstellung aus, so lässt sich auch zeigen, dass zwei unterschiedliche Dezimalbrüche niemals zur gleichen Äquivalenzklasse gehören können.

Umgekehrt lässt sich über das Prinzip der Intervallschachtelung zeigen, dass sich zu jeder Äquivalenzklassea= [(an)n∈N]∈Rein (gegebenenfalls unendlicher) Dezimalbruch finden lässt, der eben zu dieser Äquivalenzklasse gehört.

Die beiden Darstellungen sind damit äquivalent.

2.3 Der Körper der reellen Zahlen R

Übertragung der Eigenschaften von Q auf R

Die wesentlichen Eigenschaften von Q übertragen sich auf die reellen Zahlen R.

Von der Anordnung von Q ausgehend lassen sich auch auf R Ordnungsrelationen de- finieren. Dazu werden die zu Zahlen den a, b ∈ R zugehörigen Äquivalenzklassen von Cauchy-Folgen (an)n∈N, (bn)n∈N inQ betrachtet. Für alle

a := [(an)n∈N)]∈R, an∈Q∀n∈N b := [(b_n)_n∈N)]∈R, b_n∈Q∀n∈N

definiert man

a > b :⇔ ∃N ∈N: (a_n−b_n)>0 ∀n > N.

und entsprechend

a≥b :⇔ a > b oder a=b, a < b :⇔ b > a,

a≤b :⇔ b ≥a.

Analog zu Q sei dann auch aufR die Betragsfunktion gegeben als:

| · |: R→R⁺0,

|a|:=







a, a >0,

0, a= 0,

−a, a <0.

In analoger Weise sollen die elementaren Rechenoperationen von Q auf R übertragen werden. Dazu ist der folgende Hilfssatz wichtig.

Satz 2.18

Seien (an)n∈N und (bn)n∈N Cauchy-Folgen mit Grenzwerten

nlim→∞an=a und lim

n→∞bn =b.

Dann gilt (i) lim

n→∞{an+bn}=a+b, (ii) lim

n→∞{an·bn}=a·b, (iii) lim

n→∞{^a_bⁿ_n}= ^a_b, falls alle|bn| ≥α >0 und |b| 6= 0 echt positiv sind.

Beweis. Der technische Beweis wird ausgelassen.

Somit lassen sich die arithmetischen Operationen von Q auf R übertragen und man erhält das folgende Resultat.

Satz 2.19

R mit Addition und Multiplikation bildet den Körper (R,+,·).

Beweis. Die arihtmetischen Grundoperationen + und · übertragen sich direkt von Q auf R und somit sind Assoziativität und Kommutativität sowie das Distributivgesetz direkt erfüllt. Es verbleibt zu zeigen, dass die Lösungen von linearen Gleichungen exis- tieren. Sei dazu die Gleichung a+x = b mit a, b ∈ R gegeben. Die Lösung x = b−a ist folglich die Differenz zweier Cauchy-Folgen und durch eine Cauchy-Folge rationaler Zahlen approximierbar. Analog zeigt man die Lösung der Gleichunga·x=b, a6= 0.

Satz 2.20

Qliegt dicht in R, d.h. zu jedema∈Rund zu jedem >0existiert q∈Q: |a−q|< . Beweis. Nach Konstruktion von R existiert zu jedem a ∈ R eine gegen a konvergente

Cauchy-Folge (an)_n∈N inQ.

Bei den rationalen ZahlenQwurde festgestellt, dass gewisseLöcher existieren, die durch den ZahlenraumQnicht darstellbar waren. Zum Beispiel war die approximierende Folge der Lösung der Gleichung x² = 2zwar konvergent, allerdings lag der Grenzwert x=√

2 nicht inQ. Für den Körper R gilt hingegen nun folgendes Resultat.

Satz 2.21

R istvollständig, d.h. jede Cauchy-Folge in R konvergiert gegen einen Grenzwert in R. Beweis. Sei eine Cauchy-Folge (a_n)_n∈N mit Folgengliederna_n∈ R reeller Zahlen gege- ben. Nun ist zu zeigen, dass der Grenzwert dieser Folge ebenfalls in R liegt (d.h. durch eine Cauchy-Folge mit Folgenglieder in Qapproximierbar ist). Zu jedem der Folgenglie- der (die inR liegen) sei daher zunächst die approximierende Folge inQgegeben, d.h. es sei das n-te Folgenglied dargestellt durch

R3an = lim

m→∞an,m, an,m ∈Q für alle m∈N.

Da dies eine Cauchy-Folge ist, lässt sich für jedes Folgengliedaneine Schrankeknwählen, ab der die Approximation durch die Folge rationaler Zahlen so gut ist, dass gilt

|an−an,kn|< 1

n mit kn ∈N. Dies erzeugt einen neue Folge (a_n,kn)_n∈N:

2.4 Mächtigkeit von Mengen und Abzählbarkeit

2.4 Mächtigkeit von Mengen und Abzählbarkeit Da dies eine Cauchy-Folge ist, lässt sich für jedes Folgenglied a

eine Schranke k

wählen, ab der die Approximation durch die Folge rationaler Zahlen so gut ist, dass gilt

| a

a

| < 1

n mit k

2 N . Dies erzeugt einen neue Folge (a

)

:

a

a

a

a

a

. . . ! a

2 R a

a

a

a

a

. . . ! a

2 R a

a

a

a

a

. . . ! a

2 R

... . . . ! ...

a

a

a

. . . a

. . . ! a

2 R

#

n

lim

a

= a = lim

n!1

a

Die Folge (a

)

ist nun wiederum eine Cauchy-Folge (mit Folgengliedern in Q ) und hat denselben Grenzwert wie die Folge (a

)

. Dies sieht man folgendermaßen: Sei ✏ > 0 beliebig vorgegeben, so findet man ein n

2 N , so dass für alle n, m n

gilt

| a

a

| < 1

3 ✏, | a

a

| < 1 3 ✏, und somit gilt auch

| a

a

|  | a

a

| + | a

a

| + | a

a

|

 1 3 ✏ + 1

3 ✏ + 1

3 ✏ = ✏.

Sei nun

a = lim

n!1

a

der Grenzwert dieser Folge von rationalen Zahlen - der gemäß Definition in R liegt.

Dieser Grenzwert stimmt nun aber auch mit dem Grenzwert der Folge (a

)

überein, denn es gilt

| a

a |  | a

a

| + | a

a |  1

n + | a

a | ! 0 (n ! 1 ).

Dies zeigt: der Grenzwert der Cauchy-Folge (a

)

ist durch die Cauchy-Folge (a

)

von rationalen Zahlen approximierbar und somit auch in R . ⇤

2.4 Mächtigkeit von Mengen und Abzählbarkeit

Es lässt sich die Frage stellen, welche der Mengen Q und R mehr Elemente besitzt oder ob sie gleich viele Elemente haben. Dazu benötigt man zunächst eine Definition, die die Anzahl an Elementen in einer Menge greifbar macht.

Die Folge (an,kn)n∈N ist nun wiederum eine Cauchy-Folge (mit Folgengliedern in Q) und hat denselben Grenzwert wie die Folge(an)n∈N. Dies sieht man folgendermaßen: Sei >0 beliebig vorgegeben, so findet man ein n ∈N, so dass für alle n, m≥n gilt

|an−am|< 1

3, |an−an,kn|< 1 3, und somit gilt auch

|an,kn−am,km| ≤ |an,kn−an|+|an−am|+|am−am,km|

≤ 1 3+ 1

3+ 1 3=. Sei nun

a= lim

n→∞an,kn

der Grenzwert dieser Folge von rationalen Zahlen. Dieser Grenzwert stimmt nun aber auch mit dem Grenzwert der Folge (an)n∈N überein, denn es gilt

|an−a| ≤ |an−an,kn|+|an,kn−a| ≤ 1

n +|an,kn −a| →0 (n→ ∞).

Dies zeigt: der Grenzwert der Cauchy-Folge(an)n∈Nist durch die Cauchy-Folge(an,kn)n∈N

von rationalen Zahlen approximierbar und somit auch in R.

2.4 Mächtigkeit von Mengen und Abzählbarkeit

Es lässt sich die Frage stellen, welche der Mengen Q und Rmehr Elemente besitzt oder ob siegleich viele Elemente haben. Dazu benötigt man zunächst eine Definition, die die Anzahl an Elementen in einer Menge greifbar macht und speziell die Anzahl bei Mengen mit unendlich vielen Elementen (z.B. N,Z,Q,R) differenzierter auffassen lässt.