Mathematische Methoden der Physik, ¨ Ubung 15
Prof. Hans Peter B¨ uchler WS 14/15, 4 Februar 2015
1. ∇ und ∆ in Kugel- und Zylinderkoordinaten ( ¨ Ubungsstunde)
(a) Folgende Funktionen sind in Zylinderkoordinaten (r, ϕ, z) gegeben. Berechne jeweils den Gradienten ∇f und ∆f in Zylinderkoordinaten.
f 1 = ar 2 + bz 2 , f 2 = a
r , f 3 = cos ϕ r
(b) Folgende Funktionen sind in Kugelkoordinaten (r, ϕ, ϑ) gegeben. Berechne jeweils den Gradienten ∇f und ∆f in Kugelkoordinaten.
f 5 = a
r , f 6 = a e −br
r , f 7 = z
r 3 = cos ϑ r 2
2. Divergenz und Rotation in krummlinigen Koordinaten ( ¨ Ubungsstunde) In der Vorlesung wurde behandelt, wie Differentialoperatoren in krummlinige Koor- dinaten transformiert werden k¨ onnen sowie die Transformationsregeln f¨ ur Zylinder- und Kugelkoordinaten.
Bestimme die Differentialoperatoren f¨ ur die Divergenz und Rotation in Kugelkoor- dinaten.
3. Semiparabolische Koordinaten ( ¨ Ubungstunde)
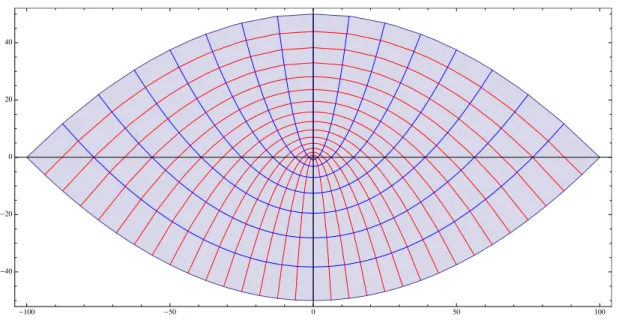
Wir betrachten in dieser Aufgabe als weiteres Beispiel f¨ ur ein Koordinatensystem die semiparabolischen Koordinaten (u 1 , u 2 , u 3 ) = (µ, ν, ϕ). Ihre Umrechnung in kartesische Koordinaten lautet:
x = µν cos ϕ, (1)
y = µν sin ϕ, (2)
z = 1
2 (µ 2 − ν 2 ). (3)
Dabei gilt µ ≥ 0 und ν ≥ 0.
(a) Berechne die Vektoren v i = ∂u ∂r
i
, ihre Betr¨ age h i = |v i | sowie die Basisvektoren e i = v i /h i .
(b) Bestimme den Gradienten in semiparabolischen Koordinaten und zeige, dass sich der Laplace-Operator in der Form
∆f = 1
µ 2 + ν 2 ∂ 2
∂µ 2 + 1 µ
∂
∂µ + ∂ 2
∂ν 2 + 1 ν
∂
∂ν + 1
µ 2 + 1 ν 2
∂ 2
∂ϕ 2
f (4)
darstellen l¨ asst.
-100 -50 0 50 100 -40
-20 0 20 40