Thermodynamik Serie 1 - Musterl¨ osung

(1)

Thermodynamik Serie 1 - Musterl¨ osung

HS 2020 Prof. P. Jetzer

M. Haney, S. Tiwari, M. Ebersold

https://www.physik.uzh.ch/de/lehre/PHY341/

Ausgeteilt am: 22.09.20 Abzugeben bis: 29.09.20

1. Reversible elektrische Zelle a)

F¨ ur die elektrische Zelle gilt p → E , V → e, i.e. der erste Hauptsatz ergibt sich zu

dU = δQ + δA = T dS − E de . (1)

Wir gehen ¨ uber zu den Variablen T und e, also schreiben dS = ∂S

∂T

e

dT + ∂S

∂e

T

de . (2) Wir erhalten:

dU = T ∂S

∂T

e

dT +

T ∂S

∂e

T

− E

de

= ∂U

∂T

e

dT + ∂U

∂e

T

de , (3) wobei sich die zweite Zeile per Definition ergibt. Da es sich bei dU um ein totales Differential handelt, muss nach dem Satz von Schwarz gelten:

∂

∂e

T ∂S

∂T

e

= ∂

∂T

T ∂S

∂e

T

− E

. (4)

Daraus erhalten wir

∂S

∂e

T

= ∂E

∂T

e

, (5) eine der sogenannten Maxwell-Relationen. Einsetzen ergibt

dU = T ∂S

∂T

_e

dT +

T ∂E

∂T

_e

− E

de . (6)

Im Vergleich mit Formel 3 sehen wir nun, dass

∂U

∂e

T

= T ∂E

∂T

e

− E . (7)

Diese Formel setzt die kalorische Zustandsgleichung U = U (T, e) mit der thermischen E = E(T, e) in Beziehung.

1

(2)

b)

Wir haben T = const. Es gilt f¨ ur die zugef¨ uhrte W¨ arme δQ = dU − δA. Also δQ = ∂U

∂e

T

de + ∂U

∂T

e

dT

| {z }

=0, da isotherm

+Ede (8)

=

∂U

∂e

T

| {z }

=T ^∂E_∂T e

−E

+E

de = T ∂E

∂T

e

de . (9)

Daraus folgt

∆Q = T Z

e1

e0

∂E

∂T

e

de . (10)

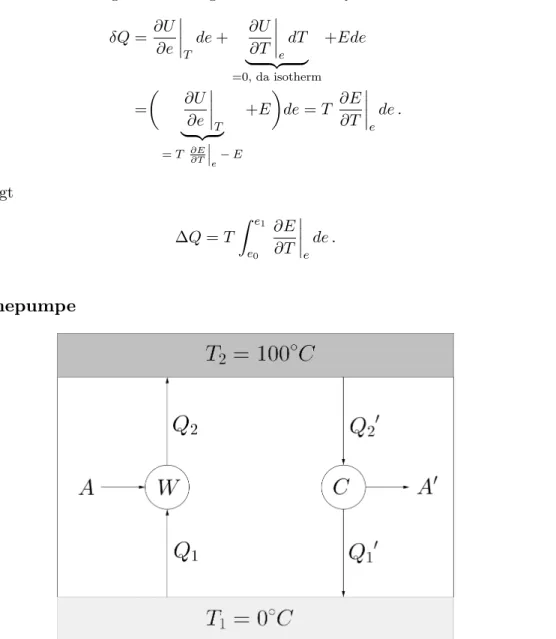
2. W¨ armepumpe

Abbildung 1: Schematische Darstellung einer Carnot-Maschine.

Betrachte eine Carnot-Maschine zwischen zwei W¨ armereservoirs der Temperatur T

₁

= 0

^◦

C und T

2

= 100

^◦

C um eine untere Grenze f¨ ur A zu finden. Wir haben Q

1

= 1cal und Q

2

= Q

₁

+ A. Gem¨ ass dem 2. HS gilt A A

⁰

. F¨ ur einen Carnot-Prozess gilt η

_C

=

_Q^A⁰

2

≤

_Q^A

2

. Also A

Q

2

≥ A

⁰

Q

2

= 1 − T

1

T

2

. (11)

Daraus finden wir

A ≥Q

₂

1 − T

1

T

₂

= (Q

1

+ A)

1 − T

1

T

₂

. (12)

2

(3)

Aufl¨ osen nach A ergibt

A ≥ Q

₁

T

₂

− T

₁

T

₁

= 1 cal 100 K

273.15 K = 0.37 cal = 1.53 J . (13) 3. Exaktes Differential

Das Differential ist nicht exakt, z.B. haben wir

∂

∂x

₃

(x

1

x

3

) 6= ∂

∂x

₁

(x

3

x

1

) . (14)

4. Rechenregeln f¨ ur partielle Ableitungen

Durch die Bedingung f (x, y, z) = 0 wird die Anzahl Freiheitsgrade um eins reduziert und das Problem h¨ angt nur noch von zwei unabh¨ angigen Variablen ab. Wir k¨ onnen nun jede Variable als Funktion der anderen beiden Variablen schreiben, da diese durch f (x, y, z) = 0 verkn¨ upft sind, also x = x(y, z ), y = y(x, z) und z = z(x, y). F¨ ur das totale Differential von x = x(y, z ) finden wir

dx = ∂x

∂y

z

dy + ∂x

∂z

y

dz, (15) das totale Differential von y = y(x, z) ergibt sich zu

dy = ∂y

∂x

z

dx + ∂y

∂z

x