Thermodynamik Serie 4 - Musterl¨ osung

Thermodynamik Serie 4 - Musterl¨ osung

HS 2020 Prof. P. Jetzer

M. Haney, S. Tiwari, M. Ebersold

https://www.physik.uzh.ch/de/lehre/PHY341/

Ausgeteilt am: 13.10.20 Abzugeben bis: 20.10.20

1. Van-der-Waals Gas

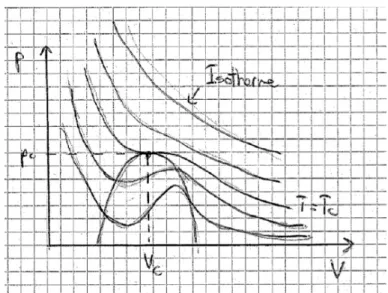
Abbildung 1: pV-Diagramm f¨ ur das Van-der-Waals Gas.

a) Am kritischen Punkt p _c , V _c , T _c hat die Isotherme p(V ) einen Wendepunkt. Es gilt also:

∂p

∂V V

,T

= ∂ ² p

∂V ² V

,T

= 0 . (1)

Wir haben somit die folgenden 3 Gleichungen:

i) p c = nRT c

V c − nb − an ²

V _c ² (van-der-Waals-Gleichung) (2) ii) − nRT c

(V c − nb) ² + 2an ²

V _c ³ = 0 (1. Ableitung) (3)

iii) 2nRT c

(V c − nb) ³ − 6an ²

V _c ⁴ = 0 (2. Ableitung) (4)

Setze ii) in iii) ein:

1

2 (V _c − nb) = V _c

3 ⇒ V _c = 3nb . (5)

Ersetze V c in Gleichung ii):

2an ²

27n ³ b ³ = nRT c

4n ² b ² ⇒ T c = 8a

27Rb . (6)

Dann lautet die Van-der-Waals-Gleichung:

p c = n 2nb

8a

27b − an ²

9n ² b ² ⇒ p c = a

27b ² . (7)

b) Die Umkehrung ist trivial, wir finden sofort b = V c

3n , (8)

a = 27

8 bRT _c = 9 8

V _c RT _c

n . (9)

c) Schreibe p = πp _c , V = vV _c , T = tT _c und dr¨ ucke in der Van-der-Waals-Gleichung p _c , V _c und T c durch a und b aus:

π a

27b ² + 1 v ²

an ² 9n ² b ²

(3nbv − nb) = 8ant

27b , (10)

an b

π 27 + 1

9v ²

(3v − 1) = 8ant

27b , (11)

und wir erhalten

π + 3

v ²

(3v − 1) = 8t . (12)

Das ist das sogenannte “Gesetz der korrespondierenden Zust¨ ande”, das heute auch uni- verselles Gasgesetz genannt wird. Dabei ist es bemerkenswert, dass die Kenntnis des kritischen Punktes allein gen¨ ugt, das Verhalten des Gases vollst¨ andig zu beschreiben.

Zwei Gase, die dieselben Werte von π, v, t haben (obwohl i. Allg. verschiedene p, V , T ), werden “im korrespondierenden Zustand”genannt.

d) Gegeben sind die Definitionen von κ _T und α:

κ _T = − 1 V

∂V

∂p T

, α = 1 V

∂V

∂T p

. (13)

Man k¨ onnte nun die Van-der-Waals Gleichung als Funktion des Volumens umschreiben.

Es ist jedoch einfacher, die Definitionen umzuformen zu κ T = − 1

V ∂p

∂V T

−1

, α = 1 V

∂T

∂V p

! −1

. (14)

und entsprechend

∂p

∂V T ,n

= − nRT

(V − nb) ² + 2an ²

V ³ = 2an ² (V − nb) ² − nRT V ³

V ³ (V − nb) ² . (16) Durch Substitution von _∂V ^∂p

_{T ,n} im Ausdruck f¨ ur κ _T bekommt man κ _T =

nRT V

(V − nb) ² − 2an ² V ²

−1

. (17)

Die van-der-Waals Gleichung als Funktion der Temperatur ist gegeben durch T(p, V ) =

p + an ² V ²

V − nb

nR , (18)

und dementsprechend

∂T

∂V p,n

= − 2an ² V ³

V − nb nR

+ V ² p + an ²

nRV ² = · · · = T V ³ − (2an/R)(V − nb) ²

V ³ (V − nb) . (19) Durch Substitution von _∂V ^∂T

p,n im Ausdruck f¨ ur α erh¨ alt man α = V ² (V − nb)

T V ³ − (2an/R)(V − nb) ² . (20)

e) F¨ ur ein ideales Gas gilt a = b = 0, dadurch reduziert sich der Ausdruck f¨ ur κ _T zu:

κ T , ideal gas = V

nRT = 1/p . (21)

Der Ausdruck f¨ ur α reduziert sich zu:

α _{ideal gas} = 1/T . (22)

f) κ _T kann f¨ ur ein van-der-Waals Gas auch negativ sein, siehe als Beispiel in Abb. 1 die unterste Kurve. Bei ansteigendem Volumen gibt es also einen Bereich in welchem auch der Druck zunimmt, wir erwarten aber einen Druckabfall, es handelt sich also um einen unphysikalischen Bereich. Zudem gibt es zu einem gegebenen Druck unterhalb p _c eine dreifache Entartung, also verschiedene L¨ osungen f¨ ur das Volumen, die Forderung nach einem stabilen System ist also verletzt. Wir werden sehen das in diesem unphysikalischen Bereich ein Phasen¨ ubergang stattfindet.

α kann tats¨ achlich negativ sein, zum Beispiel f¨ ur Wasser zwischen 0 ^◦ C und 4 ^◦ C (An-

omalie des Wassers).

2. Die thermodynamischen Potentiale des idealen Gases

Den Ausdruck f¨ ur die innere Energie erhalten wir durch Aufl¨ osen der Gleichung f¨ ur die Entro- pie (auf dem Aufgabenblatt) nach u

u = u 0

v v ₀

−

cv

e

s−s0

cv

. (23)

Die Legendre Transformation von u(s, v) in der Variablen s l¨ asst uns zur Helmholtzschen freien Energie f (T, v) ¨ ubergehen, d.h.

f (T, v) = u(T, v) − T s(T, v) , (24)

mit

T (s, v) = ∂u

∂s v

= u ₀ c v

v v 0

−

e

s−s0

cv

, (25)

wobei Gleichung (23) benutzt wurde. Der Wert T 0 ist definiert via T ₀ = T (s ₀ , V ₀ ) = u ₀

c _v . (26)

In den neuen Variabeln v und T haben die Zustandsfunktionen s und u die Form s = c _v log T

T 0

+ R log v v 0

+ s ₀ , (27)

u = u 0

v v ₀

−

cv

e ^{log(T /T}

^)+(R/c

^{) log(v/v}

⁾ = c v T . (28) Somit finden wir f¨ ur f den Ausdruck

f (T, v) = c _v T − c _v T log T

T ₀ − RT log v

v ₀ − T s ₀ . (29)

Einsetzen von T ₀ und v ₀ in Gleichung (29) definiert den Referenzwert f ₀ = f (T ₀ , v ₀ ) = u ₀ − T ₀ s ₀ , so dass gilt

f (T, v) = f 0 + (c v − s 0 ) (T − T 0 ) − T c v log T T 0

− RT log v v 0

. (30)

Eine analoge Vorgehensweise liefert uns die Gibbsche freie Energie als Legendre Transforma- tion von f (T, v) in der Variablen p. Mit Gleichung (30) finden wir

g(T, p) = f (T, p) + pv(T, p) , (31)

mit

Fassen wir f im Ausdruck (30) als Funktion der neuen Variablen T und p auf, folgt sofort

g(T, p) = f (T, p) + pv(T, p) (33)

= f 0 + (c v − s 0 ) (T − T 0 ) − T c v log T

T ₀ − RT log p 0 T

pT ₀ + RT (34)

= f 0 + (c v − s 0 ) (T − T 0 ) − T (c v + R

| {z }

c

) log T T 0

+ RT log p p 0

+ RT . (35)

Den Referenzwert g 0 = f 0 + RT 0 finden wir wiederum durch Auswerten von (33) am Refe- renzpunkt (T ₀ , p ₀ ). Die Gibbsche freie Energie f¨ ur das ideale Gas schreibt sich also

g(T, p) = g ₀ + (c _p − s ₀ ) (T − T ₀ ) − T c _p log T T 0

+ RT log p p 0

. (36)