Thermodynamik Serie 3 - Musterl¨ osung

Thermodynamik Serie 3 - Musterl¨ osung

HS 2020 Prof. P. Jetzer

M. Haney, S. Tiwari, M. Ebersold

https://www.physik.uzh.ch/de/lehre/PHY341/

Ausgeteilt am: 06.10.20 Abzugeben bis: 13.10.20

1. Carnot-Kreisprozess a)

p

v v4

1

2

4

v2

Adiabate

3

v1 v3

Isotherme

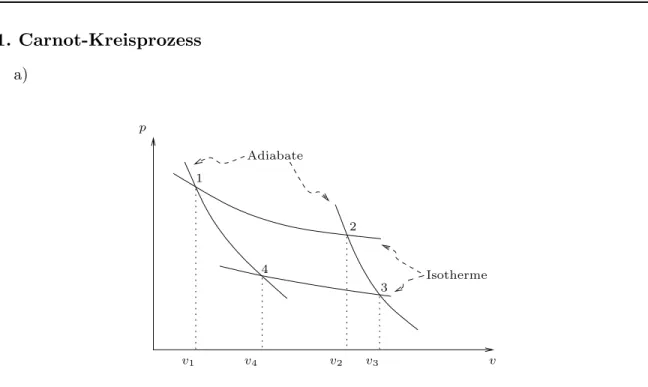
Abbildung 1: Folgende Schritte werden im Carnot-Prozess durchlaufen. Die Verwendung von Molvolumina, v_i = V_i/n, ist hier angebracht. Dadurch l¨asst sich die ideale Gasgleichung schreiben alspv=RT.

1→2 W¨ahrend der isothermen Expansion von (T1 =ϑ₁, v₁) nach (T₂ =ϑ₁, v₂) wird die Arbeit

∆a12=− Z v2

v1

pdv=−Rϑ1

Z v2

v1

dv

v =−Rϑ1logv2

v₁

nach Innen geleistet (negativ, darum positiv nach Aussen). Aus der Volumenun- abh¨angigkeit der inneren Energie des idealen Gases,

0≡ Z ₂

1

du= Z ₂

1

δq− Z _v2

v1

pdv= ∆q₁₂+ ∆a₁₂.

folgt sofort, dass der Carnot-Maschine w¨ahrend der isothermen Expansion die W¨armemenge ∆q12=−∆a12 zugef¨uhrt wird.

Bemerkung: du = δq +δa, d.h. das System leistet Arbeit falls δa < 0 (es wird Arbeit am System geleistet falls δa >0).

2→3 Da auf der Adiabaten von (T2 =ϑ1, v2) nach (T3 =ϑ2, v3) kein W¨armeaustausch stattfindet, ∆q₂₃ = 0, wird die Arbeit δa = −pdv = du = c_vdT nach Innen geleistet. Deshalb finden wir sofort

∆a23= Z 3

2

cvdT =cv(T3−T2) =−cv(ϑ1−ϑ2).

Da ϑ₁ > ϑ₂, ist ∆a₂₃ negativ und so ist die Arbeit nach Aussen abgegeben.

3→4 W¨ahrend der isothermen Kompression von (T3 =ϑ₂, v₃) nach (T₄ =ϑ₂, v₄), leistet das System die Arbeit

∆a34=Rϑ2logv₃ v4

,

wodurch effektiv Arbeit dem System zugef¨uhrt werden muss. Gleichzeitig wird die W¨armemenge ∆q34 = −∆a34 < 0 aufgenommen, was also einer W¨armeabgabe

|∆q₃₄|entspricht.

4→1 Die w¨ahrend der adiabatischen Kompression von (T4 =ϑ₂, V₄) nach (T₁ =ϑ₁, v₁) geleistete Arbeit (nach Innen) ist

∆a₄₁=c_v(ϑ₁−ϑ₂), wobei kein W¨armeaustausch stattfindet, ∆q41= 0.

Damit ist der Anfangszustand wieder erreicht. Die bei einem Umlauf am System gelei- stete Arbeita ist

a= ∆a₁₂+ ∆a₂₃+ ∆a₃₄+ ∆a₄₁=−Rϑ₁logv₂

v₁ −Rϑ₂logv₄ v₃. Mit Hilfe der Adiabatengleichungen

ϑ₁v^γ−1₂ =ϑ₂v₃^γ−1, (1) ϑ1v^γ−1₁ =ϑ2v₄^γ−1, (2) erhalten wir v₂/v₁ =v₃/v₄ und finden somit f¨ur die totale Arbeit den Ausdruck

a=−R(ϑ1−ϑ2) logv2

v₁.

Letztere ist mitϑ1 > ϑ2undv2> v1negativ, sodass die Arbeit von der Carnot-Maschine an der Umgebung geleistet wird. Mit der eingespeisten W¨arme ∆qin= ∆q12 finden wir schliesslich f¨ur den Wirkungsgrad

η= −a

∆q_in = R(ϑ₁−ϑ₂) log^v_v²

1

Rϑ₁log^v_v²

1

= 1− ϑ2

ϑ₁.

Die W¨arme ∆q34 ist reine Abw¨arme und somit ein “Abfallprodukt” des Prozesses.

b) Sobald der Kolben das minimale Volumen erreicht hat, wird der Zylindermotor an das W¨armereservoir bei der Temperaturϑ₁ angeschlossen (siehe Abbildung 2). Die Tempe- ratur des Gases ist zu diesem Zeitpunkt ebenfalls ϑ1. Daraufhin expandiert der Kolben isotherm. An einem gewissen Punkt (siehe Teilaufgabe c)) wird das Reservoir abgeh¨angt und der Kolben expandiert adiabatisch weiter. Erreicht der Kolben die maximale Aus- dehnung (TGas=ϑ2), so wird das W¨armebadϑ2angeschlossen und der Kolben zieht sich isotherm zusammen. Schliesslich wird das Bad wieder abgeh¨angt, so dass der Kolben die urspr¨ungliche Position adiabatisch erreicht.

Abbildung 2: Schematischer Ablauf des rechtslaufenden Carnot-Prozesses. Die Pfeile stellen die Bewegungsrichtung des Kolbens dar. Die adiabatischen Abschnitte sind f¨ur diesen rever- siblen Prozess isentrop.Quelle: http://de.wikipedia.org/

c) Einem Zylindermotor, welcher den Carnot-Kreisprozess zwischen ϑ₁ und ϑ₂ realisiert, sind nat¨urliche Grenzen gesetzt. Zum einen ist das maximal zul¨assige Volumen durch die Kolbengr¨osse gegeben. Diese Bedingung liefert einen maximalen Wert f¨urv₃ =v_max. Zusammen mit ϑ₂ ist damit die Position von Punkt 3 in Abbildung 1 festgelegt.

Im Punkt 1 von Abbildung 1 ist der maximal zul¨assige Druck der limitierende Faktor (p1 = pmax). Dieser h¨angt in erster Linie vom Dichtungsring am Zylinderkolben ab.

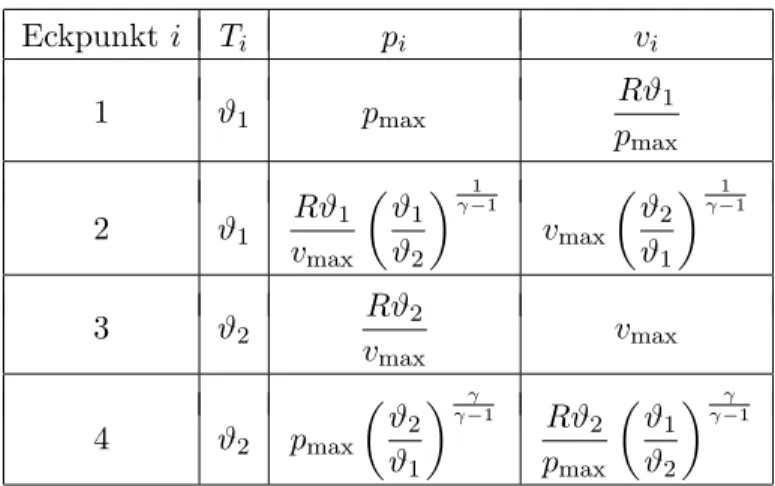
Durch die Gr¨ossen (ϑ1, ϑ₂, p_max, v_max) sind die Eckpunkte des Carnot-Kreisprozesses auf eindeutige Weise bestimmt. Nutzt man n¨amlich die Adiabatengleichungen (1) und (2) sowie die Gleichungen f¨ur die Isothermen

p1v1=p2v2 =Rϑ1, (3) p3v3=p4v4 =Rϑ2, (4) so findet man nach einigen Umformungen die genaue Position der Eckpunkte (siehe Tabelle 1).

Eckpunkti T_i p_i v_i

1 ϑ₁ p_max Rϑ₁

pmax

2 ϑ1

Rϑ1

vmax

ϑ1

ϑ2

_γ−1¹

vmax

ϑ2

ϑ1

_γ−1¹

3 ϑ₂ Rϑ₂

v_max v_max

4 ϑ2 pmax

ϑ2

ϑ1

_γ−1^γ

Rϑ2

pmax

ϑ1

ϑ2

_γ−1^γ

Tabelle 1: Eckpunkte des Carnot-Prozesses als Funktion von (ϑ1,ϑ2,pmax,vmax).

2. Escher-Wyss-Kreisprozess

a) Wir berechnen nun f¨ur einen Escher-Wyss-Kreisprozess die auf den einzelnen Zyklus- abschnitten geleisteten Arbeitsmengen und die jeweils zu-/abgef¨uhrte W¨armemenge.

Adiabate Isobare 1

2

3

4

v T

ϑ1

ϑ2

Adiabate Isobare

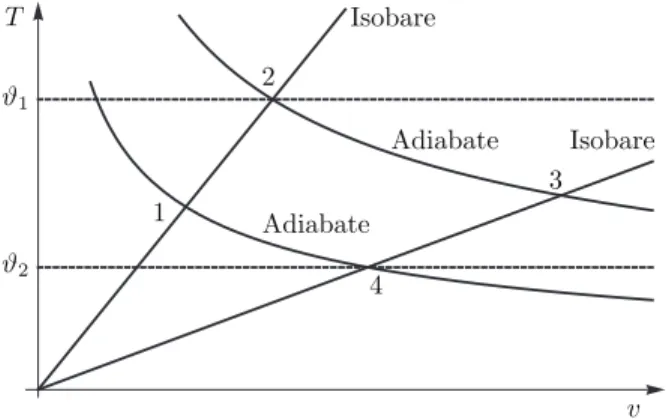
Abbildung 3: Schematische Darstellung des Escher-Wyss-Kreisprozesses. Diese Maschine wird zwischen zwei Isobaren (p= const.⇒T ∝V) und zwei adiabatischen Abschnitten betrieben.

1→2 Auf diesem Abschnitt ist der Druck konstant (p=p_A) und die Arbeit, welche am System geleistet wird, berechnet sich als

∆a12=− Z v2

v1

pAdv=−pA(v2−v1) =−R(T2−T1).

Das ist negativ, so wird Arbeit nach Aussen gemacht. Die innere Energie des idealen Gases h¨angt nur von der Temperatur ab und dessen ¨Anderung auf dem Abschnitt ist somit

∆u₁₂=c_v(T₂−T₁).

Mithilfe des ersten Hauptsatzes k¨onnen wir die dem System zugef¨uhrte W¨arme berechnen und finden

∆q₁₂= ∆u₁₂−∆a₁₂= (c_v+R)(T₂−T₁) =c_p(T₂−T₁).

2→3 Dieser Abschnitt verl¨auft adiabatisch und somit ist ∆q23= 0. Dadurch vereinfacht sich die Berechnung der zugef¨uhrten Arbeit zu

∆a₂₃= ∆u₂₃=c_v(T₃−T₂).

3→4 Wie in Abschnitt 1→2 ist der Druck konstant (p=p_B) und wir finden

∆a₃₄=− Z v4

v3

p_Bdv=−p_B(v₄−v₃) =−R(T₄−T₃), und mit dem ersten Hauptsatz

∆q₃₄= ∆u₃₄−∆a₃₄= (c_v+R)(T₄−T₃) =c_p(T₄−T₃).

4→1 Der letzte Abschnitt verl¨auft adiabatisch und somit finden wir neben ∆q41= 0,

∆a41=cv(T1−T4).

F¨ur die auf einem Kreiszyklus zugef¨uhrte Arbeit finden wir

a= ∆a12+ ∆a23+ ∆a34+ ∆a41=−cp(T2+T4−T1−T3).

Da die W¨armemenge ∆q12 die zugef¨uhrte W¨arme ins System ist, finden wir den Wir- kungsgrad als

η = −a

∆q₁₂ = cp(T2+T4−T1−T3)

c_p(T₂−T₁) = 1−T3−T4

T₂−T₁ Da entlang von Adiabaten p^1−γT^γ = const.gilt, finden wir die Relationen

p

1−γ γ

A T1 =p

1−γ γ

B T4, p

1−γ γ

A T₂ =p

1−γ γ

B T₃.

(5) Mithilfe dieser Relationen sehen wir, dass wir den Wirkungsgrad schreiben k¨onnen als

η= 1−T₄

T₁ = 1− T₃ T₂.

b) Mit den Relationen (5) l¨asst sich der Wirkungsgrad auch als Funktion der Dr¨ucke der beiden Isobaren schreiben, n¨amlich

η= 1− pB

p_A ^γ−1_γ

. (6)

Auch die Arbeit l¨asst sich als Funktion der von Aussen vorgegebenen Gr¨ossen pA,pB, ϑ₁ undϑ₂ schreiben als

a=−c_ph ϑ₁

1−p_B p_A

^γ−1_γ +ϑ₂

1−p_A p_B

^γ−1_γ i

. (7)

c) Der Kreisprozess arbeitet als Kraftmaschine f¨ur a ≤ 0. Mit a = 0 findet man den minimalen und maximalen Druck. Der maximale Druck p_B,max ist gegeben durch p_A, also p_B,max=p_A. F¨ur den minimalen Druck findet man

pB,min=pA

ϑ2

ϑ1

_γ−1^γ .

d) Den maximalen Wirkungsgrad erhalten wir offensichtlicherweise wenn der Druck pB

minimal ist, also pB =pB,min. Wenn wir dies in den Wirkungsgrad einsetzen, erhalten wir

η= 1−ϑ2

ϑ₁,

was dem Carnot-Wirkungsgrad enspricht. F¨ur diese Wahl von pB findet man nun aber, dass

a=−c_ph ϑ₁

1−ϑ₂ ϑ₁

+ϑ₂ 1−ϑ₁

ϑ₂

i= 0.

Somit arbeitet die Maschine zwar mit einem optimalen Wirkungsgrad, erzeugt aber keine Arbeit.

e) Indem wir a(ϑ1, ϑ2, pA, pB) nach pB maximieren, finden wir das optimale pB gegeben durch die Beziehung

p_B pA

=ϑ₂ ϑ1

_2(γ−1)^γ

. (8)

Indem wir dieses Ergebnis in die Ausdr¨ucke f¨ur den Wirkungsgrad (6) und die Arbeit (7) einsetzen, erhalten wir

η= 1− rϑ2

ϑ₁, a=−c_pp

ϑ₁−p ϑ₂2

.

f) Um den aus ¨okonomischer Sicht optimalen DruckpB zu bestimmen m¨ussen wir Kaa−Kq∆q12=Kaa−Kq

a η

maximieren. Indem wir durch die von pB unabh¨angige Gr¨osse cpϑ1Ka teilen, erhalten wir

(1−y)

1−ϑ2/ϑ1

y

− Kq

K_a

1−ϑ2/ϑ1

y

,

wobei wir y= (p_B/p_A)^(γ−1)/γ eingef¨uhrt haben. Dieser Ausdruck wird maximal f¨ur y=

rϑ2

ϑ1

r

1− Kq

Ka

. (9)

Aus der Beschr¨ankung der erlaubten pB-Werte erhalten wir f¨ury die Einschr¨ankung ϑ₂

ϑ1

≤y≤1.

Die rechte Ungleichung ist immer erf¨ullt f¨ur ϑ₂ < ϑ₁ und K_q < K_a. Wegen der linken Ungleichung ist die L¨osung (9) ausserhalb des erlaubten Bereiches falls

Kq

K_a >1− ϑ2

ϑ₁. Wir finden nun insgesamt

y=pB

pA

^γ−1_γ

=





 qϑ2

ϑ1

q 1−^K_K^q

a, ^K_K^q

a ≤1−^ϑ_ϑ²

1,

ϑ2

ϑ1, ^K_K^q

a >1−^ϑ_ϑ²

1, (10)

Wir erkennen, dass f¨ur K_q/K_a → 0 der ¨okonomisch optimale Arbeitsmodus f¨ur die maximale Arbeit pro Zyklus realisiert wird (Vgl. Gl. (10) f¨urKq/Ka= 0 mit (8)).

1 0 y

KAA-KQΔQ₁₂

=

=0

<1-

=1-

=1 0.4

ϑ2/ϑ1

ϑ2/ϑ1

K KQ/ A

K KQ/ A ϑ2/ϑ1

K KQ/ A ϑ2/ϑ1

K KQ/ A

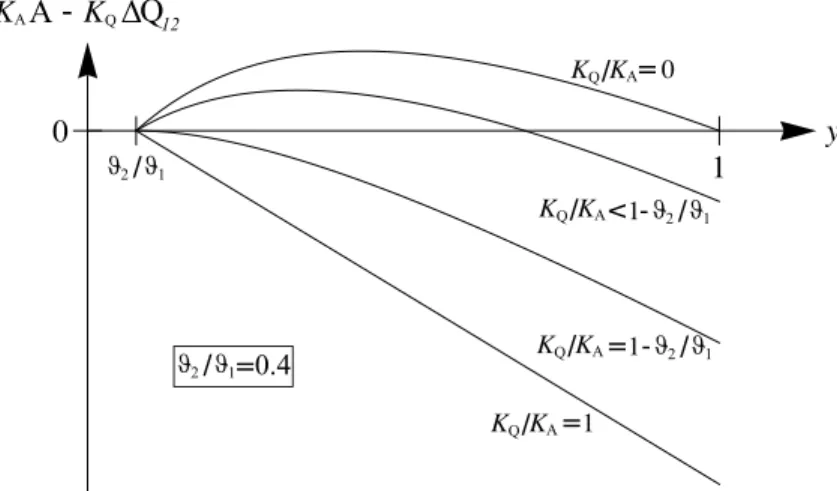
Abbildung 4: Die Gr¨osse Kaa−Kq∆q12 gilt es ¨okonomisch zu maximieren. So findet man den optimalen Druckp_B, bei dem die Escher-Wyss-Maschine betrieben werden soll. Hier wird diese Gr¨osse als Funktion von y = (pB/pA)^(γ−1)/γ f¨ur verschiedene Verh¨altnisse Kq/Ka und f¨ur ^ϑ_ϑ²

1 = 0.4 dargestellt. Nur f¨ur ^K_K^q

a ≤1−^ϑ_ϑ²

1 existiert ein Maximum>0.