Einf¨ uhrung in die Allgemeine Relativit¨ atstheorie

Dr. Oliver B¨ar WS 2009/10

Einf¨ uhrung in die Allgemeine Relativit¨ atstheorie

Ubungsblatt 3 ¨

Ubung 3.1:¨ a) F¨ur zwei VektorenU, V ∈T_p(M) kann man die sogenannte Lie-Klammer definieren durch

[U, V] := ∇_UV − ∇_VU . (1)

Offensichtlich ist [U, V] wieder ein Vektor und es gilt [U, V] = −[V, U]. Wie lauten die Komponenten [U, V]^a von [U, V]?

b) F¨ur jedes U l¨asst sich die sogenannteLie-Ableitung L_U definieren durch

L_U(V) := [U, V]. (2)

Zeigen Sie, dass diese Abbildung die Eigenschaften D1 und D2 eines Diffe- rentialoperators (→ VL) erf¨ullt, was die Bezeichnung einer Ableitung recht- fertigt. Ist f¨ur die Definition der Lie-Ableitung ein Zusammenhang n¨otig?

Ubung 3.2:¨ Gegeben sei eine Linearform ω = ω_a~e^a. Zeigen Sie, dass sich die Differenz der partiellen Ableitungen

Fab := ∂

∂x^aωb− ∂

∂x^bωa (3)

wie die Komponenten eines (0,2) Tensors transformiert. Dieser wird auch als die ¨außere Ableitung dω bezeichnet.

Ubung 3.3:¨ Autoparallele Kurven sind definiert durch die Gleichung∇_UU = 0, bzw.

d²xⁱ

dλ² + Γⁱ_jkdx^j dλ

dx^k

dλ = 0, (4)

wobei λ der Kurvenparameter ist und dxⁱ/dλ = uⁱ die Komponenten des Tangentenvektors entlang der Kurve sind.

1

a) Zeigen Sie, dass ein Parameterwechsel durch µ=f(λ) mit invertierbarem f die Gleichung (4) ¨andert zu

d²xⁱ

dµ² + Γⁱ_jkdx^j dµ

dx^k

dµ =h(µ)dxⁱ

dµ , (5)

mit

h(µ) = −d²µ dλ²

dµ dλ

2

. (6)

b) Ein Parameter wird affiner Parameter genannt wenn die Gleichung der autoparallelen Kurve die einfachere Form (4) annimmt (λ ist also ein affiner Parameter). Zeigen Sie, dass µgenau dann ein affiner Parameter ist wenn er mit λ linear zusammenh¨angt.

Ubung 3.4:¨ a) Betrachten Sie die MannigfaltigkeitR²in kartesischen Koor- dinaten. Gewinnen Sie aus den beiden Gleichungen (4) f¨urx¹ =xundx² =y eine Differentialgleichung f¨ur y(x). Zeigen Sie, dass die L¨osungen dieser Dif- ferentialgleichung durch die Geradengleichung y=mx+b gegeben ist.

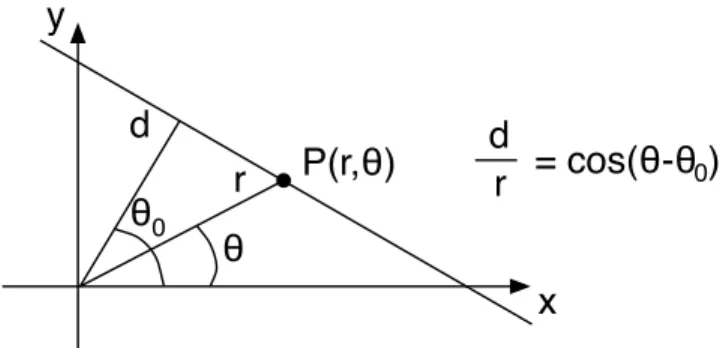
b) Betrachten Sie nun den R² in Polarkoordinaten. Gewinnen Sie aus den beiden Gleichungen (4) f¨urx¹ =r und x² =θ eine Differentialgleichung f¨ur r(θ). Zeigen Sie, dass die Geradengleichung in Polarkkoordinaten,

r(θ) = d

cos(θ−θ₀), d, θ₀ = const., (7) (siehe Abb. 1) diese Differentialgleichung l¨ost.

θ₀ θr d

P(r,θ)

x y

d

r = cos(θ-θ )₀

Abbildung 1: Geradengleichung in Polarkoordinaten

2