1 Rotation
Winkel 1.11.1.1 Bogenmaß
Das Bogenmaß eines Winkels ist die Länge des Kreisbogens mit Radius r = 1 (Einheitskreisbogen).
Gradmaß Bogenmaß
360o(Vollkreis)
180o(Halbkreis)
90o (rechter Winkel)
Tabelle 1
1.1.2 Eigenschaften des Winkels
Umrechnung
360
. 2
Vorzeichen des Winkels
(im zweidimensionalen Raum)
Der Winkel als Vektor : (Im dreidimensionalen Raum)
‚Rechte Hand Schraubenregel’
Finger Drehrichtung, Daumen Vektor
Bogenlänge s = r.
Einheit (Dimension) Da s und r beide die Einheit [m] haben, hat der Winkel im Bogenmaß keine Einheit
Gelegentlich findet statt einer Einheit den Ausdruck Rad. Dies ist aber keine echte Einheit. ist eine dimensionslose Zahl.
Beispiel 1.1
Wie groß ist der Winkel, der in der Zeit von 0h bis 2.10h a) vom Minutenzeiger b) vom Stundenzeiger ‚überstrichen’
wird? c) Welchen Weg legt die Spitze des Stundenzeigers zurück, wenn er 2m lang ist?
Lösung a:
Minutenzeiger: + 360o/ 6} = -780o = -780o / 360o = -13,61 Lösung b:
Der Stundenzeiger bewegt sich 12 Mal langsamer als der Minutenzeiger:
Lösung c:
Weg des Stundenzeigers: I s I = r I.Im]
sr
r
gegen die Uhr wie die Uhr (im Uhrzeigersinn)
r
Rotation 1.2
Die Rotation eines Massenpunktes m ist die Bewegung auf einer Kreisbahn. Unter der Rotation eines starren Körpers versteht man eine Bewegung, bei der sich alle Massepunkte auf konzentrischen
Kreisen um denselben Winkel drehen.
Dabei drehen sich alle Punkte in derselben Zeit t um denselben Winkel .
sie haben dieselbe Winkelgeschwindigkeit / t
Weiter außen liegende Punkte sind schneller als Innere Punkte, sie haben eine größere Bahngeschwindigkeit v = s / t.
1.2.1 Winkelgeschwindigkeit und Frequenz
Umlaufzeit (Periode) T [s]
Frequenz Die Frequenz f ist die Anzahl der vollen Umläufe pro Sekunde
] [ ]
s [1 1 T Hz
f ( 1 Hertz = 1 Hz = 1 Vorgang/Sekunde )
Winkelgeschwindigkeit
als Vektor: t s
1 T 2
t
Bahngeschwindigkeit v = r.als Vektor: v = r x ( s = r. v = r. / t = r.
Beispiel 1.2
Der Radius des großen Zahnrades in der Abbildung beträgt r1 = 2m, beim kleinen ist r2 = 0,8m. Das große Rad macht 3 Umdrehungen pro Sekunde.
Berechnen Sie Winkelgeschwindigkeit, Bahngeschwindigkeit und Frequenz beider Räder:
Lösung:
f1= 3 [Hz] Winkelgeschwindigkeit = f1 = 18,84 [Hz]. Bahngeschwindigkeit v1 = r1.1 = 37,68 [m/s]
Beide Räder haben dieselbe Bahngeschwindigkeit an ihrem Umfang: v1 = v2 =v2 / r2 =37,68 / 0,8 = 47,1 [Hz]
v1 = v2 r1.1 = r2.2 r12 f1 = r22 f2 f2 = r1f1 / r2 = 2 . 3 / 0,8 = 7,5 [Hz]
Beispiel 1.3
Der Sekundenzeiger einer Uhr ist genau r =1m lang. Bestimmen Sie seine Winkelgeschwindigkeit und Bahngeschwindigkeit!
Lösung:
Der Sekundenzeiger dreht sich ein Mal in 60 Sekunden: T = 60s, / T = 0,104 [Hz], v = r. = 0,104 [m/s]
Beispiel 1.4
Die Abbildung zeigt eine Anordnung von zwei Rädern zu vier
verschiedenen Zeitpunkten. Der Radius des großen Rades ist acht Mal so lang wie jener des kleinen
Rades (R =8 r.) Das große Rad dreht sich nicht. Das kleine Rad rollt am Umfang des großen Rades entlang.
a) Berechnen Sie t1, t2,, !
b) Wie viele Umdrehungen macht das kleine Rad in der Zeit
c) Die Bewegung des kleinen Rades kann man mit der Bewegung der Erde um die Sonne vergleichen: Die Zeit t1
(=Umlaufzeit der Erde) heißt dann ein Sterntag und die Zeit t2 heißt ein Sonnentag. Wie viele Sterntage und wie viele Sonnentage gibt es in unserem Beispiel?
d) Berechnen Sie die Winkelgeschwindigkeit des kleinen Rades!
Lösung a
Die Kreisbögen (Wege), die auf jedem der beiden Räder abgefahren werden sind gleich lang.
t1: Das kleine Rad hat eine volle Drehung (Bogenmaß 2)ausgeführt: sgroß=sklein2 8r.r
) t1 =
s1 s2
v1 v2
r1 r2
t = 0 t1=? t2=? t3=
tDas kleine Rad hat zum Zeitpunkt t2 eine Drehung um den Winkel 2)ausgeführt: 8r.r)
t = / 7.
Lösung b: 8 Umdrehungen (7 mal 2 : 7.( 2) = 7.( 2) = 8.2
Lösung c: 8 Sterntage, 7 Sonnentage.
Lösung d: = 2 / t1 = 16
1.2.2 Winkelbeschleunigung
Die Winkelbeschleunigung ist die Änderung der Winkelgeschwindigkeit pro Sekunde.
] [ ] s
[1
2
2 Hz
t
Beispiel 1.5
Bei einem rotierenden Rad werden zu verschiedenen Zeitpunkten folgende Drehwinkel gemessen:
Berechnen Sie die mittleren Winkelgeschwindigkeiten in den Zeitintervallen und zeigen Sie, dass die Winkelbeschleunigung konstant ist!
Lösung:
Umrechnung von Gradmaß in Bogenmaß: 5o entspricht 0,0872 [Rad]
= (t2 – t1) = 0,0872 / 0,5 = 0,1744 [Hz],
-) /t = 0,1744 / 0,5 = 0,3488 [Hz2]
= (t3 – t2) = 0,1744 /0,5 = 0,3488 [Hz],
-) /t = 0,1744 / 0,5 = 0,3488 [Hz2] = (t4 – t3) = 0,2616 / 0,5 =0,5232 [Hz]
Die Winkelbeschleunigung ist konstant.
Wir werden uns mit derartigen Aufgaben nicht weiter beschäftigen!
Aufgaben:
(1.1) Bestimmen Sie Winkelgeschwindigkeit und Bahngeschwindigkeit eines 2m langen Minutenzeigers!
(1.2) Die Räder eines Autos haben den Radius r = 40cm. Berechnen Sie Winkelgeschwindigkeit und Frequenz, wenn das Auto mit 120km/h fährt!
(1.3) Die beiden linken Zahnräder sind fest mit einander verbunden. r1 = 10m, r2 = 4m, das rechte Zahnrad, r3 = 16m greift in die Zähne des oberen linken Zahnrades.
a) Welche Räder haben dieselbe Winkelgeschwindigkeit?
b) Welche Räder haben dieselbe Bahngeschwindigkeit?
c) Rad 1 dreht sich mit der Frequenz f1. Berechnen Sie f3!
(1.4) Ein Sterntag = Umlaufzeit der Erde = 86164,091Sekunden. Wie groß ist die Bahngeschwindigkeit der Erde a) am Äquator (Radius = 6378km) und b) in Wien (geographische Breite = 48,2o) ?
c) Nehmen Sie an, ein Jahr hätte genau 365 Sonnentage. Wie viele Sterntage gibt es in einem Jahr? Wie lange würde ein solcher Sterntag dauern?
(1.5) a) Welche der drei Räder des Fahrrads haben dieselbe Bahngeschwindigkeit?
b) Welche haben dieselbe Winkelgeschwindigkeit?
c) Gegeben sei die Frequenz f3. Finden Sie einen mathematischen Ausdruck für f1! Kontrollfragen
(1.10) Bestimmen Sie das Bogenmaß folgender Winkel: 45o, 30o, 60o, 40o ! (1.12) Was versteht man unter dem Bogenmaß? Welches ist seine Einheit!
(1.13) In welchem Zusammenhang steht die Bogenlänge eines Kreisbogens mit dem Bogenmaß?
(1.14) Welches ist die Einheit der Winkelgeschwindigkeit und der Frequenz?
(1.15) Auf welchen Wegen bewegen sich die Massenpunkte eines rotierenden starren Körpers?
(1.16) Punkte eines rotierenden Körpers, die weiter ‚außen’ liegen, haben eine größere ...-geschwindigkeit (1.17) Alle Punkte eines rotierenden Körpers haben dieselbe …...-geschwindigkeit
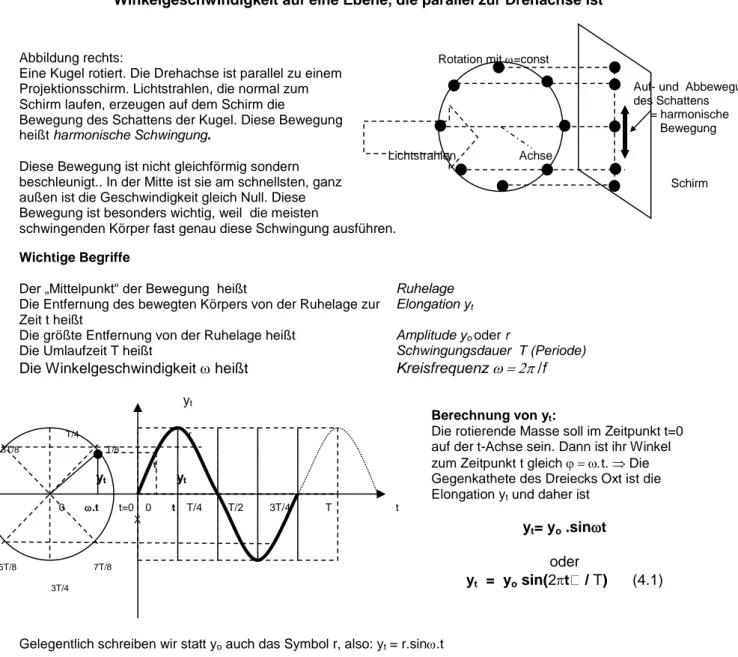
t
0
0,5
1
1,5
t3=3t t2=2t t4=4t
t1=t to=0
r1 r2 r3
Drehmoment und Trägheitsmoment 1.3
1.3.1 Wiederholung
-Kraft ist Ursache für Beschleunigung.
-Masse (Trägheit) ist Widerstand gegen Beschleunigung.
-Die resultierende Kraft ist die Vektorsumme der Einzelkräfte auf einen Körper.
-Verschwindet die Gesamtkraft, so gibt es keine Bewegung oder nur gleichförmige Bewegung.
-Übt ein Körper A auf Körper B die Kraft F aus, so übt B auf A die Kraft –F aus.
Außerdem gilt noch:
-Die Änderung des Impulses p ist gleich der Kraft mal der Wirkungszeit. p = F.t -Ohne äußere Kraft ändert sich der Impuls nicht.
Wie lauten die entsprechenden Gesetze bei der Rotation für die Winkelbeschleunigung . Welche Größen sind Ursache und Widerstand gegen Winkelbeschleunigung?
1.3.2 Drehmoment
Einige wichtige Tatsachen sind schon seit Jahrhunderten bekannt:
Hebelgesetz
Die Waage steht still (keine Rotation) wenn gilt:
Kraftarm1 mal Kraft1 Kraftarm2 mal Kraft2 r1.F1 r2.F2
Je kleiner die Masse der beide Arme im Vergleich zu m1 und m2 ist, desto genauer ist das Gesetz!
Hebelgesetz bei verschieden gerichtetem und geformtem Kraftarm
Die Waage steht wieder still (keine Rotation) wenn gilt:
Normalkraftarm1 mal Kraft1 Normalkraftarm2 mal Kraft2 r1.F1 r2.F2
Dabei ist der Kraftarm normal zur Kraft zur Kraft zu denken. Er reicht von der Achse bis zum Schnittpunkt mit der Verlängerung der Kraft.
Die Ungenauigkeit kommt wieder daher, dass die beiden Arme selbst eine Masse haben und selbst zur Kraft1 und Kraft2 auf beiden Seiten beitragen.
Um die Ursache der Winkelbeschleunigung herauszufinden, beschleunigen wir zunächst dasselbe Rad auf vier verschiedene Arten:
r r1
r r rn1 r2
rn =a rn =2a rn =2a rn2
F = X F =X F=2x F1 F2
Doppelter Normalarm Doppelter Normalarm
Doppelte Kraft rn1.F1 = rn2.F2
Winkelbeschleunigung: Winkelbeschleunigung: 2 Winkelbeschleunigung: 4 Winkelbeschleunigung=0 Der Vergleich zeigt: Die Ursache der Winkelbeschleunigung ist proportional zur Kraft und ihrem Normalarm. Das kommt vermutlich daher, dass die Kraft F nicht nur das Rad, sondern auch die hängenden Massen beschleunigt.
m a F
Kraftarm1 Kraftarm2 r1 r2 m1 m2
Kraft1 Kraft2 F1 F2
Achse
r1 r2
Normalarm1 Normalarm2
Kraft1 Kraft2 F1 F2
Definition des Drehmoments
Der Ausdruck ‚Normalarm mal Kraft’ heißt Drehmoment T (Englisch: Torque) und man sagt:
Drehmoment T ist die Ursache für Winkelbeschleunigung. Wenn T = 0 ist, gibt es entweder keine Rotation oder Rotation mit konstanter Winkelgeschwindigkeit
T = rn.F = r.F.sin I I
r Kraftarm: verbindet die Achse mit dem ‚Angriffspunkt’ der Kraft rn Normalarm: zeigt normal zur Kraft von der Achse bis zur Kraft oder zu ihrer Verlängerung. (rn =OX)
Winkel zwischen Kraft und Kraftarm: = <(r,F)
entsteht eine positive Drehung , so ist T>0, sonst T<0
Beispiel 2.1
In der Abbildung beträgt r1 = 7, r2 = 5, Í 1 I = 50o, I 2 I = 30o, m1 = 8kg, m2 = 10kg.
a) In welche Drehrichtung () wird das System beschleunigt?
b) Wie groß müsste m1 sein, damit sich das System bei unveränderten anderen Größen im Gleichgewicht befindet?
Lösung a:
Drehmoment1: T1 = -r1.G1.sin(90o-50o) = 7. 80. 0,643 = 359,9 [Nm]
Drehmoment2: T2 = r2.G2.sin(90o-30o) = -5. 100. 0,866 = -433 [Nm
Resultierendes Drehmoment: Tgesamt = -73,1 [Nm] negative Drehung
Lösung b:
Tges= T1 + T2 = 0 7.m1.10. sin40o – 433 = 0 m1 = 433 / (70.0,643)= 9,62[kg]
Beispiel 2.2
Für die Abbildung rechts gilt: r1=4m, r2=4m, =60o, m2
= 2m, m1 = m.
a) Berechnen sie das gesamte Drehmoment!
b) Um welchen Winkel muss man das System um seine horizontale Achse drehen, damit das gesamte Drehmoment verschwindet? Anleitung: Verwenden Sie die Formeln:
sin(=sincossin.cos , tan = sincos
Lösung a:
= 90o- = 30o.
Tges = +4.2m.g.sin90o - 6.m.g.sin30o = +5mg [Nm]
Lösung b:
Tges = +4.2.g. sin() - 6.g. sin() = 0
4.{sin90o.cos - cos90o.sin} = 3.{sin30o.cos cos30o.sin}
sin {-4.cos90o – 3.cos30o} = cos.{3.sin30o – 4.sin90o}
-2,6.sin-2,5. costan = 2,5 / 2,6 = 0,961 = 43,87o.
R 0
rn X Achse F Drehmoment:
T = rn.F = r.F.sinI I = r x F
= Fläche des Parallelogramms
r1 r2
r2 r1
1.3.3 Trägheitsmoment
Allgemeine Beobachtungen
Wir wollen nun den Widerstand gegen die Winkelbeschleunigung genauer untersuchen. Dazu vergleichen wir verschiedene Rotationskörper bei gleichem Drehmoment (also bei gleicher Ursache für die Winkelbeschleunigung) Beispiel 2.3
Das Drehmoment ist in allen drei Bildern dasselbe: T = rmg.
Im mittleren Bild ist die Masse des
Rotationskörpers verdoppelt. Man erhält die halbe Winkelbeschleunigung.
Rechts wurde bei gleicher Masse M der Radius des Rotationskörpers verdoppelt. Man erhält eine vier Mal kleinere Winkelbeschleunigung. Das rührt wieder daher, dass die Schwerkraft nicht nur den Rotationskörper, sondern auch m beschleunigt.
Bemerkung: Die ‚beobachtete’ Winkelbeschleunigung gilt nur für den abgebildeten Zeitpunkt. Sobald sich das Rad ein wenig dreht, ändert sich das Drehmoment T und daher auch , wie wir in aus Beispiel 2.2 erfahren haben. Der Vergleich der drei Rotationskörper bringt aber auch zu anderen Zeitpunkten dasselbe Ergebnis:
Der Widerstand gegen die Winkelbeschleunigung ist hier umgekehrt proportional zur Masse und umgekehrt proportional zum Quadrat des Radius eines zylinderförmigen Rotationskörpers.
Beispiel 2.4
Hier bleibt das Drehmoment auch zeitlich konstant: T = mrg.
Auch hier beobachtet man Ähnliches wie im obigen Beispiel:
Der Widerstand gegen die
Winkelbeschleunigung ist umgekehrt proportional zur Masse und ungefähr umgekehrt proportional zum Quadrat des Radius des Rotationskörpers.
(Das könnte daher kommen, dass wir zwar R, nicht aber r verändert haben. Wir haben also nur bei einem Teil des Rotationskörpers den Radius
verändert. Außerdem beschleunigt die Schwerkraft nicht nur den Rotationskörper, sondern auch m. )
Trägheitsmoment eines Massenpunktes
Eine theoretische Überlegung wird uns helfen, die Gesetze des Widerstands gegen die Drehbeschleunigung zu finden:
Gegeben sei ein Massenpunkt m, der keine andere Bewegung ausführen kann, als sich eine Achse 0 zu drehen.
Auf m wirke die Kraft F. Sie erzeuge ein Drehmoment T.
T = r.F = r.m.a = r.m.v / t = r.m.r.t = r2.m. .t = r2.m.
T = mr2 .
Der Term r2m heißt Trägheitsmoment des Massenpunktes m und es gilt Drehmoment = Trägheitsmoment . Winkelbeschleunigung
T =
Masse M 2M M Drehmoment: T = rmg T = rmg T = rmg Winkelbschl.:
R R 2R
r r r M 2M M m m m Bei gleichem Drehmoment gilt:
Doppelte Masse des Rotationskörpers halbe Winkelbeschleunigung Doppelter Radius des Rotationskörpers Viertel Winkelbeschleunigung
M 2M M R R 2R
r r r m m m
Winkelbeschl.
r 0 m
v
Wir vergleichen:
m a F
Translation
Kraft F ist Ursache für Beschleunigung a,
Masse m ist Widerstand gegen a T
Rotation
Drehmoment T: Ursache für Winkelbeschleunigung
Trägheitsmoment ist : Widerstand gegen .
Drehmoment ist Ursache für Winkelbeschleunigung. Verschwindet das gesamte Drehmoment für einen Rotationskörper, so dreht er sich nicht (oder lediglich mit konstanter Winkelgeschwindigkeit).
Wirken auf einen Rotationskörper mehrere Drehmomente mit derselben Achse, so ist ihre Gesamtwirkung durch ihre Summe gegeben
Der Widerstand eines Rotationskörpers gegen die Winkelbeschleunigung heißt Trägheitsmoment
Trägheitsmoment eines starren Körpers
Ein starrer Körper hat viele Massenpunkte m1, m2, m3 …….mit den Radien r1, r2, r3…………
Das Trägheitsmoment eines starren Körpers ist die Summe der Trägheitsmomente seiner Massenpunkte = ri2
.mi
Trägheitsmomente von besonderen Rotationskörpern
Die folgenden Formel werden hier ohne Beweis angegeben. Beweise sind mit Hilfe der am Vorstudienlehrgang gelehrten Integralrechnung leicht durchzuführen.
Sehr ‚dünner’ Ring
Alle Massenpunkte haben ungefähr den Abstand r von der Achse
r2.mgesamr
Zylinder
r2.mgesamr / 2
‚Dünne Platte’ (h 0)
r2.mgesamr /3
Drehmomente im täglichen Leben (Hebelwirkung)
Hebel
Türhebel
Schraubenschlüssel
r1.F1 = r2F2, wegen r1 >> r2 F1 >>
F2
Der lange Griff r1 erlaubt es, mit einer ziemlich kleinen Kraft F1 ein großes Drehmoment zu erzeugen und damit gegen die große Reibungskraft F2
zu wirken.
Meist wird bei wichtigen Verschraubungen ( z.B. bei der
Montage von Autorädern ) ein minimales Drehmoment vorgeschrieben, um die sichere Haftung der Schraube zu erreichen. Oft wird auch maximales Drehmoment angegeben, um Beschädigungen von Schraube und Mutter zu verhindern.
Professionelle Schraubenschlüssel enthalten eine Vorrichtung zur Messung des Drehmoments.
r b h
Schraubenschlüssel
Mutter F1 r1 F2
Aufgaben
(2.1) An einem Rad, sind zwei Massen aufgehängt. Ihre Gewichte erzeugen Drehmomente. Die Aufhängepunkte sind aus der Abbildung ersichtlich. Die Achse geht normal durch den
Mittelpunkt des Rades. Die linke Masse beträgt m1=10kg. Wie groß muss die rechte Masse sein, damit das Rad im Gleichgewicht bleibt. [5kg].
(2.2) Die kleinere Kraft (vertikal) beträgt 2N. Der Radius des Rades beträgt 25cm. Die größere Kraft greift im Punkt (010 )[cm] an, sie schließt mit der Horizontalen den Winkel 45oein. Die Achse
geht normal durch den Ursprung. Wie groß muss die größere Kraft gewählt werden, damit das Rad im Gleichgewicht bleibt (2.3) Die Kugel hat die Masse m= 15kg. die Masse von Knochen und Muskel wollen wir vernachlässigen. Wie groß muss die Kraft F sein, mit welcher der Muskel ziehen muss, um die Kugel im Gleichgewicht zu halten. Zeichnen Sie den
"wahren" Kraftarm ein!
(2.4)Ein Reifen der Masse m= 0,5kg mit Radius r=0,8m. Er kann sich um eine feste Achse drehen. Das
Drehmoment wird durch das Gewicht der Masse m' = 0.1kg erzeugt a) Wie groß ist das Trägheitsmoment? [0,32kgm2]
b) Das Gewicht der Masse m' erzeugt nicht nur das Drehmoment sondern bewirkt noch etwas anderes?
Was? [Die Beschleunigung von m'] c+) Wie groß ist die Winkelbeschleunigung [2,08]
d+) Wie groß ist das Drehmoment.? [0,6656]
(2.5) Die beiden "Wellräder" haben dieselbe Masse und sind um eine feste Achse drehbar. Am Anfang gibt es keine Rotation. Die Masse, die am Faden hängt ist ebenfalls in beiden Abbildungen gleich groß. Trotzdem dreht sich eines der beiden Räder nach der Zeit t doppelt so schnell wie das andere.
a)Welches der beiden Räder ist schneller und warum?
b)Welche wichtigen Rotationsgrößen sind in beiden Abbildungen gleich, welche sind verschieden?
(2.6) Gegeben sei ein "Wellrad" wie in Frage (2.5 ). Die Masse, die am Faden hängt, beträgt 0.5 kg. Die Anfangsgeschwindigkeit ist gleich Null, der große Radius beträgt 0.8m der kleine beträgt 0.4m. Nach 10s ist die Masse um 2m gesunken.
a) Bestimmen Sie Das Drehmoment, das im System wirkt, wenn es in Ruhe ist![2J]
b) Das Drehmoment bewirkt nicht nur eine Winkelbeschleunigung des Rotationskörpers sondern auch noch etwas anderes. Was?
c+) Bestimmen Sie Das Trägheitsmoment des Wellrades! [49,92]
Kontrollfragen
(2.10) Wie nennt man die Ursache für Winkelbeschleunigung?
(2.12) Wie nennt man den Widerstand gegen Winkelbeschleunigung?
(2.13) Definieren Sie das Drehmoment
20cm F=?
1cm 24cm
Der Drehimpuls L 1.4
Für die gewöhnliche Bewegung (Translation) gilt:
Kraft F ist die zeitliche Änderung des Impulses p: F = p / t. Wirkt auf ein System keine äußere Kraft (geschlossenes System), so bleibt der Gesamtimpuls erhalten.
Um ein analoges Gesetz für die Rotation zu entwickeln, erfinden wir zunächst eine neue Größe mit der Bezeichnung Drehimpuls L und sagen:
Drehmoment T ist die zeitliche Änderung des Drehimpulses L: T = L / t. Wirkt auf ein System kein äußeres Drehmoment, so bleibt der gesamt Drehimpuls erhalten.
Verwendet man L = , so ergibt sich wirklich: L / t = t = (wenn = const).
Das ein Vektor ist, ist auch der Drehimpuls L = ein Vektor in Richtung der Drehachse (rechte Hand)
Die Größe L = heißt Drehimpuls (Rotationsimpuls, Drall).
Wirkt auf ein System kein äußeres Drehmoment, so bleibt der gesamt Drehimpuls erhalten.
Wichtig! Da Lgsamt ebenfalls ein Vektor ist, bleibt auch die Richtung von Lgesamt erhalten.
Beispiel 3.1
Der abgebildete Zylinder (Masse m = 10kg, Radius r = 20cm) dreht sich 120 mal pro Minute. Wie groß ist der Drehimpuls L?
Lösung: f = 120Umdrehungen / 60s = 2Hz f = 4 = 12,56 [Hz], Zylinder = mr2 / 2 = 10.0,22 / 2 = 0,2 [kgm2] L = kgm2/s]
Beispiele für die Erhaltung des Drehimpulses
Beispiel 3.2
Die Pirouette beim Eistanzen:
Eine Eisläuferin dreht sich mit ausgebreiteten Armen mit der Winkelgeschwindigkeit um ihre vertikale Achse.
Ihr Drehimpuls ist L1 = . Zieht sie ihre Arme zum Körper, so wird das Trägheitsmoment kleiner, da die Massenpunkte der Arme jetzt kleiner Radien haben:
. Da der Drehimpuls erhalten bleibt, gilt: L1 = L2
, wegen folgt daraus
.
Die Drehbewegung wird von selbst schneller.
Beispiel 3.3
Zwei schwere Kugeln sind auf einer horizontalen Stange symmetrisch zur vertikalen Achse verschiebbar. Man versetzt die Anordnung mit in Rotation. Dabei sollen die Kugeln den Abstand r1 von der vertikalen Achse haben. Danach wird der Abstand der Kugeln von der Achse durch einen Mechanismus auf r2 verkürzt. Berechnen Sie
Vernachlässigen Sie die Masse des Gestänges!
Lösung:
Der Drehimpuls bleibt erhalten: L1 = L2 2mr1
2mr2
2 = r1 2 / r2
2
Weitere Beispiele für die Erhaltung des Drehimpulses finden wir in der folgenden Nummer über die Kreiselbewegungen!
Kreisel 1.5
Ein Kreisel ist ein Rotationskörper; seine Achse ist meist frei. Die Abbildung zeigt einen Kreisel, wie er als Spielzeug für Kinder verwendet wird.
Wir unterscheiden:
Symmetrischer Kreisel – unsymmetrischer Kreisel
Kreisel, auf den kein Drehmoment wirkt (kräftefreier Kreisel) – Kreisel unter der Wirkung eines Drehmoments
Symmetrischer Kreisel
Ohne Drehmoment
Der gesamte Drehimpuls aller Massenpunkte hat die Richtung der Drehachse und bleibt konstant.
L = const Richtung der Drehachse = const Beispiele 3.1
Beim Spielzeugkreisel mit vertikaler Achse erzeugt die Schwerkraft links und rechts je ein Drehmoment. Wegen der Symmetrie sind beide entgegengesetzt gleich und heben sich auf. Das gesamte Drehmoment verschwindet. Die Drehachse bleibt konstant.
Beispiel 3.2
Lässt man einen Fahrradkreisel mit horizontaler Drehachse los. So gibt es ebenfalls kein Drehmoment, der Kreis fällt mit unverändert horizontaler Drehachse zu Boden.
Mit Drehmoment (Präzession) Beispiel 3.3
Spielzeugkreisel mit geneigter Drehachse:
Das gesamte Drehmoment verschwindet nicht, da F1=F2 aber rn2>rn1 ist, gilt: IT1I < IT2I Das gesamte Drehmoment ist negativ. Würde der Kreisel nicht um seine Achse rotieren, so würde er ‚nach rechts’ fallen (=negatives gesamtes Drehmoment, T zeigt nach hinten)
Das Drehmoment T ändert den Drehimpuls L:
t T t L
T L
.
Die Änderung des Drehimpulses L hat dieselbe Richtung wie T. (horizontal nach hinten) Die
Spitze des Drehimpulses L beschreibt einen ‚horizontalen Kreis’. Damit ist eine Bewegung der Kreiselachse verbunden. Mann nennt sie Präzessionsbewegung.
Beispiel 3.4 Fahrradkreisel I:
Unterstützt man einen nicht rotierenden Fahrradkreisel nur am einem Ende seiner Achse (Punkt X), so wirkt ein negatives Drehmoment T (Pfeil nach hinten). Dieser Fahrradkreisel würde nach rechts zu Boden fallen.
Rotiert ein solcher Fahrradkreisel selbst um seine eigene Achse, so bewirkt das
Drehmoment T eine Änderung des Drehimpulses L. Die Änderung des Drehimpulses L = T.t ist also auch ein L+L X X L L
r F
L L
L+L r1
r2
F1 F2
rn1 rn2
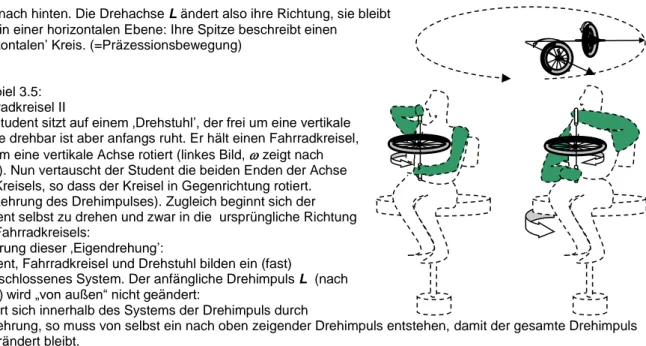
Pfeil nach hinten. Die Drehachse L ändert also ihre Richtung, sie bleibt aber in einer horizontalen Ebene: Ihre Spitze beschreibt einen
‚horizontalen’ Kreis. (=Präzessionsbewegung)
Beispiel 3.5:
Fahrradkreisel II
Ein Student sitzt auf einem ‚Drehstuhl’, der frei um eine vertikale Achse drehbar ist aber anfangs ruht. Er hält einen Fahrradkreisel, der um eine vertikale Achse rotiert (linkes Bild, zeigt nach oben). Nun vertauscht der Student die beiden Enden der Achse des Kreisels, so dass der Kreisel in Gegenrichtung rotiert.
(Umkehrung des Drehimpulses). Zugleich beginnt sich der Student selbst zu drehen und zwar in die ursprüngliche Richtung des Fahrradkreisels:
Erklärung dieser ‚Eigendrehung’:
Student, Fahrradkreisel und Drehstuhl bilden ein (fast)
abgeschlossenes System. Der anfängliche Drehimpuls L (nach oben) wird „von außen“ nicht geändert:
Ändert sich innerhalb des Systems der Drehimpuls durch
Umkehrung, so muss von selbst ein nach oben zeigender Drehimpuls entstehen, damit der gesamte Drehimpuls unverändert bleibt.
Die Erde ist ebenfalls ein (fast) symmetrischer Kreisel. Die Richtung der Rotationsachse für ihre Eigenrotation bleibt fast konstant. Da sie nicht parallel zur Achse der Rotation um die Sonne ist, werden die obere und untere Hälfte der Erde in verschiedenen Positionen verschieden lang vom Sonnenlicht bestrahlt. ( Entstehung der Jahreszeiten )
Links: Auf der nördlichen ( = oberen ) Halbkugel ist jetzt gerade Sommer Rechts: : Auf der nördlichen ( = oberen ) Halbkugel ist jetzt gerade Winter
Bemerkung: Da die Erde von der Sonne angezogen wird, wirkt auf die Erde als Kreisel ein Drehmoment.
Dies führt zu einer schwachen Präzessionsbewegung der Eigenrotationsachse der Erde. Sie ist aber für das tägliche Leben ohne Bedeutung.
Beispiel 3.6:
Foucault' sches Pendel: Die Pendelbewegung ist eine Rotation. Wird das Pendel frei aufgehängt, so ändert die Rotationsachse ihrer Richtung nicht. Die
Abbildung zeigt ein Pendel, das seinen Aufhängepunkt genau über dem Nordpol hat: Während sich die Erde unter dem Pendel hinweg dreht, bleibt die
Rotationsebene des Pendels konstant: Angenommen, das linke Bild zeigt die Erde 12h vormittags. Dann zeigt das rechte Bild die Situation um ungefähr 18h. Warum ungefähr und nicht genau?
Zusammenfassung:
Wirkt auf den symmetrischen Kreisel kein Drehmoment, so bleibt der Drehimpuls konstant und die Richtung der Drehachse bleibt erhalten
Unter der Wirkung eines Drehmoments ändert sich der Drehimpuls und die Drehachse des symmetrischen Kreisels beschreibt eine Präzessionsbewegung
Für unsymmetrische Kreisel gilt:
Die Achsen von unsymmetrischen Kreiseln führen bereits ohne Drehmoment komplizierte Bewegungen aus, obwohl sich der Drehimpuls nicht ändert.
Rotationsenergie 1.6
Die Rotation ist eine Form der Bewegung. Ein rotierender Körper hat daher kinetische Energie, auch wenn seine Achse fest ist. wir nennen diese Energie Rotationsenergie und definieren analog zur kinetischen Energie:
Die Rotationsenergie Wrot ist die Energie, die man braucht um einen Körper von der Winkelgeschwindigkeit Null auf die Winkelgeschwindigkeit zu beschleunigen
Ein Körper, der mit der Winkelgeschwindigkeit um eine Achse rotiert, „hat“ die Rotationsenergie
Wrot = /2
Beweis:
Wir beschleunigen zuerst nur einen Massenpunkt von 0 auf W = mv2/2 = mr22/2 = massenpunkt./2.
Für viele Massenpunkte müssen wir alle Energien summieren: Wges = (1++ )./2 = ges.2.
Beispiel 4.1:
Ein Rad mit der Masse m und dem Trägheitsmoment ist um eine unbeweglichen Achse drehbar und wird von Null auf beschleunigt. Es bekommt nur die Rotationsenergie Wrot = /2
Beispiel 4.2:
Ein Rad wird auf einer ebenen Straße (rollend) reibungsfrei von der Geschwindigkeit Null auf v beschleunigt. Es bekommt zwei Energien:
Die Rotationsenergie Wrot = /2 und zusätzlich noch die kinetische Energie für die Translation Wkin = mv2/2
Obwohl v=r.ist, sind die beiden Energien nicht gleich, da im allgemeinen mr2 ist
Beispiel 4.3:
Ein Reifen (Radius r, Masse m) rollt reibungsfrei auf einer schiefen Ebene (Höhenunterschied h, Länge s) zu Boden. Parallel dazu gleitet ebenfalls reibungsfrei ein Quader (Masse m) auf derselben Ebene zu Boden. Das Rad bewegt sich langsamer als der Reifen, weil sich seine potentielle Energie nicht nur in kinetische Energie sondern auch in Rotationsenergie verwandelt.
Aufgaben:
(4.1)Berechnen Sie in Beispiel 4.3 die Geschwindigkeit des Reifens am Boden und verwenden sie dazu h=4m, m=10kg, Radius = 2m)
(4.2Führen Sie Aufgabe (1.10) mit einem Vollrad statt mit einem Reifen durch!
(4.3)Wie viel Energie braucht man um, einen Reifen (r= 0.8m, m= 0.5kg von 0 auf v= 5m/s zu beschleunigen, indem man ihn
a)um eine feste Achse dreht (reine Rotation)
b)indem man ihn auf einer ebenen Straße rollt (Rotation + Translation)
(4.4) Vergleichen sie alle Größen der Translation und der Rotation und stellen Sie alle Beziehungen zwischen diesen Größen dar
( Beispiel: Translation: Geschwindigkeit v=st , Rotation: Winkelgeschwindigkeit t; v=r.
Schwerpunkt (Massenmittelpunkt) 1.7
Unterstützt man den abgebildeten Körper in seinem ‚Mittelpunkt’, so heben sich das positive Drehmoment (erzeugt durch die Kraft F1 und das negative Drehmoment (F2
) auf und das gesamte Drehmoment verschwindet. Der Körper erhält keine Winkelbeschleunigung und bleibt im Gleichgewicht.
Unterstützt man den Körper jedoch in einem anderen Punkt, so entsteht eine Winkelbeschleunigung.
Der ‚Mittelpunkt’ unseres Körpers heißt Schwerpunkt oder Massenmittelpunkt. Man kann folgende Definition angeben:
Unterstützt man ausschließlich den Schwerpunkt S eines Körpers, so verschwindet die Summe der Drehmomente aller Massenpunkte bezüglich der Schwerkraft.
Um eine Formel für s zu finden, denken wir uns zunächst einen Körper der aus drei Massenpunkten m1,m2,m3 besteht, die feste Plätze auf der x-Achse haben sollen: x1,x2x3. Die x-Achse ist normal zur Schwerkraft G. Unterstützt man in sx, so soll das gesamte Drehmoment verschwinden.
(sx – x1).m1.g + (sx – x21).m21.g + (sx – x31).m31.g = 0
sx (m1+m2+m3) = x1m1 + x2m2 + x3m3
sx = (x1m1 + x2m2 + x3m3 ) / (m1+m2+m3) = ximi / mi
Liegen die drei Punkte nicht alle auf der x-Achse, so ändert sich an der Formel nichts, da für das Drehmoment der Normalarm x bestimmend ist und nicht r.
Möchte man die ‚Höhe’ des Schwerpunkts bestimmen, also sy, so denkt man sich den ganzen Körper um 90ogedreht. Dann ist die Schwerkraft normal zur y-Achse und man hat einfach statt x ein y zu schreiben:
sy = (y1m1 + y2m2 + y3m3 ) / (m1+m2+m3) = yimi / mi
Analoges gilt für die z-Richtung:
sz = (z1m1 + z2m2 + z3m3 ) / (m1+m2+m3) = yimi / mi
i i i
z
y m
.m r s
s s
gilt
s s und z y x r mit
x
i i i i
Formel für den Schwerpunkt
Ein System von n Massenpunkten m1,m2,...mn mit den Ortsvektoren r1,r2, ...rn hat den gemeinsamen Schwerpunkt S mit den Koordinaten:
i i i
m .m r s
m1 m2 m3 x 0 x1 x2 sx x3
sx – x1>0 sx – x3<0 sx-x
y m2 y2
y1 m1 r2
sy r1 S r3 m3
y3
x1 x2 sx x3 x sx – x1>0 sx – x3<0 sx-x
1.7.1 Schwerpunkt und Drehmoment
Ein starrer Körper sei um die Achse O drehbar. Die Schwerkraft erzeuge ein Drehmoment. Dieses ist die Summe der Drehmomente aller Massenpunkte
Tges = +/-(r1 .m1.g.sin + r2.m2.g. sin +... ) =
= +/-(r1.x1 + r2.x2+ ...).g. = +/-sMgesg
Man erhält das gesamte Drehmoment eines starren Körpers, indem man sich die gesamte Masse im Schwerpunkt S denkt und dort die äußere Kraft ( z.B die Schwerkraft) angreifen lässt.
Wir sagen auch:
Die Schwerkraft greift im Schwerpunkt S an.
Tges = s.F.sin
vektoriell geschrieben:
T = s x F Beispiel 4.4:
Wie groß ist die Kraft F, mit welcher man ziehen muss, um den Arm des Krans mit seiner Last im Gleichgewicht zu halten?
Arm des Krans: m = 100kg, Länge L = 8m Masse der Last: m’ = 300kg
Winkel zwischen der Vertikalen und dem Arm des Krans: = 40o. Lösung:
Vorbemerkung: Der Winkel zwischen der Horizontalen und dem Arm des Krans beträgt = 90o – 40o = 50o
T = TPerson + TLasr + TKranarm = 0 (Gleichgewicht)
½ L.sin.F - L.sin.m’g – ½ L.sin.m.g = 0
1.7.2 Gemeinsamer Schwerpunkt mehrerer Körper
Der Körper M bestehe aus den Massenpunkten m1, m2, ...
Für seinen Schwerpunkt gilt: sx = ( m1.x1 +m2x2+.... ) / (m1 + m2 +.... ) =
=mi xi / mi m1.x1 +m2x2+....= sx.M
Der Körper M’ bestehe aus den Massenpunkte m’1, m’2, ...
Für seinen Schwerpunkt gilt: s’x = ( m’1.x’1 +m’2x’2+.... ) / (m’1 + m’2 + ) =
m’i x’i / m’i m’1.x’1 +m’2x’2+....= s’x.M’
Der gemeinsame Schwerpunkt beider Körper ist gegeben durch den Ausdruck:
Sx = ( m1.x1 +m2.x2+....+ m’1.x’1 +m’2x’2+.... ) / ( M + M’ ) = ( sxM + s’x.M’ ) / ( M + M’ ) Analoge Formel erhält man auch für Sy und Sz.
m1
r1 r2 m2
r3 m3
O
x1 x3 x2
S
s F = G
sx
m m’
sx Sx sx’