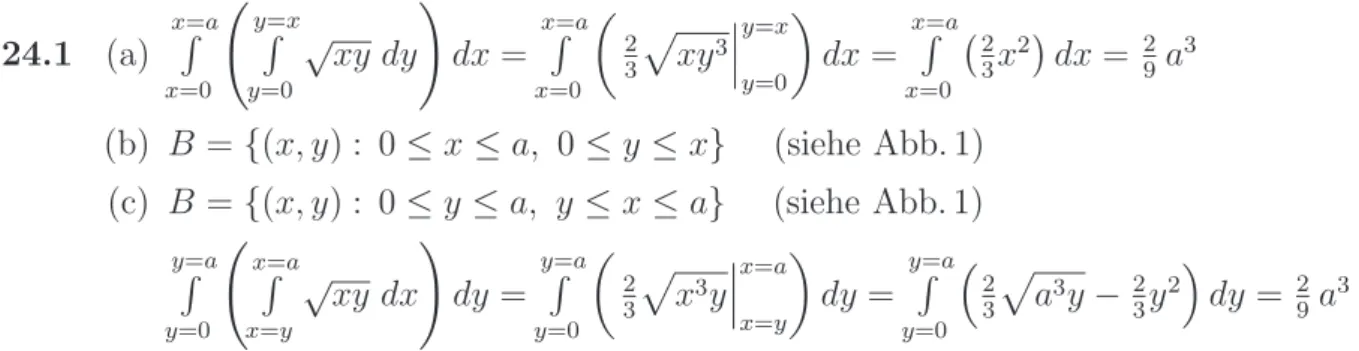L¨ osungen zur 24. ¨ Ubung

L¨ osungen zur 24. ¨ Ubung

H¨ohere Mathematik II (MB)

24.1 (a)

x=a

R

x=0 y=x

R

y=0

√xy dy

! dx=

x=a

R

x=0

2 3

pxy³

y=x y=0

dx=

x=a

R

x=0 2 3x²

dx= ²₉a³ (b) B ={(x, y) : 0 ≤x≤a, 0≤y≤x} (siehe Abb. 1)

(c) B ={(x, y) : 0 ≤y ≤a, y≤x≤a} (siehe Abb. 1)

y=a

R

y=0 x=a

R

x=y

√xy dx

! dy =

y=a

R

y=0

2 3

px³y

x=a x=y

dy =

y=a

R

y=0

2 3

pa³y−²3y²

dy= ²₉a³

24.2 Entsprechend der Integrationsgrenzen hat der Normalbereich die Darstellung B ={(x, y) : −2≤y≤0, y²−4≤x≤0}

bzw. alternativ

B ={(x, y) : −4≤x≤0, −√

x+ 4 ≤y ≤0} (siehe Abb. 1).

Hieraus findet man das Doppelintegral mit vertauschter Integrationsreihenfolge:

x=0

R

x=−4

y=0

R

y=−

√x+4

y³ dy

! dx =

x=0

R

x=−4

1 4y⁴

y=0 y=−

√x+4

dx=

x=0

R

x=−4

−¹4(x+ 4)²dx=−¹⁶3

(-4,0)

(0,-2) (a,0)

(a,a)

Abbildung 1: Aufgaben 1 und 2

24.3 (a) B ={(x, y) : 2 ≤x ≤4, ⁴_x ≤y≤x} RR

B

y db =

4

R

2 x

R

4/x

y dy

! dx=

4

R

2

1 2y²

x 4/x

dx=

4

R

2 1 2x²− ¹2

16 x²

dx= ²²₃ (b) B ={(x, y) : −1≤y≤0, y+ 1 ≤x≤e^y}

RR

B

y² db =

0

R

y=−1 e^y

R

x=y+1

y² dx

!

dy = ²³₁₂ −5e⁻¹ ≈0.07727

24.4 A= Z Z

B

1 db =

2

Z

0

√8x

Z

0

1dy dx = 16 3 ,

Z Z

B

x db = 32 5 ,

Z Z

B

y db = 8

Die Schwerpunktskoordinaten sind xS = 1 A

Z Z

B

x db , yS = 1 A

Z Z

B

y db ,

also ist S(1.2,1.5) der geometrische Schwerpunkt von B.

Rotation vonB ={(x, y) : 0 ≤x≤2, 0≤y≤√

8x} um die Gerade y = 0 : Volumen des Rotationsk¨orpers: V =πR²

0

√8x²

dx = 16π Fl¨ache von B: A= ¹⁶₃

Umfang des erzeugten Kreises: U = 2πyS = 3π, also gilt V =A·U. Rotation vonB um die Gerade x= 2 :

Volumen des Rotationsk¨orpers: V =πR⁴

0

2− ^y8²

²

dy = ¹²⁸₁₅π Fl¨ache von B: A= ¹⁶₃

Umfang des erzeugten Kreises: U = 2π(2−xS) = ⁸₅π, also gilt V =A·U. 24.5 (a) r¨aumlicher Normalbereich

B ={(x, y, z) : 0 ≤x≤4, 0≤y≤4−x, 0≤z ≤x² +y²} V =

4

Z

0 4−x

Z

0

x²+y²

Z

0

1dz dy dx=

4

Z

0 4−x

Z

0

(x²+y²)dy dx= 128 3 (b) r¨aumlicher Normalbereich

B ={(x, y, z) : 1 ≤x²+y² ≤4, 0≤z≤x+ 2} Ubergang zu Zylinderkoordinaten:¨

B ={(r, ϕ, z) : 1≤r ≤2, 0≤ϕ≤2π, 0≤z ≤x+ 2 =rcosϕ+ 2} V =

2

Z

r=1 2π

Z

ϕ=0

rcosϕ+2

Z

z=0

r dz dϕ dr=

2

Z

r=1 2π

Z

ϕ=0

(rcosϕ+ 2)r dϕ dr= 6π ≈18.85

24.6 (a) V = Z Z Z

B

1 db =

1

Z

0 x

Z

0

x+3y+1

Z

0

dz dy dx= 4 3 (b)

Z Z Z

B

x db = 23

24, d.h. xS = 23

32 = 0.719, Z Z Z

B

y db = 13

24, d.h. yS = 13

32 = 0.406, Z Z Z

B

z db = 47

24, d.h. zS = 47

32 = 1.469

Aufgaben und L¨osungen im Web : www.tu-chemnitz.de/∼ustreit

Bemerkungen an : u.streit@mathematik.tu-chemnitz.de [31. Mai 2019]