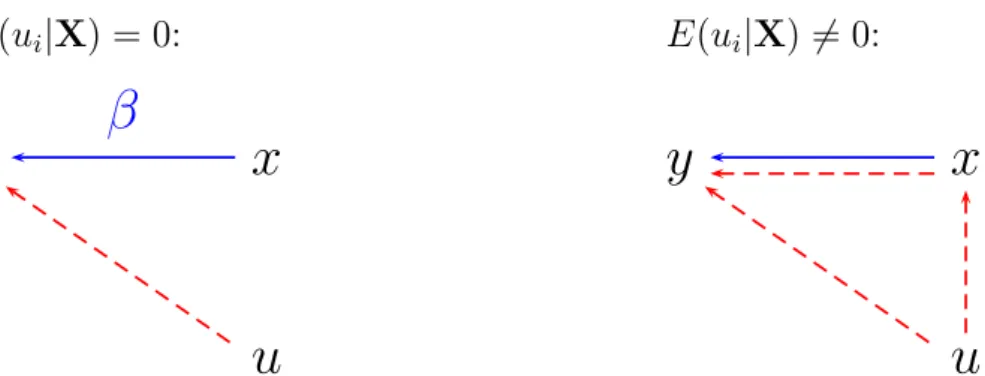Das OLS Regressionsmodell in Matrixnotation
“What I cannot create, I do not under- stand.” (Richard P. Feynman) Dieses Kapitel bietet im wesentlichen eine Wiederholung der fr¨uheren Kapitel. Wir gehen nur in einem einzigen Punkt ¨uber die fr¨uheren Kapitel hinaus, indem wir die Matrixnotation einf¨uhren. Dies vereinfacht die Darstellung der multiplen Regression ganz erheblich.
6.1 OLS-Sch¨ atzung in Matrixschreibweise
Das multiple Regressionsmodell kann in Matrixschreibweise deutlich einfacher dar- gestellt werden als unter Verwendung der bisherigen Summennotation.
Wir gehen wieder von einem einfachen linearen Zusammenhang in der Grundge- samtheit aus, d.h. von einem datengenerierenden Prozess, der durch folgende PRF beschrieben werden kann
yi =xi1β1+xi2β2+· · ·+xihβh+· · ·+xikβk+εi
wobei der erste Indexiwie ¨ublich die Beobachtung und der zweite Indexh= 1, . . . , k die Variable bezeichnet. Dar¨uber hinaus wollen wir in diesem Kapitel weiterhin annehmen, dass alle Gauss Markov Annahmen erf¨ullt seien.
F¨ur die n Beobachtungen der Stichprobe k¨onnen wir die SRF (‘Sample Regression Function’) ausf¨uhrlicher schreiben, n¨amlich f¨ur jede einzelne Beobachtung i
y1 = x11βb1 +x12βb2 +· · ·+x1kβbk+ ˆε1
y2 = x21βb1 +x22βb2 +· · ·+x2kβbk+ ˆε2
... = ... + ... + ... + ... + ...
yi = xi1βb1 +xi2βb2 +· · ·+xikβbk + ˆεi
... = ... + ... + ... + ... + ...
yn=xn1βb1+xn2βb2+· · ·+xnkβbk+ ˆεn
wobei n die Gr¨oße der Stichprobe und h die Laufvariable ¨uber die Anzahl der er- kl¨arenden Variablen (inklusive Regressionskonstante) bezeichnet (h= 1, . . . , k). Wie
1
in der Matrixschreibweise ¨ublich wird mit dem ersten Subindex die Beobachtung – also Zeile – bezeichnet (i = 1, . . . , n), und der zweite Subindex (h = 1, . . . , k) be- zeichnet die erkl¨arende Variable, also Spalte;xihbezeichnet also diei-te Beobachtung von Variableh, bzw. das Element in Zeilei und Spalte h.
Man beachte, dass wir hier keine speziellen Symbole f¨ur Regressionskonstante und Interzept eingef¨uhrt haben. Dies ist nicht erforderlich, denn das Interzept ist einfach der Koeffizient der Regressionskonstanten, d.h. eines Einsen-Vektors. Sollte die Re- gression ein Interzept enthalten ist einfach eine der x-Variablen ein Einsen-Vektor.
Dieses Gleichungssystem kann einfach in Matrixschreibweise geschrieben werden
y1
y2
...
yn
=
x11 x12 · · · x1k
x21 x22 · · · x2k ... ... ... ...
xn1 xn2 · · · xnk
βb1
βb2
...
βbk
+
ˆ ε1
ˆ ε2
...
ˆ εn
oder etwas kompakter
y =Xβˆ+ ˆε Die PRF schreiben wir analog y=Xβ+ε.
Zur Notation: Ublichen Konventionen folgend bezeichnen fettgedruckte Klein-¨ buchstaben Vektoren und fettgedruckte Großbuchstaben Matrizen.
6.1.1 Alternative Schreibweisen
Wenn wir aus der i-ten Zeile der X Matrix einenk×1 Spaltenvektor formen
xi
.
=
xi1
xi2
...
xik
kann das Modell y = Xβˆ+ ˆε alternativ auch elementenweise geschrieben werden als
yi =x′i
.
βˆ+ ˆεi = xi1 xi2 · · · xik
βb1
βb2
...
βbk
+ ˆεi
=xi1βb1+xi2βb2+· · ·+xikβbk+ ˆεi, i= 1, . . . , n
Wenn keine Gefahr von Missverst¨andnissen besteht schreiben wir im Folgenden statt xi
.
k¨urzerxi, also insgesamtnSpaltenvektoren, von denen jeder die Dimensionk×1 hat.Mit Hilfe des Spaltenvektors xi
.
kann auch dieX alternativ geschrieben werden alsX =
x′1 x′2 ...
x′n
Die k×k Matrix X′X kann auch geschrieben werden als Pn
i=1xix′i, da Xn
i=1
xix′i = Xn
i=1
xi1 xi2
...
xik
(xi1 xi2 · · · xik)
=
Pn
i=1x2i1 Pn
i=1xi1xi2 · · · Pn
i=1xi1xik
Pn
i=1xi2xi1 Pn
i=1x2i2 · · · Pn
i=1xi2xik
... ... . .. ...
Pn
i=1xikxi1 Pn
i=1xikxi2 · · · Pn i=1x2ik
=
x11 x21 · · · xn1
x12 x22 · · · xn2
... ... ... ...
x1k x2k · · · xnk
x11 x12 · · · x1k
x21 x22 · · · x2k
... ... ... ...
xn1 xn2 · · · xnk
= X′X Genauso ist X′y =P
ixiyi, weil Xn
i=1
xiyi = Xn
i=1
xi1 xi2
...
xik
yi
=
x11y1+x21y2+· · ·+xn1yn
x12y1+x22y2+· · ·+xn2yn
...
x1ky1+x2ky2+· · ·+xnkyn
=
x11 x21 · · · xn1
x12 x22 · · · xn2
... ... ... ...
x1k x2k · · · xnk
y1
y2
...
yn
= X′y
Also kann der OLS Sch¨atzer auch in Vektornotation geschrieben werden βˆ= (X′X)−1X′y=
Xn i=1
xix′i
!−1Xn i=1
xiyi
Diese Vektor-Schreibweise findet sich h¨aufig in Lehrb¨uchern.
6.2 Die OLS Sch¨ atzfunktion
Wie ¨ublich gehen wir wieder davon aus, dass der Parametervektor der Grundgesamt- heitβnicht beobachtbar ist, aber wenn wir aus der Grundgesamtheit eine Stichprobe mit dem Umfang n ziehen erwarten wir darin einen ¨ahnlichen Zusammenhang wie in der Grundgesamtheit zu finden. Unser Problem besteht also darin, eine m¨oglichst gute Sch¨atzfunktionβˆ f¨ur den ‘wahren’ Koeffizientenvektor β zu finden.
Die Grundidee der OLS–Sch¨atzung (Ordinary Least Squares) besteht darin, den Residuenvektor ˆε so zu w¨ahlen, dass die Summe der quadrierten Abweichungen in der Stichprobe (d.h. Pn
i=1εˆ2i) so klein wie m¨oglich wird. Dies ist wieder die ¨ubliche Minimierungsaufgabe.
Zur Erinnerung, die SRF y=Xβˆ+ ˆε ist ausf¨uhrlich geschrieben
y1
y2
...
yn
=
x11 x12 · · · x1k
x21 x22 · · · x2k
... ... ... ...
xn1 xn2 · · · xnk
βb1
βb2
...
βbk
+
ˆ ε1
ˆ ε2
...
ˆ εn
Die einzelnen Spalten der X-Matrix sind die erkl¨arenden Variablen, und der n×1 Vektor ˆε sind die zu minimierenden Stichprobenresiduen.
Die Summe der quadrierten Residuen kann in Matrixschreibweise einfach als inneres Produkt geschrieben werden
εˆ′εˆ= εˆ1 εˆ2 · · · εˆn
ˆ ε1
ˆ ε2
...
ˆ εn
= Xn
i=1
ˆ ε2i
Da per Definition ˆε = y−Xβˆ suchen wir den Vektor β, der die Quadratsummeˆ der Residuen minimiert. Dies wird manchmal geschrieben als
βˆ= arg minh
(y−Xβ)ˆ ′(y−Xβ)ˆ i
wobei die Funktion arg min der Bestimmung der Stelle dient, an der die Funktion (y−Xβ)ˆ ′(y−Xβ) ihr Minimum annimmt.ˆ
Die Quadratsumme der Residuen ist ˆ
ε′εˆ= (y−Xβ)ˆ ′(y−Xβ)ˆ
= (y′−βˆ′X′)(y−Xβ)ˆ
=y′y−βˆ′X′y−y′Xβˆ+βˆ′X′Xβˆ
=y′y−2βˆ′X′y+βˆ′X′Xβˆ
Man beachte, dass βˆ′X′y = (βˆ′X′y)′ = y′Xβ, weil beide Terme die Dimensionˆ (1×1) haben, also Skalare sind, und die Transponierte eines Skalars der Skalar selbst ist.
Um die Quadratsumme der Residuen zu minimieren m¨ussen wir den obigen Aus- druck nach dem Vektor βˆ ableiten und diese Ableitungen Null setzen. Dazu ben¨otigen wir zwei Rechenregeln f¨ur das Differenzieren von Matrizen.
Diese beiden Rechenregeln sind 1.
∂βˆ′X′y
∂βˆ =X′y 2.
∂βˆ′X′Xβˆ
∂βˆ = 2X′Xβˆ
und werden im Appendix zu diesem Kapitel ausf¨uhrlich erl¨autert (siehe Appendix 6.A.1 Seite 38).
Diese zwei Rechenregeln k¨onnen wir nun f¨ur unsere Minimierungsaufgabe verwen- den.
minβˆ
( ˆε′ε) = minˆ
βˆ
(y−Xβ)ˆ ′(y−Xβ)ˆ
= min
βˆ
hy′y−2βˆ′X′y+βˆ′X′Xβˆi
∂( ˆε′ε)ˆ
∂βˆ =−2X′y+ 2X′Xβˆ= 0! X′Xβˆ=X′y
Diesen Ausdruck k¨onnen wir nun einfach nach βˆl¨osen, indem wir mit der Inversen (X′X)−1 vormultiplizieren. Als Ergebnis erhalten wir den OLS-Punktsch¨atzer
βˆ= (X′X)−1X′y
Die Bedingung 2. Ordnung f¨ur ein Minimum verlangt, dass die MatrixX′X positiv definit ist. Diese Bedingung ist aufgrund der Eigenschaften der Matrix X′X unter sehr allgemeinen Bedingungen erf¨ullt, wenn X vollen Spaltenrang hat.
Ubung:¨ Schreiben Sie die MatrixX′X mit Hilfe des Summennotation ausf¨uhrlich an. Ist die Matrix X′X symmetrisch?
Wenn X eine n×k Matrix ist, ist X′ eine k×n Matrix, und X′X ist eine k×k
Matrix.
X′X =
x11 x21 · · · xn1
x12 x22 · · · xn2
... ... ... ...
x1k x2k · · · xnk
x11 x12 · · · x1k
x21 x22 · · · x2k
... ... ... ...
xn1 xn2 · · · xnk
=
Pn
i=1x2i1 Pn
i=1xi1xi2 · · · Pn
i=1xi1xik
Pn
i=1xi2xi1 Pn
i=1x2i2 · · · Pn
i=1xi2xik
... ... . .. ...
Pn
i=1xikxi1 Pn
i=1xikxi2 · · · Pn i=1x2ik
Aufgrund des Kommutativgesetzes (Pn
i=1xigxih =Pn
i=1xihxig) ist X′X eine sym- metrische k×k Matrix.
Frage: wie sieht X′X aus, wenn die erste Spalte von X die Regressionskonstante ist?
Beispiel: Die MatrixXsei einn×1 Vektor mit lauter Einsen, also einer Regression auf die Regressionskonstante
βˆ= (X′X)−1X′y
=
1 1 . . . 1
1 1...
1
−1
1 1 . . . 1
y1
y2
...
yn
= 12+ 12· · ·+ 12−1
(y1+y2 +· · ·+yn)
=n−1 Xn
i=1
yi = 1 n
Xn i=1
yi = ¯y
Die Anwendung des OLS–Sch¨atzers liefert also wie erwartet den Mittelwert.
Beispiel: Gegeben sei wieder folgende Stichprobe mit 5 Beobachtungen f¨ur x und y:
y: 2.6 1.6 4.0 3.0 4.9 x: 1.2 3.0 4.5 5.8 7.2
In Matrixschreibweise ist das Modell y=Xβˆ+ε oder ausf¨uhrlicher
2.6 1.6 4.0 3.0 4.9
=
1 1.2 1 3.0 1 4.5 1 5.8 1 7.2
βb1
βb2
! +
ˆ ε1
ˆ ε2
ˆ ε3
ˆ ε4
ˆ ε5
wobei der Koeffizient des Einsenvektors (1. Spalte) das zu berechnende Interzept ist.
Der OLS-Sch¨atzer ist βˆ= (X′X)−1X′y
=
1 1 1 1 1 1.2 3.0 4.5 5.8 7.2
1 1.2 1 3.0 1 4.5 1 5.8 1 7.2
−1
1 1 1 1 1 1.2 3.0 4.5 5.8 7.2
2.6 1.6 4.0 3.0 4.9
=
5 21.7 21.7 116.17
−1 16.1 78.6
=
1.0565 −0.1973
−0.1973 0.0455
16.1 78.6
=
1.498 0.397
Dies sind die Punktsch¨atzer βb1 und βb2. In der ¨ublichen Schreibweise b
yi = 1.498 + 0.397xi
Hinweis: Die Inverse kann z.B. einfach mit Excel berechnet werden, siehe dazu die Hinweise zu ¨Ubungsaufgabe 1 auf Seite 30.
6.3 Die Annahmen des klassischen linearen Re- gressionsmodells
Eine der wichtigsten Schlussfolgerungen der fr¨uheren Kapitel war, dass der OLS- Sch¨atzer unter denGauss-Markov Annahmen effizient – d.h. unverzerrt und varianz- minimal – ist. Dies gilt selbstverst¨andlich auch f¨ur das multiple Regressionsmodell.
Wir erinnern uns, dass wir die Gauss-Markov Annahmen einteilten in Annahmen, die die Spezifikation betreffen (z.B. Funktionsform & ‘richtige’ Variablenselektion), in solche die die X Matrix betreffen (z.B. Exogenit¨at & lineare Unabh¨angigkeit), und solche ¨uber die St¨orterme der Grundgesamtheit εi (εi ∼i.i.d.(0, σ2)).
Ein Großteil der weiteren Veranstaltung wird sich damit besch¨aftigen, was zu tun ist, wenn eine oder mehrere dieser Annahmen nicht erf¨ullt sind. Deshalb wollen wir die Gauss-Markov Annahmen nun f¨ur das allgemeinere multiple Regressionsmodell unter Zuhilfenahme der Matrixschreibweise wiederholen und etwas kompakter dar- stellen.
Der eigentliche Gauss Markov Beweis wird im Abschnitt 6.8 skizziert.
A1: Linearit¨at der PRF: Die Beobachtungen y sind eine lineare Funktion der erkl¨arenden Variablen X und der St¨orterme ε
y =Xβ+ε oder ausf¨uhrlicher
yi =β1xi1+β2xi2+· · ·+βkxik+εi
Diese Linearit¨atsannahme bezieht sich nur auf die Parameter, nicht auf die Variablen. So ist z.B.
yi =β1+β2ln(xi2) +β3x2i3+εi
linear in den Parametern, aber nicht linear in den Variablen.
Andererseits ist z.B.
yi =β1+ ln(β2)xi2+β32xi3+εi
zwar linear in den Variablen, aber nicht linear in den Parametern.
Mit OLS k¨onnen alle Modelle gesch¨atzt werden, die linear in den Parametern sind, auch wenn sie nicht linear in den Variablen sind (erstes Beispiel). Modelle, die nicht linear in den Parametern sind, werden meist mit anderen Methoden gesch¨atzt, z.B. mitMaximum Likelihood Sch¨atzern.
Insbesondere wollen wir auch annehmen, dass das Modell richtig spezifiziert ist, das heißt, dass im Modell keine relevanten erkl¨arenden Variablen fehlen, und dass keine irrelevanten erkl¨arenden Variablen vorkommen.
A2: Voller Spaltenrang: Die n×k Matrix X hat vollen Spaltenrang,1 d.h.
rk(X) = k wobei rk den Rang bezeichnet.2
Das bedeutet erstens, dass die Zahl der Beobachtungen nicht kleiner sein darf als die Zahl der zu sch¨atzenden Parameter,n ≥k, undzweitens, dass zwischen den einzelnen erkl¨arendenxVariablen (den Spalten der MatrixX) keine exak- te lineare Abh¨angigkeit besteht.3 Besteht zwischen den Spalten derX Matrix eine exakte lineare Abh¨angigkeit, spricht man von perfekter Multikollinearit¨at und der OLS-Sch¨atzer kann nicht berechnet werden, da die X′X Matrix sin- gul¨ar ist. EViews w¨urde z.B. mit der Fehlermeldung ‘Near singular matrix’
abbrechen, Stata w¨urde die linear abh¨angigen Variablen mit einer Warnmel- dung aus der Regression entfernen.
Diese Annahme stellt sicher, dass der Koeffizientenvektorβeindeutigist. Diese Bedingung kann alternativ auch folgendermaßen geschrieben werden:
Xβ(1) =Xβ(2) wenn und nur wenn β(1) =β(2)
In anderen Worten, falls X keinen vollen Spaltenrang hat ist der Koeffizi- entenvektor nicht identifiziert, die gemeinsame Verteilung von y und X ist diesem Fall mit vielen m¨oglichen Koeffizientenvektorenβˆkompatibel, es kann kein eindeutiger Koeffizientenvektor berechnet werden.
1Unter dem Spaltenrang versteht man die Anzahl linear unabh¨angiger Spaltenvektoren einer Matrix; in einer grafischen Interpretation ist der Spaltenrang die Dimension des von den Spalten- vektoren aufgespannten Vektorraums.
2Wenn man aus den Zeilen dern×k MatrixX eine nichtsingul¨arek×k Matrix bilden kann (d.h. eine Matrix, deren Determinante nicht Null ist), hatX vollen Spaltenrang.
3Eine lineare Abh¨angigkeit zwischen den Spaltenvektoren besteht, wenn mindestens ein Spal- tenvektor als Linearkombination der restlichen Spaltenvektoren dargestellt werden kann.
A3: Exogenit¨at der erkl¨arenden Variablen: Die Elemente der DatenmatrixX sind stochastisch unabh¨angig4 von den St¨ortermen ε f¨ur alle i. Das bedeutet, dass die erkl¨arenden x Variablen keinen Beitrag zur Erkl¨arung der St¨orterme εi leisten d¨urfen. Die stochastische Unabh¨angigkeit zwischen εi und den er- kl¨arendenx Variablen kann kompakt geschrieben werden als
E(εi|X) = 0
Aufgrund des Gesetzes der iterierten Erwartungen impliziert dies auch E(εi) = 0.
Man beachte, dass sich diese Annahme auf die St¨orterme der Grundgesamt- heit bezieht, nicht auf die Residuen der Stichprobe! Die Stichprobenresiduen sind aufgrund der Bedingungen erster Ordnungimmer unkorreliert mit den x Variablen.
Diese Annahme steht im Zentrum der ¨Okonometrie und wird uns noch ausf¨uhrlicher besch¨aftigen.
Annahme A3 fordert, dass die St¨orterme εi nicht nur von den individuenspe- zifischen xih stochastisch unabh¨angig sein m¨ussen, sondern von allen xjh, mit j = 1, . . . , n und h = 1, . . . , k. F¨ur Querschnittsdaten impliziert dies, dass der St¨orterm eines Individuums i stochastisch unabh¨angig sein muss von den Regressoren dieses Individuumsisowie von den Regressoren aller anderen In- dividuen j. F¨ur Zeitreihendaten bedeutet diese Annahme, dass der St¨orterm der Periodetstochastisch unabh¨angig sein muss von allenx-Variablen vergan- gener, gegenw¨artiger und zuk¨unftiger Zeitperioden!
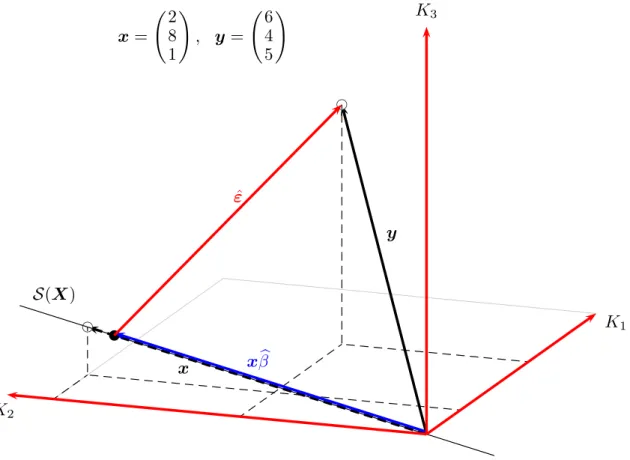
Eine intuitive Vorstellung vom Problem vermittelt Abbildung 6.1. Durch eine Korrelation zwischen xund ε wird der mit OLS gemessene Einfluss von x auf y gewissermaßen ‘verschmutzt’, OLS liefert deshalb falsche Ergebnisse.
Vereinfacht gesprochen erfordert diese Annahme, dass der datenerzeugende Prozess, der die x erzeugt, unabh¨angig vom datenerzeugende Prozess sein muss, der die St¨orterme ε erzeugt. Regressoren, die diese Annahme verlet- zen, werden endogene Regressoren genannt. Wir werden gleich zeigen, dass bei einer Verletzung dieser Annahme der OLS Sch¨atzer weder erwartungstreu noch konsistent ist.
Leider ist diese Annahme in der Praxis ziemlich h¨aufig verletzt, wichtige Bei- spiele sind
• Fehlende relevante Variablen (‘omitted variables’): wenn eine nicht in der Regression vorkommende Variable mityund mindestens einer in der Regression vorkommenden x Variable korreliert ist;5
• Simultane Kausalit¨at: wenn z.B. eine einzelne Gleichung eines Mehrglei- chungssystems (wie z.B. eine Konsumfunktion) mit OLS gesch¨atzt wird sind die Ergebnisse systematisch verzerrt;
4Stochastische Unabh¨angigkeit bedeutet, dass die gemeinsame Wahrscheinlichkeit gleich dem Produkt der Randwahrscheinlichkeiten ist, d.h.f(x, y) =f(x)f(y).
5EinSelektionsbiaskann als ein Spezialfall eines‘omitted variables bias’ angesehen werden.
Exkurs: Bedingter Erwartungswert
SeienXundU zwei Zufallsvariablen mit der gemeinsamen Dichtef(x, u). Die Rand- dichte von X und U ist definiert als
f(x) = Z
f(x, u)du bzw. f(u) = Z
f(x, u)dx Die aufX bedingte Dichte von U ist definiert
f(u|x) = f(x, u) f(x)
Zwei Zufallsvariablen sind stochastisch unabh¨angig, wenn f(x, u) =f(x)f(u)
Der Erwartungswert von U ist definiert als E(U) = R
uf(u)du, und der auf X bedingte Erwartungswert von U ist
E(U|X =x) = Z
uf(u|x)du
Wenn U und X stochastisch unabh¨angig sind folgt daraus unter bestimmten Re- gularit¨atsbedingungen, dass der auf X bedingte Erwartungswert von U gleich dem unbedingten Erwartungswert vonU ist, denn
E(U|X =x) = Z
uf(u|x)du= Z
uf(x, u) f(x) du
= Z
uf(x)f(u)
f(x) du (Unabh¨angigkeit)
= Z
uf(u)du≡E(U) wennf(x)>0.
Also folgt aus den beiden Annahmen E(U) = 0 und stochastischer Unabh¨angigkeit von X und U
E(U|X =x) = 0
Andererseits impliziert die Annahme E(U|X = x) = 0 aufgrund des Gesetzes der iterierten Erwartungen auch E(U) = 0, denn E(U) = E[E(U|X = x)] = E(0) = 0.
Die Annahme E(U|X =x) = 0 ist deshalb eine weit strengere Annahme als E(U) = 0.
¶
E(ui|X) = 0:
y x
u β
E(ui|X)6= 0:
y x
u
Abbildung 6.1: Wenn E(εi|X) = 0 misst der OLS Sch¨atzer den direkten Einfluss von x auf y (linke Grafik), der OLS Sch¨atzer ist erwartungstreu.
Falls ein Regressorxmit dem St¨orterm korreliert ist (E(εi|X)̸= 0, rechte Grafik), wird dadurch die Messung des Einflusses vonxauf ygewissermaßen ‘verschmutzt’, denn in diesem Fall misst der OLS Sch¨atzer den direkten Einfluss von x auf y sowie den indirekten Einfluss von ε uber¨ x aufy gemeinsam, der alleinige Einfluss von x auf y ist mit OLS nicht mehr korrekt messbar, d.h. der OLS Sch¨atzer liefert verzerrte Ergebnisse.
• Messfehler in den erkl¨arenden Variablen: selbst ein nicht systematischer Messfehler in einer oder mehreren x Variablen f¨uhrt zu einer Korre- lation des St¨orterms ε mit den x Variablen, und somit zu verzerrten Sch¨atzungen.
All diese Probleme werden in dem sp¨ateren Kapitel ¨uber Instrumentvariablen ausf¨uhrlich diskutiert werden.
A4: St¨orterme: Die St¨orterme der Grundgesamtheit εi sind alle unabh¨angig und identisch verteilt (independent and identically distributed) mit Erwartungswert Null und Varianz σ2
εi ∼i.i.d.(0, σ2) Diese Annahme umfasst drei einzelne Annahmen:
1. Der Erwartungswert der St¨orterme in der Grundgesamtheit ist Null E(εi) = 0
Wie schon erw¨ahnt ist diese Annahme deutlich weniger streng als die vorhin getroffenen Annahme E(εi|X) = 0, denn E(εi|X) = 0 impliziert E(εi) = 0, aber E(εi) = 0 impliziert nicht E(εi|X) = 0! F¨ur sich allein genommen ist die Annahme E(εi) = 0 nicht besonders schwerwiegend, denn man kann einfach zeigen, dass sich die Verletzung dieser Annahme nur auf die Sch¨atzung des Interzepts auswirkt, was in den meisten F¨allen keine große Bedeutung hat.
Dazu nehmen wir z.B. an, dass εi = η +vi, wobei η eine Konstante (ungleich Null) und vi ein ¨ublicher St¨orterm mit vi ∼ i.i.d.(0, σ2) ist.
Dann kann das Modellyi =β1+β2xi+εi einfach umgeschrieben werden zu
yi = (β1+η) +β2xi+vi
Der Koeffizient β2 kann in diesem Modell mit OLS effizient gesch¨atzt werden, aber es gibt keine M¨oglichkeit β1 oder η einzeln zu sch¨atzen, man kann nur die Summe (β1+η) sch¨atzen. Die Daten enthalten nicht gen¨ugend Information um β1 und η einzeln zu sch¨atzen, man sagt in solchen F¨allen, β1 und η sind nicht identifiziert. Das wichtige Kon- zept der Identifikation werden wir sp¨ater im Zusammenhang mit Sy- stemsch¨atzungen allgemeiner und ausf¨uhrlicher diskutieren.
2. Homoskedastizit¨at: Jeder St¨orterm εi hat die gleiche, endliche bedingte Varianzσ2
var(εi|X) = σ2 f¨ur allei
Ist diese Annahme nicht erf¨ullt, d.h. σi2 ̸=σj2 f¨ur i̸=j, spricht man von Heteroskedastizit¨at. Da die PRF in den meisten F¨allen nur eine lineare Approximation an die bedingte Erwartungswertfunktion (CEF) ist wird diese Annahme ziemlich h¨aufig verletzt sein. Im Kapitel zur Heteroskeda- stizit¨at werden wir sehen, dass robuste Standardfehler in solchen F¨allen manchmal geeigneter sind als OLS Standardfehler.
3. Keine Autokorrelation: Die St¨orterme εi sind untereinander stochastisch unabh¨angig,
E (εiεj|X) = 0 f¨ur i̸=j
Ist diese Annahme verletzt spricht man vonAutokorrelation.
In Vektornotation k¨onnen die beiden letzten Annahmen ¨uber die St¨orterme kompakter geschrieben werden als
var(ε|X) =σ2I
Diese vier Annahmen werden f¨ur den Gauss-Markov Beweis ben¨otigt, d.h.
wenn diese vier Annahmen erf¨ullt sind ist der OLS Sch¨atzer ein BLUE (best linear unbiased estimator, oder in anderen Worten, effizient).
A5: Normalverteilung: Die St¨ortermeε sind in der Grundgesamtheit normalver- teilt.
Dies ist keine Gauss-Markov Annahme, wenn die Gauss-Markov Annahmen A1 – A4 erf¨ullt sind ist der OLS-Sch¨atzer auch dann effizient, wenn die Nor- malverteilungsannahmenicht erf¨ullt ist.6 Außerdem sind die Stichprobenkenn- werte (wie z.B. die gesch¨atzten Koeffizienten) in großen Stichproben aufgrund des zentralen Grenzwertsatzes auch dann asymptotisch normalverteilt, wenn die St¨ortermeεnicht normalverteilt sind. Die Normalverteilungsannahme wird vor allem f¨ur Hypothesentests in kleinen Stichproben ben¨otigt.
6.4 Erwartungstreue
Offensichtlich wird sich der vorhin ermittelte Vektor βˆ = (X′X)−1X′y von Stich- probe zu Stichprobe unterscheiden, wenn wir eine andere Stichprobe ziehen, werden
6Allerdings gibt es nicht sehr viele Verteilungen außer der Normalverteilung, die die Annahme der Homoskedastizit¨at erf¨ullen.
wir auch – hoffentlich nur geringf¨ugig – andere Werte f¨ur βˆ erhalten. Deshalb sind die so berechneten Koeffizienten βˆ im Gegensatz zu den Parametern der Grund- gesamtheit β selbst wieder Zufallsvariablen, genauso wie die damit berechneten Stichprobenresiduen ˆε. Von Zufallsvariablen kann man aus der Stichprobenkenn- wertverteilung Erwartungswert und Varianz berechnen, und genau dies wollen wir im n¨achsten Schritt tun.
Insbesondere interessiert uns, ob der OLS-Sch¨atzer βˆ= (X′X)−1X′y erwartungs- treue Sch¨atzungen f¨ur β liefert, d.h., ob die aus der Stichprobe berechneten Werte βˆ ‘im Mittel’ den unbeobachtbaren β entsprechen. Dazu setzen wir wieder den
‘wahren’ Zusammenhang der Grundgesamtheit y = Xβ+ε in die Formel unseres Sch¨atzers βˆ= (X′X)−1X′y ein und bilden anschließend den Erwartungswert:
βˆ= (X′X)−1X′(Xβ+ε)
| {z }
y
= (X′X)−1X′Xβ+ (X′X)−1X′ε βˆ=β+ (X′X)−1X′ε
Wir bilden den Erwartungswert
E(β) =ˆ β+ E[(X′X)−1X′ε]
Wenn die erkl¨arenden x Variablen deterministisch (bzw. ‘fixed in repeated samp- ling’) sind, ist E((X′X)−1X′ε) = (X′X)−1X′E(ε) = 0, also ist der OLS-Sch¨atzer erwartungstreu
E(β) =ˆ β
Das gilt auch f¨ur stochastische x, allerdings ist es der Beweis nicht mehr so trivial.
F¨ur ein intuitives Verst¨andnis empfiehlt es sich, einen genaueren Blick auf denk×1 Vektor X′ε zu werfen
X′ε=
x11 x21 · · · xn1
x12 x22 · · · xn2
... ... ... ...
x1k x2k · · · xnk
ε1
ε2
...
εn
=
P
ixi1εi
P
ixi2εi
P ...
ixikεi
Man kann zeigen, dass E(P
ixihεi) = 0 (f¨ur h = 1, . . . , k) wenn die St¨orterme stochastisch unabh¨angig von den erkl¨arendenxVariablen sind. Wenn die St¨orterme also unkorreliert mit denx Variablen sind sollte also E(X′ε) = 0 sein.7
Man beachte, dass wir f¨ur die Erwartungstreue nur Annahmen A1 bis A3 ben¨otigt haben, d.h. korrekte Spezifikation, voller Spaltenrang sowie Exogenit¨at der Regres- soren (E(ε|X) = 0), nicht aber die Annahmen A4 und A5 (d.h. εi ∼ i.i.d.(0, σ2) und die Normalverteilungsannahme). Deshalb ist der OLS-Sch¨atzer selbst dann er- wartungstreu, wenn die Annahmen A4 ¨uber die St¨orterme verletzt sind.
Man beachte auch, dass (X′X)−1X′ε große ¨Ahnlichkeit mit dem Sch¨atzer f¨ur βˆ hat. Der einzige Unterschied zu βˆ = (X′X)−1X′y besteht darin, dass y durch
7Dies beweist bei stochastischenxnat¨urlich nicht, dass E[(X′X)−1X′ε] = 0, dazu m¨ussten wir weiter ausholen, aber es soll den Blick auf die richtige Stelle lenken.
ε ersetzt wurde. Intuitiv kann man sich dies folgendermaßen vorstellen: wenn im systematischen Teil des Erkl¨arungsansatzes mit den VariablenXalles erkl¨art wurde, sollten die St¨orterme ε keine nutzbare Information mehr enthalten. Deshalb sollte die Anwendung des Sch¨atzers auf die St¨orterme im Erwartungswert Null liefern.
Achtung: Wir k¨onnen die Stichprobenresiduen ˆε nicht dazu ben¨utzen um zu testen, ob die St¨orterme der Grundgesamtheit ε tats¨achlich mit den erkl¨arenden Variablen Xunkorreliert sind. Wir haben bereits gezeigt, dass die Bedingungen erster Ordnung f¨ur die Herleitung des OLS-Sch¨atzers X′εˆ= 0 implizieren, d.h. die Stichprobenkor- relation zwischen X und ˆε ist aufgrund der Konstruktion unseres Sch¨atzers immer Null, auch wenn in der Grundgesamtheit eine Korrelation zwischen ε undX beste- hen sollte!
Falls die Regression ein Interzept enth¨alt ist eine Spalte von X ein Einsen-Vektor.
Die dazugeh¨orige Bedingung erster Ordnung der Minimierung der Quadratsumme der Residuen stellt in diesem Fall sicher, dass die Summe von ˆε immer Null ist, d.h.
Pn
i=1εˆi = 0. Dies muss bei einer Sch¨atzung ohne Interzept nicht gelten!
Damit haben wir die Erwartungstreue der OLS Sch¨atzer unter den Annahmen A1 – A3 bewiesen. Als n¨achstes werden wir die Varianzen der OLS Sch¨atzer berechnen, um wieder Hypothesentests durchf¨uhren zu k¨onnen.
6.5 Sch¨ atzung der Varianz von ˆ β
Die Varianz einer skalaren Zufallsvariable βbh ist definiert als var(βbh) = E[βbh − E(βbh)]2. Die gesch¨atzten Koeffizienten βˆ bilden einen k ×1 Spaltenvektor von Zu- fallsvariablen. F¨ur Hypothesentests sowie die Berechnung von Konfidenzintervallen ben¨otigen wir unter anderem die Standardfehler der gesch¨atzten Koeffizienten, die einfach die Wurzel der Hauptdiagonalelemente der Varianz-Kovarianzmatrix von βˆ sind. Diese Varianz-Kovarianzmatrix des Vektors von Zufallsvariablenβˆist definiert als
var(β) = Eˆ h
βˆ−E(β)ˆ i h
βˆ−E(β)ˆ i′
Beispiel Wennβˆder 2×1 Koeffizientenvektor des bivariaten Modells ist erhalten wir die 2×2 Varianz-Kovarianzmatrix
var(β) = Eˆ h
βˆ−E(β)ˆ i h
βˆ−E(β)ˆ i′
= E
"
βb1−E(βb1) βb2−E(βb2)
!
βb1−E(βb1) βb2−E(βb2) #
= E[βb1−E(βb1)]2 E[βb1−E(βb1)][βb2−E(βb2)]
E[βb1 −E(βb1)][βb2−E(βb2)] E[βb2−E(βb2)]2
!
= var(βb1) cov(βb1,βb2) cov(βb1,βb2) var(βb2)
!
Die Elemente auf der Hauptdiagonale sind die Varianzen und die Elemente auf der Nebendiagonale die Kovarianzen von β.ˆ
Wir haben im vorhergehenden Abschnitt bereits gezeigt, dass unter den Gauss- Markov Annahmen βˆ=β+ (X′X)−1X′ε und E(β) =ˆ β. Deshalb ist
E[βˆ−E(β)] = E[βˆ + ((X′X)−1X′ε−β]
= E[(X′X)−1X′ε]
Unter Verwendung dieses Ergebnisses erhalten wir die Varianz-Kovarianzmatrix von βˆals
var(β) = Eˆ h
βˆ−E(β)ˆ i h
βˆ−E(β)ˆ i′
= E[(X′X)−1X′ε][(X′X)−1X′ε]′
= E[(X′X)−1X′εε′X(X′X)−1]
da (AB)′ =B′A′ sowie (A′)′ =A(siehe mathematischen Appendix).
Wenn die X deterministisch sind, sind die einzigen Zufallsvariablen in diesem Aus- druck die Elemente des Vektors der St¨orterme ε. Deshalb k¨onnen wir den Erwar- tungswertoperator direkt vor die Matrix der Zufallsvariablen εε′ schreiben
var(β) = (Xˆ ′X)−1X′E(εε′)X(X′X)−1 (6.1) Zur Berechnung der eigentlich interessierenden Varianz-Kovarianzmatrix von βˆ ben¨otigen wir also die Matrix E(εε′), die wir uns nun etwas n¨aher ansehen wol- len.
Die Elemente des n×1 Spaltenvektor der St¨ortermeε haben einen Erwartungswert von Null, d.h. E(ε) =O, bzw. ausf¨uhrlicher
E(ε) = E
ε1
ε2
...
εn
=
E(ε1) E(ε2)
...
E(εn)
=
0 0 ...
0
=O
deshalb ist E(εε′) einfach die Varianz-Kovarianzmatrix der St¨orterme.
var(ε) = E
ε1−E(ε1) ε2−E(ε2)
...
εn−E(εn)
ε1−E(ε1) ε2−E(ε2) · · · εn−E(εn)
= E
ε1
ε2
...
εn
ε1 ε2 · · · εn
= E(εε′)
=
E(ε1)2 E(ε1ε2) . . . E(ε1εn) E(ε2ε1) E(ε2)2 . . . E(ε2εn)
... ... . .. ...
E(εnε1) E(εnε2) . . . E(εn)2
=
var(ε1) cov(ε1ε2) . . . cov(ε1εn) cov(ε2ε1) var(ε2) . . . cov(ε2εn)
... ... . .. ...
cov(εnε1) cov(εnε2) . . . var(εn)
Diese Varianz-Kovarianzmatrix der Grundgesamtheit erh¨alt eine sehr einfache Form, wenn man Homoskedastizit¨at (var(εi) = σ2) und Abwesenheit von Autokorrelation (cov(εi, εj) = 0 f¨ur i̸=j) unterstellt, also
var(ε) =σ2I
denn in diesem Fall ist die Varianz-Kovarianzmatrix eine einfache Diagonalmatrix.
E(εε′) =
σ2 0 . . . 0 0 σ2 . . . 0 ... ... ... ...
0 0 . . . σ2
=σ2
1 0 . . . 0 0 1 . . . 0 ... ... ... ...
0 0 . . . 1
=σ2In
wobei In die n×n Einheitsmatrix ist.
Wie schon gesagt, diese Varianz-Kovarianzmatrix der St¨orterme εi ben¨otigen wir, um die eigentlich interessierendeVarianz-Kovarianzmatrix der gesch¨atzten OLS Ko- effizienten zu berechnen, d.h. var(β).ˆ
Dies ist unter den Annahmen E(εε′) =σ2I sehr einfach, wir brauchen nur in Glei- chung (6.1) einzusetzen
var(β) = Eˆ h
βˆ−E(β)ˆ i h
βˆ−E(β)ˆ i′
= (X′X)−1X′E(εε′)
| {z }
=σ2I
X′(X′X)−1
=σ2
(X′X)−1X′X(X′X)−1
=σ2(X′X)−1
daσ2 eine fixe Gr¨oße der Grundgesamtheit ist und dieX exogen sind. Damit haben wir einen Ausdruck f¨ur die Varianz-Kovarianzmatrix des Koeffizientenvektors, der allerdings noch von der unbeobachtbaren Varianz der St¨orterme σ2 abh¨angt. Wie fr¨uher ben¨otigen wir wieder einen Sch¨atzer ˆσ2 f¨urσ2.
6.6 Ein Sch¨ atzer f¨ ur die Varianz von ε (σ
2)
F¨ur Hypothesentests ben¨otigen wir die Standardfehler der Koeffizienten. Da der Ausdruck f¨ur die Varianz von β, var(ˆ β) =ˆ σ2(X′X)−1, noch die unbeobachtbare Varianz σ2 der Grundgesamtheit enth¨alt, ben¨otigen wir einen Sch¨atzer f¨ur σ2. Den Ansatz, den wir zur Herleitung des Sch¨atzers f¨ur β w¨ahlten, n¨amlich die Minimie- rung von ˆε′ε, k¨onnen wir hier nicht anwenden, da die Zielfunktion die Varianzˆ σ2 nicht enth¨alt.
Ein m¨oglicher Kandidat f¨ur einen solchen Sch¨atzer w¨are die Varianz der Stichpro- benresiduen, aber wie schon im bivariaten Fall kann man zeigen, dass diese einen verzerrten Sch¨atzer darstellt. Wir werden aber im folgenden Beweis zeigen, dass
ˆ
σ2 = εˆ′εˆ n−k =
P
iεˆ2i n−k
ein unverzerrter Sch¨atzer f¨ur die Varianz σ2 der St¨orterme ist, wobei k die Anzahl der erkl¨arenden Variablen (inkl. Interzept) ist; (n−k) bezeichnet wieder die Anzahl der Freiheitsgrade. Die Wurzel daraus,
ˆ σ =
s εˆ′εˆ (n−k) wird Standardfehler der Regression genannt.
Dies wollen wir nun ausf¨uhrlich zeigen und beweisen.
Die St¨orterme εi sind Zufallsvariablen, und unter den fr¨uher gemachten Annahmen ist die Varianz dieser Zufallsvariablen σ2. Aber nat¨urlich ist ε = y −Xβ nicht beobachtbar. Day=Xβˆ+ ˆεundβˆ= (X′X)−1X′ykann man f¨ur die Stichproben- Residuen schreiben
εˆ=y−Xβˆ=y−X(X′X)−1X′y=
I−X(X′X)−1X′ y
Zur Vereinfachung der Schreibweise f¨uhren wir f¨ur die n × n Matrix [I−X(X′X)−1X′] das Symbol M ein, d.h. wir definieren
M :=I−X(X′X)−1X′
Die Matrix M spielt in der ¨Okonometrie eine wichtige Rolle und wirdresiduener- zeugende Matrix genannt, da – wie soeben gezeigt – M y den Residuenvektor ˆε ergibt
ˆ
ε =M y (6.2)
d.h. Vormultiplikation des n ×1 Vektors y mit der n×n Matrix M erzeugt den Residuenvektor.
Die residuenerzeugende Matrix M hat mehrere wichtige Eigenschaften
• M ist symmetrisch, d.h. M =M′
Warum? Falls M symmetrisch ist muss gelten M =M′.
Da M′ = [I − X(X′X)−1X′]′ = I′ − (X′)′((X′X)−1)′X′ = I − X(X′X)−1X′ =M
• M ist idempotent, d.h. M M =M. Dies kann einfach durch Ausmultiplizie- ren ¨uberpr¨uft werden.8
• Die MatrizenM und X sind orthogonal, d.h. M X =O, weil M X =
I−X(X′X)−1X′
X =X −X =O Daraus folgt gemeinsam mit Gleichung (6.2) auch
ˆ
ε =M ε weil
εˆ=M y =M(Xβ+ε
| {z }
y
) = Oβ+M ε=M ε
• M ist singul¨ar mit Rangn−k(idempotente Matrizen haben mit Ausnahme der Einheitsmatrix nie vollen Rang; siehe Appendix zur Matrixalgebra). Deshalb besitztM keine Inverse und der obige Zusammenhang kann z.B. nicht benutzt werden, um aus den Residuen ˆε die St¨orterme ε zu berechnen.
Exkurs: Die Verteilung der Residuen bei normalverteilten St¨ortermen Wenn die St¨orterme ε normalverteilt sind mit ε ∼ N(0, σ2I) und die X Matrix deterministisch ist erlaubt der Zusammenhang ˆε=M εdie Verteilung der Residuen zu bestimmen.
Da jede Linearkombination normalverteilter Zufallsvariablen wieder normalverteilt ist, sind unter obigen Annahmen auch die Residuen ˆε normalverteilt, weil M ε ein linearer Zusammenhang ist.
Der Erwartungswert und die Varianz der Residuen k¨onnen ebenfalls einfach be- stimmt werden:
E( ˆε) = E(M ε)
=ME(ε)
=0
8M ist idempotent weil
M M = (I−X(X′X)−1X′)(I−X(X′X)−1X′)
=II−X(X′X)−1X′−X(X′X)−1X′+X(X′X)−1X′X(X′X)−1X′
=I−2X(X′X)−1X′+X(X′X)−1X′
=I−X(X′X)−1X′=M
und
var( ˆε) = E( ˆεεˆ′)
= E(M εε′M′)
=ME(εε′)M′
=M(σ2In)M′
=σ2M M′
=σ2M Deshalb ist
ˆ
ε∼N(0, σ2M)
Man beachte, dass f¨ur dieses Resultat alle Annahmen des klassischen linearen Re- gressionsmodells erforderlich waren, und dass die Varianz-Kovarianzmatrix der Re- siduen singul¨ar ist!
Selbst wenn die St¨orterme homoskedastisch und nicht autokorreliert sind, sind die Residuen im allgemeinen heteroskadastisch und autokorreliert, da die Nebendiago- nalelemente von var( ˆε)σ2M ungleich Null sind (d.h. E(ˆεiεˆj)̸= 0 f¨ur i ̸=j und die Hauptdiagonalelemente von M ungleich groß sind (var(ˆεi)̸=σ2 f¨ur alle i).
¶ Die residuenerzeugende Matrix M ist eng verwandt mit der Projektionsmatrix P
P :=X(X′X)−1X′ daM = [I −P].
Wenn man den y Vektor mit der Projektionsmatrix P vormultipliziert erh¨alt man die gefitteten Werte, denn yb
b
y=y−εˆ=y−M y = (I−M)y =X(X′X)−1X′y=P y
Die Projektionsmatrix P wird manchmal auch ‘Hutmatrix’ (‘hat matrix’) genannt, da sie dem y Vektor ‘einen Hut aufsetzt’.
Ebenso wie die residuenerzeugende Matrix M ist auchP eine symmetrische, idem- potente und singul¨are n×n Matrix mit Rang k.
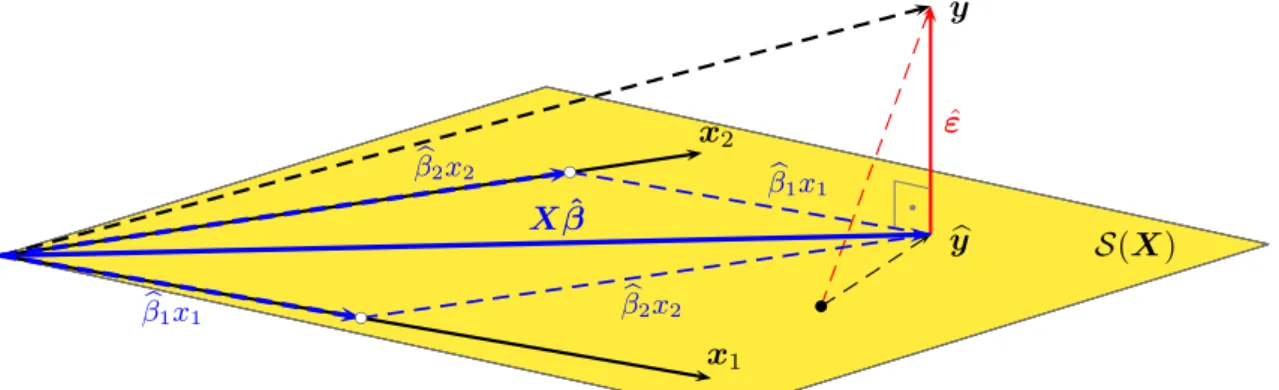
Die Bedeutung der Projektionsmatrix P und der residuenerzeugenden Matrix M wird im Abschnitt ¨uber die geometrische Interpretation des OLS-Sch¨atzers (Ab- schnitt 6.11) ausf¨uhrlich diskutiert.
Diese Ergebnisse wollen wir nun verwenden um einen erwartungstreuen Sch¨atzer ˆσ2 f¨ur das unbekannte σ2 zu ermitteln. Wir schreiben zuerst die Quadratsumme der Residuen ˆε′εˆmit Hilfe der residuenerzeugenden Matrix M an
εˆ=M y =M Xβ+M ε=M ε (da y=Xβ+ε und M X =O) εˆ′εˆ=ε′M′M ε=ε′M M ε=ε′M ε (da M sym. & idempotent ist)
F¨ur die weiteren Ausf¨uhrungen ben¨otigen wir den Spur–Operator (trace, tr): Die Spur einer symmetrischen Matrix ist definiert als die Summe der Hauptdiagonalele- mente tr(A) =a11+a22+· · ·+ann. Man kann zeigen, dass f¨ur geeignet dimensionier- te Matrizen gilt: tr(AB) = tr(BA). Da ε′M ε ein Skalar ist kann man davon die Spur nehmen ohne das Resultat zu ver¨andern. Unter Verwendung der obigen Regel k¨onnen wir also schreiben: ˆε′εˆ=ε′M ε= tr(ε′M ε) = tr(M εε′). Zur ¨Uberpr¨ufung der Erwartungstreue m¨ussen wir davon den Erwartungswert bilden:
E( ˆε′ε) = E [tr(M εεˆ ′)]
= tr [E(M εε′)] (da die Spur ein linearer Operator ist)
= tr
Mσ2I
(da M deterministisch ist und E(εε′) =σ2I)
=σ2tr(M)
=σ2tr
I −X(X′X)−1X′
(da tr(A+B) = tr(A) + tr(B))
=σ2
tr(I)−tr(X(X′X)−1X′)
(da tr(AB) = tr(BA))
=σ2
tr(I)−tr(X′X(X′X)−1)
=σ2
tr(I(n×n))−tr(I(k×k))
=σ2(n−k)
Die Varianz der Stichprobenresiduen ˜σ2ˆεi ist9
˜ σ2ˆεi = 1
n X
i
ˆ
ε2i = εˆ′εˆ n Bildet man den Erwartungswert, so folgt
E(˜σ2εˆi) = E( ˆε′ε)ˆ
n = (n−k)σ2 n
Somit untersch¨atzt die Stichprobenvarianz ˜σ2ˆεi in ihrem Erwartungswert die Popula- tionsvarianzσ2 um den Faktor (n−k)/n. Multiplizieren wir den Erwartungswert der Stichprobenvarianz mit dem Kehrwert n/(n−k), wird der ‘bias’ korrigiert und wir erhalten eine erwartungstreue Sch¨atzung der Populationsvarianz σ2. Wir definieren also ein ˆσ2
ˆ
σ2 = εˆ′εˆ n−k f¨ur das gilt
E(ˆσ2) = E( ˆε′ε)ˆ n−k =σ2
d.h. dieses ˆσ2 ist ein erwartungstreuer Sch¨atzer f¨ur die Varianz der St¨orterme σ2.■ Die Wurzel dieses Sch¨atzers f¨ur die Varianz der St¨orterme ˆσ2, d.h.
ˆ σ =
r εˆ′εˆ n−k
9Diese so definierte Stichprobenvarianz ˜σ2εˆi istkeinSch¨atzer, sondern die (Populations-) Varianz der Zufallsvariablen ˆεi. Deshalb wird durchnund nicht durchn−kdividiert.
wird Standardfehler der Sch¨atzung (Standard Error of the Regression) genannt und wird von fast allen ¨okonometrischen Software–Paketen ausgegeben.10
Damit ist unser Problem gel¨ost. Zur Erinnerung, wir hatten im letzten Abschnitt die Varianz-Kovarianz Matrix der Regressionskoeffizienten berechnet
var(β) =ˆ σ2(X′X)−1
konnten damit aber nicht viel anfangen, da σ2 ein Parameter der Grundgesamtheit – und deshalb nicht beobachtbar – ist.
Nun haben wir einen erwartungstreuen Sch¨atzer f¨ur σ2 hergeleitet, und dies erlaubt uns endlich eine erwartungstreue Sch¨atzfunktion f¨ur die Varianz-Kovarianz Matrix der OLS Sch¨atzer βˆanzugeben
c
var(β) :=ˆ σbβ2ˆ = ˆσ2(X′X)−1 = εˆ′εˆ
n−k (X′X)−1
Man beachte, dass ˆσ2 ein Sch¨atzer f¨ur die Varianz der Grundgesamtheitσ2 ist (also ein Skalar), w¨ahrend σbβ2ˆ eine k ×k Matrix mit den Sch¨atzern f¨ur die Varianzen und Kovarianzen der Koeffizienten βˆ ist. Die Wurzel der Hauptdiagonalelemente der Matrix σbβ2ˆ sind die Standardfehler der Koeffizienten.
Der Standardfehler des h-ten Koeffizienten βbh ist ˆσβb
h = ˆσ√vhh, wobei vhh das h-te Diagonalelement der Matrix (X′X)−1 ist. Da wir die Varianz aus der Stichprobe sch¨atzen ist die entsprechende Teststatistik wieder t-verteilt mit n−k Freiheitsgra- den.
Daraus folgt
t-Stat(βbh) = βbh−βh
ˆ σβb
h
= βbh−βh
ˆ
σ√vhh ∼tn−k
bzw. das Konfidenzintervall
βbh±tcα/2(ˆσ√ vhh)
Wir k¨onnen die bisherigen Ergebnisse also zusammenfassen:
Unter den Gauss-Markov Annahmen gilt
10In Stata kann mit dem postestimation Befehle(rmse)(f¨ur Root MSE) auf den Standadfehler und mite(rss)auf die Quadratsumme der Residuen zugreifen; inEViewskann mit@seauf den Standadfehler und mit @ssr (Sum of Squared Residuals) auf die Quadratsumme der Residuen zugegriffen werden. In R erh¨alt man die Quadratsumme der Residuen mitdeviance(eqname) und den Standardfehler der Regression mitsummary(eqname)$sigma.
βˆ= (X′X)−1X′y c
var(β) :=ˆ σbβ2ˆ = ˆσ2(X′X)−1 ˆ
σ2 = εˆ′εˆ n−k
F¨urεi ∼N(0, σ2) undβˆstatistisch un- abh¨angig von ˆε folgt:
βˆ∼N β, σ2(X′X)−1 t= βbh−βh
q ˆ
σ2(X′X)−1hh
∼tn−k
wobei (X′X)−1hh das h-te Diagonalelement der Matrix (X′X)−1 bezeichnet.
6.7 Die Varianz einer Linearkombination von Koeffizienten
*Um die Varianz einer Linearkombination von OLS Koeffizienten zu berechnen de- finieren wir einen k ×1 Vektor r. Durch entsprechende Wahl der Werte von von r k¨onnen wir beliebige Linearkombinationen der Parameter berechnen; wenn z.B.
r =1erhalten wir mitr′βdie Summe derβ; wennr in der Zeileheine Eins enth¨alt und sonst nur Nullen pickt r′β Element βh heraus
r′β= 1 1 1
β1
β2
β3
= X3
i=1
βi oder 0 1 0
β1
β2
β3
=β2
Definieren wir einen Skalar γ = r′β. Wir interessieren uns f¨ur die Varianz von b
γ =r′β, diese istˆ
var(bγ) =r′var(β)rˆ =σ2r′(X′X)−1r weil
var(r′β) = Eˆ
r′(βˆ−β)(βˆ−β)′r
=r′E
βˆ−β)(βˆ−β)′ r
=r′ σ2(X′X)−1 r
Beispiel F¨ur y = βb1 +βb2x2 +βb3x3 + ˆε ist die Varianz von bγ = 2βb2 −βb3 gleich var(bγ) = 4 var(βb2) + var(βb3)−4 cov(βb2,βb3). Um dies in Matrixnotation zu zeigen
definieren wir r = (0 2 −1)′ var(r′β) =ˆ 0 2 −1
var(βb1) cov(βb1,βb2) cov(βb1,βb3) cov(βb1,βb2) var(βb2) cov(βb2,βb3) cov(βb1,βb3) cov(βb3,βb2) var(βb3)
0 2
−1
=
2 cov(βb1,βb2)−cov(βb1,βb3) 2 var(bβ2)−cov(βb3,βb2) 2 cov(βb2,βb3)−var(βb3)
0 2
−1
= 4 var(βb2) + var(βb3)−4 cov(βb2,βb3)
6.8 Effizienz des OLS Sch¨ atzers
*Das Gauss Markov Theorem f¨ur die Effizienz des OLS Sch¨atzers kann nat¨urlich auch unter Zuhilfenahme der Matrixnotation bewiesen werden.
Das Gauss Markov Theorem besagt, dass bei G¨ultigkeit der Gauss Markov An- nahmen der OLS Sch¨atzer βˆ eine kleinere Varianz hat als alle alterativen linearen unverzerrten Sch¨atzfunktionen β.e
F¨ur den Beweis definieren wir eine beliebige lineare Sch¨atzfunktion βe und untersu- chen, unter welchen Bedingungen diese Sch¨atzfunktion unverzerrt ist. Sodann be- rechnen wir f¨ur diese Sch¨atzfunktion βeunter der Bedingung der Unverzerrtheit die Varianz-Kovarianzmatrix. Man kann dann relativ einfach zeigen, dass die Differenz zwischen dieser Varianz-Kovarianzmatrix und der Varianz-Kovarianzmatrix des OLS Sch¨atzers immer eine positiv-semidefinite Matrix ist.
Dies impliziert, dass f¨ur jedes einzelne Element der Sch¨atzfunktionen gilt var(βeh)−var(βbh)≥d mit d≥0
f¨ur h = 1, . . . , k. Analoges gilt auch f¨ur jede beliebige Linearkombination der Sch¨atzfunktionen.
Beweis:* Wir definieren eine beliebige lineare Sch¨atzfunktion11 βe=Cy
wobeiCeinek×nMatrix mit Konstanten ist, die eine Funktion derX sein k¨onnen,
¨ahnlich wie die (X′X)−1X′ Matrix f¨ur den OLS Sch¨atzer.
Der Sch¨atzer βeist unverzerrt, wenn
E(β) =e β Dies impliziert Restriktionen auf die Matrix C
E(β) = E(Cye )
= E(C(Xβ+ε))
=CXβ+ E(Cε)
=CXβ (wenn E(Cε) =CE(ε) = 0)
11Dieser Beweis folgt eng?, 72f.