F e 6, F e 8 [HMLN02℄, F e 10 [JJL+

Wehselwirkung auf thermodynamishe

Observable

Diplomarbeit

Dirk Müter

Fahbereih Physik

6. Dezember 2006

Inhaltsverzeihnis

1 Einleitung 4

2 TheoretisherHintergrund 5

2.1 Terme desHamilton-Oper ator s . . . 5

2.1.1 Heisenberg-Modell . . . 5

2.1.2 Zeeman-Ter m . . . 6

2.1.3 Energieeigenwert e . . . 6

2.1.4 Dzyaloshinskii-Moriya-Wehselwirkung . . . 8

2.2 Thermodynamishe Observable . . . 9

2.2.1 Magnetisierung . . . 9

2.2.2 Suszeptibilität . . . 10

2.3 Umshreiben desHamilton-Operators. . . 10

2.3.1 Umshreiben der Produktbasis . . . 10

2.3.2 Umshreiben der Operatoren . . . 11

2.4 Verringerungdes Rehenaufwands . . . 12

2.4.1 Spezielle Vereinfahungen . . . 13

3 Dzyaloshinskii-Moriya-Wehselwirkung 15 3.1 Superaustaush . . . 15

3.2 Anisotroper Austaush . . . 15

3.3 Auswahlregeln. . . 16

3.3.1 Inversion . . . 17

3.3.2 Senkrehte Spiegelebene . . . 18

3.3.3 Parallele Spiegelebene . . . 19

3.3.4 Senkrehte Rotationsahse . . . 20

3.3.5 Parallele Rotationsahse . . . 21

3.3.6 Überblik . . . 21

4 Spinringe Teil1 22 4.1 Reines Heisenberg-Modell . . . 23

4.1.1 Einuss der Temperatur . . . 24

4.1.2 Abhängigkeit vonder Wehselwirkungsstärke . . . 24

4.2 Dzyaloshinskii-Moriya-Wehselwirkung:6erSpinring (s=1/2) . . . 26

4.2.1 Bestimmung der Dzyaloshinskii-Moriya-Vektoren . . . 26

4.2.2 Entwiklung der Eigenwerte . . . 28

4.2.3 Magnetisierungund Suszeptibilität . . . 29

4.2.4 Semi-klassishe Betrahtung . . . 30

4.3 Dimerisierter6erSpinring . . . 31

4.3.1 Magnetisierungund Suszeptibilität . . . 32

4.3.2 Suszeptibilität : Positionder Peaks . . . 32

4.3.3 Eigenwerte . . . 34

4.3.4 Variationder Dimerisierung . . . 36

4.3.5 Exkurs:Sättigungsfeldstärke eines Spinrings . . . 37

4.3.6 Drehen desRinges:z-Ahse . . . 40

4.3.7 Drehen desRinges:x-Ahse . . . 40

5 Spinringe Teil2 44 5.1 Dzyaloshinskii-Moriya-Wehselwirkung:4erSpinring (s=1) . . . 44

5.1.1 Bestimmung der Dzyaloshinskii-Moriya-Vektoren . . . 44

5.1.2 Magnetisierung . . . 45

5.1.3 Suszeptibilität . . . 46

5.2 Dimerisierter4erSpinring . . . 47

5.2.1 Magnetisierungund Suszeptibilität . . . 47

5.2.2 Suszeptibilität : Positionder Peaks . . . 49

5.2.3 Suszeptibilität : Semi-klassisheErklärung . . . 51

6 Kupferdreiekskette 54 6.1 Bestimmung der Dzyaloshinskii-Moriya-Vektoren . . . 55

6.2 Magnetisierung: 9-Spin-Modell . . . 57

6.3 Magnetisierung: 12-Spin-Modell . . . 60

6.4 Dierenzkurven . . . 60

7 Zusammenfassung undAusblik 63

1 Einleitung

IndieserArbeitwerdenwehselwirkendeSpinsystemequantenmehan ishbetrahtet.Da-

zuwirdzunähstdasHeisenberg-Modelleingeführt,dasdieGrundlagezur Beshreibung

des magnetishen Verhaltens von Spinsystemen bildet. Dieses wird dann um den Zee-

man-Term erweitert, um die Dynamik des Systemsin Abhängigkeit von einem äuÿeren

Magnetfeld zu simulieren. Diesem Standardmodell wird hiernoheine weitere Wehsel-

wirkung,dieDzyaloshinskii-Moriya-Wehselwirkung,hinzugefügt.DieseWehselwirkung

stellt einen Korrekturterm dar, der das Kristallfeld unter Beahtung seiner Symmetrie

miteinbezieht . Diese Arbeit beshäftigt sih nun mit den Auswirkungen dieses Terms

auf die thermodynamish en Observablen. Zur theoretishen Untersuhung dieser Aus-

wirkungen eignen sih dabei besonders gut magnetishe Moleküle, da auf Grund ihrer

beshränktenGröÿe dienumerisheSimulation überhaupterst möglih wird.

Alsmagnetishe Moleküle bezeihnet manübliherweise Moleküle,dieeinen magnetish

aktiven Kern besitzen, z.B. paramagnetishe Ionen oder Atome. Um diesen Kern kön-

nensihdiamagnetishe Elemente benden,derenEinusshierdurhdieDzyaloshinskii-

Moriya-Wehselwirkung miteinbezogen wird. Magnetishe Moleküle liegen allgemein im

Kristallverbandvor.SinddabeidieintramolekularenWehselwirkungendeutlihstärker

als dieintermolekular en ist esmöglih, die einzelnenMoleküle losgelöst voneinander zu

betrahtenunddiemikroskopishenEigenshaftenzuberehnen.Somitkönnenaberauh

die makroskopishen Eigenshaften eines Materials aus den mikroskopishen hergeleitet

werden,dasihdiemakroskopisherfassbarenGröÿenaufGrunddervernahlässigbaren

Wehselwirkung zwishen den Molekülen als Summe über die mikroskopishen Gröÿen

ergeben.

Einige spezielle Moleküle haben in den letzten Jahren erhöhte Aufmerksamkeit in der

Forshung erfahren und auh Verwendung in der Tehnik gefunden. Ihre Synthese und

die Untersuhung ihrer magnetishen Eigenshaften wird weltweit von Physikern und

Chemikern vorangetrieben . Namentlih sind dies Eisenringe, sogenannte ferri wheels

(

F e 6

^,

F e 8

^[HMLN02℄,

F e 10

^[JJL

+

99℄,

F e 12

^[ACC

+

00℄, ...),aber auhSysteme mit an-

deren Übergangsmetallen, z.B

V 15

^[DRMMM04℄,

M n 12

^[FWK

+

01℄,

Cr 8

^[AGC

+

04℄ und

N i 4

^[Brü03℄.

Diese Arbeit befasst sih mit dem Einuss der Kristallfeldanisotropie auf die magneti-

shen Eigenshaften, vermittelt durh dieDzyaloshinskii-Moriya-Wehselwirkung. Dazu

werdenzunähstdietheoretishenGrundlagendiskutiertunddieEigenshaftenderDzya-

loshinskii-Moriya-Wehselwirkung besprohen. Anshlieÿend werden thermodynamishe

Observable, nämlih die Magnetisierung und die magnetishe Suszeptibilität , für einfa-

heSysteme (Spinringe) berehnet und derEinuss der Dzyaloshinskii-Moriya-Wehsel-

wirkung bestimmt und erläutert. Mit diesen Ergebnissen wird abshlieÿend auh eine

komplexe molekulare Kette betrahtet und die Simulation mit experimentellen Daten

abgeglihen .

2 Theoretisher Hintergrund

2.1 Terme des Hamilton-Operators

2.1.1 Heisenberg-Modell

FürdieBeshreibungmagnetisherMolekülestelltdasHeisenberg-ModelldieGrundlage

dar. Mit ihm lassen sih thermodynamishe Observable bereits in vielen Fällen ausrei-

hend präzise berehnen. Die allgemeine Form des Heisenberg-Hamiltonians sieht wie

folgtaus:

H b _Heisenberg = X

<i,j>

J ij s ~ b i · s ~ b j .

⁽¹⁾

Hierbei ist

J _ij

^{die Matrix der} Austaushparameter, die die Stärke der Wehselwirkung zwishenden einzelnen Spinsangeben.Dabei koppeln dieSpins:

•

ferromagnetishfür

J ij < 0

•

antiferromagne tish für

J ij > 0

^.

Die Kopplungallerhier betrahteten Systeme ist antiferromagne tish.

Im Falleinheitlihe rWehselwirkungsstärkeund passenderSymmetrie desSystems(z.B

bei Spinringen und -ketten) kann diese Matrix durh einen einzelnen Skalar

J

^ersetzt

werden. Dies wird in dieser Arbeit in der Diskussion der Spinringe anfänglih verwen-

det, kann jedoh auf Grund der Komplexität der anderen betrahteten Moleküle niht

beibehaltenwerden.WeitereNäherungen sinddasIsing-Modellund dasXY-Modell,die

zusammengenommen dasin diesem Abshnitt beshriebene Heisenberg-Modell ergeben.

Diese beiden Näherungen sind jedoh ebenfalls unzureihen d für die in dieser Arbeit

durhgeführten Rehnungen.

DieSummeinGleihung(1)erstrektsihüberallemiteinanderwehselwirkendenSpins,

d.h. die niht abgepaarten Spins der Elektronen in den äuÿeren Orbitalen. Damit wird

also über alle Paare

< i, j >

^{summiertfür die}

i 6 = j

^{gilt. Dieslässt sihweiter vereinfa-}

hen,wasin Kapitel 2.4erläutert wird.

Umden Heisenberg-Hamiltonian alsMatrix darstellenzukönnen,wird eineBasis benö-

tigt.Dazubietet sihhierdieProduktbasis an,dieausdemTensorproduktder Basiszu-

stände der Einteilhe noper atoren besteht

| s 1 m 1 i ⊗ | s 2 m 2 i ⊗ . . . ⊗ | s _N m _N i .

⁽²⁾

Zudem kann ein Operator

S b ²

^{eingeführtwerden, der aus demQuadrat der Summe der}

Einteilhe noperatoren

b s i

^{gebildetwird und mit dem}Hamilton-Operator vertausht

à X

i

b s i

! ²

= S b ² ,

⁽³⁾

h H, b S b ² i

= 0.

⁽⁴⁾

2.1.2 Zeeman-Term

Zur Beshreibung des Verhaltens magnetisher Moleküle in einem externen Magnetfeld

muss der Zeeman-Ter m zum Hamilton-Operator hinzugefügt werden. Dieser ist im All-

gemeinenvonder Form:

H b Zeeman = gµ B

X

i

B ~ · s b ~ i

⁽⁵⁾

Damiterhält manfür den Hamilton-Oper ator:

H b = H b _Heisenberg + H b _Zeeman = X

<i,j>

J ij s b ~ i · s ~ b j + gµ _B X

i

B ~ · s b ~ i

⁽⁶⁾

DasMagnetfeldwird nunübliherweise inRihtung derz-Ahsegelegt,wodurhnurder

z-Anteil derSpinoperato r enimZeeman-Ter mbetrahtetwerdenmuss.Stattder Summe

über dieEinteilhe noperat orenwirddazueinneuerOperator

S b z

^{deniert,derzudemmit}

H b

^und

S b ²

^{vertausht und somitdieSymmetrie des}Hamilton-Oper ators erhält

à X

i

b s ^z _i

!

= S b ^z ,

⁽⁷⁾

h H, b S b ^z i

= 0,

⁽⁸⁾

h S b ² , S b ^z i

= 0.

⁽⁹⁾

2.1.3 Energieeigenwerte

Sind die Eigenwerte und Eigenzuständ e des Hamilton-Oper ators bekannt, können die

thermodynamishenGröÿendesSystemsberehnet werden.FüreinigeSpinsystemekön-

nendieEnergieeigenwerte sogaranalytishbestimmtwerden. BeidensogenanntenPan-

taedern existiert eine Wehselwirkung gleiher Stärke aller Spins untereinander . Die

Wehselwirkungsmatrix

J ij

^enthält dementsprehend überallden gleihen Eintragauÿer aufder Hauptdiagonale, denn für

i = j

^gilt

J ii = 0

^{. Der}Hamiltonianlässtsihdannwie folgtumformen:

H b = J



 Ã X

i

b s _i

! 2

− X

i

b s ² _i



 + gµ _B B X

i

b s ^z _i

⁽¹⁰⁾

= J

"

S b ² − X

i

b s ² _i

#

+ gµ _B B S b ^z .

⁽¹¹⁾

Da alle auftretenden Operatoren miteinander kommutieren, existiert eine gemeinsame

Basis,sodassdie Eigenwerte direktermittelt werden können:

E S,M = J

"

S(S + 1) − X

i

s i (s i + 1)

#

+ gµ B BM S .

⁽¹²⁾

DieEigenwerte

S

^{ergebensihdabeiausdenmöglihenStellungenderSpins}zueinander, d.h.

S

^läuftinganzzahlige nShrittenvon

0

^bzw.

1/2

^{(jenahmöglihem}Grundzustand) bis

P

i s _i

^{. Dabeigilt für diemagnetishe} Quantenzah l

M _S = ( − S, − S + 1, ..., S − 1, S)

^.

Hierbeiistjedoh zubeahten,dassdieEigenwertenohmehrfahentartet seinkönnen.

MitdieserMethodelassensihbeispielsweisedieEigenwertevonDimeren,Dreiekenund

Tetraedern berehnen. Aber auh bei Systemen, bei denen niht alle Spins miteinander

wehselwirken, ist esmöglih, dieEigenwerte analytish zu bestimmen, falls sih die

J

^-

MatrixinBlökezerlegenlässt(sieheReferenzen[Kou97℄,[Kou98℄,[BSS00℄und[Hag03℄).

EinBeispielhierfüristdasSpinquadrat.DieIndizierungderSpinswirddabeisogewählt,

dass sih jeweils die Spins 1 und 2, sowie 3 und 4 an gegenüber liegenden Eken des

Quadratsbenden. DieWehselwirkungsmatrix nimmt dabeidiese Form an:

J ij = J ·



 



0 0 1 1 0 0 1 1 1 1 0 0 1 1 0 0



 

 .

⁽¹³⁾

DerHamiltonian fürdiesen Fall lässtsihzusammensetzen auseinem Term, indem alle

SpinsmiteinanderwehselwirkenabzüglihzweierDimerebestehendausdenSpins1und

2 bzw.3 und 4.Damitsieht der Hamilton-Operator wie folgt aus:

H b = J



 Ã ₄

X

i

b s i

! ²

− ( b s 1 + b s 2 ) ² − ( b s 3 + b s 4 ) ²



 + gµ B B X

i

b s ^z _i .

⁽¹⁴⁾

Die Eigenwerte diesesHamiltonians lauten dann

E M,S = J [S(S + 1) − S 12 (S 12 + 1) − S 34 (S 34 + 1)] + gµ B BM S .

⁽¹⁵⁾

Dabei ist

S

^{wieder der} Gesamtspin, während

S 12

^und

S 34

^die Spinstellungen der Spins 1 und 2 bzw. 3 und 4 zueinander beshreiben. So läuft beispielsweise

S 12

^{in ganzzahli-}

gen Shritten von

| s 1 − s 2 |

^bis

| s 1 + s 2 |

^{. Die zugehörige magnetishe} Quantenzahl kann

dementsprehenddie Werte

{− S 12 , − S 12 + 1, . . . , S 12 − 1, S 12 }

^annehmen.

Im allgemeinen Fall, und insbesondere unter Hinzunahme der Dzyaloshinskii-Moriya-

Wehselwirkung,könnendieEigenwertenihtanalytishberehnetwerden.Daherwerden

sie in dieserArbeitdurh exakteDiagonalisierung desHamiltonians ermittelt.

2.1.4 Dzyaloshinskii-Moriya-Wehselwirkung

Die in dieser Arbeit betrahtete anisotrope Korrektur zu den zuvor genannten Termen,

dieDzyaloshinskii-Moriya-Wehselwirkung, istvonder Form:

H b DM = X

<i,j>

D ~ ij · ³

~ b s i × s ~ b j

´

(16)

Dabeiexistiert fürjedesKreuzproduktvonwehselwirkendenSpinseinVektor

D ~

^.Dieser

VektormussdurhBetrahtung der Kristallfeldsymmetrietheoretishbestimmtwerden.

Die von Moriya hierzu beshriebenen Auswahlregeln und deren Anwendung werden in

einem späteren Abshnitt (Kap. 3) diskutiert. Nimmt man diesen Korrekturterm zum

Hamilton-Operatorhinzu,wirddiezuvorverwendeteSymmetriegebrohenunddieOpe-

ratoren

S b ^z

^und

S b ²

kommutieren niht mehr mit demHamiltonian.

h H, b S b ^z i

6

= 0,

⁽¹⁷⁾

h H, b S b ² i

6

= 0.

⁽¹⁸⁾

Daher werden dieEnergieeigenwert e hier numerish durh Diagonalisierung des Hamil-

ton-Operators bestimmt.Dieser nimmt dabei diese Forman:

H b = X

<i,j>

h J _ij s ~ b _i · s ~ b _j + D ~ _ij · ³ b ~

s _i × s ~ b _j ´i

+ gµ _B X

i

B ~ · s ~ b _i .

⁽¹⁹⁾

Betrahtet mannun den Fall ohne externes Magnetfeld, konkurrieren die ersten beiden

Terme um die Ausrihtung der Spins. Für ein Spinpaar wird der Heisenberg-Term im

Falle antiferromagne tisher Kopplung minimal,wenndieSpinsantiparallel gestelltsind.

Der Dzyaloshinskii-Moriya-Term hingegen bewirkt eine senkrehte Stellung der Spins

zueinander.Im klassishenVektormodelllässtsihder Winkel

a

^{zwishenzweiSpins für}

den die Energie extremal wird somit ausrehnen. Da durh den Heisenberg-Term keine

ausgezeihneteRaumrihtungvorgegebenwird,könnensihdieSpinssoausrihten,dass

der Einuss desDzyaloshinskii-Moriya-Terms maximalwird, d.h dasKreuzprodukt der

Spins steht antiparallel zum Dzyaloshinskii-Moriya-Vektor. Daher wird

D ~

^{durh seinen}

Betrag

D

^{ersetzt und manerhält:}

E = J ~ s 1 · s ~ 2 + D ( s ~ 1 × s ~ 2 )

⁽²⁰⁾

= J k s 1 k k s 2 k cos(a) + D k s 1 k k s 2 k sin(a).

⁽²¹⁾

Durh Dierenzierender Gleihungnah

a

^{undNullsetzen}

dE

da = − J k s 1 k k s 2 k sin(a) + D k s 1 k k s 2 k cos(a) = 0

⁽²²⁾

ergibt sihder Wert

D

J = tan a

⁽²³⁾

⇒ a = arctan µ D

J

¶

.

⁽²⁴⁾

Auf Grundder Periodizit ät desTangens wird einExtremum auhfür einen Winkel von

e a = a + π

^{erreiht. Dieser Winkel entspriht dann im} antiferromagnet ish en Fall (Ab- bildung 1(a)) demgesuhten Minimum, der andere demMinimum für ferromagnetishe

Kopplung (Abbildung1(b)).

(a)antiferromagnetisheKopplung (b)ferromagnetisheKopplung

Abb. 1:energetishgünstigste Spinstellung ohneMagnetfeld

2.2 Thermodynamishe Observable

2.2.1 Magnetisierung

Von groÿem Interesse bei der Untersuhung magnetisher Moleküle ist der Verlauf der

MagnetisierunginAbhängigkeitvomäuÿerenMagnetfeld.Sieistalsthermodynamisher

Erwartungswe rt desSpin-Operat ors deniert. Für denSpin-Operat or wird in dieserAr-

beit der Operator

S b ^z

^{verwendet, da dasMagnetfeld immer in z-Rihtung gelegt sei.Um}

Eektezubewerten, dievonderRihtung desMagnetfeldsabhängen,wird daherimmer

nur dasMolekül gedreht. Manerhält für dieMagnetisierung:

M = − gµ B

DD S b ^z EE

= − gµ B

Z Spur ³ exp h

− β H b i

· S b ^z ´

.

⁽²⁵⁾

Dabeisei

β

^{die inverse}Temperatur,

β = 1

k B T

⁽²⁶⁾

und

Z

^dieZustandsumme deskanonishen Ensembles

Z = Spur ³ exp h

− β H b i´

.

⁽²⁷⁾

2.2.2 Suszeptibilität

ZurErmittlungdesmagnetishenVerhaltenseinesMaterialseignetsihhäugbesserdie

magnetisheSuszeptibilität alsdieMagnetisierung. SieistalsAbleitungder Magnetisie-

rung nahdem Magnetfeld deniert

χ = ∂M

∂B = g ² µ ² _B β µ¿¿³

S b ^z ´ 2 ÀÀ

− DD

S b ^z EE 2 ¶

.

⁽²⁸⁾

2.3 Umshreiben des Hamilton-Operators

UmdieDiagonalisierung durhführenzu können, müssen dieimHamiltonian auftreten-

denOperatoren durhsolheersetztwerden,derenWirkungsweiseaufdieProduktbasis-

zustände numerish modellierbar ist. Zudemwird die Basis selbst an dieComputerver-

arbeitung angepasst.

2.3.1 Umshreiben derProduktbasis

DiebisherverwendetenBasiszuständebestehenausdemTensorproduktderEigenzustän-

dederEinteilhe noperatoren,vorzugsweiseder

b s ^z _i

-Operatoren.DieseBasiswirdweiterhin für dasAufstellen desHamiltonians benutzt, jedoh werdendie magnetishen Quanten-

zahlen durh so genannte Anregungen ersetzt. Dies ist eine einfahe Umformung, die

dazu dient die numerishe Verarbeitung zu erleihtern. Die alten Basiszustände sehen

wie folgtaus:

| s 1 m 1 i ⊗ | s 2 m 2 i ⊗ . . . ⊗ | s N m N i = | s 1 m 1 , s 2 m 2 , . . . , s N m N i .

⁽²⁹⁾

FürdieAnregungen

a

^gelte

a = s − m

^{,d.h.dieniedrigsteAnregungentsprihtderhöhs-}

tenmagnetishen Quantenzahl undumgekehrt,wasbeiderWirkungsweise derOperato-

ren zu beahten ist.Dieswird in dievorhergehende Formeleingesetzt unddahingehend

vereinfaht,dass nur Systeme betrahtet werden, in denen alle Teilsysteme dengleihen

Spin tragen

| s 1 m 1 , s 2 m 2 , . . . , s N m N i = | a 1 , a 2 , . . . , a N i .

⁽³⁰⁾

2.3.2 Umshreiben derOperatoren

Zum Aufstellen desHamiltonians wird die zuvor eingeführte Basisverwendet. Zunähst

müssen das Skalar- und das Kreuzprodukt aufgelöst werden. Da die Basis auh Eigen-

basis der

S b ^z

^{- und}

b s ^z _i

-Operatoren ist, müssen diese niht ersetzt werden, jedoh ist ihre Wirkungsweise der Anregungsbasisanzupassen:

b

s ^z _i | a 1 , . . . , a i , . . . , a N i = ~ (s i − a i ) | a 1 , . . . , a i , . . . , a N i ,

⁽³¹⁾

S b ^z | a 1 , a 2 , . . . , a N i = ~ X

i

(s i − a i ) | a 1 , a 2 , . . . , a N i .

⁽³²⁾

Deraufgelöste Heisenberg-Anteil desHamiltonians sieht nunwie folgt aus:

H b Heisenberg = X

<i,j>

J ij

³ b

s ^x _i b s ^x _j + s b ^y _i b s ^y _j + b s ^z _i s b ^z _j ´

.

⁽³³⁾

Die

b s ^x

^-und

b s ^y

-Operatoren werdendurhdieAuf-undAbsteigeoperatoren ersetzt,deren Wirkung aufdie Basiszuständeabzubilden ist

b s ^x = 1

2

¡ s b ⁺ + b s ⁻ ¢

,

⁽³⁴⁾

b s ^y = i

2

¡ s b ⁻ − b s ⁺ ¢

.

⁽³⁵⁾

Auhhieristzu beahten,dassihreWirkungsweise sihin der Anregungsbasisumkehrt:

b s ⁺ _i | a 1 , . . . , a i , . . . , a _N i = ~ p

a (2s − a + 1) | a 1 , . . . , a i − 1, . . . , a _N i ,

⁽³⁶⁾

b s ⁻ _i | a 1 , . . . , a _i , . . . , a _N i = ~ p

(2s − a) (a + 1) | a 1 , . . . , a _i + 1, . . . , a _N i .

⁽³⁷⁾

Manerhält sofür den umgeformten Heisenberg-Hamiltonian:

H b Heisenberg = X

<i,j>

J ij

· 1 2

³ b

s ⁺ _i b s ⁻ _j + b s ⁺ _j b s ⁻ _i ´ + b s ^z _i s b ^z _j

¸

.

⁽³⁸⁾

Analogdazu mussauhder Dzyaloshinskii-Moriya-Term umgeformt werden.Dabeiwird

ausgenutzt, dass alle paarweise auftretenden Operatoren für

i 6 = j

^{vertaushen und der}

Fall

i = j

^{wie im ersten Kapitel erwähnt} ausgeshlossenist. Es folgtdann:

H b DM = X

<i,j>

½ iD ^x _ij 2

³ b

s ⁻ _i s b ^z _j − b s ⁺ _i s b ^z _j − b s ⁻ _j b s ^z _i + s b ⁺ _j b s ^z _i ´

+ D ^y _ij 2

³

b s ⁺ _j b s ^z _i + s b ⁻ _j b s ^z _i − s b ⁺ _i b s ^z _j − b s ⁻ _i b s ^z _j ´

(39)

+ iD _ij ^z 2

³ b

s ⁺ _i b s ⁻ _j − b s ⁻ _i b s ⁺ _j ´¾

.

Nah weiterenUmformungen erhält der Termdiese Form:

H b DM = X

<i,j>

 

 b s ^z _i



 −b s ⁻ _j

³

iD _ij ^x + D ^y _ij ´ 2 + b s ⁺ _j

³

− iD ^x _ij + D _ij ^y ´ 2





+ s b ^z _j



b s ⁻ _i

³

iD ^x _ij − D _ij ^y ´ 2 − b s ⁺ _i

³

iD ^x _ij + D _ij ^y ´ 2





⁽⁴⁰⁾

+ iD _ij ^z 2

³ b

s ⁺ _i b s ⁻ _j − b s ⁻ _i b s ⁺ _j ´¾ .

Wie man sieht, ist der letzte Anteil einem Teil des Heisenberg-Hamilton ians sehr ähn-

lih, so dass sih diese für den endgültigen Hamiltonian noh zusammenfassen lassen.

Der Zeeman-Anteil muss niht verändert werdenund wird direkt übernommen. Der im

Rehner verarbeiteteHamiltonianlautet dann:

H b = X

<i,j>

 

 b s ^z _i



 −b s ⁻ _j

³ iD _ij ^x + D ^y _ij ´ 2 + b s ⁺ _j

³ − iD ^x _ij + D _ij ^y ´ 2





+ b s ^z _j



b s ⁻ _i

³

iD _ij ^x − D ^y _ij ´ 2 − b s ⁺ _i

³

iD _ij ^x + D _ij ^y ´ 2





⁽⁴¹⁾

+

· b s ⁺ _i b s ⁻ _j

µ J _ij + iD ^z _ij 2

¶

+ b s ⁻ _i b s ⁺ _j

µ J _ij − iD ^z _ij 2

¶¸

+ J ij b s ^z _i b s ^z _j o

+ gµ B B S b ^z .

2.4 Verringerung des Rehenaufwands

ZurVerkürzungder RehenzeitlassensihnoheinigeSymmetriendesHamilton-Opera-

torsausnutzen.Dader Hamiltonianeine Observableist,gilt auhnahdem Hinzufügen

desDzyaloshinskii-Moriya-Terms weiterhin, dassder Hamiltonian hermiteshist

H b = H b ^† .

⁽⁴²⁾

Daher ist es möglih nur die Hälfte des Hamiltonians zu berehnen und anshlieÿend

den adjungierten Operator zu addieren. Im Detail füllen einige Operatoren genau die

transponierteMatrixder anderen. Der komplexkonjugierteAnteil wird alleindurhdie

Vorfaktoren der Komponente n der Dzyaloshinskii-Moriya-Vektoren aus Gleihung (41)

erzeugt.Es gelten diefolgenden Beziehungen:

X

<i,j>

b

s ^z _i b s ⁻ _j = X

<i,j>

³ b s ^z _i b s ⁺ _j ´ †

,

⁽⁴³⁾

X

<i,j>

b s ^z _j b s ⁻ _i = X

<i,j>

¡ s b ^z _j b s ⁺ _i ¢ †

,

⁽⁴⁴⁾

X

<i,j>

s b ⁺ _i b s ⁻ _j = X

<i,j>

³

b s ⁻ _i b s ⁺ _j ´ †

.

⁽⁴⁵⁾

Demnahbrauhen nurdiejeweilslinken Seitender Gleihungen (43)bis(45)berehnet

zuwerdenundfürjedenangelegtenEintragindieMatrixdesHamiltoniansandertrans-

ponierten Stelle der gleihe Eintrag mit dem passenden Vorfaktor (s. Gleihung (41))

geshrieben werden.

DerIsing-Anteil

P

<i,j>

³

J ij s b ^z _i b s ^z _j ´

ist in der bisher verwendetenBasiseine Diagonalma-

trix, daherkann dieserTermauhdirekt in dieDiagonale desHamiltonians geshrieben

werden. Dain den nahfolgenden Kapiteln thermodynamishe Observable wie etwa die

Magnetisierung untersuht werden sollen, muss der Zeeman-Ter m für jede betrahtete

Magnetfeldstärkeerneut hinzugefügt werden. DieserTermistjedohwie der Ising-Term

diagonal, sodasser analogdazu verarbeitet werden kann.

BisherwurdeimmerdievolleWehselwirkungsmatrix

J ij

^{betrahtet,diesistjedohniht}

zwingend notwendig, da auf Grund der Symmetrie desHeisenberg-Terms diese Symme-

triebeziehung gilt:

J ij = J ji .

⁽⁴⁶⁾

Dementsprehen dmüssenbeiderSummierungüber

h i, j i

^{inGleihung(41)nurdiePaare}

betrahtet werden für die

j > i

^{gilt. Die} ursprünglihe Matrix wird dabei in eine obere Dreieksmatrix überführt,wobeidieverbleibendenEinträgemit2zumultiplizierensind,

da zuvor die Beiträge für

b ~s _i b ~s _j

^und

b ~s _j b ~s _i

^{gezählt wurden, nun aber nur für}

b ~s _i b ~s _j

^{. Für die}

Dzyaloshinskii-Moriya-VektorenkannaufähnliheWeisevorgegangenwerden,jedohgilt

auf GrunddesKreuzprodukte s imDzyaloshinskii-Moriya-Term:

D ~ _ij = − D ~ _ji .

⁽⁴⁷⁾

Auhhier genügt esdahernurüber diePaaremit

j > i

^zusummieren.

2.4.1 SpezielleVereinfahungen

Für Systeme, in denen alle beteiligten Komponenten den Spin

s = 1/2

^{tragen, lassen}

sih noh weitere nützlihe Vereinfahungen in den Programmablauf implementieren.

Betrahtet man zunähst die Vorfaktoren, die durh das Anwenden der

s b ^±

-Operatoren entstehen,stelltmanfest,dasssiefür

s = 1/2

^nur

0

^oder

1

^{seinkönnen,daherkannhier}

dasWurzelziehen entfallen.

Zusätzlihlässtsih dieBasissosortieren,dassdieTerme desHamiltonians,dienur

b s ^±

^-

und

s b ^z

-OperatorenenthaltennurjeweilsEinträgeoberhalboderunterhalbderHauptdia- gonaleerzeugen.Dasbedeutet,dassfür dieersten dreiTermeausGleihung(41)nurdie

Hälfte des Hamiltonians beim Aufstellen durhlaufen werden muss. Die anderenbeiden

Terme erzeugen wie bereits gesagt nur Einträge aufder Hauptdiagonalen.

Mit eben einer solhen Sortierung der Basis lässtsih das Problem noh weiter verkür-

zen.DazuwirdalserstesBasiselement,der Zustandmitder geringstenGesamtanregung

( | 0, 0, . . . , 0 i )

^{gewählt und als letztes der Zustand mit der höhsten} Gesamtanregung

( | 1, 1, . . . , 1 i )

^{. Davon ausgehend wird für das zweite Element an der Stelle}

i

^{die Anre-}

gung heraufgesetzt und beim vorletzten Basiselement die

i

^{-te Anregung} herabgesetzt.

Manerhält beispielhaftfür drei Spinsdiese Basis:

| 0, 0, 0 i | 1, 0, 0 i | 0, 1, 0 i | 1, 1, 0 i

| 0, 0, 1 i | 1, 0, 1 i | 0, 1, 1 i | 1, 1, 1 i .

⁽⁴⁸⁾

Wie man sieht,hat mit dieser Sortierung der letzte Basiszustand genau die zumersten

komplementäre Anregung. Dies gilt ebenso für den zweiten und den vorletzten Basis-

zustand und setzt sih dementsprehend für alle weiteren Paare fort. Dadurh erhält

man aber von den ersten beiden Termen aus Gleihung (41) Einträge im Hamiltonian,

dieantisymmetrish bezüglih der zweiten Hauptdiagonale (vonlinks unten nahrehts

oben) sind. Dabeierzeugen jeweilsdie

b s ^±

-Operatoren symmetrishe Einträge. Die Anti- symmetrie wird durh die

b s ^z

-Operatoren und die komplementäre Anregung erzwungen.

FürdendrittenTermausGleihung(41)erhält mandementsprehendnursymmetrishe

Einträge, da dieserja nur aus

b s ^±

-Operatoren besteht.

Zusammengefasstkannmanalsofüreins=1/2-SystemdasAufstellendesHamiltonians

sehr stark vereinfahen. Zwei Beiträge sind nur auf der Hauptdiagonalen ungleih Null

und für die anderen genügt es, ein Viertel der Matrix zu durhlaufen und die anderen

drei Viertel auf Grund der Symmetrie zu füllen.Diese Vereinfahungen lassensih aber

auhaufSystememithöherenEinzelspinsübertragen,dazumussnurdiehiervorgestellte

Sortierung der Basiszustände entsprehend angepasst werden. Ebenso ist der Vorfaktor

der beim Anwenden der

s b ^±

-Operatoren entsteht für ein System mit

s = 1

^{entweder 0}

oder

√ 2

^{und mussdamit niht imProgramm berehnet werden.Für nohgröÿere Spins}

ist letzteresjedoh niht mehrzulässig.

3 Dzyaloshinskii-Moriya-Wehselwirkung

3.1 Superaustaush

Dem Heisenberg-Modell liegt die direkte Austaushwehselwirkung zu Grunde, bei der

sih die Ordnung der Spins nur zwishen sih überlappenden Orbitalen einstellt. Die

Besetzung dieser Orbitale wird dabei durh das Pauli-Prinzip und die Coulomb-Weh -

selwirkungbestimmt.Esexistieren aber auhandere,indirekteAustaushmöglihkeiten.

Ein Beispiel ist der Superaustaush, der durh das Hubbard-Modell beshrieben wird.

DerHubbard-Hamilton ian erhält diese Form:

H b = H b t + H b U = − t X

<i,j>,σ

³

c ⁺ _i,σ c j,σ + c ⁺ _j,σ c i,σ

´

+ U X

i

n i,↑ n i,↓ .

⁽⁴⁹⁾

DabeisinddieOperatoren

c i,σ

^und

c ⁺ _i,σ

^{Vernihterbzw.ErzeugerfüreinElektronmitSpin}

σ

^und

n i

^derTeilhenzahloperat oramPlatz

i

^{.DerersteTeildes}Hamiltoniansbeshreibt einHüpfenderElektronenzwishendeneinzelnenPlätzen,wodurhsiekinetisheEnergie

gewinnen.DurhdenzweitenTermwirdderCoulombenergieRehnunggetragen,diedie

Elektronen aufbringenmüssen,um ihrenderzeitigen Platz zuverlassen.Dieses wird erst

beiantiparallel erStellungderSpinsermögliht,dadasPauli-PrinzipeinHüpfenzwishen

Orbitalen mit gleihgeriht eten Spins untersagt. Dies führtfür diesen Fall zu einer Ab-

senkungderGesamtenergiedesSystemsvonderGröÿenordnung

− 2t ² /U

^{(siehe[Ope04℄)}

und fördert eine antiferromagne tishe Anordnung der Spins. Der Superaustaush kann

dann imHeisenberg-Hamilton ian modelliert werden,indem die Austaushparameter

J ij

entsprehend modiziertwerden. Manerhält einen eektiven Hamiltonian[Maj00℄:

H b ef f = X

<i,j>

J ij s b ~ i · s ~ b j .

⁽⁵⁰⁾

3.2 Anisotroper Austaush

Im Superaustaush ndet das Hüpfen der Elektronen häug niht direkt statt, sondern

wird durh Sauerstoatome vermittelt. Die Rolle des Sauerstos kann auh durh die

Spin-Bahn-Kopplung übernommen werden, wobei der angeregte Zustandeines Ions mit

dem Grundzustand des anderen wehselwirkt. Dieser Austaush wird als anisotroper

Austaush oder Dzyaloshinskii-Moriya-Wehselwirkung bezeihnet (s. [Ope04℄) und ist

von der bereits bekannten Form:

H b DM = X

<i,j>

D ~ ij · ³

~ b s i × s ~ b j

´

.

⁽⁵¹⁾

DieseWehselwirkung kanndann,wiezuvorin Kapitel2.1gezeigtwurde,alsKorrektur-

term desHeisenberg-Modellsaufgefasst werden.

3.3 Auswahlregeln

In seinem Artikel [Mor60℄ zeigte T. Moriya wie sih die Dzyaloshinskii-Moriya-Vekto-

ren mit Hilfe der allgemeinen Kopplungstensoren berehnen lassen. Bei entsprehender

PunktsymmetriedesSystemsvereinfahensihdiese Tensoren jedohderart, dassMori-

ya hierfüreinfahe Auswahlregelnfür dieRihtung von

D ~ _ij

^{aufstellen konnte.DieseArt}

der Wehselwirkung war bereitseinige Jahre zuvor [Dzy58℄vonI.Dzyaloshinskiiphäno-

menologish hergeleitetworden.

BetrahtetmanzweimiteinanderwehselwirkendeSpinsAundB,soistihreWehselwir-

kung unter Vernahlässigung der restlihen Atome bzw. Ionen im Molekül isotrop. Der

Einuss der Umgebung kann aber niht immer übergangen werden. Umdiesen Einuss

zu bestimmen wird die Punktsymmetrie ausgehend vom Mittelpunkt der Streke AB

zwishendenbeidenSpinsbetrahtet.Moriyastellte seine AuswahlregelnfürFestkörper

auf, so dass er Randeekte vernahlässigen konnte. Will man diese Regeln bei einem

Molekülanwenden,musszunähstüberprüftwerdenwie vielderUmgebung in dieSym-

metrieüberl egungen miteinzubeziehen ist. Die Oberähe des Moleküls kann dabei eine

im Festkörper vorhandene Symmetrie brehen und daher sollten weit entfernte Atome

(Ionen)niht mehr betrahtet werden.

Im Folgenden sollendie Auswahlregelnund ihre Auswirkungan Hand von Modellsyste-

men erklärt und angewendet werden. Für diese Überlegungen wird angenomme n, dass

dieSpinsan Ionengebunden sind unddaherdieUmgebung ebenfallsausIonen besteht.

DieseWahlsollnihtdieAnwendbarkeitder Auswahlregelneinshränken,sonderndient

nur der sprahlihen Vereinfahung.

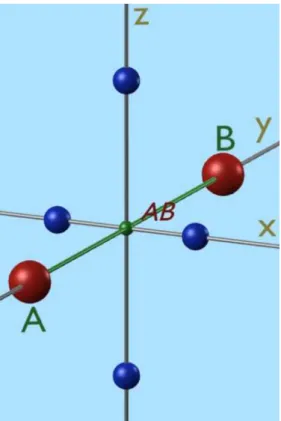
3.3.1 Inversion

Führt manamMittelpunkt zwishen den

Abb. 2: Inversionsym metrie beiden Spins eine Punktspiegelung durh

und bleibt dieAnordnung der Umgebung

dabei erhalten, liegt eine Inversionssym-

metrie vor. Moriyas erste Regel besagt,

dass es in diesem Fall keine Dzyaloshin-

skii-Moriya-Wehselwirkunggibt,alsogilt:

D ~ = ~ 0

^.

Diesistleihtverständlih,dajajederani-

sotrope Einuss eines umgebenden Ions

durh ein anderes aufgehoben wird, das

sihander entgegengesetzt en Positionim

Raumbendet.SomitliegtdergleiheFall

vor als wäre keine Umgebung vorhanden

unddieWehselwirkungistdamitreiniso-

troper Natur. Die nebenstehende Grak

beshreibt einBeispielsystemmit Inversi-

onssymmetrie. Die betrahteten Spins A

und B werden dabei durh rote und die

Umgebung durh kleinere, blaue Kugeln

symbolisiert.DerMittelpunktunddieVer-

bindungsstreke (rotes AB) zwishen den

beidenSpins sindzusätzlihgrüngekenn-

zeihnet.

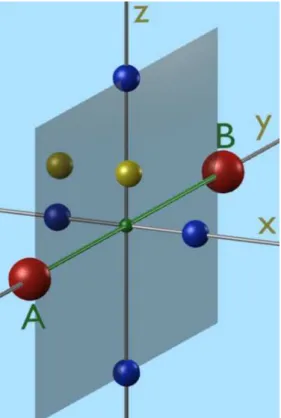
3.3.2 Senkrehte Spiegelebene

AusgehendvondemModellsystemin Ab-

Abb.3: Spiegelebene

⊥

^AB

bildung 2 wird ein weiteres Ion (gelb) in

dieUmgebungeingefügt.Dadurhwirddie

Inversionssymmetriegebrohen,dadasSys-

tem gegenüber der Inversion der z-Ahse

(

z → − z

^{) niht mehr invariant ist. Den-}

nohbleibtdieSymmetrieentlangderan-

derenbeidenAhsenerhalten.Es liegtal-

soeineSpiegelebenevor.Diesewirddurh

diex-und z-Ahsegebildetund istin der

Grak halb transparent angedeutet. Sie

istsenkrehtzurStrekeABundgehtdurh

den Mittelpunkt dieser Streke. Moriyas

zweite Regel besagt,dass dannder Dzya-

loshinskii-Moriya-Vektor in der Spiegele-

bene bzw. senkreht zur Verbindungslinie

liegt, d.h.

D ~ k

Spiegelebene oder

D ~ ⊥ AB

^.

3.3.3 Parallele Spiegelebene

Erweitert man Abbildung 2 um die gelb

Abb.4: Spiegele bene inl. AB gekennzeihnetenIonenwirdebenfallsdie

Inversionssymmetriegebrohen.EineSpie-

gelebene wie sie imvorangegangenen Ab-

shnitt beshrieben wurde existiert eben-

falls niht. Die beiden neuen Ionen lie-

geningleihenAbständenlinksundrehts

vondery-z-Ebene(halbtransparent).Da-

herbleibtdasSystemSpiegelungenandie-

serEbenegegenüberinvariant.DieseSpie-

gelebene beinhaltet diebeiden betrahte-

ten Spins undnatürlihden Mittelpunkt.

Moriya formuliert dazu, dass der Dzyalo-

shinskii-Moriya-Vektor hier senkreht zu

dieser Spiegelebene liegt, also

D ~ ⊥

^Spie-

gelebene.

DieseRegelkannmanallerdingsauhauf

das in Abb. 3 skizzierte System anwen-

den. Dies führt aber niht zu einem Wi-

derspruh, sondern beide Auswahlregeln

zusammen denieren

D ~

^{bis auf das Vor-}

zeihen.Dieerste dieserRegelnwürdefür

Abbildung 3 bedeuten, dass der Dzyalo-

shinskii-Moriya-Vektorin der x-z-Ebene liegt. Die zweite Regel lässtsih anwenden, da

auhhierdiey-z-EbeneeineSpiegelebeneist.Da

D ~

^{nunsenkrehtzuihrzeigt,folgtdass}

dieRihtung von

D ~

^die

± x

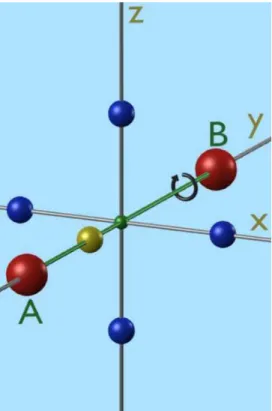
^{-Ahse ist.}

3.3.4 Senkrehte Rotationsahse

In der nebenstehenden Grak trit kei-

Abb. 5: zweifahe Rotationsahse

⊥

^AB

ne der zuvor erläuterten Regeln zu. Die

Inversionssymmetriewird durh das Feh-

lendeszweitenblauenIonsaufderx-Ah-

segebrohenundSpiegelebenensenkreht

oder parallel zu AB existieren niht, da

sih die gelb gekennzeihneten Ionen je-

weils etwas über bzw. unter der y-Ah-

se benden. Dennoh kann ein einfahes

Symmetrieelement gefunden werden. Ro-

tiert man das System (angedeutet durh

denshwarzenKreispfeil)um180

◦

umdie

x-Ahse,bleibtdieSymmetriedesSystems

erhalten. Esliegt demnah einezweifahe

RotationsahsesenkrehtzuABvor.Nah

Moriya muss der Vektor

D ~

^{senkreht zu}

dieserRotationsahseliegen,d.h.

D ~ ⊥

^Ro-

tationsahse.

Diese Regel kann wie die zuvor beshrie-

beneauhdazuverwendetwerden,den

D ~

^-

VektorimBeispielsysteminAbb.3genau-

er festzulegen. Dabei sei die z-Ahse die

zweifahe Rotationsahse, sodass zusam-

men genommen mit den Folgerungen für die senkrehte Spiegelebene der

D ~

^{-Vektor auf}

die positive oder negative Rihtung der x-Ahse festgelegt werden kann. Dies bestätigt

dasErgebnisausdemvorangegangenen Abshnitt.

3.3.5 Parallele Rotationsahse

Für die letzte Auswahlregel wurde zu Ab-

Abb. 6: n-fahe Rotationsahse

k

^AB

bildung 2 das gelb markierte Ion auf der

y-Ahse hinzugefügt und die blauen Ionen

sovershoben,dasssiealleäquidistantzum

Mittelpunktsind.DadurhlässtsihdasSys-

tem unter Symmetrieerhal tung um die y-

Ahsein90

◦

-Shrittendrehen.Fürden Fall

einern-fahenRotationsahse(

n ≥ 2

^)durh

diePunkteAundBfolgertMoriya,dassder

Dzyaloshinskii-Moriya-Vektorentlangdieser

Ahsezeigenmuss.ImnebenstehendenBei-

spiel liegt der

D ~

^-Vektor dementsprehend auf der vierfahen Rotationsahse.

Wendet man die bisher besprohenen Aus-

wahlregelnaufdiesesBeispielsysteman,er-

hältmannurfürdiezurVerbindungsstreke

paralleleSpiegelebeneeinErgebnis.Diessteht

jedohimWiderspruhzurebenerläuterten

Regel. Nimmt man beispielsweise die y-z-

Ebene alsSpiegelebene, somüsstenahder

ersten Regel

D ~

^{senkreht zu dieser Ebene,}

also aufder x-Ahseliegen. Die andereRe-

gel verlangt aber, dass

D ~

^{in Rihtung der} Rotationsahse, der y-Ahse, zeigt. Dieser Widerspruhlässtsihaberdadurh auösen,dasseinen-fahe RotationsahsealsSym-

metrieelem ent Vorrang vor der Spiegelebene hat.AmBeispiel der vierfahen Rotations-

ahselässtsihdiesauhlogishfordern,damanalsSpiegelebenesowohldiex-z-alsauh

diey-z-Ebenewählenkann.Nahder Auswahlregelmüsstedannder

D ~

^{-Vektorsenkreht}

auf beiden stehen, was aber niht möglih ist, da die beiden Ebenen bereits senkreht

zueinander sind. Folglih ist die Regel also nur anwendbar, wenn nur eine Spiegelebene

vorliegt, sonst ist dieRegelfür dieRotationsahsevorzuziehen.

3.3.6 Überblik

In der nahstehenden Tabelle sind die von Moriya aufgestellten Auswahlregeln noh

einmalzusammengefasst dargestellt.

Punktsymmetrie Rihtung von

D ~

Inversion

D ~ = ~ 0

Spiegelebene

⊥ AB D ~ ⊥

^AB

Spiegelebene durhAB

D ~ ⊥

Spiegelebene zweifahe Rotationsahse

⊥ AB D ~ ⊥

Rotationsahse n-fahe RotationsahsedurhAB

D ~ k

Rotationsahse

4 Spinringe Teil 1

Spinringe sind Ketten aus Spins mit periodishem Anshluss des letzten Spins an den

ersten. Es werden nur Wehselwirkungen zwishen den nähsten Nahbarn betrahtet

und diese Kopplung soll hier antiferromagnetish sein. Auÿerdem sollen alle Elemente

desRingsdengleihenSpintragenunddieKopplungzwishendenSpinszunähstgleih

sein.Daher gelten fürdie betrahteten Spinringediese Beshränkungen:

J ij = J > 0,

⁽⁵²⁾

s _i = s.

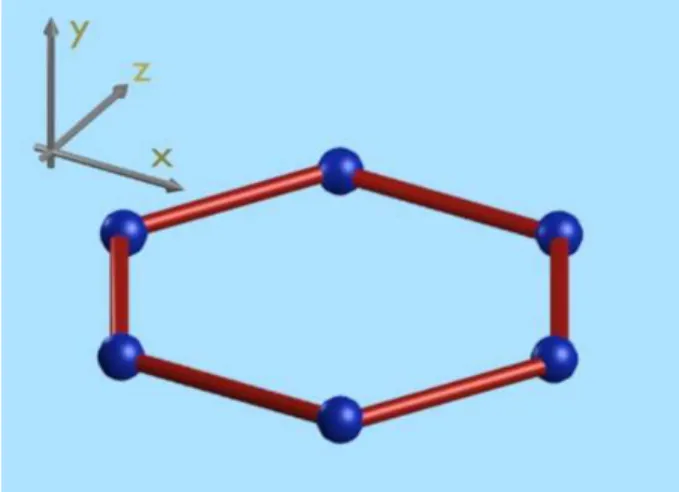
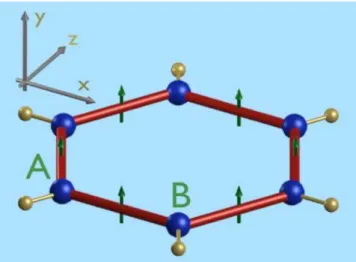
⁽⁵³⁾

Abbildung7zeigtdasBallandStik-ModelleinesSpinringesbestehendaussehsSpin.

DabeiistsinddieAtomederenElektronen denSpin tragenblaugekennzeihnet unddie

hemishen Bindungen rot.

Abb. 7: Modell eines Spinringesaus sehs Spins

Dadurh dass nur Wehselwirkungen zwishen nähsten Nahbarn betrahtet werden,

entfälltfür denHamiltonian ausGleihung (41)die Summe über

j

^{. Manerhält daher:}

H b = X

i

½ b s ^z _i

·

−b s ⁻ _{i +1} (iD x + D y )

2 + b s ⁺ _{i +1} ( − iD x + D y ) 2

¸

+ s b ^z _i +1

·

b s ⁻ _i (iD x − D y )

2 − s b ⁺ _i (iD x + D y ) 2

¸

(54)

+

· b s ⁺ _i s b ⁻ _i+1

µ J + iD _z 2

¶

+ b s ⁻ _i b s ⁺ _i+1

µ J − iD _z 2

¶¸

+ J s b ^z _i s b ^z _i +1

o

+ gµ B B S b ^z .

DabeiläuftderIndex

i

^{fürdenSpinringausAbb.(7)bis6,wobeifür}

i = 6

^dann

i+1 = 1

gesetztwird, um den Ringzushlieÿen.

4.1 Reines Heisenberg-Modell

In diesem Abshnitt werden die Magnetisierung und die Entwiklung der Energieeigen-

werte zunähstin Abwesenheitder Dzyaloshinskii-Moriya-Wehselwirkung exemplarish

für einen Spinring aus sehs Spins mit

s = 1/2

^{betrahtet. Die} Energieeigenwer te ver- ändern sih in Abhängigkeit des externen Magnetfelds. Da der Heisenberg-Term vom

Magnetfeld unabhängig ist, trägt zu dieser Entwiklung nur der Zeeman-Ter m bei. Ab-

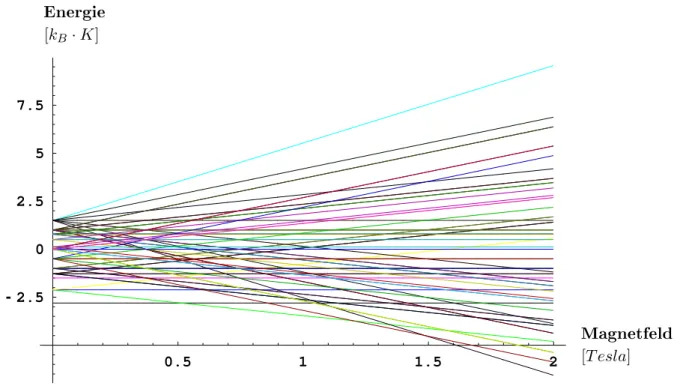
bildung8zeigtdieEnergieeigenwerteinAbhängigvomangelegtenMagnetfeld.DieKopp-

lungsstärke

J

^{sei dabei}

1 K · k B

^.

0.5 1 1.5 2

- 2.5 0 2.5 5 7.5

PSfragreplaements

Energie

Magnetfeld

[k B · K]

[T esla]

Abb.8: Eigenwertentwiklungfür den 6er-Spinring,

J = 1 k _B · K

DieinAbb.8gezeigtenEigenwerteentwikelnsihlinearmit steigendemMagnetfeld,da

jaauhderZeeman-TermlinearimB-Feldist.DemnahkönnendensinkendenEigenwer-

ten Zustände mit negativer magnetisher Quantenzahl

M

^{und den steigenden Zustände}

mit positiver magnetisher Quantenzah l zugeordnet werden. Zu den konstant bleiben-

den Eigenwerten gehören daher Zuständemit

M = 0

^{. Es wird ebenso deutlih, dassdie}

mehrfahe Entartung der Eigenwerte durh das Anlegen eines Magnetfeldes zum Teil

aufgehoben wird.

Dadurhdassfür den Austaushparameter

J

^{einpositiver Wertgewähltwurde, handelt}

es sih um einen antiferromagne tishen Spinring, d.h. die Spins sind im Grundzustand

bei

B = 0

antiparallel ausgerihtet und es gilt

S = 0

^{. Dieser} Grundzustand hat damit die magnetishe Quantenzah l

M = 0

^{. Der Beweis hierzu ist in Referenz [LM62℄ zu n-}

den. Durh die Erhöhung der Magnetfeldstärke sinkt ein höherer Energieeigenwer t mit

M < 0

^{unterdenWertdes}antiferromagne tishenGrundzustands.Beidiesemlevel-ros- sing ändert sihsomit der Grundzustand,wasauhin einem sprunghaftenAnstiegder

Magnetisierungresultiert.

Für denhier betrahteten 6er-Spinring kann sih der Grundzustand mit steigender Ma-

gnetfeldstärkedreimal ändern, sodass dieMagnetisierungdrei sprunghafteAnstiegebis

zumErreihenderSättigungsmagnet isie r ungverzeihnet.Abbildung9zeigtdiekomplet-

te Magnetisierungskurve.

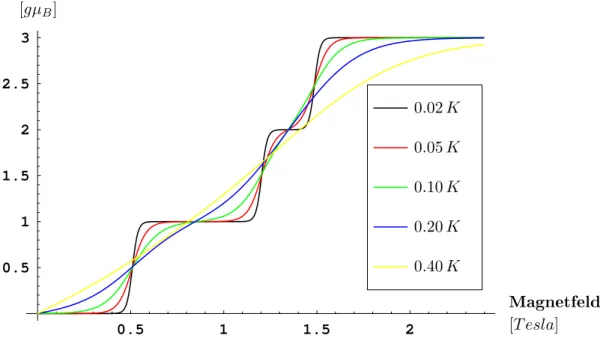
4.1.1 Einuss derTemperatur

Betrahtet man die Formel für die Magnetisierung wird deutlih, dass die Temperatur

auf der sih dasSystem bendet einen wesentlihen Einuss auf dieForm der Magneti-

sierungskurve hat

M = − gµ B

Z Sp µ

exp

·

− 1 k _B T H b

¸

· S b ^z

¶

.

⁽⁵⁵⁾

Thermishe Fluktuationen stören dabei die Ausrihtung der Spins am Magnetfeld. Da-

her können die quantenmehan ishen Eekte, d.h. dieMagnetisierungssprünge, nur bei

Temperaturen nahgewiesen werden, für die Heisenberg-Koppl ung gegenüber der ther-

mishen Energie überwiegt, d.h.

T ≪ | J/k B |

^. Andernfalls werden die Sprünge derart verwisht,dasssie niht mehr zuerkennen sind. InAbbildung 10ist dieMagnetisierung

für vershiedeneTemperaturen dargestellt.

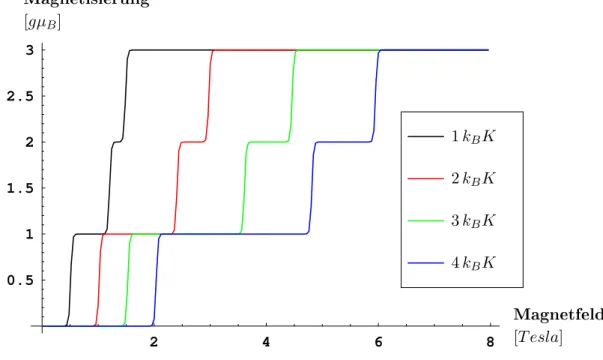
4.1.2 Abhängigkeit von der Wehselwirkungsstärke

Wie aus dem Hamilton-Operator des Heisenberg-Modells (s. Gleihung (6)) ersihtlih

ist,hängtderEinuss einesexternenMagnetfeldsaufdieMagnetisierungvonder Stärke

derAustaushparameterab.FürhöhereWehselwirkungsstärkenmussderZeeman-Ter m

gröÿer,d.h. dieMagnetfeldstärke erhöht werden, um eineÄnderung desGrundzustands

herbeizuführen. DamitvershiebensihdieMagnetisierungssprüngezuhöherenFeldstär-

ken und der Abstand zwishen den Sprüngenwird ebenfallsgröÿer. Abbildung 11 zeigt

diesen Eektfür vershiedeneAustaushparameter

J

^.

0.5 1 1.5 2 0.5

1 1.5 2 2.5 3

PSfragreplaements

Magnetisierung

Magnetfeld

[gµ B ]

[T esla]

Abb. 9: vollständigeMagnetisierungskurve für

T = 0.02K

^und

J = 1 k _B · K

0.5 1 1.5 2

0.5 1 1.5 2 2.5 3

PSfragreplaements

Magnetisierung

Magnetfeld

[gµ B ]

[T esla]

0.02 K 0.05 K 0.10 K 0.20 K 0.40 K

Abb. 10:Magnetisierungsverlauf in Abhängigkeit von der Temperatur,

J = 1 k _B · K

2 4 6 8 0.5

1 1.5 2 2.5 3

PSfragreplaements

Magnetisierung

Magnetfeld

[gµ B ]

[T esla]

1 k B K 2 k B K 3 k _B K 4 k _B K

Abb. 11: Magnetisierungfürvershiedene Austaushparameter

J

^,

T = 0.02 K

4.2 Dzyaloshinskii-Moriya-Wehselwirkung: 6er Spinring (s=1/2)

EssollnunderEinussderDzyaloshinskii-Moriya-WehselwirkungamBeispieldesSpin-

rings aussehs

s = 1/2

^{-Spins betrahtet werden. Dazuwird die Stärke der Wehselwir-}

kungvariiertundderSpinringimMagnetfeldgedreht.InsbesonderesollendieseErgebnis-

semit demreinenHeisenberg-Modellverglihen werden. Füralle Rehnungen in diesem

und dem nähsten Kapitel wird, sofern niht anders angegeben, für die Austaushpara-

meterdesHeisenberg-ModellseinWertvon

1 K · k B

^{undfürdieTemperatur}

0.02 K

^ange-

nommen. Die Dzyaloshinskii-Moriya-Wehselwirkung wird wie zuvor beshrieben durh

dasKristallfeld erzeugt, daher wurden zum Spinring ausAbbildung 7 magnetish niht

aktive Elemente hinzugefügt, um die Anwesenheit dieser Anisotropie zu gewährleisten.

Diese Elemente sind so angeordnet, dass sie die gleihe Symmetrie wie der magnetish

relevante Teil desRings haben.Das im folgenden untersuhte Beispiel ist in Abbildung

12 dargestellt.

4.2.1 Bestimmung derDzyaloshinskii-Moriya-Vektoren

Zunähstistesnotwendiganhandder zuvorerläuterten AuswahlregelndieRihtungder

Dzyaloshinskii-Moriya-Vektorenzubestimmen.DieseRegeln(s.3.3.6)werdendahersuk-

zessive abgearbeite tund bewertet.

Durhden MittelpunktdesRingesgeht einesehsfaheRotationsahse.Dahergenügtes

füreinPaar vonSpinsdieDzyaloshinskii-Moriya-Vektorenzubestimmen,da durheine

Drehung um 60

◦

um diese Ahseder Spinring in sihselbst überführt wird (vgl. [KC02℄

und [DRMMM04℄). Betrahtetman nun diebeiden Spins Aund Bin Abbildung 12,er-

kennt man,dassdieumliegenden Ionen dieInversionssymmetriebrehen,d.h. dieDzya-

loshinskii-Moriya-Wehselwirkung kannhier vorliegen.

Abb. 12:6er Spinringmit

D ~

^-Vektoren

WeiterhinndetmanzwishendenSpinsAundBeineSpiegelebene,diedenRingmittig

durhläuft, die Streke AB imMittelpunkt tritund zudem senkreht zu dieserStreke

ist.DamitsindalleVoraussetzungenfürdiezweiteAuswahlregelerfülltundesfolgt,dass

die

D ~

^{-Vektoren senkreht zu AB liegen müssen. Dies kann durh die dritte Regel noh}

weiter eingeshränkt werden.

EineparalleleSpiegelebene, diedieSpinsAundBenthält,bildetder Ringselbst. Daher

müssendie

D ~

^{-VektorenauhsenkrehtzumRingsein.Esistauhmögliheinezweifahe}

Rotationsahsesenkreht zu ABzu nden, jedoh liefertdies keine neuen Erkenntnisse.

Einen-fahe Rotationsahsehingegenexistiert niht.DamitistdieAhseaufder die

D ~

^-

Vektoren liegen müssen bestimmt, die Ausrihtung (

+y

^oder

− y

^{-Rihtung in Abb. 12)}

andieserAhsekannfreigewähltwerdenundbeeinusstdiemagnetishenEigenshaften

niht.Dabeiwerdendie

D ~

^{-Vektorenalle in dieselbe Rihtung gelegt,um die Symmetrie}

des Hamilton-Operator s niht unnötig zu reduzieren. Die Dzyaloshinskii-Moriya-Vekto-

ren sindin Abbildung 12 grün gekennzeihnet aufder Mitte der Bindung dargestellt.

NahMoriyaistdieStärkeder Dzyaloshinskii-Moriya-Wehselwirkung relativzur Stärke

der Heisenberg-Koppl ung vonder Ordnung:

D = ∆g/g · J.

⁽⁵⁶⁾

Dabei ist

g

^dasgyromagnetishe Moment desfreien Elektrons und

∆g

^{die Abweihung}

von diesem Wert für das gebundene Elektron. Übliherweise liegt dieses Verhältnis bei

einem Wertvonetwa10%. Daherwird fürdieBetrahtung derEnergieeigenwerte dieser

Wertangenomme n, beider anshlieÿendenDiskussionderMagnetisierungaber auhva-

riiert.

ZusätzlihistbeiderRehnungdaraufzuahten,dassfür

J _ij

^{eine obere}Dreieksmatrix verwendet wird. Dies hat aber zur Folge, dass für die Bindung des sehsten mit dem

ersten Spin der Dzyaloshinskii-Moriya-Vektor

D ~ 16

^{bearbeitet wird. Inder Abbildung ist}

aber der Vektor

D ~ 61

^{parallel zu den anderen. Beim Anlegen der} Dzyaloshinskii-Moriya- Matrixmuss dementsprehend daraufgeahtetwerden,dass

D ~ 16 = − D ~ 61

^gilt.

4.2.2 Entwiklung der Eigenwerte

In diesem Abshnitt werden die Auswirkungen der Dzyaloshinskii-Moriya-Wehselwir-

kungaufdieEntwiklungder Energieeigenwer te desSpinringsbetrahtet. Abbildung 13

zeigt das gesamte Eigenwertspe ktrum mit den gleihen Parameter n wie in Abb. 8. Das

Magnetfeld liegtdabeisenkreht zu den

D ~

^-Vektorenan.

0.5 1 1.5 2

- 2.5 0 2.5 5 7.5

PSfragreplaements

Energie

Magnetfeld

[k B · K]

[T esla]

Abb. 13:Eigenwertentwiklungmit Dzyaloshinskii-Moriya-Wehselwirkung,

D = 10% J

^,

J = 1 k _B · K

DasEnergiespektrum sheintsihauf denersten Bliknur wenigvondemohne Dzyalo-

shinskii-Moriya-Wehselwirkung zuuntersheiden.AbweihungensindbeigeringenFeld-

stärken zu sehen, hier wird die Entartung der Energienivea us bei

B = 0

^{zum Teil auf-}

gehoben.Umfeststellenzukönnen,welhen Einuss diesaufdasmagnetisheVerhalten

desRingshat,wirdnundieMagnetisierungbetrahtet.Hierbeiistauÿerdeminteressant,

ob sih die aus den Grundzustandsänderungen resultierenden Magnetisierungssprünge

vershieben oder breiter werden.

4.2.3 Magnetisierung undSuszeptibilität

Wie im vorangegangenen Kapitel erwähnt wurde, sollte die Stärke der Dzyaloshinskii-

Moriya-Wehselwirkungbeietwa10%derHeisenberg-Kopplungliegen,jedohwird jetzt

dieStärke umdiesen Wertvariiertum dieAuswirkungen dieserWehselwirkung zu ver-

deutlihen. Zudem handelt es sih bei diesem Wert um eine Abshätzung, so dass der

tatsählihe Wert in der Natur davon abweihen kann. Abbildung 14 zeigt hierzu den

Verlauf der Magnetisierung in Abhängigkeit des externen Magnetfelds für vershiedene

Stärken der Wehselwirkung. Die Legende der Grak gibtdabei dieStärke als Prozent-

satzdes Austaushparameters

J

^an.

0.5 1 1.5 2

0.5 1 1.5 2 2.5 3

PSfragreplaements

Magnetisierung

Magnetfeld

[gµ B ]

[T esla]

0% J 5% J 10% J 15% J 20% J 30% J

Abb. 14:Magnetisierungskurven fürvershiedene Stärken von

D

^,

T = 0.02 K

^,

J = 1 k _B · K

Wiemansieht,führteineErhöhungderStärkederWehselwirkungzueinerVershiebung

des Magnetisierungssprungs. Hier ist nun die Betrahtung der Ableitung der Magneti-

sierung, der magnetishen Suszeptibilität , sinnvoll. Die Sprünge in der Magnetisierung

korrelieren dabei mit einzelnen Peaks in der Suszeptibilität , wobei auh hier die Peaks

vershoben seinsollten.Abbildung15 zeigtnundiekorrespondierende nSuszeptibilität s-

0.5 1 1.5 2 0.5

1 1.5 2 2.5 3

PSfragreplaements

Suszeptibilität

Magnetfeld

£ gµ B · T esla ^{− 1} ¤

[T esla]

0% J 5% J 10% J 15% J 20% J 30% J

Abb. 15:Suszeptibilitätskurven für vershiedene Stärken von

D

^,

T = 0.02 K

^,

J = 1 k _B · K

kurven zu Grak 14. Die Suszeptibilität wurde dabei als Dierenzenquotient aus den

Magnetisierungsdaten berehnet:

χ = ∆M

∆B .

⁽⁵⁷⁾

Die Suszeptibilität skurven in Abb.15 zeigen das erwartete Verhalten, vor allem beim

erstenPeakistzuerkennen,dassbeihöhererStärkederWehselwirkungeinestarkeVer-

shiebung stattndet. Dieses Verhalten wurde auh von Konstantinidis am Vanadium-

Molekül

V 15

^{[KC02℄ gefunden.} Interessant ist nun, dassklassish betrahtetdie Dzyalo- shinskii-Moriya-Wehselwirkung bei der vorliegenden

S 6

^{-Symmetrie des Rings aus rein}

geometrishen Gründen überhauptkeinenEinuss habendürfte (vgl.Ref.[CAJ02℄).

4.2.4 Semi-klassishe Betrahtung

Zur Erklärung sei nun ein klassisher Grundzustand gegeben, wie er in Grak 16 dar-

gestellt ist. Dieser Zustand ist niht der einzig möglihe, dennoh lässt sih an diesem

Zustandder Einuss der Geometrie desRings verdeutlihen.DadieDzyaloshinskii-Mo-

riya-Vektorenbereitsfestgelegt wurden,wurdein derAbbildung aufdieDarstellungder

Liganden verzihtet. Die Spins stehen antiparallel zueinander, sind jedoh leiht ver-

kantet, was durh die Dzyaloshinskii-Moriya-Wehselwirkung bewirkt wird. Dies führt

auÿerdem zu einem shwahen Ferromagnetismus. Hierauf und auf die Annahmen, die

für diesesModell gemaht werden, wird in Kapitel5.2.3 ausführlih eingegangen.

Bildet man nun das Kreuzprodukt ei-

Abb. 16:Mögliher Grundzustand des 6er

Spinrings bei

B = 0

nesSpinsmitdemnähsten,erhältman

einenVektor,derentwederparalleloder

antiparallelzum

D ~

^{-Vektors steht.In ei-}

nem Umlauf über den Ring ndet man

gleihvieleparallelewieantiparallel eVek-

toren, so dass sih die Beiträge gegen-

seitigaufheben.Dieslässtsih auh auf

ZuständemitgeklapptenSpinsübertra-

gen,dadabeidasKreuzproduktdesge-

klapptenSpinsmitdemeinenNahbarn

in dem Maÿe gröÿer wird wie das mit

demanderenNahbarnkleiner(vgl.Ka-

pitel 5.2.3). Für diese klassishen Zu-

ständewärederEinussderDzyaloshinskii-Moriya-Wehselwirkungsomitnihtexistent.

Da hier jedoh quantenmehan ish exakt gerehnet wurde, lassen sih Abweihungen

feststellen. Um aber ein System zu betrahten, dessen Verhalten auh klassish erklärt

werden kann wird nun der Spinring, wie in [CAJ02℄ vorgeshlagen, dimerisiert.

4.3 Dimerisierter 6er Spinring

Abb.17: DimerisierterSpinringmit

D ~

^-Vektoren

Der Spinring des vorangegangenen Kapitels wird nun dahin gehend verändert, dass je-

weilszweiSpins einenDimer bilden und diese Dimeremit den anderen verbundensind.

Die Bindungen imDimer sinddamit stärker als diezwishenden Dimeren (s. Abb.17).

Stattder bisherigen

S 6

^{-Symmetriendet mannunnoheine}

C 3

-Symmetrie,womit auh

für dieBestimmung der Dzyaloshinskii-Moriya-Vektoren nur noh der Ringalsparallele

Spiegelebene zur Verfügung steht.

ErgebnisdieserBetrahtung ist,dassdie

D ~

^{-VektorenimmernohindiegleiheRihtung}

zeigen wie zuvor. Da aber die Stärke der Dzyaloshinskii-Moriya-Wehselwirkung von

den Austaushparametern des Heisenberg-Modells abhängt, sind die Vektoren wie in

Abb.17dargestelltvershiedenlang.Somitkönnen sihauhklassishdieBeiträgeniht

gegenseitigaufheben undes bleibt einNettobeitrag übrig.

4.3.1 Magnetisierung undSuszeptibilität

Danun eingröÿerereektiver Beitrag der Dzyaloshinskii-Moriya-Wehselwirkung zu er-

warten ist, sollte sih dies auh in der Magnetisierung wiederspiegeln. Abbildung 18

zeigtdieMagnetisierungskurven fürdiegleihenWehselwirkungsstärkenwieimvorigen

Kapitel (vgl. Abb. 14). Die Austaushparameter wurden für die Dimerbindungen auf

J 1 = 1.25 K · k _B

^{und für die} Inter-Dimerbindungen auf

J 2 = 0.75 K · k _B

^{gesetzt. Die}

Temperatur von

0.02 K

^wurde beibehalten.

In Abb. 18 sieht man nun einen weiteren Eekt. Die Sprünge sind vershmiert, d.h.

sieerstreken sihüber ein gröÿeresFeldstärkenintervall alszuvor.Diesähnelt in gewis-

sem Maÿe dem Einuss der Temperatur (vgl. Abbildung 10). Da die Vershiebung der

Magnetisierungssprünge inAbb.18 nihtgut zuerkennen ist,solltedieBetrahtungder

Suszeptibilität hier hilfreih sein. InGrak 19sind die korrespondierende nSuszeptibili-

tätskurven aufgetragen.

Wie man sieht, werden die Peaks für höhere Stärken der Dzyaloshinskii-Moriya-Weh-

selwirkung deutlih breiter, auh die Vershiebung der Peaks ist gut zu erkennen. Diese

Vershiebungsollim nahfolgenden Unterkapitelgenaueruntersuht werden.

4.3.2 Suszeptibilität: Position der Peaks

Für die drei möglihen Magnetisierungssprünge des 6er-Spinrings werden nun die Ma-

gnetfeldstärken bestimmt, bei denen die Mitte des Magnetisierungssprunge s zu nden

ist.Dazu ist eszwekmäÿiger die magnetishe Suszeptibilität nah Formel (57)aus den

berehneten Magnetisierungsdaten zu ermitteln und diePosition des Maximums zu be-

stimmen. Die nahfolgenden drei Graken (Abb. 20) zeigen dazu die Peakpositionen

in Abhängigkeit von der Stärke der Dzyaloshinskii-Moriya-Wehselwirkung für alle drei

Peaks.

ManbeobahteteineVershiebungzukleinerenFeldstärkenbeim erstenPeak,jedohzu

gröÿeren beim zweiten und dritten Peak. An Hand eines Spinringes aus vier Spins mit

s = 1

^{wird dazuimKapitel 5.2.3ein}semi-klassishesModell vorgestellt.AndieserStelle solldaher aufeine Erklärung verzihtetwerden, da sih an einem System mit gröÿerem

Spin dieErläuterun g einfaher undanshauliher gestaltet.

0.5 1 1.5 2 0.5

1 1.5 2 2.5 3

PSfragreplaements

Magnetisierung

Magnetfeld

[gµ B ]

[T esla]

0% J 5% J 10% J 15% J 20% J 30% J

Abb. 18:Magnetisierungfür vershiedene Stärken von

D

^,

T = 0.02 K

^,

J ₁ = 1.25 k _B · K

^,

J ₂ = 0.75 k _B · K

0.5 1 1.5 2

1 2 3 4 5 6 7

PSfragreplaements

Suszeptibilität

Magnetfeld

£ gµ B · T esla ^{− 1} ¤

[T esla]

0% J 5% J 10% J 15% J 20% J 30% J

Abb. 19:Suszeptibilitätfürvershiedene Stärken von

D

^,

T = 0.02 K

^,

J ₁ = 1.25 k _B · K

^,

J ₂ = 0.75 k _B · K

5 10 15 20 25 30 0.61

0.62 0.63

PSfragreplaements

Magnetfeld

[T esla]

Stärke(DM)

[% J ]

(a)1.Peak

5 10 15 20 25 30 1.225

1.235 1.24

PSfragreplaement s

Magnetfeld

[T esla]

Stärke(DM)

[% J ]

(b)2.Peak

5 10 15 20 25 30 1.49

1.495 1.505 1.51 1.515 1.52

PSfragreplaement s

Magnetfeld

[T esla]

Stärke(DM)

[% J ]

()3.Peak

Abb.20: Suszeptibilität:Peakmaximumabhängig von

D

4.3.3 Eigenwerte

Inder Magnetisierung hattedieDzyaloshinskii-Moriya-Wehselwirkung nuneinen deut-

lih höheren Einuss. Daher kann davon ausgegangen werden, dass sih auh in der

Entwiklung der Energieeigenwerte eine Veränderung zeigen sollte. Grak 21 zeigt das

Energiespektrumfür dendimerisiertenSpinring miteiner StärkederDzyaloshinskii-Mo-

riya-Wehselwirkung von 10%der Heisenberg-Kopplung.

Auh hier erkennt man wie in Abb. 13, dass bei

B = 0

^{die Entartung für einige Ei-}

genwerte aufgehoben wird.Interessanterist aber, dassan Stelle deslevel-rossings ein

anti-level-ro ssing zu sehenist,d.h.dieEnergieniveaus stoÿensihin diesemPunktab

(

→

energy-level repulsion). Der Magnetisierungssprung ndet hier an der Stelle statt, an der sih die Energienivea us kreuzen würden, jedoh gibt es jetzt niht mehr einen

sharf abgegrenzte n Übergang, sondern einÜbergangsintervall.Die beiden Energienive-

ausnähernsihbeimanti-level-rossingeinander an,wodurh sihder Abstandüberein