Pr¨ufung aus Wahrscheinlichkeitstheorie und Statistik (2VU) MASCHINENBAUER
29.6.2004
GRUPPE A - L¨osungen
1. Es sind nur zwei Ereignisse m¨oglich: Entweder man wartet oder man wartet nicht.
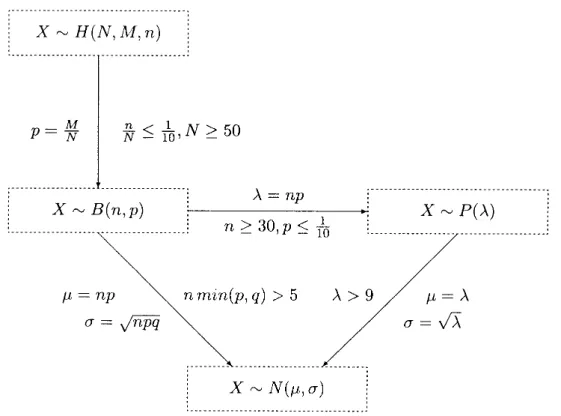
Wir legen also eine Binomialverteilung zugrunde. Die Erfolgswahrscheinlichkeit ist die Wahrscheinlichkeit, sofort 2 Minuten pro Stunde zu telefonieren; also ist p = 602 = 301 womit q = 1−p = 2930. Mit n = 90.000 k¨onnen wir die Binomialverteilung durch eine Normalverteilung approximieren (siehe auch Abb. 1):
Abbildung 1: Approximationen von diskreten Verteilungen
µ=np= 90000 1
30 = 3000 σ=√
npq = r
300029 30 =√
2900
Um nicht warten zu m¨ussen, muss man einer der 3100 sein, die gleichzeitig telefonieren k¨onnen. Wir suchen also, mit X = 3100, die Wahrscheinlichkeit
P(x≤X) wobei X ∼N(µ, σ).
Wir transformieren X auf eine N(0,1)-verteilte ZufallsvariableZ: Z = X−µ
σ = 3100−3000
√2900 = 1.85695.
1
Damit ist
P(x≤3100) =P(z ≤1.85695) =φ(1.85695)≈0.9683.
2. Die grunds¨atzliche ¨Uberlegung ist: Wenn man von 100 Schuhen einen Schuh zieht, befinden sich noch 99 Schuhe f¨ur den n¨achsten Zug im Kasten. Von diesen 99 Schuhen kommt genau einer in Frage, mit dem bereits gezogenen Schuh ein Paar zu bilden.
Wird einer der 98 Schuhe gezogen, die kein Paar mit dem ersten bilden, befinden sich f¨ur den n¨achsten Zug noch 98 Schuhe im Kasten, von denen nun genau zwei in Frage kommen, mit einem der beiden bereits gezogenen Schuhe ein Paar zu bilden usw.
(a)
Zug 1 2 3 4 5 . . . 20 Wahrscheinlichkeit 1 9899 9698 9497 9296 . . . 6281
Zur Erkl¨arung: Im ersten Zug ist es egal, was man zieht, im zweiten Zug hat man 98 M¨oglichkeiten, einen Schuh zu ziehen, der kein Paar mit dem ersten bildet. Nun hat man zwei verschiedene Schuhe und hat daher im dritten Zug zwei Schuhe im Kasten, die ein Paar mit einem der beiden bilden w¨urden, also bilden 96 Schuhe von den verbliebenen 98 kein Paar mit einem der beiden usw.
Die Wahrscheinlichkeit kein Paar zu ziehen ist also das Produkt der Wahrschein- lichkeiten in obiger Tabelle:
98 99 · 96
98· 94 97· 92
96·. . .·62
81 = 80!
100! ·(100·98·. . .·62) = 80!
100! ·
50
Y
n=31
2n = 0.0922
(b) Nun m¨ussen wir genau ein Paar ziehen. Mit ¨ahnlichen ¨Uberlegungen wie oben, kommen wir zu folgender Tabelle, in der wir 19 F¨alle unterscheiden, je nachdem in welchem Zug der zweite Schuh zu einem bereits Entnommenen gezogen wird:
Zug 1 2 3 4 5 . . . 19 20 Wahrscheinlichkeit 1 991 9898 9697 9496 . . . 6682 6481 1 9899 982 9697 9496 . . . 6682 6481 1 9899 9698 973 9496 . . . 6682 6481
...
1 9899 9698 9497 9296 . . . 6482 1981
Die Wahrscheinlichkeit genau ein Paar zu ziehen ist dann die Summe der Produkte der Wahrscheinlichkeiten der einzelnen F¨alle:
98·96·. . .·64
99·98·. . .·81 ·(1 + 2 +. . .+ 19) = 80!
100! ·
50
Y
n=32
2n·
19
X
k=1
k= 0.2826
2
3. Wir haben gegeben
x= 18, sx = 3, m= 10 y= 22, sy = 6, n = 17
Zuerst m¨ussen wir testen, ob wir Gleichheit der Varianzen annehmen k¨onnen. Das machen wir mit einem F-Test.
Zu testen ist also die Hypothese
H0 :σx =σy Die Teststatistik im F-Test ist
F = s2x s2y d.h. wir erhalten
f = 32
62 = 0.25.
H0 wird verworfen, wenn
f ≤Fm−1,n−1,α/2
oder
f ≥Fm−1,n−1,1−α/2.
In unserem Fall erhalten wir F9,16,0.005 = 0.1617 und F9,16,0.995 = 4.3838. Damit liegt f = 0.25 nicht im kritischen Bereich. H0 kann also nicht verworfen werden, es gibt keine signifikanten Unterschiede in den Varianzen.
Somit k¨onnen wir den exakten t-Test anwenden.
Die Teststatistik im exakten t-Test ist
T = X−Y
q
SP2 m1 + 1n
wobei SP2 = (m−1)sm+n−22x+(n−1)s2y die gepoolte empirische Varianz ist.
Mit SP2 = 26.28 erhalten wir
t = 18−22
q
26.28 101 + 171
=−1.9579
F¨ur den P-Wert der zweiseitigen Hypothese H0 :µX =µY erhalten wir p= 2(1−Ftν(|t|)) = 2(1−Ft25(1.9579)) = 2(1−0.9693) = 0.0614.
H0 wird verworfen, wenn p≤α oder|t| ≥tν,1−α/2. Wegen 0.06146≤0.01
bzw.
1.95796≥2.7874
k¨onnen wir H0 also nicht verwerfen. Der Test sagt somit aus, dass sich die mittleren Lebensdauern nicht unterscheiden.
3
4. (a) Den Sch¨atzer ˆσ2 entnimmt man der ANOVA-Tabelle: ˆσ2 = 1.077
(b) Die Koeffizienten der Regressionsgerade sind ˆa =−0.09634 und ˆb = 0.999. Somit ist die Regressionsgerade
y =−0.09634 + 0.999x Das Bestimmtheitsmaß ist R2 = 0.999
(c) Die Teststatistik f¨ur die Hypothese H0 :a=a0 mit a0 = 0 ist Ta= aˆ−a0
s.e.(ˆa) mit s.e.(ˆa) = ˆσ s
1
n + x2 (n−1)s2x Somit erhalten wir
ta = −0.09634
√1.077· q 1
100+ 99·28.976752.52 2
= 0.2156
H0 wird verworfen, wenn |ta| ≥ tn−2,1−α/2 ist. Wegen t98,0.995 = 2,6269 kann H0 nicht verworfen werden.
Die Teststatistik f¨ur die Hypothese H00 :b=b0 mit b0 = 1 ist Tb =
ˆb−b0
s.e.(ˆb) mit s.e.(ˆb) = σˆ p(n−1)s2x Somit erhalten wir
tb = 0.999−1
√1.077
√
99·28.97672
=−0.2778
H00 wird verworfen, wenn |tb| ≥ tn−2,1−α/2 ist. Wegen t98,0.995 = 2,6269 kann H00 nicht verworfen werden.
4