Freie Universit¨at Berlin WS 2005/2006
Volltext
Abbildung
ÄHNLICHE DOKUMENTE
Ausserdem wird man bei einer Messung eines in positiver y-Richtung polarisierten Neutrons in der H¨alfte der F¨alle ebenfalls eine Polarisierung in die positive x-Richtung
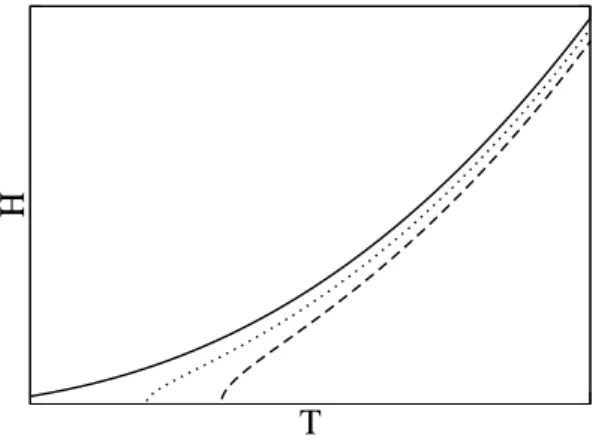
Ihr Zusammenhang erschließt sich ¨ uber die gemischten partiellen Ableitungen der Entropie nach ihren nat¨ urlichen Variablen.. Die Achsen sind nicht
Deutlich erkennbar ist, dass f¨ur T < T C in einem endlichen Intervall von h zu einem Wert des ¨außeren Feldes drei Werte der Magnetisierung existieren.. Diese Kurve ist
Dieses Ergebnis war in gewissem Sinne zu erwarten, da x und y uber eine Koordinatentransformation in Beziehung stehen und deshalb auch nicht unabh¨angig ¨ sein k¨onnen. Daß x und
In diesem Fall hat sich die Geschwindigkeit des Teilchens asymptotisch derjenigen der Wand angen¨ahert, sodaß kein weiterer Stoß mehr statt finden bzw.. die Wand vom Teilchen erst
Berechnen Sie zun¨achst die (kanonische) Zustandssumme und vergleichen Sie anschliessend die sich daraus ergebende Besetzungswahrschein- lichkeit, den Oszillator im n-ten
Ausserdem wird man bei einer Messung eines in positiver y-Richtung polarisierten Neutrons in der H¨alfte der F¨alle ebenfalls eine Polarisierung in die positive x-Richtung
Im folgenden Schritt wird es isobar bis zu seinem urspr¨ unglichen Volumen komprimiert.. Schließlich wird der Druck isochor so lange erh¨oht, bis das Gas wieder in