Freie Universit¨at Berlin WS 2005/2006

(1)

Freie Universit¨at Berlin WS 2005/2006

Fachbereich Physik 25.01.2006

Statistische Physik - Theorie der W¨ arme

(PD Dr. M. Falcke)

Ubungsblatt 12: ¨ Ferromagnet

L¨ osungen

Aufgabe 1

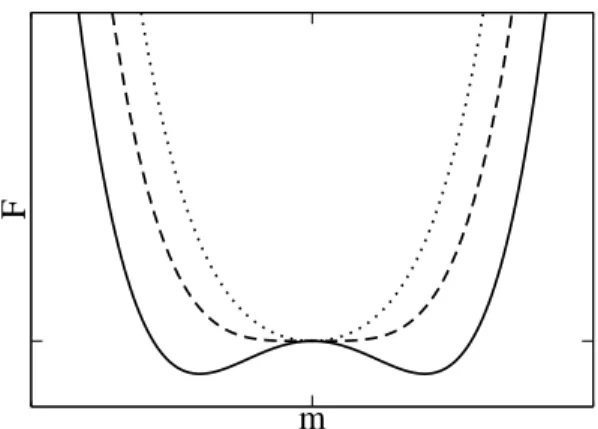
a. Abbildung 1 stellt die freie Energie f¨ ur die drei Bereiche T < T

C

, T = T

C

und T > T

C

dar.

Deutlich erkennbar ist die bistabile Form von F f¨ur T < T

C

.

m

F

Abbildung 1: Freie Energie F als Funktion der Magnetisierung m bei h = 0 f¨ur T < T

C

(durchgezogen), T = T

C

(gestrichelt) und T > T

C

(gepunktet).

b. Aus der Minimierung von F folgt die notwendige Bedingung 0 = am + bm

³

. Diese Gleichung besitzt die L¨osungen

m = 0 , m = ± r

− a b = ±

r a

0

b

T

C

− T T

C

. (1)

Gleichung (1) zeigt, dass von Null verschiedene Extrema nur f¨ur T < T

C

auftreten k¨onnen. Das Minimum, dass bei m = 0 f¨ ur T ≥ T

C

existiert, geht in ein lokales Maximum f¨ur T < T

C

¨ uber.

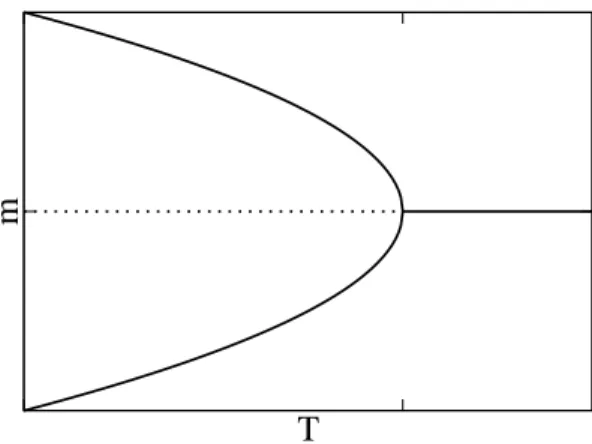
Dies ist in Abbildung 2 verdeutlicht.

c. Um F als Funktion der Temperatur zu untersuchen, setzen wir die L¨osungen f¨ ur m(T ) aus Gleichung (1) in die Definition von F ein. Da F ≡ 0 f¨ ur m = 0, betrachten wir im folgenden nur den Bereich T < T

C

F (T ) N = a

0

2 T − T

C

T

C

a

0

b

T

C

− T T

C

+ b 4

a

²₀

b

²

T

C

− T T

C

2

= − a

²₀

4b

T

C

− T T

C

2

. (2)

Daraus ergibt sich die Entropie zu S(T ) = −

∂F

∂T

N

= a

²₀

N 2b

T − T

C

T

_C²

(3)

und die W¨armekapazit¨at bei konstantem Volumen zu C

V

= −T ∂

²

F

∂T

²

= a

²₀

N 2b

T

_C²

. (4)

(2)

T

m

Abbildung 2: Extrema der Magnetisierng m als Funktion der Temperatur bei h = 0. Die Minima sind als durchgezogene Linien, das Maximum als gestrichelte Linie gezeichnet.

Abbildung 3 stellt die W¨armekapazit¨at als Funktion der Temperatur dar. Da m = 0 f¨ ur T > T

C

, verschwindet dort auch die Wärmekapazität. Somit springt die Wärmekapazität am kritischen Punkt um ∆C

V

= a

²₀

N/(2bT

C

).

T

C

V

T_C

Abbildung 3: W¨armekapazit¨at C

V

als Funktion der Temperatur bei h = 0.

d. Bei endlichem h folgt aus der Minimierung von F der Zusammenhang h = ma + bm

³

. Daraus finden wir durch Ableiten nach h f¨ ur die Suzeptibilit¨at

1 = aχ + 3m

²

bχ

²

⇔ χ = 1

a + 3bm

²

, (5)

so dass

χ =

(

_T_C

a0(T−TC)

, T > T

C TC

2a0(T−TC)

, T < T

C

. (6) Am kritischen Punkt divergiert die Suszeptibilit¨at.

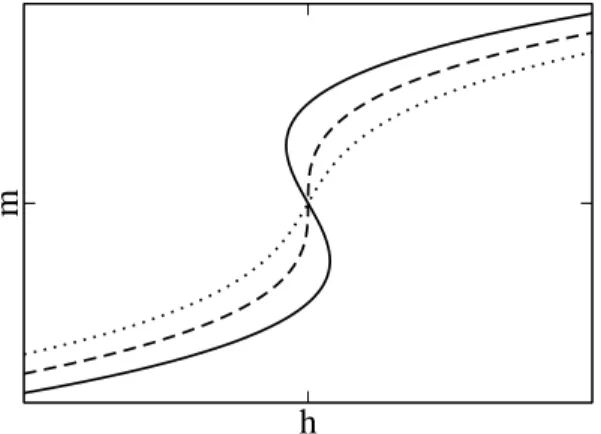
e. Abbildung 4 zeigt die Magnetisierung bei endlichem ¨außeren Feld f¨ur verschiedene Tempera- turbereiche. Die Bedingungen a < 0, a = 0 und a > 0 entsprechen jeweils T < T

C

, T = T

C

und T > T

C

. Deutlich erkennbar ist, dass f¨ur T < T

C

in einem endlichen Intervall von h zu

einem Wert des ¨außeren Feldes drei Werte der Magnetisierung existieren. Diese Kurve ist die

Grundlage f¨ ur das Ph¨anomen der Hysterese.

(3)

h

m

Abbildung 4: Magnetisierung m als Funktion des ¨außeren Feldes h f¨ ur T < T

C

(durchgezogen), T = T

C

(gestrichelt) und T > T

C

(gepunktet)

, Aufgabe 2

a. Aus der Definition der Zustandssumme Z

N

= Sp exp(−βH) folgt Z

N

= X

s1=±1

· · · X

sN=±1

exp β

N−1

X

i=1

J

i

s

i

s

i+1

!

= X

s1=±1

· · · X

sN

−1=±1

X

sN=±1

exp β

N−2

X

i=1

J

i

s

i

s

i+1

!

exp (βJ

N−1

s

N−1

s

N

)

= X

s1=±1

· · · X

sN−1=±1

exp β

N−2

X

i=1

J

i

s

i

s

i+1

!

2 cosh (βJ

N−1

s

N−1

)

= 2 cosh (βJ

N−1

) Z

N−1

,

(7)

da s

N−1

= ±1 und cosh(x) = cosh(−x). Damit erhalten wir Z

N

= Z

2

N−1

Y

k=2

2 cosh (βJ

k

) . (8)

Verwenden wir schließlich Z

2

= X

s1=±1

X

s2=±2

exp (βJ

1

s

1

s

2

) = 2 · 2 cosh (βJ

1

) , (9) so ergibt sich die kanonische Zustandssumme zu

Z

N

= 2

N−1

Y

k=1

2 cosh (βJ

k

) = 2 [2 cosh (βJ )]

^N⁻¹

, (10) wobei wir in der letzten Umformung J = const gesetzt haben.

b. Die freie Energie pro Spin lautet f = F

N = − k

B

T

N ln 2 − k

B

T (N − 1)

N ln [2 cosh (βJ )] ≈ −k

B

T ln [2 cosh (βJ )] . (11) Damit erhalten wir f¨ur die Entropie pro Spin

s = S N = −

∂f

∂T

N

≈ k

B

ln [2 cosh (βJ )] − J

T tanh (βJ) (12)

(4)

und f¨ ur die innere Energie pro Spin u = U

N = − ∂

N ∂β ln Z

N

= −J tanh (βJ ) . (13)

Die W¨armekapazit¨at pro Spin folgt schließlich zu c

V

= C

V

N = ∂u

∂T = J

²

k

B

T

²

1 cosh

²

(βJ ) . (14)

Die N¨aherungen beziehen sich auf den Limes N → ∞.

c. Der dritte Hauptsatz der Thermodynamik besagt, dass die Entropie pro Teilchen im Grenzfall T → 0 verschwindet. Dies ist in der Tat erf¨ullt, da

T

lim

→0

s = lim

T→0

k

B

ln [2 cosh (βJ )] − J

T tanh (βJ )

= 0 . (15)

F¨ur T → 0 gilt β → ∞, so dass 2 cosh(βJ ) = exp(βJ ) + exp(−βJ ) ≈ exp(βJ ). Daher divergiert der erste Term in Gleichung (15) wie

T

lim

→0

k

B

ln [2 cosh (βJ )] ≈ J

T . (16)

Auf der anderen Seite ist lim

β→∞

tanh(βJ) = 1, woraus mit Gleichung (16) die Behauptung (15) folgt.

d. Setzen wir τ

i

:= s

i

s

i+1

, so gilt wegen s

²_i

= 1

G(i, n) = hs

i

s

i+n

i = hs

i

s

i+1

s

i+1

· · · s

i+n−1

s

i+n−1

s

i+n

i = hτ

i

· · · τ

i+n−1

i . (17) Die Zustandssumme l¨aßt sich mit der Bindungsvariablen τ als

Z

N

= 2 X

τ1=±1

. . . X

τN−1=±1

exp β

N−1

X

i=1

J

i

τ

i

!

, (18)

schreiben, wobei der Faktor 2 daher kommt, daß die Werte τ

i

= ±1 f¨ur jedes Paar s

i

s

i+1

zweimal angenommen werden. F¨ur die Korrelationsfunktion erhalten wir

G(i, n) = 1 Z

N

∂

∂βJ

i

· · · ∂

∂βJ

i+n−1

Z

N

= 1 Z

N

"

_i+n−1

Y

k=i

∂

∂βJ

k

# Z

N

=

i+n−1

Y

k=i

tanh(βJ

k

) . (19)

e. Werten wir Gleichung (19) f¨ur konstantes J aus, so erhalten wir

G(i, n) = tanh

ⁿ

(βJ) . (20)

Damit finden wir f¨ur die Korrelationsl¨ange ξ aus dem Ansatz G(i, n) = exp(−n/ξ) ξ

⁻¹

= − ln [tanh(βJ)] = ln

1 + e

⁻^2βJ

1 − e

⁻^2βJ

≈ ln 1 + 2e

⁻^2βJ

+ e

⁻^4βJ

≈ 2e

⁻^2βJ

. Hier haben wir in der letzten Zeile die f¨ ur |x| ≪ 1 (β ≫ 1) g¨ ultigen Approximationen

1 1 − x ≈ 1 + x und ln(1 + x) ≈ x benutzt und den Term e

⁻^4βJ

vernachl¨assigt. Die Korrelationsl¨ange

ξ = 1

2 e

^2βJ