mit regul¨ arem (n − 1)-dimensionalem Rand ∂V und nach außen gerichteter Einheitsnormale ξ gilt f¨ ur eine stetig differenzierbare Funktion f

(1)

Hauptsatz f¨ ur Mehrfachintegrale

F¨ ur einen regul¨ aren Bereich V ⊂ R

ⁿ

mit regul¨ arem (n − 1)-dimensionalem Rand ∂V und nach außen gerichteter Einheitsnormale ξ gilt f¨ ur eine stetig differenzierbare Funktion f

Z

V

∂

_ν

f = Z

∂V

f ξ

_ν

, ν = 1, . . . , n .

Fasst man diese Gleichungen zusammen, so erh¨ alt man die vektorielle Identit¨ at

Z

V

grad f = Z

∂V

f ξ .

Die Glattheitsvoraussetzungen k¨ onnen abgeschw¨ acht werden, indem man

die Integrale ¨ uber geeignete Grenzprozesse definiert.

(2)

Beweis

Approximation durch eine st¨ uckweise lineare Funktion auf einer Triangulierung von V

ξ

(3)

Aufhebung von Randtermen im Inneren nur ein Dreieck bzw.

Tetraeder zu betrachten

dreidimensionaler Fall

_a

b c

f : 1 im Ursprung •

0 an anderen Eckpunkten ◦

f linear: bestimmt durch Werte an den Eckpunkten

Linearit¨ at = ⇒ o.B.d.A f null an 3 Eckpunkten

(4)

(i) linke Seite R

V

grad f :

bestimme g = grad f aus Richtungsableitungen a

^t

g = b

^t

g = c

^t

g = 0 − 1 = −1 Cramersche Regel = ⇒

g

₁

=

−1 a

2

a

3

−1 b

₂

b

₃

−1 c

2

c

3

det(a, b, c)

= [−b

₂

c

3

− c

2

a

3

− a

2

b

3

+ c

2

b

3

+ a

2

c

3

+ b

2

a

3

]/(6 vol V ) analoge Berechnung von g

2

, g

3

erste Komponente der linken Seite Z

V

grad f

1

= 1

6 [. . .]

(5)

(ii) rechte Seite R

∂V

f ξ:

betrachte von a,b aufgespannte Seitenfl¨ ache S : (s , t) 7→ sa + tb Normale: ξ = −a × b/|a × b|

Fl¨ achenelement dS = |a × b| dt ds f (sa + tb) = 1 − s − t = ⇒

Z

S

f ξ = (b × a) Z

1

0

Z

1−s 0

1 − s − t dt ds = 1

6 (b × a)

analoge Berechnung f¨ ur die von b, c bzw. c, a aufgespannten Seitenfl¨ achen;

f null auf vierter Seitenfl¨ ache = ⇒ Z

∂V

f ξ = 1

6 (b × a + c × b + a × c)

Ubereinstimmung der ersten Komponente mit [. . .] ¨

(6)

Beispiel

Hauptsatz f¨ ur das Quadrat V = [0, 1]

²

: Z

1

0

Z

1 0

grad f (x, y) dxdy = R

₁

0

f (1, y) − f (0, y) dy R

1

0

f (x, 1) − f (x, 0) dx

!

ξ = (±1, 0), (0, ±1) , ξ

_v

jeweils nur auf zwei gegen¨ uberliegenden Randkomponenten 6= 0

V ξ

(7)

Komponenten der Identit¨ at univariater Hauptsatz z.B.

Z

1 0





1

Z

0

f

_x

(x, y) dx



 dy =

1

Z

0

[f (x, y)]

^x=1_x=0

dy

(8)

Beispiel

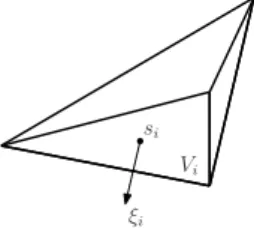
Illustration des Hauptsatzes f¨ ur einen Simplex V ⊆ R

ⁿ

, begrenzt durch (n − 1)-dimensionale

Simplizes V

_i

,, i = 1, . . . , n + 1

ξ

i

: nach außen gerichtete Einheitsnormale, s

i

: Schwerpunkt von V

i

si

ξi

Vi

(9)

(i) konstante Funktion f (x) = b:

Hauptsatz = ⇒

0 = X

i

vol

n−1

(V

i

)ξ

i

(ii) lineare Funktion f (x) = a

^t

x:

Hauptsatz = ⇒

vol

_n

(V ) a = X

i

vol

n−1

(V

_i

)(a

^t

s

_i

)ξ

_i

,

denn f¨ ur einen Simplex mit Schwerpunkt s ist die Quadraturformel Z

S

f ≈ vol(S )f (s)

f¨ ur lineare Funktionen f exakt

(10)

Beispiel

Illustration des Hauptsatzes f¨ ur Kugel mit Radius R und Oberfl¨ ache S = ∂V

Volumen- und Fl¨ achenelement (Kugelkoordinaten)

dV = r

²

sin ϑ drdϑdϕ, dS = R

²

sin ϑ dϑdϕ ξ = (x , y, z )

^t

/R

Hauptsatz = ⇒ Z

R

0

Z

π 0

Z

2π 0

grad f (r , ϑ, ϕ) r

²

sin ϑ dϕdϑdr

= R

²

Z

_π

0

Z

_2π

0

f (R, ϑ, ϕ)





sin ϑ cos ϕ sin ϑ sin ϕ

cos ϑ





| {z }

ξ

sin ϑ dϕdϑ

(11)

z.B.:

f (x, y , z) = xz

²

= R

³

sin ϑ cos ϕ cos

²

ϑ mit

grad f (x, y , z) =



 z

²

0 2xz



 , f (x, y, z)ξ = 1 R



 x

²

z

²

xyz

²

xz

³



 erste Komponente des Hauptsatzes

Z

R 0

Z

_π

0

Z

_2π

0

(r cos ϑ)

²

r

²

sin ϑ dϕdϑdr = 4 15 πR

⁵

R

²

Z

π 0

Z

2π 0

1 R (R sin ϑ cos ϕ)

²

(R cos ϑ)

²

sin ϑ dϕdϑ = 4

15 πR

⁵