Grundfragen des Mathematikunterrichts
Online-Lektion 3: Grundformen mathematischen Arbeitens:
Modellieren und Probleml•osen
Maja Cetic / Kora Deweis-Weidlinger / Andreas Vohns
Sommersemester 2019
•Ubersicht
Grundformen mathematischen Arbeitens
Im Fokus: Anwenden und Modellieren (Fortsetzung)
Im Fokus: Probleml•osen
Modellierungskreislauf 2Modellierungskreislauf 2 Mathematik
10
nach Maaß (2005, S. 117)
Grundfragen des Mathematikunterrichts
Grundformen Modellbilden 2019S 4
Modellierungskreislauf 3
Blum (2010b, S. 43)
Wenn im Folgenden vommathematischen Modellierendie Rede ist, sind die Schritte 2, 3, 5 und 6 dieses Kreislaufs gemeint.
VonModellierungsaufgabenspreche ich, wenn substanzielle Anforderungen in Bezug auf diesen Teil des Bearbeitens involviert sind...“
Modellieren: AufgabenebeneAnforderungen auf Aufgabenebene Mathematik
2
Zum Geburtstag hat die Mutter sechs Liter Kakao gekocht. Jedes Kind bekommt einen ½ Liter Becher. Wie viele Kinder sind es?
Man stelle sich das einmal bildlich vor:
Die Kinder führen beidhändig Halbliterkrüge Kakao zum Mund hin und die Mutter steht in der Küche und versucht, aus dem Kakaoverbrauch zu erschließen, wie viele Gäste ihre Tochter wohl eingeladen hat!
(Spiegel und Selter (2003) zitiert nach B¨uchter und Leuders, 2005)
Grundfragen des Mathematikunterrichts
Grundformen Modellbilden 2019S 6
Abgrenzung: Eingekleidete Aufgaben 11/ 2H¨uhner legen in 11/ 2Tagen 11/ 2Eier.
Wie viele Eier legt ein Huhn pro Tag?
Jahnke (2001, S. 5):
Nat¨urlich dient die H¨uhneraufgabe nicht dazu, die Legeleistung von Hennen zu berechnen oder betriebswirtschaftliche Aussagen ¨uber Legebatterien
mathematisch abzusichern.
Wer so tut, macht sich zurecht l¨acherlich. Eingekleidete Aufgaben offenbaren in der Regel nichts ¨uber nicht-mathematische Sachverhalte.
Das ist nicht ihre Funktion oder sollte sie nicht sein.
Sie k¨onnen aber Mathematik veranschaulichen, einen mathematischen Satz oder Sachverhalt oder ein mathematisches Verfahren.
Modellieren: Aufgabenebene
Kriterien/Leitfragen f•ur”gute Modellierungsaufgaben“
Kriterien/Leitfragen f•ur”gute Modellierungsaufgaben“
É Modellierungspotenzial:Modellierungspotenzial: Spielt der gegebene Realit•atsbezug eine Rolle f•ur die L•osung der Aufgabe? Ist z.B. (relativ zum Vorwissen der Sch•uler(innen)) die (bewusste) Bildung eines Realmodells erforderlich?
É Authentizit•at:Authentizit•at: Werden Dinge bearbeitet, die es in der Realit•at gibt? Hat/h•atte die bearbeitete Frage auch au erhalb des Unterrichts ihre Berechtigung?
Ist/w•are das erzielte Ergebnis au erhalb von Unterricht relevant?
É Anregung:Anregung: Ist die Aufgabe f•ur die Sch•uler(innen) interessant/anregend (z.B.
durch lokale Bez•uge,
”Sch•uler(innen)n•ahe“, Ungew•ohnlichkeit)?
É Relevanz:Relevanz: Wie stark lassen sich die Sch•uler(innen) individuell, pers•onlich auf die Aufgabe ein / nehmen sich der Fragestellung als ihrer eigenen an?
É Offenheit:Offenheit: Inwieweit sind Realmodell und mathematisches Modell noch zu entwickeln oder (relativ zum Vorwissen der Sch•uler(innen)) bereits eindeutig vorgegeben?
(Greefrath, 2007, S. 27ff)
Grundfragen des Mathematikunterrichts
Grundformen Modellbilden 2019S 8
Modellieren: Aufgabenebene
Authentische Modellierungsaufgaben
Authentische Modellierungsaufgaben m•ussen echte, sowohl einfache als auch komplexe Anwendungsbez•uge von Mathematik aufzeigen.
Sie m•ussen vor allem (nicht jede einzelne f•ur sich, aber alle zusammen) die Teilprozesse des Modellierens
Teilprozesse des Modellierens ber•ucksichtigen:
É in Realsituationen eigene Fragen stellen,
É beim Mathematisieren •uber Vereinfachungen entscheiden,
Modellannahmen machen, zwischen Modellen w•ahlen (→Offenheit),
É im Modell arbeiten (und dabei ggf. der Realsituation Hinweise f•ur die L•osung entnehmen),
É Ergebnisse kritisch hinterfragen und das gesamte Modell bewerten (→ Reflexion),
É die Fragestellung oder das Modell revidieren und erneut mit dem Modellieren beginnen.
(B•uchter & Leuders, 2005, S. 76)
Modellieren: Herausforderungen auf Lernendenseite DISUM: Beobachtungen
”aus Labor und Unterricht“
DISUM: Beobachtungen
”aus Labor und Unterricht“
É Alle Schritte im Modellierungskreislauf sind potentielle kognitive H•urden f•ur Lernende, variierend je nach Aufgabe.
É Lernende benutzen i. a. keine bewussten L•osungsstrategien und sind bei auftretenden Schwierigkeiten oft hilflos.
É Es gibt einen fundamentalen Unterschied zwischen dem
”Alleine-Arbeiten“ von Lernenden und selbst•andigem Arbeiten mit Lehrpersonenunterst•utzung; im ersteren Fall sind Lernende oft
•uberfordert und geben schnell auf.
(Blum, 2010b)
Grundfragen des Mathematikunterrichts
Grundformen Modellbilden 2019S 10
Modellieren: Herausforderungen auf Lernendenseite DISUM: Empfehlungen
DISUM: Empfehlungen
É Teil-Kompetenzen des Modellierens sollten gezielt mithilfe geeigneter Aufgaben gef•ordert werden.
É Lernende sollten ad•aquate Strategien zum L•osen von Modellierungsaufgaben an die Hand gegeben werden.
É Lehrpersonen sollten mehr •uber Diagnose- und
Interventionsm•oglichkeiten beim Modellieren erfahren (→Herausforderungen auf Lehrpersonenseite).
(Blum, 2010b)
Modellieren: Empfehlung
”Teilkompetenzf¨orderung“
DISUM: Empfehlungen
É Teil-Kompetenzen des Modellierens sollten gezielt mithilfe geeigneter Aufgaben gef¨ordert werden.
Mathematik
Empfehlung: Teilkompetenzfördernde Aufgaben
3
(Schukajlow, 2009)
Grundfragen des Mathematikunterrichts
Grundformen Modellbilden 2019S 12
Modellieren: Empfehlung
”Teilkompetenzf¨orderung“
Bezug zu den M8-Standards:
É H1: Darstellen, Modellbilden
Darstellen meint die ¨Ubertragung gegebener mathematischer Sachverhalte in eine (andere) mathematische Repr¨asentation(sform).
Modellbilden erfordert ¨uber das Darstellen hinaus, in einem gegebenen Sachverhalt die relevanten mathematischen Beziehungen zu erkennen, Annahmen zu treffen, Vereinfachungen vorzunehmen u. ¨A.
É H3: Interpretieren
Interpretieren meint, aus mathematischen Darstellungen Fakten,
Zusammenh¨ange oder Sachverhalte zu erkennen und darzulegen sowie mathematische Sachverhalte und Beziehungen im jeweiligen Kontext zu deuten.
Standards M-8: Beispiel zum Modellieren
Anhand einer Landkarte soll der Inhalt der Fläche Österreichs näherungsweise ermittelt werden. (Quelle: http://www.statistik.at)
Zeichne in obige Abbildung elementare geometrische Figuren ein, die sich für eine näherungsweise Ermittlung des Flächeninhalts Österreichs gut eignen!
(Peschek, 2012, S. 50)
Grundfragen des Mathematikunterrichts
Grundformen Modellbilden 2019S 14
Standards: Beispiele zum Darstellen
Eine Plakatsäule hat die Form eines Zylinders mit aufgesetztem Kegel. Die Höhe des Zylinders ist ungefähr dreimal so groß wie der Durchmesser, die Höhe des Kegels ungefähr halb so groß wie der Durchmesser.
Fertige eine Schrägriss-Skizze der Plakatsäule an!
Rationale Zahlen kann man in Dezimaldarstellung oder Bruchdarstellung anschreiben.
Schreibe die Zahl 4
7 in Dezimaldarstellung an!
Schreibe die Zahl 0,20 in Bruchdarstellung an!
(Peschek, 2012, S. 46, S. 50)
Standards: Beispiel zum Interpretieren
Die nebenstehende Figur zeigt einen Kegel.
Was wird durch (R2 H r2 h)
3
berechnet?
Es sind:
P1: Preis eines Fernsehers im Jahre 2008
P2: Preis eines Fernsehers vergleichbarer Qualität im Jahre 2010 Was bedeutet 0,35
P P P
1 1
2 ?
(Schneider, 2012, S. 92)
Grundfragen des Mathematikunterrichts
Grundformen Modellbilden 2019S 16
Modellieren: Empfehlung
”Teilkompetenzf¨orderung“
Validieren
Mathematik
Empfehlung: Teilkompetenzfördernde Aufgaben
4
(Maaß , 2007)
Bezug zu den M8-Standards:
”Reflektieren umfasst das Nachdenken ¨uber [...] mathematische Modelle (Modellannahmen, Idealisierungen, Aussagekraft, Grenzen des Modells, Modellalternativen) im jeweiligen Kontext sowie das Nachdenken ¨uber (vorgegebene) Interpretationen, Argumentationen oder Begr¨undungen.“
Modellieren: Empfehlung
”Ad¨aquate Strategien“
Vereinfachter Modellierungskreislauf
Mathematik
Empfehlung: Adäquate Strategien
(Schukajlow, 2009)5 Grundfragen des Mathematikunterrichts
Grundformen Modellbilden 2019S 18
Modellieren: Empfehlung
”Ad¨aquate Strategien“
Weitere strategische Hilfestellungen
(hinreichend offene Aufgaben vorausgesetzt)
(B¨uchter & Leuders, 2005)
Modellieren: Herausforderungen auf Lehrpersonenseite DISUM: Beobachtungen”aus Labor und Unterricht“
DISUM: Beobachtungen”aus Labor und Unterricht“
É Lehrerpersonen halten sich aufgrund bestimmter p•adagogischer Vorpr•agungen bei lernendenzentriertem Unterricht zu stark zur•uck (keine Intervention in Gruppenarbeitsphasen).
É Wenn sie eingreifen, geben sie zu oft direkte inhaltliche Hilfen, statt blo strategisch einzugreifen (Prinzip der”minimalen Hilfe“ nach Aebli wird verletzt).
É Sie setzen oft ihre eigene spezielle Variante der Aufgabenl•osung bei den Lernenden durch, weil ihre Interventionen massiv von dieser L•osungsvariante gepr•agt sind.
É Lehrpersonen stimulieren kaum L•osungsstrategien bei Lernenden, obwohl gerade f•ur Modellierungsaufgaben wirksame strategische Instrumente zur Verf•ugung stehen (Modellbildungskreisl•aufe, Strategieschemata).
(Blum, 2010b)
Grundfragen des Mathematikunterrichts
Grundformen Modellbilden 2019S 20
Modellieren: Herausforderungen auf Lehrpersonenseite DISUM: Empfehlungen
DISUM: Empfehlungen
É •Ubergreifend: Problem-Wahrnehmung und -Bewusstsein st•arken.
É Lehrerpersonenrolle beim sch•uler(innen)zentrierten Unterricht
•uberdenken.
É M•oglichkeiten gestufter Hilfestellung kennen lernen, Erfahrungen mit unterschiedlichen Modellbildungskreisl•aufen als strategische
Hilfsmittel (f•ur Lehrpersonen und Lernende) sammeln lassen.
É Erfahrungen in der Exploration des”task space“ von (offeneren) Modellierungsaufgaben sammeln lassen (Welche verschiedenen L•osungsans•atze sind denkbar, m•oglich?).
É Geeignete Unterrichtsformen /
”Best Practice“-Unterrichtsskripte kennen lernen.
(Blum, 2010b)
Modellieren: Empfehlung
”Lehrpersonenrolle“
Hilbert Meyer <> Werner Blum
Empfehlungen: Lehrer(innen)rolle
(Blum, 2010a)6
Grundfragen des Mathematikunterrichts
Grundformen Modellbilden 2019S 22
Modellieren: Empfehlung
”Gestufte Hilfen“
Mathematik
Empfehlungen: Gestufte Hilfen (nach Maaß 2007)
Ziel: möglichst stark selbstständigkeitserhaltende Intervention
Motivationshilfen
„Du wirst das schon schaffen!“
„Versuch es doch mal!“
Rückmeldungshilfen
„Da bist Du auf dem richtigen Weg.“
„Da musst Du nochmal nachrechnen.“
allgemein‐strategische Hilfen
„Lies Dir die Aufgabe genau durch!“
„Mach Dir eine Skizze!“
„Schreib Dir gegebene Daten heraus!“
„Welche Daten benötigst Du, wie kannst Du sie erhalten?“
„Überlege Dir, an welcher Stelle des Modellierungsprozesses Du jetzt stehst!“
„Überlege Dir, welcher Schritt beim Modellieren als nächster kommt!“
DISUM: Eher geringe (praktische) Bedeutung
(Maaß , 2007)
Modellieren: Empfehlung
”Gestufte Hilfen“
Mathematik
Empfehlungen: Gestufte Hilfen (nach Maaß 2007)
Ziel: möglichst stark selbstständigkeitserhaltende Intervention
inhaltsorientierte strategische Hilfen
„Welche Werte fehlen Dir? Versuche, Angaben dafür zu schätzen!“
„Welche Bedeutung hat dieser Wert für das Lösen der Aufgabe?“
„Überlege Dir, ob dieses Ergebnis bezogen auf das Ausgangsproblem sinnvoll ist!“
inhaltliche Hilfen
„Stelle einen Zusammenhang zwischen diesen beiden Werten her!“
„Wird der Erdgasverbrauch in den nächsten Jahren gleich bleiben, steigen oder sinken?“
„Berücksichtige auch, dass in den nächsten Jahren die Ölvorkommen geringer werden.“
17
(Maa , 2007)
Grundfragen des Mathematikunterrichts
Grundformen Modellbilden 2019S 24
Modellieren: Empfehlungen
”Unterrichtssetting“
”Best Practice“ Unterrichtsskript (TIMSS/DISUM)
”Best Practice“ Unterrichtsskript (TIMSS/DISUM) 1. Vorstellung des Beispiels im Plenum
2. Einzelarbeit 3. Gruppenarbeit
4. Individuelles Aufschreiben von L•osungen 5. Pr•asentation der L•osungen im Plenum
6. Vergleich der L•osungen und reflektierender R•uckblick
Phasen 4. und 5. lassen sich durch Gruppenl•osungen ersetzen, dann kann Gruppenpuzzle sinnvoll sein.
(Blum, 2010b)
Modellieren: Empfehlung
”Unterrichtssetting“
Empfehlungen: Unterrichtssetting
(Schukajlow, 2009)7 Grundfragen des Mathematikunterrichts
Grundformen Modellbilden 2019S 26
Anwenden und Modellieren: Wozu?
Traditionell: Sachrechnen
Drei”Sinngebungen“ (nach: Winter, 2003):
É Sachrechnen als Lernstoff
(Nahezu) Unmittelbar alltagspraktisch verwendbare Mathematik, Umgang mit Gr¨oß en, Prozentrechnung, elementar(st)e Statistik
É Sachrechnen als Lernprinzip
Lernpsychologische Bedeutung, als motivierender Einstieg, zur Veranschaulichung von (abstrakten) Begriffen durch Verk¨orperung in Sachsituationen
É Sachrechnen als Lernziel: Bef¨ahigung zur Umwelterschließ ung Sachrechnen im Dienst vonSachkunde: Mit Mathematik / durch Mathematisierung wird etwas Relevantes ¨uber die Welt (und die Rolle von Mathematik in der Welt) gelernt
Probleml•osen: Einstiegsbeispiel
Aufgabenstellung
1. Legen Sie mit den Ziffernkartenzweidreistellige Zahlen und addieren Sie diese. Versuchen Sie, als Summe genau 1000 zu erhalten.
1 2 3 4 5 6 7 8 9
2. Legen Sie mit den Ziffernkartendreidreistellige Zahlen und addieren Sie diese. Versuchen Sie,
a) eine m•oglichst gro e Summe zu erzeugen, b) eine m•oglichst kleine Summe zu erzeugen,
c) mit der Summe m•oglichst nah an 1000 heranzukommen.
3. •Uberlegen Sie: Warum ist die Summe 1000 nicht m•oglich?
Grundfragen des Mathematikunterrichts
Grundformen Probleml•osen 2019S 28
Was ist ein Problem?
Duncker (1935, S. 1):
EinProblementsteht z. B. dann, wenn ein Lebewesen ein Ziel hat und nicht weiß, wie es diese Ziel erreichen soll. Wo immer der gegebene Zustand nicht durch blo es Handeln (Ausf•uhren selbstverst•andlicher Operationen) in den erstrebten Zustand •uberf•uhren l•asst, wird das Denken auf den Plan gerufen. Ihm liegt es ob, ein vermittelndes Handeln zuallererst zu
konzipieren.
B•uchter und Leuders (2005, S. 28):
Eine Probleml•oseaufgabe (auch kurz: Problem) ist die Aufforderung, eine L•osung zu finden, ohne dass ein passendes L•osungsverfahren auf der Hand liegt.
Was ist ein Problem?
Objektive und subjektive Probleme (Sill, 2006)
Der Begriff”Problem“ wird in der Didaktik in zwei Bedeutungen verwendet:
Unter Problem wird einmal im Sinne einerobjektiven Kategorieeine besonders schwierige und anspruchsvolle Anforderung verstanden.
Damit sind Problem und Aufgabe (als sofort l•osbare Anforderung) einander nachgeordnete Begriffe.
Sinnvoller in Bezug auf den Lernprozess von Sch•ulern scheint mir die andere Verwendung der Begriffs Problem zu sein, bei der unter Problem im Sinne einer subjektiven Kategorieeine Aufgabe verstanden wird, die durch den jeweiligen L•oser nicht unmittelbar bearbeitet werden kann.
In diesem Fall ist ein Problem eine spezielle Aufgabe, die durchaus einfach bzw.
elementar sein kann.
Grundfragen des Mathematikunterrichts
Grundformen Probleml•osen 2019S 30
Was ist ein Problem?
Didaktik der Geometrie 5.6
Jürgen Roth
Was ist ein Problem?
Anfangszustand Zielzustand
(Routine-)Aufgabe
Algorithmus
Anfangszustand Zielzustand
Problem
?
http://www.juergen-roth.de/lehre/skripte/did_grundlagen/fachdidaktische_grundlagen.pdf
Ein Problemlöser kenntkeine Lösung der Aufgabe, also weder einen Operator noch eine Operatorkette, die den Anfangszustand in den Zielzustand überführt.
Quelle: Roth (2016)
Grundformen Probleml¨osen 2019S 31
Was ist ein Problem?
Didaktik der Geometrie 5.8
Jürgen Roth
objektivsubjektiv
Problemtypen im Geometrieunterricht
Interpolationsprobleme
1. Anfangszustand (das Gegebene) genau definiert 2. Zielzustand (das Gesuchte) genau definiert
3. Problemlöser verfügtüber Operationen, die eine Lösung des Problems gestatten.
Quelle: Roth (2016) Grundfragen des Mathematikunterrichts
Grundformen Probleml¨osen 2019S 32
Wozu Probleml¨osen?
Kadunz und Str¨aß er (2009): im Kontext”entdeckenden Lernens“ (Winter, 1991)
É zul¨assige(re)s Bild von Mathematik (kreativer, oft unsichtbarer Teil)
É Eigenst¨andigkeit als”Bedingung der M¨oglichkeit“ pers¨onlicher Einsichtsgewinnung
É subjektives Erfolgserleben kann zu Identifikation mit Fragestellungen und verbundenem Kontext f¨uhren
É Suchen von L¨osungsans¨atzen f¨uhrt zur Reorganisation von Wissen und Probleml¨osen wird damit zum ¨Ubungsfeld
Auch: ¨Ahnlich wie
”Sachrechnen“ / Mathematisches Modellieren:
É ”Zweck an sich“ (vgl.→allgemeine Lernzielenach Winter (1975))
É Mittel zu anderen Zwecken, insbesondere
É Erarbeitung neuer (Routine-)Verfahren
É Entdecken neuer Sachverhalte, Finden von Begr¨undungen / Beweisen
Heuristik
”Kunst des Probleml¨osens“
Im Angebot:
É heuristische Strategien
É bereichs¨ubergreifende
É bereichsspezifische (in den Lernbereichsdidaktiken Thema)
É heuristische Hilfsmittel
É L¨osungspl¨ane
É (gestufte) Hilfen (dieselben wie beim Modellieren)
Grundfragen des Mathematikunterrichts
Grundformen Probleml¨osen 2019S 34
Heuristische Strategien
176 Jürgen Roth• Fachdidaktische Grundlagen
Heuristische Strategien
Vorwärtsarbeiten
Was ist gegeben?
Was weiß ich über das Gegebene?
Was kann ich daraus ermitteln?
Rückwärtsarbeiten Was ist gesucht?
Was weiß ich über das Gesuchte?
Was benötige ich, um das Gesuchte zu ermitteln?
Invarianzprinzip
Was ändert sich nicht?
Was haben alle Objekte gemeinsam?
Zerlegungsprinzip
Welche Teilfragen sind zu lösen? (Zerlegen) Abarbeiten der Teilprobleme
Kombination
Quelle: Roth (2016)
Grundformen Probleml¨osen 2019S 35
Heuristische Strategien
177 Jürgen Roth• Fachdidaktische Grundlagen
Heuristische Strategien
Analogiebildung
Hast du schon einmal etwas Ähnliches gelöst?
Lassen sich Lösungsschritte übernehmen?
Suchraumeingrenzung
In welchen Grenzen liegt das Ergebnis?
Systematisches Probieren Ziel-Mittel-Analyse
Welche (heuristischen) Hilfsmittel können auf dem Weg zum Ziel hilfreich sein?
Spezialisieren, Grenzfälle ausloten Vom Besonderen zum Allgemeinen Konkretisieren
Beispiele analysieren
Quelle: Roth (2016) Grundfragen des Mathematikunterrichts
Grundformen Probleml¨osen 2019S 36
Heuristische Hilfsmittel
178 Jürgen Roth• Fachdidaktische Grundlagen
Heuristische Hilfsmittel
Tabelle
Ausprobieren!
Welche Werte sollen in die Tabelle eingetragen werden?
Informative Figur
Hilft beim Verständnis des Problems.
Beim Zeichnen wird deutlich, welche Informationen zur Lösung benötigt werden.
Gleichung / Term
Beziehungen der Informationen werden verknüpft dargestellt.
Nicht immer notwendig!
𝑛𝑛+ (𝑛𝑛+ 1) + (𝑛𝑛+ 2)
=3𝑛𝑛+ 3
= 3�(𝑛𝑛+ 1)
𝒏𝒏 𝒏𝒏+𝟏𝟏 𝒏𝒏+𝟐𝟐 Summe
1 2 3 6
5 6 7 18
9 10 11 30
Beispiel:Was gilt für die Summe dreier aufeinanderfolgender natürlicher Zahlen?
Quelle: Roth (2016)
L¨osungsplan (P ´olya)
182 Jürgen Roth• Fachdidaktische Grundlagen
Wie sucht man die Lösung?
Pólya, G. (19954): Die Schule des Denkens. Francke Verlag, Umschlaginnenseite
Quelle: Roth (2016) Grundfragen des Mathematikunterrichts
Grundformen Probleml¨osen 2019S 38
L¨osungsplan (P ´olya)
181 Jürgen Roth• Fachdidaktische Grundlagen
Wie sucht man die Lösung?
Erstens
Du musst die Aufgabe verstehen.
Zweitens
Suche den Zusammenhang zwischen den Daten und der Unbekannten.
Du musst vielleicht Hilfsaufgaben betrachten, wenn ein unmittelbarer Zusammenhang nicht gefunden werden kann.
Du musst schließlich einen Plan der Lösung erhalten.
Drittens
Führedeinen Plan aus.
Viertens
Prüfe die erhaltene Lösung.
Pólya, G. (19954): Die Schule des Denkens. Francke Verlag, Umschlaginnenseite
Quelle: Roth (2016)
Problem 2:
Denken Sie sich vier beliebige nat•urliche Zahlen aus.
Zwei davon haben immer eine Differenz, die durch drei teilbar ist.
Warum stimmt das?
Grundfragen des Mathematikunterrichts
Grundformen Probleml•osen 2019S 40
Problem 2:
Denken Sie sich vier beliebige nat•urliche Zahlen aus.
Zwei davon haben immer eine Differenz, die durch drei teilbar ist.
Warum stimmt das?
Wie sucht man die Lösung?
Pólya, G. (19954): Die Schule des Denkens. Francke Verlag, Umschlaginnenseite
Problem 2:
Denken Sie sich vier beliebige nat•urliche Zahlen aus.
Zwei davon haben immer eine Differenz, die durch drei teilbar ist.
Warum stimmt das?
184 Jürgen Roth • Fachdidaktische Grundlagen
Wie sucht man die Lösung?
Pólya, G. (19954): Die Schule des Denkens. Francke Verlag, Umschlaginnenseite
Grundfragen des Mathematikunterrichts
Grundformen Probleml•osen 2019S 42
Problem 2:
Denken Sie sich vier beliebige nat•urliche Zahlen aus.
Zwei davon haben immer eine Differenz, die durch drei teilbar ist. Warum stimmt das?
Wie sucht man die Lösung?
Pólya, G. (19954): Die Schule des Denkens. Francke Verlag, Umschlaginnenseite
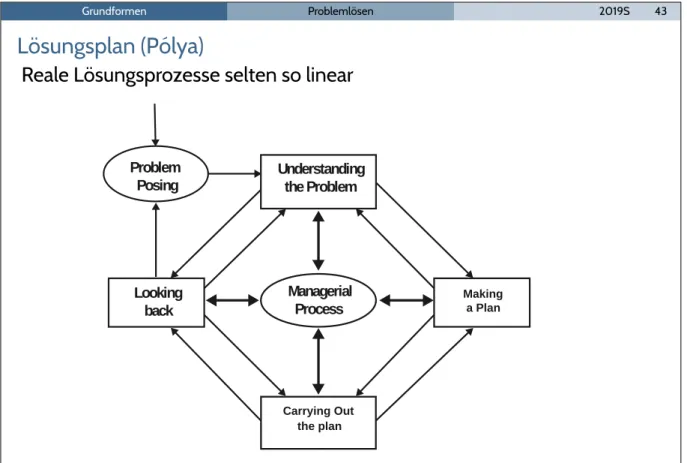
L¨osungsplan (P ´olya)
Reale L¨osungsprozesse selten so linear288 F. Heinrich et al.
entsprechen Variablen, deren Wirkungen auf die Problemlösefähigkeiten der Schülerin- nen und Schüler teilweise anhand empirischer Befunde belegt werden können (vgl. Collet 2009).
Making a Plan
Understanding the Problem Problem
Posing
Looking
back Managerial
Process
Carrying Out the plan
Abb. 10.1 Verlaufsmodell nach Fernandez, Hadaway und Wilson (1994)
Vor, während und nach der selbstregulierten Problembearbeitung Orientierungsgrundlagen auf unterschiedlichem Niveau
Problem- stellung
Self-Monitoring und Steuerung der Problembearbeitung -Volitionale Strategien
-Lernstrategien L
E R N A U F G A B E
Reflexion über -Inhalte -Vorgehen Motivation Emotion Selbstwirk- samkeit
Kompetenz- zuwachs
Vo r ... Während... Nach...
Analyse &
Planung Problem - Lesen - Analysieren
lösung
Planen mit Beweglichkeits- eigenschaften
Ausführung
Problem Problem-
- Mathe- matisieren - Verarbeiten mit bereichsspezifis- chem Wissen und Fähigkeiten
Kontrolle
- Kontrollieren - Inter- pretieren - Validieren Motivation
Emotion Selbstwirk- samkeit
Abb. 10.2 Prozessmodell selbstregulierten Problemlösens (Collet 2009)
Grundfragen des Mathematikunterrichts
Grundformen Probleml¨osen 2019S 44
Probleml¨osen lernen
...kann man nur dadurch, dass man Probleme l¨ost.
Flankierend / unterst¨utzend: Heurismen vermitteln durch
É Implizite Gew¨ohnung an heuristische Vorgehensweisen und zugeh¨orige typischen Fragestellungen
É Zu lernende Strategie an Hand von ausgearbeiteten Musteraufgaben explizit vorstellen
É ¨Ubungsphase mit Aufgaben unterschiedlicher Schwierigkeit, in denen die neue Strategie bewusst angewandt werden soll
É Reflexion ¨uber L¨osungsprozesse anregen, etwa durch Dokumentation entlang von Pl¨anen
(Heinrich, Bruder & Bauer, 2015)
Blum, W. (2010a). Kann mathematische Modellieren selbständig gelernt werden? Ergebnisse aus der Lehr-/Lernforschung. Paderborn. Zugriff unter https://goo.gl/2LuWHE
Blum, W. (2010b). Modellierungsaufgaben im Mathematikunterricht: Herausforderung für Schüler und Lehrer.Praxis der Mathematik in der Schule,52(34), 42–48.
Büchter, A. & Leuders, T. (2005).Mathematikaufgaben selbst entwickeln: Lernen fördern - Leistung überprüfen.
Berlin: Cornelsen Scriptor.
Duncker, K. (1935).Zur Psychologie des produktiven Denkens. Berlin: Springer.
Fernandez, M. L., Hadaway, N. & Wilson, J. W. (1994). Problem solving: Managing it all.The Mathematics Teacher, 87, 195–199.(3).
Greefrath, G. (2007).Modellieren lernen mit offenen realitätsnahen Aufgaben (2., unveränd. Au .). Köln:
Aulis-Verl. Deubner.
Heinrich, F., Bruder, R. & Bauer, C. (2015). Problemlösen lernen. In R. Bruder, L. Hefendehl-Hebeker, B. Schmidt-Thieme & H.-G. Weigand (Hrsg.),Handbuch der Mathematikdidaktik(S. 279–301). Berlin, Heidelberg: Springer.
Jahnke, T. (2001). Kleines Aufgabenbrevier: Zur Klasi zierung von Aufgaben im Mathematikunterricht.
Potsdam: Pädagogisches Landesinstitut Brandeburg. Zugriff unter https://goo.gl/RyHJG9 Kadunz, G. & Sträßer, R. (2009).Didaktik der Geometrie in der Sekundarstufe I(3., korr. Au .). Hildesheim:
Franzbecker.
Maaß, K. (2005). Modellieren im Mathematikunterricht der Sekundarstufe I.Journal für Mathematik- Didaktik,26(2), 114–142.
Maaß, K. (2007).Mathematisches Modellieren: Aufgaben für die Sekundarstufe I. Berlin: Cornelsen Scriptor.
Peschek, W. (2012). Darstellen, Modellbilden. In B. Kröp & E. Schneider (Hrsg.),Standards Mathematik unter der Lupe(S. 41–58). München: Pro l-Verl.
Pólya, G. (1995).Schule des Denkens: Vom Lösen mathematischer Probleme(4. Au .). Tübingen: Francke.
Roth, J. (2016).Fachdidaktische Grundlagen: Vorlesungsfolien. Koblenz. Zugriff unter https://goo.gl/tE1iPs Schneider, E. (2012). Interpretieren. In B. Kröp & E. Schneider (Hrsg.),Standards Mathematik unter der
Lupe(S. 79–98). München: Pro l-Verl.
Schukajlow, S. (2009). Selbständigkeitsorientierter Unterricht mit Modellierungsaufgaben. Wien. Zugriff unter https://goo.gl/9NpJTM
Spiegel, H. & Selter, C. (2003).Kinder & Mathematik: Was Erwachsene wissen sollten. Seelze-Velber: Kall- meyer.
Winter, H. (1975). Allgemeine Lernziele für den Mathematikunterricht?Zentralblatt für Didaktik der Ma- thematik, (7), 106–116.
Winter, H. (1991).Entdeckendes Lernen im Mathematikunterricht: Einblicke in die Ideengeschichte und ihre Bedeutung für die Pädagogik(2., verb. Au .). Braunschweig: Vieweg.
Winter, H. (2003).Sachrechnen in der Grundschule: Problematik des Sachrechnens ; Funktionen des Sachrech- nens ; Unterrichtsprojekte(6. Au .). Frankfurt am Main: Cornelsen Scriptor.