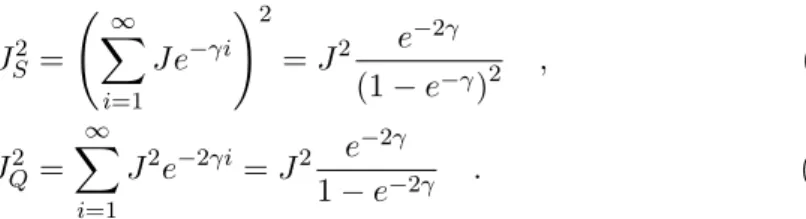Quantenmechanische Berechnung von Autokorrelationsfunktionen im Zentralspinmodell f¨ur unendlich große Spinb¨ader

Quantenmechanische Berechnung von Autokorrelationsfunktionen

im Zentralspinmodell f¨ ur unendlich große Spinb¨ ader

Masterarbeit

zur Erlangung des akademischen Grades Master of Science

vorgelegt von

Robin R¨ohrig

geboren in Arnsberg

Lehrstuhl f¨ ur Theoretische Physik I Fakult¨ at Physik

Technische Universit¨ at Dortmund

2017

2. Gutachter : Prof. Dr. Frithjof B. Anders

Datum des Einreichens der Arbeit: 26. September 2017

Kurzfassung

Das Zentrale Thema dieser Arbeit ist die quantenmechanische Berechnung von Autokor- relationsfunktionen im thermodynamischen Limes mit iterierten Bewegungsgleichungen im Zentralspinmodell. Dieses Modell beschreibt die Dynamik eines zentralen Spins in einem Bad aus Kernspins, die besonders im Bezug auf die Realisierung von Qubits eine wichtige Rolle spielt. Die Schwierigkeit besteht darin, dass in realistischen Systemen eine sehr große Anzahl wechselwirkender Badspins vorhanden ist. Quantenmechanische Berechnungen, die ann¨ ahernd realistische Badgr¨ oßen erfassen k¨ onnen, sind sehr limi- tiert in der berechenbaren Zeit. Mit einer klassischen Betrachtung ist es jedoch bereits gelungen, Autokorrelationen sogar f¨ ur ein unendlich großes Spinbad zu berechnen und dabei trotzdem sehr lange Zeiten zu erreichen.

Aufbauend auf diesen effizienten klassischen Algorithmen wird eine quantenmechani- sche Operatorbasis hergeleitet, die ebenfalls eine Betrachtung im thermodynamischen Limes erlaubt und dabei die Berechnung l¨ angerer Zeiten erm¨ oglicht, als etablierte Me- thoden f¨ ur große B¨ ader. Die n¨ otigen Anpassungen f¨ ur den ¨ Ubergang von der klassischen zur quantenmechanischen Beschreibung werden dabei motiviert und erl¨ autert. Die Re- sultate werden anschließend mit etablierten Methoden verglichen, wobei sich eine sehr gute ¨ Ubereinstimmung f¨ ur kurze Zeiten zeigt. Ein Vergleich f¨ ur l¨ angere Zeiten wird anschließend f¨ ur kleine B¨ ader durchgef¨ uhrt. Die Auswirkungen eines externen Magnet- feldes, welches auf den Zentralspin wirkt, werden abschließend analysiert.

Abstract

The main topic of this thesis is the quantum mechanical calculation of autocorrelation functions in the theromdinamic limit using iterated equations of motion in the central spin model. This model describes the dynamics of a central spin surrounded by a bath of nuclear spins, which is especially relevant for the realization of qubits. The main difficulty is caused by the large number of interacting bath spins in a realistic system.

Quantum mechanical approaches that can describe a relevant number of nuclear spins are restricted to very limited times. However, with a classical approach it is now possible to calculate autocorrelations for long times, even for infinite baths.

Using these efficient algorithms, a quantum mechanical operator basis will be derived that also allows a calculation for an infinite bath while reaching longer times than other methods for large spin baths. For this, the adjustments needed to achive the transition from the classical to the quantum mechanical description are motivated and explained.

Then, comparisons of the results with other methods are presented, which show a good

agreement for small times. A comparison for longer times is made afterwards using

small baths. Finally, the influence of a magnetic field, that acts on the central spin, is

analyzed.

Inhaltsverzeichnis

Inhaltsverzeichnis IV

1 Einleitung 1

2 Zentralspinmodell 3

3 Iterierte Bewegungsgleichungen 7

4 Direkte Basisentwicklung 11

4.1 Basisoperator . . . . 11

4.2 Allgemeine Basis-Entwicklung und Trunkierung . . . . 12

4.3 Resultate . . . . 15

4.3.1 Exakte L¨ osung . . . . 15

4.3.2 Trunkierte L¨ osung . . . . 18

5 Approximative Basisentwicklung f¨ ur große B¨ ader 21 5.1 Orthonormale Felder und Lanczos-Rekursion . . . . 21

5.2 Basisoperatoren mit Hermitepolynomen . . . . 23

5.3 Allgemeine Basisentwicklung . . . . 26

5.4 Ubergang zu bosonischen Leiteroperatoren . . . . ¨ 28

5.4.1 Leiteroperatoren der Hermitepolynome . . . . 29

5.4.2 Zentralspin-Matrizen des Hamiltonoperators . . . . 30

5.4.2.1 Multiplikation . . . . 30

5.4.2.2 Kommutation . . . . 31

5.4.3 Effektiver Hamiltonoperator . . . . 32

5.4.4 Konsistenz der Approximation . . . . 35

5.4.5 Trunkierungsschema . . . . 38

5.5 Resultate . . . . 38

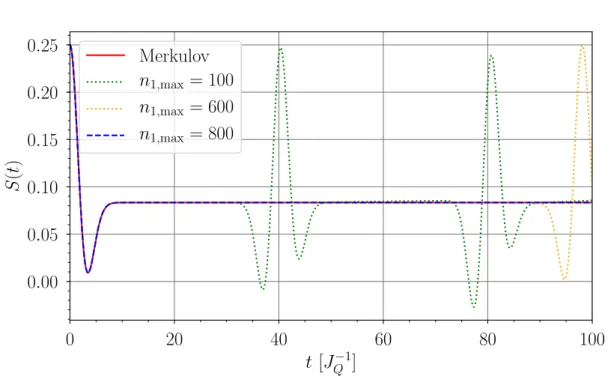
5.5.1 Eingefrorenes Overhauserfeld und Merkulov-L¨ osung . . . . 39

5.5.2 Dynamisches Overhauserfeld . . . . 41

5.5.2.1 Stufe j = 1 . . . . 42

5.5.2.2 Stufe j = 2 . . . . 45

5.5.2.3 Stufe j = 3 . . . . 48

5.5.2.4 Simulation mit Magnetfeld . . . . 51

6 Zusammenfassung und Ausblick 55 A Approximative Basisentwicklung f¨ ur große B¨ ader 59

A.1 Leiteroperatoren der Hermite-Polynome . . . . 59

A.2 Direkte Zeitentwicklung . . . . 60

A.2.1 0. Ordnung . . . . 60

A.2.2 1. und 2. Ordnung . . . . 60

A.2.3 3. und 4. Ordnung . . . . 61

A.2.4 6. Ordnung . . . . 62

Quellenverzeichnis 65

Kapitel 1

Einleitung

Ein klassischer Computer arbeitet bekanntermaßen mit einem Bin¨ arsystem aus Bits, welche entweder den Wert Eins oder Null annehmen k¨ onnen. Ein vergleichbares Zwei- Niveau-System kann auch quantenmechanisch betrachtet werden und wird Quanten- bit, oder kurz Qubit, genannt. Durch die Eigenschaften der ¨ Uberlagerung und Ver- schr¨ ankung sind mit Qubits Algorithmen denkbar, die spezielle Aufgaben deutlich ef- fizienter l¨ osen als herk¨ ommliche Computer.

Der Shor-Algorithmus [1, 2] erm¨ oglicht zum Beispiel durch eine Primfaktorzerle- gung in polynomialer Zeit kryptographische Verschl¨ usselungen zu dechiffrieren, die mit heutigen Computern wegen der schlechten Laufzeit als praktisch nicht dechiffrierbar gelten. Ein weiteres Beispiel ist der Grover-Algorithmus, welcher die Suche in einer großen Datenbank von einer linearen Laufzeit auf eine Laufzeit proportional zur Qua- dratwurzel der Datenbankeintr¨ age reduziert [3].

Damit ein physikalisches System f¨ ur einen Qubit in Frage kommt, muss es die be- kannten DiVincenzo-Kriterien erf¨ ullen [4]. Es gibt viele Ans¨ atze, jedoch erf¨ ullt bisher kein Kandidat alle dieser Kriterien. Ein vielversprechendes System ist ein lokalisier- tes Elektron eingeschlossen in einem Quantenpunkt, wobei durch den Elektronenspin mit den Zust¨ anden ↑ und ↓ ein Zwei-Niveau-System gegeben ist. Quantenpunkte wur- den schon in fr¨ uheren Arbeiten theoretisch [5, 6] und in einer Vielzahl von Expe- rimenten [6–9] untersucht. Das Elektron ist dabei von Kernspins des Substrats des Quantenpunktes umgeben. Ein h¨ aufig verwendetes Material ist zu Beispiel GaAs [6–

8]. Die umgebenden Kernspins f¨ uhren zur Dekoh¨ arenz des Elektronenspins, wodurch die Information des anf¨ anglichen Zustands verloren geht. Um m¨ oglichst viele Gatter- Operationen durchf¨ uhren zu k¨ onnen, ist deswegen eines der DiVincenzo-Kriterien eine lange Koh¨ arenzzeit. Darum ist es essentiell zun¨ achst den Dekoh¨ arenzprozess zu ver- stehen, um Maßnahmen zu entwickeln, welche die Koh¨ arenzzeit verl¨ angern, wie zum Beispiel durch Pulssequenzen [10].

In einem Quantenpunkt ist die dominierende Kopplung zwischen Elektronenspin

und Kernspins ¨ uber die Hyperfein-Wechselwirkung gegeben [6]. Dabei wirken die Kern-

spins als ein Bad auf den Elektronenspin. Ein geeignetes Modell um die Dynamik des

Elektronenspins in so einem System zu beschreiben ist das sogenannte Zentralspinmo-

dell [6, 11], das von Gaudin eingef¨ uhrt wurde [12, 13].

F¨ ur die Berechnung experimentell relevanter Observablen mit diesem Modell, wie zum Beispiel der Autokorrelationsfunktion, wurden eine Reihe verschiedener Ans¨ atze entwickelt. F¨ ur kleine B¨ ader mit bis zu N = 20 Spins kann eine Simulation ¨ uber exak- te Diagonalisierung (ED) [6] oder Chebyshev-Expansion (CET) [14–16] durchgef¨ uhrt werden. Dabei sind auch Simulationen langer Zeiten m¨ oglich. F¨ ur stark polarisierte Anfangszust¨ ande ist ebenfalls eine analytische L¨ osung ¨ uber den algebraischen Bethe- Ansatz m¨ oglich [13, 17]. F¨ ur unpolarisierte Anfangszust¨ ande kann eine L¨ osung ¨ uber den Bethe-Ansatz in Kombination mit einem direkten Monte-Carlo-Sampling f¨ ur sehr schwache bis starke Magnetfelder und B¨ ader mit bis zu N = 48 Kernspins erreicht wer- den [18, 19]. Realistische Badgr¨ oßen liegen jedoch f¨ ur einen Quantenpunkt bei N ≈ 10 ⁴ bis 10 ⁶ Kernspins [6, 11, 20, 21], weswegen es anderer Methoden zur Berechnung bedarf.

Die Zeitentwicklung des Zentralspins f¨ ur gr¨ oßere B¨ ader mit bis zu N = 1000 Kern- spins kann ¨ uber die Methode der Dichtematrix-Renormierungsgruppe (DMRG) berech- net werden, jedoch nur f¨ ur eine sehr begrenzte Zeit [22, 23]. F¨ ur eine rein klassische Berechnung des Zentralspinmodells [11, 24] ist das Bewegungsgleichungssystem deutlich einfacher zu l¨ osen. Das erm¨ oglicht auch lange Zeiten f¨ ur große B¨ ader, sogar im ther- modynamischen Limes, zu berechnen [25]. Jedoch werden dabei quantenmechanische Effekte offensichtlich nicht beachtet.

Die Ergebnisse von Fauseweh et al. in Ref. [25] haben die Effizienz einer vollkom- men klassischen Simulation allerdings deutlich erh¨ oht. Ein approximativer Ansatz ist dabei orthonormale Felder aus Spinoperatoren einzuf¨ uhren, die mithilfe des bekannten Lanczos-Algorithmus [26] hierarchisch aufgebaut sind. Dies liefert ein effizient l¨ osbares Bewegungsgleichungssystem auch bei Badgr¨ oßen N → ∞ . Diese Arbeit setzt hier an und ¨ uberf¨ uhrt diese Methodik in eine voll quantenmechanische Betrachtung. Dabei liegt der Fokus auf der Entwicklung einer passenden Operatorbasis mit den hierarchischen Feldern.

Dazu wird in Kapitel 2 zun¨ achst das Zentralspinmodell eingef¨ uhrt und erl¨ autert.

F¨ ur die Zeitentwicklung wird in dieser Arbeit die Methode der iterierten Bewegungs- gleichungen genutzt. Sie wird in Kapitel 3 zun¨ achst vollkommen allgemein hergeleitet.

Anschließend werden noch einige f¨ ur das Zentralspinmodell spezifische Eigenschaften dieser Methode beschrieben.

In Kapitel 4 wird zun¨ achst ein direkter, nicht-approximativer Ansatz f¨ ur eine Ope- ratorbasis ohne hierarchische Felder betrachtet. Dieser zeigt die Schwierigkeiten einer exakten quantenmechanischen Beschreibung.

Kapitel 5 besch¨ aftigt sich anschließend mit der Entwicklung der voll quantenmecha- nischen Berechnung ¨ uber die Methode der hierarchischen, orthonormalen Felder. Dabei sind zus¨ atzliche Annahmen im Vergleich zur klassischen Lanczos-Methode n¨ otig, die haupts¨ achlich auf den Ergebnissen von Seifert et al. in Ref. [27] basieren. Anschließend werden die Resultate der approximativen Methode pr¨ asentiert und mit etablierten Me- thoden wie der DMRG und der CET verglichen. Zus¨ atzlich wird noch der Einfluss von einem externen Magnetfeld diskutiert.

Die Ergebnisse dieser Arbeit werden abschließend in Kapitel 6 zusammengefasst

und ein Ausblick f¨ ur weitere Forschungsm¨ oglichkeiten gegeben.

Kapitel 2

Zentralspinmodell

Die Hyperfein-Wechselwirkung zwischen einem Elektronen- oder Lochspin ˆ S ₀ , umge- ben von einem Bad aus Kernspins ˆ S _i in einem Quantenpunkt, l¨ asst sich sehr gut ¨ uber das Zentralspinmodell beschreiben. Eingef¨ uhrt von Michel Gaudin ist es auch unter dem Namen Gaudin-Modell bekannt [12, 13]. Der Hamiltonoperator f¨ ur die quanten- mechanische Beschreibung des Systems ist in diesem Modell durch

H ˆ = ˆ S 0 N

X

i=1

J i S ˆ i (2.1)

gegeben, wobei S 0 der Zentralspin mit der Spinquantenzahl S = 1/2 ist. Die Kopp- lungskonstanten J _i beschreiben die St¨ arke der als isotrop angenommenen Hyperfein- Wechselwirkung zwischen S ₀ und N Badspins S _i , die in dieser Arbeit ebenfalls einen Spin S = 1/2 besitzen. Es sei an dieser Stelle darauf hingewiesen, dass die Kernspins in einem realistischen Quantenpunkt eine h¨ ohere Spinquantenzahl besitzen. F¨ ur die Spins im h¨ aufig genutzten Halbleiter GaAs gilt zum Beispiel S _GaAs = 3/2 [21, 28]. Die Summe

B ˆ =

N

X

i=1

J i S ˆ i (2.2)

wirkt wie ein effektives Magnetfeld auf den Zentralspin und wird auch als Overhauser- Feld bezeichnet. Die Dipol-Dipol-Wechselwirkungen zwischen den einzelnen Kernspins werden hier vernachl¨ assigt, da deren typische Zeitskala ein bis zwei Gr¨ oßenordnungen gr¨ oßer als die Zeitskala der betrachteten Hyperfein-Wechselwirkung ist [6].

Wird zus¨ atzlich der Einfluss eines externen Magnetfeldes betrachtet, ist das magne-

tische Moment der Kerne im Quantenpunkt im Vergleich zum Elektron gew¨ ohnlich um

drei Gr¨ oßenordnungen kleiner [24], weswegen hier nur die Wechselwirkung des Magnet-

feldes mit dem Zentralspin beachtet wird. Dies f¨ uhrt zum erweiterten Hamiltonoperator

H ˆ ^α (h) = ˆ H − h S ˆ ₀ ^α (2.3)

mit der Magnetfeldst¨ arke h in Richtung der Komponente α.

Die Aufenthaltswahrscheinlichkeit des Zentralspins am Ort r _i kann durch die Ver- teilung

| Ψ(r _i ) | ² ∝ exp h

− r _i R

m i

, m ∈ { 1, 2 } (2.4)

beschrieben werden [14, 29, 30]. Dabei gibt R den charakteristischen Radius der hy- perfein koppelnden Kernspins an. Die Wellenfunktion Ψ beschreibt f¨ ur m = 1 einen wasserstoff-¨ ahnlichen s Zustand, w¨ ahrend p = 2 einen gaußverteilten Verlauf mit Bohr- Radius R darstellt. Die Gr¨ oße N 0 beschreibt nun die Anzahl der Kernspins innerhalb des Radius R. In d Dimensionen ist dann (r _i /R) ^d = i/N ₀ = γi. In dieser Arbeit wird die gaußverteilte Wellenfunktion f¨ ur einen zweidimensionalen Quantenpunkt verwen- det, sodass m = d = 2 gilt, was letztendlich die exponentielle Verteilung [25, 27, 29]

J i = J e

(2.5)

f¨ ur die Kopplungen liefert. Dabei ist i ∈ { 1 .. N } . Die Energiekonstante J wird so gew¨ ahlt, dass

J _Q ² :=

N

X

i=1

J _i ² = 1 (2.6)

gilt. Dadurch dass in dieser Arbeit nat¨ urliche Einheiten ( ~ = 1) betrachtet werden, legt J _Q die nat¨ urliche Energieskala und gleichzeitig eine Zeitskala fest. Deshalb wird die Simulationszeit t in den folgenden Kapiteln immer in der Einheit 1/J Q angegeben, welche im Experiment der Gr¨ oßenordnung einer Nanosekunde entspricht [31]. Weiter- hin wird das Verh¨ altnis der Gesamtanzahl der Spins N zu der Anzahl der Spins N ₀ innerhalb des Wahrscheinlichkeitsradius R ¨ uber

x := N N 0

(2.7) definiert, sodass γ = x/N gilt. Damit ist die geringste Kopplung ¨ uber J N ∝ exp( − x) gegeben. In dieser Arbeit werden unter anderem auch potentiell unendliche B¨ ader be- trachtet, f¨ ur die x → ∞ gilt. Auch f¨ ur diese Systeme existiert nur eine endliche, von γ abh¨ angige Anzahl N eff der Kernspins die effektiv an den physikalischen Prozessen beteiligt ist [25]. Um dies zu zeigen wird zun¨ achst die Summe

J _S :=

N

X

i=1

J _i (2.8)

eingef¨ uhrt. Bei einer Betrachtung mit konstanten Kopplungen J _i = C gilt offensichtlich

J _S ² = C ² N ² , sowie J _Q ² = C ² N , wodurch deutlich wird, dass der Quotient J _S ² /J _Q ² = N

die Anzahl der Badspins wiedergibt. Dieses Vorgehen kann nun ebenfalls f¨ ur die expo-

nentiellen Kopplungen (2.5) durchgef¨ uhrt werden. Es ergibt sich im Limes unendlicher

B¨ ader

J _S ² =

∞

X

i=1

J e

! 2

= J ² e

(1 − e

) ² , (2.9a)

J _Q ² =

∞

X

i=1

J ² e

= J ² e

1 − e

. (2.9b)

Der Quotient dieser beiden Gr¨ oßen liefert nun auch f¨ ur die exponentiellen Kopplungen die Anzahl der Kernspins. Jedoch konvergiert diese f¨ ur γ > 0 gegen den Effektivwert

N eff = J _S ²

J _Q ² = 1 − e

(1 − e

) ² = 2

γ + O (γ ⁰ ) . (2.10)

Im letzten Schritt wurde angenommen, dass γ 1 gilt. Diese Annahme ist hier legitim, da f¨ ur einen Quantenpunkt typischerweise N eff ≈ 10 ⁴ bis 10 ⁶ und somit γ ≈ 10

bis 10

gilt.

Haupts¨ achlich werden in dieser Arbeit die normierten exponentiellen Kopplungen (2.5) verwendet. Basierend auf Ref. [24] wird jedoch im Zusammenhang mit Magnet- feldern auch ein Vergleich von Simulationen mit der linear abfallenden Kopplungsver- teilung

J _i =

r 6N 2N ² + 3N + 1

N + 1 − i

N J _Q (2.11)

durchgef¨ uhrt.

0 200 400 600 800 1000

i 0.00

0.05 0.10 0.15 0.20 0.25 0.30

J

/J

γ = 5 · 10

γ = 1 · 10

γ = 5 · 10

γ = 1 · 10

linear

Abbildung 2.1: Darstellung der exponentiellen Kopplungskonstanten (2.5) f¨ ur verschie-

dene Parameter γ und der linearen Kopplung (2.11) bei N = 1000 Spins. Die Kopp-

lungen sind dabei ¨ uber den Faktor J _Q

(2.6) normiert.

Zur Veranschaulichung ist die normierte Kopplungskonstante J _i /J _Q f¨ ur verschiedene γ bei einer Anzahl von N = 1000 Spins in Abbildung 2.1 dargestellt. F¨ ur große γ liefern offensichtlich nur wenige, stark koppelnde Kernspins die komplette Dynamik, da die Kopplungskonstanten f¨ ur gr¨ oßere i schnell abfallen. F¨ ur realistischere γ hingegen wird der deutlich schw¨ achere Abfall der Kopplungsst¨ arke sichtbar und damit auch der steigende Einfluss von immer mehr Kernspins. Dabei bestimmen die schw¨ acheren Kopplungen das Langzeitverhalten des Zentralspins [25, 29, 32].

In dieser Arbeit wird die zz-Autokorrelationsfunktion als Observable genutzt. Sie ist durch

S(t) := D

S ˆ ₀ ^z (t) ˆ S ₀ ^z (0) E

= 1

4 Tr ( ˆ ρˆ σ ₀ ^z (t)ˆ σ ₀ ^z (0)) (2.12) definiert. Diese Autokorrelation beschreibt die ¨ Anderung des Zustands der z-Kom- ponente des Zentralspins ˆ S ₀ ^z (t) zum Startzustand ˆ S ₀ ^z (0). Nun ist zu beachten, dass die charakteristische thermische Energie k B T der Umgebung im Experiment mindes- tens eine Gr¨ oßenordnung ¨ uber der intrinsischen Energie des Quantenpunktes liegt [8].

Demnach ist es eine realistische Annahme eine unendliche Temperatur und somit ein v¨ ollig ungeordnetes Bad zu betrachten. Diese initialen Bedingungen entsprechen dem Dichteoperator

ˆ ρ = 1

dim H 1 . (2.13)

Dabei beschreibt H den Hilbertraum des betrachteten Systems. Da Zentralspin und Kernspins einen Spin S = 1/2 besitzen, ist dessen Dimension hier durch dim H = 2 ^{N +1} gegeben.

Nun muss eine Methode eingef¨ uhrt werden, mit der die Zeitentwicklung der z- Komponente des Zentralspins ˆ S ₀ ^z (t) im vorgestellten Modell durchgef¨ uhrt werden kann.

Diese wird im n¨ achsten Kapitel erl¨ autert.

Kapitel 3

Iterierte Bewegungsgleichungen

Die Methode der iterierten Bewegungsgleichungen bietet eine relativ einfache M¨ oglich- keit, ein Bewegungsgleichungssystem f¨ ur einen zeitabh¨ angigen Operator aufzustellen, welches mit bekannten Verfahren wie Runge-Kutta oder exakter Diagonalisierung gel¨ ost werden kann. Deshalb soll sie in dieser Arbeit f¨ ur die Zeitentwicklung des Zentralspins zum Einsatz kommen. Dazu wird die Methodik zun¨ achst f¨ ur allgemeine zeitabh¨ angige Operatoren erl¨ autert. Anschließend wird kurz Bezug auf das in Kapitel 2 eingef¨ uhrte Zentralspin-Modell genommen.

Ausgangspunkt f¨ ur die Zeitentwicklung mit iterierten Bewegungsgleichungen ist die Heisenberg-Gleichung. Diese besagt f¨ ur die Ableitung des zeitabh¨ angigen Operators O ˆ _i (t) im Heisenberg-Bild, dass

d

dt O ˆ i (t) = i

h H, ˆ O ˆ i (t) i

= i L O ˆ i (t) (3.1)

gilt. Dabei ist L der Liouville-Superoperator, welcher eine k¨ urzere Schreibweise f¨ ur die Kommutation eines Operators mit dem Hamiltonoperator darstellt. Es kann nun eine orthonormale Basis B = { ˆ b 0 , ˆ b 1 , ˆ b 2 , ... ˆ b K } mit den Operatoren ˆ b _k im Schr¨ odinger-Bild gefunden werden, mit welcher der zeitabh¨ angige Operator durch die Reihe

O ˆ i (t) = X

k

ξ _ik (t)ˆ b k (3.2)

dargestellt werden kann. Damit ist die Zeitabh¨ angigkeit nun durch die skalaren Koef- fizienten ξ _ik (t) bestimmt, die zum Zeitpunkt t = 0 durch

ξ ik (0) =

( 1, k = i

0, k 6 = i (3.3)

gegeben sind. Initial gilt demnach ˆ O i (0) = ˆ b 0 . Um ˆ O i (t) in der Zeit zu entwickeln,

muss nun eine passende Basis gefunden und ein Bewegungsgleichungssystem f¨ ur die

Koeffizenten der Basisoperatoren ξ ik (t) aufgestellt werden. Die Idee der iterierten Be-

wegungsgleichungen ist, das gesuchte Bewegungsgleichungssystem durch iteratives An-

wenden des Liouville-Operators auf den initialen Operator ˆ b ₀ aufzubauen. Sie basiert

darauf, dass bei jeder Anwendung auf einen allgemeinen Operator aus der Untermenge B sub ⊂ B nach

L ˆ b _i = X

k

Γ _ik ˆ b _k (3.4)

neue Operatoren b _k ∈ B mit den Koeffizienten Γ _ik entstehen. Durch das iterative An- wenden kann B sub so schrittweise erweitert und durch Γ _ik das gesuchte Bewegungsglei- chungssystem aufgebaut werden.

Dazu wird nun zun¨ achst die initiale Menge B 0 = { ˆ b 0 } ⊂ B definiert. Durch ein- malige Anwendung des Liouville-Operators entstehen nach (3.4) bekanntlich die neuen Basisoperatoren ˆ b _k , welche in der neuen Menge B 1 ⊂ B enthalten sind. Die erweiter- te Menge der Basisoperatoren nach einem Iterationsschritt ergibt sich sodann aus der Vereinigung

B ¹ gesamt = B 0 ∪ B 1 . (3.5)

Ist B l ⊆ B die Menge der Basisoperatoren, die durch die l-te Anwendung des Liouville- Operators entsteht, so gilt demnach allgemein f¨ ur die Menge aller Basisoperatoren nach L Anwendungen

B gesamt ^L =

L

[

l=0

B l . (3.6)

Nun ist nach Gleichung (3.4) die Zeitableitung des Basisoperators ˆ b i uber die Koef- ¨ fizienten Γ _ik an die Basisoperatoren ˆ b _k gekoppelt. Dies kann genutzt werden, um das f¨ ur die zeitabh¨ angigen Koeffizienten ξ ik (t) aus Gleichung (3.2) gesuchte Bewegungs- gleichungssystem aufzustellen. Dazu wird nun (3.2) in die Heisenberg-Gleichung (3.1) eingesetzt. Dadurch gilt

d dt

X

k

ξ _ik (t)ˆ b _k = i X

k

ξ _ik (t) L ˆ b _k (3.7a)

= i X

k

ξ _ik (t) X

j

Γ _kj ˆ b _j . (3.7b)

Dabei wird im zweiten Schritt nur die Definition (3.4) eingesetzt. Da k und j uber ¨ dieselben Werte laufen, k¨ onnen die Indizes vertauscht werden, sodass gilt

d dt

X

k

ξ _ik (t)ˆ b _k = i X

k,j

ξ _ij (t)Γ _jk ˆ b _k (3.7c)

⇔ d

dt (ξ _i (t)) ^T ˆ b = i (ξ _i (t)) ^T Γ ˆ b . (3.7d) Durch Vergleich der Koeffizienten der Basisoperator-Vektoren ˆ b und transponieren auf beiden Seiten der Gleichung (3.7d) ergibt sich das finale Bewegungsgleichungssystem

d

dt ξ _i (t) = iΓ ^T ξ _i (t) , (3.7e)

wobei die Matrix Γ quadratisch ist und nach L Iterationsschritten die Dimension

B gesamt ^L

×

B gesamt ^L

hat. Diese Matrix soll in dieser Arbeit als Liouville-Matrix be- zeichnet werden.

Um mithilfe von (3.7e) den gew¨ unschten Operator ˆ O _i (t) sinnvoll in der Zeit entwi- ckeln zu k¨ onnen, muss f¨ ur die iterativ entstehende Basis B ein Skalarprodukt definiert werden, f¨ ur das

L ˆ b i

ˆ b j

= ˆ b i

L ˆ b j

(3.8) gilt. Dann ist die Matrix Γ hermitesch [33], wodurch sie lediglich reelle Eigenwerte besitzt und eine exponentielle Divergenz in der Zeitentwicklung ausgeschlossen ist. Ein Skalarprodukt, welches die Eigenschaft (3.8) erf¨ ullt, ist durch

A ˆ | B ˆ

:= 1 dim H Tr

A ˆ

B ˆ

(3.9) definiert, wie eine kurze Rechnung zeigt. Da der Normierungsfaktor 1/ dim H f¨ ur den Beweis von (3.8) zun¨ achst irrelevant ist, soll hier nur die Spur betrachtet werden. Dann gilt

Tr

L A ˆ

B ˆ

= Tr

H ˆ A ˆ − A ˆ H ˆ

B ˆ

(3.10a)

= Tr

A ˆ

H ˆ

B ˆ − H ˆ

A ˆ

B ˆ

(3.10b)

= Tr A ˆ

H ˆ B ˆ − B ˆ H ˆ

(3.10c)

= Tr

A ˆ

L B ˆ

. (3.10d)

Demnach erf¨ ullt die Spur die Eigenschaft (3.8) f¨ ur beliebige Operatoren. Dabei ist je- doch zu beachten, dass die Definition des Skalarprodukts (3.9) nur f¨ ur Operatoren mit lokal endlich-dimensionalen Hilbertr¨ aumen sinnvoll ist. Da in dieser Arbeit allerdings nur Spinoperatoren betrachtet werden, ist diese Bedingung erf¨ ullt. Bilden nun die Ba- sisoperatoren zus¨ atzlich eine Orthonormalbasis, so sind die Matrixelemente ¨ uber

L ˆ b i

ˆ b j

= X

k

Γ _ik ˆ b _k

ˆ b j

= X

k

Γ _ik δ _kj = Γ ij = Γ

_ji (3.11) definiert.

Im Zentralspin-Modell, welches in Kapitel 2 beschrieben wird, ist der zeitabh¨ angige Operator durch die z-Komponente des Zentralspins ˆ σ ^z ₀ (t) gegeben. Damit ist der initiale Basisoperator f¨ ur die iterierten Bewegungsgleichungen durch

ˆ b 0 = ˆ σ ₀ ^z (0) = ˆ σ ₀ ^z (3.12)

bestimmt. Nun enth¨ alt der Hamiltonoperator (2.1) nur Spin-Operatoren, wodurch die

gesamte Basisentwicklung durch Operationen der Spin-Algebra f¨ ur S = 1/2 durch-

gef¨ uhrt werden kann. Dabei soll in dieser Arbeit, mit den (2 × 2)-Einheitsmatrizen 1 2

und m ∈ { 0,1,2,3 } , die Definition ˆ σ _j ^m =

j−1

O

i=0

1 2

!

⊗ σ ˜ ˆ _j ^m ⊗





N

O

i=j+1

1 2



 (3.13)

gelten. F¨ ur die Pauli-Matrizen werden in dieser Arbeit außerdem die beiden ¨ aquivalenten Notationen

ˆ

σ ⁰ _j ≡ 1 σ ˆ _j ¹ ≡ σ ˆ ^x _j σ ˆ _j ² ≡ ˆ σ _j ^y σ ˆ ³ _j ≡ σ ˆ ^z _j (3.14) genutzt. F¨ ur die Entwicklung der Basisoperatoren in den folgenden Kapiteln sind au- ßerdem noch die bekannten Relationen

h ˆ σ _i ^α , σ ˆ _j ^β i

= 2i X

ζ

_αβζ ˆ σ _i ^ζ δ _ij , (3.15a)

ˆ σ _i ^α σ ˆ _j ^β =



i X

ζ

_αβζ σ ˆ _i ^ζ + σ _i ⁰ δ _αβ



 δ ij + ˆ σ _j ^β σ ˆ ^α _i (1 − δ ij ) (3.15b) essentiell, wobei griechische Buchstaben in dieser Arbeit immer Elemente der Menge der dreidimensionalen Raumrichtungen { x,y,z } sind.

In den folgenden zwei Kapiteln wird nun die Methode der iterierten Bewegungsglei-

chungen f¨ ur das Zentralspinmodell angewendet. Dabei liegt der Fokus der Betrachtung

auf zwei unterschiedlichen Ans¨ atzen f¨ ur die Definition von Basisoperatoren. Deren An-

zahl bestimmt die Gr¨ oße des zu l¨ osenden Bewegungsgleichungssystems und ist somit der

limitierende Faktor. Dabei ist wichtig, wie die Basisgr¨ oße in der Zeit t und Systemgr¨ oße

N skaliert.

Kapitel 4

Direkte Basisentwicklung

Wird der Liouville-Operator iterativ auf den initialen Basisoperator ˆ σ ^z ₀ angewendet, so sind die neu entstehenden Operatoren im Allgemeinen Produkte von Pauli-Matrizen.

Ein naiver Ansatz f¨ ur eine Basis f¨ ur die iterierter Bewegungsgleichungen ist nun, die Basisoperatoren direkt ¨ uber diese Spinoperatorprodukte zu definieren.

4.1 Basisoperator

Ein beliebiges Produkt von Spinoperatoren kann wegen der Relationen (3.15a) und (3.15b) immer so zusammengefasst werden, dass maximal ein Operator pro Platz i vorhanden ist. Dessen Komponente kann die Werte m _k,i ∈ { 0,1,2,3 } annehmen. Dabei bedeutet m _k,i ∈ { 1,2,3 } , dass dieser Platz besetzt ist, und m _k,i = 0, dass dort der triviale Operator ˆ σ _i ⁰ steht. Da die Reihenfolge der Operatoren an unterschiedlichen Pl¨ atzen irrelevant ist, kann ein allgemeiner Basisoperator nun durch

ˆ b _k :=

N

Y

i=0

ˆ

σ _i ^m

= ˆ σ ₀ ^m

· σ ˆ ^m ₁

· ... · σ ˆ ^m _N

(4.1)

dargestellt werden. F¨ ur den initialen Basisoperator ˆ b ₀ = ˆ σ ₀ ^z gilt demnach in dieser Dar- stellung m _0,i = 0 ∀ i ∈ { 1 ... N } und m _0,0 = 3. Damit eine einfache Berechnung der Matrixelemente f¨ ur die Liouville-Matrix nach (3.11) m¨ oglich ist, m¨ ussen diese Ope- ratoren orthonormal zueinander sein, was nun im Bezug auf das Skalarprodukt (3.9) gezeigt werden soll.

Da die Pauli-Matrizen hermitesch sind und die Reihenfolge der Operatoren irrele- vant ist, ist ein allgemeiner Basisoperator nach

ˆ b

_k =

N

Y

i=0

ˆ σ _i ^m

!

=

N

Y

i=0

ˆ σ ^m _i

=

N

Y

i=0

ˆ

σ _i ^m

= ˆ b k (4.2)

ebenfalls hermitesch. Wird nun das Skalarprodukt zweier allgemeiner Basisoperatoren

gebildet, so gilt nach ˆ b _k

ˆ b _l

= 1

2 ^N+1 Tr

N

Y

i=0

ˆ σ ^m _i

ˆ σ _i ^m

!

(4.3a)

= 1

2 ^N+1

N

Y

i=0

Tr

σ ˜ ˆ ^m _i

˜ ˆ σ ^m _i

(4.3b)

= 1

2 ^N+1

N

Y

i=0

2δ _m

_m

(4.3c)

= δ _kl , (4.3d)

dass diese Orthonormal zueinander sind. Dabei ist zu beachten, dass im zweiten Schritt die auf dem Hilbertraum H ^2×2 definierten Pauli-Matrizen ˜ σ ˆ ^m _i eingesetzt wurden. Die gew¨ ahlte Definition der Basisoperatoren liefert demnach eine Orthonormalbasis, welche nun f¨ ur die Anwendung der iterierten Bewegungsgleichungen genutzt wird.

4.2 Allgemeine Basis-Entwicklung und Trunkierung

Um die Entwicklung der Basis in jedem Iterationsschritt besser zu verstehen, ist es hilfreich, die Anwendung des Liouville-Operators auf einen allgemeinen Basisoperator zu betrachten. Dies liefert

L ˆ b k =

N

X

j=1

J j

"

S ˆ ₀ ^α S ˆ _j ^α ,

N

Y

i=0

ˆ σ _i ^m

#

(4.4a)

=

N

X

j=1

J _j "

S ˆ ^α ₀ ,

N

Y

i=0

ˆ σ _i ^m

#

S ˆ ^α _j + ˆ S ₀ ^α

"

S ˆ ^α _j ,

N

Y

i=0

ˆ σ _i ^m

#!

(4.4b)

=

N

X

j=1

J _j 2





h S ˆ ₀ ^α , σ ˆ ₀ ^m

i Y ^N

i=1

ˆ

σ ^m _i

σ ˆ _j ^α + ˆ σ ₀ ^α

j−1

Y

i=0

ˆ σ _i ^m

h

S ˆ _j ^α , σ ˆ _j ^m

i Y ^N

l=j+1

ˆ σ _l ^m



 (4.4c)

= i

N

X

j=1

X

γ

J _j

2 _αm

_γ (1 − δ _m

₀ )

=: ˜ ˆ b

z }| { ˆ

σ ^γ ₀

N

Y

i=1

ˆ

σ _i ^m

σ ˆ _j ^α (4.4d)

+ i

N

X

j=1

X

γ

J j

2 αm

γ (1 − δ m

0 )ˆ σ ^α ₀

j−1

Y

i=0

ˆ σ _i ^m

σ ˆ _j ^γ

N

Y

l=j+1

ˆ

σ ^m _l

. (4.4e)

Der Anteil (4.4d) der allgemeinen Basisentwicklung beinhaltet nun die Erkenntnis, dass

nach n 6 N Iterationsschritten der iterierten Bewegungsgleichungen die Basisoperato-

ren mit der gr¨ oßten Anzahl besetzter Pl¨ atze aus genau (n + 1) Pauli-Matrizen mit

4.2. Allgemeine Basis-Entwicklung und Trunkierung

m _k,i 6 = 0 bestehen. Um dies zu zeigen werden die in (4.4d) definierten, neuen Basisope- ratoren ˜ ˆ b ^αγ _k,j betrachtet. F¨ ur diese gilt allgemein

N

X

j=1

˜ ˆ b ^αγ _k,j =

N

X

j=1

ˆ σ ₀ ^γ

N

Y

i=1

ˆ

σ _i ^m

σ ˆ ^α _j . (4.5)

Der Ausgangspunkt ist nun zun¨ achst der initiale Basisoperator ˆ b 0 , f¨ ur den m 0,i = 0 f¨ ur i > 0 gilt. Da demnach alle Pl¨ atze i ∈ { 1, ... ,N } dieses Operators unbesetzt sind, besetzt die Pauli-Matrix ˆ σ ^α _j , die aus der Anwendung des Liouville-Operators auf ˆ b ₀ entsteht, in den neuen Basisoperatoren offensichtlich einen zus¨ atzlichen Platz. Dadurch haben diese Operatoren nach einem Iterationsschritt nun zwei besetzte Pl¨ atze und sind durch

˜ ˆ b ^αγ _0,j = ˆ σ ₀ ^γ σ ˆ _j ^α (4.6) gegeben. Vor dem n-ten Iterationsschritt haben die Basisoperatoren mit der maximalen Anzahl an besetzten Pl¨ atzen demnach genau n besetzte und (N + 1 − n) unbesetzte Pl¨ atze. Solange nun n 6 N gilt, haben diese Basisoperatoren somit mindestens einen unbesetzten Platz. Da j ¨ uber alle Pl¨ atze im Bad l¨ auft, wird es mindestens ein j geben sodass der unbesetzte Platz nach

˜ ˆ b ^αγ _k,j = ˆ σ ₀ ^γ · σ ˆ ^m ₁

· ... · σ ˆ _j−1 ^m

· 1 · σ ˆ _j+1 ^m

· ... · σ ˆ _N ^m

· σ ˆ ^α _j (4.7a)

= ˆ σ ₀ ^γ · σ ˆ ^m ₁

· ... · σ ˆ ^m _j−1

· ˆ σ ^α _j · σ ˆ ^m _j+1

· ... · σ ˆ _N ^m

(4.7b) besetzt wird. Der neu entstandene Operator (4.7b) hat demnach eine Pauli-Matrix zus¨ atzlich. Im Umkehrschluss besitzen die maximal besetzten Basisoperatoren im Fall n = (N + 1) keinen unbesetzten Platz mehr, wodurch sich am Platz j nach der Relation (3.15b) entweder nur die Komponente ¨ andert, oder im Fall α = m _k,j eine Einheitsmatrix entsteht und dieser demnach nicht mehr besetzt ist.

Durch die Wahl der Basisoperatoren ˆ b _k ist direkt ersichtlich, dass f¨ ur ein endliches System nur eine endliche Anzahl an Basisoperatoren ben¨ otigt wird, da nur endlich viele Kombinationen der ˆ σ ^m _i

existieren. Nun ist jedoch ebenfalls gezeigt, dass die Anzahl der entstehenden Basisoperatoren f¨ ur eine unendliche Systemgr¨ oße divergiert. Dadurch ist in diesem Fall eine Trunkierung notwendig. Jedoch zeigt sich im n¨ achsten Abschnitt, dass die Basisgr¨ oße f¨ ur die definierten Operatoren exponentiell mit der Badgr¨ oße N ansteigt, wodurch ebenfalls bei endlichen Systemen schon f¨ ur relativ kleine Badgr¨ oßen eine Trunkierung notwendig wird.

Wird die Anzahl der Basisoperatoren S B und der von Null verschiedenen Eintr¨ age

S LM der Liouville-Matrix in Abh¨ angigkeit der Badgr¨ oße N betrachtet, so k¨ onnen Ska-

lierungsfunktionen gefunden werden. Die Paulimatrizen an einem Platz haben vier

m¨ ogliche verschiedene Komponenten. Da bei einer exakten Berechnung vermutlich alle

Kombinationen der Badspins vorkommen, wird eine Skalierung in der Gr¨ oßenordnung

O (4 ^N ) liegen. Bei Betrachtung von Tabelle 4.1 best¨ atigt sich diese Annahme. Dabei

N S _B (N ) S _LM (N ) ^S

^(N) / S

(N)

0 1 0 0,000

1 4 8 2,000

2 15 48 3,200

3 64 288 4,500

4 255 1536 6,024

5 1024 7680 7,500

6 4095 36864 9,002

7 16384 172032 10,500

8 65535 786432 12,000

9 262144 3538944 13,500

10 1048575 15728640 15,000

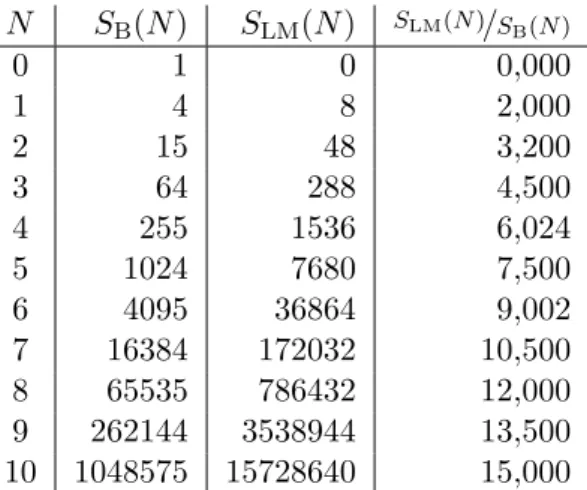
Tabelle 4.1: Skalierung S _B (N ) der Anzahl der Basisoperatoren und S _LM (N ) der Anzahl der von Null verschiedenen Matrixeintr¨ age in Abh¨ angigkeit der Badgr¨ oße N sowie der Quotient beider Werte.

entsteht f¨ ur gerade N f¨ ur N > 0 ein zus¨ atzlicher konstanter Faktor. Es ergibt sich quantitativ

S _B (N ) = 4 ^N − ((N + 1) mod 2) f¨ ur N > 0 . (4.8) Um die Skalierung der Anzahl der von Null verschiedenen Eintr¨ age der Liouville-Matrix S LM (N ) in Abh¨ angigkeit der Badgr¨ oße zu erhalten ist eine Betrachtung des Quotienten der Anzahl dieser Eintr¨ age und S _B (N ) hilfreich, welcher in Abbildung 4.1 dargestellt ist. Mit der Ausnahme von N = 1 folgt der Quotient f¨ ur ungerade Badgr¨ oßen der linearen Funktion

f (N ) = 3

2 N . (4.9)

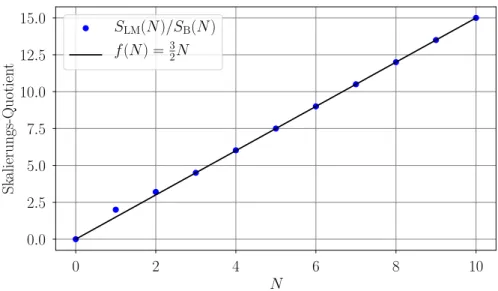
F¨ ur gerade Badgr¨ oßen ist eine Abweichung zu erkennen, welche durch den Summanden S mod (N ) = − ((N + 1) mod 2) entsteht. Da dieser jedoch konstant ist, wird die Abwei- chung f¨ ur gr¨ oßer werdende N schnell vernachl¨ assigbar klein. F¨ ur große Badgr¨ oßen kann demnach die Anzahl der Matrixelemente durch die Skalierungsfunktion

S _LM (N ) ≈ 3

2 N · S _B (N) = 3

2 N · 4 ^N (4.10)

angegeben werden. Eine Skalierung der Anzahl der Matrixeintr¨ age von der Ordnung O (N · 4 ^N ) limitiert die l¨ osbare Badgr¨ oße sehr stark, da schon f¨ ur kleine B¨ ader sehr große Speichermengen f¨ ur die Berechnung des Bewegungsgleichungssystems n¨ otig sind.

An dieser Stelle wird die Wichtigkeit eines geeigneten Trunkierungsschemas ersicht-

lich. Die Skalierungen der Basis S B (N ) und der von Null verschiedenen Matrixeintr¨ age

S LM (N ) gelten f¨ ur die exakte Berechnung des Problems. Die Trunkierung dient dazu,

eine approximative L¨ osung zu erhalten, welche mit weniger Basisoperatoren auskommt,

4.3. Resultate

0 2 4 6 8 10

N 0.0

2.5 5.0 7.5 10.0 12.5 15.0

Sk alierungs-Quotien t

S

(N )/S

(N ) f(N ) =

N

Abbildung 4.1: Differenzenquotient der Skalierungsfunktionen S LM (N )/S B (N ) mit Ver- gleichsgeraden f (N ) = ³ / 2 N.

dabei jedoch immer noch m¨ oglichst nah an der exakten L¨ osung liegt. Nun ist die Anzahl der besetzten Pl¨ atze A (b _k ) eines Basisoperators ˆ b _k ein Ansatzpunkt f¨ ur dieses Schema.

Eine einfache Trunkierung besteht darin einen Basisoperator ˆ b _k nur dann zur Basis hinzuzuf¨ ugen, wenn

A (b _k ) < P _max , (4.11) wobei P max der maximalen Anzahl der Spinoperatoren verschiedener Pl¨ atze in diesem Operator entspricht.

Dieser Ansatz wird nun dazu genutzt mittels der iterierten Bewegungsgleichungen die Zeitentwicklung des Zentralspins zu simulieren. Die Resultate werden im n¨ achsten Kapitel diskutiert.

4.3 Resultate

Bevor auf das zuvor erl¨ auterte Trunkierungsschema n¨ aher eingegangen wird, werden einige ¨ Uberlegungen zu exakten L¨ osungen angestellt. Dabei wird unter anderem auch die Wahl verschiedener Parameter x f¨ ur die Kopplungskonstanten J i betrachtet.

4.3.1 Exakte L¨ osung

Als exakte L¨ osung wird hier der Fall P max = (N + 1) bezeichnet. Da im Hamiltonope-

rator nur (N + 1) verschiedene Pl¨ atze betrachtet werden, k¨ onnen auch nur maximal so

viele Pl¨ atze durch einen Basisoperator beschrieben werden. Demnach werden durch die

iterierten Bewegungsgleichungen alle n¨ otigen Basisoperatoren f¨ ur die Zeitentwicklung

bestimmt und damit auch alle Wechselwirkungsprozesse beachtet.

0 5 10 15 20 25 t [J

]

0.00 0.05 0.10 0.15 0.20 0.25

S ( t )

x = 0, 5 x = 1, 0 x = 2, 0 x = 4, 0

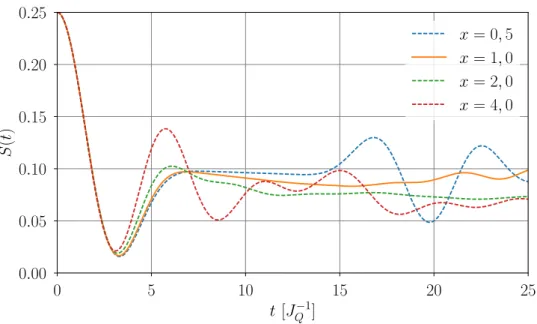
Abbildung 4.2: Vergleich der exakten L¨ osung mit der Methode der iterierten Bewe- gungsgleichungen f¨ ur verschiedene Parameter x. Dabei ist die Badgr¨ oße N = 10.

Nun muss zun¨ achst ein passender Parameter x f¨ ur die Kopplungsverteilung gew¨ ahlt werden. Um den Einfluss dieser Gr¨ oße genauer zu analysieren sind in Abbildung 4.2 Simulationen f¨ ur verschiedene x dargestellt. Die Badgr¨ oße betr¨ agt dabei N = 10 Kern- spins. F¨ ur x = 0,5 verl¨ auft die Kopplungsverteilung relativ flach. Dadurch sind die Kopplungen lange von derselben Gr¨ oßenordnung, wie schon aus Abbildung 2.1 deutlich wird. Der charakteristische Abfall der Autokorrelation nach dem ersten Minimum ist deswegen relativ gering. Da das betrachtete System endlich ist, sind jedoch nach kurzer Zeit relativ starke Schwankungen zu sehen. Sie entstehen dadurch, dass das System nur aus sehr wenigen Badspins besteht und werden auch Finite-Size-Effekte genannt. Da ein Quantenpunkt jedoch aus N ≈ 10 ⁴ bis 10 ⁶ Kernspins besteht sind diese Effekte nicht realistisch. F¨ ur große x ist die Dynamik nur durch sehr wenige Kernspins domi- niert, wodurch die Autokorrelation schrittweise in eine Oszillation ¨ ubergeht. Dies ist ebenfalls unrealistisch f¨ ur einen Quantenpunkt.

Hier wird nun x = 1 und somit N = N 0 gew¨ ahlt, wodurch die kleinste Kopplung durch J _N = J _Q /e gegeben ist. Diese Wahl stellt einen guten Kompromiss dar, um auf der Zeitskala bis t _max , bei der die Finite-Size-Effekte auftreten, eine Dynamik des Zentralspins zu erkennen, ohne dabei die Anzahl der einflussreichen Kernspins zu stark zu beschr¨ anken.

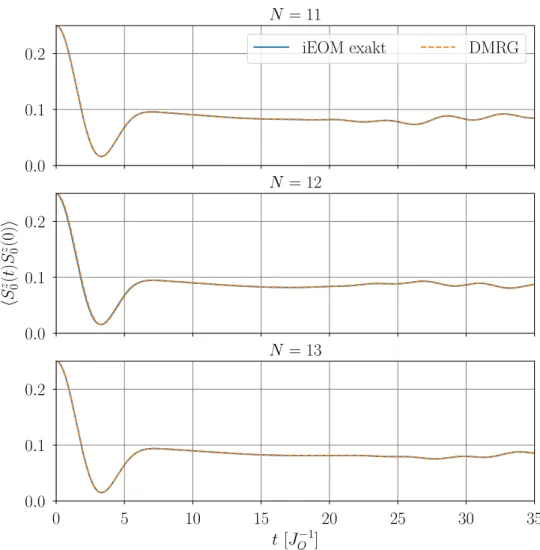
Abbildung 4.3 zeigt nun die exakte Zeitentwicklung mit der Methode der iterier-

ten Bewegungsgleichung (iEOM) f¨ ur verschiedene Badgr¨ oßen N bis t = 35J _Q

. Da-

bei wird jeweils mit einer Simulation ¨ uber den Dichtematrix-Renormierungsgruppen-

Formalismus (DMRG) [22] verglichen. Die Ergebnisse stimmen hier genau mit denen

der iterierten Bewegungsgleichungen ¨ uberein, wodurch best¨ atigt wird, dass die Metho-

4.3. Resultate

0.0 0.1 0.2

N = 11

iEOM exakt DMRG

0.0 0.1 0.2

h S

( t ) S

(0) i

N = 12

0 5 10 15 20 25 30 35

t [J

] 0.0

0.1 0.2

N = 13

Abbildung 4.3: Exakte L¨ osung mit den iterierten Bewegungsgleichungen (iEOM) f¨ ur x = 1 im Vergleich mit einer Simulation ¨ uber der Methode der Dichtematrix- Renormierungsgruppe (DMRG) f¨ ur verschiedene Badgr¨ oßen N .

de korrekte Ergebnisse liefert. Dabei werden die Finite-Size-Effekte durch die leichten Oszillationen f¨ ur gr¨ oßere Zeiten sichtbar. F¨ ur Ansteigende Badgr¨ oßen treten sie offen- sichtlich immer sp¨ ater in der Zeitentwicklung auf.

Die Umsetzung der iterierten Bewegungsgleichungen ist bei einer numerischen Be-

rechnung relativ effizient in der Zeit, jedoch Speicherintensiv. Die Dauer f¨ ur das hier

gr¨ oßte exakt berechnete Bad von N = 13 Spins liegt mit dem genutzten Programm

bei etwa 24 Stunden. Der ben¨ otigte RAM-Speicher kann ¨ uber die Skalierungsfunktio-

nen (4.8) und (4.10) abgesch¨ atzt werden. Da die Liouville-Matrix zu großen Teilen aus

Nullen besteht, wird die Speicherung des Bewegungsgleichungssystems ¨ uber eine d¨ unn

besetzte (sparse) Matrix umgesetzt. Diese speichert nicht jeden einzelnen Eintrag, son-

dern nur die von Null verschiedenen. Dazu sind zwei Long Integer mit jeweils 8 Byte

2 4 6 8 10 12 14 t [J _Q ^{− 1} ]

0 100 200

Arb eitsp eic her [GB]

Minimal ben¨otigter Arbeitsspeicher M min (N ) 256GB

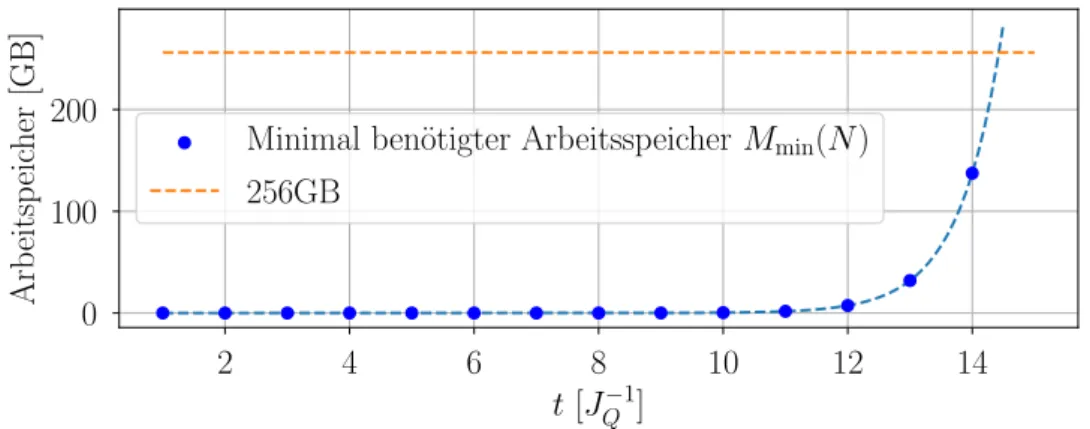
Abbildung 4.4: Minimal ben¨ otigter Arbeitsspeicher in Abh¨ angigkeit der Badgr¨ oße N f¨ ur eine exakte Berechnung mit der Autokorrelationsfunktion mit den iterierten Bewe- gungsgleichungen.

n¨ otig um die Position des Eintrags zu bestimmen. Dessen Wert wird in einer Fließkom- mazahl mit doppelter Genauigkeit (Double) gespeichert welche ebenfalls 8 Byte groß ist.

Dies liefert f¨ ur die Matrix ein Speicheraufkommen von M _LM (N ) = 24 · S _LM Bytes. Da die Zeitentwicklung mit einem Runge-Kutta-Verfahren vierter Ordnung durchgef¨ uhrt wird, muss ebenfalls ein Vektor gespeichert werden. Dies wird ¨ uber ein Array umge- setzt, wodurch f¨ ur diesen Anteil M _B (N ) = 8 · S _B Bytes ben¨ otigt werden. Insgesamt gilt demnach

M _min (N ) = M _LM (N ) + M _B (N ) = 24 · S _LM + 8 · S _B Bytes (4.12) Die Skalierung des Speicherbedarfs ist in Abbildung 4.4 zusammen mit dem f¨ ur diese Arbeit maximal verf¨ ugbaren Speicher dargestellt. Offensichtlich steigt die ben¨ otigte Speichermenge rasant an. Es zeigt sich, dass die Anzahl der Kernspins hier auf maximal N = 14 begrenzt ist. Dass in diesem Kapitel nur maximal N = 13 Badspins betrachtet werden liegt daran, dass das verwendete Programm bez¨ uglich des Speicherbedarfs nicht vollst¨ andig optimiert ist.

Nun wird das zuvor vorgestellte Trunkierungsschema angewendet um die Anzahl der zu l¨ osenden Bewegungsgleichungen zu verringern.

4.3.2 Trunkierte L¨ osung

Da im vorigen Kapitel gezeigt wurde, dass die exakte L¨ osung der iterierten Bewegungs-

gleichungen mit denen etablierter Methoden ¨ ubereinstimmen, werden nun diese zum

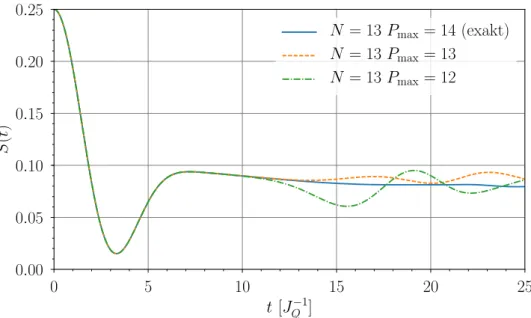
Vergleich f¨ ur die trunkierten L¨ osungen genutzt. In Abbildung 4.5 wird die maximale

Platzzahl P max f¨ ur eine feste Anzahl Badspins N variiert. Der Vergleich zeigt, dass

die gew¨ ahlte Trunkierungsmethode nicht geeignet ist. Schon f¨ ur P _max = N zeigen die

Verl¨ aufe nach anf¨ anglicher ¨ Ubereinstimmung große Abweichungen. Ein Grund hierf¨ ur

ist, dass bei dem genutzten Schema die Kopplungsst¨ arke missachtet wird. Basisope-

ratoren, die P > P _max besetzte Pl¨ atze haben, koppeln nach (4.4) nicht zwangsl¨ aufig

4.3. Resultate

0 5 10 15 20 25

t [J

] 0.00

0.05 0.10 0.15 0.20 0.25

S ( t )

N = 13 P

= 14 (exakt) N = 13 P

= 13

N = 13 P

= 12

Abbildung 4.5: Vergleich einer exakten L¨ osung mit der Methode der iterierten Bewe- gungsgleichungen mit zwei trunkierten L¨ osungen f¨ ur verschiedenen Badgr¨ oßen N . schw¨ acher an den Zentralspin als jene, die aus P ≤ P _max Pauli-Matrizen bestehen.

Aus diesem Grund ist die Relevanz der einzelnen Operatoren nicht an die Anzahl der beschreibenden Pl¨ atze gebunden. Eine Idee bei der Trunkierung ist weiterhin, dass die Anzahl der besetzten Pl¨ atze durch die Anzahl der Anwendungen des Hamiltonoperators gegeben ist. Dadurch, dass die Operatoren mit n besetzten Pl¨ atzen erst nach (n − 1) Iterationsschritten auftreten, wurde deren Einfluss auf das Kurzzeitverhalten des Zen- tralspins als sehr gering eingesch¨ atzt. Jedoch akkumuliert sich der Einfluss offensichtlich so stark, dass signifikante Abweichungen entstehen.

Uberlegungen zu neuen Trunkierungsschemata bieten voraussichtlich noch Opti- ¨

mierungsm¨ oglichkeiten f¨ ur den direkten Ansatz. Da die Skalierung der zu l¨ osenden

Bewegungsgleichungen in dieser Basis jedoch allgemein sehr schlecht ist, wird hier auf

die Verbesserung der Trunkierung verzichtet. Eine bessere M¨ oglichkeit die Gr¨ oße des

Problems signifikant zu verringern ist durch die Basisoperatoren selbst gegeben. Die im

folgenden Kapitel vorgestellte Definition nutzt N¨ aherungen f¨ ur den Limes großer B¨ ader,

wodurch auch realistische Badgr¨ oßen zug¨ anglich werden, ohne dabei mehr Ressourcen

zu ben¨ otigen als bisher.

Kapitel 5

Approximative Basisentwicklung f¨ ur große B¨ ader

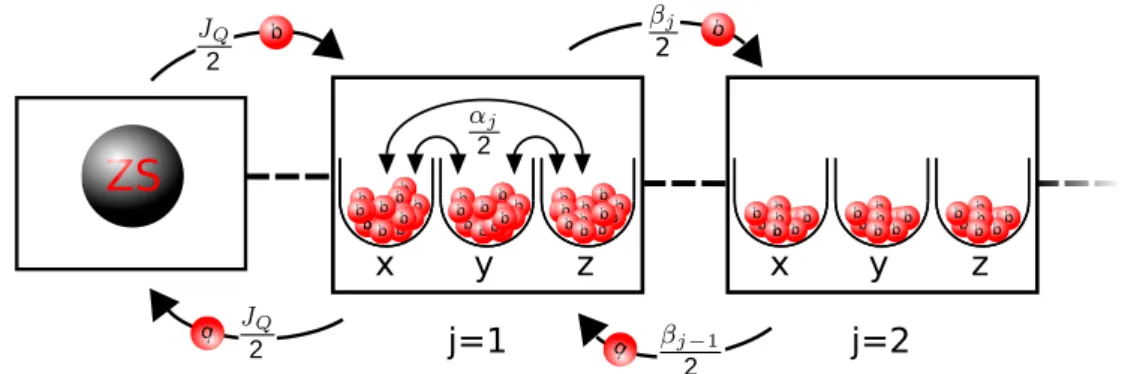
Die Struktur der neuen Basisoperatoren, welche in diesem Kapitel f¨ ur die Zeitent- wicklung des Zentralspins genutzt werden, basiert auf der Idee des Lanczos-Verfahrens in Ref. [25]. Dabei werden nicht wie zuvor die Spinoperatorprodukte direkt betrach- tet, sondern Felder ˆ P j eingef¨ uhrt. Diese sind, ¨ ahnlich zum Overhauserfeld, ¨ uber eine gewichtete Summe ¨ uber alle Badspins definiert. F¨ ur die Konstruktion der neuen Basis- operatoren bleibt der Zentralspinanteil im Vergleich zum direkten Ansatz unber¨ uhrt, jedoch wird der Badanteil ¨ uber Produkte aus den Komponenten ˆ P _j ^α der Felder be- schrieben. Der Index j beschreibt dabei die Stufe der Kopplungsfaktoren, die durch orthogonale Polynome p j (J i ) der Kopplungskonstanten J i definiert sind. Diese Polyno- me werden ¨ uber die Lanczos-Rekursion [26] bestimmt. Der Ansatz bietet den Vorteil, dass viele Badspin-Kombinationen, die beim direkten Ansatz in Kapitel 4 jeweils als eigenst¨ andige Basisoperatoren betrachtet wurden, nun in einem einzigen Basisoperator zusammengefasst werden. Dadurch wird die Gr¨ oße des zu l¨ osenden Differentialglei- chungssystems signifikant reduziert. Um jedoch alle relevanten Wechselwirkungen zu erfassen, werden h¨ ohere Potenzen der ˆ P _j ^α ben¨ otigt. Dabei wird die direkte Berechnung von Skalarprodukt und Erwartungswert schnell sehr aufw¨ andig. Um einen einfache- ren Zugang zu fast beliebigen Potenzen zu erhalten, wird im Laufe dieses Kapitels die Repr¨ asentation des Badanteils der neuen Basisoperatoren durch normierte Hermitepo- lynome der Feldkomponenten ˆ P _j ^α motiviert.

5.1 Orthonormale Felder und Lanczos-Rekursion

Zun¨ achst werden die Felder ˆ P

eingef¨ uhrt. Diese sind ¨ uber die gewichtete Summe P ˆ _j :=

N

X

i=1

p _j (J _i ) ˆ σ _i , j ∈ { 1, 2, 3, ... } (5.1)

mit den Polynomen p j (J i ) in Abh¨ angigkeit der Kopplungskonstanten J i gegeben. Die

Definition weicht um einen Faktor 2 vom klassischen Ansatz in Ref. [25] ab. Damit

diese Felder orthonormal sind, m¨ ussen die Polynome p _j orthonormal bez¨ uglich des Skalarprodukts

(p j | p _k ) :=

N

X

i=1

p j (J i )p _k (J i ) = ^! δ _jk (5.2)

sein. Eine Polynombasis, die dies erf¨ ullt, kann ¨ uber den bekannten Lanczos-Algorithmus [26] bestimmt werden. Dazu wird zun¨ achst das Startpolynom p 1 (J i ) := J i definiert. Die Idee des Algorithmus besteht grunds¨ atzlich darin, das Startpolynom iterativ mit sei- nem Argument J _i zu multiplizieren und das entstehende Polynom ˜ p _j+1 (J _i ) = J _i p _j (J _i ) mit dem Gram-Schmidt-Verfahren im Bezug auf alle vorherigen Polynome zu ortho- normieren. Daraus ergibt sich die Rekursionsformel

J i p j (J i ) = β j p j+1 (J i ) + α j p j (J i ) + β j−1 p j−1 (J i ) , (5.3) wobei p 0 (J i ) := 0 gilt. Die Faktoren α j und β j sind die Lanczos-Koeffizienten, welche im Rahmen der Orthonormierung entstehen und durch

β j−1 = (˜ p j+1 | p j−1 ) (5.4a)

α _j := (˜ p _j+1 | p _j ) (5.4b)

β j :=

q

| p ˜ j+1 − α j p j − β j−1 p j−1 | ² (5.4c) gegeben sind. F¨ ur diese gilt α _j , β _j ∝ √ γ. Die Rekursion kann somit ebenfalls ¨ uber die tridiagonale Matrix

T =











α ₁ β ₁ 0 0 . . . β ₁ α ₂ β ₂ 0 . . . 0 β 2 α 3 β 3 . . . .. . .. . . .. ... ...











(5.5)

und den Vektor der orthonormalen Polynome

p(J i ) = (p 1 (J i ), p 2 (J i ), ... p n (J i )) ^T (5.6) durch

J _i p(J _i ) = T p(J _i ) (5.7)

dargestellt werden. Durch dieses Verfahren ergibt sich eine Basis P = { p 1 , .., p n } aus

reellen Polynomen, welche orthonormal bez¨ uglich des Skalaprodukts (5.2) sind. F¨ ur die

5.2. Basisoperatoren mit Hermitepolynomen

orthonormalen Felder ˆ P _j gilt mit dem zuvor definierten Skalarprodukt (3.9) somit P ˆ _j ^α

P ˆ _k ^β

= 1

2 ^{N +1} Tr





N

X

n,m=1

p _j (J _n )p _k (J _m )ˆ σ ^α _n σ ˆ ^β _m



 (5.8a)

= 1

2 ^{N +1}

N

X

n,m=1

p j (J n )p _k (J m )Tr

ˆ σ _n ^α ˆ σ _m ^β

(5.8b)

=

N

X

n=1

p _j (J _n )p _k (J _n )δ _αβ (5.8c)

= δ jk δ αβ . (5.8d)

Im folgenden Kapitel wird nun die bereits erw¨ ahnte Einf¨ uhrung normierter Hermitepo- lynome motiviert, um einen einfachen Zugang auch f¨ ur h¨ ohere Potenzen der Feldkom- ponenten ˆ P _j ^α zu erhalten.

5.2 Basisoperatoren mit Hermitepolynomen

Die Felder ˆ P j bestehen aus gewichteten Summen von Spinoperatoren. Die Berech- nung h¨ oherer Potenzen dieser Felder ¨ uber das Skalarprodukt (3.9) ist wegen der Spur uber die Spinoperatoren sehr aufw¨ ¨ andig, da viele verschiedene Operator-Kontraktionen einen Beitrag liefern. Wie in Ref. [27] von Seifert et al. gezeigt kann dies jedoch stark vereinfacht werden, sobald eine große Anzahl Badspins betrachtet wird. Diese Vor- aussetzung ist hier f¨ ur die orthonormalen Felder ˆ P _j gegeben, wenn ein System mit N eff → ∞ repr¨ asentiert wird. Dabei wurde in Kapitel 2 bereits festgestellt, dass die ef- fektive Badspin-Anzahl N _eff wegen der exponentiellen Kopplungen f¨ ur große B¨ ader ¨ uber den Parameter γ bestimmt ist. Nach Seifert et al. ist nun der f¨ uhrende Beitrag in der effektiven Badgr¨ oße N eff bei der Berechnung der Spur unter Annahme einer Gaußver- teilung ¨ uber alle paarweisen Kontraktionen der Spins gegeben. Dazu wird anhand eines einfachen Beispiels zun¨ achst gezeigt, dass die Reihenfolge der orthonormalen Felder ˆ P _j ^α bei der Auswertung der Spur in f¨ uhrender Ordnung irrelevant ist. Es gilt

h P ˆ ₁ ^α , P ˆ ₁ ^β i

=

N

X

i,j=1

p 1 (J i )p 1 (J j ) h

ˆ σ ^α _i , σ ˆ ^β _j

i

(5.9a)

= α 1 N

X

i=1

p 1 (J i ) h

ˆ σ _i ^α , σ ˆ _i ^β

i + β 1

N

X

i=1

p 2 (J i ) h

ˆ σ _i ^α , σ ˆ _i ^β

i

(5.9b)

= X

α,β,γ

αβγ

α 1 P ˆ ₁ ^γ + β 1 P ˆ ₂ ^γ

(5.9c)

= ˆ I ^γ . (5.9d)

Wird nun das Skalarprodukt dieses Ergebnisses gebildet ergibt sich I ˆ ^γ

I ˆ ^γ

= α ² ₁ P ˆ ₁ ^γ

P ˆ ₁ ^γ

+ 2α 1 β 1

P ˆ ₁ ^γ P ˆ ₂ ^γ

+ β ₁ ²

P ˆ ₂ ^γ P ˆ ₂ ^γ

(5.10a)

= α ² ₁ + β ₁ ² (5.10b)

∝ γ (5.10c)

∝ N _eff

. (5.10d)

Damit verschwindet der Kommutator f¨ ur N eff → ∞ . Weiterhin ist die Summe ¨ uber N eff

nicht-verschwindende Spin-Kontraktionen proportional zu N _eff . Die f¨ uhrende Ordnung in N _eff ist somit ¨ uber die Maximierung der Kontraktionen bestimmt. Bei einer großen Anzahl von Spinoperatoren ist diese Maximierung durch die Kontraktionen aller nicht- verschwindenden Paare gegeben. Weiterhin ist bekannt, dass der Erwartungswert von Produkten gaußverteilter Variablen ebenfalls durch die Berechnung aller paarweisen Kontraktionen gegeben ist [34, 35]. Diese Eigenschaften k¨ onnen nach Seifert et al.

nun dazu genutzt werden, die Spur der Produkte aus den Feldkomponenten ˆ P _j ^α in f¨ uhrender Ordnung in N _eff uber Gauß-Integrale zu bestimmen und damit sowohl das ¨ Skalarprodukt als auch den Erwartungswert des Badanteils der neuen Basisoperatoren zu berechnen.

Nun werden zun¨ achst die normierten Hermitepolynome H _n (x) = 1

√ n!

H ˜ _n (x) (5.11)

eingef¨ uhrt. Dabei sind die nicht-normierten Hermitepolynome durch H ˜ _n (x) = ( − 1) ⁿ e

d ⁿ

dx ⁿ e

(5.12)

definiert [36]. Diese erf¨ ullen die bekannten Relationen

H ˜ n+1 (x) = x H ˜ n (x) − n H ˜ n−1 , (5.13a) d

dx H ˜ _n (x) = n H ˜ n−1 (x) . (5.13b) Dadurch folgt f¨ ur die normierten Hermitepolynome direkt

xH n (x) = √

nH n−1 (x) + √

n + 1H n+1 (x) , (5.14a) d

dx H _n (x) = √

nH n−1 (x) . (5.14b)

Diese Relationen bieten einen einfachen Zugang zu h¨ oheren Potenzen des Arguments, was im Laufe dieses Kapitels f¨ ur die orthonormalen Felder genutzt wird. Weiterhin gilt f¨ ur die normierten Hermitepolynome die Orthonormalit¨ atsbeziehung

√ 1 2π

Z

−∞

H _n (x)H _m (x)e

2

2

dx = δ _nm . (5.15)

5.2. Basisoperatoren mit Hermitepolynomen

bez¨ uglich der Gewichtsfunktion w(x) = ( √

2π)

exp − x ² /2 .

Nach Seifert et al. wird die N¨ aherung f¨ ur die Berechnung der Spur ¨ uber Gauß- Integrale f¨ ur N _eff → ∞ exakt. Das bedeutet, dass f¨ ur die Hermitepolynome, welche nun als Argument einzelne Komponenten der othornormalen Felder besitzen, die Relation

H _n

( ˆ P _j ^α )

H _m

( ˆ P _j ^α )

= 1

dim H Tr

H _n

( ˆ P _j ^α )

H _m

( ˆ P _j ^α )

(5.16a)

= 1

√ 2π Z

R

H n

(P _j ^α )H m

(P _j ^α )e

( ^P

)

dP _j ^α (5.16b)

= δ _m

_n

(5.16c)

gegeben ist und sie somit ebenfalls orthonormal bez¨ uglich des Skalarproduktes (3.9) sind. Hier wird ausgenutzt, dass die Hermitepolynome der Feldkomponenten ˆ P _j ^α her- mitesch sind. An dieser Stelle soll noch einmal betont werden, dass es sich um eine vollkommen quantenmechanische Betrachtung handelt, obwohl die Feldkomponenten P _j ^α in (5.16b) keine Operatoren mehr darstellen, sondern reelle Variablen. Es wird hier lediglich die f¨ uhrende Ordnung in N _eff der Spur von quantenmechanischen Spins ¨ uber das Gaußintegral bestimmt. Im Fall N _eff < ∞ ist diese Beziehung zwar nicht mehr exakt, stellt f¨ ur große B¨ ader allerdings immer noch eine gute Approximation dar.

Nun k¨ onnen die neuen Basisoperatoren definiert werden. Da die Pauli-Matrizen des Badanteils ¨ uber die Feldkomponenten ˆ P _j ^α beschrieben sind, wird auf die Indi- zierung des Platzes vom Zentralspin verzichtet und dieser nur noch durch ˆ σ _m mit m ∈ { 0,1,2,3 } dargestellt. Allgemein ist ein neuer Basisoperator mit der Kurzschreib- weise H n

:= H n

( ˆ P _j ^α ) durch

ˆ b

_m := ˆ σ _m H n

H n

H n

H n

...

| {z }

=:A

= σ m J

Y

j=1

Y

α

H n

, α ∈ { x, y, z } , (5.17) gegeben. Das J-Tupel n = (n 1,x , n 1,y , ..., n J,z ) definiert dabei die Grade der Hermi- tepolynome im jeweiligen Basisoperator. Es sei hier noch einmal betont, dass deren Reihenfolge nach Seifert et al. in f¨ uhrender Ordnung in N _eff nicht relevant ist.

Dass die neuen Basisoperatoren ˆ b

_m orthonormal bez¨ uglich des Skalarprodukts (3.9) sind, kann mit (5.16) gezeigt werden. Es gilt

ˆ b

_k

ˆ b

_l

= 1

dim H Tr





J

Y

j=1

Y

α

σ _k H _n

σ _l H _m



 (5.18a)

= 1

2 Tr (σ _k σ _l ) 1 2 ^N Tr





J

Y

j=1

Y

α

H _n

H _m



 (5.18b)

= δ _kl δ

. (5.18c)

Die Grundvoraussetzungen f¨ ur eine Basisentwicklung mit den iterierten Bewegungs-

gleichungen sind nun geschaffen. Im folgenden Kapitel wird diese zun¨ achst allgemein

betrachtet.