Dann ist H= Ne X j=1 pj2 2me+ Nn X i=1 pi2 2Mi+ 1 4π0  X i<j e2 |~ri−~rj| +X i<j e2ZiZj R~i−R~j −X i<j e2Zi R~i−~rj

1.5 Elektronen im Festk¨orper

Bis jetzt habe wir eineadiabatische Approximation benutzt, d.h. die kineti- sche Energie der Atome vernachl¨assigt bzw. als kleine St¨orung angenommen Born-Oppenheimer Approximation, mit der Hamilton-Funktion

H=^X

i

p_i²

2M_i +U(R~₁, ~R₂,· · ·, ~R_n)

Angenommen, daß wir jetzt Elektronen aus dem Grundzustand anregen k¨onnen. Dann ist

H=

Ne

X

j=1

p_j² 2m_e+

Nn

X

i=1

p_i² 2M_i+ 1

4π₀



X

i<j

e²

|~r_i−~r_j| +^X

i<j

e²Z_iZ_j

R~_i−R~_j −^X

i<j

e²Z_i

R~_i−~r_j





mit den folgenden Bezeichnungen:

N_e := Anzahl der Elektronen N_n := Anzahl der Kerne

₀ = Elektrische Feldkonstante, 4π₀ = 1 inCGS-System Z_i = Ladung des i-ten Kernes

Und hier wird keine Spin-Orbit Kopplunggenommen.

Wir k¨onnen es weiter vereinfachen, indem wir annehmen, daß die inneren Elektronen stark gebunden sind und wir damit ¨außere Elektronen und Ionen haben. Die Ionen seien auf festen Gitterpl¨atzen (auf jeden Fall im Moment).

Es gibt zwei Zug¨ange:

• Einteilchen, Quasi-Teilchen

• kollektiv

Angenommen, die Ionen seien fixiert und die Wechselwirkung mit den Elek- tronen seiV(~r). Wir vernachl¨assigen zun¨achst die Elektron-Elektron Wech- selwirkung, die man sp¨ater als Korrektur einf¨uhren kann.

¯ h²

2m∇²ψ_i(~r) +V(~r)ψ_i(~r) =_iψ_i(~r) ψ_i(~r): Elektronwellenfunktion

V(~r): Potentialenergie, die einen Anteil enthalten m¨oge, der den Hintergrund von negativer Ladung neutralisiert.

Angenommen weiter, daß wir das Problem f¨urψ_i(~r) schon gel¨ost. Dies ergibt eine orthogonale Menge von Ein-Elektron Zust¨anden ψ_i. Wir f¨uhren nun Erzeugungsoperator b⁺_i f¨ur die Erzeugung eines Elektrons im Zustandψi:

H=^X

i

_ib⁺_i b_i+V_e−e,

wobei V_e−e die Elektron-Elektron Wechselwirkung bezeichnet.

Alternativ k¨onnen wir sowiel wie m¨oglich der Elektron-Elektron Wechselwir- kung in V(~r) stecken. Damit erhalten wir Einteilchen-Wellenfunktion und

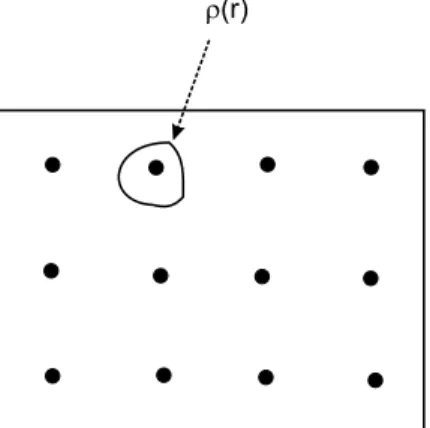
Abbildung 1.27: Mittlere Ladungsdichte

die b⁺_i erzeugt Quasiteilchen. Um V(~r) zu finden k¨onnte man etwa eine Hartree-Fock N¨ahrunganwenden. Definieren wir die Mittlere Ladungsdichte f¨ur das i-te Elektron

ρ(~r⁰) =e

j6=i

X

j

ψ^∗_j(~r⁰)ψ_j(~r⁰) und

−eψ_j(~r⁰)²

ist die mittlere Ladungsdichte eines Punktes~r, die durch das i-te Elektron erzeugt wird.

Hartree-N¨ahrung

¯ h²

2m∇²ψi(~r) +V(~r)

| {z }

Ionen

ψi(~r) + 1 4π₀

Z eρ(~r⁰)

|~r−~r⁰|d³r⁰ψi(~r) =iψi(~r)

1 4π0

R eρ(~r⁰)

|~r−~r⁰|d³r⁰ ist die mittlere Potentialenergie zwischen einem Elektron und dem Rest.

Wegen desPauli-Prinzipserhalten wir jedoch noch einen extra Anteil (Hartree- Fock N¨ahrung):

−^X

j6=i

e² 4π₀ψ_j(~r)

Z ψ_i^∗(~r)ψ_j(~r)

|~r−~r⁰| d³r⁰ (N ichtlokales P otential) Nun gilt es dasKoppman-Theorem, das besagt:

1.

< ψ|H_w|ψ >

< ψ|ψ > 6=^X

i

_i

ψ= 1

√N!(ψ_i) = 1

√N!

ψi(1) · · · ψi(N) ... . .. ... ψ_N(1) · · · ψ_N(N)

Hwist diewahreHamilton-Funktion undψ_iist die approximative Wel- lenfunktion.

2. Wenn wir ein Elektron, dessen Zustand zun¨achstψ_i ist, zuψ_i anregen und alle anderen Wellenfunktionen unver¨andert lassen, dann ist die Energie¨anderung

< ψ|H_w|ψ >

< ψ|ψ > =_j−_i

d.h. _i kann als eine Einteilchenenergie aufgefaßt werden, solange wir nur an ¨Anderung der Energie interessiert sind, wenn wir das System anregen. Zum Beispiel kann man f¨ur die spezifische W¨arme _i als die Energie eines Elektrons nehmen.

Das Programm sieht also wie folgt aus: Nehme

¯ h²

2m∇²+V(~r)

!

ψi(~r) =iψi(~r),

wobei V(~r) die Ionen und eine mittlere Elektron-Elektron Wechselwirkung beinhaltet.

V(~r) muß die Eigenschaft haben:

V(~r) =V(~r+~an) f¨ur jeden Bravais-Gittervektor~a_n

1.5.1 Bloch’scher Satz

SeiV(~r+~a_n) =V(~r) und betrachten wir

−¯h²

2m∇²+V(~r)

!

ψ_ν(~r) =_νψ_ν(~r)

Dann ist ψ_ν(~r+~a_n) ebenfalls eine Eigenfunktion mit Energie_ν. Wennν nicht entartet ist, dann ist

ψ_ν(~r+~a_n) =c⁽ⁿ⁾ψ_ν(~r), c⁽ⁿ⁾= 1

Falls _ν entartet ist, dann haben wir eine Menge {ψ_ν(~r)} von Wellenfunk- tionen mit derselben Energie:

ψµ(~r+~an) =^X

ν

c⁽ⁿ⁾_µνψν(~r) Falls wir die Wellenfunktionen orthonomieren, dann gilt

< ψ_µ(~r+~a_n)|ψ_ν(~r+~a_n)>=δ_µν damit ist

< ψ_µ(~r+~a_n)|ψ_ν(~r+~a_n)> ^def= <^X

ν

c^∗_µν⁽ⁿ⁾ψ_ν(~r)|^X

γ

c⁽ⁿ⁾_λγψ_γ(~r)>

= ^X

νγ

c^∗_µν⁽ⁿ⁾c⁽ⁿ⁾_λγ < ψν(~r)|ψγ(~r)>

| {z }

δνγ

= ^X

γ

c^∗_µγ⁽ⁿ⁾c⁽ⁿ⁾_λγ

= δ_µλ Fassen wirc⁽ⁿ⁾µν, c⁽ⁿ⁾_λγ als Matrix auf:

c⁽ⁿ⁾c⁽ⁿ⁾⁺= 1

=⇒ c⁽ⁿ⁾ ist unit¨ar Matrix.

Es gilt

c⁽ⁿ⁾c^{(m) !}=c^(m)c⁽ⁿ⁾ ψ_µ((~r+~a_n) +~a_m) ^def= ^X

ν

c⁽ⁿ⁾_µνψ_ν(~r)

def= ^X

νλ

c⁽ⁿ⁾_µνc^(m)_νλ ψ_λ(~r)

= ^X

νλ

c^(m)_µν c⁽ⁿ⁾_νλψ_λ(~r)

Damit haben wir eine Menge von unit¨aren Matrizen, die kommutieren. Dar- aus folgt:

• Wir k¨onnen alle diese Matrizen simultan durch dieselbe unit¨are Trans- formation diagonalisieren.

• Wir k¨onnen die entarteten Wellenfunktionen ψν(~r) so w¨ahlen, daß ψ_ν(~r+~a_n) =c⁽ⁿ⁾ψ_ν(~r)

• c^(m+n)=c^(m)c⁽ⁿ⁾=c⁽ⁿ⁾c^(m) Da~an=n1~a1+n2~a2+n3~a3 ist, folgt:

c⁽ⁿ⁾_ν =^hc⁽¹⁾_ν ^in1hc⁽²⁾_ν ^in2hc⁽³⁾_ν ⁱⁿ³ Definieren wir nun

c⁽¹⁾_ν =: e^iθ1,ν c⁽²⁾_ν =: e^iθ2,ν c⁽³⁾_ν =: e^iθ3,ν

=⇒ c⁽ⁿ⁾_ν =e^{i(n1θ1,ν+n2θ2,ν+n3θ3,ν)} Suchen wir nun einen Vektor ~k mit der Eigenschaft:

θ_1,ν =~k^ν~a₁, θ_2,ν =~k^ν~a₂, θ_3,ν =~k^ν~a₃

Erinnern wir uns, daß die primitiven reziproken Gittervektoren~b₁,~b₂,~b₃ die Eigenschaft

~a_i~bj = 2πδ_ij haben. Definieren wir

~k^ν := 1 2π

θ_1,ν~b1+θ_2,ν~b2+θ_3,ν~b3

=⇒ c⁽ⁿ⁾_ν =eⁱ(ⁿ1~k^ν~a1+n2~k^ν~a2+n3~k^ν~a3) =e^i~kν~an

ψ_ν(~r+~a_n) =e^i~kν~anψ_ν(~r)

Nun soll ψ_ν die periodische Bedingung gen¨ugen. Betrachten wir eine kubi- sche Einheit mit einer Kantenl¨ange L, dann ist der Wellenvektor

~k^ν = 2π

L (m₁, m₂, m₃), wobei m_i eine ganze Zahl ist.

Sei ~L=n₁L~e₁+n₂L~e₂+n₃L~e₃

=⇒

ψ_ν(~r+~L) =e^i~kν~Lψ_ν(~r) =e^{i2π(m1n1+m2n2+m3n3)}ψ_ν(~r) =ψ_ν(~r) Definieren wir nun udurch

ψν(~r) =e^i~kν~ru_~kν(~r)

=⇒

ψ_ν(~r+~a_n) =e^i~kν~rψ_ν(~r) =e^{i~kν~r+i~kν~an}u_~kν(~r)

=⇒

u_~kν(~r+~a_n) =u_~kν(~r) f¨ur alle Bravais-Gittervektoren~a_n

Wir schreiben nun die Elektroneneigenfunktion in der Bloch’schen Form ψ_~k, s

|{z}

Spin

(~r) =e^i~k~ru_~k,s(~r),

wobeiu_~k,s(~r) die Periodizit¨at des Gitters aufweist. Wir betrachten den fol- gende Zustand

ψ_~k+~g(~r) = eⁱ(^~k+~g)^~ru_~k+~g,s(~r)

= e^i~k~re^i~q~ru_~k+~g,s(~r)

| {z }

∗

e^i~k~ru_~k,s0(~r)

*:e^i~q~ru_~k+~g,s(~r) hat die Periodizit¨at des Gitters:

e^i~g(~r+~an)=e^i~g~reⁱ

2πn

z}|{~g~a_n =e^i~g~r

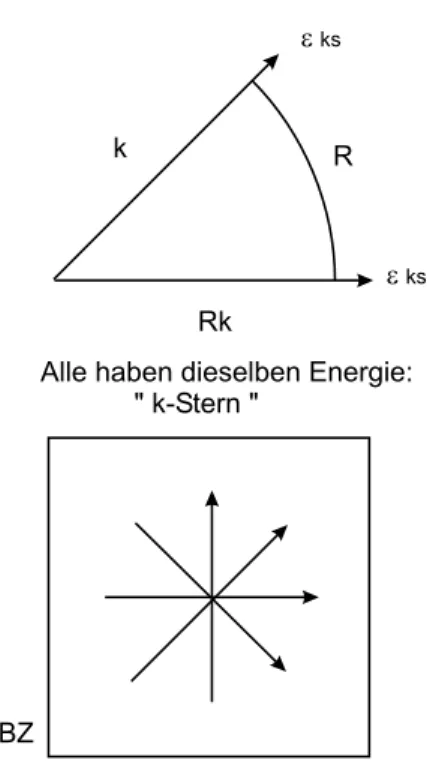
Wir k¨onnen also jedenBlockzustand als einen Blockzustand mit Wellenvek- tor~k in der ersten B.Z. schreiben. Damit brauchen wir nur die Wellenvek- toren in der ersten B.Z. zu betrachten.

Die Schr¨odingergleichung ist nun

−¯h²

2m∇²+V(~r)

!

ψ_~k,s(~r) =_~k,sψ_~k,s(~r)

Um die symmetrischen Eigenschaften der Blochzust¨ande zu erhalten, be- trachten wir ψ_~k,s^∗ (~r). Falls ψ_~k,s(~r) ein Eigenzustand des Systems ist, dann auchψ_~k,s^∗ (~r) mit derselben Energie _~k,s

ψ_~k,s(~r) = e^i~k~ru_~k,s(~r) ψ_~k,s^∗ (~r) = e^−i~k~ru_~k,s^∗ (~r) Definieren wir

u_~k,s^∗ (~r) :=u

−~k,s⁰(~r)

=⇒

ψ_~k,s^∗ (~r) =ψ

−~k,s⁰(~r)

Es gibt also stets eine Entartung zwischen einem Elektronenzustand mit Wellenvektor~k und einem anderen Elekronenzustand mit Wellenvektor −~k d.h.

_~k,s hat eine Inversionssymmetrie in~k-Raum, die unabh¨angig von der Sym- metrie des Kristalls ist. (Zur Erinnerung: F¨ur Phononen gibt es eine ¨ahnliche Symmetrieω_~k,σ =ω_−~k,σ)

Sei R eine Rotation, Reflexion oder Invertierung des Kristalls (d.h. eine der Symmetrieoperatoren). Man kann sichR denken als eine Rotation eines Vektors:

R~a_n=~a_m

oder als die Rotation einer Kontour einer Wellenfunktion im Raum anstatt der Rotation des Kristalls

ψ⁰(~r) =P_Rψ(~r) =ψ(R⁻¹~r) F¨ur einen Blochzustand

P_Rψ_~ks(~r) = P_Re^i~k~ru_~k,s(~r)

= e^i~kR−1~ru_~k,s(R⁻¹~r)

∗∗= eⁱ(R~k)~ru_R~k,s(~r)

**: R ist unit¨ar mit R⁻¹ =R⁺; u_~k,s(R⁻¹~r) := u_R~k,s(~r), da es die Periodi- zit¨at des Gitters hat.

u_~k,s(R⁻¹(~r+~a_n)) = u_~k,s(R⁻¹~r+R⁻¹~a_n)

=u_~k,s(R⁻¹~r+~a_m) = u_~k,s(R⁻¹~r)

Wenn der Kristall eine Rotationssymmetrie hat, dann hat _~k,s dieselbe Ro- tationssymmetrie im ~k-Raum. Was ist nun derelektrische Strom, der durch ein Elektron in einem Blochzustand getragen wird?

ψ_~k,s(~r) =e^i~k~ru_~k,s(~r) Zustand f¨ur den gesamten Kristall ψ_~k,s(~r, t) =eⁱ(^~k~r−ωt)u_~k,s(~r) Modulierte laufende Welle.

D.h. das Elektron im Blochzustand ψ_~ks wird nicht gestreut zu einem ande- ren Zustand mit~k⁰ durch die Atome des Kristalls

=⇒ Das Elektron verst¨arkt sich wie ein freies Elektron.

Wahrscheinlichkeitsflußdichte S bzgl. des Zustandesψ_~k,s ist S_~k,s(~r) = ¯h

2mi

ψ_~k,s^∗ ∇ψ_~k,s−ψ_~k,s∇ψ_~k,s^∗

F¨ur eine ebene Welle e^i~k~r S_~k,s(~r) = ¯h

2mi

i~k+i~kψ^∗ψ= ¯h~k m ψ^∗ψ

| {z }

1

(^klassisch= p~ m =~v)

Um die Abh¨angigkeit von~raufheben, normieren wirS(~r) ¨uber den gesamten

Raum: _R

S_~ksd³r

Rψ^∗ψd³r :=~v(~k, s)

Abbildung 1.28: Symmetrie der Energie von dem Kristall mit Rotationssym- metrie

Betrachten wir die Schr¨odinger Gleichung und differenzieren nach der x- Komponente von~k:

∇²∂ψ_~k,s

∂k_x +2m

¯ h²

"

∂_~ks

∂k_xψ_~k,s+_~ks−V∂ψ_~k,s

∂k_x

#

= 0 Nun istψ_~k,s(~r) =e^i~k~ru_~k,s(~r)

=⇒ ^∂ψ_∂k^~k,s_x =ixψ_~k,s+e^{i~k~r ∂u}_∂k^~k,s

x Damit haben wir 2i∂ψ_~k,s

∂k_x +2m

¯ h²

∂_~ks

∂k_xψ_~k,s+

∇²+2m

¯ h²

_~ks−V∂u_~k,s

∂k_x e^i~k~r = 0 Multiplizieren wir es mitψ^∗

2iψ_~k,s^∗ ∂ψ_~k,s

∂k_x +2m

¯ h²

∂_~ks

∂k_xψ_~k,s^∗ ψ_~k,s+ψ_~k,s^∗

∇²+2m

¯ h²

_~ks−V∂u_~k,s

∂k_x e^i~k~r = 0 Integrieren wir diese Gleichung ¨uber den gesamten Raum

2i Z

ψ_~k,s^∗ ∂ψ_~k,s

∂k_x d³r+2m

¯ h²

Z ∂_~ks

∂k_xψ_~k,s^∗ ψ_~k,sd³r+

Z ψ_~k,s^∗

∇²+2m

¯ h²

_~ks−V∂u_~k,s

∂k_x e^i~k~rd³r= 0 Mit der Anwendung von dem Green’schen Satz bekommen wir

Z ψ_~k,s^∗

∇²+2m

¯ h²

_~ks−V∂u_~k,s

∂k_x e^i~k~rd³r =

Z ∂u_~k,s

∂k_x e^i~k~r

∇²+2m

¯ h²

_~ks−Vψ_~k,s^∗ d³r = 0^∗

*:ψ_~k,s^∗ erf¨ullt dieselbe Schr¨odinger Funktion wie ψ_~k,s Damit also

i Z

ψ_~ks^∗ ∂ψ_~ks

∂k_x d³r =−m

¯ h²

∂_~ks

∂k_x Z

ψ_~k,s^∗ ψ_~k,sd³r

v_x = 1

¯ h

∂_~ks

∂k_x Gruppengeschwindigkeit

Die Geschwindigkeit eines Elektronen im Band verschwindet bei ~k = 0 so- wie an der Zonengrenze. Wir k¨onnen nun ein Wellenpaket konstruieren f¨ur

Abbildung 1.29:

ein Elektron mit Wellenpaket, das in R zentriert und dessen dominanter Wellenvektor ~k0 ist

ψ= ^X

veck

A(~k)ψ_~ks(~r, t) =sum_veckA(~k)e^i~k~re^−iω~kstu_~k,s(~r)

Nehmen wir an, daß das Wellenpaket scharf um~k0 ist, dann ist ψ(~r, t)∼=e^i~k0~re^{−iω~k0,st X}

veck

A(~k)eⁱ(^~k−~k0)^~re⁻ⁱ(^~k−~k0)^∂ω~ks_∂~k ^tu_~k

0,s(~r)

1.5.2 Spin-Orbit Kopplung Sei

H= p²

2m +V(~r) +Hs.o., wobei

Hs.o. := ¯h

4m²c²σ× ∇V(~r)·p mit p=−i¯h∇ und

σ= (σx, σy, σz) σ_x = 0 1

1 0

!

, σ_x = 0 −i i 0

!

, σ_x = 1 0 0 1

!

Der Spin-Orbit Anteil Hs.o. der Hamiltonfunktion hat die Periodizit¨at des Gitters, d.h.

Hs.o.(~r) =Hs.o.(~r+~a_n) Der Bloch’sche Satz gilt auch bei diesem Fall und damit

ψ_~ks =e^i~k~ru_~ks(~r) mit

u_~ks =u^↑_~ks(~r) 1 0

!

+u^↓_~ks(~r) 0 1

!

Weiter gilt

v_~ks= 1

¯ h

∂_~ks

∂k , ¯hdk

dt =−eE _~ks=

−~ks

Um dies zu zeigen, definieren wir den Operator Q:=σ_yK,

wobeiK Operator zu Komplex konjugieren ist. Dann ist Kp=pK

und die Spin-Matrizen antikommutieren:

σ_iσ_j+σ_jσ_i = 1 mit i, j ∈ {x, y, z}

Also,HQ=QHund somit

Hψ_~ks=_~ksψ_~ks

=⇒ QHψ_~ks =_~ksQψ_~ks

=⇒ HQψ_~ks =_~ksQψ_~ks

=⇒ Qψ_~ks ist Eigenzustand mit demselben Energieeigenwert_~ks wieψ_~ks Nun ist

Qψ_~ks = Qe^i~k~ru_~ks(~r)

= e^−i~k~rσ_yu_~ks^∗ (~r)

= ψ

−~ks⁰, wobei σyu_~ks^∗ (~r) hat die Periodizit¨at des Gitters.

Nun ist Hψ_−~ks0 =_~ksψ_−~ks0 und wir k¨onnen damit s’=s w¨ahlen.

_~ks =_−~ks

Nehmen wir nun an, daßV(~r) sehr schwach ist im Bezug auf die ¨außeren Elektronen der Atomen. Damit k¨onnen wir mit einfachen ebenen Wellen f¨ur die Blochzust¨ande starten und V(~r) als eine St¨orung betrachten.

ψ_~k= 1

Ve^i~k~r =|~k >, 0 = ¯hk² 2m St¨orungstheorie (nicht entartet)

(~k) =₀(~k)+< ~k|V|~k >+ ^X

~k⁰6=~k

< ~k|V|~k⁰ >² ₀(~k)−₀(~k⁰) +· · · F¨urV(~r) schreiben wir

V(~r) =^X

~g

e^i~q~rV_~g dann ist

< ~k|V|~k > = 1 V

Z e^−i~k~r



X

~g

e^i~q~rV_~g



e^i~k~rd³r

= 1

V Z

V(~r)d³r

=: V₀ und

< ~k|V|~k⁰ > = 1 V

Z e^−i~k~r



X

~g

e^i~q~rV_~g



e^i~k0~rd³r

= 1

V ·V ^X

~g

V_~gδ_~k,~k0+~g Wir erhalten also immer Probleme, wenn

~k⁰ =~k−~g

Abbildung 1.30:

und

₀(~k) =₀(~k⁰)

Wir m¨ussen also entartete St¨orungstheorie in der N¨ahe der Zonengrenze machen. Dazu brauchen wir den wirklichen Blochzustand f¨ur das System

ψ_~ks(~r) =^X

~g

α_s(~g)|~k+~g >

Seien_~ks der exakte Eigenwert f¨ur den Blochzustandψ_~ks: Hψ_~ks=_~ksψ_~ks

Betrachten wir zun¨achstH= _2m^p2 +V(~r):

Hψ_~ks = p²

2m +V(~r)

! X

~g

α_s(~g)|~k+~g >

=



X

~g

α_s(~g)₀(~k+~g) +^X

~g

α_s(~g)V



|~k+~g >

=! _~ksα_s(~g)|~k+~g >

Multiplizieren wir es von links mit< ~k|: X

~g

α_s(~g)₀(~k+~g)< ~k|~k+~g >

| {z }

αs(0)+0(~k)

+^X

~g

α_s(~g)< ~k|V|~k+~g >=_~ksα_s(0)

Wenn wir es mit< ~k+~g| statt < ~k| multiplizieren, dann haben wir:

αs(~g)0(~k+~g) +^X

~g⁰

αs(~g⁰)< ~k+~g|V|~k+~g⁰ >=_~ksαs(~g)

=⇒

α_s(0) = −1 ₀(~k)−_~ks

X

~g

α_s(~g)< ~k|V|~k+~g >

und

α_s(~g) = −1 ₀(~k+~g)−_~ks

X

~g⁰

α_s(~g⁰)< ~k+~g|V|~k+~g⁰ >

Sei also ~k nahe der Zonengrenze von BZ (∼π/a), dann sind die wichtigen

~g-Vektoren~g= 0 und~g =−2π/a·~e=~g₁

=⇒

αs(0)0(~k) +αs(0)< ~k|V|~k >+αs(~g1)< ~k|V|~k+~g1>=αs(0)_~ks

α_s(0)₀(~k) +α_s(0)

V0

z }| {

< ~k|V|~k >+α_s(~g₁)

V₋~g1

z }| {

< ~k|V|~k+~g₁>=α_s(0)_~ks α_s(~g₁)₀(~k+~g1)+α_s(0)< ~k+~g₁|V|~k >

| {z }

V~g1

+α_s(~g₁)< ~k+~g₁|V|~k+~g₁ >

| {z }

V0

=α_s(~g₁)_~ks Definiere:

˜

₀(~k) :=₀(~k) +V₀

=⇒

˜

₀(~k)−_~ksα_s(0) +V_−~g1

| {z }

V_~g^∗

α_s(~g₁) = 0

V_~g1α_s(0) +˜₀(~k+~g₁)−_~ksα_s(~g₁)

Nun muß

˜

₀(~k)−_~ks V_~g^∗ V_~g1 ˜₀(~k+~g₁)−_~ks

= 0

=⇒

_~ks^± = 1 2

˜₀(~k) + ˜₀(~k+~g₁)±1 2

r

˜

₀(~k) + ˜₀(~k+~g₁)²+ 4V_~g1² Und in der N¨ahe an der Zonengrenze gibt es N¨ahrung f¨ur_~ks:

_~ks^± ≈˜₀(~k) +const·(k−π/2)²±V_~g1±const·(k−π/2)²+O((k−π/2)³) Also, an der Zonengrenze :

_~ks^± = ˜0(~k)±V_~g1

und wenn (k−π/2)² klein ist, ist das Band parabolisch.

Abbildung 1.31:

Abbildung 1.32:

1.5.3 Tight-Binding Approximation

Angenommen, ein Elektron eines isolierten Atoms habe die Orbitale φ_α(~r).

Beispielsweise f¨ur das H-Atom: φ_1s(~r). Die Wellenfunktion eines H₂ Mo- lek¨uls kann man approximativ als eine Linearkombination der atomaren Or- bitale schreiben.

ψ^±(~r) =φ_1s(~r−~r₁)±φ_1s(~r−~r₂)

Versuchen wir einen ¨ahnlichen Ansatz im Festk¨orper zu machen, mit der Annahme, daß die ¨Uberlappung zwischen den Atomen schwach ist. Sei H

Abbildung 1.33: Schwacher ¨Uberlapp des Potentials

die Hamiltonfunktion eines Elektrons im Festk¨orper:

H=−¯h²

2m∇²+V(~r)

mit V(~r) =^P_nv(~r−~a_n), wobeiv(~r) das Potential eines isolierten Atoms.

Sei φ_α(~r) die L¨osung f¨ur die Schr¨odingergleichung:

−¯h²

2m∇²+V(~r)

!

φ_α(~r) =E_αφ_α(~r)

E_α undφ_α(~r) sind also der Eigenwert und die Wellenfunktion einesisolier- ten Atoms.

Sei ψ_~kα((~r) die Eigenfunktion des Elektron im Festk¨orper:

ψ_~kα((~r) =^X

n

A_nφ_α(~r−~a_n) ψ_~kα((~r) muß ein Blochzustand sein:

An= 1

√Ne^i~k~an

=⇒ ψ_~kα(~r) = 1

√N X

n

e^i~k~anφ_α(~r−~a_n) ψ_~kα(~r)

e^i~k~r = 1

√N X

n

e^{i~k(~an−~r)}φ_α(~r−~a_n) =:u_~kα(~r), da es die Periodizit¨at des Gitters hat.

=⇒ e^i~k~ru_~kα(~r)