Quantenchemische Untersuchungen an Initialreaktionen zur Bildung von Borosilazankeramiken Diplomarbeit von Silke Reinhardt aus Datteln Bonn, im April


Quantenchemische Untersuchungen an Initialreaktionen zur Bildung von

Borosilazankeramiken

Diplomarbeit

Silke Reinhardt von Datteln aus

Bonn, im April 1998

Ich versichere, da ich diese Arbeit eigenstandig verfat und keine anderen als die angegebenen Quellen und Hilfsmittel benutzt sowie Zitate als solche kenntlich gemacht habe.

Bonn, den

Referentin: Frau Priv.-Doz. Dr. Christel M. Marian Korreferentin: Frau Prof. Dr. Sigrid D. Peyerimho

Meinen Eltern und meiner Gromutter

Inhaltsverzeichnis

Einleitung 1

1 Thermodynamik und Kinetik 3

1.1 Die Theorie des aktivierten Komplexes . . . 4

1.2 Ubergangszustande aus Theorie und Rechnung . . . 9

2 Angewandte Methoden 13

2.1 Energiebestimmungen . . . 13

2.1.1 Die SCF-Methode . . . 13

2.1.2 Die semiempirischen Methoden MNDO und AM1 . . . 19

2.1.3 Dichtefunktionaltheorie . . . 21

2.1.4 Storungstheorie . . . 25

2.2 Verfahren zur Lokalisierung stationarer Punkte . . . 30

2.2.1 Gradienten und Hesse-Matrizen . . . 30

2.2.2 Optimierung ohne Gradienten . . . 31

2.2.3 Das lineare Modell . . . 32

2.2.4 Das quadratische Modell . . . 32

3 Die Rechnungen 35

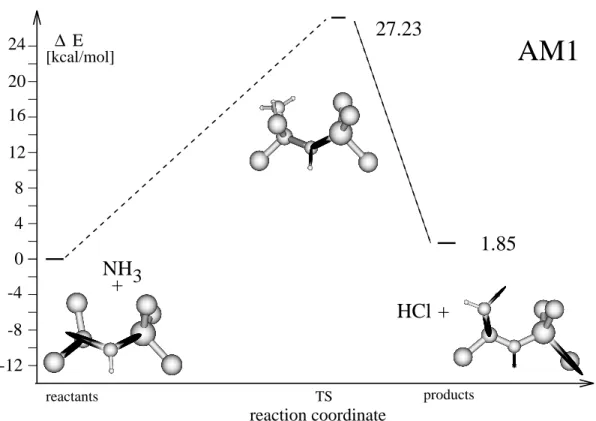
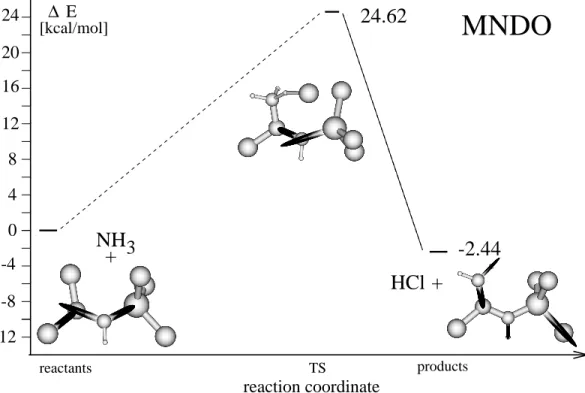
3.1 Abschatzung der Verlalichkeit . . . 35

3.1.1 Ergebnisse der Rechnungen mit AM1, MNDO und MNDO/d . . 36

3.1.2 Ergebnisse der Hartree-Fock-Rechnungen . . . 43

3.1.3 Ergebnisse der Rechnungen mit Dichtefunktionalen . . . 55

3.1.4 Ergebnisse der Rechnungen mit Mller-Plesset Storungstheorie . 63 3.2 Kettenverlangerung - Bor/Siliciumseite . . . 79

3.2.1 Reaktionen von TADB mit einem Ammoniakmolekul . . . 79

3.2.2 Reaktionen von TADB mit zwei Ammoniakmolekulen . . . 88

3.2.3 Die Reaktion eines aminierten TADB mit einem weiteren TADB Molekul . . . 93

3.3 Kettenverzweigung . . . 94

Zusammenfassung und Ausblick 95

Danksagung 105

i

Einleitung

Im Rahmen des Sonderforschungsbereiches 408, \Festkorper ohne Translationssymme- trie", haben es sich die Teilprojekte B und C zur Aufgabe gemacht, Aussagen uber die Struktur amorpher Festkorper zu treen. Diese Arbeit, \Quantenchemische Untersu- chungen an Initialreaktionen zur Bildung von Borosilazankeramiken", fugt sich in das Teilprojekt C2 dieses Sonderforschungsbereiches ein. An dieser Stelle werden zunachst einige Grundlagen erlautert, um anschlieend zu skizzieren, warum aus der quanten- chemischen Untersuchung einer Initialreaktion Informationen uber die Struktur eines amorphen Festkorpers gezogen werden konnen.

Ein amorpher Festkorper wird sehr haug als Gegenteil eines kristallinen Festkorpers deniert. [1] Diese Denition sagt aus, da in einem amorphen Festkorper weder Ele- mentarzellen noch Translationssymmetrie vorhanden sind, die eine Kristallstruktur ausmachen. In [2] wird amorph dagegen als ein Adjektiv deniert, mit dem man die re- gellose Anordnung molekularer Bausteine in einem Festkorper beschreiben kann. Diese Denition erweckt den Anschein, da es in einem amorphen Festkorper keine geord- neten Bereiche gibt. Es wird aber angenommen, da in einem amorphen Festkorper bestimmte Verknupfungen zwischen verschiedenen Atomen bevorzugt sind und daher auch von Nahordnung zu sprechen ist. [3]

Bei kristallinen Festkorpern ist es unproblematisch, Aussagen uber die Struktur zu ma- chen. Die Sonden, die dabei zur Strukturaufklarung benutzt werden, liefern bei amor- phen Festkorpern aber kaum Informationen. Mit der Rontgenbeugung ist es moglich, die Fernordnung einer kristallinen Substanz zu bestimmen. Da bei amorphen Fest- korpern aber keine Translationssymmetrie existiert und somit auch keine Netzebenen vorhanden sind, an denen die Rontgenstrahlung gebeugt wird, fuhrt diese Analysen- methode nicht zu Ergebnissen. Mit der IR- und der NMR-Spektroskopie besteht bei kristallinen Festkorpern die Moglichkeit, Aussagen uber die nachsten Nachbarn einer Atomsorte zu machen. Wenn ein IR-Spektrum einer amorphen Substanz aufgenommen wird, erhalt man aber i.a. nur drei breite Banden, die man den Streckschwingungen, den Biegeschwingungen und den Gerustschwingungen zuordnen kann. Es ist sehr schwie- rig, solche Spektren zu interpretieren. [3] Ahnliche Probleme tauchen auch bei der Festkoper-NMR-Spektroskopie auf. Aufgrund der vielen verschiedenen, aber ahnlichen chemischen Umgebungen einer Atomsorte, werden hier mehrere Signale mit ahnlichen chemischen Verschiebungen, d.h. breite Resonanzen, erhalten. [4]

Im Rahmen dieses Sonderforschungsbereiches ist es von besonderen Interesse, nahere Informationen uber die Strukturen von Keramiken zu bekommen, die im Arbeitskreis um Prof. Jansen entwickelt wurden. Diese Keramiken haben eine herausragende Hit- zebestandigkeit, weisen eine hohe Oxidationsstabilitat und eine gute Thermoschockre- sistenz auf und sind auerdem wenig sprode.

1

Eine Zugangsmoglichkeit zu solchen keramischen Hochleistungswerkstoen ist die sog.

Polymerroute, in der polymere Vorlaufer thermisch zersetzt werden. [5, 6] Die Darstel- lung des Polymers, das fur die Darstellung der Keramik notig ist, verlauft uber die Ver- netzung von molekularen Vorlaufern (Precusoren), die alle Elemente des gewunschten Festkorpers enthalten. Diese Darstellungsweise wurde mit dem Hintergrund entwickelt, da bestimmte molekulare Einheiten aus den Precursoren in der Keramik vorhanden sind und somit eine hohe Stabilitat des Werkstos erhalten wird.

Die Keramik, die fur diese Arbeit von besonderem Interesse ist, ist Si³B³N⁷. Ihre Dar- stellung gelingt wie folgt: Zunachst wird der Precursor TADB ([(Trichlorosilyl)amino]- dichloroboran) bei -78 C mit Ammoniak zum Polymer umgesetzt. Nachdem das Po- lymer gereinigt wurde, wird es im stromenden Ammoniak auf 1000 C erhitzt.[6]

Cl³Si^;NH^;BCl²+ ^;NH!3 Si³B³N⁷ (1)

Uber die Struktur dieser Keramik ist bisher wenig bekannt. Mit Hilfe der NMR- Spektroskopie konnte gezeigt werden, da Bor trigonal von Sticksto umgeben ist und Silicium tetraedrisch. Genaue Informationen zur Koordination von Sticksto liegen noch nicht vor. ¹⁵N-NMR-Spektren von Si³B³N⁷ mit unterschiedlicher Isotopenmar- kierung weisen jedoch darauf hin, da die Si-N-B-Einheit aus dem Precursor erhal- ten bleibt. Weitere Hinweise uber die Koordination des Stickstos in dieser Keramik konnen durch die Klarung des Verlaufs der Initialreaktion gewonnen werden. Daher stellen sich zur weiteren Strukturaufklarung die folgenden Fragen: Findet die Substitu- tion der Chloratome bei der Reaktion mit Ammoniak oder wahrend der Pyrolyse statt?

Werden bei der Reaktion mit Ammoniak zunachst die Chloratome an der Bor- oder an der Siliciumseite substituiert? Findet der Angri eines zweiten TADB-Molekuls am Sticksto des ersten TADB bevorzugt mit der Silicium- oder mit der Borseite statt? Da diese Fragen experimentell schwierig zu beantworten sind, liegt eine quantenchemische Untersuchung dieser Initialreaktion nahe.

Grundlagen dieser Betrachtung sind Kenntnisse der Physikalischen Chemie einerseits sowie die Methoden der Theoretischen Chemie andererseits. Diese Grundlagen sollen in den beiden folgenden Kapiteln naher erlautert werden. Anschlieend werden dann die Ergebnisse der Rechnungen vorgestellt, die gemacht wurden, um die Reaktionen von TADB mit einem und mit zwei Ammoniakmolekulen zu untersuchen.

Kapitel 1

Thermodynamik und Kinetik einer chemischen Reaktion

In Rahmen dieser Arbeit soll die Initialreaktion zur Darstellung einer Si³B³N⁷-Keramik untersucht werden. Zunachst werden dazu die Reaktionen von TADB mit einem und zwei Molekulen Ammoniak betrachtet. Die theoretischen Grundlagen, die zur Beschrei- bung chemischer Reaktionen notig sind, liefern die Thermodynamik und die Reakti- onsdynamik. [7] Die wichtigsten Grundlagen sollen in diesem Kapitel kurz erlautert werden.

Durch die Thermodynamik und die Reaktionsdynamik werden verschiedene Gesichts- punkte einer chemischen Reaktion beschrieben. Mit Hilfe der Thermodynamik konnen Aussagen daruber gemacht werden, wo das Gleichgewicht einer chemischen Reakti- on liegt. In der Reaktionsdynamik wird die zeitliche Entwicklung einer Reaktion in Abhangigkeit von der Temperatur genauer betrachtet. Mit der Reaktionsdynamik kann also beschrieben werden, wie schnell eine Reaktion ablauft.

Eine fruhe Theorie der Reaktionsdynamik fur Gasphasenreaktionen ist die klassische Stotheorie. Sie geht davon aus, da die Reaktionsgeschwindigkeit proportional ist (a) zur AnzahlA der Stoe, die die Reaktionspartner untereinander erleiden

(b) zur Wahrscheinlichkeit, da bei einem Sto genugend Energie vorhanden ist, damit eine Reaktion erfolgen kann

Voraussetzung fur diese Annahmen ist, da ein Sto nur dann zu einer Reaktion fuhren kann, wenn die kinetische Energie, mit der sich die Stopartner nahern, mindestens der Aktivierungsenergie der Reaktion Ea entspricht. Nach der Boltzmann-Verteilung ist bei der TemperaturT der Anteil der Stoe mit der Mindestenergie Eaproportional zu e^;Ea=RT. Fur die Reaktionsgeschwindigkeit folgt daraus:

k^R =A(T)e^;Ea=RT (1.1)

Dabei ist zu bedenken, da die StozahlA ebenfalls temperaturabhangig ist. Ein Pro- blem der klassischen Stotheorie ist, da es notig ist, zur Bestimmung der Stozahl den sog. Stoquerschnitt einzufuhren; wenn von einem Modell mit harten Kugeln ausgegangen wird, wird als =(RA+RB)² deniert, wobei RA undRB die Radi- en der stoenden Molekule sind. Wenn man einen realistischeren Fall betrachten will, der sicherlich nicht mit festen Kugeln beschrieben werden kann, wird die Berechnung des Stoquerschnitts sehr viel aufwendiger. Aus diesem Grund wurde Eyring 1934 eine andere Theorie entwickelt, die Theorie des aktivierten Komplexes.[8]

3

1.1 Die Theorie des aktivierten Komplexes

Mit Hilfe der Theorie des aktivierten Komplexes wurde von Eyring ein Weg aufgezeigt, wie sich bei Kenntnis der Potentialhyperache die Geschwindigkeitskonstante einer Reaktion berechnen lat. Dabei geht man nicht, wie bei der Stotheorie, vom Verhalten der einzelnen Molekule aus, sondern nimmt die Statistische Thermodynamik zu Hilfe.

Um die Grundlagen der Theorie des aktivierten Komplexes naher zu erlautern, wird von einer einfachen bimolekularen Reaktion ausgegangen:

A+BC ^!AB+C (1.2)

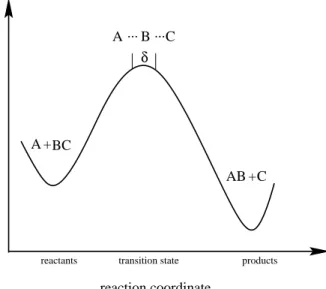
Dabei wird die Annahme gemacht, da wahrend der gesamten chemischen Reaktion die Kerne der drei Atome auf einer Geraden liegen, die Reaktion also kollinear ist. Der Ablauf der Reaktion wird so sein, da sich A annahert und sich dabei die Bindung BC lockert. Es wird dann ein aktivierter Komplex ABC durchlaufen. Dieser aktivierte Komplex zerfallt entweder wieder in die Edukte, oder reagiert zuAB undC weiter. Der Reaktionsweg wird symbolisiert durch:

A+BC ^!A+BC *) ABC *) AB+C^!AB +C (1.3) Die energetischen Verhaltnisse konnen wie folgt beschrieben werden: Wenn A noch weit entfernt ist, bendet sich das Molekul BC in einem Energieminimum. Nahert sich A, so steigt die Energie langsam an, bis der Sattelpunkt erreicht ist. Verringert sich der Abstand zwischen A und B weiter, so nimmt bei gleichzeitiger Aufweitung des BC- Abstands die Energie ab, bis sich das neugebildete Molekul AB in einer Energiemulde bendet.

E

reactants transition state products

reaction coordinate δ

A ... B ... C

A +BC

AB + C

Abbildung 1.1: Schematische Darstellung der potentiellen Energie als Funktion der Reaktionskoordinate

Um die Reaktionsgeschwindigkeit mit der Eyring-Theorie zu berechnen, behandelt man den aktivierten Komplex, der im Bereich vorliegt, wie eine eigene Molekulart. Im weiteren Verlauf wird er als M^y bezeichnet. Auerdem nimmt man an, da alle Re- aktanden, die den Ubergangszustand erreichen, in Produkte uberfuhrt werden. Sobald

sich aber AB und C gebildet haben, kann die Ruckreaktion stattnden. So kann es dann zu einer Gleichgewichtseinstellung kommen.

A+BC *) M^y*) AB+C (1.4)

Das Kernstuck dieser Theorie ist, da die Hin- und Ruckreaktion als unabhangig von- einander betrachtet werden. Das heit, die Geschwindigkeit der Hinreaktion wird nur durch die Anzahl der Stoe zwischen Aund BC bestimmt, unabhangig davon, ob sich das Gleichgewicht fur die gesamte Reaktion schon eingestellt oder nicht. Eine weitere Annahme der Theorie von Eyring ist, da sich ein Gleichgewicht zwischen den Edukten und dem aktivierten Komplex ausbildet. Die Gleichgewichtskonstante fur die Hinreak- tion ist dann:

K = [M^y]

[A][BC] (1.5)

Fur die Konzentration des aktivierten Komplexes erhalt man daher:

[M^y] =K[A][BC] (1.6)

Die Konzentration des aktivierten Komplexes ist vernachlassigbar klein im Vergleich zu der Konzentration der Edukte und Produkte, weil er sehr schnell durchlaufen wird.

Die Konzentration ist daher nicht mebar und mu in der o.g. Gleichung substituiert werden. Ausgangspunkt fur diese Substitution ist die mittlere Geschwindigkeit, mit der sich die Komplexe durch den Ubergangszustand bewegen. Sie lat sich aus der Maxwell-VerteilungF (v) berechnen.

v =^{Z 1}

0

vF(v)dv=

s2kT

m^{y (1.7)}

In dieser Gleichung ist m^y die Masse des aktivierten Komplexes, k die Boltzmann- Konstante und T die Temperatur.

Da der Ubergangszustand langs der Strecke existiert, kann nun die Zeit bestimmt werden, in der der Ubergangszustand durchlaufen wird:

t =

v ⁼

(2kT=m^y)¹⁼² (1.8)

Daraus kann nun die Reaktionsgeschwindigkeit r ermittelt werden. Sie lat sich aus- drucken als die Stomenge, die pro Volumen- und Zeiteinheit nach rechts ubergeht.

Man bedenke dabei, da im Gleichgewicht der Ubergangszustand ebenso haug von links nach rechts durchlaufen wird wie von rechts nach links. Daher ist nur die halbe Konzentration des aktivierten Komplexes einzusetzen.

r _{= 12} [M^y_{] = 12} [M^y]1

s2kT

m^{y (1.9)}

Durch Einsetzen von Gleichung (1:6) erhalt man:

r _{= 12} K[A][BC]1

s2kT

m^{y (1.10)}

Andererseits lat sich die Reaktionsgeschwindigkeit beschreiben durch

r= k^R[A][BC]: (1.11)

Damit ergibt sich die Geschwindigkeitskonstante kR der Gesamtreaktion zu:

k^R = K

s kT

2m^{y (1.12)}

Die Geschwindigkeitskonstante kR der Reaktion lat sich also bestimmen, wenn die GleichgewichtskonstanteK und die Groeberechnet werden konnen. Zur Berechnung notig sind Grundlagen der Statistischen Thermodynamik. Sie sollen an dieser Stelle kurz erlautert werden.

Die kanonische Zustandssumme eines System ist deniert als Summe uber alle Zustande eines Systems bei einer bestimmten Zusammensetzung und einem bestimmten Volu- men.

Z =^X

j e^;Ej=kT (1.13)

Ej ist die quantenmechanische Energie des makroskopischen Systems, wenn es sich in dem mikroskopischen Zustand j bendet.

In einem idealen Gas gibt es keine Wechselwirkungen zwischen den Teilchen. Fur ein Gas mit N ununterscheidbaren, nicht-wechselwirkenden Molekeln kann die Zustands- summe angegeben werden als:

Z =^X

j e^;Ej=kT = z^N

N! (1.14)

mit

z =^X

s e^;s=kT =^X

s e^{;tr;t+rot;r+vib;u+el;v=kT} (1.15) als molekularer Zustandssumme. Eine gute Naherung ist, die molekulare Energiesals Summe der Translations-, Rotations-, Vibrations- und elektronischen Energie darzu- stellen:

s =tr;t+rot;r+vib;u+el;v (1.16)

t;r;u;v in dieser Gleichung geben die translatorischen, vibratorischen, rotatorischen und elektronischen Zustande an. Das heit also, die molekulare Zustandssumme z ist darstellbar als Produkt der translatorischen, vibronischen, rotatorischen und elektro- nischen Zustandssummen.

z =ztrzrotzvibzel (1.17)

Fur ein ideales Gas konnen diese Zustandssummen ermittelt werden. Wenn man einen Kasten mit dem VolumenV betrachtet ergibt sich fur die Zustandssumme der Trans- lation:

ztr = (2mkT)³⁼²V: (1.18)

Die Zustandssumme der Vibration fur ein Molekul mit (3N^;6) Freiheitsgraden ist in der Naherung des harmonischen Oszillators:

zvib =^3Yn;6

s⁼¹ zvib;s=^3Yn;6

s⁼¹

1^;e^;1^{hs=kT (1.19)}

Die Zustandssumme der Rotation fur ein polyatomares Molekul ist:

zrot= ^{1=2 2}kT

h

!

3=²

(IaIbIc)¹⁼² (1.20)

Ia;Ib und Ic sind die Tragheitsmomente des Molekuls bezuglich seiner Haupttragheits- achsen, gibt die Anzahl der ununterscheidbaren Orientierungen des Molekuls an, die durch Rotation um molekulare Drehachsen erhalten werden.

Fur die elektronische Zustandssumme wird eine grobe Naherung angenommen. Es wird davon ausgegangen, da bei Raumtemperatur nur der elektronische Grundzustand be- setzt ist.zel wird daher alsgel;oangesetzt, wobeigel;odie Entartung des Grundzustands angibt.

An dieser Stelle ist es nun moglich, die Herleitung der Gleichung, mit der die Geschwin- digkeitskonstante einer Reaktion berechnet werden kann, fortzufuhren. Zunachst gilt es, eine Bestimmungsgleichung fur die Gleichgewichtskonstante K zu ermitteln. Nach der Boltzmann-Verteilung ist die Besetzung des Ubergangszustands gegeben als:

NM^y

NANBC = zM^y

zAzBCe^;E0y=kT (1.21)

Wenn jedes N in dieser Gleichung durch das Produkt aus Loschmidtzahl und Volumen (NLV) dividiert wird, erhalt man die Konzentrationen der jeweiligen Molekule. Das ist dann in die Gleichung (1:5) fur die Gleichgewichtskonstante einzusetzen und man erhalt:

K = zM^y=NLV

(zA=NLV)(zBC=NLV)e^;E0y=kT (1.22) Die Zustandssumme des Ubergangszustands ist gegeben alszM^y =ztr^y zrot^y z^y_vibz_el^y. Der aktivierte Komplex zeichnet sich dadurch aus, da die Zustandssumme der Vibration geschrieben werden kann als

z^y_vib =z_vib^y0 zrc; (1.23)

wobei zrc die Zustandssumme fur die Bewegung des aktivierten Komplexes entlang der Reaktionskoordinate und z_vib^y0 das Produkt uber (3N ^;6) Schwingungsmoden bei linearen Molekulen oder (3N ^; 7) Schwingungsmoden bei sonstigen Molekulen ist.

Die Gesamtzustandssumme des Ubergangszustands kann daher auch alszM^y =z_M ^yzrc

ausgedruckt werden. Die Bewegung des aktivierten Komplexes entlang der Reaktion- koordinate kann als als Translation in einem eindimensionalen Kasten der Lange beschrieben werden.

zrc=2m^ykT¹⁼²=h (1.24)

Fur die Gleichgewichtskonstante ergibt sich daher:

K =

z_M^y=NLV2m^ykT¹⁼²=h

(zA=NLV)(zBC=NLV) e^;E0y=kT (1.25) Nach Einsetzen dieses Ausdrucks in die Gleichung (1:12) fur die Geschwindigkeitskon- stante k^R, erhalt man:

k^R = kT h

z_M ^y=NLV

(zA=NLV)(zBC=NLV) e^;Ey0=kT (1.26) Mit diesem Ausdruck ist es nun moglich, die Geschwindigkeitskonstante der oben genannten Elementarreaktion zu bestimmen. Das Ziel, etwas uber die Temperatu- rabhangigkeit einer Reaktion aussagen zu konnen, wurde mit der Herleitung dieser Formel erreicht. Die Geschwindigkeitskonstante lat sich berechnen. Wenn man die Massen vonA;BC undM^y (zur Bestimmung der Tragheitsmomente) und ihre Gleich- gewichtsgeometrien (zur Ermittlung der Schwingungsfrequenzen) kennt und Informa- tionen uber die Entartungen der Grundzustande hat.

Mit den eingefuhrten Gleichungen, besteht nun die Moglichkeit eine Brucke zur Ther- modynamik zu schlagen. Wenn eine Pseudo-Gleichgewichtskonstante K^ydeniert wird als:

K^y=

z_M^y=NLV

(zA=NLV)(zBC=NLV) e^;E0y=kT; (1.27) die sich dadurch auszeichnet, da die Zustandssumme zrc des aktivierten Komplexes vernachlassigt wurde, ist es moglich, die Freie Standard-Aktivierungsenthalpie G^y

G^y =^;RT lnK^y (1.28)

sowie Standard-Aktivierungsenthalpie H^y und Standard-Aktivierungsentropie S^y

G^y = H^y;TS^y (1.29)

anzugeben. Wenn diese Gleichungen nun in die Formel fur die Geschwindigkeitskon- stante (1:26) eingesetzt werden, wird die Abhangigkeit der Geschwindigkeitskonstanten von der Temperatur ersichtlich.

k^R = kT

h e^;Gy=RT = kT

h e^;Hy=RTe^Sy=R (1.30)

Ein Vergleich mit der Arrhenius-Gleichung

kR=A(T)e^EA=RT (1.31)

zeigt, da die Aktivierungsenergie EA der Standard-Aktivierungsenthalpie entspricht und der praexponentielle FaktorAgleich ^kT_h e^Sy=Rist. Es ist nun moglich, eine Verbin- dung zur klassischen Stotheorie herzustellen; dort wurde der FaktorA(T) als Stozahl deniert. Bei einem Sto nahern sich die Teilchen und verringern damit die Unordnung des Gases. Das heit, ein Sto entspricht einer Entropieerniedrigung und S^yhat einen negativen Wert. Die Entropieerniedrigung ist besonders bei solchen Stoen stark nega- tiv, bei denen die Stopartner sich in einer wohldenierten gegenseitigen Orientierung annahern. Der praexponentielle FaktorAhat dann einen sehr kleinen Wert. Diese Aus- wirkungen konnen in der Stotheorie durch einen sterischen Faktor P berucksichtigt werden, der in den den FaktorAmit einbezogen wird.

1.2 Vergleich der Ubergangszustande aus Theorie und Rechnung

An dieser Stelle kommt die Frage auf, inwieweit die im Rahmen dieser Arbeit be- rechneten Ubergangszustande mit denen aus der Theorie des aktivierten Komplexes

ubereinstimmen.

Um die Ubergangsstruktur zu bestimmen, wird ein Sattelpunkt erster Ordung auf der Potentialhyperache gesucht, der zwei Energieminima voneinander trennt. Dabei wird i.a. der Weg minimaler Energie gewahlt. Diese Ubergangsstruktur entspricht nicht dem

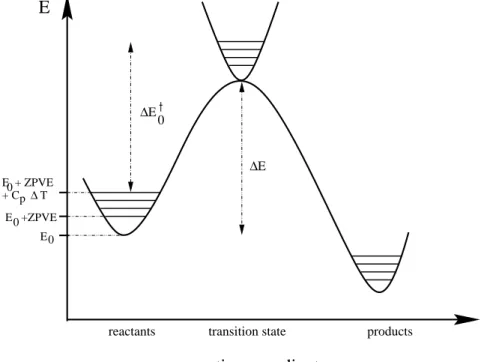
Ubergangszustand aus der Eyring-Theorie, denn der Ubergangszustand nach Eyring ist ein Maximum an Freier Enthalpie auf der Reaktionskoordinate, der zwei Freie- Enthalpie-Minima voneinander trennt. Um den Zusammenhang zwischen Energie und Freier Enthalpie darzustellen, ist es notig, die Enthalpie H zu denieren.[9]

H = U +pV = U +nRT (1.32)

U ist in diesem Fall die folgende Summe:

U =^X(E + ZPV E+CvT) (1.33) Mit den Methoden, die im folgenden Kapitel beschrieben werden, ist es moglich, sta- tionare Punkte auf einer \schwingungslosen" Energiehyperache zu lokalisieren. Um die Innere Energie U zu bestimmen, ist es daher notig, zu der berechneten potenti- ellen Energie die Nullpunktsschwingungsenergie ZPV E = ^12P_ihi, sowie die Energie CvT zu addieren. Durch die Addition der Energie CvT wird beschrieben, da sich die Molekule in angeregten Zustanden benden konnen. Die Berechnung dieses Terms gelingt wieder uber Zustandssummen. Man erhalt fur ein ideales Gas:

Cv;tr = 32nR (1.34)

Cv;rot =

( nR lineare Molekule

3=2nR nicht^;lineare Molekule (1.35)

Cv;el = 0 (1.36)

Cv;vib = ^3NX;6

s⁼¹ nR hs

kT

!

2 e^hs=kT

(e^{hs=kT ;}1)² (1.37)

(1.38) Um die Innere Energie naherungsweise zu berechnen, ist es also notig, die Schwingungs- frequenzen zu berechnen. Das gelingt in der Naherung des harmonischen Oszillators

uber die Kraftkonstanten einer Bindung. Die Kraftkonstanten sind die zweiten Ablei- tungen der potentiellen Energie bezuglich der Kernkoordinaten.

Um aus diesem Ausdruck fur die Energie die Enthalpie zu berechnen, mu noch der Term nRT zu U hinzuzuaddiert werden, wobei n die Anderung der Anzahl der Molekel wahrend der Reaktion angibt.

E

reactants transition state products

reaction coordinate

+ C T

E 0 +ZPVE E0

p∆ E0 + ZPVE

∆E0

∆E

Abbildung 1.2: Darstellung des Zusammenhangs zwischen der berechneten Gesamt- energie und der Energie aus dem Experiment

mit :

E⁰ = berechnete Energie des Edukts ZPV E = Nullpunktsenergie

Cp = Warmekapazitat (Cp =Cv+nR) EA = Aktivierungsenergie

E^0y= Energiedierenz zwischen den berechneten Energien von Edukt und Ubergangs- zustand

Um von der Enthalpie zur Freien Enthalpie zu kommen, mu bedacht werden, da sich Gvon H um die GroeTS unterscheidet.

G= H^;TS (1.39)

Die Entropie des Molekuls oder des Ubergangszustands wird, genauso wie die Warme- kapazitat, uber Zustandssummen bestimmt. Fur ein ideales Gas erhalt man:

Str = 52nR+nRln

2

4(2m)³⁼²

h^{3 (}kT)⁵⁼² p

3

5 (1.40)

Srot = 32nR+nRlnzrot nicht^;lineare Molekule (1.41) Svib = nR^vib;sT e^{;vib;s1=T ;}1^;nRln1^;e^;vib;s=T (1.42)

Sel = nRlngel;⁰ (1.43)

(1.44)

Inwieweit die berechnete Ubergangsstruktur und der Ubergangszustand nach Eyring

ubereinstimmen, bestimmt mageblich die Entropie. Wenn eine Reaktion eine rela- tiv hohe Energiebarriere hat und sich der Entropieterm wahrend der Reaktion wenig

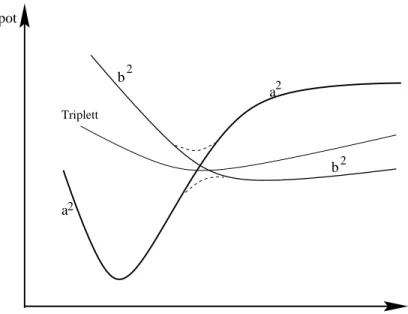
andert, entspricht der Ubergangszustand nach Eyring ungefahr dem Maximum der potentiellen Gesamtenergie der Reaktion. Die beiden gefundenen Strukturen werden dann im wesentlichen ubereinstimmen. Fur eine Reaktion mit einer relativ niedrigen Barriere und einem sich stark andernden Entropieterm kann sich die Geometrie des berechneten Ubergangszustands sehr stark von der theoretischen unterscheiden. [9]

Abbildung 1.3: Einu des Entropieterms auf die freie Enthalpie (aus [9]) Um die Anderung der Entropie zu bestimmen, kann eine naherungsweise Berechnung der Entropie mit dem Gaussian-Programmpaket durchgefuhrt werden, in der die o.g.

Zusammenhange genutzt werden.

Kapitel 2

Angewandte Methoden

In diesem Kapitel sollen die grundlegenden Methoden vorgestellt werden, die benutzt wurden, um Aussagen zur Reaktion von TADB mit Ammoniak zu machen. Im er- sten Teilbereich werden die SCF-Methode, die semiempirischen Methoden AM1 und MNDO, die Dichtefunktionaltheorie sowie die Storungstheorie naher erlautert. Mit die- sen Methoden ist es moglich, die elektronische Schrodingergleichung fur ein Molekul an einer vorgegebenen Geometrie naherungsweise zu losen. Wenn die elektronische Schrodingergleichung fur verschiedene Kernkoordinaten gelost wird, kann die Potenti- alhyperache ermittelt werden.

Um die Reaktionsenthalpie einer Reaktion zu bestimmen, ist es notig, die Minima und Sattelpunkte auf der Potentialhyperache zu nden. Aus diesem Grund werden im zweiten Teil dieses Kapitels die Methoden vorgestellt, die benutzt wurden, um stati- onare Punkte auf der Energiehyperache zu lokalisieren. Durch die Energieminimierung gelangt man zu den optimierten Geometrien der Molekule, denn je kleiner die Energie eines Molekuls, desto stabiler ist auch seine Geometrie.

2.1 Energiebestimmungen

Zur Bestimmung der Energiewerte der Molekule wurden in dieser Arbeit zwei quan- tenchemische Methoden genutzt, die semiempirischen und die ab-initio-Verfahren. Der Unterschied zwischen den beiden Ansatzen ist folgender. In den ab-initio-Rechnungen werden alle Integrale berechnet, bei den semiempirischen Verfahren dagegen wird die Zahl der zu berechnenden Integrale dadurch reduziert, da ein Teil der Integrale voll- kommen vernachlaigt und ein anderer Teil mittels experimentell oder rechnerisch be- stimmte Parameter naherungsweise ermittelt wird. Diese Verminderung der Anzahl der zu berechnenden Integrale wirkt sich massiv auf den Rechenaufwand aus.

2.1.1 Die SCF-Methode

Die SCF-(Self-Consistent-Field-)Methode, die eng mit den Namen D. Hartree, V. Fock, J.C. Slater, C.C.J. Roothaan und G.G. Hall verknupft ist, [10, 11, 12, 13, 14] bildet eine wesentliche Grundlage fur alle im Rahmen dieser Arbeit genutzten Verfahren und soll daher in ihren Grundzugen beschrieben werden.

13

Um die Energie eines Molekuls zu berechnen, mu man die Schrodingergleichung losen.

H^ (x¹xn;X¹Xk) = E (x¹xn;X¹Xk) (2.1) Fur die hier zu behandelnden Falle genugt es, die nichtrelativistische, zeitunabhangige Schrodingergleichung zu betrachten, weil die Zustande stationar sind und die Systeme keine Atome mit hoher Ordnungszahl enthalten, bei denen relativistische Korrektu- ren notwendig waren. Auerdem wird die Gultigkeit der Born-Oppenheimer-Naherung angenommen.[15] Die Born-Oppenheimer-Naherung setzt voraus, da sich die im Ver- gleich zu den schnellen Elektronen sehr viel schwereren Kerne langsam bewegen und die Bewegung der Elektronen nicht an die der Kerne gekoppelt ist. Die Elektronen eines Molekuls bewegen sich demnach im Feld der xierten Kerne. Unter diesen Vorausset- zungen kann ein Separationsansatz fur die Schrodingergleichung angewandt werden:

(x¹xn;X¹Xk) = el(x¹xn) Kerne(X¹Xk) (2.2)

H^ = ^Hel+ ^HKerne (2.3)

Die Schrodinger-Gleichung fur festgelegte Kernkoordinaten ist losbar. Der elektronische Hamilton-Operator hat folgende Gestalt:

H^ = ^X

^;

12^r2;

X

A

ZA

rA

!

+^X

<

r1 + ^X

A<B

ZAZB

RAB (2.4)

A und B bezeichnen die Kerne, und die Elektronen und Z ist die jeweilige Kernla- dungszahl. Durch den ersten Summanden wird die kinetische Energie der Elektronen beschrieben, mit dem zweiten die attraktive Wechselwirkung zwischen den Kernen und den Elektronen. Die letzten beiden Summanden beschreiben die Abstoung zwischen den Elektronen und zwischen den Kernen. Man kann die ersten beiden Summanden zusammenfassen und erhalt:

H^ = ^X

h+^X

<

r1 +VKerne (2.5)

Ausgangspunkt fur die Herleitung der Hartree-Fock-Gleichungen ist, die Wellenfunkti- on el als Determinante von Spinorbitalen i (Slaterdeterminante) darzustellen. Spi- norbitale sind Einelektronenfunktionen, die neben den drei Raumkoordinaten, auch die Spinkoordinate des jeweiligen Elektrons enthalten.

el(x¹xn) = ^j12nⁱ (2.6)

Die Energie einer Wellenfunktion ist gegeben als Erwartungswert E[ el] des Hamilton- Operators ^H

E[ el] = ^{h elj}H^^j elⁱ

h el^j elⁱ : (2.7)

Die Energie E ist also ein Funktional der Wellenfunktion el und somit auch ein Funktional der Spinorbitale i. Die Herleitung der Hartree-Fock-Gleichungen gelingt

uber die Minimierung des EnergiefunktionalsE[^fi^g] durch Variation der Spinorbitale i

@@i

h el^jH^^j elⁱ

h el^j elⁱ ; (2.8)

mit der Nebenbedingung, da die Spinorbitale orthogonal zueinander sind

hi^jjⁱ=ij: (2.9)

Diese Nebenbedingung wird unter Verwendung von Lagrange-Multiplikatorenab in die Gleichung (2:93) eingefuhrt:

L(x¹xn) = ^{h elj}H^^j elⁱ

h el^j el^{i ;} n

X

a⁼¹ n

X

b⁼¹ab(^ha^jb^i;ab) (2.10) Die Energie wird minimal, wenn die erste Ableitung vonLverschwindet. Nach Diagona- lisierung der Matrix der Lagrangeschen Multiplikatorenab , erhalt man die kanonische Hartree-Fock-Gleichung

F^ i =ii (2.11)

Sie ist eine Eigenwertgleichung mit den Spinorbitalen als Eigenfunktionen und den Energien der Spinorbitale als Eigenwerte. Nach Koopmans Theorem entspricht die Energie¹ der Energie, die benotigt wird um das Elektron aus dem Spinorbital¹ zu entfernen. [16] Der Fock-Operator, der ein eektiver Einelektronenoperator ist, ist wie folgt deniert:

F^ = ^h+ ^G (2.12)

Der erste Term des Fock-Operators, ^h, ist ein echter Einelektronenoperator h^() =^;1

2^r2;

X

A

ZA

rA (2.13)

Mit ihm wird die kinetische Energie der einzelnen Elekronen sowie ihre Anziehung durch die Kerne beschrieben. Der Operator ^G ist wie folgt deniert:

G^ =^X

i Ji^;Ki (2.14)

wobeiJi der Coulomboperator undKi der Austauschoperator ist. Der Coulombopera- tor soll an dieser Stelle dadurch beschrieben werden, da er auf das Spinorbitalj(1) wirkt.

Ji(1)j(1) = ^Z _i (2) 1r¹²i(2)d²j(1) (2.15) Durch ihn wird die potentielle Energie, die aufgrund der \Elektronenverteilung" ^ji^j2

entsteht, beschrieben. Das heit also, da der Operator das eektive Potential eines Elektrons beschreibt, das sich im repulsiven Feld der anderen Elektronen bendet.

Ki(1)j(1) =^Z _i (2) 1r¹²j(2)d²i(1) (2.16)

ist der sog. Austauschoperator, der hier auch beispielhaft auf das Spinorbital j(1) wirkt. Dieser Operator resultiert aus dem Austauschprinzip, was man sehr gut daran sieht, da er, im Vergleich zum Coulomboperator, die Elektronen 1 und 2 rechts von r^;112 austauscht. Bis zu diesem Punkt wurde die Herleitung der Hartree-Fock-Gleichung mit Spinorbitalen durchgefuhrt. Es gibt zwei verschiedene Arten von Spinorbitalen, die restricted- und die unrestricted-Spinorbitale. Bei den restricted-Spinorbitalen ben- den sich die Elektronen mit alpha- und beta-Spin in den gleichen Ortsorbitalen, bei den unrestricted-Spinorbitalen dagegen besetzen die Elektronen mit alpha- und beta- Spin jeweils unterschiedliche Ortsorbitale. Zur weiteren Vereinfachung wird nun die Hartree-Fock-Gleichung fur Spinorbitale durch Integration uber die Spinfunktionen in die Hartree-Fock-Gleichung fur Raumorbitale umgeformt. Dazu werden restricted- Spinorbitale und ein geschloenschaliges System angenommen, so da dienElektronen n=2-Raumorbitale doppelt besetzen. Man erhalt:

F^ = ^h+^Xn=2

i⁼¹2Ji^;Ki (2.17)

Die exakten Losungen der Hartree-Fock-Gleichung, die eine Integro-Dierentialgleichung ist, sind exakte Hartree-Fock Spinorbitale. In der Praxis, und das ist das Problem, ist diese Gleichung nur fur Atome losbar. Eine Naherung die gemacht wird, um die Hartree- Fock Gleichung zu losen ist, die Darstellung der Molekulorbitale als Linearkombination einer endlichen Anzahl von Atomorbitalen. Diese Methode wird als LCAO-Methode (linear combination of atomic orbitals) bezeichnet.

i =^X

ci (2.18)

Durch den LCAO-Ansatz wird die ursprungliche Integro-Dierentialgleichung (2.11) in eine Matrixgleichung uberfuhrt, die sog. Roothaan-Hall-Gleichung.

X

ci

Z (1) ^F (1)(1)d¹ =^1X

ci

Z (1)(1)d¹ (2.19) Durch Einbringen der sog. "Dichtematrix" ist es moglich, die Roothaan-Hall-Gleichung weiter zu vereinfachen. Die Dichtematrix wird erhalten, wenn man in die Denition fur die Ladungsdichte

(r) = 2^N=X2

a ^j i(r)^j2 (2.20)

in Gleichung (2.18) einsetzt. Damit ergibt sich (r) = ^X

P(r)(r) (2.21)

mit

P = 2^N=X2

a cac_a (2.22)

als Dichtematrix. Wenn diese Denition nun in die Roothaan-Hall-Gleichung eingesetzt wird, ergibt sich

F = ^h+^X

P

(^j)^;1

2 (^j) (2.23)

mit

(^j) =^Z (1)(1)r^;112(2)(2) (2.24) Um die Roothaan-Hall-Gleichung moglichst einfach losen zu konnen, sind noch einige Umformungen notig. Sie liefern zum Schlu folgendes Ergebnis:

FC =SCi (2.25)

C ist die Koezientenmatrix, die nach Diagonalisierung die Koezienten ci aus Glei- chung 2.18 als Diagonalelemente enthalt. S ist die Uberlappmatrix mit den Elementen

S =^Z (r)(r)dr (2.26)

Da die Basisfunktionen, die in der LCAO-Naherung benutzt wurden, zwar normiert, aber nicht orthogonal zueinander sind, mu die Uberlappmatrix noch diagonalisiert werden. Dazu wird wie folgt vorgegangen. Man wahlt eine KoezientenmatrixC⁰, die mit der alten Koezientenmatrix in folgendem Zusammenhang steht:

C =S^(;12)C⁰ (2.27)

Einsetzen dieses Ausdrucks fur C in die Roothaan-Gleichung (2:25) liefert:

FS^(;12)C⁰ =SS^;21C⁰i (2.28)

(2.29) Multiplizieren von links mit der adjungierten vonS^(;12), S^(;12)y ergibt:

S^(;12)yFS^(;12)C⁰ =S^(;12)ySS^(;12)C⁰i (2.30) Wenn nun eine neue MatrixF⁰ deniert wird, mit

F⁰ =S^(;12)yFS^(;12) (2.31)

und man beachtet, da

S^(;12)ySS^(;21) = 1; (2.32)

erhalt man die transformierte Roothaan-Hall-Gleichung

F⁰C⁰ =C⁰i (2.33)

An dieser Stelle soll das SCF-Verfahren kurz zu erlautert werden.

1. Das Molekul mit seinen Kernkoordinaten und Ordnungszahlen, sowie der Basis- satz werden gewahlt.

2. Alle benotigten IntegraleS,h und (^j) werden berechnet.

3. Die Uberlappmatrix S wird orthogonalisiert.

4. Eine Annahme fur die Dichtematrix, der sog. initial guessP, wird berechnet.

5. Die Matrix ^G wird aus der Dichtematrix P und den Zweielektronenintegralen berechnet.

6. Die Matrix ^Gund der Einelektronenhamiltonoperator ^h werden zur Fockmatrix kombiniert.

7. Die transformierte Fock-Matrix ^F⁰ wird berechnet.

8. Um die Energien der MO's zu erhalten, wird das Eigenproblem aus Gleichung (2.33) gelost.

9. Die Koezientenmatrix C wird aus C =S^(;12)C⁰ berechnet.

10. Die DichtematrixP wird aus der Koezientenmatrix bestimmt.

11. Nun wird uberpruft, ob die Dichtematrix konvergiert ist, d.h. ob die Dichtema- trix aus 4. mit der aus dem letztem Schritt bis auf einen vorgegebenen Konver- genzschwellwert ubereinstimmt. Wenn keine Konvergenz eingetreten ist, wird mit Schritt 5. fortgefahren.

12. Wenn Konvergenz erreicht wurde, werden aus den erhaltenen Losungen fur C,P und ^F⁰ Energien, Dipolmomente etc. bestimmt

Es wird also ein Basissatz gewahlt, und die Koezientenci bei der LCAO werden durch einen initial guess ermittelt. Der einfachste initial guess, der auch als bare nucleus ap- proachbezeichnet wird, ist eine Nullmatrix fur die DichtematrixP zu wahlen. Aquiva- lent dazu ist es, alle Elektron-Elektron-Wechselwirkungen zu vernachlassigen und den Fock-Operator F als Einelektronenhamiltonoperator ^h zu nahern. Da aber die Mo- lekulorbitale eines N-Elektronensystems vollkommen anders aussehen konnen als die des korrespondierenden \Einelektronenmolekuls", konvergiert ein SCF mit dieser Wahl von Startorbitalen haug nicht. Eine andere Moglichkeit fur den initial guess besteht darin, eine extended-Huckelrechnung fur das jeweilige Molekul durchzufuhren. Da auch hierbei die Zweielektronenintegrale vernachlassigt werden, konnen sehr schnell genaher- te Orbitale berechnet werden. Aus den so erhaltenen Huckelorbitalen wird eine erste Dichtematrix bestimmt, aus der dann die transformierte Fock-Matrix F⁰ berechnet werden kann.

Der initial guess der Dichtematrix, der im Gaussian-Programmpaket gemacht wird, hangt von der angewandten Methode und von den Elementen des betrachteten Systems ab und ist entweder eine INDO intermediate neglect of dierential overlap-, CNDO complete neglect of dierential overlap oder eine extended-Huckelrechnung.

Im Turbomole wird die erste Dichtematrix ebenfalls dadurch erhalten, da eine extended- Huckelrechnung durchgefuhrt wird.

Ein Nachteil der SCF-Methode besteht darin, da die Korrelation von Elektronen nicht berucksichtigt wird. Die sog. Elektronenkorrelationsenergie, die als Dierenz zwischen dem exakten Eigenwert eines feldfreien nichtrelativistischen Hamiltonoperators und dem Erwartungswert der Hartree-Fock-Naherung deniert ist, beschreibt den Fehler, der durch die Vernachlaigung der Elektronenkorrelation entsteht. Dieser Korrelati- onsfehler kann dadurch erklart werden, da in der Hartree-Fock-Methode die Elektron- Elektron-Wechselwirkung durch ein gemitteltes Potential beschrieben wird, was nicht

der Realitat entspricht. Elektronen mit gleichem Spin sind zwar durch das Pauli-Prinzip korreliert, nicht aber Elektronen mit unterschiedlichen Spins. Aus Erfahrung kann man sagen, da SCF-Rechnungen mit einem kleinen Basissatz zu lange und solche in einer groen Basis, mit der man nahe an das Hartree-Fock-Limit kommt, zu kurze Bindun- gen liefern. In der Praxis verwendet man daher mittelgroe Basissatze, mit denen man aufgrund von Fehlerkompensation zu guten Ergebnissen fur Bindungslangen kommt.

2.1.2 Die semiempirischen Methoden MNDO und AM1

Mit den semiempirischen Verfahren sollte erreicht werden, chemische Fragestellun- gen mit weniger Rechenaufwand zu losen als mit den ab-initio-Verfahren und dabei trotzdem Korrelationseekte zu berucksichtigen. MNDO (Modied Neglect of Diato- mic Overlap) [17] und AM1 (Austin Model 1) [18, 19, 20] sind semiempirische Metho- den, die als Naherungen zur allgemeinen Roothaan-Hall-Gleichung angesehen werden konnen. Der geringere Rechenaufwand wird dadurch erreicht, da die Integrale, die zum Aufbau der Fock-Matrix benotigt werden, nicht exakt berechnet werden. Sie werden durch parametrisierte Ausdrucke genahert, die an experimentelle Werte angepat wur- den, oder sie werden, wie die Drei- und Vierzentrenintegrale, vollstandig vernachlaigt.

Dreizentrenintegrale treten z.B. bei den Elektron-Kern-Wechselwirkungsintegralen auf, wenn keines der Orbitale sich an dem Kern bendet, auf den sich der Operator bezieht.

Bei den Elektron-Elektron-Wechselwirkungsintegralen treten nicht nur Drei- sondern auch Vierzentrenintegrale auf. Diese Vierzentrenintegrale sind Zweielektronenintegrale (^j), bei denen sich die Spinorbitale an vier verschiedenen Zentren (Kernen) ben- den. Durch die Anpassung der Parameter fur die Integralberechnung an experimentelle Werte wie Dipolmomente, Bildungsenthalpien, Ionisierungsenergien und Geometrien wird erreicht, da relativ gute Ergebnisse fur die Molekule erhalten werden, die den Mo- lekulen ahneln, mit denen die Parametrisierung durchgefuhrt wurde. Im Umkehrschlu wird nun aber auch das Problem der semiempirischen Verfahren sichtbar. Wenn die zu berechnenden Molekule stark von denen abweichen, mit denen die Parametrisierung durchgefuhrt wurde, konnen die Ergebnisse sehr stark von den experimentellen Werten abweichen.

Um zu zeigen, welche Naherungen bei den semiempirischen Methoden gemacht werden, sollen hier die Approximationen von MNDO vorgestellt werden, welches von Dewar und Thiel entwickelt wurde: [17]

Mit der MNDO-Methode ist es grundsatzlich nur moglich, geschlossenschalige Molekule zu berechnen. Bei der Naherung werden nur die Valenzelektronen berucksichtigt. Von den Valenzelektronen wird angenommen, da sie sich in einem eektiven Feld von Ker- nen und Rumpfelektronen bewegen. Daraus ergibt sich, da die Valenzmolekulorbitale i durch eine Linearkombination aus dem minimalen Basissatz der Valenzatomorbitale i dargestellt werden konnen.

Die Diagonalelemente der Fockmatrix in der MNDO-Naherung sehen wie folgt aus, wenn man beachtet, da sich die Atomorbitale und an Atom A und sowie

sich an Atom B benden:

F =U+^X

B V;B+^XA

P[(^j)^; 1

2 (^j)] +^X

B

X

;P(^j) (2.34) U beschreibt die kinetische Energie eines Elektrons in dem Atomorbital an Atom

B. V;B ist die potentiellen Energie, die ein Elektron in durch die Anziehung des Feldes der Rumpfelektronen und Kerne erfahrt. Die Summe dieser beiden Energien ist die Einzentren-Einelektronenenergie. Die Einzentren-Zweielektronenintegrale sind das Coulombintegral (^j) und das Austauschintegral (^j). Fur die Auerdiagonal- terme der Fockmatrix, die aber Orbitale am gleichen Atom betrachten, gilt:

F =^X

B V;B+ 12P[^;(^j) + 3(^j)] +^X

B

X

;P(^j) (2.35) V;B beschreibt hier die Anziehung des Elektrons, das sich in an Atom A be- ndet und durch den core von Kern B angezogen wird. (^j) sind Zweizentren- Zweielektronen-Repulsionsintegrale.

Die Wechselwirkungen zwischen Elektronen in Orbitalen an verschiedenen Atomen wird durch die Auerdiagonalelemente

F =^; 1 2

A

X

B

X

P(^j) (2.36)

beschrieben. ist dabei ein Zweizentren-Einelektronen-Core-Resonanzintegral.

Der Core-Core-Repulsionsterm ist bei MNDO eine Funktion des Elektron-Elektron- Repulsionintegrals.

Damit vereinfachen sich die Roothaan-Hall-Gleichungen fur geschlossenschalige Syste- me

b

X

(F^;iS)ci = 0 (2.37)

zu

m

X

(F^;i)ci = 0; (2.38)

wobei das Kronecker-Delta ist.

Der Unterschied zwischen AM1, das auch von Dewar und Thiel entwickelt wurde, und MNDO besteht darin, da mit AM1 im Gegensatz zu MNDO auch Wasserstobrucken- bindungen beschrieben werden konnen. Das Problem der Wasserstobruckenbindungen wurde ursprunglich dadurch gelost, da der Term in der MNDO-Naherung, der die Core-Core-Repulsion beschreibt, modiziert wurde. Dadurch war es moglich, Korre- lationseekte bei groeren Abstanden der Kerne, besser zu beschreiben. Nachtraglich wurde dann fur AM1 auch die Parametrisierung und die Optimierungstechnik geandert, um die Rechnungen ezienter zu machen.

Ein Problem dieser beiden semiempirischen Methoden ist, da eine Minimalbasis be- nutzt wird, die nur Basisfunktionen fur s- und p-Orbitale enthalt. Polarisationseekte und hypervalente Bindungen von Hauptgruppenelementen konnen daher nicht beschrie- ben werden. Aus diesem Grund erweiterte Thiel die Parametrisierung von MNDO auch aufd-Funktionen. [21, 22] Die sog. MNDO/d-Parametrisierung existiert mittlerweile fur alle Elemente der dritten Periode, auer fur Argon, fur die Elemente der Zink-Gruppe sowie fur Brom un Iod.

2.1.3 Dichtefunktionaltheorie

Mit der Dichtefunktionaltheorie wurde eine Methode zur Energie- und Geometriebes- timmung von Molekulen unter Beachtung der Elektronenkorrelationsenergie entwickelt.

Eine aktuellen Uberblick zu diesem Thema bietet. [23] Sie bildet oftmals eine gute Al- ternative zu korrelierten ab-initio-Methoden, bei geringerem Rechenaufwand.

Die Dichtefunktionaltheorie kann nicht zu den ab-initio-Methoden gezahlt werden, weil das Dichtefunktional empirisch bestimmt wird. Auf der anderen Seite werden hier keine Integrale vernachlassigt wie bei den semiempirischen Methoden, so da doch eher eine Verwandtschaft zu den ab-initio-Methoden besteht. Im folgenden sollen die Grundzuge der Dichtefunktionaltheorie erlautert werden.

Kohn-Hohenberg-Theoreme I und II

Um die Energie eines N-Elektronensystems zu bestimmen, wird die stationare elek- tronische Schrodingergleichung, mit dem Hamiltonoperator (2:6) benutzt. Es ist hier sinnvoll, diesen Operator in einer etwas anderen Form zu schreiben

H^ = ^T + ^Vne+ ^Vee (2.39)

T^=^XN

;

12^r2

(2.40)

V^ne=^;X

X

A

ZA

rA =^X

v(r) (2.41)

T^ ist der Operator der kinetischen Energie, ^Vne der Operator fur die attraktive Wech- selwirkung zwischen Kernen und Elektronen.

V^ee= ^XN

<

r1 (2.42)

ist der Operator fur die Elektron-Elektron-Repulsion.

In der Dichtefunktionaltheorie wird nun ein anderer Ansatz zur Bestimmung der Ener- gie gewahlt als bei der Hartree-Fock-Theorie. Anstatt die Energie uber die Wellen- funktion zu bestimmen, wird die Energie als Funktional der Einelektronendichte(

r

i) deniert. Die Einelektronendichte beschreibt als nicht-negative Funktion die Dichte von Elektronen, sprich ihre Anzahl pro Volumeneinheit. Sie steht in Relation zur Wel- lenfunktion = (x¹;x²;x³;;xN)

(

r

^{1) =NZ j (x1;x2;x3;;x}N)^j2ds¹dx²dxN (2.43) wobei die Koordinatenxi die Raumkoordinatenri und die Spinkoordinatensi des i-ten Elektrons umfassen. Wenn uber den gesamten Raum integriert wird, erhalt man die Anzahl an Elektronen.

Z (

r

^)d

r

^{=N (2.44)}

Zwei Theoreme, die von Kohn und Hohenberg 1964 aufgestellt wurden, [24] sind fur die Dichtefunktionaltheorie von grundlegender Bedeutung:

1. Theorem:

Das externe Potential v(

r

) welches in (2:41) deniert wurde, wird bis auf eine additive Konstante durch die Elektronendichte (

r

) bestimmt.

Das heit, da der Hamiltonoperator dann eindeutig bestimmt ist, wenn das externe Potentialv(

r

) sowie N bekannt sind. N ergibt sich aus der Normierung der Elektronen- dichte in Gleichung (2:44). Durch (

r

) wird also die Grundzustandswellenfunktion eindeutig bestimmt. Aus diesem Grund ist es auch nicht ohne weiteres moglich, mit der DFT elektronisch angeregte Zustande zu berechnen. Zu einem bestimmten Potential v(

r

) ergibt sich damit ein von abhangiges Energiefunktional

E[] =^Z (

r

)v(

r

)d

r

+T [] +Vee[]: (2.45) Dabei fat man T[] und Vee[] zu dem sog. Kohn-Hohenberg-FunktionalFHK[] zu- sammen:

FHK[] =T [] +Vee[] (2.46)

Der Term Vee[], der die Elektron-Elektron-Wechselwirkung beschreibt, enthalt dabei zwei Beitrage. Ein Beitrag beschreibt die klassische Coulombwechselwirkung J[] und der andere die Austausch- und Korrelationswechselwirkung.

2. Theorem:

Mit diesem Theorem ist das Variationsprinzip auch auf die Elektronen- dichte anwendbar.

Die Energie, die aus einer willkurlichen Dichte berechnet wurde, ist also stets groer oder gleich der wahren Grundzustandsenergie:

E⁰ Ev[~] (2.47)

Die Kohn-Sham-Gleichungen

Die Kohn-Hohenberg-Theoreme postulieren, da es moglich ist, uber die Elektronen- dichte die Grundzustandsenergie eines N-Elektronensystems zu berechnen. Sie sagen allerdings nichts uber den Weg der Berechnung aus. Im Jahre 1965 verhalfen Kohn und Sham der Dichtefunktionaltheorie zu einer praktischen Anwendbarkeit auf Atom- und Molekulberechungen. [25]

Ansatz zur Losung des Problems ist die Aufstellung einer Ein-Determinanten-Wellen- funktion fur ein N-Elektronensystem. Wechselwirkungen zwischen den Elektronen wer- den dabei zunachst nicht zugelassen (Index s). Daher besteht nun die Moglichkeit, die kinetische EnergieTsund die Elektronendichte (

r

) exakt zu berechnen. Bei einem nichtwechselwirkenden System werden die BesetzungszahlennifurN Elektronen gleich Eins gesetzt. Fur orthonormierte Orbitale erhalt man im allgemeinen Fall:

Tww =^X

i

Z ni_i ^;1₂^r2id (2.48)