Bachelorarbeit Monte-Carlo-Simulationen an Fe

Monte-Carlo-Simulationen an Fe ₃₀ -Schichtsystemen

Katrin Jahns Fachbereich Physik

4. Juni 2006

Inhaltsverzeichnis

1 Einleitung 3

2 Statistische Physik 5

2.1 Statistische Mechanik . . . 5

2.2 Ubergangswahrscheinlichkeit¨ . . . 5

2.3 Equilibrium . . . 6

2.4 Thermodynamische Observable . . . 7

2.4.1 Innere Energie . . . 7

2.4.2 Freie Energie . . . 7

2.4.3 Magnetisierung . . . 8

2.4.4 Spezifische W¨arme . . . 8

3 Monte-Carlo-Simulation 9 3.1 Allgemeiner Erwartungswert . . . 9

3.2 Importance Sampling . . . 10

3.2.1 Markov-Kette . . . 11

3.2.2 Ergodizit¨at . . . 11

3.2.3 Detailed Balance . . . 12

3.3 Akzeptanzraten . . . 13

3.4 Metropolis - Algorithmus . . . 14

4 Betrachtungen an einem Fe30 - Molek¨ul 17 4.1 Grundlagen . . . 18

4.1.1 Klassisches Heisenberg-Modell . . . 18

4.1.2 Allgemeine Betrachtungen des{Mo₇₂Fe₃₀}-Molek¨uls . . . 19

4.2 Simulationsergebnisse . . . 20

4.2.1 Magnetisierung . . . 20

4.2.2 Innere Energie und Spezifische W¨arme . . . 25

4.3 Zusammenfassung und Ergebnisse . . . 28

5 Betrachtungen an Fe30-Schichtsystemen 28 5.1 Struktur der Fe₃₀-Schichtsysteme . . . 29

5.2 Periodische Randbedingungen . . . 30

5.3 Betrachtungen an Clustern . . . 31

5.3.1 Magnetisierung in Abh¨angigkeit von der Temperatur bei B = 0,1 T . . . 32

5.3.2 Spezifische W¨arme in Abh¨angigkeit von der Temperatur bei B = 0 T . . . 32 5.4 Zusammenfassung und Ergebnisse . . . 34

6 Zusammenfassung und Ausblick 35

7 Abstract 37

A Wechselwirkungsmatrix und Nummerierung der Spins 38

Literatur 40

1 Einleitung

Heutzutage spielen Simulationsverfahren zur Bestimmung von physikalischen Eigenschaften eine wichtige Rolle. Neben der Best¨atigung von experimentellen Messergebnissen dienen sie auch dazu, Messungen in solchen Bereichen zu simu- lieren, die experimentell noch nicht zug¨anglich sind. Außerdem k¨onnen durch Simulationen Kosten- und Zeiteinsparungen erzielt werden, da durch virtuelle Experimente das Verhalten von Systemen charakterisiert und m¨ogliche Messbe- reiche eingeschr¨ankt werden k¨onnen.

Eine der Standartsimulationen ist die sogenannte Monte-Carlo-Methode, auf die in dieser Arbeit auch genauer eingegangen wird. Eigentlich f¨ur die Berechnung von komplizierten Integralen in der Mathematik gedacht, findet sie inzwischen auch Anwendung in der Forschung der modernen Physik. Sie ist eine stocha- stische Simulationsmethode und von daher eng mit der Statistischen Physik verkn¨upft.

Besonders in der Quantenmechanik spielen Simulationen eine sehr große Rol- le. Oftmals ist die Dimension des betrachteten Hilbertraumes eines Spinsystems viel zu groß, um die zugeh¨orige Hamiltonmatrix zu diagonalisieren. Das in dieser Arbeit betrachtete Molek¨ul hat zum Beispiel einen Hilbertraum der Dimension 6³⁰. Auch in naher Zukunft wird es nicht m¨oglich sein, die entsprechende Ha- miltonmatrix zu diagonalisieren. Das Problem liegt darin, dass Berechnungen an Matrizen dieser Gr¨oßenordnung viel mehr Speicherplatz ben¨otigen als mit der zur Verf¨ugung stehenden Hardware realisiert werden kann.

Ein anderer wichtiger Aspekt dieser Arbeit ist die Betrachtung von magneti- schen Molek¨ulen. Bei diesen herrscht eine sehr starke Wechselwirkung inner- halb des Molek¨uls w¨ahrend die Wechselwirkung zwischen einzelnen Molek¨ulen im Vergleich dazu relativ klein ist. Inzwischen ist es gelungen, solche Molek¨ule nach Vorgaben zu synthetisieren und Experimente mit diesen durchzuf¨uhren.

Die Untersuchung solcher Molek¨ule ist aus mehreren Gr¨unden interessant. Auf der einen Seite sind sie von grundlegendem physikalischen Interesse aufgrund ihrer magnetischen Eigenschaften, auf der anderen Seite spielen sie aber auch in Anwendungsbereichen eine wichtige Rolle, wie zum Beispiel bei der Entwick- lung von neuen magnetischen Datentr¨agern.

In dieser Arbeit wird das Molek¨ul {Mo₇₂Fe30} genauer betrachtet. Klassische Behandlungen durch deterministische und stochastische W¨armebadkopplung haben bei diesem Molek¨ul schon sehr gute Ergebnisse erbracht [1]. Nun werden in dieser Arbeit numerische Untersuchungen durchgef¨uhrt.

In Kapitel 2 erfolgt zun¨achst eine kurze Einf¨uhrung in die statistische Physik, wobei lediglich auf einige Aspekte eingegangen wird, die f¨ur die Monte-Carlo- Methode und die in dieser Arbeit durchgef¨uhrten Betrachtungen von Bedeutung

sind. Die Monte-Carlo-Methode wird anschließend in Kapitel 3 genauer un- tersucht. Außerdem wird ein Standartalgorithmus, der sogenannte Metropolis- Algorithmus, vorgestellt.

Anschließend wird die Monte-Carlo-Methode sowohl auf ein{Mo₇₂Fe30}-Molek¨ul (siehe Kapitel4) als auch auf Cluster, die aus mehreren{Mo₇₂Fe₃₀}-Molek¨ulen bestehen (siehe Kapitel5), angewendet. Den Abschluss dieser Arbeit bildet eine kurze Zusammenfassung der Ergebnisse.

2 Statistische Physik

Als erstes werden die Grundlagen der Statistischen Physik vorgestellt welche f¨ur Monte-Carlo-Techniken von grundlegender Bedeutung sind. Daf¨ur erfolgt zun¨achst eine Betrachtung der Statistischen Mechanik (Kapitel 2.1). Im An- schluss daran werden in Kapitel2.4einige Observable eingef¨uhrt, die f¨ur die in dieser Arbeit durchgef¨uhrten Simulationen von Bedeutung sind.

2.1 Statistische Mechanik

In der Statistischen Mechanik werden mikroskopische Systeme beschrieben, die aus einer großen Anzahl an Partikeln, wie etwa Molek¨ulen oder Atomen, beste- hen. Die Statistik liegt darin, dass zumeist eine sehr große Anzahl an Teilchen betrachtet werden muss.

F¨ur diese Arbeit sind ausschließlich Systeme von Interesse, bei denen die Hamil- tonfunktionH des Systems in jedem m¨oglichen Zustandµdie Zustandsenergie E_µ definiert, so dass gilt

E_µ≡H(µ) . (2.1)

Außerdem muss ein thermisches W¨armebad vorliegen, welches die Energie des Systems so lange hebt oder senkt bis sich W¨armebad und System im thermo- dynamischen Gleichgewicht befinden. Die Wechselwirkung zwischen W¨armebad und System ist dabei sehr klein, reicht aber trotzdem aus, das thermodynami- sche Gleichgewicht hervorzurufen.

2.2 Ubergangswahrscheinlichkeit¨

Wenn sich ein System in einem Zustand µ befindet, dann ist die Wahrschein- lichkeit, dass das System innerhalb einer Zeitspannedtvon µin den Zustandν wechselt, gegeben durch

R(µ→ν)dt . (2.2)

Hierbei bezeichnetR(µ→ν) die ¨Ubergangswahrscheinlichkeit f¨ur den Wechsel von µnachν. F¨ur die meisten realen Systeme ist diese ¨Ubergangsrate

zeitunabh¨angig, darum wird sie auch im weiteren Verlauf dieser Arbeit als zei- tunabh¨angig angenommen [2].

Die Wahrscheinlichkeit, dass sich ein System zu einem bestimmten Zeitpunktt im Zustandµ befindet, wird wµ(t) genannt. Betrachtet man nun die zeitliche Entwicklung des Systems, dann gilt der Zusamenhang

dw_µ(t) dt =X

ν

[wν(t)R(ν →µ)−wµ(t)R(µ→ν)] . (2.3)

wν(t)R(ν→µ) stellt dabei die ¨Ubergangswahrscheinlichkeit dar, mit der von einem Zustandνin den Zustandµgewechselt wird.wµ(t)R(µ→ν) beschreibt die ¨Ubergangswahrscheinlichkeit, mit welcher der Zustandµverlassen wird. Die Summe der einzelnen Wahrscheinlichkeiten muß genau gleich Eins sein:

X

µ

wµ(t) = 1 . (2.4)

Dies bedeutet, dass sich das System zu jedem Zeitpunkt in irgend einem Zu- stand befinden muß.

Nach [3] lassen sich aus den wµ(t) allgemeine makroskopische Eigenschaften des vorliegenden Systems ermitteln. F¨ur den Erwartungswert der Observablen Q im Zustandµgilt der Zusammenhang

hQi=X

µ

Qµwµ(t) . (2.5)

Nach Festlegung derwµ(t) und der Zust¨andeQµ k¨onnen nun die Erwartungs- wertehQi bestimmt werden.

2.3 Equilibrium

Der Begriff des Equilibriums ist ein zentraler Bestandteil dieser Arbeit. Be- findet sich ein System im Equilibrium, dann ist es ausgeglichen. In Gleichung (2.3) sind dann beide Translationsraten gleich, so dass allewµkonstant bleiben.

Das System erf¨ahrt nun keine St¨orungen mehr, die es aus dem Gleichgewicht werfen. In dieser Arbeit wird von Systemen ausgegangen, die das Equilibrium nicht mehr verlassen, wenn sie es einmal erreicht haben.

Befindet sich das System im Gleichgewicht, dann gilt f¨ur die Besetzungswahr- scheinlichkeitpµ eines Zustandes der Zusammenhang

pµ= lim

t→∞wµ(t) . (2.6)

F¨ur ein System, welches sich im thermodynamischen Gleichgewicht mit seinem W¨armebad befindet, gilt f¨ur die Besetzungswahrscheinlichkeit die Boltzmann- Statistik mit

pµ= 1

Ze−E_µ/k_BT , (2.7)

wobeiE_µdie Energie des Systems im Zustandµ,k_Bdie Boltzmann-Konstante, T die Temperatur des W¨armebades und Z die Zustandssumme ist. Der Term 1/k_BT wird oftmals auchβ genannt.

Die ZustandssummeZ ist definiert zu Z=X

µ

e−E_µ/k_BT =X

µ

e−βE_µ (2.8)

und spielt bei der Herleitung einiger Observablen eine wichtige Rolle.

Unter Einbeziehung der Boltzmann-Verteilung und der Definition der Zustands- summe l¨aßt sich Gleichung (2.5) schreiben als

hQi=X

µ

Qµwµ(t) = 1 Z

X

µ

Qµe−βE_µ . (2.9)

2.4 Thermodynamische Observable

Die Zustandssumme nach Gleichung (2.8) ist der Ausgangspunkt f¨ur die Be- trachtung einiger Observablen. Im Folgenden wird auf die Innere Energie, die Magnetisierung und die Spezifische W¨arme n¨aher eingegangen. F¨ur diese Obser- vable werden sp¨ater Monte-Carlo-Simulationen durchgef¨uhrt. W¨ahrend der Si- mulationen wird angenommen, dass die Systeme an ein thermisches W¨armebad gekoppelt sind. Des Weiteren werden sowohl die Teilchenzahl N als auch das VolumenV des Systems als konstant angenommen. Das zugeh¨orige statistische Ensemble ist die Kanonische Gesamtheit.

2.4.1 Innere Energie

In Kapitel2.1wurde eingef¨uhrt, dass die Definition der Zustandsfunktion ¨uber die zugeh¨orige HamiltonfunktionHerfolgt (siehe Gleichung (2.1)). In der Ther- modynamik wird die mittlere EnergiehEi als innere EnergieU bezeichnet und ist definiert zu

U = 1 Z

X

µ

Eµe−βE_µ . (2.10)

Des Weiteren ist U nach Gleichung (2.8) als Ableitung des nat¨urlichen Loga- rithmus der Zustandssumme darstellbar:

U =−1 Z

∂lnZ

∂β (2.11)

Nach Gleichung (2.1) folgt f¨ur die innere Energie

U =hEi=hHi . (2.12)

2.4.2 Freie Energie

Die spezifische W¨arme C ist die Ableitung der inneren Energie nach der Tem- peraturT und l¨asst sich somit schreiben als

C= ∂U

∂T =kBβ²∂U

∂β =kBβ²∂²lnZ

∂β² . (2.13)

Des weiteren besteht zwischenC und der EntropieS der folgende Zusammen- hang:

C=T∂S

∂T =β∂S

∂β (2.14)

F¨ur die Entropie erh¨alt man nach Gleichsetzen von (2.13) und (2.14) und Inte- gration nachβ den folgenden Ausdruck:

S=−k_Bβ∂lnZ

∂β +k_BlnZ (2.15)

Uber die Gleichungen (2.11) und (2.14) kann nun die freie Energie¨ F definiert werden:

F =U −T S=−k_BlnZ (2.16)

2.4.3 Magnetisierung

Das magnetische Moment pro Volumeneinheit in einem Stoff wird als Magne- tisierung M_µ eines Systems im Zustand µ bezeichnet. Hergeleitet wird sie aus der potentiellen Energie eines magnetischen Momentsµin einem externen Feld, gegeben durchµ·B:

(M_µ)_j =−∂E_µ

∂Bj

. (2.17)

B_j bezeichnet hier die Komponente des B-Feldes in j-Richtung. Betrachtet man o.B.d.A. das Magnetfeld in z-Richtung mitB=B0·ez, ergibt sich f¨ur die Magnetisierung der Term

Mµ=−∂E_µ

∂Bz

. (2.18)

Nach Gleichung (2.9) ergibt sich die mittlere MagnetisierunghMi zu hMi= 1

Z X

µ

Mµe−βE_µ . (2.19)

2.4.4 Spezifische W¨arme

Die Spezifische W¨arme C ist ein Maß f¨ur die ¨Anderung von U und somit f¨ur die im System auftretenden Fluktuationen. Nach Gleichung (2.13) l¨asst sichC in Abh¨angigkeit der Varianz vonhEi schreiben zu

C =kBβ²∂²lnZ

∂β² =kBβ² ∂

∂β 1

Z

∂Z

∂β

=kBβ²

"

1 Z

∂²Z

∂β² − 1 Z²

∂Z

∂β 2#

.

(2.20) Hierbei beschreibt

"

1 Z

∂²Z

∂β² − 1 Z²

∂Z

∂β 2#

die Varianz inE.

Betrachtet man wieder Gleichung (2.9), dann kann der Zusammenhang E²

= 1 Z

X

µ

E_µ²e−βE_µ = 1 Z

∂²Z

∂β² (2.21)

f¨ur E²

aufgestellt werden. Somit kann C als Varianz der mittleren Energie dargestellt werden:

C=kBβ²

E²

− hEi²

. (2.22)

3 Monte-Carlo-Simulation

3.1 Allgemeiner Erwartungswert

Das Hauptziel bei thermodynamischen Monte-Carlo-Simulationen ist die Be- stimmung des ErwartungswerteshQieiner ObservableQ, wie zum Beispiel der Magnetisierung. Wie in Kapitel2.1schon beschrieben wurde, geschieht dieses, indem man ¨uber alle Zust¨ande µ des Systems summiert und jeden einzelnen Wert mit seiner Wahrscheinlichkeit gem¨aß der Boltzmann-Verteilung wichtet:

hQi= P

µQ_µe−βE_µ P

µe−βE_µ (3.1)

Allerdings ist dieses so nur in kleineren Systemen anwendbar, da Speicherkapa- zit¨at und Rechnerleistung leider nur endlich sind. Bei gr¨oßeren Systemen erfolgt eine Mittelung ¨uber einige ausgew¨ahlte Zust¨ande, wobei kleinere Ungenauigkei- ten hier in Kauf genommen werden.

Bei Monte-Carlo-Simulationen wird zun¨achst ein Satz an Zust¨anden ausgew¨ahlt.

Diese unterliegen einer Wahrscheinlichkeitsverteilung pµ (siehe Kapitel 3.2).

Betrachtet man M Zust¨ande µ1, ..., µ_M, so l¨asst sich der Erwartungswert Q_M bestimmen zu

QM = PM

i=1Qµip⁻¹_µie−βE_µi P_M

j=1p⁻¹µje−βE_µj . (3.2)

Entspricht die Anzahl M der betrachteten Zust¨ande genau der Anzahl der Zust¨ande des Systems, dann istQM =hQi.

In der Praxis tritt nun allerdings das Problem auf, dass bei der Betrachtung von S¨atzen an Zust¨anden gewaltige Dimensionen auftreten. Selbst sehr schnel- le Rechner brauchen oft Tage, um f¨ur solche Systeme Berechnungen durch- zuf¨uhren.

Betrachtet man zum Beispiel ein kleines, dreidimensionales kubisches System mit 10×10×10 Spins, dann h¨atte das System eine Dimension von 2¹⁰⁰⁰ ∼= 10³⁰⁰ - davon k¨onnten bei Simulationen nur etwa 10⁸ Zust¨ande ber¨ucksichtigt werden.

Trotz dieses scheinbar enormen Verlustes an Informationen liefern Simulationen sehr gute Ergebnisse.

Der Grund daf¨ur ist, dass die Summen aus Gleichung (3.2) von einigen wenigen diskreten Zust¨anden dominiert werden k¨onnen. Dieses tritt vor allem bei klei- nen Temperaturen auf. Hier reicht die vorhandene thermische Energie nicht aus,

das System in h¨ohere angeregte Zust¨ande zu versetzen. Somit befindet sich das System entweder im Grundzustand oder in den ersten angeregten Zust¨anden.

Wenn es nun bei der Berechnung vonQM m¨oglich ist, diese dominanten Zust¨ande zu identifizieren, dann wird das Ergebnis sehr nahe an dem wahren Erwartungs- wert liegen.

Ein solcher dominanter Zustand wird alsimportant state bezeichnet. Den ent- sprechenden Algorithmus, der vorwiegend solche Zust¨ande betrachtet, nennt manImportance Sampling.

3.2 Importance Sampling

Der Erwartungswert stellt die Mittelung ¨uber alle Zust¨ande eines Systems dar, die w¨ahrend einer Messung auftreten. Wie beschrieben, ist es aber meist aus technischen Gr¨unden nicht m¨oglich, alle Zust¨ande eines Systems zu ber¨uck- sichtigen. Allerdings kann davon ausgegangen werden, dass w¨ahrend der Dauer einer Messung auch nicht alle m¨oglichen Zust¨ande durchlaufen werden. Letztlich wird der Erwartungswert von nur wenigen, abereffektiven Zust¨anden bestimmt.

Unter Effektivit¨at wird hier verstanden, dass der Zustand relativ oft eingenom- men wird, also ein

important state ist. Die Selektion solcher effektiven Zust¨ande nennt man Im- portance sampling.

Um dieses zu erreichen, generiert man die Zust¨ande mit ihren zugeh¨origen Boltzmann-Wahrscheinlichkeiten. Wenn man nun ¨uber einen Zeitraum mittelt, dann treten dieimportant states gem¨aß ihrer Boltzmann-Gewichtung

pµ= 1

Ze−βE_µ (3.3)

auf. Mit dieser Definition der Wahrscheinlichkeitsverteilungpµvereinfacht sich Gleichung (3.2) zu

QM = 1 M

M

X

i=1

Qµi . (3.4)

Bemerkenswert ist, dass die Boltzmann-Gewichtung in dieser Definition nicht mehr auftaucht.

F¨ur Systeme, die die meiste Zeit in einigen wenigen Zust¨anden verharren, l¨asst sich Gleichung (3.4) sehr gut anwenden. Diese Zust¨ande entsprechen n¨amlich ge- nau den Zust¨anden, die nach der Boltzmann-Verteilung am h¨aufigsten vorkom- men. Des weiteren entspricht die Frequenz, mit der diese Zust¨ande ausgew¨ahlt werden, genau der Zeit, die das reale System in diesen Zust¨anden verharren w¨urde.

Die Generierung dieser Zust¨ande erfolgt nach einem Algorithmus, der im n¨achsten Kapitel genauer erl¨autert wird.

3.2.1 Markov-Kette

Einer der wichtigsten Komponenten der Monte-Carlo-Simulation ist die Ge- nerierung von Zust¨anden gem¨aß einer vorgegebenen Wahrscheinlichkeitsvertei- lung, der Boltzmann-Verteilung. Allerdings reicht es nicht, Zust¨ande zu generie- ren, die proportional zu e−βE_µ sind, da so keine Selektion von einigen effekti- ven Zust¨anden statt finden w¨urde und man somit wieder nahezu alle Zust¨ande betrachtet. Die Wahrscheinlichlichkeit des Auftretens eines Zustandes w¨are so gering, dass sich keine dominanten Zust¨ande herausbilden w¨urden.

Statt dessen erfolgt die Generierung der Zust¨ande bei Monte-Carlo-Simulationen durch einenMarkov-Prozess. Dieser generiert zufallsbasiert aus einem Zustand µeinen Zustandν. Hierbei ist zu beachten, dassµnicht immer in den gleichen Zustandν ¨ubergeht da die Zust¨ande zuf¨allig erzeugt werden.

Die Wahrscheinlichkeit, dass µ in den Zustand ν ubergeht, bezeichnet man¨ als ¨UbergangswahrscheinlichkeitP(µ→ν). Damit tats¨achlich die Generierung neuer Zust¨ande statt findet, m¨ussen drei grundlegende Kriterien erf¨ullt sein:

1. Die ¨Ubergangswahrscheinlichkeiten d¨urfen nicht zeitlich variieren.

2. Die ¨Ubergangswahrscheinlichkeiten m¨ussen unabh¨angig von allen Zust¨anden außer µ undν sein.

3. Die Bedingung X

ν

P(µ→ν) = 1 (3.5)

muss erf¨ullt sein, da der Prozess immer einen neuen Zustand generiert.

Hierbei kann das System auch im alten Zustand verharren.

Wenn man mehrere Markov-Prozesse iterativ aneinanderreiht, dann erh¨alt man die sogenannte Markov-Kette. Diese wird bei Monte-Carlo-Simulationen ver- wendet, um Zust¨ande gem¨aß einer spezifizierten Verteilung zu generieren.

Im weiteren Verlauf dieser Arbeit werden mit Hilfe der Markov-Kette Zust¨ande generiert, die nach einer gewissen Zeit der Boltzmann-Verteilung unterliegen und sich somit im Equilibrium befinden.

Im weiteren werden nun zwei Bedingungen behandelt, die f¨ur das zu simulieren- de System zwangsweise erf¨ullt sein m¨ussen. Dieses sind zum einen die Forderung derErgodizit¨at und zum anderen die detailed-balance-Bedingung.

3.2.2 Ergodizit¨at

Ergodizit¨at erfordert, dass aus jedem beliebigen Zustand µ der Zustand ν ir- gendwie erreicht werden kann. Dabei ist die Anzahl der Zwischenschritte nicht

von Bedeutung. Wichtig ist nur, dass sich das System irgendwann im Zustand ν befindet. Ein solches System bezeichnet man dann alsergodisch.

Betrachten wir nun ein System: Jeder Zustand des Systemsν ist entsprechend seiner Boltzmann-Wahrscheinlichkeitpν gewichtet, die von Null verschieden ist.

Angenommen, es existiert ein Zustandµ, von dem aus der Zustand ν niemals erreicht werden kann, unabh¨angig davon wie lange man wartet oder ¨uber wel- che Zwischenschritte man geht. Somit ist das System nicht ergodisch wenn es sich irgendwann im Zustandµbefindet. Die Wahrscheinlichkeit, dassνerreicht wird, w¨are n¨amlich in diesesm Fall Null und nicht, wie gefordert,pν.

F¨ur Systeme, die durch Monte-Carlo-Simulationen untersucht werden sollen, muss Ergodizit¨at gegeben sein. Dieses bedeutet nicht, dass zwischen Zust¨anden die ¨Ubergangswahrscheinlichkeit zwangsweise ungleich Null sein muss. Relevant ist nur, dass mindestens ein m¨oglicher Weg existiert, um vom Zustand ν zum Zustandµ zu gelangen.

3.2.3 Detailed Balance

Diedetailed-balance-Bedingungist daf¨ur verantwortlich, dass die von der Markov- Kette generierten Zust¨ande gem¨aß der Boltzmann-Verteilung gewichtet sind.

Ist das Equilibrium erreicht, dann muss die Wahrscheinlichkeit f¨ur einen Wech- sel in einen neuen Zustand und das Verlassen eines Zustandes gleich sein:

X

ν

p_µP(µ→ν) =X

ν

p_νP(ν →µ) (3.6)

Unter Ber¨ucksichtigung der Gleichung (3.5) folgt:

pµ=X

ν

pνP(ν →µ) (3.7)

Allerdings ist diese Definition noch nicht ausreichend. Sie gew¨ahrleistet noch nicht, dass die Wahrscheinlichkeitsverteilung gem¨aß Gleichung (3.7) aus jedem Zustand des Systems heraus generiert werden kann. Die M¨oglichkeit der Heraus- bildung eines dynamischen Equilibriums, in dem sich die Wahrscheinlichkeits- verteilung innerhalb einiger fester Werte ver¨andert, ist durch diese Definition nicht ausgeschlossen.¹

Um dieses Problem zu l¨osen, f¨uhrt man die detailed-balance-Bedingung ein.

Diese ist definiert zu

p_µP(µ→ν) =p_νP(ν →µ) . (3.8)

Diese Bedingung erf¨ullt ebenfalls Gleichung (3.6).² Sie besagt, dass das Sy- stem durchschnittlich genau so oft von ν nach µ wie von µ nach ν wechselt.

1Eine ausf¨uhrliche Herleitung dieses Sachverhaltes ist in [2] nachzulesen.

2Uberpr¨¨ ufung: Summierung von Gleichung (3.8) auf beiden Seiten ¨uberν.

Dynamische Ver¨anderungen der Wahrscheinlichkeiten der Zust¨ande sind somit ausgeschlossen, das dynamische Equilibrium kann nicht auftreten.

Um nun Zust¨ande im Equilibrium zu generieren, m¨ussen lediglich die Wahr- scheinlichkeiten an Gleichung 3.8 angepasst werden. Die Zust¨ande sollen gem¨aß der Boltzmann-Statistik gewichtet werden, darum werden die Wahrscheinlich- keiten gem¨aß Gleichung (3.3) gew¨ahlt. Ber¨ucksichtigt man dieses, dann l¨asst sich Gleichung (3.8) umformen zu

P(µ→ν) P(ν →µ) = p_ν

p_µ = e−β(E_ν−E_µ) . (3.9)

Nach einer gen¨ugend großen Wartezeit im Equilibrium wird die Markov-Kette nun unter Forderung von Ergodizit¨at und detailed balance Zust¨ande produzie- ren, die der Boltzmann-Verteilung entsprechen.

3.3 Akzeptanzraten

Wenn nun ein Satz an ¨Ubergangswahrscheinlichkeiten P(µ→ν) gegeben ist, dann ist es problemlos m¨oglich, mit Hilfe der Markov-Kette Zust¨ande gem¨aß der Boltzmann-Verteilung zu generieren. Allerdings ist noch unklar, wie der Markov-Prozess genau gew¨ahlt werden muss. Da sich reale Systeme sehr oft stark von idealen Systemen unterscheiden ist es oftmals nicht sofort offensicht- lich ob Algorithmen wie etwa der Metropolis-Algorithmus (siehe Kapitel 3.4) zu physikalisch sinnvollen Ergebnissen f¨uhren.

Allerdings stellt sich heraus, dass jeder beliebige Algorithmus zur Erzeugung von Zust¨anden unter gewissen Umst¨anden gew¨ahlt werden kann. Hierzu wird der Begriff derAkzeptanzrate(auchacceptance ratio) eingef¨uhrt. Die Idee dahin- ter ist, die ¨Ubergangswahrscheinlichkeit in zwei Teile aufzuspalten. P(µ→ν) l¨asst sich somit schreiben als

P(µ→ν) =g(µ→ν)A(µ→ν) . (3.10)

g(µ→ν) stellt hier die Wahrscheinlichkeit dar, dass der Markov-Prozess aus dem Startzustand µ den Zustand ν generiert. Die Akzeptanzrate ist durch A(µ→ν) gegeben. Sie kann frei zwischen Null und Eins gew¨ahlt werden. Somit wird immer nur f¨ur einen Bruchteil aller F¨alle in den neuen Zustand gewech- selt. Die Wahl der Null ist ¨aquivalent zu der Formulierung P(µ→ν) = 1, das System w¨urde f¨ur alle Zeiten im Zustandµverharren.

Durch die Definition der Akzeptanzrate kanng(µ→ν) nun v¨ollig frei gew¨ahlt werden. Nach Gleichung (3.9) muss nur der Quotient der ¨Ubergangswahrschein- lichkeiten einer Vorgabe gen¨ugen. Demnach ergibt sich f¨ur den Quotienten der Ubergangswahrscheinlichkeiten unter Ber¨¨ ucksichtigung von Gleichung (3.10)

P(µ→ν)

P(ν →µ) = g(µ→ν)A(µ→ν)

g(ν →µ)A(ν→µ) . (3.11)

F¨ur den Quotienten der Akzeptanzraten gilt nach [2] der Zusammenhang 0< A(µ→ν)

A(ν→µ) <1 . (3.12)

Die Wahrscheinlichkeiteng(µ→ν) undg(ν →µ) k¨onnen nun beliebig gew¨ahlt werden. Außerdem ist Gleichung (3.5) erf¨ullt, denn das System endet bei jedem Markov-Prozess in irgend einem Zustand.

Somit werden durch Markov-Prozesse zufallsbasiert neue Zust¨andeνbei gegebe- nen Zust¨andenµunter einem Satz von Wahrscheinlichkeiteng(µ→ν) erzeugt.

Diese Zust¨ande werden dann, abh¨angig von der AkzeptanzrateA(µ→ν), ent- weder akzeptiert oder abgelehnt. Die Akzeptanzrate wird dabei so gew¨ahlt, dass Gleichung (3.11) erf¨ullt ist.

Somit sind alle Bedingungen f¨ur die ¨Ubergangswahrscheinlichkeiten, wie sie in Kapitel 3.2.1 dargestellt wurden, erf¨ullt. Die Markov-Kette generiert nun nach Erreichen des Equilibriums eine Menge an Zust¨anden, die der Boltzmann- Verteilung unterliegen.

Offen bleibt nun noch die Frage, wie die Akzeptanzraten im Optimalfall gew¨ahlt werden m¨ussen. Bei der Wahl eines niedrigen Wertes wird der Algorithmus die meiste Zeit in einigen wenigen Zust¨anden verharren. Selbst bei einer sehr ho- hen Zahl an Durchl¨aufen ist die Anzahl der ¨Uberg¨ange gering. Allerdings war das Ziel die Erzeugung von einer großen Bandbreite an Zust¨anden. Aus diesem Grund m¨ussen die Akzeptanzraten so groß wie m¨oglich gew¨ahlt werden.³ Der”ideale Algorithmus“ generiert immer direkt Zust¨ande gem¨aß der

gew¨unschten Zustandsverteilung, und die Akzeptanzrate ist immer Eins. Bei einem

”guten Algorithmus“ hat die Akzeptanzrate einen Wert, der sehr nah an Eins liegt.

Ein solcher

”guter Algorithmus“ ist derMetropolis-Algorithmus, der im n¨achsten Abschnitt vorgestellt wird.

3.4 Metropolis - Algorithmus

Der Metropolis-Algorithmus wurde im Jahre 1953 von Nicolas Metropolis und seinen Co-Autoren vorgestellt [4]. Er ist einer der bekanntesten und am h¨aufigsten benutzten Monte-Carlo-Algorithmen.

Der Algorithmus verl¨auft genauso ab, wie es in Kapitel 3.3 beschrieben wur- de: Zuerst wird ein Satz an Wahrscheinlichkeiten g(µ→ν) gew¨ahlt, wobei jede Wahrscheinlichkeit einen ¨Ubergang von µ nach ν repr¨asentiert. Danach

3Eine Herleitung dazu ist in [2] zu finden.

erfolgt die Wahl der Akzeptanzrate A(µ→ν), so dass Gleichung (3.12) die detailed-balance-Bedingung (3.9) erf¨ullt. Nun erzeugt der Algorithmus wieder- holt Zust¨ande ν, die dann entweder akzeptiert oder verworfen werden. Wenn der neue Zustand akzeptiert wird, dann wechselt das System in diesen neuen Zustandν, und der Prozess beginnt von vorne.

Bei der Wahl der Auswahlwahrscheinlichgeiten g(µ→ν) kommt eine Eigen- schaft des Metropolis-Algorithmus zum Einsatz: Alle erlaubten Wahrschein- lichkeiten werden gleich groß, alle anderen zu Null gew¨ahlt. Welche Zust¨ande dabei erlaubt sind, muss vorher definiert werden.

Eine M¨oglichkeit zur Auswahl von erlaubten Zust¨anden ist diesingle-spin-flip- dynamic. Sie besagt, dass nur Zust¨ande erlaubt sind, die sich vom vorherigen Zustand in der Neuausrichtung eines Spins unterscheiden. Simuliert man ein System mit N Spins, dann kann bei jedem Markov-Prozess einer dieser N Spins

”flippen“. Es entstehen also N m¨ogliche Zust¨ande ν, die vom Zustand µ aus erreicht werden k¨onnen. Demnach gibt es also genau N Auswahlwahrscheinlich- geiteng(µ→ν) ungleich Null, und jede einzelne hat den Wert

g(µ→ν) = 1

N . (3.13)

Mit dieser Definition der Auswahlwahrscheinlichkeiten nimmt die detailed-balance- Bedingung aus Gleichung (3.9) die folgende Form an:

P(µ→ν)

P(ν →µ) = A(µ→ν)

A(ν→µ) = e−β(Eν−Eµ) . (3.14) Damit nun der Algorithmus so effektiv wie m¨oglich arbeitet, m¨ussen die Ak- zeptanzraten so groß wie m¨oglich gew¨ahlt werden. Dazu wird die gr¨oßere der beiden Raten aus (3.14) auf den maximal m¨oglichen Wert, n¨amlich auf Eins, gesetzt. Nun wird die andere Rate so gew¨ahlt, dass Gleichung (3.14) erf¨ullt ist.

Betrachtet man zum Beispiel zwei Zust¨ande µ und ν mit Eµ < Eν, dann ist A(ν →µ) die gr¨oßere der beiden Raten und wird auf Eins gesetzt. Die an- dere Rate,A(µ→ν), nimmt den Wert e−β(E_ν−Eµ) an. Somit gilt f¨ur den optimalen Algorithmus:

A(µ→ν) =







e−β(E_ν −Eµ) fallsE_ν −E_µ>0

1 sonst.

(3.15) Liegt der neue Zustand energetisch niedriger oder auf gleicher Ebene, dann wird automatisch in den neuen Zustand gewechselt. Sollte er energetisch h¨oher lie- gen, dann wird er mit seiner Wahrscheinlichkeit akzeptiert. Bei zunehmender Energiedifferenz sinkt die Akzeptanz.

Jeder Algorithmus, der auf der Definition der Akzeptanzraten nach Gleichung (3.15) basiert, wird Metropolis-Algorithmus genannt. Alle Simulationen, die im

Verlauf dieser Arbeit durchgef¨uhrt werden, basieren auf dieser Definition der Akzeptanzraten um Zust¨ande gem¨aß der Boltzmann-Verteilung zu generieren.

Der inkrementelle Ablauf des Metropolis-Algorithmus, so wie er im weiteren Verlauf dieser Arbeit realisiert wird, l¨asst sich wie folgt beschreiben:⁴

1. W¨ahle einen Startzustand.

2. W¨ahle zuf¨allig einen Spin.

3. Berechne die Energie des neuen Zustandes mit geflipptem Spin und berechne ∆E.

4. Gilt ∆E < 0, dann wechsel in den neuen Zustand und starte erneut bei 2, ansonsten generiere eine Zufallszahlr mit 0≤r <1.

5. Gilt r <e−β∆E, dann gehe ¨uber in den neuen Zustand, ansonsten bleibe im alten.

6. Fahre fort bei 2.

4Siehe hierzu auch [5].

4 Betrachtungen an einem Fe

- Molek¨ ul

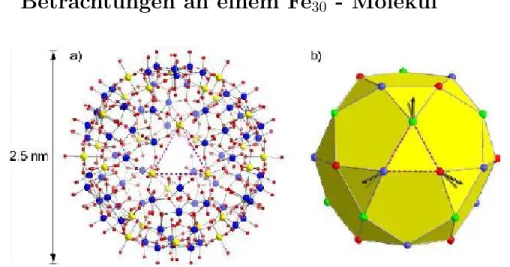
Abbildung 1: links: Chemische Struktur: Aufbau des Molek¨uls; rechts:

Magnetische Struktur: Die 30 Fe³⁺-Ionen sind in der Form eines Icosedode- caeder angeordnet. ¨Ubernommen aus [6].

Bisher wurden Monte-Carlo-Simulationen nur theoretisch betrachtet. In diesem Kapitel werden nun Simulationen an einem Molek¨ul durchgef¨uhrt. Es handelt sich hierbei um das Molek¨ul mit der Strukturformel

[M o₇₂F e₃₀O₂₅₂(M o₂O₇(H₂O))₂(M o₂O₈H₂(H₂O))(CH₃COO)₁₂(H₂O)₉₁]×

150H2O ={M o₇₂F e30} ×150H2O,

welches {Mo₇₂Fe₃₀} genannt wird. Es ist mit einem Durchmesser von etwa 2,5 nm das bis dato gr¨oßte synthetisierte paramagnetische Molek¨ul. In Ab- bildung 1 ist sowohl die chemische (links) als auch die magnetische (rechts) Struktur dieses Molek¨uls dargestellt.

Im linken Teilbild von Abbildung 1 sind Fe³⁺-Ionen durch gelbe Kugeln, Mo- Atome durch blaue Kugeln und O-Atome durch rote Kugeln vertreten. Die einzelnen Fe-Atome sind ¨uber O-Mo-O-Br¨ucken miteinander verbunden.

Betrachtet man nur die Fe³⁺-Ionen, so bilden diese einen Icosedodecaeder, auf dessen Eckpunkten jeweils immer ein Fe³⁺-Ion sitzt. Dieses ist in Abbildung 1 rechts zu sehen. F¨ur magnetische Prozesse sind nur diese 30 Fe³⁺-Ionen von Bedeutung. Des weiteren ist in dieser Abbildung noch die Grundzustandskon- figuration der Spins, erkennbar an den Pfeilen, dargestellt.

Das betrachtete System umfasst, wie schon beschrieben, 30 Fe³⁺-Ionen mit einem Spin von S=5/2. Demnach ist die Dimension des betrachteten Hilber- traumes

D (H) = (2S+ 1)^N = 6³⁰ . (4.1)

Bis heute ist es unm¨oglich, die Hamiltonmatrix dieses Systems zu diagona- lisieren und somit das System quantenmechanisch exakt zu l¨osen. Aus diesem Grunde w¨ahlt man die Monte-Carlo-Technik zur statistischen Beschreibung des Systems.

Zun¨achst wird nun das klassische Heisenberg-Modell vorgestellt. Anschließend werden einige allgemeine Betrachtungen des Molek¨uls vorgenommen. Nach die- sen allgemeinen ¨Uberlegungen werden die Simulationsergebnisse aufgezeigt und erl¨autert.

4.1 Grundlagen

4.1.1 Klassisches Heisenberg-Modell

Das in diesem Zusammenhang betrachtete Molek¨ul l¨asst sich durch das klassi- sche Heisenberg-Modell beschreiben. Dieses beschreibt die Wechselwirkung zwi- schen unmittelbar benachbarten Spins. Geht man von einem isotropen System aus, dann ist der HamiltonoperatorH gegeben zu

H=−2X

hi,ji

JijSi·Sj−gµB

X

i

B·Si , (4.2)

wobei die Summehi, ji uber eindeutig benachbarte Paare l¨¨ auft. Außerdem ist Jij die Kopplungskonstante zwischen zwei Nachbarn, g der Land´e-Faktor und µB das Bohrsche Magneton.

Der zweite Summand stellt den Zeeman-Term dar und tritt nur bei einem an- gelegten MagnetfeldB in Kraft. Dabei wird B o.B.d.A. als ein externes Ma- gnetfeldB0 in z-Richtung angenommen.

In Gleichung (4.2) werden die Spins S wie klassische Vektoren behandelt. Da sie betragsm¨aßig gleich groß sind, gilt die folgende Beziehung mit e_i als Ein- heitsvektor, der beliebig im Raum orientiert ist:

Si=|S_i|ei=p

S(S+ 1)ei . (4.3)

Der Betrag des Spins wurde hier durch eine Herleitung aus dem quantenme- chanischen Spinoperator repr¨asentiert. Alternativ kann er auch zu

|S_i|=S (4.4)

angenommen werden, was den Limes von Gleichung (4.3) f¨ur wachsende Spins darstellt. In dieser Arbeit wird allerdings nur der erste Fall weiter untersucht.

Simulationsergebnisse und Erl¨auterungen zu dem zweiten Fall sind in [5] zu finden.

Da in dieser Arbeit nur isotrope Kopplungen betrachtet werden, kann J als klassische Kopplungsmatrix aufgefasst werden, und es gilt

Jc=|S|²J =S(S+ 1)J . (4.5)

Ber¨ucksichtigt man Gleichungen (4.2), (4.3) und (4.5), dann l¨asst sich die Ha- miltonfunktion darstellen als

H=−2J_cX

hi,ji

e_i·e_j−gµ_B|S|X

i

B·e_i (4.6)

Abbildung 2:Geometrie des Icosido- decaeders. ¨Ubernommen aus [7].

Abbildung 3: Spinkonfiguration.

Ubernommen aus [7].¨

4.1.2 Allgemeine Betrachtungen des {Mo₇₂Fe₃₀}-Molek¨uls

Nun wird das{Mo₇₂Fe₃₀}-Molek¨ul etwas genauer betrachtet. Wie schon erw¨ahnt sitzen die 30 Fe³⁺-Ionen auf den Eckpunkten eines Icosidodecaeders. Dieser ist aus gleichseitigen Drei- und F¨unfecken aufgebaut, siehe dazu auch Abbildung 2.

”Klappt“ man den Icosidodecaeder auseinander, dann erh¨alt man eine Darstel- lung wie in Abbildung 3. Hier ist deutlich zu erkennen, dass jeder Spin genau vier Nachbarspins besitzt. Diese Darstellung ist besonders n¨utzlich beim Er- stellen der Wechselwirkungsmatrix. Nach geschicktem Durchnummerieren der einzelnen Positionen l¨asst sich sofort sagen, welche Spins wechselwirken; die Wechselwirkungsmatrix kann problemlos erstellt werden. Die Nummerierung der Positionen kann hierbei frei gew¨ahlt werden. Allerdings ist man letztend- lich bestrebt eine Matrix aufzustellen, bei der die Eintr¨age m¨oglichst nah an der Diagonalen liegen. Im Anhang ist sowohl eine Variation von Abbildung 3 mit Angabe der Nummerierung der Positionen zu finden als auch die f¨ur die Simulationen verwendete Wechselwirkungsmatrix

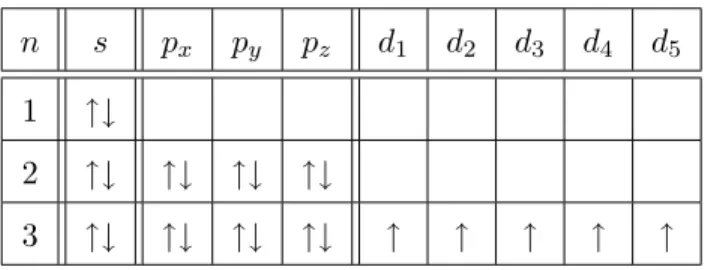
Der Spin der Fe³⁺-Ionen ergibt sich aus den Hundtschen Regeln. In Tabelle 1 ist die Elektronenkonfiguration des Fe³⁺-Ions dargestellt.

n s px py pz d1 d2 d3 d4 d5

1 ↑↓

2 ↑↓ ↑↓ ↑↓ ↑↓

3 ↑↓ ↑↓ ↑↓ ↑↓ ↑ ↑ ↑ ↑ ↑

Tabelle 1: Elektronenkonfiguration desF e³⁺-Atoms

Hierbei ist n die Hauptquantenzahl und s, pi und di sind die Orbitale der zul¨assigen Quantenzahll. Energetisch ist es am g¨unstigen, die 5 Elektronen in den 5 d-Orbitalen anzuordnen und den einzelnen Spins die Spinquantenzahl m_s= +1/2 zuzuweisen. Somit ergibt sich der Gesamtspin zu S = 5/2.

4.2 Simulationsergebnisse

In den nun folgenden Kapiteln werden Monte-Carlo-Simulationen f¨ur das {Mo₇₂Fe30}-Molek¨ul durchgef¨uhrt und diskutiert. Vor allem sind solche Gr¨oßen interessant, f¨ur die auch experimentelle Ergebnisse vorhanden sind. An dieser Stelle werden die Magnetisierung, die Innere Energie und die Spezifische W¨arme genauer betrachtet.

Bei allen Messungen, bei denen die Temperaturabh¨angigkeit untersucht wird, werden Simulationen f¨ur einen Temperaturbereich von 0 K bis 40 K durch- gef¨uhrt. Außerdem wird die Anzahl der Metropolisschritte (

”sweeps“) auf 1.000.000 festgelegt, wobei die Aufnahme von Simulationswerten erst nach 20.000 sweeps beginnt. Dieses Warten l¨aßt sich dadurch begr¨unden, dass das System erst eine gewisse Zeit braucht um das Equilibium zu erreichen. Nach [5]

liegt das Equilibrium zwar schon fr¨uher vor, allerdings k¨onnen in einer Sprache wie Java oder Fortran weit mehr sweeps realisiert werden als in Matlab, und darum f¨uhrt die Wahl eines etwas h¨oheren Startwertes in diesem Fall nicht zu einem Ergebnisverlust. Eher werden die bestimmten Werte genauer, da effektiv

¨

uber eine gr¨oßere Anzahl an Simulationswerten gemittelt wird.

Die benachbarten Fe-Atome sind ¨uber O-Mo-O-Br¨ucken miteinander gekoppelt.

Außerdem sind die Abst¨ande zwischen den einzelnen Fe-Atomen konstant. Die allgemeine Kopplungskonstante J_c wird daher zu J_c/k_B = −1,57 K festge- legt [7]. Dieses entspricht antiferromagnetischer Kopplung. Allerdings h¨angt das Vorzeichen der Kopplungskonstanten auch von der Definition des Vorzeichens der Hamiltonfunktion ab, und kann daher, nach Anpassung der Hamiltonfunk- tion, gegebenenfalls auch positiv sein. Der Land´e-Faktor wird angenommen zu g= 1,974.

4.2.1 Magnetisierung

Zun¨achst wird die Magnetisierung des Molek¨uls genauer untersucht. In Kapitel 2.4.3 wurden schon allgemeine Betrachtungen der Magnetisierung durchgef¨uhrt.

Nach den Gleichungen (2.12), (2.18) und (4.6) ergibt sich f¨ur die Magnetisierung der Zusammenhang

M =gµ_B|S|X

i

e^z_i , (4.7)

wobei der Vektore^z_i den Einheitsvektor des Spins i in Richtung des Magnetfel- des (hier: z-Richtung) darstellt.

0 5 10 15 20 25 30 35 40 0

10 20 30 40 50 60 70 80

B [T]

M/(g. µ B)

Messwerte bei T=1mK

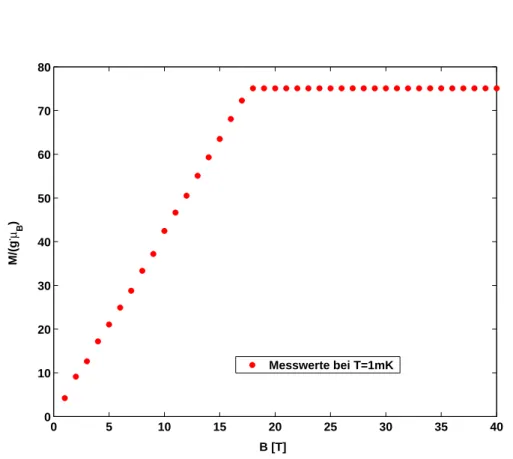
Abbildung 4: Magnetisierung in Abh¨angigkeit vom angelegten Magnetfeld bei T = 1 mK; der Knick bei 17,7 K entsteht durch die Einf¨uhrung der im Text beschriebenen Randbedingung.

Im Folgenden werden nun Simulationsergebnisse f¨ur verschiedene Randbedin- gungen betrachtet. Drei F¨alle sind dabei von besonderem Interesse:

1. Untersuchung der Magnetisierung in Abh¨angigkeit vom angelegten Ma- gnetfeld beiT = 0 K (Grundzustand)

2. Untersuchung der Magnetisierung in Abh¨angigkeit vom angelegten Ma- gnetfeld bei bei konstanter Temperatur (T 6= 0 K)

3. Untersuchung der Magnetisierung in Abh¨angigkeit von der Temperatur bei konstantem Magnetfeld

Zu 1: Untersuchung der Magnetisierung in Abh¨angigkeit vom ange- legten Magnetfeld bei T = 0 K (Grundzustand)

Zun¨achst wird nun untersucht, wie die Magnetisierung vom angelegten Ma- gnetfeld bei T = 0 K abh¨angt. Betrachtet man die exakte L¨osung (siehe dazu [7]), dann wird f¨ur kleine Magnetfelder ein linearer Anstieg der Magnetisierung erwartet. Dieser Anstieg ist dadurch zu erkl¨aren, dass sich die Spins bei stei- gendem Magnetfeld immer weiter ausrichten, bis sie schließlich alle parallel zum angelegten Magnetfeld stehen. Dieses ist bei einem Wert vonBc = 17,7 T der

Fall. Ab diesem Wert tritt eine S¨attigung ein, die Magnetisierung liegt nun bei dem quantenmechanisch maximal erlaubten Wert vonMmax = 30gµBS.

In dem betrachteten Fall nach Gleichung (4.3) wird diese Randbedingung nicht automatisch ber¨ucksichtigt. Darum muss die Magnetisierung ab Bc = 17,7 T k¨unstlich aufM_max = 30gµ_BS gesetzt werden [5].

In Abbildung 4 sind die Simulationsergebnisse f¨ur T = 1 mK im Bereich von 0 T bis 40 T dargestellt. Aus programmiertechnischen Gr¨unden (Division durch die 0) kann die Kurve nicht genau bei T = 0 K aufgenommen werden, somit wird ein Wert sehr nahe des Nullpunkts angenommen.

Deutlich erkennt man den linearen Anstieg bis etwa 18 K. Zwar wird der pro- gnostizierte Knick k¨unstlich durch die Festsetzung von M_max herbeigef¨uhrt, allerdings f¨ugt sich dieser harmonisch in die Kurve ein und ruft keine Spr¨unge hervor.

F¨ur sehr tiefe Temperaturen scheint das verwendete Modell also sehr gut das Verhalten der Magnetisierung in Abh¨angigkeit von dem angelegten Magnetfeld zu repr¨asentieren.

Zus¨atzlich zu dem hier betrachteten Modell kann der Spin auch nach Gleichung (4.4) zu S angenommen werden. In diesem Fall wird der quantenmechanische Grenzwert bei Bc automatisch ber¨ucksichtigt. Allerdings entsprechen die Kur- ven nur f¨ur Temperaturen naheT = 0 K dem erwarteten Verlauf [5]. Aus diesem Grunde werden im weiteren Verlauf dieser Arbeit keine n¨aheren Betrachtungen zu dieser Wahl des Spins durchgef¨uhrt.

Zu 2: Untersuchung der Magnetisierung in Abh¨angigkeit vom an- gelegten Magnetfeld bei bei konstanter Temperatur (T 6= 0 K)

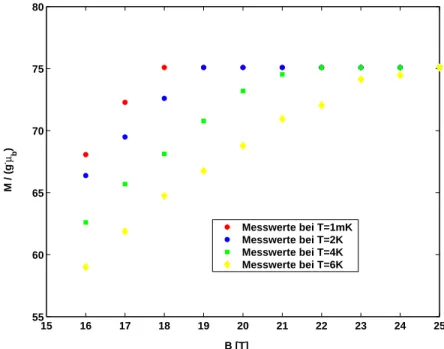
Nun wird untersucht, wie sich die in 4 betrachtete Kurve bei Variation der Tem- peratur ver¨andert. Dazu wird die Simulation mehrfach mit unterschiedlichen Temperaturen durchgef¨uhrt, die entsprechenden Kurven sind in Abbildung ??

zu finden. Der S¨attigungsbereich musste in diesem Fall wiederum nachtr¨aglich hinzugef¨ugt werden.

Auch bei diesen Kurven ist deutlich der lineare Anstieg bei kleinen Magnet- feldern zu erkennen. Bei steigender Temperatur ist zu erkennen, dass sowohl die Steigung als auch der lineare Wertebereich abnimmt. Außerdem verschiebt sich B_c hin zu gr¨oßeren Werten. Die Spins sind also erst bei einem gr¨oßeren angelegten Magnetfeld parallel zu diesem ausgerichtet. In Abbildung 6 ist der Bereich um den quantenmechanischen Grenzwert noch einmal vergr¨oßert dar- gestellt. Die soeben beschriebenen Beobachtungen sind hier noch einmal klarer zu erkennen.

0 5 10 15 20 25 30 35 40 0

10 20 30 40 50 60 70 80

B [T]

M / (g.µB)

Messwerte bei T=1mK Messwerte bei T=2K Messwerte bei T=4K Messwerte bei T=6K

Abbildung 5:Magnetisierung in Abh¨angigkeit vom angelegten Magnetfeld bei unterschiedlichen Temperaturen; der Knick bei 17,7 K entsteht durch die Einf¨uhrung der im Text beschriebenen Randbedingung.

15 16 17 18 19 20 21 22 23 24 25

55 60 65 70 75 80

Messwerte bei T=1mK Messwerte bei T=2K Messwerte bei T=4K Messwerte bei T=6K

B [T]

M / (g.µb)

Abbildung 6:Genauere Betrachtung der quantenmechanischen Grenze bei der Magnetisierung in Abh¨angigkeit vom angelegten Magnetfeld bei unter- schiedlichen Temperaturen.

0 5 10 15 20 25 30 35 40 0

10 20 30 40 50 60 70

T [K]

M / (g. µ B)

Messwerte bei B=1T Messwerte bei B=7T Messwerte bei B=9T Messwerte bei B=14T

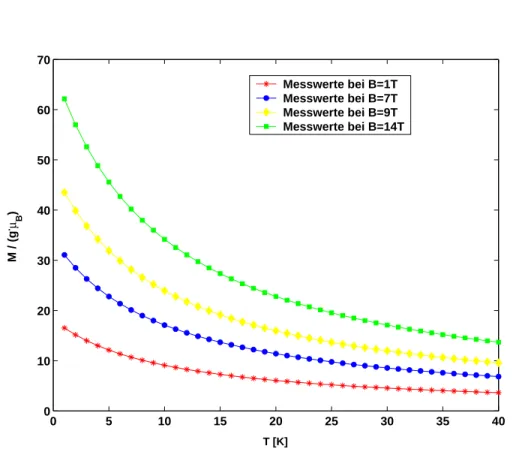
Abbildung 7: Magnetisierung in Abh¨angigkeit von der Temperatur bei unter- schiedlichen angelegten Magnetfeldern.

Zu 3: Untersuchung der Magnetisierung in Abh¨angigkeit von der Temperatur bei konstantem Magnetfeld

Bei der letzten Betrachtung der Magnetisierung wird nun ein konstantes Ma- gnetfeld angenommen und die Temperatur in 1 K-Schritten im Bereich von 0 K bis 40 K variiert.

Klassisch wird bei dieser Messung ein Abfall der Magnetisierungskurve zu h¨oheren Temperaturen hin erwartet. Bei steigender Temperatur k¨onnen sich die einzelnen Spins zunehmend unabh¨angig von ihren Nachbarspins frei im Raum bewegen. Die thermische Energie dominiert den Zeeman-Term immer st¨arker, bis schließlich alle Spins komplett zuf¨allig im Raum verteilt sind, die Magneti- sierungskurve hat ein absolutes Minimum erreicht.

Bei einer quantenmechanischen Betrachtung l¨asst sich der Abfall dadurch er- kl¨aren, dass bei kleinen Temperaturen die Spins st¨arker in Magnetfeldrichtung ausgerichtet sind als bei h¨oheren Temperaturen. Hierf¨ur ist der Zeeman-Term verantwortlich. BeiT = 0 K liegt somit ein Maximum der Magnetisierung vor.

Erh¨oht man nun die Temperatur, dann erhalten die Spins so viel Energie, dass sie sich unabh¨angig von den anderen Spins frei im Raum ausrichten k¨onnen und die Magnetisierung abnimmt.

0 5 10 15 20 25 30 35 40

−1000

−900

−800

−700

−600

−500

−400

−300

−200

−100 0

T [K]

E [k B]

Messwerte bei B=0T MesTswerte bei B=7T Messwerte bei B=9T Messwerte bei B=14T

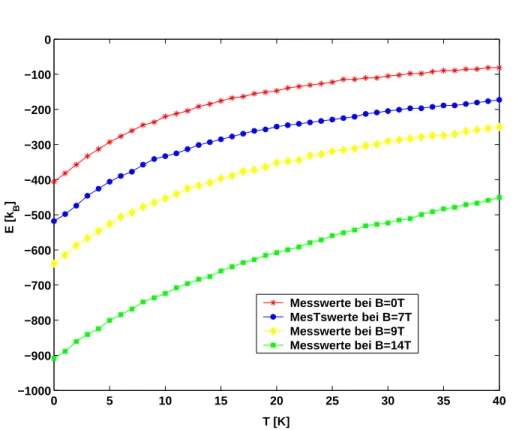
Abbildung 8: Innere Energie in Abh¨angigkeit von der Temperatur bei unter- schiedlichen angelegten Magnetfeldern.

In Abbildung 7 sind die entsprechenden Kurven dargestellt. Wie erwartet ist eine abfallende Kurve zu sehen. Je h¨oher das angelegte Magnetfeld ist, desto h¨oher ist auch die Grundzustandsmagnetisierung beiT = 0 K. Dieser Anstieg ist linear und analog zu den Betrachtungen, die an Hand von Abbildung 5 durchgef¨uhrt wurden.

Zusammengefasst kann gesagt werden, dass das klassische Heisenberg-Modell unter den hier eingef¨uhrten Randbedingungen sehr gut die theoretischen ¨Uber- legungen zum Verhalten der Magnetisierung best¨atigt.

4.2.2 Innere Energie und Spezifische W¨arme

An dieser Stelle werden nun die Innere Energie und die Spezifische W¨arme genauer untersucht. Nach Gleichung (2.12) kann die Innere Energie berechnet werden durch

hEi=hHi . (4.8)

Dieses bedeutet, dass die Innere Energie direkt durch Bildung des Mittelwertes

¨uber eine bestimmte Anzahl an sweeps berechnet werden kann. In diesem Fall wird, wie schon fr¨uher beschrieben, ¨uber 980.000 sweeps nach Erreichen des

0 5 10 15 20 25 30 35 40 0

5 10 15 20 25 30 35

T [K]

C [k B]

Messwerte bei B=1T Messwerte bei B=7T Messwerte bei B=9T Messwerte bei B=14T

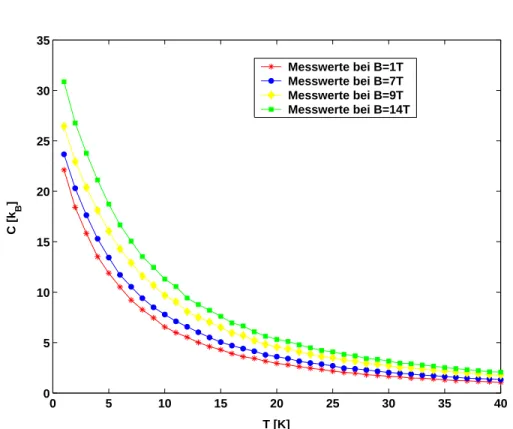
Abbildung 9: Spezifische W¨arme in Abh¨angigkeit von der Temperatur bei un- terschiedlichen angelegten Magnetfeldern.

Equilibriums gemittelt.

In Abbildung 8 ist die Innere Energie in Abh¨angigkeit von der Termperatur bei verschiedenen angelegten Magnetfeldern dargestellt. Es ergibt sich ein kontinu- ierlicher, ansteigender Kurvenverlauf. Bei gr¨oßer werdendem Magnetfeld ist die Innere Energie nach kleineren Werten hin verschoben.

Die Spezifische W¨arme berechnet sich nach Gleichung (2.22) zu C=kBβ²

E²

− hEi²

. (4.9)

Des weiteren l¨asst sie sich nach Gleichung (2.13) als Ableitung der Inneren Energie nach T bestimmen.

In Abbildung 9 sind die Simulationsergebnisse f¨ur die Spezifische W¨arme dar- gestellt. Deutlich ist der Zusammenhang zwischen der Inneren Energie und der Spezifischen W¨arme zu erkennen: f¨ur kleine Temperaturen nimmt die Steigung der Kurven der Inneren Energie ab; die Kurve der Spezifischen W¨arme f¨allt also in diesem Bereich recht deutlich. Bei gr¨oßer werdender Temperatur verringert sich der Steigungsabfall der Kurve der Inneren Energie, bei der Spezifischen

0 5 10 15 20 25 30 35 40 0

1 2 3 4 5 6 7 8 9

T [K]

∆ C [k B]

C(T,B=7T)−C(T,B=0T) C(T,B=9T)−C(T,B=0T) C(T,B=14T)−C(T,B=0T)

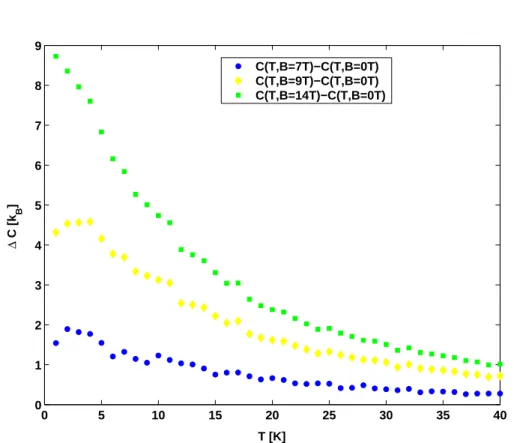
Abbildung 10: Differenz ∆C = C(T, B)−C(T, B= 0 T) der Spezifischen W¨arme bei unterschiedlichen angelegten Magnetfeldern.

W¨arme f¨allt die Kurve nur noch schwach ab.

Um den phononischen Anteil der Spezifischen W¨arme auszublenden, kann die Differenz ∆C = C(T, B)−C(T, B= 0 T) gebildet werden. Nach dem De- bey’schen Modell ist dieser unabh¨angig vom externen Magnetfeld, und kann darum durch Differenzbildung eliminiert werden [3]. Somit kann auch allein die magnetfeldabh¨angige Spezifische W¨arme untersucht werden.

In Abbildung 10 ist genau dieses dargestellt. Je gr¨oßer das angelegte Magnetfeld, desto h¨oher verl¨auft die Kurve von ∆C f¨ur gr¨oßere T. In diesem Fall streuen die Werte st¨arker als bei den anderen Teilversuchen, was durch die Differenz- bildung von bereits fehlerbehafteten Gr¨oßen kommt.

Auch das Verhalten der Inneren Energie und der Spezifischen W¨arme kann durch das klassische Heisenberg-Modell beschrieben werden. Somit scheint das klassische Heisenberg-Modell also sehr gut geeignet zu sein, die magnetischen Eigenschaften des betrachteten Molek¨uls zu beschreiben.

4.3 Zusammenfassung und Ergebnisse

In diesem Kapitel wurden an Hand von Monte-Carlo-Simulationen die magne- tischen Eigenschaften eines {Mo₇₂Fe30}-Molek¨uls betrachtet. Es wurde unter- sucht, inwieweit das klassische Heisenberg Modell dieses Molek¨ul beschreibt.

Dazu erfolgte zun¨achst eine genauere Betrachtung des Verhaltens der Magneti- sierung sowohl in Abh¨angigkeit von der Temperatur als auch in Abh¨angigkeit von dem angelegten Magnetfeld. Anschließend wurden Simulationen zur Be- trachtung der Inneren Energie und der Spezifischen W¨arme vorgenommen.

Die Simulationsergebnisse best¨atigen, dass die magnetischen Eigenschaften des Molek¨uls durch das klassische Heisenberg-Modell beschrieben werden kann. Al- le Kurven, die durch die Simulationswerte entstanden sind, entsprechen den vor der Simulation durchgef¨uhrten ¨Uberlegungen. Nur bei dem Ausblenden des phononischen Anteils bei der Betrachtung der Spezifischen W¨arme sind etwas gr¨oßere Streuungen in den Werten erkennbar.

5 Betrachtungen an Fe

-Schichtsystemen

Nachdem bisher die Eigenschaften von einzelnen{Mo₇₂Fe30}-Molek¨ulen unter- sucht wurden, steht in diesem Kapitel nun die Betrachtung von {Mo₇₂Fe₃₀}- Clustern im Vordergrund. Hierzu werden Simulationen f¨ur zwei verschiedene Cluster, n¨amlich ein 2x2- und ein 4x4-Cluster, mit unterschiedlichen Kopplun- gen zwischen den einzelnen Molek¨ulen durchgef¨uhrt. Das gr¨oßte Problem bei diesen Betrachtungen liegt an der Laufzeit f¨ur die jeweiligen Simulationen. Bei einem einzelnen Molek¨ul dauert ein Simulationsdurchlauf auf dem verwende- ten Computer f¨ur einen Bereich von 0 K bis 50 K in etwa 1 Stunde. Da die Laufzeit ungef¨ahr linear mit der Anzahl der Molek¨ule im Cluster zunimmt, betr¨agt die Laufzeit f¨ur das 2x2-Cluster etwa 4 Stunden, f¨ur das 4x4-Cluster etwa 16 Stunden. Das n¨achstgr¨oßere 5x5-Cluster w¨urde schon eine Laufzeit von 25 Stunden bedeuten und wird an dieser Stelle auch nicht betrachtet. Bei den hier untersuchten Clustern werden nur einige signifikante Eigenschaften be- trachtet, n¨amlich die Magnetisierung in Abh¨angigkeit von der Temperatur bei B = 0,1 T sowie die Spezifische W¨arme in Abh¨angigkeit von der Temperatur beiB = 0 T.

Das Simulationsprogramm, das f¨ur die Simulationen f¨ur ein Molek¨ul geschrie- ben wurde, muss nun auch ver¨andert werden. Dazu wird eine zweite Wech- selwirkungsmatrix erstellt, die zus¨atzlich die Kopplung mit den Atomen eines anderen Molek¨uls beinhaltet⁵. Außerdem muss die Berechnung des Hamilton- operators so angepasst werden, dass auch der f¨unfte Nachbar bei Spins, die mit einem Spin des Nachbarmolek¨uls wechselwirken, ber¨ucksichtigt wird.

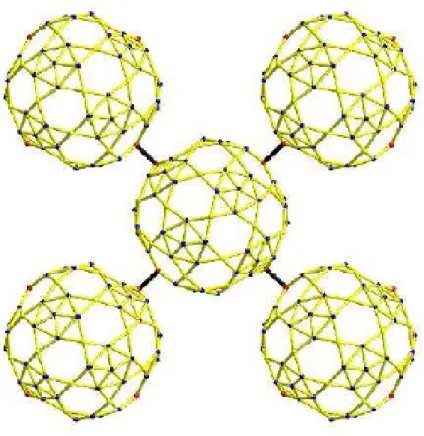
Abbildung 11:Aufbau einer Schicht des{Mo72Fe30}-Clusters. Jedes Molek¨ul ist mit seinen vier n¨achsten Nachbarn ¨uber antiferromagnetische Kopplung verbunden.

Ubernommen aus [6].¨

5.1 Struktur der Fe30-Schichtsysteme

Fe30-Schichtsysteme bestehen aus parallelen Schichten, die aus {Mo₇₂Fe30}- Clustern bestehen. In den einzelnen Clustern sind die {Mo₇₂Fe30}-Molek¨ule

¨uber Sauerstoffbr¨ucken mit ihren Nachbarn verbunden, zwischen ihnen herrscht eine starke antiferromagnetische Kopplung [6]. In Abbildung (11) ist ein solches Cluster mit 5 Molek¨ulen dargestellt.

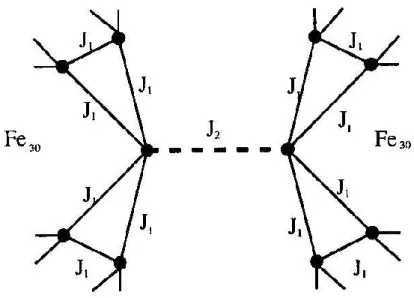
In Abbildung 12 ist die Kopplung der Spins zwischen zwei Molek¨ulen sowie innerhalb eines Molek¨uls zu sehen. Die Spins, die mit dem Nachbarmolek¨ul ge- koppelt sind, haben 5 Nachbarspins zum Wechselwirken. Innerhalb des Molek¨uls tr¨agt die KopplungskonstanteJ1den WertJ1 =−1,57. Die Kopplungskonstan- teJ₂ wird in den folgenden Teilversuchen variiert.

5Da diese Matrix dreidimensional ist wurde darauf verzichtet, sie im Anhang mit anzuge- ben.

Abbildung 12: Wechselwirkung zwischen zwei{Mo₇₂Fe₃₀}-Molek¨ulen. Erkenn- bar ist sowohl die Kopplung innerhalb des Molek¨uls ¨uber J₁ sowie die Kopplung beider Molek¨ule ¨uberJ2. ¨Ubernommen aus [6].

5.2 Periodische Randbedingungen

Um Simulationen an den Clustern durchf¨uhren zu k¨onnen, m¨ussen periodische Randbedingungen eingef¨uhrt werden. Ansonsten h¨atten die ¨außersten Spins, die normalerweise mit einem Nachbarmolek¨ul wechselwirken w¨urden, keinen f¨unften Nachbarn.

In Abbildung 13 ist ein 2x2-Cluster dargestellt, mit dessen Hilfe nun die Idee der periodischen Randbedingung erkl¨art wird. Jedem der 16 Spins, der bei der Kopplung mit einem Nachbaratom beteiligt ist, wird mit einem entsprechenden Wert w von 1 bis 16 belegt.

Ein Spin auf dem Rand wechselwirkt nun mit dem ihm im Cluster genau ge- gen¨uberliegenden Spin. In diesem Fall w¨urde nun bei periodischen Randbedin- gungen der Spin 1 mit dem Spin 7 wechselwirken, der Spin 13 mit dem Spin 11, der Spin 2 mit Spin 16, der Spin 6 mit Spin 12 und umgekehrt.⁶ Bei einem gr¨oßeren Cluster sind die ¨Uberlegungen analog.

6Alternativ h¨atte jedem Molek¨ul eine Zahl von 1 bis 4 zugewiesen werden k¨onnen, und zus¨atzlich dazu w¨are bei jedem Molek¨ul eine Nummerierung der Spins von 1 bis 4 erfolgt. Der Spin 3 im Molek¨ul 3 h¨atte dann den Wertw = 3 + 4 + 4 = 11, was der Nummerierung in Abbildung 13 entspricht. Hier w¨urde nun immer der Spin 1 mit dem Spin 3, der Spin 2 mit Spin 4 und umgekehrt wechselwirken.

1 2

3 4

14

16 15

5

6

7 8

9 10

11 12

13

Abbildung 13: Erkl¨arung der periodischen Randbedingung. Komponenten ent- nommen aus [6].

5.3 Betrachtungen an Clustern

Zun¨achst wird ein Cluster mit 4 Molek¨ulen untersucht. Ein solches Cluster ist auch in Abbildung 13 zu sehen. Insgesamt besitzt dieses System also 4·30 = 120 Spins. Anschließend erfolgt die Betrachtung eines Clusters mit 16 Molek¨ulen, also 16·30 = 480 Spins.

Wie schon in4 wird die Temperatur in 1 K-Schritten von 0 K bis 40 K gemes- sen. Bei allen Messungen, wo eine Untersuchung der Temperaturabh¨angigkeit erfolgt, werden Simulationen f¨ur einen Temperaturbereich von 0 K bis 40 K durchgef¨uhrt. Außerdem werden Messungen f¨ur verschiedene Werte der Kopp- lungskonstanten J₂ durchgef¨uhrt. Diese kann die Werte -150 K, -15 K und -1,57 K annehnmen.

0 5 10 15 20 25 30 35 40 5

10 15 20 25 30 35 40

T [K]

M / (g. µ B)

Messwerte bei J

c=−150K, −15K und −1,57K

Abbildung 14:Magnetisierung der Cluster in Abh¨angigkeit von der Temperatur beiB= 0,1 T.

5.3.1 Magnetisierung in Abh¨angigkeit von der Temperatur bei B = 0,1 T

Als erstes wird die Magnetisierung der Cluster in Anh¨angigkeit von der Tem- peratur untersucht. In Abbildung 14 ist das Ergebnis der Simulation sowohl f¨ur das 2x2-Cluster als auch f¨ur das 4x4-Cluster zu sehen. Die Magnetisierungskur- ve entspricht ziemlich genau den Kurven aus Abbildung 7, also den Ergebnissen f¨ur ein einzelnes{Mo₇₂Fe30}-Molek¨ul. Außerdem sind die Kurven f¨ur alle Kopp- lungen identisch, darum wurde an dieser Stelle auch nur ein Diagramm erstellt.

An dieser Stelle werden keine weiteren Betrachtungen f¨ur die Magnetisierung durchgef¨uhrt. Allerdings sind noch weitere gehende Untersuchungen zum Ver- halten der Magnetisierung erforderlich.

5.3.2 Spezifische W¨arme in Abh¨angigkeit von der Temperatur bei B = 0 T

In den Abbildungen 15 und 16 sind die Simulationswerte f¨ur die Untersuchung der Spezifischen W¨arme einmal f¨ur das 2x2-Cluster und einmal f¨ur das 4x4- Cluster dargestellt. Diese Kurven unterscheiden sich sehr stark von der Kurve der Spezifischen W¨arme eines einzelnen Molek¨uls, siehe Abbildung 9. Bei allen

0 5 10 15 20 25 30 35 40 0

5 10 15 20 25 30 35 40

T [K]

C [k B]

Messwerte bei J_c=−150K Messwerte bei J

c=−15K Messwerte bei J

c=−1,57K

Abbildung 15: Spezifische W¨arme des 2x2-Clusters in Abh¨angigkeit von der Temperatur beiB= 0 T.

0 5 10 15 20 25 30 35 40

0 10 20 30 40 50 60

M / (g.µ B)

T [K]

Messwerte bei J c=−150K Messwerte bei J

c=−15K Messwerte bei J

c=−1,57K

Abbildung 16: Spezifische W¨arme des 4x4-Clusters in Abh¨angigkeit von der Temperatur beiB= 0 T.

drei Kopplungen ist ein stark ausgepr¨agtes Peak zu sehen. Dieses Peak ver- schiebt sich bei gr¨oßerer Kopplung zu h¨oheren Temperaturen hin. Nach diesem Peak verl¨auft die Kurve wieder ¨ahnlich wie in Abbildung 9.

Vermutlich handelt es sich bei dem vorliegenden Peak um einen Phasen¨ubergang.

Hierzu sind weitere Untersuchungen erforderlich, die an dieser Stelle allerdings nicht durchgef¨uhrt werden.

5.4 Zusammenfassung und Ergebnisse

In diesem Kapitel wurden die magnetische Eigenschaften f¨ur zwei unterschiedli- che Cluster aus{Mo₇₂Fe₃₀}-Molek¨ulen genauer untersucht. W¨ahrend die Kurve der Magnetisierung bei den Clustern keine großen Unterschiede zu der Kurve des Einzelmolek¨uls aufweist, tritt bei der Spezifischen W¨arme ein stark ausge- pr¨agtes Peak auf. Beide Sachverhalte erfordern noch weitere Untersuchungen.