Monte-Carlo-Simulation mit Copula
Quantitatives Risikomanagement
vorgelegt von
Kevin Schellkes und Christian Hendricks
Bergische Universität Wuppertal Fachbereich C - Stochastik Dozent: M.Sc. Brice Hakwa
29. August 2010
Inhaltsverzeichnis
1 Einleitung 2
2 Korrelationsansatz 2
2.1 Herleitung . . . 2
2.2 Portfoliowert in K Tagen . . . 4
2.3 Monte-Carlo-Simulation mit Korrelationsansatz . . . 4
3 Copulaansatz 5 3.1 Gauÿ-Copula . . . 5
3.2 t-Copula . . . 6
3.3 Tailabhängkeit Gauÿ- und t-Copula . . . 7
3.4 Simulation der Renditen . . . 8
3.4.1 Bestimmung der Randverteilungen . . . 10
3.4.2 Copula-Parameterschätzung . . . 12
3.4.3 Praktische Umsetzung mit einer Monte-Carlo-Simulation . . . 14
4 Numerische Tests 15 4.1 Berechnung des Value at Risk . . . 15
4.2 Backtest . . . 16
5 Fazit 17
1 Einleitung
Ziel dieser Arbeit ist es, basierend auf dem Working Paper von Patrick Deuÿ zum Thema Measuring the Value at Risk of a Stock Portfolio - The Copula Approach zwei Verfahren vorzustellen, mit denen an Hand von Monte-Carlo-Simulationen der Value at Risk eines Akti- enportfolios ermittelt werden kann. Das erste Verfahren baut auf dem herkömmlichen Ansatz auf, eine lineare Abhängigkeitsstruktur der Aktienrenditen anzunehmen, während der zweite Ansatz die Abhängigkeit mittels einer Copula erklärt.
2 Korrelationsansatz
2.1 Herleitung
Der Standardansatz geht von einer Aktienkursbewegung aus, die sich gemäÿ der folgenden stochastischen Dierentialgleichung entwickelt:
dSti = µi(St, t)dt+σi(St, t)idWti für0≤t≤T und i= 1, ...I
Die Bewegung der Aktie i wird also durch einen deterministischen Updrift und eine Zufalls- komponente in Form eines Wiener Prozesses Wti ermittelt, wobei Wti ∼ N(0, t) verteilt ist.
Wählt man die Funktionenµi(St, t) undσi(St, t) fest, ergibt sich die Darstellung
Sti = S0iµidt+σiS0idWti für 0≤t≤T mit der analytischen Lösung
Sti = S0iexp
(µi−12σ2i)
| {z }
=:αi
t+σiWti)
(1)
⇔ln(SStii 0
) = αit+σiWti (2)
In Matrixschreibweise, mit
St := (St1, ..., StI) α := (α1, ..., αI) Wt := (Wt1, ..., WtI)
D :=
σ1 0
...
0 σI
lässt sich die Lösung umschreiben
St =
S01
...
S0I
exp
α1
...
αI
t+
σ1 0
...
0 σI
Wt1
...
WtI
Man erkennt leicht, dass die einzelnen Aktienkurse zum Zeitpunkt t unabhängig voneinander sind. In der Realität trit dieses Verhalten allerdings nicht zu. Daher wollen wir im Folgenden annehmen, dass eine Korrelation innerhalb der Aktienkursdynamik besteht. Sie kann durch die Kovarianzmatrix Σ der beobachteten logarithmischen Renditen beschrieben werden und ermöglicht die Modellierung einer linearen Abhängigkeitsstruktur.
Σ =
ρ1,1σ1σ1 . . . ρ1,Iσ1σI
... ... ...
ρI,1σIσ1 . . . ρI,IσIσI
=
σ1 0
...
0 σI
1 ρi,j
...
ρj,i 1
σ1 0
...
0 σI
Ziel ist es nun, einen Zufallsvektor Y ∈ RI zu erzeugen, der der Verteilung Y ∼ N(αt,Σt) genügt1.Y :=αt+ ΣWt erfüllt diese Bedingung nicht, daαt+ ΣWt∼N(αt,ΣΣTt). Erst die Cholesky-Zerlegung von Σ =LLT führt auf das gewünschte Ergebnis:
at+LWt ∼ N(αt, LLTt)
∼ N(αt,Σt)
1gem. (2) , um logarithmische Renditen zu simulieren
2.2 Portfoliowert in K Tagen
Nun möchten wir mittels Monte-Carlo-Simulation den Wert unseres Portfolios in K Tagen vorhersagen. Um verlässliche Daten zu erhalten, sollte die Anzahl N der ins Modell einieÿenden logarithmischen Tagesrenditen deutlich gröÿer sein als der vorherzusagende Zeitraum K. An dieser Stelle werden die täglichen log-Renditen auf den Zeitraum K transformiert, so dass später in der Simulationt= 1 gesetzt werden kann, um den Assetkurs zum Zeitpunkt K zu erhalten.
Wird mit γi(l) für i = 1, ..., I und l = 1, ..., N die logarithmische Tagesrendite der Aktie i bezeichnet, lässt sich die K-Tagesrendite mitδK :=N−1
K
durch
γi,k =
K
X
n=1
γi(kK+n) für k= 0, ..., δK
berechnen. Gilt hierbeiN modK =c mit c6= 0, so werden die letzten c Datensätze vernach- lässigt und nicht weiter berücksichtigt. Der Erwartungswertschätzer der K-Tagesrenditen von Aktie i ist gegeben durch
γiK = 1 δK+ 1
δK
X
k=0
γi,k
Als Parameter für unsere spätere Simulation erhalten wir damit αK :=
γ1K
...
γIK
. Die Kovari- anzmatrix wird aus der transformierten Beobachtungsmatrix XK := (γi,k)i=1,...,I
k=0,...,δK
gewonnen.
In Matlab z.B. mit dem Befehl cov(XK). Nachdem die Parameter geschätzt wurden, kann der Portfoliowert2 in K-Tagen mit einer Monte-Carlo-Simulation berechnet werden.
2.3 Monte-Carlo-Simulation mit Korrelationsansatz Algorithmus 1: Monte-Carlo mit Korrelationsansatz
transformiere Beobachtungsmatrix auf logarithmische K-Tagesrenditen
Schätze die Verteilungsparameter αK und ΣK aus der neuen Beobachtungsmatrix for j= 1→R do
ermittle Y =(y1, ..., yI)∼N(αK,ΣK) fori= 1→I do
Sˆji =S0iexp(yi) end for
Sˆj = 1IPI
l=1Sˆjl (Portfoliowert in der j-ten Simulation) end for
Sˆ= R1 PR
l=1Sˆl (Portfoliowert gem. Monte-Carlo)
2für ein gleichgewichtetes Portfolio
3 Copulaansatz
Im vorherigen Modell wurde eine lineare Abhängigkeit der einzelnen Renditen in Form der Korrelation unterstellt. Es ist allerdings fragwürdig, ob damit alle Formen der Abhängigkeit erklärt werden können. Im folgenden Beispiel sind Realisationen von 2 Zufallsvariablen ange- geben. In beiden Plots weisen die Zufallsvariablen neben den gleichen Randverteilungen auch die gleiche Korrelation auf. Dennoch sind die Abhängigkeitsstrukturen unterschiedlich, was besonders deutlich im unteren und oberen Randbereich zu erkennen ist. Bei Nutzung des Kor- relationsansatzes würde nur die lineare Abhängigkeit in Form der Korrelation berücksichtigt.
Daher wird in diesem Abschnitt die Abhängigkeitsstruktur mittels einer Copula modelliert, die in der Lage ist auch komplexere Abhängigkeitsstrukturen zu erfassen. Wir verwenden dabei die Gauÿ- und t-Copula.
Abbildung 1: Embrechts' Fallacies (siehe [1]) 3.1 Gauÿ-Copula
Die Gauÿ-Copula ist deniert durch eine multivariate Normalverteilung φI(0, P) := φIP der Dimension I mit Korrelationsmatrix P, sowie der univariaten Standardnormalverteilung als Randverteilungenφ.
CPGa(v1, ..., vI) = φIP(φ−1(v1), ..., φ−1(vI))
=
Z φ−1(v1)
−∞
. . .
Z φ−1(vI)
−∞
1
(2π)1/2|P|1/2 exp −12zTP−1z
dz1. . . dzI
mit |P|als Determinante von P und zi =φ−1(vi) für i= 1, ..., I Die Dichte der Gauÿ-Copula ist
cGaP (v1, ..., vI) = |P|−1/2 exp −12zT(P−1−IdI)z
3.2 t-Copula
Weitgehend analog zur Gauÿ-Copula ist die t-Copula deniert. Sie hat neben der Korrelatios- matrix P die Anzahl der Freiheitsgradeν als weiteren Parameter.
Cν,Pt (v1, ..., vI) = tIν,P(t−1ν (v1), ..., t−1ν (vI))
=
Z t−1ν (v1)
−∞
. . .
Z t−1ν (vI)
−∞
Γ(ν+I 2 ) Γ(ν
2)√
(νπ)I|P|
1 +zTPν−1z ν+I2
dz1. . . dzI
mit Γ als Gammafunktion undzi =t−1ν (vi). Die Dichte der t-Copula ist
ctν,P(v1, ..., vI) = |P|−1/2
Γ(ν+I 2 ) Γ(ν
2)
Γ(ν 2) Γ(ν+1 2 )
I
1+zTP−1z ν
−ν+I 2
QI
i=1 1+z2i ν
!−ν+1 2
0 0.2 0.4 0.6 0.8 1
0 0.5 10 0.5 1
X Verteilungsfunktion Gauß−Copula mit ρ=0.5
Y 0 0.2 0.4 0.6 0.8 1
0 0.5 10 1 2 3
X Dichtefunktion Gauß−Copula mit ρ=0.5
Y
0 0.2 0.4 0.6 0.8 1
0 0.5 10 0.5 1
X Verteilungsfunktion t−Copula mit ρ=0.5 und ν=5
Y 0 0.2 0.4 0.6 0.8 1
0 0.5 10 2 4
X Dichtefunktion t−Copula mit ρ=0.5 und ν=5
Y
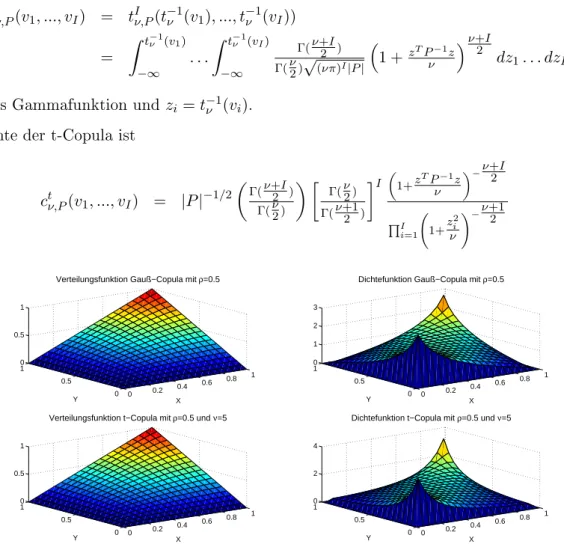
Abbildung 2: Verteilungs- und Dichtefunktion der bivariaten Gauÿ- und t-Copula
3.3 Tailabhängkeit Gauÿ- und t-Copula
Bei der Simulation eines Portfolios sind für uns vor allem die Wahrscheinlichkeiten von ex- tremen Verlusten von Bedeutung. Eine Maÿzahl für diese Extrema ist der untere bzw. obere Tail-Abhängigkeitskoezient.
Denition 1. allgemeine Tailabhängigkeit Für zwei stetige Zufallsvariablen X und Y mit RandverteilungenFX undFY ist, sofern der Limes existiert, der untere Abhängigkeitskoezient deniert durch
λL(X, Y) := lim
q→0+P(X ≤FX−1(q)|Y ≤FY−1(q)) und der obere Koezient durch
λU(X, Y) := lim
q→1−P(X > FX−1(q)|Y > FY−1(q))
Denition 2. Tailabhängigkeit mit Copula Für zwei stetige Zufallsvariablen X und Y mit Randverteilungen FX,FY und Copula C ist für q =FX(a) = FY(b) der untere Abhängigkeits- koezient deniert durch
λL:= lim
q→0+
C(q, q) q und der obere Koezient durch
λU := lim
q→1−
1−2q+C(q, q) 1−q
Ist die Korrelation zwischen zwei Zufallsvariablen 6= ±1, so folgt für die Gauÿ-Copula λL = λU = 0. Daraus folgt, dass selbst bei einer extrem starken positiven oder negativen Korrela- tion 6= ±1 zweier Zufallsvariablen, extreme Ausprägungen bei der Gauÿ-Copula unabhängig voneinader auftreten. Auf Grund dieser asymptotischen Unabhängigkeit eignet sie sich nicht zur Modellierung von Risiken mit Tail-Abhängigkeiten. Bei der t-Copula gilt für ρ >−1 stets λ >0. Extreme Ausprägungen treten also tendenziell gleichzeitig auf, was die t-Copula geeignet erscheinen lässt, um Risiken mit Tail-Abhängigkeit zu simulieren3.
3gem. [5]
3.4 Simulation der Renditen
Die Simulation der Gauÿ- und t-Copula erfolgt weitgehend analog und wird an dieser Stelle mit Hilfe des Satzes von Sklar dargestellt.
Satz 1. Satz von Sklar Sei F eine gemeinsame Verteilungsfunktion mit Randverteilungen F1, ..., FI, dann gibt es eine Copula derart, dass
F(z1, ..., zI) = C(F1(z1), ..., FI(zI))
für alle z1, ..., zI ∈R. Falls die Randverteilungen stetig sind, ist C eindeutig. Andernfals ist C nur auf dem kartesischen Produkt der Wertebereiche vonFi füri= 1, ..., I eindeutig bestimmt.
Mit Hilde des Satzes von Sklar kann die Simulation der Renditen grob in 2 Schritte aufgeteilt werden.
Schritt 1: Modellierung der Einzelrenditen bzw. der Randverteilungen F1, ..., FI
Schritt 2: Wahl einer geeigneten Copula, sowie Anpassung ihrer Parameter - Modellierung der Abhängigkeit der Einzelrisiken
Abbildung 3: Aufspaltung nach Sklar
Denieren wir V1 :=F1(Z1), ..., VI :=FI(ZI), ergibt sich aus dem Satz von Sklar eine Berech- nungsmethode der Copula durch die Inversen der Randverteilungen
C(v1, ..., vI) =F(F1−1(v1), ..., FI−1(vI)) Algorithmus 2: Simulation Copula
1. GeneriereZ ∼F und erhalte Realisationz= (z1, ..., zI)T
2. Wende Randverteilung Fi auf jeden Eintrag zi des Vektors z an und erhalte v = (F1(z1), ..., FI(zI))T
Der Vektor v erfüllt v∼C, denn:
Z ∼F verteilt undZi ∼Fi verteilt, wobeiFi eine stetige und monoton wachsende Randver- teilung ist. Daraus folgt, dass Vi ∼ U(0,1)verteilt, also gilt für die gemeinsame Verteilungs-
funktionFV
FV(v1, ..., vI) = P(V1≤v1, ..., VI ≤vI)
= P(F1(Z1)≤v1, ..., FI(ZI)≤vI)
= P(Z1 ≤F1−1(v1), ..., ZI ≤FI−1(vI))
= F(F1−1(v1), ..., FI−1(vI))
FürF =φIP undFi−1=φ−1 bzw.F =tρ,ν undFi−1 =t−1ν ergeben sich damit die Gauÿ- bzw.
t-Copula.
Um damit unsere logarithmischen Renditen X = (X1, ..., XI) ∼ FX mit der entsprechenden Verteilung zu ermitteln, führen wir die Schritte 1 und 2 in umgekehrter Reihenfolge aus und es ergibt sich der folgende Algorithmus:
Algorithmus 3: Simulation abhängiger Renditen
1. GeneriereV ∼C mit Algorithmus 2 und erhalte Realisationv= (v1, ..., vI)T
2. Wende Inverse der empirischen RandverteilungFi auf jeden Eintragvi des Vektors v an und erhaltex= (F1−1(v1), ..., FI−1(vI))T
Der erhaltene Vektor x erfüllt die gewünschte Verteilung und simuliert damit die logarithmi- schen Renditen mit der entsprechenden Abhängigkeit, denn:
FX(x1, ..., xI) = P(X1≤x1, ..., XI ≤xI)
= P(F1−1(V1)≤x1, ..., FI−1(VI)≤xI)
= P(v1 ≤F1(x1), ..., vI ≤FI(xI))
= C(F1(x1), ..., FI(xI))da V ∼C
3.4.1 Bestimmung der Randverteilungen
Zur Simulation der Randverteilungen bieten es sich an, entweder eine Verteilungsannahme zu machen und daraufhin die Parameter zu schätzen oder alternativ die empirischen Randvertei- lungen zu nutzen. Wir wollen uns innerhalb dieser Arbeit auf die zweite Variante beschränken.
Die empirischen Randverteilungen werden aus den historischen Daten ermittelt. Bezeichnen wir mitX := (xi,j)i=1,...,I
j=1,...,N die Beobachtungsmatrix, die an Eintrag i, j die logarithmische Ta- gesrendite der Aktie i in der j-ten Beobachtung enthält, so ist die empirische Randverteilung deniert durch:
Denition 3. empirische Randverteilung Fi,N(x) := 1
N + 1
N
X
n=1
1{xi,n≤x}(x) für i= 1, ..., I
1{xi,n≤x}(x) bezeichnet dabei die Indikatorfunktion. Es wird durch den Faktor N + 1dividiert, um Fi,N ∈[0,1) zu gewährleisten.
Sie kann ezient und einfach für die einzelnen Beobachtungen xi,j für i = 1, ..., I und j = 1, ..., N berechnet werden, wenn man ausnutzt, dass
N
X
n=1
1{xi,n≤x}(xi,j) = rank(xi,j)
⇔Fi,N(xi,j) = rank(xi,j) N + 1
In Matlab kann die Berechnung mit folgender Funktion implementiert werden:
function U = Randverteilung(data) [I,N] = size(data);
U = zeros(I,N);
for i=1 : I
temp1 = [data(i,:)', (1:N)'];
temp1 = sortrows(temp1,1);
temp1 = [temp1, (1:N)'./(N+1)];
temp1 = sortrows(temp1,2);
U(i,:)= temp1(:,3)';
end
Damit erhalten wir die Randverteilungsmatrix U = (ui,j)i=1,...,I
j=1,...,N mit ui,j = Fi,N(xi,j) der Beobachtungen.
−0.030 −0.02 −0.01 0 0.01 0.02 0.03 0.2
0.4 0.6 0.8 1
FDt. Telekom,40(x)
−0.030 −0.02 −0.01 0 0.01 0.02 0.03 0.04 0.05 0.2
0.4 0.6 0.8 1
logarithmische Rendite FRWE,40(x)
−0.20 −0.15 −0.1 −0.05 0 0.05 0.1 0.15
0.2 0.4 0.6 0.8 1
FDt. Telekom, 1000(x)
−0.20 −0.15 −0.1 −0.05 0 0.05 0.1 0.15
0.2 0.4 0.6 0.8 1
FRWE,1000(x)
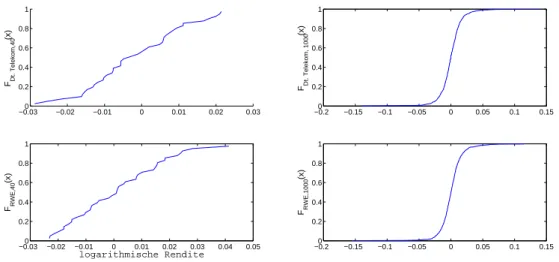
Abbildung 4: empirische Randverteilgungen
3.4.2 Copula-Parameterschätzung
Um die Copula gemäÿ Algorithmus 2 simulieren zu können, müssen die Parameter der Copula erst entsprechend geschätzt werden. Bei der Gauÿ-Copula gilt es die Korrelationskoezienten und bei der t-Copula neben den Korrelationskoezienten noch die Anzahl der Freiheitsgrade zu schätzen.
Maximum-Likelihood-Methode
Wir bedienen uns an dieser Stelle des Maximum-Likelihood-Schätzers. Idee dieses Schätzers ist es, diejenigen Parameter zu wählen, die auf Grund der gemachten Beobachtungen bzw. Reali- sationen am plausibelsten erscheinen. Wird mit θ der Parameter der Copula und werden mit θi für i = 1, ..., I die Parameter der Randverteilungen bezeichnet, so lässt sich unter der An- nahme, dass von stochastisch unabhängigen, identisch verteilten Beobachtungen ausgegangen wird, der Maximum-Likelihood-Schätzer als Maximum der folgenden Funktion aufschreiben
L(x, θ, θ1, ..., θI) =
N
Y
i=1
c(F1(x1,i, θ1), ..., FI(xI,i, θI), θ)
I
Y
j=1
fi(xj,i, θj) wobei c die Dichte der Copula ist, mit
c(v1, ..., vI, θ) = ∂IC(v1, ..., vI, θ)
∂v1...∂vI
Nutzt man aus, dass der Logarithmus monoton ist und das Maximum der logarithmischen Dichte an der gleichen Stelle angenommen wird wie von der nicht logarithmierten Rendite und vernachlässigen wir die Dichten der Randverteilungen, da ihre Parameter schon implizit durch die empirischen Randverteilungen geschätzt wurden, so folgt der Log-Maximum-Likelihood- Schätzer
l(x, θ) =
N
X
i=1
ln(c(F1(x1,i), ..., FI(xI,i), θ))
Da die genauen Randverteilungen nicht bekannt sind, sondern nur ihre empirischen Randver- teilungen, die in der Matrix U berechnet wurden, wird mit den Pseudorealisationen der Rand- verteilungen in den beobachteten Realisationen gearbeitet. Es wird die sogenannte Pseude-Log- Maximum-Likelihoodfunktion bezüglichθ maximiert
l(x, θ) =
N
X
i=1
ln(c(u1,i, ..., uI,i, θ))mit uk,j =Fk(xk,j)
Gauÿ-Copula-Parameterschätzung
Das Maximum des Log-Likelihood-Schätzers kann bei der Gauÿcopula4 für den Parameter P mittels
φ−1(U) :=
φ−1(u1,1) . . . φ−1(u1,N) ... ... ...
φ−1(uI,1) . . . φ−1(uI,N)
4gem. [4] Beispiel 5.53
und der Korrelation der Einträge vonφ−1(U)gefunden werden Pˆ =ρ(φ−1(U))
Algorithmus 4: Parameterschätzung Gauÿ-Copula
1. Bestimme die empirischen VerteilungsfunktionenFi,N für i= 1, ..., I
2. Wende die erhaltenen Verteilunsfunktionen auf die Beobachtungsmatrix X an und speichere Ergebnisse in U ∈RI×N
3. Transformiere U aufφ−1(U)
4. Berechne die KorrelationsmatrixPˆ ∈[−1,1]I×I von φ−1(U) t-Copula-Parameterschätzung
Der Parameter P der t-Copula kann über die Beziehung zum Kendall'schen Rangkorrelati- onskoezienten τ gewonnen werden Pˆ = sin(π2τ(U)). Die Freiheitsgrade ν werden mittels Maximum-Likelihood-Methode geschätzt
maxν l(x, ν,Pˆ) Algorithmus 5: Parameterschätzung t-Copula
1. Bestimme die empirischen VerteilungsfunktionenFi,N für i= 1, ..., I
2. Wende die erhaltenen Verteilunsfunktionen auf die Beobachtungsmatrix X an und speichere Ergebnisse in U ∈RI×N
3. Berechne die Kendall'schen Rangkorrelationskoezienten mit Pˆ = sin(π2τ(U))und erhaltePˆ ∈[−1,1]I×I
4. Maximiere den Log-Maximum-Likelidhoodschätzer max
ν l(x, ν,Pˆ)mit geeigneten nu- merischen Methoden
3.4.3 Praktische Umsetzung mit einer Monte-Carlo-Simulation
Nachdem jetzt alle Einzelschritte beschrieben wurden, müssen diese noch praktisch umgesetzt werden. Da wir, ähnlich wie im 2. Kapitel zur Simulation an Hand des Korrelationsansatzes, auch diesmal den Portfoliowert in K Tagen simulieren möchten, gilt es zunächst die täglichen log-Renditen in logarithmische K-Tagesrenditen zu transformieren. Dies erfolgt analog zu dem bereits bekannten Ansatz aus dem vorherigen Kapitel. Ausgehend von der nun erhaltenen Be- obachtunsmatrixXK werden die empirischen Randverteilungen berechnet, so dass wir die zur Beobachtungmatrix gehörenden Randverteilungsrealisationen in MatrixUK ∈RI×δK erhalten.
Nachdem die Copulaparameter geschätzt wurden, kann im Anschluss der Vektor v ∼ C mit Algorithmus 2 simuliert werden. Dieser wird, gemäÿ Algorithmus 3, in die inversen Randver- teilungen eingesetzt. Hierbei ergibt sich das Problem, dass wir nur eine diskrete Darstellung der einzelnenFi−1 für die Beobachtungen kennen, so dass im Allgemeinen gilt Fi−1(vi) 6=xi,j
für alle j ∈ {1, ..., N}. Ist N groÿ genug, so sind die Randverteilungen fast kontinuierlich, so dass
Fi−1(vi) ≈ xi,j∗
i für (3)
ji∗ = min
j∈{1,...,δK}|ui,j−vi| für i= 1, ..., I (4) also
Fi−1(vi) ≈ Fi−1(ui,j∗
i) =xi,j∗
i (5)
gilt. Somit erhalten wir eine Annäherung an die inversen Randverteilungen. Alternativ könnte man die Zwischenräume auch interpolieren.
Führt man die Einzelschritte R-mal hintereinander aus und ermittelt aus den erhaltenen Rendi- ten den Portfoliowert5, erhält man zusammengefasst den folgenden Monte-Carlo-Algorithmus:
Algorithmus 6: Monte-Carlo-Simulation mit Copula
transformiere Beobachtungsmatrix auf logarithmische K-Tagesrenditen berechne empirische Randverteilungsmatrix UK
schätze Copula-Parameter for j= 1→R do
erhalte Vektorx= (x1, ..., xI) aus Algorithmus 3 unter Verwendung von (4) und (5) fori= 1→I do
Sˆji =S0iexp(xi) end for
Sˆj = 1IPI
l=1Sˆjl (Portfoliowert in der j-ten Simulation) end for
Sˆ= R1 PR
l=1Sˆl (Portfoliowert gem. Monte-Carlo)
5für ein gleichgewichtetes Portfolio
4 Numerische Tests
4.1 Berechnung des Value at Risk
Innerhalb des Risikomanagements ist allerdings nicht der Portfoliowert von primären Interesse, sondern vielmehr das Risikokapital, das auf Grund gesetzlicher Bestimmungen ermittelt wer- den muss (z.B. zur Errechnung des Mindestkapitals/Solvenzkapitals). Der Value at Risk (VaR) dient diesbezüglich als Maÿzahl des Risikos.
Denition 4. Value at Risk
V aR(X, α) := FX−1(α)
FX−1 = min{x|FX(x)≥α}
wobei FX−1 die Quantilfunktion der Verteilungsfunktion FX bezeichnet.
Interpretieren lässt sich der VaR als Verlust, der mit der Mindestwahrscheinlichkeit α nicht überschritten wird. Vice versa beträgt die Wahrscheinlichkeit, dass Verluste, die gröÿer als der VaR sind, höchstens 1−α.
Um den VaR praktisch berechnen zu können, benötigen wir nicht den Portfoliowert, sondern die einzelnen AusgängeSˆj fürj= 1, ..., Raus den Portfoliosimulationen, um daraus die Dichte approximieren zu können. Die folgenden numerischen Experimente geben immer den prozen- tualen Wert des Portfolios gegenüber dem Anfangswert von 1 bzw. 100%6 an. Das Portfolio besteht aus den Aktien der 4 Gesellschaften Dt. Telekom AG, RWE AG, BMW AG und In- neon AG mit jeweils identischer Gewichtung und N = 1158 in der Zeit vom 02.01.2007 bis 29.07.2011.
0.7 VaR 0.9 1 1.1 1.2 1.3 1.4 1.5
0 1 2 3 4 5 6
K=20
0.7 VaR 1 1.2 1.4 1.6 1.8
0 2 4 6 8 10 12
K=10
Gewinn
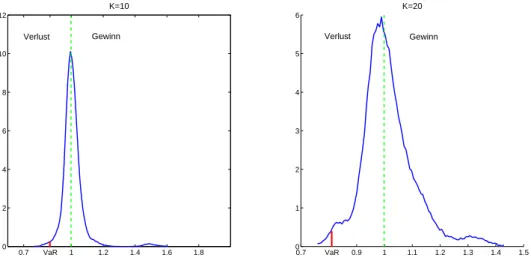
Verlust Verlust Gewinn
Abbildung 5: Dichte und VaR bei 100.000 Simulationen mit t-Copula fürα= 0.99 Da die Verluste auf der linken Seite der Dichtefunktion liegen, wird der Value at Risk mittels Matlab mitV aRα= quantile( ˆSr,1−α) berechnet.
6indem AktienstartwerteS0i= 1gesetzt wurden
Tage Kondenzniveau COP Gauÿ-Copula COP t-Copula COR
K= 5 α= 0.99 0.9076 0.9044 0.9245
K= 10 α= 0.99 0.8703 0.8655 0.8899
K= 20 α= 0.99 0.8158 0.8105 0.8394
Tabelle 1: VaR - Berechnung
Der VaR unter Verwendung der Copula-Ansätze ist gegenüber dem Korrelationsansatz in bei- den Zeitperioden niedriger. Im Vergleich der beiden Copulaansätze ist der VaR der t-Copula geringer. Für den Praktiker bedeutet dies, dass bei der Verwendung der Copulas mehr Risiko- kapital vorgehalten werden muss.
4.2 Backtest
Im vorherigen Abschnitt konnte experimentell festgestellt werden, dass bei Verwendung der Copulaansätze in der Praxis mehr Risikokapital bereitgestellt werden musste. Es stellt sich die Frage, ob dieses wirklich gemacht werden muss. Dies wollen wir innerhalb eines Backtests beantworten.
0 20 40 60 80 100 120
−0.2
−0.15
−0.1
−0.05 0 0.05 0.1 0.15 0.2 0.25
K = 10
0 10 20 30 40 50 60
−0.25
−0.2
−0.15
−0.1
−0.05 0 0.05 0.1 0.15 0.2 0.25
K = 20
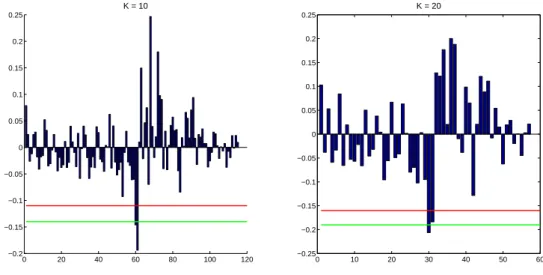
Abbildung 6: Backtest mit historischen logarithmierten K-Tages-Renditen
Betrachtet man die historischen logarithmischen Renditen im Vergleich zum VaR mit beiden Ansätzen, so ist zu erkennen, dass der Korrelationsansatz (rote Linie) schlechter abschneidet als die Copulaansätze (grüne Linie). Obwohl auch der VaR mittels Copula nicht alle Renditen abdecken kann, deckt er sie dennoch besser ab als der Korrelationsansatz. Das Risiko wird beim Korrelationsansatz deutlich unterschätzt, was dafür spricht, dass nicht alle Abhängigkeiten durch die Korrelation erfasst wurden.
Es bleibt noch zu klären, welche der beiden Copulaansätze bessere Ergebnisse erzielt. Gemäÿ der Arbeit von Patrick Deuÿ erzielt die t-Copula bessere Ergebnisse, was er auf die starke untere Tailabhängigkeit der Aktienrenditen zurückführt, die durch die t-Copula besser abgebildet werden kann. Ob wirklich eine Tailabhängigkeit besteht, soll an dieser Stelle an einem Beispiel mit dem unteren Tailabhängigkeitsschätzer getestet werden.
Denition 5. Tailabhängigkeitsschätzer7
bλL(q) := #{(x, y)∈Beob.:x < FX−1(q)∧y < FY−1(q)}
#{(x, y)∈Beob.:y < FY−1(q)}
bλU(q) := #{(x, y)∈Beob.:x > FX−1(q)∧y > FY−1(q)}
#{(x, y)∈Beob.:y > FY−1(q)}
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
q
Bedingte Wahrscheinlichkeit
Abbildung 7: unterer Tailabhängigkeitsschätzer für tägliche logarithmische Renditen der Tele- kom AG und RWE AG
Es zeigt sich, dass im Testdatensatz eine starke untere Tailabhängigkeit herrscht und für die- sen Datensatz die These der unteren Tailabhängigkeit von Aktienrenditen als wahr angesehen werden kann.
5 Fazit
Innerhalb dieser Arbeit wurde sowohl der Korrelationsansatz und auch der Copulaansatz zur Ermittlung des Value at Risk eines Portfolios praxisnah vorgestellt.
In dem anschlieÿenden numerischen Experiment konnte die Überlegenheit des Copulaansat- zes, auch komplexere Abhängigkeitsstrukturen zu erfassen, an realen Daten getestet werden.
Der Backtest zeigte, dass der herkömmliche Korrelationsansatz das Risiko systematisch un- terschätzt. Diese Unterschätzung führt im Praxiseinsatz zu zu niedrigen Risikokapitalreserven und hat bei Börsencrashs unter Umständen dramatische Auswirkungen auf die Unternehmen.
Daher sollte der Copulaansatz, trotz eventuell höherer Kapitalkosten, dem Korrelationansatz vorgezogen werden.
7gem. [2]
Literatur
[1] Abhängigkeitsmessung: Neuere Entwicklungen und Anwen-
dungen, (03. Dezember 2007) www.statistik.wiso.uni −
erlangen.de/lehre/diplom/versicherungsoekonomie/cops.pdf, Matthias Fischer [2] Abhängigkeitsmodell anhand von Copulas, (28. Januar 2010) www.opt.math.tu −
graz.ac.at/ cela/V orlesungen/Risk09−10/praesentationSchitteretal.pdf, Lisa Stadl- müller, Christian Schitter, Peter Scheibelhofer, Wolfgang Draxler
[3] Measuring the Value at Risk of a Stock Portfolio - The Copula Approach, (Januar 2009) www.imacm.uni−wuppertal.de/f ileadmin/imacm/preprints/amna0902.pdf, Patrick Deuÿ
[4] Quantitative Risk Management, (26. September 2005), A. McNeil, R. Frey, P.Embrechts [5] Risikoanalyse: Modellierung, Beurteilung und Management von Risiken mit Praxisbei-
spielen, Auage: 1 (15. September 2009), Claudia Cottin, Sebastian Döhler
![Abbildung 1: Embrechts' Fallacies (siehe [1]) 3.1 Gauÿ-Copula](https://thumb-eu.123doks.com/thumbv2/1library_info/4365324.1576660/6.892.120.785.386.700/abbildung-embrechts-fallacies-siehe-gauÿ-copula.webp)