4 Elementare Funktionen

(1)

4 Elementare Funktionen

In diesem Kapitel werden elementare Funktionen, die u.a. zur Beschreibung von physikalischen Vorgängen notwendig sind, angegeben und allgemeine Funktionseigenschaften zur Charakterisierung dieser Funktionen bereitgestellt. Neben den Polynomen werden die gebrochenrationalen Funktionen qualitativ diskutiert. Potenz- und Wurzelfunktionen sowie Exponential- und Logarithmusfunktion werden im Zusammenhang mit wichtigen Anwendungen eingeführt. Zur Beschreibung von Wechselspannungen bzw. harmonischen Schwingungen werden die trigonometrischen Funktionen mit den zugehörigen Umkehr- funktionen eingeführt.

4.1 Allgemeine Funktionseigenschaften

4.1

In diesem Abschnitt werden grundlegende Begriﬀ wie z.B. Funktion und Umkehrfunk- tion, Nullstellen und Symmetrieverhalten als auch Monotonieverhalten wiederholt. Diese Eigenschaften werden anschließend zur Beschreibung elementarer Funktionen verwendet.

4.1.1 Grundbegriﬀe

Für die mathematische Formulierung naturwissenschaftlicher Gesetzmäßigkei- ten ist der Begriff derFunktionunentbehrlich. Nahezu alle quantitativen Aus- sagen werden in Form eines funktionalen Zusammenhangs aufgestellt. Bevor der Begriff der Funktion mathematisch präzisiert wird, soll seine zentrale Stel- lung anhand technischer Beispiele sichtbar gemacht werden.

Beispiel 4.1 (Weg-Zeit-Diagramm):Bewegungsabl¨aufe werden in sog.Weg- Zeit-Diagrammenwie in Abb. 4.1 graphisch dargestellt.

s(t)

t0 t1 t2 t3 t Abb. 4.1.Weg-Zeit-Diagramm

Im Intervall t₀ ≤ t ≤ t₁ findet eine beschleunigte Bewegung, im Intervall t₁ ≤ t ≤ t₂ eine gleichförmige Bewegung und im Intervall t₂ ≤ t ≤ t₃ eine abgebremste Bewegung statt. Charakteristisch für den dargestellten Vorgang ist, dass zu jedem Zeitpunkt t ∈ [t₀, t₃] der Ort s(t) eindeutig bestimmt ist.

Durch diese Zuordnung wird eineFunktiondeﬁniert.

(2)

Deﬁnition: (Funktion).SeiID⊂IReine Teilmenge vonIR.Unter einer reellen Funktionf auf IDversteht man eine Abbildung

f : ID → IR x → f(x).

Die Abbildung f bildet jedes Element ausIDeindeutig auf ein Element inIR ab.

Die Menge ID heißt Deﬁnitionsbereich von f und die Menge IR der Zielbereichvonf. Die Menge

VW:=f(ID) :={f(x) :x∈ID}

heißt derWertebereichvonf. Man nenntf(x)den Funktionswert oder Funktionsausdruck an der Stellex.

Zur graphischen Darstellung einer Funktion verwenden wir das kartesische Ko- ordinatensystem IR×IR = {(x, y) :x ∈IR, y ∈IR}, in dem jeder Punkt P der Ebene durch ein Zahlenpaar(x, y)eindeutig beschrieben wird. Zur geome- trischen Veranschaulichung der Funktion zeichnet man die Menge der Punkte (x, f(x))in ein Koordinatensystem und erh¨alt so die zugeh¨orige Kurve.

Deﬁnition: Unter dem Graphen G_f einer Funktion f : ID → IR mit x→f(x)verstehen wir die Menge aller Paare(x, y):

G_f:={(x, y) :x∈ID und y=f(x)}.

Beispiele f¨ur Funktionen aus der Technik:

Beispiel 4.2 (Freier Fall): Das Weg-Zeit-Gesetz beim freien Fall aus der H¨ohes₀ mit Anfangsgeschwindigkeitv₀ lautet

s(t) = 1

2g t²+v₀t+s₀, t≥0, wenng= 9,81_s^m₂ die Erdbeschleunigung ist.

Beispiel 4.3 (Plattenkondensator):Wird an einem Plattenkondensator eine LadungQangelegt, so ist die resultierende Spannung

U(Q) = 1 CQ, wennC die Kapazit¨at des Kondensators ist.

(3)

Beispiel 4.4 (Gleichstromkreis):In einem elektrischen Gleichstromkreis ist die Stromst¨arke Iabh¨angig von der angelegten GleichspannungU. Es gilt

I(U) = U R,

wennR der Ohmsche Widerstand der Schaltung ist.

Beispiel 4.5 (W¨armeausdehnung von Gasen (Gay-Lussac)):IstV₀das Volumen eines idealen Gases bei TemperaturT₀,so gilt bei konstantem Druck pf¨ur das Volumen bei der TemperaturT

V(T) =V₀(1 +γ (T −T₀)), T ≥T₀, wennγ die W¨armeausdehnungskonstante ist.

Beispiel 4.6 (Barometrische Höhenformel):Für den Luftdruck pin der Höhehüber dem Erdboden gilt näherungsweise

p(h) =p₀e⁻^H^h, h≥0, wennH = _ρ^p⁰

0·g ≈8km undp₀, ρ₀ Luftdruck und -dichte am Erdboden sind.

Diesen physikalischen Gesetzmäßigkeiten ist gemeinsam, dass zu einer unab- hängigen Größet, Q, U, T, hdie physikalische Größes(t),U(Q),I(U), V(T) bzw.p(h)eindeutigberechenbar ist. Man spricht daher auch oftmals von der unabhängigen Variablenxund derabhängigen Variablen(= Funktion)f(x).

Mathematische Beispiele:

Beispiel 4.7. f :IR→IR mitx→f(x) =cheißtkonstante Funktion.

Beispiel 4.8. id_IR:IR→IR mitx→id_IR(x) =xheißtidentische Funktion.

Beispiel 4.9. abs:IR→IR mitx→abs(x) =|x|heißt Betragsfunktion.

7. Konstante Funktion 8. Identische Funktion 9. Betragsfunktion

(4)

Beispiel 4.10.sqr:IR→IR mitx→sqr(x) =x² heißtQuadratfunktion.

Beispiel 4.11.sqrt:IR_≥₀→IR mitx→sqrt(x) =√

xheißtWurzelfunktion.

Beispiel 4.12.exp :IR→IR mitx→exp (x) =e^xheißtExponentialfunktion.

10. Quadratfunktion 11. Wurzelfunktion 12. Exponentialfunktion

Beispiel 4.13.sin :IR→IR mitx→sin (x)heißtSinusfunktion.

13. Sinusfunktion

^! ^Achtung: Es gibt auch Funktionen, die man nicht zeichnen kann:

Beispiel 4.14.f :IR→IR mitx→f(x) =

0 falls x rational 1 falls x irrational.

Bemerkung:Im Hinblick auf die Programmierung bzw. der Anwendung von Maple ist zu unterscheiden zwischen einer Funktion und einem Ausdruck (bzw. Funktionsausdruck): Z.B.sqrt(x) ist ein Ausdruck f¨ur √

x, welcher zu gegebenemxdie Wurzel ausxdarstellt. Hingegen istsqrt eine Funktion, die an einer Stellexausgewertet werden kann. Eine Funktion ist mehr als nur der Funktionsausdruck: Jede Funktion besteht aus Deﬁnitionsbereich, Zielbereich und einer Funktionszuweisung.

Anwendungsbeispiel 4.15 (Logarithmische Darstellungen).

Häufig werden in Physik und Technik logarithmische oder doppel-logarithmische Darstellungen der Messergebnisse verwendet, um exponentielle, potenzielle oder logarithmische Gesetzmäßigkeiten aufzuzeigen.

(5)

(1) Liegt ein exponentielles Gesetz vor y=c a^x,

so liefert eine logarithmische Skalierung dery-Achse log(y) =log(c) +x·log(a)

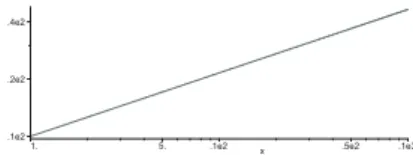
als Graphen eine Gerade mit der Steigunglog(a)und dem Achsenabschnitt log(c). Dabei d¨urfen die Funktionswerte nur positive Werte enthalten, da der Logarithmus nur f¨ur positive reelle Zahlen deﬁniert ist. Beispielswei- se wird durch die logarithmische Skalierung der y-Achse eine allgemeine Exponentialfunktiony= 10·4⁻^xals Gerade gezeichnet.

Abb. 4.2.Logarithmische Darstellung der Funktiony= 10·4⁻^x.

(2) Liegt eine allgemeine Potenzfunktion vor y=a x^b,

dann liefert eine doppel-logarithmische Auftragung log(y) =log(a) +b·log(x)

als Graphen eine Gerade mit der Steigung b und dem Achsenabschnitt log(a). Sowohl derx-Bereich als auch die zugehörigen Funktionswerte dür- fen nur positive Werte enthalten, da der Logarithmus nur für positive reelle Zahlen definiert ist. Eine doppel-logarithmische Auftragung der Potenz- funktiony= 10x¹³ liefert die folgende Gerade:

Abb. 4.3.Doppel-logarithmische Darstellung der Funktiony= 10x¹3.

(3) Liegt ein logarithmisches Gesetz der Formy=a log(x)+bvor, dann liefert die logarithmische Auftragung derx-Achse eine Gerade mit der Steigung aund dem Achsenabschnitt b.

(6)

4.1.2 Allgemeine Funktionseigenschaften Nullstellen

Deﬁnition:Eine Funktionf besitzt inx₀ eine Nullstelle,wenn f(x₀) = 0.

Beispiele 4.16:

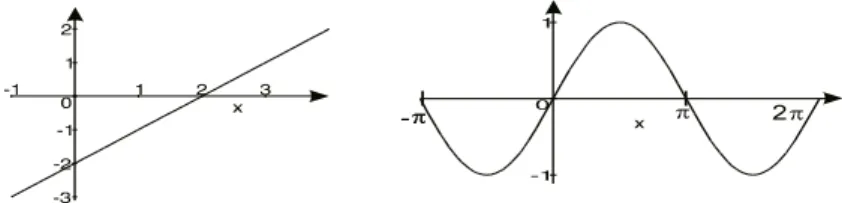
1 Die Funktionf(x) =x−2schneidet diex-Achse an der Stellex₀= 2.

2 Die Funktionf(x) = sin (x)hat unendlich viele Nullstellen :0,±π,±2π, . . .

Abb. 4.4.Nullstellen von Funktionen

Symmetrieverhalten

Definition:Eine Funktionf mit symmetrischem Definitionsbereich heißt gerade,wenn für alle x∈IDgilt

f(−x) =f(x).

Bemerkung:Die Funktionskurve einer geraden Funktion istspiegelsymme- trischzury-Achse.

Beispiele 4.17:

1 Die Funktionf(x) =x² ist gerade.

2 Die Funktionf(x) = cosxist gerade.

3 Jede Potenzfunktionf(x) =xⁿ mit gerademnist gerade.

(7)

Abb. 4.5.Gerade Funktionenx²und cos(x): Spiegelsymmetrisch zur y-Achse

Definition:Eine Funktionf mit symmetrischem Definitionsbereich heißt ungerade, wenn für alle x∈IDgilt

f(−x) =−f(x).

Bemerkung:Die Funktionskurve einer ungeraden Funktion ist punktsym- metrischzum Ursprung.

Beispiele 4.18:

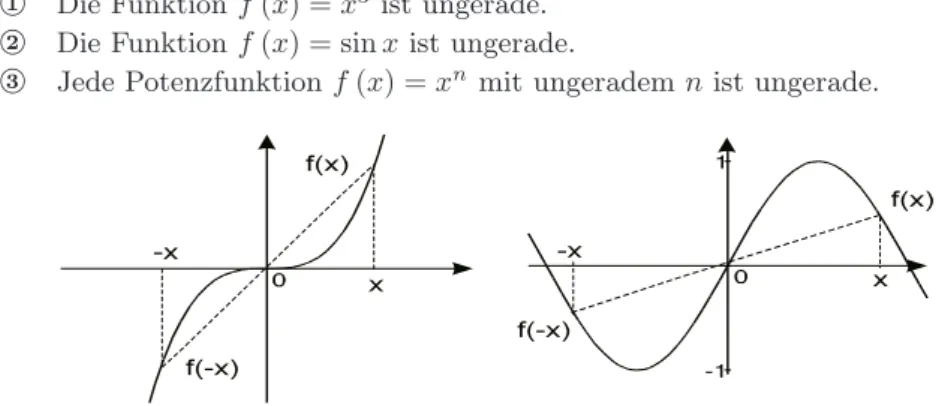
1 Die Funktionf(x) =x³ist ungerade.

2 Die Funktionf(x) = sinxist ungerade.

3 Jede Potenzfunktionf(x) =xⁿ mit ungeradem nist ungerade.

Abb. 4.6.Ungerade Funktionenx³und sin(x): Spiegelsymmetrisch zum Ursprung

Monotonie

Deﬁnition:Eine Funktionf :ID→IRheißt

monoton wachsend,falls f(x₁)≤f(x₂). streng monoton wachsend,falls f(x₁)< f(x₂). monoton fallend,falls f(x₁)≥f(x₂). streng monoton fallend,falls f(x₁)> f(x₂). f¨ur alle x₁, x₂∈IDmit x₁< x₂ gilt.

(8)

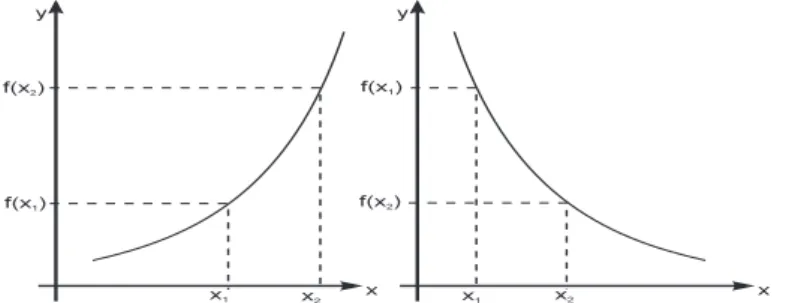
Bemerkung:Eine streng monoton wachsende Funktionf (Abb. 4.7 (a)) hat also die Eigenschaft, dass zum kleinerenx-Wert der kleinere Funktionswert ge- hört. Bei einer streng monoton fallenden Funktion (Abb. 4.7 (b)) ist es genau umgekehrt: Zum kleinerenx-Wert gehört der größere Funktionswert.

Abb. 4.7.Streng monoton wachsende (a) und streng monoton fallende (b) Funktionen

Beispiele 4.19:

1 Streng monoton wachsende Funktionen:

(i) Jede Gerade mit positiver Steigung.

(ii) Die Funktion f(x) =x³.

(iii) Die Funktion f :IR_≥0→IR mitf(t) =y₀

1−e⁻^t/t⁰ .

2 Der Ladevorgang eines Kondensators entspricht einer streng monoton wach- senden Funktion: Beim Laden eines Kondensators C ¨uber einem Widerstand R mit der Spannung U₀ ist der Zeitverlauf der Spannung am Kondensator gegeben durch

U(t) =U₀

1−e⁻^t/RC

. 3 Streng monoton fallende Funktionen:

(i) Jede Gerade mit negativer Steigung.

(ii) Die Funktion f :IR→IR mitf(t) =y₀e⁻^t/t⁰.

4 Der radioaktive Zerfall entspricht einer streng monoton fallenden Funktion:

Beim radioaktiven Zerfall nimmt die Anzahl der Atomkernen(t)nach dem Ex- ponentialgesetzn(t) =n₀e⁻^t/t⁰ mit der Zeit ab.

6 Die quadratische Funktion f : IR → IR mit x → f(x) = x² ist weder monoton fallend noch monoton wachsend. Schr¨ankt man sie jedoch auf ein Teilintervall IR_≥₀ oder IR_≤₀ ein, so ist sie dort monoton:

f₊:IR_≥₀→IR mitx→f₊(x) =x²ist streng monoton wachsend.

f₋:IR_≤0→IR mitx→f₋(x) =x² ist streng monoton fallend.

(9)

Periodizit¨at

Deﬁnition: Eine Funktion f : ID → IR heißt periodisch mit Periode p >0, wenn f(x+p) =f(x) f¨ur alle x∈ID.

Beispiele 4.20:

1 Die Sinusfunktionsin: IR→IR mitx→sin (x)ist periodisch mit der Pe- riode2π.Die Kosinusfunktioncos: IR→IR mitx→cos(x)ist periodisch mit Periode2π(siehe§4.6).

2 Die Tangens- und Kotangensfunktion, die wir in §4.6 noch n¨aher bespre- chen werden, sind periodisch mit Periodeπ.

4.1.3 Umkehrfunktion (inverse Funktion)

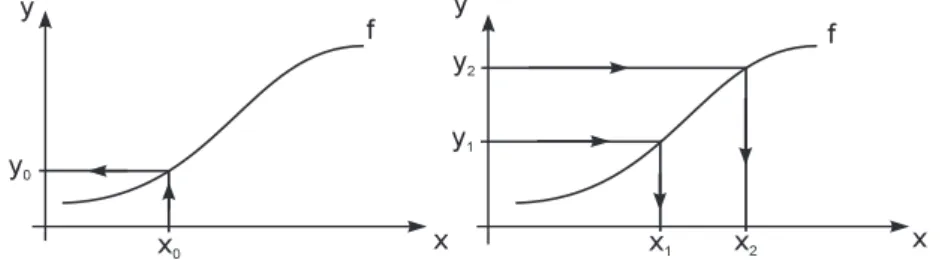
Eine Funktion f ordnet jeder Zahlx₀ ihres Deﬁnitionsbereiches ID eindeutig einen Wert y₀ =f(x₀) zu. Diese Zuordnung ist in Abb. 4.8 durch den Pfeil vonx₀nachy₀gekennzeichnet.

Abb. 4.8.Zuordnung und Umkehrzuordnung

Häufig stellt sich das umgekehrte Problem. Zu gegebenem Funktionswert (y- Wert) ist der zugehörigex-Wert zu bestimmen. In Abb. 4.8 ist diese Umkehrung der Problematik durch die Umkehrung der Pfeile gekennzeichnet. Gegeben sind y₁ undy₂, gesucht sind die zugehörigenx₁undx₂.Zu gegebenemy-Wert aus dem Wertebereich vonf kann genau einx-Wert angegeben werden, wenn die Funktion die Eigenschaft hat, dass ausx₁=x₂ stets folgtf(x₁)=f(x₂).

(10)

Deﬁnition:

(1) Eine Funktion f :IDf →VWf heißt umkehrbar, wenn aus x₁ =x₂ stets folgt f(x₁)=f(x₂).

(2) Ist die Funktionf umkehrbar, so gibt es zu jedemy∈VW_f genau ein x∈IDf.Diese eindeutige Zuordnung y→xliefert eine Funktion, die Umkehrfunktion (inverse Funktion)

f⁻¹:VW_f →ID_f.

^! ^Achtung: Nicht jede Funktion ist umkehrbar, wie Beispiel 4.21 zeigt.

Beispiele 4.21:

1 Die Funktionf₁ :IR → IR mitf₁(x) = x² ist nicht umkehrbar, da f¨ur x₀= 0 f(x₀) =x²₀=f(−x₀)aberx₀=−x₀ (Abb. 4.9 (a)).

2 Die Funktionf₂:IR_≥₀→IR mitf₂(x) =x²istnichtumkehrbar. Obwohl man den Definitionsbereich so eingeschränkt hat, dassf₂eine streng monoton wachsende Funktion ist, so gibt es doch für die negativen y-Werte keine zugehörigenx-Werte.

3 Die Funktion f₃ :IR_≥0 →IR_≥0 mit f₃(x) = x² ist umkehrbar. f₃ ist auf dem Deﬁnitionsbereich eine streng monoton wachsende Funktion und der Zielbereich f¨allt mit dem Wertebereich zusammen. Jedem Werty aus dem Zielbereich kann eindeutig einxzugeordnet werden (Abb. 4.9 (b)).

Abb. 4.9.Umkehrung der Funktiony=x²

Bemerkung:Anhand des Beispiels erkennt man, dass eine Funktion nicht nur durch eine Funktionsvorschrift charakterisiert werden kann, sondern Deﬁniti- onsbereichundZielbereich dazugeh¨oren.

(11)

Visualisierung: Auf der Homepage beﬁndet sich eine Anima- tion, in welcher der Graph der Umkehrfunktion bestimmt wird.

Die Umkehrfunktion f⁻¹ ist eine Abbildung vom Wertebereich der Funktion f in den Definitionsbereich der Funktionf. Durch das Vertauschen der Variablen erhält man aber wieder eine Abbildung, in welcher der Definitionsbereich auf der x-Achse und der Wertebereich auf der y- Achse abgetragen wird. In Konsequenz bedeutet dies, dass man den Graph der Funktionf so dreht, dass diey-Achse zurx-Achse wird, um den Graphen der Umkehrfunktion zu erhalten.

In vielen (aber nicht allen) Fällen kann man für umkehrbare Funktionen eine explizite Zuordnungsvorschrift für die Umkehrfunktion wie folgt angeben:

Bestimmung der Funktionsgleichung der Umkehrfunktion (1) Man schr¨ankt den Deﬁnitionsbereich der Funktion ID_f so ein, dass f

in dem eingeschränkten Definitionsbereich streng monoton verläuft.

(2) Man schr¨ankt den Zielbereich auf den Wertebereich der Funktion VWf

ein. Damit erh¨alt man eine umkehrbare Funktion!

(3) Man löst die Funktionsgleichungy =f(x) nach der Variablenx auf und erhält die aufgelöste Form x=g(y).

(4) Durch formales Vertauschen der beiden Variablen x und y gewinnt man die Zuordnungsvorschrift der Umkehrfunktion

f⁻¹(x) =y=g(x).

Beispiele 4.22:

1 f :IR→IR mitf(x) = 2x+ 1.

Wie man aus dem Funktionsgraphen entnimmt, stelltf eine Gerade dar.

f ist auf ganz IR streng monoton steigend mit dem Wertebereich IR; daher istf umkehrbar!

Durch Auﬂ¨osen von

y= 2x+ 1 nachxfolgt

x= 1 2y−1

2.

Durch formales Vertauschen vonxundyerh¨alt man die Umkehrfunktion f⁻¹:IR→IR mitf⁻¹(x) = ¹₂x−¹₂.

(12)

Abb. 4.10.Funktionf(x) = ¹₂x+1 und Umkehrfunktionf⁻¹(x) =¹

2x−¹₂

2 f : [0,∞)→[1,∞)mit f(x) = 1 +x².

f ist auf dem Deﬁnitionsbereich ID = [0,∞) streng monoton wachsend und der Zielbereich f¨allt mit dem Wertebereich VW = [1,∞) zusammen.

Auﬂ¨osen der Funktionsgleichung

y= 1 +x² nachxliefert

x=± y−1.

Da nur positive x-Werte durch den Deﬁnitionsbereich zugelassen sind, entf¨allt das Minuszeichen! Vertauschen vonxundy liefert:

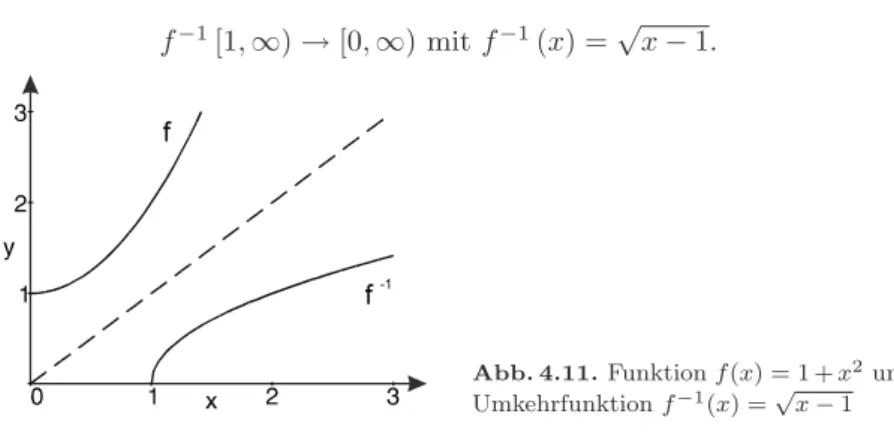
f⁻¹[1,∞)→[0,∞)mit f⁻¹(x) =√ x−1.

Abb. 4.11.Funktionf(x) = 1 +x²und Umkehrfunktionf⁻¹(x) =√

x−1

Zusammenfassung ¨uber die Umkehrung einer Funktion

(1) Jede streng monoton wachsende oder fallende Funktionf :IDf →VWf

ist umkehrbar.

(2) Bei der Umkehrung einer Funktion werden Deﬁnitions- und Wertebe- reich miteinander vertauscht.

(3) Zeichnerisch erh¨alt man das Schaubild der Umkehrfunktion durch Spiegelung vonf an der Winkelhalbierendeny=x.

(13)

Zur Charakterisierung der umkehrbaren Funktionen f¨uhren wir noch die fol- genden Begriﬀe ein:

Deﬁnition:Sei f :ID_f →VW_f eine Funktion.f heißt (1) injektiv,falls gilt: x₁=x₂ ⇒ f(x₁)=f(x₂).

(2) surjektiv,falls es zu jedemy∈VWf einx∈IDf gibt mit y=f(x).

(3) bijektiv,falls gilt: f ist injektiv und surjektiv.

Man nennt die Injektivität einer Funktion auch die Eineindeutigkeit einer Funktion. Sie bedeutet, dass eine Parallele zurx-Achse den Graphen der Funk- tion höchstens einmal schneidet. Eine Funktion f ist surjektiv, wenn zu jedem Wert y aus dem Zielbereich mindestens einx aus dem Definitionsbereich gefunden wird, welches auf yabgebildet wird.

Beispiele 4.23:

1 Die Funktionf :IR→IR mitf(x) =x²ist weder injektiv, noch surjektiv.

Denn sowohl x als auch −x f¨uhren zu dem selben Funktionswert. Die Funktion ist auch nicht surjektiv, da zu den negativen y-Werten keine zugeh¨origenx-Werte gibt.

2 Die Funktionf :IR_≥₀→IR mitf(x) =x²ist injektiv, aber nicht surjektiv, da z.B. zuy= (−1)keinxaus dem Deﬁnitionsbereich gefunden wird mitx²=−1.

3 Die Funktionf :IR_≥₀→IR_≥₀ ist bijektiv.

Die bijektiven Funktionen sind genau die umkehrbaren Funktionen:

Satz:Zu einer Funktionf existiert die Umkehrfunktion genau dann, wenn f bijektiv ist.