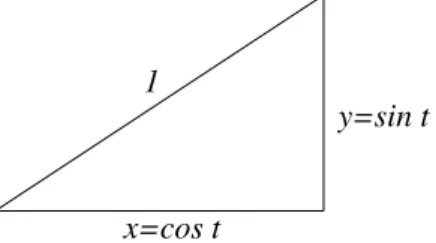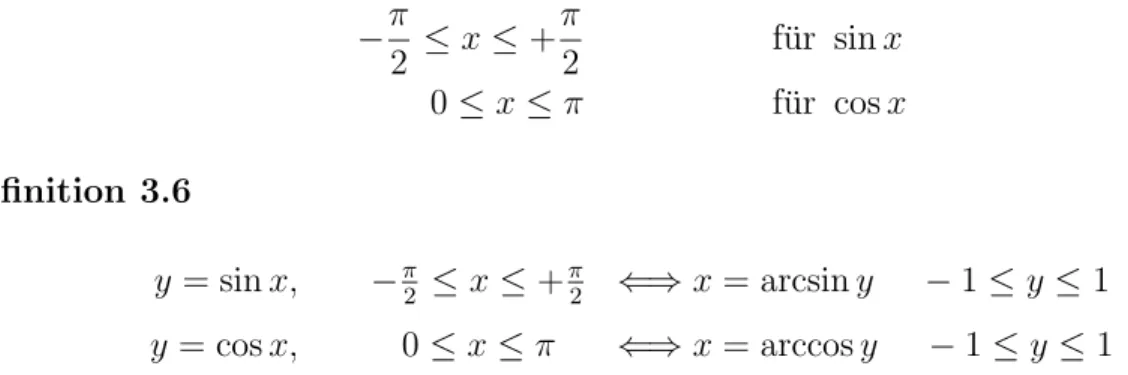Kapitel 3 Elementare Funktionen

Kapitel 3

Elementare Funktionen

3.1 Polynome

Definition 3.1 Eine Funktion f : → heißt Polynom vom Grad n, wenn es Zahlen a

, a

, . . . , a

∈ gibt, a

̸ = 0, so dass

f (x) = a

+ a

x + a

x

+ . . . + a

x

=

!

i=0

a

x

Die a

heißen Koeffizienten des Polynoms.

Beispiel 3.1

f (x) = 0 Nullfunktion (hat keinen Grad) f (x) = a

(a

̸ = 0) “Grad 0”

f (x) = a

+ a

x Polynom vom Grad 1 → lineare Funktion f (x) = a

+ a

x + a

x

Polynom vom Grad 2 → quadratische Funktion Addition und Subtraktion:

!

k=0

a

x

±

!

k=0

b

x

=

!

k=0

(a

± b

)x

Koeffizientenvergleich Wenn f¨ur alle x ∈ D gilt

!

k=0

a

x

=

!

k=0

b

x

folgt a

= b

(0 ≤ k ≤ n) (3.1)

Der Beweis dieser Behauptung folgt in Beispiel 3.4.

Beispiel 3.2 Es gilt

x

+ 3x

+ 7x + 2 = αx

+ (3β + u)x

+ 3x

+ γx + ω genau dann, wenn α = 1, 3β + u = 0, γ = 7, ω = 2.

Faktorisierung:

x

+ ax + c = (x − x

)(x − x

)

= x

− (x

+ x

)

" #$ %

a

x + x

x

"#$%

c

Woraus sich ergibt

a = − x

− x

, c = x

· x

Nullstellen eines Polynoms

Als Nullstellen eines Polynoms bezeichnet man die Werte x

f¨ur die gilt: f (x

) = 0.

Beispiel 3.3

f (x) Nullstellen

x

− 3x + 2 = (x − 1)(x − 2) 1 und 2 (einfach)

(x + 1)

-1 (doppelt)

(x − a)

a (n-fach)

Definition 3.2

Sei f ein Polynom vom Grad n. Dann nennt man x

∈ eine k-fache Nullstelle von f , wenn es ein Polynom g vom Grad n − k gibt mit

f (x) = (x − x

)

g (x) und g(x

) ̸ = 0

Sind x

, x

, . . . , x

verschiedene reelle Nullstellen der jeweiligen Vielfachheit k

, k

, . . . , k

, so gilt die Produktdarstellung

f (x) = (x − x

)

· (x − x

)

· . . . · (x − x

)

· q(x)

mit einem Polynom q(x) vom Grad n − k

− k

− . . . − k

, das in keine Nullstellen besitzt.

Satz 3.1 Jedes Polynom vom Grad n mit n ≥ 1 hat h¨ochstens n reelle Nullstellen.

Beweis:

Grad f = n = k

+ k

+ . . . + k

+ Grad q

d. h., die Anzahl der Nullstellen betr¨agt k

+ k

+ . . . + k

= n − Grad q ≤ n.

Beispiel 3.4 Polynominterpolation

Wieviele Punkte (x, y) sind notwendig, um ein Polynom vom Grad n eindeutig zu bestim- men? Zum Beispiel k¨onnte man Geraden oder Parabeln betrachten und vermuten, dass die Anzahl der notwendigen Punkte n + 1 betr¨agt.

Die Vermutung ist richtig, da zwei Polynome f und g von Grad ≤ n, die an (n + 1) ver- schiedenen Stellen (x

, y

), (x

, y

), . . . , (x

, y

) ¨ubereinstimmen, identisch sind. Denn das Polynom h = f − g ist h¨ochstens vom Grad n und hat n + 1 Nullstellen (x

, x

, . . . , x

), woraus sich ergibt, dass h = 0 sein muss.

Diese ¨ Uberlegung beweist auch Gl. (3.1).

Polynome komplexer Zahlen

Im Allgemeinen ist wegen des Restpolynoms q die Anzahl der Nullstellen in unbestimmt (n ist die obere Grenze). Wir haben aber gesehen, dass q komplexe Nullstellen haben kann. Eine naheliegende Frage ist daher, wieviele Nullstellen ein Polynom in hat. Dazu betrachten wir ein Polynom vom Grad n ≥ 1

f(z) =

!

i=0

a

z

wobei z ∈ , a

∈ und a

̸ = 0.

Dann gilt der Fundamentalsatz der Algebra (nach F. Gauß, ohne Beweis) Satz 3.2 Ein Polynom vom Grad n ≥ 0 besitzt genau n Nullstellen in . (Dabei wird jede Nullstelle so oft gez¨ahlt, wie ihre Vielfachheit angibt.) D. h. wir k¨onnen schreiben

f (z) = a

(z − w

)

· (z − w

)

· · · (z − w

)

mit n = &

j=1

k

.

Satz 3.2 wird als Fundamentalsatz bezeichnet, da er zeigt, dass die komplexen Zahlen

einen formalen Abschluss bilden. Das bedeutet, man braucht keine ¨ubergeordnete Zah-

lenmenge (z. B. “hyperkomplexe” Zahlen), um alle Eigenschaften und Rechenoperationen

von Polynomen durchzuf¨uhren. Dies gilt ebenso f¨ur alle anderen Arten von Funktionen.

(Beachte: Es gibt zwar mehrkomponentige Gr¨oßen, z. B. Vektoren v = (v

, v

)

, aber die Elemente v

, v

∈ .)

Konjungiert komplexe Nullstellen Sei nun

f (z) =

!

k=0

a

z

ein Polynom mit den reellen Koeffizienten a

∈ . Dann ist

f (z

) =

!

k=0

a

z

= f

(z) d. h., wenn

0 = f (z

) ist z

ebenfalls eine Nullstelle:

0

= f

(z

) = f (z

) = 0 (3.2) Die komplexen Nullstellen von f(z) treten stets als Paare z

, z

auf. Ein reelles Polynom, dessen Grad eine ungerade Zahl ist, hat also mindestens eine reelle Nullstelle.

Beispiel 3.5

f(z) =

!

i=0

a

z

mit a

∈ , z ∈ .

Im Falle n = 1 ergibt sich

f(x) = a

+ a

z = 0

a

̸ = 0

→ z = − a

/a

1 reelle Nullstelle Im Falle n = 2 ergibt sich

f (z) = z

+ pz + q = 0 z

= − p

2 ± √

D mit D = p

4 − q

→ D > 0 2 reelle Nullstellen

D = 0 1 doppelte reelle Nullstelle D < 0 2 komplexe Nullstellen

F¨ur n = 3, 4 existieren l¨angliche Formeln f¨ur Nullstellen.

F¨ur n ≥ 5 gibt es keine allgemeinen L¨osungen.

Oft kennt man eine Nullstelle x

eines Polynoms, d. h.

f (x) = (x − x

)g(x) (3.3)

mit Grad(g) = Grad(f ) − 1.

g (x) = f(x)

x − x

f¨ur x ̸ = x

(3.4)

Die Funktion g (x) kann durch Polynomdivision berechnet werden.

3.2 Rationale Funktionen

Definition 3.3

f (x) = p(x)

q(x) = a

x

+ . . . + a

x + a

b

x

+ . . . + b

x + b

(mit a

̸ = 0, b

̸ = 0) D = \{ NS von q }

Sei x

eine k-fache Nullstelle von q und p(x

) ̸ = 0. Dann heißt x

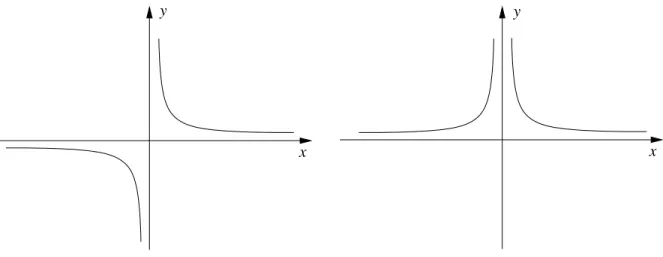
k-facher Pol von f . Beispiel 3.6 Pole von 1/x und 1/x

.

y y

x x

Abbildung 3.1: Polstellen von 1/x und 1/x

Polynomdivision

Sei f = p/q eine rationale Funktion mit Grad p ≥ Grad q.

Dann gilt

p(x)

q(x) = h(x) + r(x) q(x)

mit einem Polynom h(x) (dem “ganzen Anteil”) und einem Restpolynom r(x).

Dabei gilt entweder r(x) ≡ 0 oder Grad r < Grad q.

Beispiel 3.7 Sei x

= 2 eine Nullstelle von

f (x) = x

− 4x

+ 5x − 2 = (x − 2) · g(x) so ist g (x) durch eine Polynomdivision bestimmbar:

x

− 4x

+ 5x − 2 : x − 2 = x

− 2x + 1 x

− 2x

− 2x

+ 5x

− 2x

+ 4x x − 2 Dies bedeutet

g(x) = x

− 2x + 1 = (x − 1)

Es entsteht kein Restpolynom (also r(x) = 0), da x

= 2 eine Nullstelle ist.

Beispiel 3.8

x

− 4x

+ 5x − 2 : (x

+ 1) = x − 4 + 4x + 2 x

+ 1 x

+ x

− 4x

+ 4x − 2

− 4x

− 4 4x + 2 Test:

'

x − 4 + 4x + 2 x

+ 1

(

(x

+ 1) =

(x − 4)(x

+ 1) + 4x + 2 = x

− x − 4x

− 4 + 4x + 2

= x

− 4x

+ 5x + 2

Es ergibt sich ein Restpolynom r(x) = 4x + 2. Der Grad r = 1 ist (um 1) kleiner als der

Grad des Nennerpolynoms q = 2.

3.3 Kreisfunktionen: Sinus und Cosinus

Diese Funktionen werden auch trigonometrische oder Winkelfunktionen genannt.

z y

x 1

P(x, y)

Abbildung 3.2: Einheitskreis x

+ y

= 1

Der Einheitskreis x

+y

= 1 beschreibt einen Kreis, dessen Mittelpunkt sich im Nullpunkt N = (0, 0) des Koordinatensystems befindet. Der Abstand (Radius) zwischen Mittelpunkt und einem beliebigen Punkt P auf dem Kreisumfang ist 1. Die L¨ange des Kreisumfangs betr¨agt 2π ≈ 6, 28.

Der Winkel α zwischen dem positiven Teil der x-Achse und dem Radius NP liegt zwischen 0

und 360

. F¨ur das Bogenmaß t, also der Bogen zwischen dem Punkt (1, 0) und P (x, y), gilt α/360 = t/2π. Das Bogenmaß betr¨agt demnach

t = 2πα/360

Das Bogenmaß t ist also sowohl die L¨ange des Kreisbogens, wie auch selbst ein Maß f¨ur den Winkel α. Weiterhin gilt, dass P (x, y) = P (x(t), y(t)).

Definition 3.4 Jedem Winkel t (im Bogenmaß) entspricht eindeutig ein Punkt P (x, y) auf dem Einheitskreis, dessen Koordinaten x und y durch die Kreisfunktionen

x = x(t) = cos t “Cosinus”

y = y(t) = sin t “Sinus”

gegeben sind.

Eigenschaften:

1. Wertebereich

| cos t | ≤ 1

| sin t | ≤ 1

1

x=cos t

y=sin t

Abbildung 3.3: Das rechtwinklige Dreieck aus dem Einheitskreis cos

t + sin

t = 1 Satz von Pythagoras

2. Periodizit¨ at:

cos t = cos(t + 2π) = cos(t + k · 2π)

sin t = sin(t + k · 2π) mit k ∈ Sinus und Cosinus sind periodisch mit der Periode 2π.

Allgemein heißt eine Funktion periodisch mit Periode T , wenn gilt f (x) = f (x + T )

x

−1 1

y

Abbildung 3.4: Die periodischen Fuktionen Sinus (durchgezogene Linie) und Cosinus (gestri- chelte Linie)

t 0 π/2 π 3π/2 2π π/6 π/4 π/3

sin t 0 1 − 1 − 1 0 1/2 1/ √ 2 √

3/2

cos t 1 0 0 0 1 √

3/2 1/ √

2 1/2

3. Symmetrie:

Es gilt:

sin t = − sin( − t) ungerade cos t = cos( − t) gerade

sin(t + π/2) = cos t cos(t + π/2) = − sin t Cosinus und Sinus sind zueinander um π/2 verschoben.

Polarkoordinaten

y

x r

P ϕ

Abbildung 3.5: Der Punkt P

“Pol” bei (0, 0), Polarachse bzgl. der der Winkel ϕ definiert wird.

Ublicherweise ist ¨ − π < ϕ ≤ π.

P = P (r, ϕ) = P (x, y)

Die Umrechnung von kartesischen Koordinaten in Polarkoordinaten erfolgt ¨uber x = r cos ϕ

y = r sin ϕ mit

r

= x

+ y

r = )

x

+ y

Beispiel 3.9

kartesisch(x, y) polar(r, ϕ) (1, 1) ( √

2, π/4)

(0, 3) (3, π/2)

Additionstheoreme

Satz 3.3 F¨ur alle x, y ∈ gilt

(1) sin(x + y) = sin x cos y + cos x sin y (2) cos(x + y) = cos x cos y − sin x sin y Beweis von (2):

P

Q x

y

Abbildung 3.6: Skizze der Punkte Wir betrachten zwei Punkte P und Q mit den Koordinaten

P = (1, 0)

Q = (cos(x + y), sin(x + y))

Der Abstand d zwischen zwei Punkten A = (x

, y

) und B = (x

, y

), genauer gesagt ihr Abstandsquadrat d

berechnet sich aus

d

(A, B) = (x

− x

)

+ (y

− y

)

F¨ur P und Q ergibt sich also

d

(P, Q) = (1 − cos(x + y))

+ (0 − sin(x + y))

= 1 − 2 cos(x + y) + cos

(x + y) + sin

(x + y)

= 2 − 2 cos(x + y) (3.5)

Nun nehmen wir eine Drehung der Koordinaten vor.

Der Abstand d ¨andert sich dabei nicht.

(P, Q) → (P

, Q

) d

(P, Q) = d

(P

, Q

) Die neuen Koordinaten der Punkte P

und Q

lauten

P

= (cos(x), − sin(x))

Q

= (cos(y), sin(y))

Die Formel f¨ur das Abstandsquadrat in den neuen Koordinaten lautet d

= (cos x − cos y)

+ (sin y + sin x)

= cos

x + cos

y − 2 cos x cos y + sin

x + sin

y + 2 sin x sin y

= 2 − 2 cos x cos y + 2 sin x sin y (3.6)

Da sich das Abstandsquadrat durch die Koordinatendrehung nicht ¨andert, muss Gl. (3.5) und (3.6) ¨ubereinstimmen:

2 − 2 cos(x + y) = 2 − 2 cos x cos y + 2 sin x sin y woraus sich ergibt

cos(x + y) = cos x cos y − sin x sin y (3.7)

Beweis von (1):

Wie gezeigt gilt

cos(x + π

2 ) = − sin x sin(x + π

2 ) = cos x Daraus folgt

sin(x + y) = − cos(x + y + π 2 )

= − cos x cos(y + π

2 ) + sin x sin(y + π 2 )

= cos x sin y + sin x cos y (3.8)

Man kann mit Hilfe der Additionstheoreme noch mehr Beziehungen zeigen, z. B.:

sin(2x) = 2 cos x sin x

cos(2x) = cos

x − sin

x

Harmonische Schwingungen

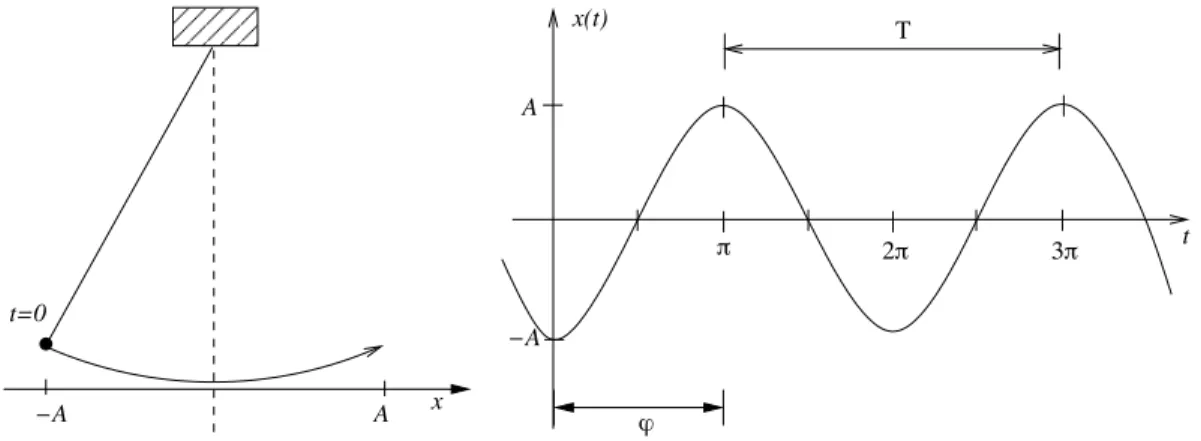
Sinus und Cosinus sind nicht nur rein mathematische Konstrukte. Mit ihrer Hilfe lassen sich auch viele nat¨urliche Ph¨anomene beschreiben, unter anderem harmonische Schwin- gungen.

−A A x

t=0

A

−A x(t)

t

ϕ

π 2π 3π

T

Abbildung 3.7: Bewegung des Pendels im Raum und mit der Zeit Eine harmonische Schwingung wird beschrieben durch die Gleichung

x(t) = A · cos(ωt + ϕ) t : Zeit

A : Amplitude (Maximalauslenkung) ϕ : Phase (F¨ur x(0) = − A ist ϕ = π)

ω : Kreisfrequenz (Anzahl der Schwingungen im Zeitintervall 2π) T : Periode (Schwingungsdauer)

Es gilt

ω = 2π

T

Tangens- und Cotangensfunktionen

Neben Sinus und Cosinus gibt es noch zwei weitere Winkelfunktionen.

Definition 3.5 Tangens:

x *−→ tan x = sin x cos x wobei f¨ur den Definitionsbereich gilt

= / { Nullstellen des cos }

= / {± π 2 , ± 3 π

2 , ± 5 π 2 , . . . } Cotangens:

x *−→ cot x = cos x

sin x = 1 tan(x) wobei f¨ur den Definitionsbereich gilt

= / { Nullstellen des sin }

= / { 0, ± π, ± 2π, . . . }

Periodizit¨ at

Sinus und Cosinus sind 2π-periodisch. Gilt dies auch f¨ur Tangens bzw. Cotangens?

Wegen

tan(x + π) = sin(x + π)

cos(x + π) = − sin x

− cos x = tan x sind Tangens und Cotangens (Beweis analog) also π-periodisch.

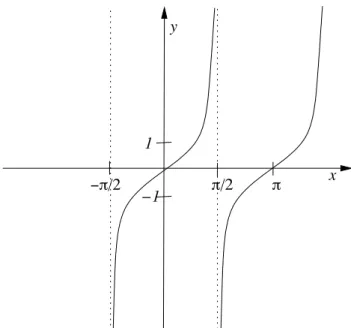
Aus der Wertetabelle f¨ur den Tangens

x 0 π/4 − π/4 → π/2 − ε → − π/2 + ε → π/2 + ε → − π/2 − ε

tan x 0 1 − 1 + ∞ −∞ −∞ + ∞

erhalten wir den Graphen

y

x 1

−π/2 −1 π/2 π

Abbildung 3.8: Die Tangens-Funktion

Analog bekommen wir f¨ur den Cotangens:

x π/2 π/4 3π/4 0 + ε 0 − ε π − ε π + ε

cot x 0 1 − 1 + ∞ −∞ −∞ + ∞

1

−1

t cot t

−π/2 π/2 π

Abbildung 3.9: Die Cotangens-Funktion

Die Umkehrfunktion der Kreisfunktion

Die Umkehrung ist nur in beschr¨ankten Definitionsbereichen m¨oglich.

x

−1 1

y

Abbildung 3.10: Die periodischen Funktionen Sinus (durchgezogene Linie) und Cosinus (gestri- chelte Linie)

Die ¨ubliche Wahl des Definitionsbereiches ist

− π

2 ≤ x ≤ + π

2 f¨ur sin x

0 ≤ x ≤ π f¨ur cos x Definition 3.6

y = sin x, −

≤ x ≤ +

⇐⇒ x = arcsin y − 1 ≤ y ≤ 1 y = cos x, 0 ≤ x ≤ π ⇐⇒ x = arccos y − 1 ≤ y ≤ 1 Die entstehenden Funktionen nennt man Arcus- oder zyklometrische Funktionen.

x y

1

−1

arc sin x

y

1 x

−1

arc cos x

−π/2 π/2

π/2

Abbildung 3.11: Die periodischen Fuktionen Arcsinus und Arccosinus

Beispiel 3.10 t = arcsin x bedeutet: t ist der Winkel im Bogenmaß, dessen Sinus den

Wert x besitzt. So ist arcsin 0 = 0, arcsin 1 = π/2 und arccos 0 = π/2.

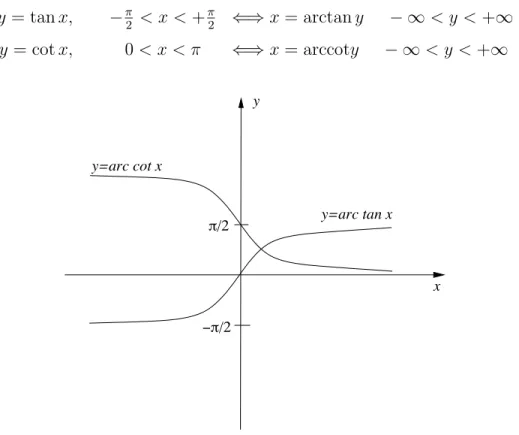
Die Umkehrung von Tangens und Cotangens verl¨auft analog.

x

cot t=cos x/sin x tan x=sin x/cos x y

−π/2 π/2 π

Abbildung 3.12: Die periodischen Fuktionen Tangens und Cotangens

Definition 3.7

y = tan x, −

< x < +

⇐⇒ x = arctan y − ∞ < y < + ∞ y = cot x, 0 < x < π ⇐⇒ x = arccoty − ∞ < y < + ∞

y=arc cot x

y=arc tan x

x y

−π/2 π/2

Abbildung 3.13: Die periodischen Fuktionen Arctangens und Arccotangens