Kapitel 4 Elementare Anregungen

Elementare Anregungen

Warum bildet eine große Anzahl von Kupfer-Atomen einen metallischen Kristall und nicht eine ungeordnete glasartige Struktur oder gar eine Fl¨ussigkeit? Erstaunlicherweise kann ei- ne so fundamentale Frage mit theoretischen Hilfsmitteln nicht ohne weiteres beantwortet werden, da dies die L¨osung des Vielteilchenproblems aus einer großen Anzahl von Kupfer- kernen und Elektronen erfordern w¨urde, - ein schlichtweg unm¨ogliches Unterfangen. Der ubliche Zugang ist daher, den Grundzustand zu erraten und dann seine Energie zu berech-¨ nen. Falls diese niedriger ist als die Energie vieler anderer Zust¨ande, k¨onnen wir berechtigte Hoffnung haben, dass es sich tats¨achlich um den Grundzustand handelt. Experimentelle Untersuchungen sind aber zur Best¨atigung des Grundzustandes unerl¨asslich. So zeigen z.B.

R¨ontgenstrukturuntersuchungen, dass Kupfer eine kubisch fl¨achenzentrierte Struktur ein- nimmt. Diese Struktur kann also als Ausgangspunkt f¨ur die theoretische Behandlung von Kupfer verwendet werden. Nat¨urlich k¨onnen Experimente niemals am absoluten Tempera- turnullpunkt durchgef¨uhrt werden und k¨onnen somit - strenggenommen - auch keine Aussage

¨

uber den Grundzustand machen. Dass eine ¨Anderung der Struktur von Kupfer bei Tempe- raturen im Milli-Kelvin-Bereich auftritt, ist allerdings ¨uberaus unwahrscheinlich. Wesentlich subtiler ist die Frage nach dem elektronischen Grundzustand. Wie wir in Kap. 2 gesehen haben, k¨onnen z.B. magnetische Ordnung oder Supraleitung bei extrem tiefen Temperatu- ren auftreten. Der elektronische Grundzustand kann also nicht generell aus experimentellen Untersuchungen bestimmt werden.

F¨ur einen Vergleich mit dem Experiment ist also meist nicht die Grundzustandsenergie von Bedeutung, sondern die Antwort des Systems auf ¨außere Einfl¨usse. Mit der spezifischen W¨arme z.B. misst man die ¨Anderung der Energie bei Er¨ohung der Temperatur. Mit der magnetischen Suszeptibilit¨at misst man die ¨Anderung der Magnetisierung bei Anlegen eines Magnetfeldes. Bei diesen Experimenten wird die Probe von einem energetisch tiefliegen- den Zustand in einen angeregten Zustand h¨oherer Energie ¨ubergef¨uhrt. Eine theoretische Behandlung derartiger Prozesse geht vom Konzept der elementaren Anregungen aus. Der Grundzustand wird dabei g¨anzlich außer Acht gelassen und der Prozess, bei dem das System in einen Zustand h¨oherer Energie ¨uberf¨uhrt wird, als Erzeugung eines

”Etwas“ aufgefasst, wo vorher

”Nichts“ war. Der einfachste derartige Prozess ist die Erzeugung von elementaren Anregungen.

49

Der Nutzen des Konzeptes der elementaren Anregungen r¨uhrt von einer einfachen Ei- genschaft her, die die meisten Vielteilchensysteme gemeinsam haben: Nehmen wir an, dass es zwei angeregte Zust¨ande der Energie ǫ1 und ǫ2 oberhalb der Grundzustandsenergie g¨abe.

Es ist dann h¨aufig der Fall, dass es ebenfalls einen angeregten Zustand der Energie ǫ3 gibt, wobei sich ǫ3 nur wenig von ǫ1 +ǫ2 unterscheidet: ǫ3 = (ǫ1 +ǫ2) + ∆ǫ. Wir sagen dann, dass alle Anregungen, die in den ersten zwei Zust¨anden enthalten waren, jetzt gemeinsam vorhanden sind. ∆ǫ ist die Wechselwirkungsenergie. ǫ1 and ǫ2 setzen sich i.A. ebenfalls aus Anregungen niedrigerer Energie zusammen. Falls das nicht der Fall ist, die Anregungen also nicht weiter unterteilt werden k¨onnen, spricht man von elementaren Anregungen. Falls die Wechselwirkungsenergie klein ist, kann man die meisten angeregten Zust¨ande des Festk¨orpers mit vertretbarer Genauigkeit als Ensemble elementarer Anregungen auffassen. Das bedeutet eine weitreichende Vereinfachung des urspr¨unglichen Bildes, in dem wir ein Spektrum von Energiezust¨anden ohne bestimmte Relation zueinander vorliegen hatten.

Gelegentlich wird zwischen zwei Arten von elementaren Anregungen, Quasiteilchen- Anregungen und kollektiven Anregungen unterschieden, obwohl eine solche Unterteilung nicht streng m¨oglich ist. Die Anregung eines Elektrons von einem Zustand unterhalb der Fermienergie in einen Zustand oberhalb der Fermienergie wird im Falle des freien Fermigases als Teilchen-Anregung bezeichnet, im Falle der Fermifl¨ussigkeit als Quasiteilchen-Anregung (Kap. 3; das Quasiteilchen hat nur eine endliche Lebensdauer). Ein einfaches Beispiel f¨ur eine kollektive Anregung ist eine Schallwelle in einem Festk¨orper. Wegen der starken inter- atomaren Kr¨afte im Festk¨orper macht es wenig Sinn, die Bewegung eines einzelnen Atoms zu beschreiben. Der Impuls, den wir einem einzelnen Atom zuf¨uhren, wird so schnell an die Nachbarn weitergegeben, dass es schon nach kurzer Zeit schwierig w¨are festzustellen, welches Atom urspr¨unglich angestoßen wurde. Die gesamte Schallwelle wird hingegen nur langsam abgeschw¨acht und ist somit ein besser geeignetes Bild einer Anregung. Da eine Schallwelle durch die Angabe der Koordinaten aller Atome des Festk¨orpers bestimmt ist, spricht man von einer kollektiven Anregung.

Im Folgenden werden wir eine Reihe von elementaren Anregungen auf einfachem Ni- veau einf¨uhren. Eine strengere quantenmechanische Beschreibung erfolgt anhand von zwei Beispielen in Abschnitt 4.2.

4.1 Uberblick ¨

4.1.1 Elektronisches Quasiteilchen

Elektronische Quasiteilchen sind die in Kap. 3 eingef¨uhrten elementaren Anregungen eines Systems wechselwirkender Elektronen. Sie werden auch als Quasielektron bzw. Quasiloch bezeichnet. In der ph¨anomenologischen Theorie der Landau’schen Fermifl¨ussigkeit wurde die Art der Wechselwirkung zwischen den Elektronen nicht n¨aher spezifiziert. In einer mi- kroskopischen Theorie kann ¨uber die Wahl des Hamiltonoperators in Glg. 3.67 eine Vielzahl von verschiedenen Wechselwirkungen ber¨ucksichtigt werden. Ein Beispiel, auf das wir in Abschnitt 5.2 noch weiter eingehen werden, ist das Quasiteilchen

”schweres Elektron im Kondo-System“. Wie schon im Abschnitt 2.1 gesagt, kann die Masse dieses Quasiteilchens

im Vergleich zur Masse des freien Elektrons um zwei bis drei Gr¨oßenordnungen erh¨oht sein.

4.1.2 Phonon

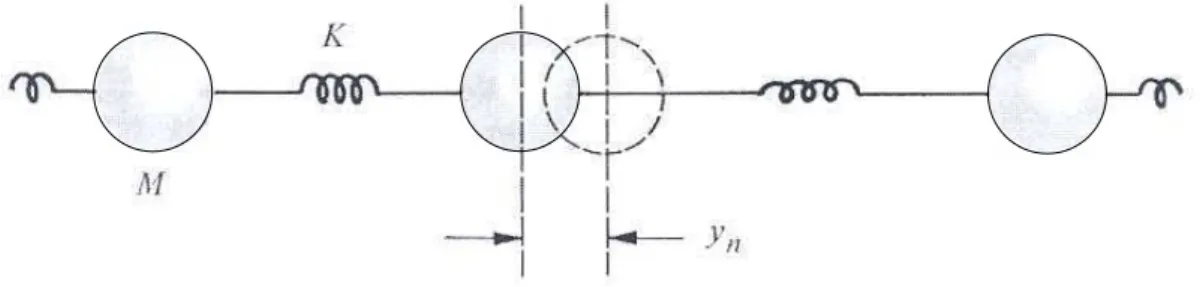
Wir f¨uhren hier die Phononen ¨uber ihr klassisches Analogon, die Gitterschwingung ein. Wir betrachten eine lineare Kette aus gleichen MassenM, die ¨uber Federn der FederkonstanteK gem¨aß Abb. 4.1 verbunden sind. Die Auslenkung der n-ten Masse aus ihrer Gleichgewichts-

Abbildung 4.1: Kette aus gleichen Massen und Federn.

lage werde mityn bezeichnet. Die Bewegungsgleichungen des Systems lauten Md²yn

dt² = K[(yn+1−yn)−(yn−yn−1)]

= K(y_n+1−2y_n+y_n−1). (4.1)

Diese Gleichungen k¨onnen f¨ur gegebene Randbedingungen mit Hilfe von zylindrischen Bes- selfunktionen J_n gel¨ost werden. Die Rekursionsrelationen der J_n lauten

dJ_n

dt =−1

2[Jn+1(t)−Jn−1(t)], (4.2) woraus man durch nochmalige Anwendung von d/dt die Relation

d²Jn

dt² = 1

4[Jn+2(t)−2Jn(t) +Jn−2(t)] (4.3) erh¨alt. Eine L¨osung von Glg. (4.1) ist

yn(t) =J2n(ωmt), (4.4)

wobei

ω_m² = 4K/M, (4.5)

wovon man sich durch Einsetzen von Glg. (4.4) in Glg. (4.1), das mehrmalige Umbenennen von Indizes, die totale Differentiation nacht vonJ_n(z(t)) mit z(t) =ω_mtund schließlich den Vergleich mit Glg. (4.3) ¨uberzeugen kann.

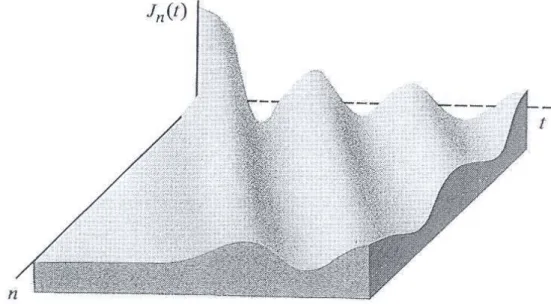
Die L¨osung f¨ur den Fall, dass wir eine Masse (z.B. die zu n = 0) auslenken und dann loslassen, ist in Abb. 4.2 dargestellt. Die Auslenkung der 0-ten Masse y0, die durch J0(ωmt)

gegeben ist, zeigt Oszillationen, die rasch mit der Zeit abklingen. Schon nach wenigen Oszil- lationen verl¨auft y0(t) wie t^−1/2cos(ωmt). Die Bewegung einer (z.B. der 0-ten) Komponente des Systems zeigt also kein teilchenartiges Verhalten, das sich ja durch konstante Geschwin- digkeit auszeichnen w¨urde.

Abbildung 4.2: Die Besselfunktionen sind L¨osungen der Bewegungsgleichungen (4.1).

Besser als elementare Anregungen geeignet sind die Normalmoden der Schwingungen des Systems. Nehmen wir an, dass wir

yn(t)∼e^i(ωt+kna) (4.6)

schreiben k¨onnen, wobei ω eine Funktion der Wellenzahl k ist und a der Gleichgewichtsab- stand zweier Massen. Glg. (4.6) erf¨ullt die Bewegungsgleichungen (4.1), falls

−ω²M =K(e^ika+e^−ika−2), (4.7) falls also

ω =±ωmsin (1

2ka). (4.8)

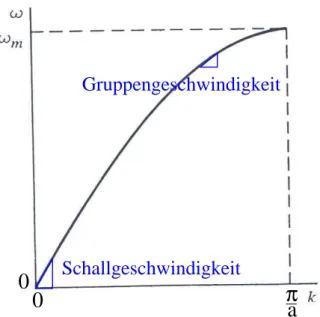
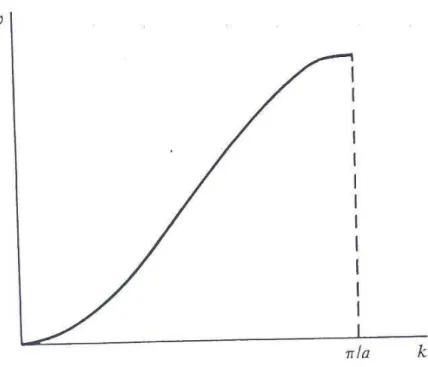
Der Maximalwert von ω, ωm, ist wieder durch Glg. (4.5) gegeben. Glg. (4.7) erh¨alt man durch Einsetzen von Glg. (4.6) in Glg. (4.1), Glg. (4.8) folgt mit Ber¨ucksichtigung von cosx= (e^ix+e^−ix)/2 und sin²x= (1−cos(2x))/2. Die L¨osung (4.6) stellt eine propagierende Welle der Frequenzω, der Wellenzahl k und der Wellenl¨angeλ= 2π/kdar. Die Gruppenge- schwindigkeit v ist durch dω/dk gegeben. Sie ist die lokale Steigung der Kurve in Abb. 4.3, die die Dispersionsrelation in Glg. (4.8) darstellt. Bei kleinemkist die Steigung konstant und entspricht der Schallgeschwindigkeit. Beiω =ωm f¨allt die Gruppengeschwindigkeit auf null.

Dies erkl¨art, warum die Besselfunktions-L¨osung Glg. (4.4) nach kurzer Zeit in eine Oszilla- tion der Frequenz ωm zerf¨allt: Die Besselfunktion kann als ¨Uberlagerung von Wellen aller

π a

Schallgeschwindigkeit Gruppengeschwindigkeit

0 0

Abbildung 4.3: Dispersionskurve der linearen Kette aus Abb. 4.1.

Wellenzahlen betrachtet werden. Die Wellen niedriger Frequenz haben eine große Gruppen- geschwindigkeit und entfernen sich schnell vom 0-ten Massenpunkt weg. Nur die Welle der Frequenz ω_m kann sich nicht fortbewegen und bleibt daher am Ort des 0-ten Massepunktes erhalten.

Das einfache Modell der linearen Kette kann ohne weiteres auf kompliziertere Systeme ubertragen werden, z.B. auf Systeme mit drei Dimensionen, mit unterschiedlichen Atom-¨ sorten oder mit Wechselwirkungen, die nicht nur zwischen den n¨achsten Nachbarn wirken.

Solange die R¨uckstellkr¨afte proportional zur Auslenkung bleiben, haben die L¨osungen die Form von Glg. (4.6).

Das Phonon ist das quantenmechanische Analogon der mit Glg. (4.6) beschriebenen Git- terschwingung. Ein einzelnes Phonon der Kreisfrequenzωhat die Energie~ω. Eine klassische Gitterschwingung von großer Amplitude entspricht der quantenmechanischen Situation, wo viele Phononen der gleichen Mode vorliegen. Ein solches Ensemble von Phononen hat gewisse Ahnlichkeit mit einem Gas aus Teilchen. Daher werden Phononen oft auch als Quasiteilchen¨ bezeichnet.

In Abschnitt 4.2.1 werden wir die Phononen mit Hilfe des Formalismus der zweiten Quan- tisierung (oder Fock-Darstellung) noch eingehender behandeln.

4.1.3 Soliton

Im realen Festk¨orper ergibt sich aufgrund der Abstoßung zwischen den Atomr¨umpfen ein anharmonisches Potenzial. Die Bewegungsgleichungen (4.1) sind dann nicht mehr linear in der Auslenkung. Bei kleinen Auslenkungen f¨uhrt dies nur zu kleinen Korrekturen und eine Beschreibung mit Phononen ist adequat. Bei großen Auslenkungen entsteht dadurch aber eine v¨ollig neue Familie von elementaren Anregungen, die solit¨aren Wellen oder Solitonen.

Dies sind Anregungen, in denen eine lokale Druckwelle den Festk¨orper durchl¨auft. Die Atome werden nur kurzzeitig ausgelenkt und nehmen nach Durchlaufen der Druckwelle wieder ihre urspr¨ungliche station¨are Lage ein.

Solit¨are Wellen kommen auch in klassischen Systemen vor, sind also kein rein quanten- mechanisches Ph¨anomen. Allerdings k¨onnen solit¨are Wellen unter bestimmten Umst¨anden teilchen¨ahnlich miteinander wechselwirken: Sie behalten dann bei einer Kollision ihre Gestalt bei. Deshalb werden sie oft als Quasiteilchen betrachtet.

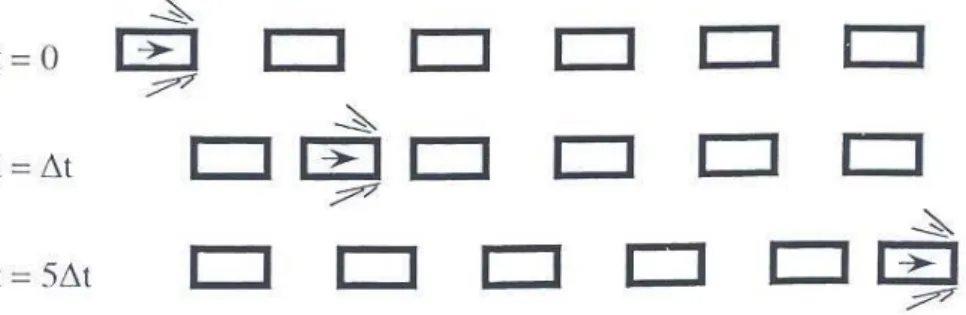
Das einfachste Modell, das solit¨are L¨osungen zul¨asst, ist eine eindimensionale Anordnung harter St¨abchen, wie sie in Abb. 4.4 skizziert ist. Durch einen Schlag auf das St¨abchen ganz

Abbildung 4.4: Die solit¨are Welle breitet sich durch eine Folge elastischer St¨oße von links nach rechts aus.

links wird dieses in Bewegung versetzt und auf das benachbarte St¨abchen schlagen, das seinerseits wieder auf das n¨achste St¨abchen schl¨agt. Eine solit¨are Druckwelle wird die ganze Anordnung durchlaufen und alle bis auf das letzte (rechteste) St¨abchen im Ruhezustand hinterlassen. Die Ausbreitungsgeschwindigkeit der Welle h¨angt einzig von der St¨arke des anf¨anglichen Schlags ab und kann jeden positiven Wert annehmen. Die Welle ist immer auf einem einzigen St¨abchen lokalisiert, im Gegensatz zur Schallwelle in einem harmonischen System, die immer g¨anzlich delokalisiert ist.

Ein oft verwendetes Modell, das zwischen den Grenzf¨allen des harmonischen Potenzials und dem Potenzial zwischen harten K¨orpern interpoliert, ist die sog. Toda-Kette. Ihr Erfinder Toda schlug das Potenzial

V(r) =ar+ a

be^−br (4.9)

vor, wobei r der Abstand zwischen zwei K¨orpern ist. Wenn b→0 und dabei ab=cendlich ist, erh¨alt man daraus durch Reihenentwicklung der Exponentialfunktion (exp(x) = 1 + x¹/1! +x²/2! +...) das harmonische Potenzial

V(r) = a b + 1

2cr². (4.10)

Falls hingegenb → ∞und dabei ab=cendlich ist, ergibt sich das Potenzial zwischen harten K¨orpern, das durch

V → ∞ , r ≤0

V →0 , r >0 (4.11)

gegeben ist. F¨ur allgemeine Werte von b betrachten wir eine Kette mit Gleichgewichts- abst¨anden D zwischen den Massen, wobei das Potenzial P

nV(Rn −Rn−1 −D) zwischen Massen am Ort Rn und Rn−1 wirkt. In der Notation der Auslenkungen von der Gleichge- wichtslage yn=Rn−nD ergeben sich die Bewegungsgleichungen zu

Md²yn

dt² =−a(e^{−b(yn+1−yn)}−e^{−b(yn−yn−1)}). (4.12) Mit yn−yn−1 ≡rn erhalten wir

Md²rn

dt² =a(−e^−brn+1+ 2e^−brn−e^−brn−1). (4.13) Eine einfache L¨osung dieser Gleichungen ist die propagierende Welle, f¨ur die

e^−brn−1 = sinh²µ

cosh²(µn±βt) (4.14)

gilt, wobei β = p

ab/Msinhµ und µ eine Zahl ist, die sowohl die Amplitude als auch die r¨aumliche Ausdehnung der Welle bestimmt. Da die Funktion 1/cosh²(µn±βt) außer f¨ur kleine Argumente klein ist (1/coshx= 2/(e^x+e^−x)), ist die Breite der solit¨aren Welle, f¨ur die rn ∼f(nD−vt) gilt, etwa D/µ. Die Geschwindigkeit der Welle ist

v =βD µ =D

rab

M(sinhµ

µ ). (4.15)

F¨ur solit¨are Wellen mit großer Amplitude dominieren die Charakteristika des Potenzials harter K¨orper (Glg. (4.11)) und die Geschwindigkeit wird sehr groß (sinhx= (e^x−e^−x)/2).

F¨ur kleine Amplituden zwischen benachbarten Massen ist sinhµ/µ→1 (aus Reihenentwick- lung: e^x = 1 +x+...) und wir erhalten die Schallgeschwindigkeit der harmonischen Kette Dp

(ab/M).

Das Beispiel der Toda-Kette zeigt, wie die Ber¨ucksichtigung von Nichtlinearit¨aten die elementaren Anregungen eines Systems qualitativ ver¨andert. Zur vollst¨andigen L¨osung des klassischen Problems muss auf elliptische Jacobi-Funktionen zur¨uckgegriffen werden, was sich als sehr aufw¨andig gestaltet. Auch die quantenmechanische Behandlung ist ¨uberaus nichttrivial.

Solitonen in konjugierten Polymeren

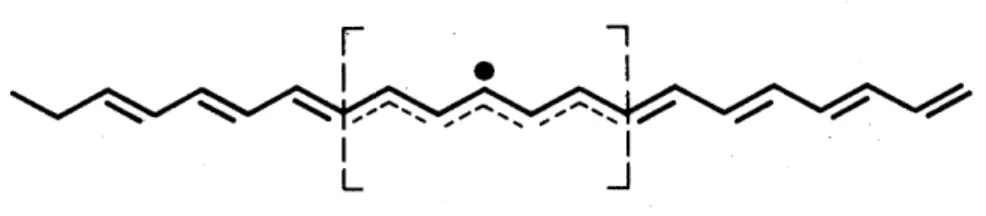
In konjugierten Polymeren wie Polyacetylen alternieren Einfach- und Doppelbindungen zwi- schen den Kohlenstoffatomen. Damit ergibt sich ein zweifach entarteter Grundzustand, da die Doppelbindungen entweder zwischen dem 1. und 2., 3. und 4., ... oder zwischen dem 2. und 3., 4. und 5., ... Kohlenstoffatom auftreten k¨onnen. Ein Soliton ist hier eine Dom¨anenwand zwischen diesen beiden Grundzust¨anden (Abb. 4.5).

Abbildung 4.5: Schematische Darstellung eines neutralen Solitons in trans-(CH)x [Heeger, Rev. Mod. Phys. 60 (1988) 781)]

Magnetische Solitonen

Es gibt auch ein magnetisches Analogon zu mechanischen Solitonen. Ein einfaches Beispiel ist eine antiferromagnetische Ising-artige Kette, die durch den Hamiltonoperator

H =−2JX

i>j

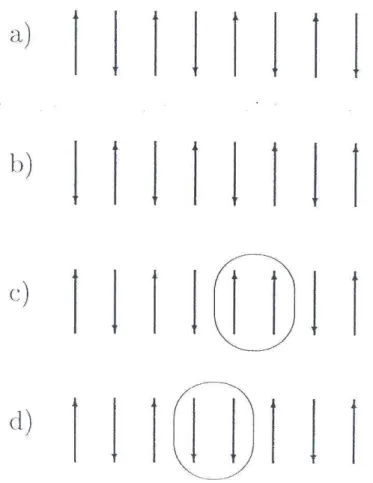
(aS_i^zS_j^z+bS_i^yS_j^y+cS_i^xS_j^x) (4.16) mit negativer AustauschkonstanteJ (antiferromagnetische Kopplung) und wesentlich st¨arker Kopplung in z-Richtung als in x- und y-Richtung (b =c≪ a) beschrieben wird. Der N´eel- Grundzustand dieses Systems ist zweifach entartet, da die zwei in Abb. 4.6 (a) und (b) gezeig- ten Anordnungen der Spins m¨oglich sind. Die niederenergetischen Anregungen sind magneti- sche Solitonen (oder Dom¨anenw¨ande) zwischen den zwei verschiedenen N´eel-Grundzust¨anden (c). Die nichtverschwindende Spinkopplung entlang der x- undy-Achse (b =c >0) sorgt f¨ur die Bewegung des Solitons entlang der Kette (d). Eine tight binding-N¨aherung ergibt f¨ur die Geschwindigkeit des Solitons

v =−4abJsin(2ak). (4.17)

4.1.4 Magnon

In einem Ferromagneten aus lokalen Momenten zeigen unterhalb der Curie-Temperatur alle diese lokalen magnetischen Momente in etwa in die gleiche Richtung, die wir mitzbezeichnen.

Vereinfachend kann man annehmen, dass das effektive Magnetfeld, das ein magnetisches Moment auf dem Gitterplatz ~l sp¨urt, von der Orientierung der Momente seiner n¨achsten Nachbarn abh¨angt:

H~_~l=AX

~l^′

~µ~l^′. (4.18)

A ist eine Konstante, ~µ~l^′ ist das zum Gitterplatz ~l^′ geh¨orende magnetische Moment. Die Summe geht ¨uber die n¨achsten Nachbarn. Das Drehmoment ~µ_~l×H~_~l, das dieses Feld auf das Moment auf dem Gitterplatz~laus¨ubt, f¨uhrt zu einer zeitlichen ¨Anderung des Drehimpulses und, da das magnetische Moment eines Atoms proportional zum Dreimpuls ist, auch zu einer zeitlichen ¨Anderung des magnetischen Moments

d~µ_~l

dt ∼~µ_~l×H~_~l=AX

~l^′

~µ_~l×~µ~l^′. (4.19)

Abbildung 4.6: Grundzust¨ande des Ising-Modells in (a) und (b) und niederenergetische Solitonen-Anregungen in (c) und (d).

Wieder suchen wir nach einer wellenf¨ormigen L¨osung dieser Differentialgleichungen. Unter der Annahme, dass die Auslenkungen der ~µ_~l aus derz-Richtung klein sind, schreiben wir

~µ_~l=~µz+~µ_⊥e^{i(ωt+~k·~l)}. (4.20)

~µzzeigt in diez-Richtung. Die Komponenten in derx−y-Ebene~µ⊥=~µx+i~µy sind komplexe Zahlen. Einsetzen von Glg. (4.20) in Glg. (4.19) und Vernachl¨assigen der Terme in ~µ²_⊥ liefert

iω~µ_⊥∼~µ_z×~µ_⊥X

l~^′′

(e^{i~k·l~′′}−1). (4.21)

l~^′′ sind Vektoren, die den Gitterplatz~lmit seinen n¨achsten Nachbarn verbinden. In einem Kristall mit Inversionssymmetrie vereinfacht sich die Summe zu

−2X

l~^′′

sin²(1

2~k·l~^′′). (4.22)

Damit ergibt sich die Kreisfrequenz, mit der ~µ_⊥ in der x−y-Ebene rotiert zu

ω ∼ |~µz|X

l~^′′

sin²(1

2~k·l~^′′). (4.23)

Die Phasendifferenz zweier Atome im Abstand rvoneinander ist~k·~r. Die hier beschriebene Situation ist schematisch in Abb. 4.7 dargestellt. Die Pfeile zeigen die Richtungen an, in die ~µzeigt, wenn man in Richtung k entlang einer Kette von Atomen fortschreitet. Da das magnetische Moment ~µ meist vom Spin eines Elektrons herr¨uhrt, werden die Wellen als Spinwellen bezeichnet. Die Quanteneinheit der Spinwelle ist das Magnon.

Abbildung 4.7: Schematische Darstellung einer Spinwelle.

Der wichtigste Unterschied zwischen Phononen und Magnonen ist ihre unterschiedliche Dispersionsrelationω(~k) f¨ur kleine Werte von~k (Abb. 4.8). W¨ahrend die Gruppengeschwin- digkeit dω/dk f¨ur Phononen f¨ur~k → 0 gegen eine Konstante tendiert, geht sie im Fall von Magnonen gegen null.

Zur Ableitung von Glg. (4.23) waren N¨aherungen n¨otig. Das bedeutet, dass die Spinwel- len, die wir erhalten haben, keine exakten Eigenzust¨ande des Systems sind sondern dass sie nach einer gewissen Zeit zerfallen werden. Dass wir kein brauchbares Modell eines Fer- romagneten finden k¨onnen, das exakt gel¨ost werden kann, zeigt schon, wie kompliziert das Problem Magnetismus ist.

Magnonen treten auch in Antiferromagneten mit lokatisierten Momenten auf. Ihre theo- retische Beschreibung ist aber noch aufw¨andiger. Eine andere Art von Spinwellen tritt in metallischen Ferro- oder Antiferromagneten auf, wo die Spinwelle nicht von lokalisierten ma- gnetischen Momenten, sondern von den Spins der Leitungselektronen getragen wird. Sowohl lokale als auch itinerante (ferromagnetische) Spinwellen werden wir in Abschnitt 4.2.2 noch genauer betrachten.

Abbildung 4.8: Dispersionskurve f¨ur Magnonen.

4.1.5 Paramagnon

Man geht derzeit davon aus, dass in der Umgebung von quantenkritischen Punkten (Ab- schnitt 2.2) magnetische Spinfluktuationen, deren Quanteneinheit das Paramagnon ist, von besonderer Bedeutung sind. Paramagnonen sind bosonische Quasiteilchen. In einem Metall, das noch nicht magnetisch geordnet ist, fluktuiert die Magnetisierung M(R, t) stark. In der~ N¨ahe des Phasen¨ubergangs breitet sich eine (antiferromagnetische) Fluktuation etwa folgen- dermaßen aus:

M(R, t)~ ∼cos(Q~ ·R)e~ ^−R

2

Dte^−Dtξ2 1

t^3/2. (4.24)

Qbeschreibt die Modulation des Antiferromagneten, ξ ist die typische Gr¨oße eines magneti- sierten Bereichs und wird als Korrelationsl¨ange bezeichnet. Durch die Elektronen werden die Fluktuationen stark ged¨ampft, was durch die D¨ampfungskonstante D ber¨ucksichtigt wird.

Im oberen Teilbild von Abb. 4.9 ist M(x, t) f¨ur ein System dargestellt, in dem ξ ungef¨ahr drei Perioden der Magnetisierung betr¨agt. Die Fluktuationen zerfallen nach kurzer Zeit und haben nur eine kurze Reichweite. Eine derartige Situation liegt z.B. im paramagnetischen Zustand in der N¨ahe des quantenkritischen Punktes von CePd2Si2 vor (vgl. Abb. 2.7). F¨ur ξ = ∞, wie es an einem Quantenphasen¨ubergang auftritt, klingen die magnetischen Fluk- tuationen nur sehr langsam ab (unteres Teilbild von Abb. 4.9).

Die magnetischen Fluktuationen verursachen ihrerseits wieder eine effektive Wechselwir- kung zwischen den Elektronen. Ein solcher Prozess ist in Abb. 4.10 dargestellt: Ein Elektron am Ort ~r1 erzeugt zum Zeitpunkt t1 eine Spinfluktuation M(~r−~r1, t−t1), wobei sich die Richtung seines Spins ¨andert. Zum Zeitpunktt2 absorbiert ein anderes Elektron die Spinfluk- tuation wieder. Die effektive Wechselwirkung ist beiT = 0 proportional zuM(~r2−~r1, t2−t1).

60 KAPITEL 4. ELEMENTARE ANREGUNGEN

!6 F!! ! * !*

!&! *! <*F !R

&ÊõÆH36Ê4ÆN5 âêÆiÈ

Ã

Å6Å ÍË

Ã

:ÁÊ49>021ëÊ43ˆ021*Èx5

Ã

҉Ê4ÆHÈ;3ˆ:;021Ô҉ÆH9ÉWË4Ê4ÆiÈ

3ˆ: ÈHÍFúÑ4Ç*ÈWÑ436ÆHÉ;ȶË>36Æ$â

Ã

҉Ê4ÆHÈ;3ˆ: 36ÆNÉ;Ñ4ÊÒ5 F43

7 H]: È

Ã

ÉWÇ®Ï &ÊaË>ÆNÉ

X·øà 14ÆaË>ÆJ:1 à : ÆNÊ]øÑ ð ÆHÉWÒ Ã Ê4Ò: ð ÉWÆH3YÈ;ÆHȼ:;3ˆ021ÔÆN3YÊÆC÷]Å6Ñ4Ç*È;Ñ Ã é

ÈW3Y9Ê(á‰Ï

ÿ

Ï>ÌK9ÅYÒÆHÊË4ÆHÉW5

Ã

ì‰ÆNÊ

Ã

Ñ:

5 F43

7

Hö0H9:F

ÛE3 H*Æ

T

è Ö 3kG

Æ T

è Ö

G Ø

æ G

ð

ÆN:W0214ÉWÆH3

ð

È·Ë43YÆ(âê9>Ë>Ñ4Å

Ã

ÈW3Y9ÊëË4ÆN:À/±Ê*È;3YÌKÆHÉWÉW9‰5

Ã

ÒÊ4ÆiÈWÆHÊÍ

3ˆ: ÈË>36Æ#ÈZè43ˆ:;021ÆîxÉJø9ì‰Æ#ÆN3YÊÆN:ö5

Ã

҉Ê4ÆHÈ;3ˆ:;3YÆNÉ ÈWÆHÊ

ÿ

ÆHé

ÉWÆH3ˆ021:HÏ Â Ñ4É2021ÀË43YÆÄÅ6ÆNÇÈWÉ;9Ê4ÆHÊ

Î

ÆHÉ2Ë>ÆNÊ·Ë>36Æ÷PÅ6Ñ4Ç*ÈWÑ Ã ÈW3Y9Ê4ÆHÊ

: È

Ã

É;Ƿ҉ÆNË øà 5aè>̈ÈNÍ*Ë>36Æç*È øà ÉWljƱË>36ÆJ: ÆJ:ÄYmjÆHÇ*ÈW:

ð

ÆJ: ÈW365a5‚ÈË>36Æ

 ø

Ã

5aè>ÌKÑÊ4Ò:;lj9Ê: È

Ã

Ê*È;Æ

Ï

x t

x t

&5 9 ð ÆHÉWÆHÊ

ÿ

36ňËô36: È,5 F!

7

H$ÌWøÑ4ÉxÆH36ÊÔç>: ÈWÆH5Ë

Ã

É;ÒÆN: È;ÆHÅ6ÅYÈHÍ

36ÊöË>ÆN5 Ë43YÆ7[Á9‰ÉWÉ;ÆNÅ

Ã

È;369‰Ê.: Å&øà ÊÒlÆ

Ñ4Ê4ÒÆiÌ ø

Ã

14É :_¶ÆNÉ;369>Ë>ÆNÊ

Ë>ÆNɱâ

Ã

ÒÊ4ÆiÈW3ˆ: 36ÆHÉWÑ4Ê4Ò

ð

ÆHÈ;Écø

Ã

҉ÈHÏ

Â

3Yƾ÷]Å6Ñ4Ç*È;Ñ

Ã

È;369Ê4ÆHÊ(áHÆHÉ;Ì

Ã

ÅYé

Å6ÆHÊêÊ

Ã

021ÇÑ4É;áNÆHÉJ®ÆH3YȱÑ4ÊËï1

Ãlð

ÆHÊïÊÑ4ÉÆH36Ê4ƼÇÑ4ÉWáHƂ7±ÆH3ˆ021>é

Î

ÆH3YÈ;ƉÏ

ÂxÃ

ÒÆH҉ÆNÊü3ˆ: È·Ë43YÆ [Á9‰ÉWÉ;ÆNÅ

Ã

È;369‰Ê.: Å&ø

Ã

Ê҉Æ

Ë>36ÉWÆHÇ*È

à 5

Ñ Ã Ê*È;ÆHÊè41 Ã :;ÆHÊ

ø

Ñ ð ÆNÉ;Ò Ã Ê4ÒÑ4ÊÆHÊË>Å63ˆ0216FKÑ4Ê*ÈWÆHÉWÆN: ÿ 36ňËH2ÍNÑ4ÊË

Ë>36Æ$5

Ã

҉Ê4ÆHÈ;3ˆ:;021ÆHÊ·÷]Å6Ñ4Ç*È;Ñ

Ã

È;369Ê4ÆHÊÀÇÅY36Ê4ÒÆHÊ·Ê*Ñɗ:;ÆH14ÉÅ

Ã

Ê4Òlé

: Ã 5

Éð

Ï

Â

36Æ5

Ã

ÒÊ4ÆiÈW36:W0214ÆNÊÁ÷]Å6Ñ4Ç*È;Ñ

Ã

È;369Ê4ÆHÊÁñ‰ÆNÉ;ÑÉW:

Ã

0214ÆNÊÁ3Y1É;ÆNÉW:;ÆH3YÈW:

Î

36ÆNË4ÆHÉÆN36Ê4ÆíÆm®ÆNÇÈW36ñ‰ÆöóõÆN021.: ÆNÅ

Î

36ÉWÇÑ4Ê4Ò#á

Î

3ˆ:W0214ÆHÊ8Ë4ÆHÊ

ÄÅYÆNÇ*È;ÉW9‰Ê4ÆNÊÏÄ36ÊÄÅ6ÆHÇ*ÈWÉ;9Ê Ç Ã ÊÊöálÏ ÿ Ï Ã 5 É;È " áHÑ45

J®ÆN3YÈ;è4Ñ4ÊÇÈ

;Þ

ÆH36Ê4Ƽçè436Ê>úÑÇÈWÑ

Ã

ÈW369‰Ê 5 F Ö

Þ7

Ö

;Þ

H—ÆHÉ;é

áNÆHÑ4ÒÆHÊÍË

Éð

ÆN3øà Ê.Ë>ÆHÉ;ȱ: 3ˆ021(Ë43YƼ7$3ˆ021*È;ÑÊ4ÒÀ:;ÆH36Ê4ÆJ:$çè436Ê:HÏ

J®Ñ5 J®ÆH3YÈWè4Ñ4Ê4Ç*È

ZG Éð

:;9‰É

ð

36ÆHÉ;È·Ë

Ã

ÊÊ ÆN3YÊ

Ã

ÊË4ÆHÉWÆN:CÄÅ6ÆHÇ*é

ÈWÉ;9ÊëË>36ƞçè436Ê>ú.Ñ4Ç*È;Ñ

Ã

È;369‰Ê

Î

36ÆNË>ÆNÉHÏ

Â

3YÆ|çÈJøà ÉWljÆCË>36ÆN:;ÆHɼÆḦé

ÌKÆNÇÈW36ñ‰ÆHÊïóëÆJ021: ÆNÅ

Î

3YÉWÇÑ4Ê4Ҟ3ˆ: È/F

ð

ÆN3 \0]Ü=H±è4ÉW9‰è®9‰É;È;369Ê

à Å

áNÑ 5 F G Ö Þ 7 G Ö Þ

HwÍ3ˆ: È Ã Åˆ: 9 à 5 Ñ Ã Ê*ÈWÆHÊ4è41 à :;ÆHÊ

ø

Ñ ð ÆHÉ;é

Ò Ã Ê4Ò ð ÆN3 ]$# ð ÆN:;9‰Ê.Ë>ÆHÉ2:: È Ã ÉWǞÑ4ÊËô1 Éð ÆNÊôÆN36Ê4ÆÅ Ã Ê4҉Æ

7$ÆN3ˆ021

Î

ÆH3YÈWÆlÏ

%P&d6RT (TxM/(P!i/() T60 d"+-#

: ȶË>36ƗóëÆJ021:;ÆHÅ

Î

36É;ÇÑ4Ê4Ò$á

Î

3ˆ:;0214ÆNʂË>ÆNÊÀÄÅYÆNÇ*È;ÉW9‰Ê4ÆNʾ: È

Ã

ÉWÇ.Í

:;9

ð

ÆHÆH36Ê>ú.Ñ4ìlÈ!3614É!lj9‰Å6Å6ÆHÇ*ÈW3YñÆN:—û,ÆHÉW1

Ã

ÅYÈWÆHÊêË>36ƾÄ36҉ÆNÊ:W021

Ã

̈ÈWÆHÊ

ñ9‰ÊüâêÆHÈ

Ã

Å6Å6ÆHÊÏ &ÊüÆH36Ê4ÆNɂ÷4ÆNÉ;5a3Yú,øÑ:W:;3YÒljÆN3©Èx1

Ãlð

ÆHÊýË43YÆ

Î

360214é

ÈW36Ò: È;ÆHÊÁÇ9‰Å6Å6ÆHÇ*È;36ñ‰ÆNÊ!/±ÊÉ;ÆN҉Ñ4Ê4ÒÆHÊÍcË>36Æ Ñ Ã :;3YÈ;ÆN3Yň0214ÆNÊÍw҉ÆNÉ Ã Ë>Æ

Ë43YÆxÄ36҉ÆNÊ:W021

Ã

̈ÈWÆHÊCñ‰9ʞÆH36Ê4áNÆHÅ6Ê4ÆHʞÄÅ6ÆHÇ*È;ÉW9‰Ê4ÆNÊωóõÆHÊÊ(Ë

Ã

҉Æié

ÒÆHÊêË>36ƼÄÅ6ÆHÇ*ÈWÉ;9Ê4ÆHÊô: 3ˆ021ôÊ*ÑÉ$3YÊÆN3YÊÆHÉ Â 365aÆNÊ: 369Ê ð Æ Î

ÆH҉ÆNÊ

Çø9Ê4Ê4ÆHÊÍ

Î

ÆHÉ2Ë>ÆHÊÔçè3YÊêÑÊËïÐ

Ã

Ë>Ñ4Ê4Òañ9‰Êêá

Î

ÆN3pÑ4Ê*È;ÆNÉW:W021436ÆNË>é

Å63ˆ0214ÆNÊ|þpÆN36Å6021ÆHʞÈWÉ

Ã

Ê:;è.9É ÈW3YÆNÉ ÈNÏ

/±Ñ4ÌÆH36Ê4Æ

Ã

ÊË>ÆHÉWÆ·ç9É ÈWÆHÊêñ9‰Ê Ñ Ã

: 3YÈ;ÆN36Å6021ÆHÊÍ4Ë>36ƾ36Êêá

Î

ÆH3

Â

365aÆHÊ:;369‰Ê4ÆNÊ

ð

ÆH3149‰14ÆNÊâ

Ã

ÒÊ4ÆiÈ;ÌKÆHňË>ÆHÉWÊ

Î

36021*ÈW3YÒ

Î

ÆHÉ2Ë>ÆHÊÍ

Ç9‰Ê4Ê*ÈWƼ1436ÆHɱÊ43ˆ021*ȱÆH36Ê4ÒÆHÒ Ã Ê4ÒÆHÊ7Fg: 36ÆN14Æ¾Ë Ã áNÑ

H" ÿ ÆN3Y5 : 9҉ÆHé

Ê Ã

Ê4Ê*È;ÆNʂÌKÉ

Ã

Ç*ÈW3Y9Ê

Ã

Å6ÆNÊ Ñ Ã

Ê*ÈWÆHÊ41

Ã

Å6ÅYÆm®ÆNÇ*ÈPÆHÊ*È2: ÈWÆH14ÆNÊÀÇ9‰Å6Å6ÆHÇ*é

ÈW36ñ‰Æ¾/±ÊÉ;ÆN҉Ñ4Ê4ÒÆHÊê5a3YÈ!á‰Ï

ÿ

ÏjÊ*ÑÉ!ÆH36Ê4ÆN5

Â

ÉW3©È;È;ÆNÅPË>ÆNÉxÐ

Ã

Ë>Ñ4ÊÒ

ÆN36Ê4ÆN:xÄÅ6ÆHÇ*ÈWÉ;9Ê:iÏj÷±øÑ4ɼ3614É;ÆÀÄÊ*ÈWË4ÆN02ÇÑ4Ê4Ò

Î

Ñ4É2Ë>ÆÀË4ÆHÉX±9

ð

ÆNÅ©é

èÉ;ÆN36:¾3YÊ1=>:;36ÇýØNååBA

Ã

Êý7¼Ï

ÿ

Ï]Ð

Ã

Ñ4Ò14Å636ÊÍ

W

Ï,Ð,Ï,ç*È 9É;5aÆNÉø

ÑÊË

Â

Ïjà!Ï®þ$: Ñ43ñÆHÉWÅ63YÆN14ÆHÊÏ

&Ê Ë>ÆHÉ9X·ø

Ã

14Æüñ9‰Êí5

Ã

҉Ê4ÆHÈ;3ˆ:W0214ÆHÊ Ñ Ã

Ê*È;ÆNÊ4è41

Ã

: ÆNÊ]øÑ ð ÆHÉ;é

Ò®ø

Ã

Ê4ÒÆHÊ 36Ê#âêÆiÈ

Ã

Å6Å6ÆHÊ

Î

ÆNÉWË>ÆNÊ ÆH36Ê4ÆüÒ

Ã

Ê4áHÆý7±ÆH3614Æýñ9‰Ê

Ã

Ê>é

95

Ã

Å6ÆHÊÁÄ36ÒÆHÊ:W021

Ã

̈ÈWÆHÊ

ð

ÆH9

ð.Ã

021*È;ÆHÈHÏJ÷!øÑ4ɶË>36ÆÑ4Ê҉Æ

Î ø914Ê4Å63ˆ0214Æ

þPÆH5aè®ÆHÉ

Ã

ÈWÑ4É

Ãlð 1pø

Ã

Ê4҉36ÒljÆH3YÈ!Ë>ÆJ:xóö3ˆË>ÆHÉ2: È

Ã

ÊË4ÆN:ÁÑ4ÊË

Ã

ÊË>ÆNÉ;ÆNÉ

îxÉcø9‰ìÆHÊÍ Ã‰ð ÆNÉ Ã Ñ021òÌWøÑ4ɂË>36ÆaçÑ4è4É Ã Å6ÆN3©ÈWÑ4Ê4Ò ð ÆN3,È;36ÆiÌKÆNÊëþPÆH5Cé

è®ÆHÉ Ã ÈWÑ4ÉWÆHÊ 36: È

Î Ã 14É2:;0214ÆN36Ê4Å636021üË Ã :ÀóëÆJ021:;ÆHň: è3YÆNÅá

Î

3ˆ:;021ÆHÊ

Ñ Ã

:;3©ÈWÆH36ň0214ÆHÊÑ4Ê.ËÔÇ9‰Å6Å6ÆHÇ*È;36ñ‰ÆNÊ5

Ã

҉ÊÆiÈ;3ˆ:W0214ÆHÊï÷]Å6Ñ4Ç*È;Ñ

Ã

È;369‰é

ÊÆHÊüñ‰ÆNÉ

Ã

Ê*È

Î

9É ÈWÅY3ˆ021Ïjû!36ÆNÅYƞÄm®ÆNÇ*È;Æ|:;36ÊËüË

Ãlð

ÆH3—Ê49>021üÊ43ˆ021*È

ñÆHÉ2: È

Ã

ÊË4ÆHÊÏ

Ä36Êíç>021

Î

ÆHÉWè4Ñ4Ê4Ç*È(Ë4ÆHÉ÷49‰É2:W021*ÑÊ4Ò

Ã

ÊöÇ9‰ÉWÉ;ÆNÅ63YÆNÉ ÈWÆHÊ âêÆié

È Ã

Å6Å6ÆHÊ :;3YÊ.Ë8: ÆN3YÈ3614É;ÆNÉ ÄÊÈ2Ë>ÆN02ÇÑ4ÊÒ 365 5 Ã

14ÉWÆ ØJåBAÚ#Ë>36Æ

W 9>021ÈWÆH5aè®ÆHÉ Ã ÈWÑ4ÉW:;Ñ4è4É Ã Å6ÆN3©ÈWÆHÉNÏ Â 36ÆJ: Æõâ à ÈWÆHÉW3 à Å636ÆHÊñ‰ÆNÉ;Å636ÆHÉWÆHÊ

3614ÉWÆHÊóö3ˆË>ÆHÉ2: È

Ã

ÊË

ð

ÆH3±ñ36ÆHÅ$1pø914ÆHÉWÆHÊäþPÆH5aè®ÆHÉ

Ã

È;ÑÉ;ÆNÊFKá‰Ï

ÿ Ï

ð

ÆH3®0

Ã

ωåB>U[í36Ê('

ÿÃ

G

à—Ñ

æ

) H Ã

ň:

ð

ÆN3ñ‰9É;1ÆHÉ

ð

ÆHÇ

Ã

Ê4Ê*ÈWÆHʞçÑ>é

èÉ

Ã

ÅYÆN3YÈ;ÆHÉWÊÏç36Æa: 36ÊËõË

Ã

5a3©È¼:;ÆH14É

Î

3ˆ021*È;36Ò|ÌWøÑ4ɂË>36ƞÄÊ*È

Î

3ˆ02Ç*é

Å6Ñ4ÊÒÊ4ÆNÑ4ÆHÉ

Ã

Ñ4ÌCçÑ4èÉ

Ã

ÅYÆN3YÈ;Ñ4Ê4Ò

ðÃ

:;36ÆHÉWÆHÊË>ÆNÉ(þPÆN0214Ê9‰Å69‰Ò3YÆNÊÍ

36Ê: ð ÆN:;9‰ÊË>ÆNÉ;ÆÀË Ã : 36Ƃ5a3YȼË>ÆH5 ð 36ÅYÅ636҉ÆNÊ|ú,øÑ:;:;36҉ÆNÊòç*È;3ˆ02Ç>: È;9Um

ÒÆHÇpøÑ414ÅYÈ

Î

ÆHÉ2Ë>ÆNÊïÇø9‰Ê4Ê4ÆNÊÏÄ36Ê4ƂÄÉ;ÇÅ&ø

Ã

ÉWÑ4Ê4Òa3614ÉWÆN:: ÆNÅ©È2:

Ã

5aÆHÊ

û,ÆNÉ;1

Ã

ÅYÈ;ÆNÊ:iÍlË

à : Ã

Å6Å6ÆHʾÊ9‰ÉW5

Ã

Å6ÆHÊ Ñ Ã

: 3YÈWÆH36ň0214ÆHÊ45a9>Ë>ÆNÅ6ÅYÆHÊáNÑ

Î

3ˆË>ÆNÉW:;è4ÉWÆN0214ÆNÊ:W0214ÆH36Ê*ÈHÍ,3ˆ: È

ð

3ˆ:;14ÆHÉ-8 ÆJË>9>021 Ê9021 Ê43ˆ021*Èa҉Æié

Å6Ñ4Ê҉ÆHÊÏė:—3ˆ: ȐË>ÑÉW021

Ã

Ñ:—5 ø9‰Ò‰Å63ˆ021ÍË

à ì Ã

Ñ021|13YÆNɐË43YÆx÷]ÅYÑÇé

ÈWÑ

Ã

ÈW369‰Ê4ÆNÊÊ

Ã

14ÆÔÆH36Ê4ÆH5 Ñ Ã

ÊÈWÆHÊ4è1

Ã

:;ÆHʶøÑ ð ÆNÉ;Ò

Ã

Ê4Ò

Î

3ˆ021*È;36Ò

:;36ÊËõ9>Ë>ÆHÉCË Ã ìòË>36Æ(ÄÅ6ÆHÇ*È;ÉW9‰Ê4ÆNÊøà 14Ê4Å63ˆ021

Î

36ƞ36ÊýÆH36Ê4ÆNÉ·ÐpÑ>È é

ÈW36Ê4҉ÆNÉ ú,øÑ.:;:;36҉ljÆN3YÈÁ36Êäçè436ÊÑ4Ê.Ë Ð Ã

Ë>Ñ4ÊÒòáNÆHÉ;Ì

Ã

Å6Å6ÆHÊÏ

ð

1436ÆNÉ

ÆN36Ê4ÆÒ

Ã

ÊáêÊ4ÆHÑ4ÆÔç>9‰É;È;Æêñ‰9Ê ÄÅ6ÆH5aÆHÊ*È

Ã

É;È;ÆH36ň0214ÆNÊëÆN36Ê4Æê7$9‰Å6Å6Æ

:;è436ÆHÅYȐ9Ë4ÆHÉ9

ð

Ë>36ÆN:;ÆN:1[Á9‰Ê4áNÆHè>È$Ò

Ã

ɐÊ43ˆ021È

Ã

Ê҉Æ

Î

ÆHÊ.Ë>ÆiÈ

Î

ÆNÉ é

Ë4ÆHÊÇ

Ã

Ê4ÊÍ43ˆ: È

Ã

Å6Å6ÆHÉ2Ë>36Ê4Ò:,Ê9021ñø9‰Å6Å636Ò¼9UmjÆHÊÏ

&Ž®´x¬a­i«&¡‰¦•w¯s]j¬ô u—• J¢&  ¡’J¯»4j°±+*N¦£SŸY­iœ®¯ (;j°±

›

­N£~¥F’W•w¯

´x*¬ô s• ’&qc’J¯°±=tÁ

›  ­N¢&’W£S¤Ÿ~“Á“¼’W•¦*œu u .Hœ¨w­i• Ÿ©  ¡®¯

Ž­i«&¦*• ’-,/.0®¯ 21C‹ o3121E$cš;

"

p]ªp  ¥F’W•&œü¦œ>KtÁ ¹4 x¸N  ¥4¯/ ¡Uq‰¢&ŸS¥ÔŸ~œõ¦*œ*¢&’W• ’W•544’WŸS«76¯/$E

‹ o3121c™Jš;

9‰‘> ¸N¡œ’&q‰¢&’Wœ.¯ ¡Uq‰¢&ŸS¥J­N£SŸ©¢&  ¡’µ¶£ ¸­H«&« ’W•98;:*¯/1HŒBo¾‹ o3121c™Nš;

<

j

›  n œ>’;• ¢&Nœ®¯ ¡?q‰¢&ŸS 2¢º®l­"qF¯‰Œc–À‹= W«wNo31>1>?Jš;

@BACADA

n

•&« Ÿ~¥F’2£>¨;¦*•»l¦¿*• ­N£S’2Ÿ~«&¦*œ*§¯B ¡?q‰¢&Ÿ~¥¾ŸSœ‚¦*œ*¢&’W• ’W•94>’2ŸS«

ACACA



ACADA

n

•&« Ÿ~¥F’2£¨W¦“8ŸS’2¢FE2¸­H¡*• ŸS§J’;œêŽH”4’2£S¿• ’2ŸS¢ ¡Uq‰¢&Ÿ~¥¯ ¡Uq¢&Ÿ~¥žŸ~œ

¦*œ*¢&’W• ’W•G4>’2ŸS«

ACACA



Abbildung 4.9: Orts- und zeitabh¨angige Magnetisierung f¨ur zwei Spinfluktuationen mit un- terschiedlicher Korrelationsl¨ange [Rosch, Physik in unserer Zeit 30 (1999) 118].

Beim Quantenphasen¨ubergang, wo ξ = ∞, ist sie gem¨ass Glg. (4.24) besonders groß und langreichweitig. Wie bereits in Abschnitt 2.3.2 erw¨ahnt kann diese effektive Wechselwirkung auch anziehend sein und zu Supraleitung f¨uhren.

!&! *! <*F !R

&ÊõÆH36Ê4ÆN5 âêÆiÈ

Ã

Å6Å ÍË

Ã

:ÁÊ49>021ëÊ43ˆ021*Èx5

Ã

҉Ê4ÆHÈ;3ˆ:;021Ô҉ÆH9ÉWË4Ê4ÆiÈ

3ˆ: ÈHÍFúÑ4Ç*ÈWÑ436ÆHÉ;ȶË>36Æ$â

Ã

҉Ê4ÆHÈ;3ˆ: 36ÆNÉ;Ñ4ÊÒ5 F43

7

H]: È

Ã

ÉWÇ®Ï &ÊaË>ÆNÉ

X·ø

Ã

14ÆaË>ÆJ:1

Ã

: ÆNÊ]øÑ ð

ÆHÉWÒ

Ã

Ê4Ò:

ð

ÉWÆH3YÈ;ÆHȼ:;3ˆ021ÔÆN3YÊÆC÷]Å6Ñ4Ç*È;Ñ

à é

ÈW3Y9Ê(á‰Ï

ÿ

Ï>ÌK9ÅYÒÆHÊË4ÆHÉW5

Ã

ì‰ÆNÊ

Ã

Ñ:

5 F43

7

Hö0H9:F

ÛE3 H*Æ

T

è Ö

3kG

Æ T

è Ö

G Ø

æ G

ð

ÆN:W0214ÉWÆH3

ð

È·Ë43YÆ(âê9>Ë>Ñ4Å

Ã

ÈW3Y9ÊëË4ÆN:À/±Ê*È;3YÌKÆHÉWÉW9‰5

Ã

ÒÊ4ÆiÈWÆHÊÍ

3ˆ: ÈË>36Æ#ÈZè43ˆ:;021ÆîxÉJø9ì‰Æ#ÆN3YÊÆN:ö5

Ã

҉Ê4ÆHÈ;3ˆ:;3YÆNÉ ÈWÆHÊ

ÿ

ÆHé

ÉWÆH3ˆ021:HÏ

Â

Ñ4É2021ÀË43YÆÄÅ6ÆNÇÈWÉ;9Ê4ÆHÊ

Î

ÆHÉ2Ë>ÆNÊ·Ë>36Æ÷PÅ6Ñ4Ç*ÈWÑ

Ã

ÈW3Y9Ê4ÆHÊ

: È

Ã

É;Ƿ҉ÆNË ø

Ã

5aè>̈ÈNÍ*Ë>36Æç*È ø

Ã

ÉWljƱË>36ÆJ: ÆJ:ÄYmjÆHÇ*ÈW:

ð

ÆJ: ÈW365a5‚ÈË>36Æ

 ø

Ã

5aè>ÌKÑÊ4Ò:;lj9Ê: È

Ã

Ê*È;Æ

Ï

&5 9 ð

ÆHÉWÆHÊ

ÿ

36ňËô36: È,5 F!

7

H$ÌWøÑ4ÉxÆH36ÊÔç>: ÈWÆH5Ë

Ã

É;ÒÆN: È;ÆHÅ6ÅYÈHÍ

36ÊöË>ÆN5 Ë43YÆ7[Á9‰ÉWÉ;ÆNÅ

Ã

È;369‰Ê.: Å&ø

Ã

ÊÒlÆ

Ñ4Ê4ÒÆiÌ ø

Ã

14É :_¶ÆNÉ;369>Ë>ÆNÊ

Ë>ÆNɱâ

Ã

ÒÊ4ÆiÈW3ˆ: 36ÆHÉWÑ4Ê4Ò

ð

ÆHÈ;Écøà ҉ÈHÏ

Â

3Yƾ÷]Å6Ñ4Ç*È;Ñ

Ã

È;369Ê4ÆHÊ(áHÆHÉ;Ì

Ã

ÅYé

Å6ÆHÊêÊ

Ã

021ÇÑ4É;áNÆHÉJ®ÆH3YȱÑ4ÊËï1

Ãlð

ÆHÊïÊÑ4ÉÆH36Ê4ƼÇÑ4ÉWáHƂ7±ÆH3ˆ021>é

Î

ÆH3YÈ;ƉÏ

ÂxÃ

ÒÆH҉ÆNÊü3ˆ: È·Ë43YÆ [Á9‰ÉWÉ;ÆNÅ

Ã

È;369‰Ê.: Å&ø

Ã

Ê҉Æ

Ë>36ÉWÆHÇ*È

à 5

Ñ Ã

Ê*È;ÆHÊè41

Ã

:;ÆHÊ

ø

Ñ ð

ÆNÉ;Ò

Ã

Ê4ÒÑ4ÊÆHÊË>Å63ˆ0216FKÑ4Ê*ÈWÆHÉWÆN:

ÿ

36ňËH2ÍNÑ4ÊË

Ë>36Æ$5

Ã

҉Ê4ÆHÈ;3ˆ:;021ÆHÊ·÷]Å6Ñ4Ç*È;Ñ

Ã

È;369Ê4ÆHÊÀÇÅY36Ê4ÒÆHÊ·Ê*Ñɗ:;ÆH14ÉÅ

Ã

Ê4Òlé

: Ã 5

Éð

Ï

Â

36Æ5

Ã

ÒÊ4ÆiÈW36:W0214ÆNÊÁ÷]Å6Ñ4Ç*È;Ñ

Ã

È;369Ê4ÆHÊÁñ‰ÆNÉ;ÑÉW:

Ã

0214ÆNÊÁ3Y1É;ÆNÉW:;ÆH3YÈW:

Î

36ÆNË4ÆHÉÆN36Ê4ÆíÆm®ÆNÇÈW36ñ‰ÆöóõÆN021.: ÆNÅ

Î

36ÉWÇÑ4Ê4Ò#á

Î

3ˆ:W0214ÆHÊ8Ë4ÆHÊ

ÄÅYÆNÇ*È;ÉW9‰Ê4ÆNÊÏÄ36ÊÄÅ6ÆHÇ*ÈWÉ;9Ê Ç Ã

ÊÊöálÏ

ÿ Ï Ã 5 É;È

"

áHÑ45

J®ÆN3YÈ;è4Ñ4ÊÇÈ

;Þ

ÆH36Ê4Ƽçè436Ê>úÑÇÈWÑ

Ã

ÈW369‰Ê 5 F Ö

Þ7

Ö

;Þ

H—ÆHÉ;é

áNÆHÑ4ÒÆHÊÍË

Éð

ÆN3ø

Ã

Ê.Ë>ÆHÉ;ȱ: 3ˆ021(Ë43YƼ7$3ˆ021*È;ÑÊ4ÒÀ:;ÆH36Ê4ÆJ:$çè436Ê:HÏ

2 2

Spinfluktuation r t r t

_{1 1}

J®Ñ5 J®ÆH3YÈWè4Ñ4Ê4Ç*È

ZG

Éð

:;9‰É

ð

36ÆHÉ;È·Ë

Ã

ÊÊ ÆN3YÊ

Ã

ÊË4ÆHÉWÆN:CÄÅ6ÆHÇ*é

ÈWÉ;9ÊëË>36ƞçè436Ê>ú.Ñ4Ç*È;Ñ

Ã

È;369‰Ê

Î

36ÆNË>ÆNÉHÏ

Â

3YÆ|çÈJø

Ã

ÉWljÆCË>36ÆN:;ÆHɼÆḦé

ÌKÆNÇÈW36ñ‰ÆHÊïóëÆJ021: ÆNÅ

Î

3YÉWÇÑ4Ê4Ҟ3ˆ: È/F

ð

ÆN3 \0]Ü=H±è4ÉW9‰è®9‰É;È;369Ê

à Å

áNÑ 5 F G Ö Þ

7

G Ö Þ

HwÍ3ˆ: È

Ã

ň: 9

à 5 Ñ Ã

Ê*ÈWÆHÊ4è41

Ã

:;ÆHÊ Ñø ð

ÆHÉ;é

Ò Ã Ê4Ò

ð

ÆN3

]$#

ð

ÆN:;9‰Ê.Ë>ÆHÉ2:: È

Ã

ÉWǞÑ4ÊËô1

Éð

ÆNÊôÆN36Ê4ÆÅ

Ã

Ê4҉Æ

7$ÆN3ˆ021

Î

ÆH3YÈWÆlÏ

: ȶË>36ƗóëÆJ021:;ÆHÅ

Î

36É;ÇÑ4Ê4Ò$á

Î

3ˆ:;0214ÆNʂË>ÆNÊÀÄÅYÆNÇ*È;ÉW9‰Ê4ÆNʾ: È

Ã

ÉWÇ.Í

:;9

ð

ÆHÆH36Ê>ú.Ñ4ìlÈ!3614É!lj9‰Å6Å6ÆHÇ*ÈW3YñÆN:—û,ÆHÉW1

Ã

ÅYÈWÆHÊêË>36ƾÄ36҉ÆNÊ:W021

Ã

̈ÈWÆHÊ

ñ9‰ÊüâêÆHÈ

Ã

Å6Å6ÆHÊÏ &ÊüÆH36Ê4ÆNɂ÷4ÆNÉ;5a3Yú,øÑ:W:;3YÒljÆN3©Èx1

Ãlð

ÆHÊýË43YÆ

Î

360214é

ÈW36Ò: È;ÆHÊÁÇ9‰Å6Å6ÆHÇ*È;36ñ‰ÆNÊ!/±ÊÉ;ÆN҉Ñ4Ê4ÒÆHÊÍcË>36Æ Ñ Ã

:;3YÈ;ÆN3Yň0214ÆNÊÍw҉ÆNÉ

Ã

Ë>Æ

Ë43YÆxÄ36҉ÆNÊ:W021

Ã

̈ÈWÆHÊCñ‰9ʞÆH36Ê4áNÆHÅ6Ê4ÆHʞÄÅ6ÆHÇ*È;ÉW9‰Ê4ÆNÊωóõÆHÊÊ(Ë

Ã

҉Æié

ÒÆHÊêË>36ƼÄÅ6ÆHÇ*ÈWÉ;9Ê4ÆHÊô: 3ˆ021ôÊ*ÑÉ$3YÊÆN3YÊÆHÉ

Â

365aÆNÊ: 369Ê

ð Æ Î

ÆH҉ÆNÊ

Çø9Ê4Ê4ÆHÊÍ

Î

ÆHÉ2Ë>ÆHÊÔçè3YÊêÑÊËïÐ

Ã

Ë>Ñ4Ê4Òañ9‰Êêá

Î

ÆN3pÑ4Ê*È;ÆNÉW:W021436ÆNË>é

Å63ˆ0214ÆNÊ|þpÆN36Å6021ÆHʞÈWÉ

Ã

Ê:;è.9É ÈW3YÆNÉ ÈNÏ

/±Ñ4ÌÆH36Ê4Æ

Ã

ÊË>ÆHÉWÆ·ç9É ÈWÆHÊêñ9‰Ê Ñ Ã

: 3YÈ;ÆN36Å6021ÆHÊÍ4Ë>36ƾ36Êêá

Î

ÆH3

Â

365aÆHÊ:;369‰Ê4ÆNÊ

ð

ÆH3149‰14ÆNÊâ

Ã

ÒÊ4ÆiÈ;ÌKÆHňË>ÆHÉWÊ

Î

36021*ÈW3YÒ

Î

ÆHÉ2Ë>ÆHÊÍ

Ç9‰Ê4Ê*ÈWƼ1436ÆHɱÊ43ˆ021*ȱÆH36Ê4ÒÆHÒ

Ã

Ê4ÒÆHÊ7Fg: 36ÆN14ƾË

Ã

áNÑ

H"

ÿ

ÆN3Y5 : 9҉ÆHé

Ê Ã

Ê4Ê*È;ÆNʂÌKÉ

Ã

Ç*ÈW3Y9Ê

Ã

Å6ÆNÊ Ñ Ã

Ê*ÈWÆHÊ41

Ã

Å6ÅYÆm®ÆNÇ*ÈPÆHÊ*È2: ÈWÆH14ÆNÊÀÇ9‰Å6Å6ÆHÇ*é

ÈW36ñ‰Æ¾/±ÊÉ;ÆN҉Ñ4Ê4ÒÆHÊê5a3YÈ!á‰Ï

ÿ

ÏjÊ*ÑÉ!ÆH36Ê4ÆN5

Â

ÉW3©È;È;ÆNÅPË>ÆNÉxÐ

Ã

Ë>Ñ4ÊÒ

ÆN36Ê4ÆN:xÄÅ6ÆHÇ*ÈWÉ;9Ê:iÏj÷±øÑ4ɼ3614É;ÆÀÄÊ*ÈWË4ÆN02ÇÑ4Ê4Ò

Î

Ñ4É2Ë>ÆÀË4ÆHÉX±9

ð

ÆNÅ©é

èÉ;ÆN36:¾3YÊ1=>:;36ÇýØNååBA

Ã

Êý7¼Ï

ÿ

Ï]Ð

Ã

Ñ4Ò14Å636ÊÍ

W

Ï,Ð,Ï,ç*È

ø

9É;5aÆNÉ

ÑÊË

Â

Ïjà!Ï®þ$: Ñ43ñÆHÉWÅ63YÆN14ÆHÊÏ

&Ê Ë>ÆHÉ9X·ø

Ã

14Æüñ9‰Êí5

Ã

҉Ê4ÆHÈ;3ˆ:W0214ÆHÊ Ñ Ã

Ê*È;ÆNÊ4è41

Ã

: ÆNÊ]øÑ ð

ÆHÉ;é

Ò®ø

Ã

Ê4ÒÆHÊ 36Ê#âêÆiÈ

Ã

Å6Å6ÆHÊ

Î

ÆNÉWË>ÆNÊ ÆH36Ê4ÆüÒ

Ã

Ê4áHÆý7±ÆH3614Æýñ9‰Ê

Ã

Ê>é

95

Ã

Å6ÆHÊÁÄ36ÒÆHÊ:W021

Ã

̈ÈWÆHÊ

ð

ÆH9

ð.Ã

021*È;ÆHÈHÏJ÷!øÑ4ɶË>36ÆÑ4Ê҉Æ

Î ø914Ê4Å63ˆ0214Æ

þPÆH5aè®ÆHÉ

Ã

ÈWÑ4É

Ãlð 1pø

Ã

Ê4҉36ÒljÆH3YÈ!Ë>ÆJ:xóö3ˆË>ÆHÉ2: È

Ã

ÊË4ÆN:ÁÑ4ÊË

Ã

ÊË>ÆNÉ;ÆNÉ

îxÉcø9‰ìÆHÊÍ

Éð ÆNÉ

Ã

Ñ021òÌWøÑ4ɂË>36ÆaçÑ4è4É

Ã

Å6ÆN3©ÈWÑ4Ê4Ò

ð

ÆN3,È;36ÆiÌKÆNÊëþPÆH5Cé

è®ÆHÉ

Ã

ÈWÑ4ÉWÆHÊ 36: È

Î Ã

14É2:;0214ÆN36Ê4Å636021üË

Ã

:ÀóëÆJ021:;ÆHň: è3YÆNÅá

Î

3ˆ:;021ÆHÊ

Ñ Ã

:;3©ÈWÆH36ň0214ÆHÊÑ4Ê.ËÔÇ9‰Å6Å6ÆHÇ*È;36ñ‰ÆNÊ5

Ã

҉ÊÆiÈ;3ˆ:W0214ÆHÊï÷]Å6Ñ4Ç*È;Ñ

Ã

È;369‰é

ÊÆHÊüñ‰ÆNÉ

Ã

Ê*È

Î

9É ÈWÅY3ˆ021Ïjû!36ÆNÅYƞÄm®ÆNÇ*È;Æ|:;36ÊËüË

Ãlð

ÆH3—Ê49>021üÊ43ˆ021*È

ñÆHÉ2: È

Ã

ÊË4ÆHÊÏ

Ä36Êíç>021

Î

ÆHÉWè4Ñ4Ê4Ç*È(Ë4ÆHÉ÷49‰É2:W021*ÑÊ4Ò

Ã

ÊöÇ9‰ÉWÉ;ÆNÅ63YÆNÉ ÈWÆHÊ âêÆié

È Ã

Å6Å6ÆHÊ :;3YÊ.Ë8: ÆN3YÈ3614É;ÆNÉ ÄÊÈ2Ë>ÆN02ÇÑ4ÊÒ 365 5 Ã

14ÉWÆ ØJåBAÚ#Ë>36Æ

W

9>021ÈWÆH5aè®ÆHÉ

Ã

ÈWÑ4ÉW:;Ñ4è4É

Ã

Å6ÆN3©ÈWÆHÉNÏ

Â

36ÆJ: Æõâ

Ã

ÈWÆHÉW3

Ã

Å636ÆHÊñ‰ÆNÉ;Å636ÆHÉWÆHÊ

3614ÉWÆHÊóö3ˆË>ÆHÉ2: È

Ã

ÊË

ð

ÆH3±ñ36ÆHÅ$1pø914ÆHÉWÆHÊäþPÆH5aè®ÆHÉ

Ã

È;ÑÉ;ÆNÊFKá‰Ï

ÿ Ï

ð

ÆH3®0

Ã

ωåB>U[í36Ê('

ÿÃ

G

à—Ñ

æ

) H Ã

ň:

ð

ÆN3ñ‰9É;1ÆHÉ

ð

ÆHÇ

Ã

Ê4Ê*ÈWÆHʞçÑ>é

èÉ

Ã

ÅYÆN3YÈ;ÆHÉWÊÏç36Æa: 36ÊËõË

Ã

5a3©È¼:;ÆH14É

Î

3ˆ021*È;36Ò|ÌWøÑ4ɂË>36ƞÄÊ*È

Î

3ˆ02Ç*é

Å6Ñ4ÊÒÊ4ÆNÑ4ÆHÉ

Ã

Ñ4ÌCçÑ4èÉ

Ã

ÅYÆN3YÈ;Ñ4Ê4Ò

ðÃ

:;36ÆHÉWÆHÊË>ÆNÉ(þPÆN0214Ê9‰Å69‰Ò3YÆNÊÍ

36Ê:

ð

ÆN:;9‰ÊË>ÆNÉ;ÆÀË

Ã

: 36Ƃ5a3YȼË>ÆH5

ð

36ÅYÅ636҉ÆNÊ|ú,øÑ:;:;36҉ÆNÊòç*È;3ˆ02Ç>: È;9Um

ÒÆHÇpøÑ414ÅYÈ

Î

ÆHÉ2Ë>ÆNÊïÇø9‰Ê4Ê4ÆNÊÏÄ36Ê4ƂÄÉ;ÇÅ&ø

Ã

ÉWÑ4Ê4Òa3614ÉWÆN:: ÆNÅ©È2:

Ã

5aÆHÊ

û,ÆNÉ;1

Ã

ÅYÈ;ÆNÊ:iÍlË

à : Ã

Å6Å6ÆHʾÊ9‰ÉW5

Ã

Å6ÆHÊ Ñ Ã

: 3YÈWÆH36ň0214ÆHÊ45a9>Ë>ÆNÅ6ÅYÆHÊáNÑ

Î

3ˆË>ÆNÉW:;è4ÉWÆN0214ÆNÊ:W0214ÆH36Ê*ÈHÍ,3ˆ: È

ð

3ˆ:;14ÆHÉ-8 ÆJË>9>021 Ê9021 Ê43ˆ021*Èa҉Æié

Å6Ñ4Ê҉ÆHÊÏė:—3ˆ: ȐË>ÑÉW021

Ã

Ñ:—5 9‰Ò‰Å63ˆ021ÍËø

à ì Ã

Ñ021|13YÆNɐË43YÆx÷]ÅYÑÇé

ÈWÑ

Ã

ÈW369‰Ê4ÆNÊÊ

Ã

14ÆÔÆH36Ê4ÆH5 Ñ Ã

ÊÈWÆHÊ4è1

Ã

:;ÆHʶøÑ ð

ÆNÉ;Ò

Ã

Ê4Ò

Î

3ˆ021*È;36Ò

:;36ÊËõ9>Ë>ÆHÉCË

Ã

ìòË>36Æ(ÄÅ6ÆHÇ*È;ÉW9‰Ê4ÆNÊø

Ã

14Ê4Å63ˆ021

Î

36ƞ36ÊýÆH36Ê4ÆNÉ·ÐpÑ>È é

ÈW36Ê4҉ÆNÉ ú,øÑ.:;:;36҉ljÆN3YÈÁ36Êäçè436ÊÑ4Ê.Ë Ð Ã

Ë>Ñ4ÊÒòáNÆHÉ;Ì

Ã

Å6Å6ÆHÊÏ

ð

1436ÆNÉ

ÆN36Ê4ÆÒ

Ã

ÊáêÊ4ÆHÑ4ÆÔç>9‰É;È;Æêñ‰9Ê ÄÅ6ÆH5aÆHÊ*È

Ã

É;È;ÆH36ň0214ÆNÊëÆN36Ê4Æê7$9‰Å6Å6Æ

:;è436ÆHÅYȐ9Ë4ÆHÉ9

ð

Ë>36ÆN:;ÆN:1[Á9‰Ê4áNÆHè>È$Ò

Ã

ɐÊ43ˆ021È

Ã

Ê҉Æ

Î

ÆHÊ.Ë>ÆiÈ

Î

ÆNÉ é

Ë4ÆHÊÇ

Ã

Ê4ÊÍ43ˆ: È

Ã

Å6Å6ÆHÉ2Ë>36Ê4Ò:,Ê9021ñø9‰Å6Å636Ò¼9UmjÆHÊÏ

&Ž®´x¬a­i«&¡‰¦•w¯s]j¬ô u—• J¢&  ¡’J¯»4j°±+*N¦£SŸY­iœ®¯ (;j°±

›

­N£~¥F’W•w¯

´x*¬ô s• ’&qc’J¯°±=tÁ

›  ­N¢&’W£S¤Ÿ~“Á“¼’W•¦*œu u .Hœ¨w­i• Ÿ©  ¡®¯

Ž­i«&¦*• ’-,/.0®¯ 21C‹ o3121E$cš;

"

p]ªp  ¥F’W•&œü¦œ>KtÁ ¹4 x¸N  ¥4¯/ ¡Uq‰¢&ŸS¥ÔŸ~œõ¦*œ*¢&’W• ’W•544’WŸS«76¯/$E

‹ o3121c™Jš;

9‰‘>

¸

N¡œ’&q‰¢&’Wœ.¯ ¡Uq‰¢&ŸS¥J­N£SŸ©¢&  ¡’µ¶£

¸

­H«&« ’W•98;:*¯/1HŒBo¾‹ o3121c™Nš;

<

j

›  n

œ>’;• ¢&Nœ®¯ ¡?q‰¢&ŸS 2¢º®l­"qF¯‰Œc–À‹= W«wNo31>1>?Jš;

@BACADA

n

•&« Ÿ~¥F’2£>¨;¦*•»l¦¿*• ­N£S’2Ÿ~«&¦*œ*§¯B ¡?q‰¢&Ÿ~¥¾ŸSœ‚¦*œ*¢&’W• ’W•94>’2ŸS«

ACACA



ACADA

n

•&« Ÿ~¥F’2£¨W¦“8ŸS’2¢FE2¸­H¡*• ŸS§J’;œêŽH”4’2£S¿• ’2ŸS¢ ¡Uq‰¢&Ÿ~¥¯ ¡Uq¢&Ÿ~¥žŸ~œ

¦*œ*¢&’W• ’W•G4>’2ŸS«

ACACA



D

Abbildung 4.10: Diagrammatische Darstellung einer Spinfluktuation [Rosch, Physik in un- serer Zeit 30 (1999) 118.

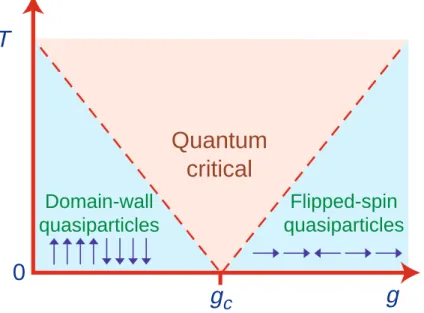
4.1.6 Domain-wall- und Flipped-spin-Quasiteilchen

Die Ising-Kette im transversalen Magnetfeld wird mit dem Hamiltonoperator HI =−JX

j

(g ^↔σ^x_j +^↔σ^z_j^↔σ^z_j+1) (4.25)