1 Abbildung 1: Laplace-Gleichung in zwei Raumdimensionen

−0.2 0 0.2 0.4 0.6 0.8 1 1.2 0

0.2 0.4 0.6 0.8 1 1.2

x

y

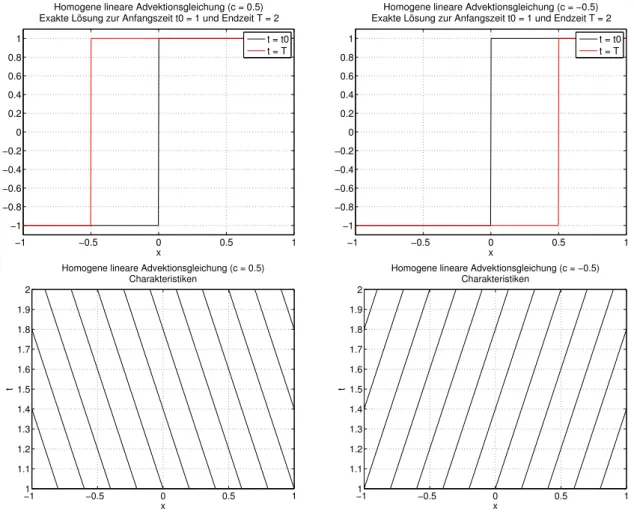
Werte der vorgegebenen Funktion

Wert r(0) = 0 Wert r(x) = x² Wert r(1) = 1

Abbildung 1: Laplace-Gleichung in zwei Raumdimensionen. Vorgegebene Lösungswerte am Rand des Einheitsquadrates.

Abbildung 2: Zweidimensionale Laplace-Gleichung unter inhomogenen Dirichlet- Randbedingungen und entsprechende Poisson-Gleichung unter homogenen Dirichlet- Randbedingungen. Approximationen an Lösungswerte basierend auf Sinus-Reihenansatz.

Abbildung 3: Zweidimensionale Poisson-Gleichung mit normierter rechter Seite unter ho- mogenen Dirichlet-Randbedingungen. Approximationen an Funktionswerte von∆w basie- rend auf Sinus-Reihenansatz für Lösung w; im Inneren des Einheitsquadrates ist Funktion näherunsweise Eins, am Rand gleich Null.

Abbildung 4: Gray–Scott-Gleichungen in zwei Raumdimensionen unter periodischen Rand- bedingungen. Anfangsbedingungen und numerisch berechnete Lösungswerte (t=1000).

Abbildung 5: Gray–Scott-Gleichungen in zwei Raumdimensionen unter periodischen Rand- bedingungen. Numerisch berechnete Lösungswerte (zweite Komponente,t=2000).

0 0.5 1 1.5 0

0.2 0.4 0.6 0.8 1

x

|ψ(x,t)|2

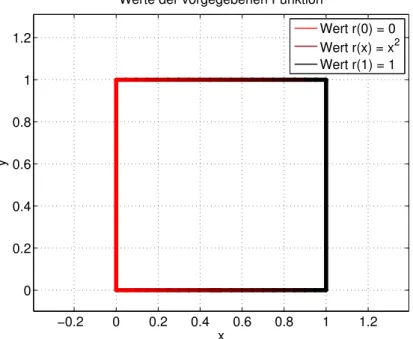
Nonlinear Schrödinger equation (ε = 0.01, ω = 2, θ = 1) Integrator "embedded" (p = 2, Strang / Lie−Trotter) Solution at time t = 3 (Tol = 0.1, N = 1720, FFTs = 3444, M = 8192)

0 0.5 1 1.5

0 0.2 0.4 0.6 0.8 1

x

|ψ(x,t)|2

Nonlinear Schrödinger equation (ε = 0.01, ω = 2, θ = 1) Integrator "embedded" (p = 2, Strang / Lie−Trotter) Solution at time t = 3 (Tol = 0.01, N = 6828, FFTs = 13658, M = 8192)

0 0.5 1 1.5

0 0.2 0.4 0.6 0.8 1

x

|ψ(x,t)|2

Nonlinear Schrödinger equation (ε = 0.01, ω = 2, θ = 1) Integrator "embedded" (p = 2, Strang / Lie−Trotter) Solution at time t = 3 (Tol = 0.001, N = 7566, FFTs = 15134, M = 8192)

0 0.5 1 1.5

0 0.2 0.4 0.6 0.8 1

x

|ψ(x,t)|2

Nonlinear Schrödinger equation (ε = 0.01, ω = 2, θ = 1) Integrator "embedded" (p = 2, Strang / Lie−Trotter) Solution at time t = 3 (Tol = 0.0001, N = 12466, FFTs = 24936, M = 8192)

Abbildung 6: Eindimensionale nichtlinearen Schrödinger-Gleichung im semi-klassischen Re- gime. Mittels lokaler Schrittweitensteuerung numerisch berechnete Lösungswerte; für hinrei- chend kleine Toleranzen beobachtet man ein konsistentes Resultat.

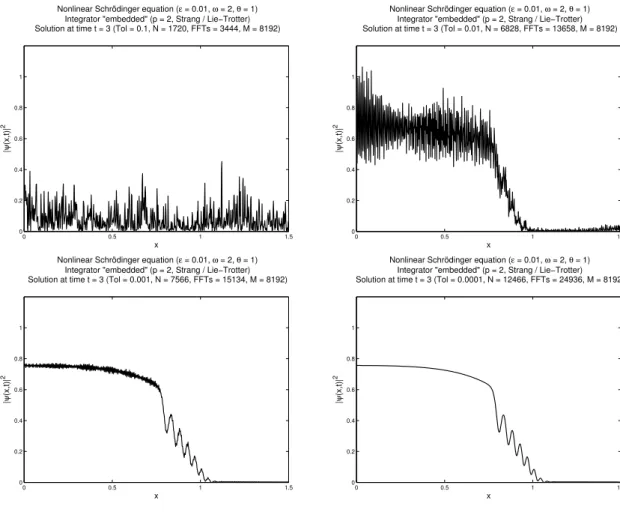
Abbildung 7: Zweidimensionale Gross–Pitaevskii-Gleichung mit zusätzlichem Rotationsterm.

Numerische berechnete Lösungwerte.

−2 −1.5 −1 −0.5 0 0.5 1 1.5 2

−5

−4

−3

−2

−1 0 1 2 3 4 5

x

y

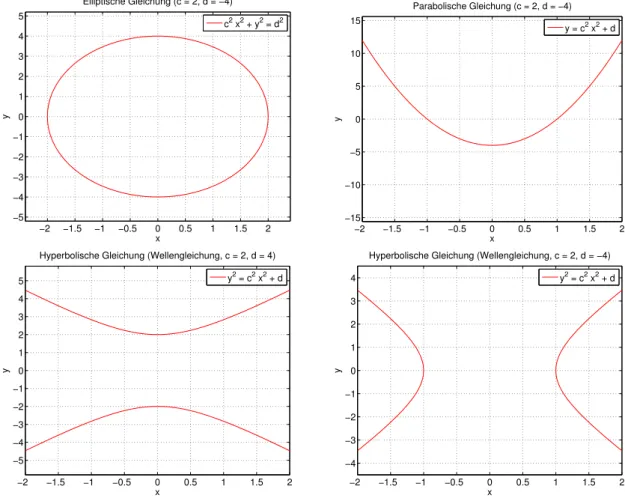
Elliptische Gleichung (c = 2, d = −4)

c² x² + y² = d²

−2 −1.5 −1 −0.5 0 0.5 1 1.5 2

−15

−10

−5 0 5 10 15

x

y

Parabolische Gleichung (c = 2, d = −4) y = c² x² + d

−2 −1.5 −1 −0.5 0 0.5 1 1.5 2

−5

−4

−3

−2

−1 0 1 2 3 4 5

x

y

Hyperbolische Gleichung (Wellengleichung, c = 2, d = 4) y² = c² x² + d

−2 −1.5 −1 −0.5 0 0.5 1 1.5 2

−4

−3

−2

−1 0 1 2 3 4

x

y

Hyperbolische Gleichung (Wellengleichung, c = 2, d = −4) y² = c² x² + d

Abbildung 8: Elementare lineare partielle Differentialgleichungen und zugehörige Gleichun- gen für Polynome in zwei Variablen.

−10 −0.5 0 0.5 1 0.2

0.4 0.6 0.8 1

x

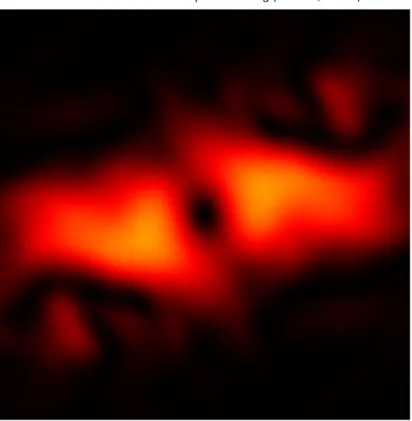
Homogene lineare Advektionsgleichung (c = 0.5) Exakte Lösung zur Anfangszeit t0 = 1 und Endzeit T = 2

t = t0 t = T

−10 −0.5 0 0.5 1

0.2 0.4 0.6 0.8 1

x

Homogene lineare Advektionsgleichung (c = −0.5) Exakte Lösung zur Anfangszeit t0 = 1 und Endzeit T = 2

t = t0 t = T

−11 −0.5 0 0.5 1

1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2

x

t

Homogene lineare Advektionsgleichung (c = 0.5) Charakteristiken

−11 −0.5 0 0.5 1

1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2

x

t

Homogene lineare Advektionsgleichung (c = −0.5) Charakteristiken

Abbildung 9: Klassische Lösungenu∈C¹(R×[t₀,T],R) von eindimensionalen homogenen li- nearen Advektionsgleichungen mit positiven bzw. negativen Ausbreitungsgeschwindigkeiten.

−1 −0.5 0 0.5 1

−1

−0.8

−0.6

−0.4

−0.2 0 0.2 0.4 0.6 0.8 1

x

Homogene lineare Advektionsgleichung (c = 0.5) Exakte Lösung zur Anfangszeit t0 = 1 und Endzeit T = 2

t = t0 t = T

−1 −0.5 0 0.5 1

−1

−0.8

−0.6

−0.4

−0.2 0 0.2 0.4 0.6 0.8 1

x

Homogene lineare Advektionsgleichung (c = −0.5) Exakte Lösung zur Anfangszeit t0 = 1 und Endzeit T = 2

t = t0 t = T

−11 −0.5 0 0.5 1

1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2

x

t

Homogene lineare Advektionsgleichung (c = 0.5) Charakteristiken

−11 −0.5 0 0.5 1

1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2

x

t

Homogene lineare Advektionsgleichung (c = −0.5) Charakteristiken

Abbildung 10: Verallgemeinerte Lösungen von eindimensionalen homogenen linearen Ad- vektionsgleichungen mit positiven bzw. negativen Ausbreitungsgeschwindigkeiten. Zugehö- rige Charakteristiken {(ξ(t),t)∈R×[t₀,T] :u(ξ(t),t)=u(ξ0,t₀)} sind durch Geraden gegeben.

−10 −0.5 0 0.5 1 0.2

0.4 0.6 0.8 1

x

Burgers−Gleichung (f(u) = c u², c = 0.5)

Numerische Lösung zur Anfangszeit t0 = 1 und Endzeit T = 1.18 t = t0 t = T

−10 −0.5 0 0.5 1

0.2 0.4 0.6 0.8 1

x

Advektionsgleichung (f(u) = c u, c = 0.5)

Numerische Lösung zur Anfangszeit t0 = 1 und Endzeit T = 1.18

t = t0 t = T u0(x+c(t−t0))

−11 −0.5 0 0.5 1

1.02 1.04 1.06 1.08 1.1 1.12 1.14 1.16 1.18

x

t

Burgers−Gleichung (f(u) = c u², c = 0.5) Charakteristiken

−11 −0.5 0 0.5 1

1.02 1.04 1.06 1.08 1.1 1.12 1.14 1.16 1.18

x

t

Advektionsgleichung (f(u) = c u, c = 0.5) Charakteristiken

Abbildung 11: Eindimensionale Burgers-Gleichung mit Ausbildung von Stoßwellen und Vergleich mit linearer Advektionsgleichung. Numerische Approximation mittels Upwind-

−10 −0.5 0 0.5 1 0.2

0.4 0.6 0.8 1

x

Burgers−Gleichung (f(u) = c u², c = −0.5) Numerische Lösung zur Anfangszeit t0 = 1 und Endzeit T = 1.18

t = t0 t = T

−10 −0.5 0 0.5 1

0.2 0.4 0.6 0.8 1

x

Advektionsgleichung (f(u) = c u, c = −0.5) Numerische Lösung zur Anfangszeit t0 = 1 und Endzeit T = 1.18

t = t0 t = T u0(x+c(t−t0))

−11 −0.5 0 0.5 1

1.02 1.04 1.06 1.08 1.1 1.12 1.14 1.16 1.18

x

t

Burgers−Gleichung (f(u) = c u², c = −0.5) Charakteristiken

−11 −0.5 0 0.5 1

1.02 1.04 1.06 1.08 1.1 1.12 1.14 1.16 1.18

x

t

Advektionsgleichung (f(u) = c u, c = −0.5) Charakteristiken

Abbildung 12: Eindimensionale Burgers-Gleichung mit Ausbildung von Stoßwellen und Vergleich mit linearer Advektionsgleichung. Numerische Approximation mittels Upwind- Verfahren (dämpfende Eigenschaften).

−10 −0.5 0 0.5 1 0.2

0.4 0.6 0.8 1

x

Viskose Burgers−Gleichung (ε = 0.1, f(u) = c u², c = 0.5) Numerische Lösung zur Anfangszeit t0 = 1 und Endzeit T = 1.18

t = t0 t = T

−10 −0.5 0 0.5 1

0.2 0.4 0.6 0.8 1

x

Viskose Burgers−Gleichung (ε = 0.1, f(u) = c u², c = −0.5) Numerische Lösung zur Anfangszeit t0 = 1 und Endzeit T = 1.18

t = t0 t = T

−10 −0.5 0 0.5 1

0.2 0.4 0.6 0.8 1

x

Viskose Burgers−Gleichung (ε = 0.001, f(u) = c u², c = 0.5) Numerische Lösung zur Anfangszeit t0 = 1 und Endzeit T = 1.18

t = t0 t = T

−10 −0.5 0 0.5 1

0.2 0.4 0.6 0.8 1

x

Viskose Burgers−Gleichung (ε = 0.001, f(u) = c u², c = −0.5) Numerische Lösung zur Anfangszeit t0 = 1 und Endzeit T = 1.18

t = t0 t = T

0.4 0.6 0.8 1

Viskose Burgers−Gleichung (ε = 0.0001, f(u) = c u², c = 0.5) Numerische Lösung zur Anfangszeit t0 = 1 und Endzeit T = 1.18

t = t0 t = T

0.4 0.6 0.8 1

Viskose Burgers−Gleichung (ε = 0.0001, f(u) = c u², c = −0.5) Numerische Lösung zur Anfangszeit t0 = 1 und Endzeit T = 1.18

t = t0 t = T

−10 −0.5 0 0.5 1 0.2

0.4 0.6 0.8 1

x

Diffusions−Advektions−Gleichung (ε = 0.1, f(u) = c u, c = 0.5) Numerische Lösung zur Anfangszeit t0 = 1 und Endzeit T = 1.18

t = t0 t = T u0(x+c(t−t0))

−10 −0.5 0 0.5 1

0.2 0.4 0.6 0.8 1

x

Diffusions−Advektions−Gleichung (ε = 0.1, f(u) = c u, c = −0.5) Numerische Lösung zur Anfangszeit t0 = 1 und Endzeit T = 1.18

t = t0 t = T u0(x+c(t−t0))

−10 −0.5 0 0.5 1

0.2 0.4 0.6 0.8 1

x

Diffusions−Advektions−Gleichung (ε = 0.001, f(u) = c u, c = 0.5) Numerische Lösung zur Anfangszeit t0 = 1 und Endzeit T = 1.18

t = t0 t = T u0(x+c(t−t0))

−10 −0.5 0 0.5 1

0.2 0.4 0.6 0.8 1

x

Diffusions−Advektions−Gleichung (ε = 0.001, f(u) = c u, c = −0.5) Numerische Lösung zur Anfangszeit t0 = 1 und Endzeit T = 1.18

t = t0 t = T u0(x+c(t−t0))

0.2 0.4 0.6 0.8 1

Diffusions−Advektions−Gleichung (ε = 0.0001, f(u) = c u, c = 0.5) Numerische Lösung zur Anfangszeit t0 = 1 und Endzeit T = 1.18

t = t0 t = T u0(x+c(t−t0))

0.2 0.4 0.6 0.8 1

Diffusions−Advektions−Gleichung (ε = 0.0001, f(u) = c u, c = −0.5) Numerische Lösung zur Anfangszeit t0 = 1 und Endzeit T = 1.18

t = t0 t = T u0(x+c(t−t0))

−30 −2 −1 0 1 2 3 0.5

1 1.5 2 2.5 3

x

t

Integrationsbereich (c = 2)

0 0.5 1 1.5 2 2.5 3

−3

−2

−1 0 1 2 3

t

x

Integrationsbereich (c = 2)

−30 −2 −1 0 1 2 3

0.5 1 1.5 2 2.5 3

x

t

Integrationsbereich (c = −2)

0 0.5 1 1.5 2 2.5 3

−3

−2

−1 0 1 2 3

t

x

Integrationsbereich (c = −2)

Abbildung 15: Integrationsbereiche für positive und negative Ausbreitungsgeschwindigkei-