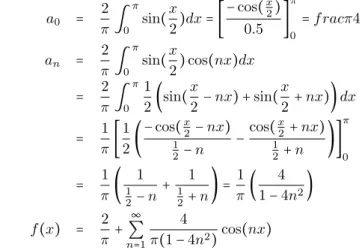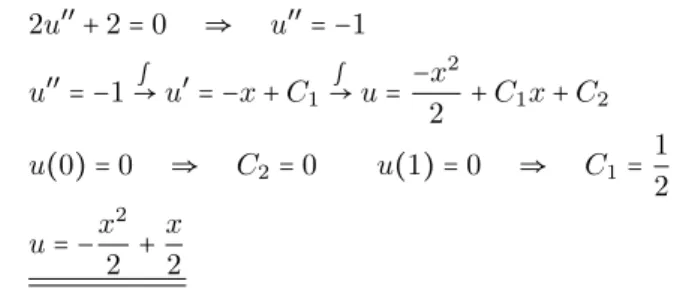1 Laplace - Transformation

Zusammenfassung Analysis 3

Patrik Rohner, rohnerpa@student.ethz.ch 9. Januar 2009

1 Laplace - Transformation

Die Laplace Transformation ist f¨ ur t ≥ 0 folgendermassen de- finiert:

F (s) = L[f (t )] = ∫

∞ 0

f (t) ⋅ e ^{− st} dt

Originalfunktion f (t) Bildfunktion F (s) = L[f (t)]

t ⁿ (n = 0, 1, 2, . . .) _s

^n!

n = 0 → f (t) = 1 ¹ _s n = 1 → f (t) = t _s ¹

e ^at _{s −} ¹ _a

sin (at) _s

₊ ^a _a

cos (at) _s

₊ ^s _a

sinh(at) _s

− ^a a

cosh (at) _s

₋ ^s _a

H(t − a) (a > 0) e ^{− as} /s δ(t − a) (a > 0) e ^{− as}

δ(t) 1

Tabelle 1: Grundlegende Laplace - Transformationen

1.1 Eigenschaften

1.1.1 Linearit¨ at

L[λf + µg] = λL[f ] + µL[g] λ, µ ∈ R 1.1.2 Verschiebungssatz

f (t) = e ^{− at} ⋅ g(t) Ð→ ^L F (s) = G(s + a) 1.1.3 Ableitungsregel

L [ df

dt ] = sF(s) − f (0) L [

d ² f

dt ² ] = s ² F (s) − sf (0) − f ˙ (0) L [

d ³ f

dt ³ ] = s ³ F (s) − s ² f (0) − s f ˙ (0) − f ¨ (0) L [

d ⁿ f

dt ⁿ ] = s ⁿ F(s) −

n − 1

∑

j = 0

s ^{n − 1 − j} d ^j F (0) dt ^j

1.1.4 Faltungssatz

(f ∗ g)(t ) = ∫

t 0

(t − t ^′ )g(t ^′ )dt ^′ = L ^{− 1} [G(s) ⋅ F (s)] t > 0 Die Faltung von f (t) und g(t) erf¨ ullt folgende Eigenschaften:

f ∗ g = g ∗ f , L[f ∗ g] = L[f ] ∗ L[g]

1.1.5 Zweite Ableitungsregel

L[t ⁿ f ](s) = (−1) ⁿ d ⁿ

ds ⁿ (F (s)) 1.1.6 Integrationssatz

L [∫

t 0

f (τ )dτ ] (s) = 1 s (F(s)) 1.1.7 Zweiter Verschiebungssatz

L ^{− 1} [e ^{− as} F(s)] = H (t − a)f (t − a) 1.1.8 Ahnlichkeitssatz ¨

L[f (t)] = F(s) Ô⇒ L[f(at)] = 1 a ⋅ F (

s a )

▸ Streckung (a < 1)

▸ Stauchung (a > 1)

▸ Vorgehen s in F (s) durch s/a ersetzen und mit 1/a multiplizieren.

1.1.9 Wurzelsatz

L ^{− 1} [F( √

s)] = 1

√ 4πt ³ ∫

∞ 0

ξe ⁻

2 4t

f (ξ)dξ

▸ L ^{− 1} [e ^{− a √ s} ] = a

√

4πt ³ e ⁻

2 4t

▸ L ^{− 1} [ 1

√ s e ^{− a √ s} ] = 1

√ πt e ⁻

2 4t

Originalfunktion f (t) Bildfunktion F (s) = L[f (t)]

e

− 1 a

1 s ( s − a )

t ⋅ e ^at _{( s −} ¹ _{a )}

e

− e

a − b

1 ( s − a )( s − b )

(1 + at) ⋅ e ^at _{( s −} ^s _{a )}

a ⋅ e

− b ⋅ e

a − b

( s − a )( s s − b ) t

⋅ e

( n − 1 ) !

( s − 1 a )

(n = 1, 2, 3, . . .) sin (at + b) ^{sin ( b )⋅} _s ^s

⁺ ₊ ^a _a ^⋅

^{cos ( b )}

cos (at + b) ^{cos ( b )⋅} _s ^s

+ ⁻ a ^{a ⋅}

^{sin ( b )} sin ( at )

t arctan( ^a _s )

√ 1 π ⋅ t

√ 1 s

2 ⋅ √ ¹ π

1 s √ s

Tabelle 2: Weitere Laplace - Transformationen

1.2 Differenzialgleichungen

(i) Laplacetransformierte der einzelnen Summenden bilden.

(Ableitungsregel verwenden)

(ii) Anfangsbedingungen einsetzen, nach F(s) aufl¨ osen.

(iii) R¨ ucktransformieren. (PBZ / Faltungssatz verwenden) 1.2.1 Das L¨ osen einer ODE mittels Laplace - Transfor-

mation

/ L¨ osen Sie die folgende ODE mittels Laplace - Transfor- mation:

dx(t)

dt + 2x(t) = t , x(0) = a

dx(t)

dt + 2x(t) = t Ð→ ^L sX(s) − X (0)

² = a

+2X (s) = 1 s ² X (s) = 1

s ² (2 + s) + a 2 + s

L

Ð→ x(t) = t ∗ e ^{− 2t} + a ⋅ e ^{− 2t}

Der Faltung ergibt

t ∗ e ^{− 2t} = ∫

t 0

(t − t ^′ )e ^{− 2t} dt ^′ = [ te ^{− 2t}

−2 ]

t

0

− ∫

t 0

t ^′

® ↓

e ^{− 2t}

± ↑

dt ^′

= [ te ^{− 2t}

−2 ]

t

0

− [ t ^′ e ^{− 2t}

−2 ]

t

0

+ ∫

t 0

e ^{− 2t}

−2 dt ^′

= t 2 + [

e ^{− 2t}

4 ]

t

0

= t 2 −

1 4 +

e ^{− 2t} 4 Somit ist die gesuchte Funktion

x(t) = (a + 1 4 )e ^{− 2t} +

t 2 −

1 4

/ L¨ osen Sie die folgende ODE mittels Laplace - Transfor- mation:

˙

y + y = cos(t) , y(0) = 1

˙

y + y = cos(t) Ð→ ^L sY (s) − y(0) + Y (s) = s s ² + 1

Y (s) = s

(s ² + 1)(s + 1) − 1 s + 1

Die Partialbruchzerlegung des Bruches erfolgt mit dem Ansatz f¨ ur komplex konjugierte Nullstellen, also _{( s}

+ 1 ^s )( s + 1 ) = ^As _s

⁺ + ^B 1 +

C

s + 1 und liefert s = (As + B )(s + 1) + (s ² + 1)(C). Der Koeffi- zientenvergleich f¨ uhrt auf _{( s}

_{+ 1} ^s _{)( s + 1 )} = ¹ _{2 s}

^s _{+ 1} + ¹ _{2 s}

¹ _{+ 1} − ¹ _{2 s +} ¹ ₁ und somit gilt

Y (s) = 1 2

s s ² + 1 +

1 2

1 s ² + 1 −

3 2

1 s + 1

Die Laplace - R¨ ucktransformation liefert das gesuchte Resultat y(s) = 1

2 cos(t) + 1

2 sin(t) − 3 2 e ^{− t}

1.2.2 Das L¨ osen einer PDE mittels Laplace - Transfor- mation

/ L¨ osen Sie f¨ ur 0 ≤ x < 1 mittels Laplacetransformation in der Variablen t das folgende Anfangsrandwertproblem:

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

u tt − c ² u xx = 0 f¨ ur x > 0, t > 0 u x (0, t) = f (t) f¨ ur t > 0 lim _{x →∞} u(x, t) = 0 f¨ ur t > 0 u(x, 0) = u t (x, 0) = 0 f¨ ur x > 0 , wobei f eine vorgegebene Funktion ist.

Laplacetransformation mit Ableitungregel ergibt L[u _tt ] = s ² U (x, s) − sU (x,0)

´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶

= 0

− U _t (x, 0)

´¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¶

= 0

= s ² U (x, s)

Somit folgt die ODE

U xx (x, s) − s ²

c ² U (x, s) = 0 Diese hat die L¨ osung

U (x, s) = A ₁ e

^x + A ₂ e ⁻

^x

Mit lim x →∞ u(x, t) = 0 ⇒ lim x →∞ U(x, s) = 0 muss A 1 = 0 sein. Aus u x (0, t) = f (t) ⇒ U x (0, s) = F (s) folgt A 2 =

− _s ^c F (s) und somit

U (x, s) = − c

s F (s)e ⁻

^x

Nun wenden wir die Regel L [∫ 0 ^t f (τ)dτ ] (s) = ¹ _s (F(s)) an, in diesem Fall gilt L ^{− 1} [− ^c _s F (s)] = −c ∫

t

0 f(τ)dτ .

Aus dem 2. Verschiebungssatz L ^{− 1} [e ^{− as} F (s)] = H (t − a)f (t − a) ergibt die R¨ ucktransformation von e ⁻

^x eine Ver- schiebung im Argument. Die L¨ osung lautet sodann

u(x, t) = H (t − x

c ) ⋅ (−c ∫

t −

0

f (τ )dτ )

2 Fourier - Reihen

2.1 Multiple Choice Fragen # 1

2.1.1 Periodizit¨ at

ˆ Die Funktionen sin (cx) , cos (cx) , tan (cx) , cos (πx) , e ^{√ 2ix} , e ^{( ix )} , sin (x)cos (x) , _sin ¹ _{( x )} sind periodisch.

ˆ Die Funktionen sin (x ² ) , arcsin (x) , arctan(cx) , cosh (x) , arcsin (πx) , e ^{i √ x} sind nicht periodisch.

ˆ Die Funktionen tan(x) , cos ² (x) , sin(2x) sind π- periodisch.

ˆ Die Funktion sin(mx) ist ^2π _m -periodisch.

ˆ Sind f, g π-periodisch, dann auch f + g.

ˆ Ist f (x) π-periodisch, so ist sin(f(x)) ebenfalls π- periodisch.

ˆ Ist f (x) a-periodisch und g(x) b-periodisch, so ist f (g(x)) b-periodisch, g(f (x)) aber a-periodisch

.

ˆ Ist f (x) n-periodisch und g(x) k-periodisch, n > k, so ist f(x)g(x) mindestens (kgV (n, k))-periodisch.

ˆ Ist f(x) u-periodisch und g(x) v-periodisch,, so ist f (x) + g(x) (kgV (u, v))-periodisch.

2.1.2 gerade oder ungerade?

ˆ Die Funktionen cos(ax) , cosh(ax) , sin(x ² ) , sin(x) tan(x) , Re(e ^{i sin ( x )} )

sind gerade.

ˆ Die Funktionen sin(ax) , tan(ax) , sinh(ax) , tanh(ax) , sin(x)cos(x) , sinh(sin(x)) sind ungerade.

ˆ Das Produkt von 2 geraden Funktionen ist auch eine gerade Funktion.

ˆ Das Produkt von 2 ungeraden Funktionen ist eine gerade Funktion.

ˆ Das Produkt einer geraden und einer ungeraden Funkti- on ist eine gerade Funktion.

ˆ Ist f gerade, dann ist f ^′ ungerade und f ^′′ wieder gerade.

ˆ sin(sin(x)) → ungerade und 2π-periodisch.

ˆ sin(cos(x)) → gerade und 2π-periodisch.

ˆ cos(cos(x)) → gerade und π-periodisch.

ˆ cos(sin(x)) → gerade und π-periodisch.

ˆ tan(sin(x)) = ^sin _cos ⁽ ₍ ^sin _sin ⁽ ₍ ^x _x ⁾⁾ ₎₎ → ungerade , p = 2π.

ˆ tan(cos(x)) = _cos ^{sin (} ₍ ^cos _cos ⁽ ₍ ^x _x ⁾⁾ ₎₎ → ungerade , p = 2π.

2.2 Reelle Darstellung

2.2.1 Periodenl¨ ange p = 2π

Anstelle vom Interval -π bis π k¨ onnte man auch 0 bis 2π w¨ ahlen.

f (x) = a 0

2 +

∞

∑

n = 1

(a _n cos(nx) + b _n sin(nx)) a ₀ =

1 π ∫

π

− π

f (x)dx a n =

1 π ∫

π

− π f (x) cos(nx)dx, (n ≥ 0) b n =

1 π ∫

π

− π

f (x) sin(nx)dx, (n ≥ 1)

▸ ungerade Funktion, a _n = 0:

f (x) =

∞

∑

n = 1

b _n sin(nx)

b n = 2 π

π

∫

0

f (x) sin(nx)dx (n ≥ 1)

▸ gerade Funktion, b n = 0:

f (x) = a 0

2 +

∞

∑

n = 1

a n cos(nx)

a _n = 2 π

π

∫

0

f (x) cos(nx)dx (n ≥ 0)

2.2.2 Periodenl¨ ange p = L

f (x) = a ₀

2 +

∞

∑

n = 1

(a _n cos( 2πn

L x) + b _n sin 2πn L x) a 0 =

2 L ∫

L 2

−

f (x)dx a _n =

2 L ∫

L 2

−

f (x) cos( 2πn

L x)dx, (n ≥ 0) b n =

2 L ∫

L 2

−

f (x) sin( 2πn

L x)dx, (n ≥ 1)

▸ ungerade Funktion, a n = 0:

f (x) =

∞

∑

n = 1

b n sin( 2πn L x) b n =

4 L

L / 2

∫

0

f (x) sin( 2πnx

L )dx (n ≥ 1)

▸ gerade Funktion, b n = 0:

f (x) = a ₀

2 +

∞

∑

n = 1

a _n cos( 2πn L x) a _n =

4 L

L / 2

∫

0

f (x) cos( 2πn

L x)dx (n ≥ 0)

2.3 Komplexe Darstellung

2.3.1 Periodenl¨ ange p = 2π f (x) =

∞

∑

n =−∞

c n e ^inx c n = 1 2π ∫

2π 0

e ^{− inx} f (x)dx

2.3.2 Periodenl¨ ange p = L f (x) =

∞

∑

n =−∞ c n e

^x c n = 1 L ∫

L

0 e ⁻

^x f (x)dx

1

nur wenn a ≠ b; cos(cos(x)) ist π-periodisch

2

i sin(x) =

(e

− e

) ist gerade, so auch Re(e

)

2.4 Umrechnung zwischen den Darstellungen

▸ a 0 = 2c 0 ▸ a n = c n + c ₋ n ▸ b n = i(c n − c ₋ n )

▸ c _n =

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

a

− ib

2 n > 0

a

2 n = 0

a

+ ib

2 n < 0

Hierbei wird oft die Vorzeichenfunktion sgn() verwendet:

sgn(x) =

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

1 n > 0 0 n = 0

−1 n < 0

/ Beispiel: c k = ∫

1

0 e ^x ⋅ e ^{− 2πikx} dx Ô⇒ a k , b k

c k = ∫

1 0

e ^x ⋅ e ^{− 2πikx} dx =

e − 1

1 + 4π ² k ² (1 + 2πik) f(x) = (e − 1)

∞

∑

k =−∞

1 + 2πik

1 + 4π ² k ² ⋅ e ^2πikx

= (e − 1)

∞

∑

k =−∞

1 + 2πik

1 + 4π ² k ² ⋅ (cos(2πkx) − i sin(2πkx))

= (e − 1)[ 1

®

k = 0

+2

∞

∑

k = 1

1 ⋅ cos(2πkx) 1 + 4π ² k ²

´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶

R

( 1 + 2πik )⋅ 2

( 1 + 2πik )= 0

−

2πk ⋅ sin(2πkx) 1 + 4π ² k ²

´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶

R

( 1 + 2πik )= 0

( 1 + 2πik )⋅ 2

]

2.5 Orthgonalit¨ atsrelationen

e ^{± πin} =

⎧ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎩

1 n gerade

−1 n ungerade

∫

π

− π

e ^inx ⋅ e ^{− ikx} =

⎧ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎩

0 n ≠ k 2π n = k

= δ _n,k ⋅ 2π

δ n,k =

⎧ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎩

0 n ≠ k 1 n = k / Beispiel: 1

2π ∫

π

− π

(e ^iax + 4e ^3ix ) ⋅ e ^{− inx} = δ _a,n + 4δ _3,n

F¨ ur n, k ∈ N 0 gilt:

(i) ∫

π

− π cos(kx) ⋅ cos(nx)dx =

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

2π n = k = 0 π n = k ≠ 0 0 n ≠ k

(ii) ∫

π

− π

sin(kx) ⋅ sin(nx)dx =

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

0 n = k = 0 π n = k ≠ 0 0 n ≠ k (iii) ∫

π

− π sin(kx) ⋅ cos(nx)dx = 0

2.6 Multiple Choice Fragen # 2

Abbildung 1: Die Funktionen f 1 (links) und f 2 (rechts) / Funktion 1: Sei f 1(x) = ∑ ^∞ _{n = 1} a n sin(πnx) die Fourier- reihe zu f 1. f 1 ist ungerade und hat Periodenl¨ ange 2 (an der allg. Formel f¨ ur die Fourierreihen ersichtlich) Somit gilt:

a n = 4 L ⋅ ∫

L / 2 0

f 1(x) sin( 2πnx

L )dx = 2 ⋅ ∫

1 0

1 sin(πnx)dx a 1 = 2 ⋅ ∫

1

0 1 sin(πx)dx ≠ 0

Definiert man die Fourierreihe von 0 bis ∞, so gilt

f 1(x) = ∑ ^∞

n = 1

a _n sin(πnx) = ∑ ^∞

n = 0

a _{2n + 1} sin((2n + 1)πx)

, da im Integral sich ∫ sin(πnx) sich alternierend aufl¨ ost.

/ Funktion 2: Sei f 2(x) = ^a ₂

+ ∑ ^∞ _{n = 1} a n cos(πnx) die Fou- rierreihe zu f 2. f 2 ist gerade und hat widerum Periodenl¨ ange 2

a ₀ = 2 L ∫

L / 2

− L / 2

f (x)dx = ∫

1

− 1

f (x)dx

= ∫

0

− 1 (x + 1)dx + ∫

1

0 (x − 1)dx = [ x ²

2 + x]

0

− 1

+ [x − x ²

2 ]

1

0

= 1

/ Funktion 3: Sei f 3(x) = ∑ ^∞ _{n = 1} b n sin(πnx) die Fourierrei- he zur Funktion f 3(x ) = ∫ 0 ^x g(x)dx − x. Weder lim _{n →∞} n ² a _n noch lim _{n →∞} n ² b _n werden 0.

/ Funktion 4: Sei f 4(x) = ∑ ^∞ _{n = 1} a _n cos(2πnx) die Fourier- reihe zur Funktion f 4 und sei g4(x) = ^df4 _dx die Ableitung eben dieser Funktion f 4.

Frage: Verschwindet der nullte Koeffizient von g4 ? Antwort: Ja, da f 4 eine gerade Funktion ist, wird g4 zur ungeraden Funktion und somit gilt a ₀ ⊂ a _n = 0.

/ Funktion 5: Sei f 5(x) = ^a ₂

+ ∑ ^∞ _{k = 1} a _k cos(kπx) + b k sin(kπx) die Fourierreihe zur Funktion f 4. Man sieht, dass wenn man die Funktion fortsetzt, sie ungerade ist. Also gilt a k = 0∀ k ∈ N 0 .

Abbildung 2: Die Funktion f 5

F¨ ur b k folgt b k = 2 ∫

L / 2 0

f (x) sin(πnx)dx = 2 ∫

1 0

f (x) sin(πnx)dx

= 2 ∫

0.5 0

1 ⋅ sin(πnx)dx = −2 ⋅ [

cos(πnx) πn ]

0.5

0

= 2

πn (1 − cos( πn 2 )) =

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

2

πn n ungerade

4

πn n = 2, 6, 10 . . . 0 n = 0, 4, 8 . . .

2.7 Konvergenzsatz

Eine 2π-periodische Funktion kann durch eine Fourier-Reihe dargestellt werden, wenn diese st¨ uckweise glatt ist, d.h. wenn sie ¨ uberall stetig diffenenzierbar ist, bis auf einzelne Sprung- punkte ξ _i .

Abbildung 3: Der Graph einer st¨ uckweise glatten Funktion Der Konvergenzsatz besagt nun:

Die Fourier-Reihe einer periodischen, st¨ uckweise glatten Funktion f konvergiert in jedem Punkt und es gilt

a ₀ 2 +

∞

∑

K = 1

[a k cos(kx) + b k sin(kx)] =

=

⎧ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎩

f (x) x Stetigkeitsstelle

1

2 lim _{x → ξ}

(f (x)) + ¹ ₂ lim _{x → ξ}

(f (x)) x Sprungstelle ξ

2.8 Allgemeine Umformungen

In den Formeln f¨ ur die Fourier - Koeffizienten k¨ onnen und sol- len jeweils die folgenden Umformungen vollzogen werden:

∞

∑

n = 1

cos(nπ) =

∞

∑

n = 1

(−1) ⁿ n ∈ Z

∞

∑

n = 1

sin( ^nπ ₂ )

n =

∞

∑

n = 0

(−1) ⁿ 1

2n + 1 n ∈ Z

2.9 L¨ osen einer PDE durch Fourieransatz

y(x) = A 0

2 +

∞

∑

n = 1

A n ⋅ cos(nx) + B n ⋅ sin(nx) y(x) ^′ =

∞

∑

n = 1

−A n ⋅ n ⋅ sin(nx) + B n ⋅ n ⋅ cos(nx) y(x) ^′′ =

∞

∑

n = 1

−A _n ⋅ n ² ⋅ cos(nx) − B _n ⋅ n ² ⋅ sin(nx)

2.9.1 Vorgehen

1. Einsetzen des Fourieransatzes in die homogene PDE 2. Berechnen der Koeffizienten a ₀ , a _n und b _n durch 2π-

periodische Fortsezung der rechten Seite

3. Einsetzen der Koeffizienten in die Gleichung f¨ ur die Fou- rierreihe f(x) = ^a ₂

+ ∑ ^∞ _{n = 1} a n ⋅ cos(nx) + b n ⋅ sin(nx) 4. Koeffizientenvergleich ⇒ A 0 , A n und B n

5. Koeffizienten in den Ansatz einsetzen

/ Beispiel: Bestimmen sie durch Fourieransatz die 2π- periodischen L¨ osungen von

y ^′′ − y = ∣sin( x 2 )∣

Der Fourieransatz in die homogene PDE eingesetzt ergibt

− A 0

2 +

∞

∑

n = 1

−A _n (n ² + 1) ⋅ cos(nx) − B _n (n ² + 1) ⋅ sin(nx)

Die rechte Seite ist eine gerade Funktion, womit b n = 0 ist.

a 0 = 2 π ∫

π 0 sin( x

2 )dx = [

− cos( ^x ₂ ) 0.5 ]

π

0

= f racπ4 a n =

2 π ∫

π 0

sin( x

2 ) cos(nx)dx

= 2 π ∫

π 0

1 2 (sin( x

2 − nx) + sin( x

2 + nx)) dx

= 1 π [

1 2 (

− cos( ^x ₂ − nx)

1

2 − n −

cos( ^x ₂ + nx)

1

2 + n )]

π

0

= 1 π (

1

1 2 − n +

1

1 2 + n ) =

1 π (

4 1 − 4n ² ) f (x) =

2 π +

∞

∑

n = 1

4 π(1 − 4n ² )

cos(nx)

Nun gilt es, bei den unterstrichenen Termen einen Koeffi- zientenvergleich durchzuf¨ uhren

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

A 0 = − _π ⁴

A _n = − _{π ( 1 − 4n}

⁴ _{)( n}

_{+ 1 )} B n = 0

Damit lautet die ursr¨ unglich gesuchte Funktion y(x) = − 2

π +

∞

∑

n = 1

−

4

π(1 − 4n ² )(n ² + 1) cos(nx)

2.10 Fourier - Transformation

f ˆ (k) = ∫

R

f (x)e ^{− ikx} dx f (x) =

1 2π ∫

R

f ˆ (k)e ^ikx dk

N¨ utzliche Rechnungen

ˆ ∫

R

e ^{− ax}

e ^{− ikx} dx = e ⁻

2 4a

√ _π

a

ˆ ∫

R

e ^{−( ak}

^{+ bk + c )} dk =

√ _π

a e

2 4a

− c

ˆ ∫

R

e ^{−∣ x}

^∣ dx =

√ π

ˆ ∫

R

1

1 + k

dk = π

/ Beispiel zum L¨ osen von PDE’s:

u t = u xx + 2u x + 3u transformiert ergibt:

ˆ

u t = (ik) ² u ˆ + 2ik u ˆ + 3ˆ u

2.10.1 L¨ osen von Integralen mit Fouriertrafo Zu berechnen:

∫

∞

−∞

(t cos(t) − sin(t)) sin( ^t ₂ )

t ² dt

Aus einer vorigen Fouriertrafo ist bekannt:

Ô⇒ f (x) = 1 2π ∫

∞

−∞ 2i k cos(k) − sin(k) k ² e ^ikx dk Die letzte Gleichung wird nun umgeformt:

f (x) = 1 2π ∫

∞

−∞ 2i k cos(k) − sin(k) k ² e ^ikx dk

= i 1 π ∫

∞

−∞

k cos(k) − sin(k)

k ² cos(kx) dk

´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶

=

( x )= 0

f ( x )

− 1 π ∫

∞

−∞

k cos(k) − sin(k)

k ² sin(kx) dk

= − 1 π ∫

∞

−∞

k cos(k) − sin(k)

k ² sin(kx) dk Es gilt also f (x) = − ¹ _π ∫ _−∞ ^∞

k cos ( k )− sin ( k )

k

sin(kx) dk . In dieser Gleichung setzen wir x = ¹ ₂ und formen sie anschliessend um:

f (1/2)

´¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¶

=

= − 1 π ∫

∞

−∞

k cos(k) − sin(k)

k ² sin(k/2) dk

Ô⇒ ∫

∞

−∞

k cos(k) − sin(k)

k ² sin(k/2) dk = −

π

2

3 PDE :: Einleitung

3.1 ODE :: R¨ uckblick

Das L¨ osen der homogenen Diffenentialgleichung erfolgt mit dem Ansatz u = c 1 e ^λt . Dies sei f¨ ur folgende 2 F¨ alle gezeigt:

u tt − ω ² u = 0 ⇒ u(t) = c 1 e ^ωt + c 2 e ^{− ωt} = 0 u _tt + ω ² u = 0 ⇒ u(t) = c ₁ e ^iωt + c ₂ e ^{− iωt} = 0

u(t) = d 1 cos(ωt) + d 2 sin(ωt) = 0

3.2 Klassifizierung der PDE

ˆ Ordnung = h¨ ochste Ableitung der unbekannten Funk- tion

ˆ Linearit¨ at

– linear Die Koeffizienten vor den Ableitungen sind nicht von der gesuchten Funktion abh¨ angig.

Beispiel: u _t = b oder auch u _tt − c ² u _xx

– quasilinear Wenn die Ableitungen h¨ ochster Ord- nung linear sind und die Koeffizientenfunktionen vor der h¨ ochsten Ableitung von niedrigeren Ablei- tungen und der unbekannten Funktion abh¨ angen Beispiel: u _t + uu _x = 0 (reibungsfreie Burgersglei- chung)

– nichtlinear Eine nichtlineare PDE enth¨ alt Pro- dukte der abh¨ angigen Variablen und/oder ihrer Ab- leitungen.

Beispiel: u t + uu x = µu xx

3.3 Klassifikation von linearen PDE’s 2.Ord- nung

au _xx + bu _xy + cu _yy = f

⎡ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎣

dx dy 0

0 dx dy

a b c

⎤ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎦

´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶

A

⎡ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎣ u xx

u xy

u _yy

⎤ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎦

=

⎡ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎣ d(u x ) d(u y ) f

⎤ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎦

Ist A regul¨ ar, so hat man eine eindeutige L¨ osung; ist det(A) = 0, so gibt es ∞-viele L¨ osungen.

Wann ist det(A) = 0 ?

det(A) = c(dx) ² + a(dy) ² − bdxdy = 0 0 = a( dy

dx ) ² − b( dy dx ) + c

Die Diskriminatnte D = b ² − 4ac bestimmt nun die Anzahl der L¨ osungen und den Typ der PDE.

3.3.1 Der Typ der PDE Die Diskriminante lautet

D = b ² − 4ac Sie kennzeichnet den Typ der PDE.

ˆ Elliptisch D < 0 keine reelle L¨ osung

z.B. ∆u = 0 (Laplace-Gleichung), ∆u − f = 0 (Poisson- Gleichung)

ˆ Parabolisch D = 0 1 reelle L¨ osung z.B. u x − u yy = 0 (W¨ armeleitungsgleichung)

ˆ Hyperbolisch D > 0 2 reelle L¨ osungen z.B. u _xx − c ² u _yy = 0 (Wellengleichung)

3.4 Variabelntransformation

Allgemeiner Ansatz

⎛

⎜

⎝ ξ η

⎞

⎟

⎠

=

⎡ ⎢

⎢ ⎢

⎢ ⎢

⎣ a b c d

⎤ ⎥

⎥ ⎥

⎥ ⎥

⎦

⎛

⎜

⎝ x t

⎞

⎟

⎠

wobei det(A) ≠ 0 sein muss, wegen R¨ ucktransformation Beispiel

u tt + 2u xt − 2u xx = 0

1. Aus dem allgemeinen Ansatz ergibt sich, dass:

u x = au ξ + cu η

u t = bu ξ + du η

und

u xx = a ² u ξξ + 2acu ξη + c ² u ηη

u xt = abu ξξ + (ad + bc)u ξη + cdu ηη

u tt = b ² u ξξ + 2bdu ξη + d ² u ηη

2. Einsetzen in die PDG und a,b,c,d so w¨ ahlen, dass u ξη = 0 herauskommt.

3. Es folgt:

b = (−1 ±

√ 2)a d = (−1 ±

√ 2)c Man w¨ ahle a=1, b =

√ 2 − 1, c=1 und d = −

√ 2 − 1.

Man sieht, dass die Determinante so nicht verschwindet.

Die L¨ osung der Gleichung lautet nun:

u(ξ, η) = F (ξ) + G(η) Nach der R¨ ucksubstitution folgt:

4. u(x, t) = F(x + (

√

2 − 1)t) + G(x + (−

√ 2 − 1)t) Satz

Sei Au xx + Bu xy + Cu yy = 0, dann gibt es eine Koordinaten- transformation

⎧ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎩

x ^′ = ax + by a, b, c, d ∈ R y ^′ = cx + dy

so dass sich die PDG auf die Form:

A ^′ u x

x

+ B ^′ u x

y

+ Cu y

y

= 0

bringen l¨ asst, dann und nur dann wenn (B ² − 4AC) und (B ^{′ 2} − 4A ^′ C ^′ ) das gleiche Vorzeichen haben.

B ² − 4AC < 0 elliptisch B ² − 4AC = 0 parabolisch B ² − 4AC > 0 hyperbolisch

Die Variabeltransformation ¨ andert den Typ nicht.

3.5 Typ eines Systems zweier quasilinearer PDE’s

Das folgende System zweier quasilinearer PDE’s

⎧ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎩

f 1 = a1u x + b1u y + c1v x + d1v y

f 2 = a2u x + b2u y + c2v x + d2v y

mit den Unbekannten u(x, y) und v(x, y) hat die Diskrimi- nante

D =(a1d2 − a2d1 + b1c2 − b2c1) ²

− 4(a1c2 − a2c1)(b1d2 − b2d1)

3.6 Die Bestimmung des anzuwendenden Schemas

1. Anfangs- und Randbedingungen:

PDE mit partiellen Ableitungen ersten und zweiten Gra- des nach den beiden Variablen.

AB: u(x, 0) = f (x) RB:

ˆ Dirichlet RB: (Werte auf dem Rand) RB muss nicht homogen sein:

u(0, t) = 0 u(L, t) = 0 Ô⇒ Separation der Variablen

ˆ Neumann RB: (Normalenableitungen) RB muss nicht homogen sein:

u _x (0, t) = 0 u _x (L, t) = 0 Ô⇒ Separation der Variablen

ˆ Periodische RB:

u(x, t) = u(x + L, t) Ô⇒ Fourier-Reihen Ansatz

2. Anfangswertprobleme in R oder R ⁿ (ohne RB)

PDE mit partiellen Ableitungen beliebigen Grades nach beiden Variablen.

Homogene PDE Bsp.: u t − ∆u = 0 AB: u(x, 0) = f (x)

Ô⇒ Fourier-Transformation in x

3. Anfangs- und Randbedingungen:

PDE mit partiellen Ableitungen beliebigen Grades nach beiden Variablen.

Homogene PDE Bsp.: u tt − u xx = 0 AB: u(x, 0) = u t (x, 0) = 0

RB: Sind von folgender Form (von t abh¨ angig):

u(0, t) = f (t) lim x →∞ u(x, t) = 0 Ô⇒ Laplace-Transformation in t

4. Lineare und quasilinieare partielle Differenzialgleichun- gen erster Ordnung.

Ô⇒ Methode der Charakteristiken

3.7 Die Methode der Charakteristiken

3.7.1 Algorithmus

⎧ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎩

u _t + c(x, t, u)u _x = d(x, t, u) , t ≥ 0, u(x, 0) = f (x)

1. F¨ ur jedes x ₀ l¨ ose man das System:

˙

x(t) = c(x(t), t, z(t)), (1)

˙

z(t) = d(x(t), t, z(t)), (2)

mit Anfangsbedingungen x(0) = x 0 , z(0) = z 0 = f (x 0 ) 2. Die L¨ osung ist implizit durch die Gleichung

u(x(t), t) = z(t) gegeben

3. Um u(x, t) zu bestimmen, finde man x 0 , so dass f¨ ur die L¨ osung von (1), (2) mit dieser Anfangsbedingung x(t) = x.

Jede durch t parametriesierte Kurve t → (t, x(t), z(t)), die das System (1), (2) erf¨ ullt, heisst Charakteristik 3.7.2 Beispiel

⎧ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎩

u _t − uu _x = 0 , t ≥ 0, u(x, 0) = f (x)

In diesem Fall ist: c(x, t, z) = z und d = 0

Gleichungen der Charakteristiken: x(t) = −z(t) ˙ und z(t) = ˙ 0 L¨ osungen mit folgenden AB: x(0) = x 0 , z(0) = f (x 0 ) x(t) = x 0 − f (x 0 )t, und z(t) = f (x 0 )

L¨ osung des Anfangswertproblems ist implizit:

u(x, t) = f (x 0 ), und x = x 0 − f (x 0 )t

3.8 Inhomogene PDE’s

3.8.1 Beispiel

⎧ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎩

u t − αu xx = sin(x) t > 0, x ∈ R u(x, 0) = 0 x ∈ R 3.8.2 Vorgehen

1. L¨ osung des inhomogenen Problems schreiben als u(x, t) = u(x, t) + ˜ U (x, t), wobei U (x, t) die partikul¨ are L¨ osung des inhomogenen Problems ist, und u ˜ die allge- meine L¨ osung des homogenen Problems.

2. Finde partikul¨ are L¨ osung 3. L¨ ose das homogene Problem 3.8.3 L¨ osungsweg

1. 0 − αU ^′′ = sin(x) → U = ^sin _α ^{( x )} 2. u ˜ t − α˜ u xx = 0

t = 0 → u(x, 0) = u(x, ˜ 0) + _αsin ¹ _{( x )} = 0

⎧ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎩

˜

u(x, 0) = − _{α sin} ¹ _{( x )} (= f (x))

˜

u _t − α˜ u _xx = 0

3. u(x, t ˜ ) = ∫ R K t (x − x ^′ )f (x ^′ )dx ^′

4. u(x, t) = − _α ¹ ∫ R K t (x − x ^′ ) sin(x ^′ )dx ^′ + ¹ _α sin(x)

3.9 Separation der Variabeln SdV

u(x, t) = X (x)T(t)

u x = X ^′ T u xx = X ^′′ T u t = X T ˙ u tt = X T ¨

ˆ Die so erhaltenen Ableitungen in die PDE einsetzen und so umstellen, dass alle von x und von t abh¨ angigen Ter- me getrennt sind.

ˆ Aus den Randbedingungen entscheiden, ob K <, =, > 0 ist und L¨ osung hinschreiben.

▶ X ^′′

X = K ⇒ X ^′′ − KX = 0

⇒

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

X(x) = A 1 e ^ωx + A 2 e ^{− ωx} (K = ω ² > 0) X(x) = A 1 cos(ωx) + A 2 sin(ωx) (K = −ω ² < 0) X(x) = A ₁ x + A ₂ (K = 0)

▶ −

Y ^′′

Y = K ⇒ Y ^′′ + KY = 0

⇒

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

Y (y) = B 1 cos(ωx) + B 2 sin(ωx) (K = ω ² > 0) Y (y) = B 1 e ^ωx + B 2 e ^{− ωx} (K = −ω ² < 0) Y (y) = B ₁ x + B ₂ (K = 0)

▶ X ^′

X = K ⇒ X ^′ − KX = 0

⇒

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

X(x) = A 1 e ^ω

^t (K = ω ² > 0) X(x) = A 1 e ^{− ω}

^t (K = −ω ² < 0)

X(x) = A ₁ (K = 0)

▶ −

Y ^′

Y = K ⇒ Y ^′ + KY = 0

⇒

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

Y (y) = B 1 e ^{− ω}

^t (K = ω ² > 0) Y (y) = B ₁ e ^ω

^t (K = −ω ² < 0)

Y (y) = B ₁ (K = 0)

ˆ Restliche Anfangs- und Randbedingungen einbauen, um auf die L¨ osung zu kommen.

ˆ Wichtig: Konstanten immer wieder zusammenfassen.

/ Beispiel # 1

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

u _xx + u _yy = 0 u(0, y) = u(L, y) = 0

u(x, 0) = 0 L > 0 u(x, L) = −3 sin(4π _L ^x )

Gesucht: L¨ osungen der Form u(x, y) = f (x)g(y).

Vorgehen 1. ^f _f

₍ ⁽ _x ^x ₎ ⁾ = − ^g

′′

( y ) g ( y ) = C

2. f (x) =

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

A 1 e ^{√ Cx} + A 2 e ^{− √ Cx} (C > 0) A 1 cos( √

−Cx) + A 2 sin( √

−Cx) (C < 0)

A ₁ x + A ₂ (C = 0)

und g(y) =

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

B ₁ e ^{√ − Cy} + B ₂ e ^{− √ − Cy} (C < 0) B 1 cos √

Cy + B 2 sin √

Cy (C > 0) B 1 y + B 2 (C = 0) 3. aus u(0, y) = u(L, y) = 0 folgt, dass f(0)=f(L)=0 gilt.

Nur die L¨ osung f¨ ur C < 0 macht sinn f¨ ur diese Forde- rung.

4. Es folgt A ₁ = 0 und aus A ₂ sin √

−CL = 0, dass

√

−CL = kπ, also f (x) = A 2 sin( ^kπx _L ) 5. da C < 0 ist g(y) = B 1 e ^{kπy / L} + B 2 e ^{− kπy / L} 6. aus u(x, 0) = 0 folgt dass g(0) = 0 also B 1 = −B 2

7. u(x, y) = A sin( ^kπx _L ) sinh( ^kπy _L )

8. aus einsetzen folgt noch dass k=4 und A = _sinh ⁻ ₍ ³ _{4π )} 9. Die L¨ osung ist also u(x, y) = _sinh ⁻ ₍ ³ _{4π )} sin( ^4πx _L ) sinh( ^4πy _L )

/ Beispiel # 2

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

∆u(x, y) = 0 0 < x < π 0 < y < π u(x, 0) = u(x, π) = u(0, y) = 0

u x (π, y) = sin(y)

Gesucht: L¨ osungen der Form u(x, y) = X(x)Y (y).

Vorgehen

1. X ^′′ Y + XY ^′′ = 0 ⇒ ^X

′′

X = − ^Y

′′

Y = K

2. aus u(x, 0) = u(x, π) weiss man: u periodisch in y und K > 0

3. X (x) = A 1 e ^ωx + A 2 e ^{− ωx} und Y (y) = B 1 cos(ωy) + B 2 sin(ωy)

4. Y (0) = 0 = B 1 , sowie Y (π) = 0 = B 2 sin(ωπ) und daher ω = k ∈ G

5. X (0) = 0 zeigt: A 1 = −A 2

6. u(x, y) = (A 1 e ^kx − A 1 e ^{− kx} )(B 2 sin(ky))

=(C 1 sinh(kx))(B 2 sin(ky)) = D 1 (sinh(kx) sin(ky)) 7. u x (π, y) = D 1 ⋅ k ⋅ cosh(kπ) sin(ky) = sin(y) , womit

k = 1 sein muss

8. D 1 = _cosh ¹ _{( π )} in die allgemeine Gl. einsetzen 9. Die L¨ osung lautet somit u(x, y) = ^{sinh (} _cosh ^{kx )} ₍ ^sin _{π )} ^{( ky )} Weitere Funktionen und ihre L¨ osungen

▶ y g ˙

g = K ⇒ g(y) = A 1 ⋅ y ^K

▶ f ^′

e ^x f = K ⇒ f (x) = B ₁ ⋅ e ^{K ⋅ e}

▶

f ^′′ − f k

f = K (k > 0) ⇒ f ^′′ − f (k + K) = 0

⇒

⎧ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎩

f (x) = A 1 e ^{√ k + ω}

^x + A 2 e ^{− √ k + ω}

^x (K = ω ² > 0) f (x) = B 1 cos(

√

ω ² − kx) + B 2 sin(

√

ω ² − kx)(K = −ω ² < 0)

4 W¨ armeleitungsgleichung

... das Standart - Beispiel f¨ ur parabolische PDE’s.

u t − αu xx = 0 (−∞ < x < ∞) u _t − a ² u _xx = 0 (−∞ < x < ∞)

4.1 Ans¨ atze mit RB’s (t > 0, x ∈ (0, l))

ˆ u(0, t) = u(l, t) = 0

u(x, t) = ∑ ^∞ _{n = 1} c n sin( ^nπx _l )e ^{− α}

2π2t l2

ˆ u _x (0, t) = u _x (l, t) = 0

u(x, t) = ∑ ^∞ _{n = 0} c _n cos( ^nπx _l )e ^{− α}

2π2t l2

ˆ u(0, t) = u x (l, t) = 0

u(x, t) = ∑ ^∞ _{n = 0} c _n sin(ω _n x)e ^{− αω}

^t ω n = ^{π ( 1} _2l ^{+ 2n )} n = 0, 1, ...

4.2 L¨ osung des Anfangwertproblems

⎧ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎩

u _t − αu _xx = 0 − ∞ < x < ∞ u(x,0) = f (x) − ∞ < x < ∞

u(x, t) =

∞

∫

−∞

K t (x − x ^′ )f (x ^′ )dx ^′ mit W¨ armeleitungskern

K _t (x − x ^′ ) = 1

√

4παt e ⁻

2 4αt

Der W¨ armeleitungskern erf¨ ullt:

1. ∫ ^∞

−∞ K _t (x − x ^′ )dx = 1 2. K t (x − x ^′ ) > 0

/ Zwei St¨ abe, die zusammengef¨ ugt werden

f (x) =

⎧ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎩

T 1 x > 0 T ₂ x < 0

liefert f¨ ur T 1 = −T 2 ≡ T Ô⇒ u(x, t) = T ⋅ erf (

x

√ 2αt ) mit: erf (z) = √ ¹ 2π

z

− ∫ z

e ⁻

2 2

dy

Falls T 1 ≠ T 2

u(x, t) = ^T

⁺ ₂ ^T

+ ^T

⁻ ₂ ^T

erf ( √ ^x 2αt )

4.3 Skalierung

/ W¨ armeleitung in einem d¨ unnen Stab Die Ausgangslage ist

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

u _t = a ² u _xx

u(x, 0) = U A = const. x ∈ [0, L] Ziel t = 0 ⇒ 1 u(0, t) = U W = const. t > 0 Ziel t → ∞ ⇒ 0 u _x (L, t) = 0 da isoliert

1. L¨ ange dimensionslos machen von [0, L] → [0, 1] mit

˜ x = _L ^x

v(˜ x, t) = u(L˜ x, t) − U _W U A − U W

⎧ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎩

v(˜ x, 0) = 1 v(0, t) = 0 v t = u t ⋅

1 U A − U W

v _{x ˜} = L ⋅ u _x ⋅ 1 U A − U W

v x˜ ˜ x = L ² ⋅ u xx ⋅ 1 U A − U W

In u t = a ² u xx eingesetzt ergibt das (U A − U W ) ⋅ v t = a ² ⋅

U A − U W

L ² ⋅ v x˜ ˜ x ⇒ v t = a ² L ² ⋅ v x˜ ˜ x

2. Temperatur dimensionslos machen von [U W , U A ] → [0, 1] mit ˜ t = _τ ^t τ muss ^L _a

sein

τ v t = v x˜ ˜ x

Die neue Funktion w(˜ x, t) = ˜ v(˜ x, τ t) ˜ f¨ uhrt zu w ˜ t τ v _t = w _{x˜ ˜ x} ⇒ w ˜ t = w _{˜ x˜ x} Das Problem nach der Skalierung lautet also nun

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

w ˜ t = w ˜ x˜ x

w(x, 0) = 1 x ∈ [0, 1]

w(0, ˜ t) = 0 τ > 0 w ˜ t (L, ˜ t) = 0 τ > 0

/ W¨ armeleitung im geschlossenen Draht Die Aufgabenstellung

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

PDE: v t = a ² v xx

AB: v(x, 0) =

⎧ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎩

V 1 0 ≤ x < L V 2 L ≤ x < 2L RB: v(0, t) = v(2L, t)

soll auf die Problemstellung

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

PDE: u _t = v _xx

AB: u(x, 0) =

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

1 0 < x < ^π ₂

−1 ^π ₂ < x < ^3π ₂ 1 ^3π ₂ < x < 2π RB1 u(0, t) = u(2π, t)

umskaliert werden. Ansatz dazu ist w(x, t) = v( Lx

π , βt).

Ableiten nach t und einsetzen in die PDE ergibt w t = βv t = βa ² v xx = βa ² v xx = βa ² π ²

L ² w xx .

Um a wegzuskalieren, muss man β = ( _πa ^L ) ² setzen.

In den Ansatz eingesetzt ergibt das w(x, t) = v( Lx

π , ( L

πa ) ² t) Ô⇒ v(x, t) = w( πx L , (

πa L ) ² t).

Die Translation von u zu v wird beschrieben durch u(x, t) = w(x + ^π ₂ , t) − ^V

⁻ ₂ ^V

V

− V

2

. , womit die Skalierung beendet ist.

4.4 L¨ osung der Anfangsrandwertaufgabe

/ W¨ armeleitung im geschlossenen Draht

Abbildung 4: W¨ armeleitung im geschlossenen Draht der L¨ ange 2π

Falls das Problem noch nicht skaliert ist, zuerst umskalieren.

Die Aufgabenstellung lautet

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎩

u(x, t) x ∈ [0, 2π] t ≥ 0 PDE: u t = u xx

AB: u(x, 0) = f (x) =

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

1 0 < x < ^π ₂

−1 ^π ₂ < x < ^3π ₂ 1 ^3π ₂ < x < 2π RB1: u(0, t) = u(2π, t)

RB2: u _x (0, t) = u _x (2π, t) RB3: u _xx (0, t) = u _xx (2π, t)

Vorgehen

1. Separation der Variabeln u(x, t) = X (x)T(t) in die PDE eingesetzt ergibt das

T ˙ T =

X ^′′

X = K = const.

Dies f¨ uhrt auf die 2 ODE’s T ˙ = KT X ^′′ = KX

Da u 2π-periodisch in x ist (aus RB1), muss eine peri- odische L¨ osung f¨ ur X gelten. Darum muss K < 0 sein.

Wir setzen K = −ω ² .

Daraus ergeben sich nun die L¨ osungen der ODE’s X ^′′ + ω ² X = 0 Ô⇒ X = A cos(wx) + B sin(wx)

T ˙ + ω ² T = 0 Ô⇒ T = Ce ^{− ω}

^t

X und T in den SdV - Ansatz u(x, t) = X(x)T (t) ein- gesetzt ergibt die Basisfunktion u _k . Mit k ∶= ω _k und A ^′ _k = C _k ⋅ A _k und B _k ^′ = C _k ⋅ B _k lautet sie

u _k (x, t) = e ^{− k}

^t (A ^′ _k cos(kx) + B _k ^′ sin(kx)) 2. Superposition Die PDE ist linear und homogen, wo-

mit das Superpositionsprinzip gilt. Dasselbe gilt auch f¨ ur die RB. Die erhaltene Basisfunktion erf¨ ullt beide dieser Gleichungen, womit man duch Superposition die L¨ osung erh¨ alt.

u(x, t) =

∞

∑

k = 0

u k (x, t)

=

∞

∑

k = 0

e ^{− k}

^t (A ^′ _k cos(kx) + B _k ^′ sin(kx)) 3. Erf¨ ullen der AB Einseten der superponierten L¨ osung in

die AB f¨ uhrt zu u(x, 0) = f (x)

=

∞

∑

k = 0

(A ^′ _k cos(kx) + B _k ^′ sin(kx))

was eine Fourier - Reihe darstellt. Also muss f (x) in eine Fourier - Reihe entwickelt werden.

Zeichnet man die Funktion auf, so erkennt man, dass sie gerade ist. Also berechnet man die Fourier - Koeffizien- ten f¨ ur eine gerade Funktion und f¨ uhrt den Koeffizien- tenvergleich durch.

B _k ^′ = 0 A ^′ _k =

2 π

π

∫

0

f (x) cos(kx)dx

= 2 π (

π / 2

∫

0

cos(kx)dx −

π

∫

π / 2

cos(kx)dx)

= 4

πk sin( πk 2 ) f (x) =

∞

∑

k = 0

(−1) ^k 4

π(2k + 1) cos((2k + 1)x) = u(x, 0) In u(x, t) eingesetzt ergibt das die L¨ osung

u(x, t) = 4 π ⋅

∞

∑

k = 0

(−1) ^k 1

2k + 1 cos((2k + 1)x) ⋅ e ^{−( 2k + 1 )}

^t / W¨ armeleitung in einer Kugel

Die W¨ armeleitungsgleichung in 3-D lautet u t = ∆u(x, y, z) ∈ B t > 0 Die Randbedingung ist

u(x, y, z, t) = u _W (x, y, z) ∈ ∂B und die Anfangsbedingung

u(x, y, z, 0) = u A (x, y, z) ∈ B Umskalierung mit v = _u ^{u − u}

A

− u

f¨ uhrt auf

PDE: v t = ∆v

RB: v(x, y, z, t) = 0 ∈ ∂B

AB: v(x, y, z, 0) = 1 ∈ B

Man nimmt Radialsymmetrie an und ¨ ubertr¨ agt das Pro- blem in sph¨ arische Koordinaten (Abh¨ angigkeit von r). Mit SdV erh¨ alt man so die Basisl¨ osung

v n (r, t) = B n

1 r sin( nπ

r 0

r)e

−n2π2 r2

0

t

Es wird wiederum superponiert, und das erf¨ ullen der AB (inhomogen) f¨ uhrt zur L¨ osung, die man noch in die Gleichung f¨ ur die Skalierung einzusetzen hat, um u(r, t) zu bekommen.

v(r, t) = − 1 r

2r 0

π

∞

∑

n = 1

(−1) ⁿ n sin( nπ

r ₀ r)e

−n2π2 r2

0

t

4.5 Superpositionsprinzip

Gen¨ ugen u A und u B denselben homogenen linea- ren Anfangs- und Randbedingungen sowie dersel- ben linearen, homogenen PDE, so ist

u = αu A + βu B

eine L¨ osung der PDE und der Rand- und Anfangs- bedingung.

ˆ homogene PDE = keinen konstanten Term

ˆ homogene AB, RB = linear in u und ohne konstanten Term

4.6 Beispielaufgaben

/ Beispiel # 1: Drahtschleife im W¨ armebad

Aufgabenstellung: Die Drahtschleife mit Radius R wird zur Zeit t = 0 aus dem W¨ armebad mit W¨ armefunktion h(x, y) =

x

R T ₀ genommen und k¨ uhlt nach dem W¨ armeleitungsgesetz u t = a ² u ss

ab. L¨ osen Sie das Anfangswertproblem f¨ ur u.

Separation der Variabeln mit u t = T S ˙ und u s s = T S ^′′ f¨ uhrt

auf T ˙

T = a ² S ^′′

S = K

Da die Funktion in s 2πR-periodisch ist (Umfang), muss C in S ^′′ − _a ^C

S = 0 negativ sein, um periodische L¨ osungen zu bekommen.

S(s) = A 1 cos( ω

a s) + A 2 sin( ω a s)

,wobei ^ω _a s = 2πn sein muss, mit n ∈ Z . Also ist ω = ^2πna _s = ^na _R und die einzelnen ODE’s werden

S(s) = A ₁ cos( n

R s) + A ₂ sin( n R s) T (t) = B 1 e ^{− ω}

^t = B 1 e ⁻

2a2 R2

t

u _n (s, t) = S(s)T(t) = (C ₁ cos( n

R s) + C ₂ sin( n R s))e ⁻

2a2 R2

t

Superposition heisst hier, dass die Basisfunktion u n in eine Fourierreihe entwickelt wird.

u(s, t) =

∞

∑

n = 1

°

Spos

(D n cos( n

R s) + E n sin( n R s))e ⁻

2a2 R2

t

Die Anfangsbedingung liefert die Funktion h(x, y) = _R ^x T ₀ , wobei in cyl. Koordinaten x = R cos( _R ^s ) ist und deshalb h(x, y) = T 0 cos( _R ^s ). Diese ist auch gleich u(s, 0), womit der Koeffizientenvergleich

u(s, 0) = T 0 cos( s R ) =

∞

∑

n = 1

D n cos( n

R s) + E n sin( n R s) folgende Resultate bringt

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

E n = 0 ∀n da links keine Sinusterme D 1 = T 0 n = 1 womit ¨ Ubereinstimmung herrscht D _n = 0 n ≠ 1 f¨ ur alle andern n

Diese Resultate einsetzen f¨ uhrt direkt zur L¨ osung u(s, 0) = T ₀ cos( s

R )e ⁻

2 R2

t

/ Beispiel # 2: Abk¨ uhlung der Erde

⎧ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎨

⎪ ⎪

⎪ ⎪

⎪ ⎪

⎪ ⎩

PDE: u t = α∆u x ∈ B , t > 0 RB: u(x, t) = 0 ∣x∣ = 1 , t > 0 AB: u(x, 0) = 1 − ∣x ² ∣

Zeigen Sie, dass

u n (x, t) = 1

r sin(πnr)e ^{− απ}

ⁿ

^t

ist, f¨ ur n ∈ Z . Und finden Sie mit der AB die L¨ osung des Problems.

Vorgehen

Es handelt sich um ein Kugelsymmetrisches Problem, alos ver- wenden wir Kugelkoordinaten. In diesen lautet der Laplace - Operator, der f¨ ur Kugelsymmetrie nur vom Radius abh¨ angt

∆u = u rr + 2 r u r

Wir bestimmen v , gem¨ ass u(r, t) = ^{v ( r,t} _r ⁾ und leiten u ab u(r, t) = v

r u _r (r, t) = v _r

r − v r ² u rr (r, t) = v rr

r − v r

r ² − v r

r ² + 2 v r ³ = v rr

r − 2 v r

r ² + 2 v r ³

∆u = u rr + 2 r u r =

v rr

r − 2 v r

r ² + 2 v r ³ +

2 r (

v r

r − v r ² ) =

v rr

r ,womit f¨ ur u _t = α∆u folgt, dass v _t = αv _rr . ¨ Uber Superposition und einsetzen der RB v(1, t) = 0 folgt die gesuchte allgemeine L¨ osung u _n .

Diese wird nun f¨ ur die AB superponiert, und die AB wird in eine Fourier - Reihe entwickelt. Das Finden der Fourier - Koeffizienten B n in die allgemine L¨ osung

u n (x, t) = B n

r sin(πnr)e ^{− απ}

ⁿ

^t

eingesetzt l¨ ost das Anfangswertproblem.