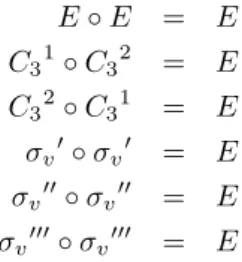π − aus derDeuteronspaltung bei π − Einfang)

4 Übungsblatt Kern und Teilchenphysik

4.1 (intrinsischeParität des

π ⁻

aus derDeuteronspaltung bei

π ⁻

Einfang)

Wir betrachtendieTeilchenreaktion:

π ⁻ + d → n + n

hierbei wirdein

π ⁻

eingefangen, welches ein Deuteron spaltet. DieParität sollerhaltenbleiben,d.h.

P in = P f i

^{.DasDeuteronbesitzeeinenSpinvon}

S = 1

und sei ein gebundener s-Zustand von

p

^und

n

^{, d.h.}

l = 0

^{. Zudem sei (durch}

experimentelle Ergebnisse)bekannt, dassdasPionin Ruhein einen s-Zustand

eigefangenwird.D.h.auchfürdasPiongilt

l = 0

^{. Fürdie initialParitätgilt:}

P in = P d · P π ⁻ · (−1) ^{l πd} = P π ⁻

da

P d = +1

^{(DieParitätderNukleonenistgleich,d.h.ProtonundNeutron}

haben die gleiche Parität, für ein zusammengesetztes System gilt

P 12 = P 1 · P 2 · (−1) ^{l 12}

^{, in diesem Fall ist}

l 12 = 0

^und

P 1 = P 2 ⇒ P 1 · P 2 = +1

^{, da die}

MultiplikationzweierElemente mitgleichemVorzeichenimmeretwaspositives

liefert)und

l πd = 0

^.

DienalParitätergibtsichmit:

P f i = P n · P n

| {z }

+1

· (−1) ^{l 2 n} = (−1) ^{l 2 n}

Ausder Bedingung

P in = P f i

^{, d.h.der} Paritätserhaltung folgtalsofür die intrinsischeParitätdes

π ⁻

^:

P π = (−1) ^{l 2 n}

esistnun

l 2n

^{zubestimmen.Diesistmöglichüberdie}Drehimpulserhaltung

J in = J f i

^,wobei:

J in = L + I d = l πd + 1 = 1 J f i = L + I 2n = l 2n + I 2n

mit dem Kernspin

I

^{(wir besitzen keine} Elektronenspins (Spin des Pions

s π ⁻ = 0

^),daherkeine

S

^).

Esgiltalso:

l 2n + I 2n = 1

Dasbedeutetalso,dassesvierverschiedeneKombinationsmöglichkeitenfür

l 2n = 0, 1, 2

^und

I 2n = 0, 1

^gibt,umden Gesamtdrehimpuls

1

^{zuerzeugen.Wir}

wissen, dassdie Gesamtwellenfunktionantisymmetrisch

(−1)

^{seinmuss, daher}

folgt:

l 2n I 2n

^{Vorzeichenbei}Teilchenvertauschungin den

J

^-Zuständen

1 0 (−1) · (−1) = +1

0 1 (+1) · (+1) = +1

1 1 (−1) · (+1) = −1

2 1 (+1) · (+1) = +1

Hierausfolgt,dassdieeinzigeMöglichkeit

l 2n = 1

^und

I 2n = 1

^{ist,somitgilt}

also:

P f i = (−1) ^{l 2 n} = −1

undwirerhaltendieintrinsischeParitätfürdasPion mit:

P π − = −1

4.2 (

C _3v

-SymmetrieoperationeneinesgleichseitigenDrei- ecks)

Abbildung1:Spiegelebenen(

σ ⁰ , σ ⁰⁰ , σ ⁰⁰⁰

^)desgleichseitigenDreiecks,Drehungen um

120 ^◦

^(imUhrzeigersinn)überführen

1 → 3, 3 → 2, 2 → 1

^{undDrehungenum}

240 ^◦

^überführen

1 → 2, 3 → 1, 2 → 3

^{,dieIdentitätliefertdasgleicheDreieck.}

Esistzuzeigen,dassdie

6

Symmetrie-OperationeneineGruppebildenund zusätzlichist die Multiplikationstafelder Gruppezu konstruieren.Die

6

^mög-

lichenSymmetrieoperationensind

E, C 3 1 , C 3 2 , σ v 0 , σ v 00 , σ v 000

, d.h.dieIdentität,

eine Drehung um

120 ^◦

^{, eine Drehung um}

240 ^◦

^{(die Drehung um}

360 ^◦

^wäre

wieder die Identität)und drei Spiegelebenen,welchejeweilsvoneinerder Sei-

tenhalbierendenzueinerEckedesDreieckslaufen.

ZuerstbetrachtenwirdieGruppeneigenschaften:

1)Abgeschlossenheit

DieAbgeschlossenheitwirddurch dieuntenfolgendeMultiplikationstabelle

gewährleistet.

Wirsuchen dasEinselementfürdieseGruppe.DieIdentitätkannsofortals

Einselementidentiziertwerden.Dieskannmanauchnutzen,umschnelleinige

Elemente indieMultiplikationstabelleeinzutragen.Esgilt:

A ◦ E = E ◦ A = A

3)InversesElement

Wir prüfen,ob jedes Element derGruppeein inversesbesitzt. Diesist der

Fall,wenn

A ◦ A ^{− 1} = A ^{− 1} ◦ A = E

dies lässt sich leicht mit Hilfe der unten folgenden Multiplikationstabelle

zeigen,esgilt:

E ◦ E = E C 3 1

◦ C 3 2

= E C 3 2

◦ C 3 1

= E σ v 0 ◦ σ v 0 = E σ v 00 ◦ σ v 00 = E σ v 000 ◦ σ v 000 = E

DieSpiegelungensindalsozusichselbstinvers,dieIdentitättrivialerWeise

auchunddieInversen derDrehungensindjeweilsdieanderenDrehungen.

4)Assoziativgesetz

DasAssoziativgesetzgiltallgemeinfürdieMatrizenmultiplikation,alsoauch

speziellfürdieMultiplikationderMatrizender

C 3v

^{-Gruppe,welchedurch Ma-}

trizen dargestelltwerdenkönnen,d.h.esgilt:

[A ◦ B] ◦ C = A ◦ [B ◦ C]

5)Multiplikationstabelle

DieMultiplikationstabelleergibtsichausderBetrachtungdesgleichseitigen

Dreiecks und Anwendung der Symmetrieoperationen,wobei die Elemente der

Tabellejeweilshintereinanderausgeführtwerden,wobeizuerstdasElementauf

dery-AchseunddanndasElementauf derx-Achseausgeführtwird.

C 3v E C 3 1

C 3 2

σ v 0 σ v 00 σ v 000

E E C 3 1

C 3 2

σ v 0 σ v 00 σ v 000

C 3 1 C 3 1 C 3 2 E σ v 000 σ v 0 σ v 00

C 3 2

C 3 2

E C 3 1

σ v 00 σ v 000 σ v 0

σ v 0 σ v 0 σ v 00 σ v 000 E C 3 1 C 3 2

σ v 00 σ v 00 σ v 000 σ v 0 C 3 2

E C 3 1

σ v 000 σ v 000 σ v 0 σ v 00 C 3 1 C 3 2 E

6)Kommutativgesetz

WenneineGruppeunter einerOperationkommutativist,danngilt:

A ◦ B = B ◦ A

füralle ElementederGruppe.

Um zu zeigen, dass die Gruppe nicht abelsch ist, reicht es für eines der

Elementezuzeigen,dassdiesesnichtkommutativist,dainabelschenGruppen

dieElemente kommutieren,wirwählen:

σ v 0 · C 3 1

= σ v 00

C 3

1 · σ v 0 = σ v 000

esgiltalso:

σ v 0 · C 3 1

6= C 3 1

· σ v 0

somitistdieGruppenichtabelsch.

7)eindimensionaleDarstellung

Einemöglichenicht-trivialeeindimensionaleDarstellungist:

A = f E, C 3 1

, C 3 3

= 1 B = f (σ v 0 , σ v 00 , σ v 000 ) = −1

wobei

1

^hierdasEinselement,und

1

^inverszu

1

^und

−1

^inverszu

−1

^ist.Es

ergibtsichalsMultiplikationstabelleindiesemFall:

A A A B B B

A 1 1 1 −1 −1 −1

A 1 1 1 −1 −1 −1

A 1 1 1 −1 −1 −1

B −1 −1 −1 1 1 1

B −1 −1 −1 1 1 1

B −1 −1 −1 1 1 1

8)Darstellunggetreu?

EineDarstellungistgetreu,wenneseinenisomorphenZusammenhangzwi-

schen Symmetrieoperation und eindimensionaler Darstellung gibt. Wenn also

dieDarstellung

f

^{injektiv undsurjektiv,alsobijektiv istundzudem}

f

^einHo-

momorphismusist.WirzeigendurcheinGegenbeispiel,dassdiesnichtderFall

ist.Esgilt:

f (E) = 1 f C 3 1

= 1

hierausmüssteimFalldergetreuenDarstellungfolgen:

E = C 3 1

diesistjedochnichtderFall!DieDarstellungistalsonichtgetreu.