Skript zur Vorlesung
“Physik auf dem Computer”
JP Dr. A. Arnold Universität Stuttgart Institut für Computerphysik
unter Mithilfe von
Dr. O. Lenz
Sommersemester 2014
Ich danke H. Menke, M. Kuron, J. Landsgesell, K. Szuttor und A. Weyman für zahlreiche Korrekturen.
Dieses Skript und alle Quelldateien sind unter einer Creative Commons-Lizenz vom Typ Namensnennung-Weitergabe unter gleichen Bedingungen 3.0 Deutschland zugänglich.
Um eine Kopie dieser Lizenz einzusehen, konsultieren Sie http://creativecommons.
org/licenses/by-sa/3.0/de/ oder wenden Sie sich schriftlich an Creative Com- mons, 444 Castro Street, Suite 900, Mountain View, California, 94041, USA.
CC BY:C
Inhaltsverzeichnis
1 Einleitung 7
1.1 Über dieses Skript . . . . 8
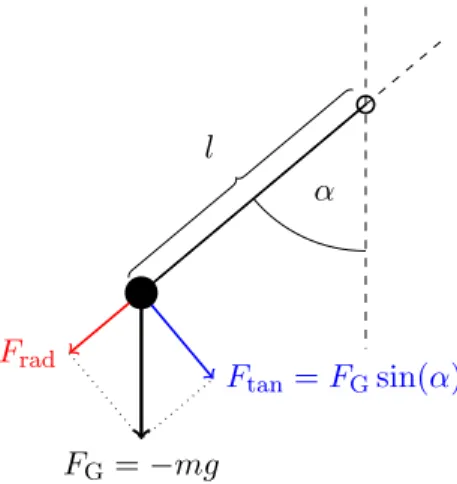
1.2 Beispiel: Fadenpendel . . . . 10
1.2.1 Modell . . . . 10
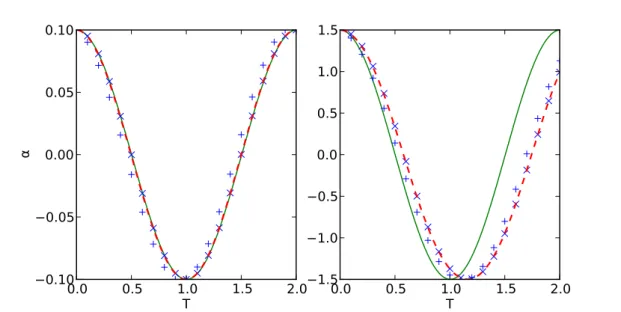
1.2.2 Näherung: der harmonische Oszillator . . . . 11
1.2.3 Numerische Lösung . . . . 12
2 Lineare Algebra I 17 2.1 Dreiecksmatrizen . . . . 17
2.2 Gaußelimination . . . . 18
2.3 Matrixinversion . . . . 20
2.4 LU-Zerlegung . . . . 21
2.5 Cholesky-Zerlegung . . . . 22
2.6 Bandmatrizen . . . . 23
3 Darstellung von Funktionen 25 3.1 Horner-Schema . . . . 25
3.2 Taylorreihen . . . . 26
3.3 Polynom- oder Lagrangeinterpolation . . . . 27
3.3.1 Lagrangepolynome . . . . 29
3.3.2 Baryzentrische Darstellung . . . . 30
3.3.3 Neville-Aitken-Schema . . . . 30
3.3.4 Newtonsche Darstellung . . . . 31
3.3.5 Chebyshev-Stützstellen . . . . 32
3.4 Splines . . . . 32
3.5 Fourierreihen . . . . 35
3.5.1 Komplexe Fourierreihen . . . . 35
3.5.2 Reelle Fourierreihen . . . . 37
3.5.3 Diskrete Fouriertransformation . . . . 39
3.5.4 Schnelle Fouriertransformation . . . . 42
3.6 Wavelets . . . . 43
4 Datenanalyse und Signalverarbeitung 47 4.1 Kontinuierliche Fouriertransformation . . . . 47
4.1.1 Numerische kontinuierliche Fouriertransformation . . . . 50
4.1.2 Abtasttheorem . . . . 52
4.2 Faltungen . . . . 52
4.2.1 Antwort zeitinvarianter linearer Systeme . . . . 55
4.3 Kreuz- und Autokorrelation . . . . 55
4.3.1 Kreuzkorrelationsfunktion . . . . 56
4.3.2 Autokorrelationsfunktion . . . . 59
4.4 Messfehlerabschätzung . . . . 61
4.4.1 Fehler bei der Messung korrelierter Daten . . . . 63
4.4.2 Binning-Analyse . . . . 64
4.5 Ausgleichsrechnung, Methode der kleinsten Quadrate . . . . 66
5 Nichtlineare Gleichungssysteme 71 5.1 Sukzessive Substitution . . . . 71
5.1.1 Beispiel . . . . 73
5.2 Newtonverfahren in einer Dimension . . . . 74
5.2.1 Beispiel . . . . 75
5.2.2 Wurzelziehen . . . . 76
5.2.3 Nullstellen von Polynomen . . . . 76
5.3 Sekantenmethode . . . . 77
5.4 Bisektion . . . . 78
5.4.1 Beispiel . . . . 79
5.5 Regula falsi . . . . 79
5.6 Newtonverfahren in mehreren Dimensionen . . . . 81
5.6.1 Gedämpftes Newtonverfahren . . . . 82
6 Numerisches Differenzieren und Integrieren 83 6.1 Numerisches Differenzieren . . . . 83
6.1.1 Näherungen höherer Ordnung und höhere Ableitungen . . . . 84
6.1.2 Genauigkeit . . . . 85
6.1.3 Beispiel: Besselsche Differentialgleichung . . . . 86
6.2 Quadratur: numerische Integration . . . . 88
6.2.1 Newton-Cotes-Formeln . . . . 91
6.2.2 Zusammengesetzte Newton-Cotes-Formeln . . . . 93
6.2.3 Beispiel: Besselfunktion . . . . 95
6.2.4 Romberg-Integration . . . . 96
6.2.5 Beispiel: Fehlerintegral . . . . 97
6.2.6 Gauß-Quadratur . . . 100
6.2.7 Unendliche Integrale und Singularitäten . . . 102
6.2.8 Mehrdimensionale Integration, Monte-Carlo-Integration . . . 104
6.2.9 Beispiel: Monte-Carlo-Integration von π . . . 105
6.2.10 Quasi-Monte-Carlo-Integration . . . 106
6.2.11 Beispiel: Quasi-Monte-Carlo-Integration von π . . . 108
Inhaltsverzeichnis
7 Zufallszahlen 111
7.1 Pseudozufallszahlen . . . 111
7.1.1 Linearer Kongruenzgenerator . . . 112
7.1.2 Verzögerter Fibonaccigenerator . . . 114
7.2 Qualitätsanalyse . . . 115
7.2.1 Statistiktests . . . 116
7.2.2 Poincaré-Schnitte . . . 118
7.2.3 Fouriertest . . . 119
7.2.4 Autokorrelationstest . . . 119
7.3 Andere Verteilungen . . . 120
7.3.1 Verwerfungsmethode . . . 120
7.3.2 Inversionsmethode . . . 123
7.3.3 Zufällige Punkte auf Kugel und Kugeloberfläche . . . 125
7.4 Beispiel: Random walk . . . 126
7.5 Beispiel: Perkolation . . . 132
8 Lineare Algebra II 137 8.1 Iterative Gleichungslöser . . . 138
8.1.1 Jacobiverfahren . . . 139
8.1.2 Gauß-Seidel-Verfahren . . . 141
8.1.3 Relaxationsverfahren . . . 142
8.2 QR-Zerlegung und Orthogonalisierung . . . 144
8.2.1 Gram-Schmidt-Verfahren . . . 144
8.2.2 Householder-Verfahren . . . 148
8.2.3 Givens-Rotationen . . . 152
8.3 Eigenwerte . . . 155
8.3.1 Vektoriteration . . . 155
8.3.2 QR-Algorithmus . . . 157
8.3.3 Inverse Iteration . . . 159
9 Optimierung 161 9.1 Pseudoinverse . . . 163
9.2 Nichtlineare Optimierung . . . 164
9.2.1 Verfahren des steilsten Abstiegs . . . 165
9.2.2 Schrittweitensteuerung . . . 165
9.2.3 CG-Verfahren . . . 167
9.2.4 Nebenbedingungen und Straffunktionen . . . 170
9.3 Lineare Programme und Simplexalgorithmus . . . 173
9.4 Globale Optimierung . . . 178
9.4.1 Simulated annealing . . . 184
9.4.2 Genetische Algorithmen . . . 187
10 Differentialgleichungen 189
10.1 Gewöhnliche Differentialgleichungen . . . 189
10.1.1 Runge-Kutta-Verfahren . . . 190
10.1.2 Beispiel: Lotka-Volterra-Gleichungen . . . 194
10.1.3 Velocity-Verlet-Verfahren . . . 196
10.1.4 Beispiel: 3-Körperproblem . . . 198
10.2 Partielle Differentialgleichungen . . . 200
10.2.1 Finite-Differenzen-Methode — Wärmeleitungsgleichung . . . 200
10.2.2 Finite-Elemente-Methode . . . 204
10.2.3 Lösung mittels Fouriertransformation — Poisson-Gleichung . . . . 207
10.2.4 Lösung der Poisson-Boltzmann-Gleichung . . . 210
1 Einleitung
In dieser Vorlesung geht es darum, wie der Computer in der modernen Physik eingesetzt wird, um neue Erkenntnisse zu gewinnen. Klassisch war die Physik ein Zusammenspiel aus Experiment und Theorie. Die Theorie macht Vorhersagen, die im Experiment überprüft werden. Umgekehrt kann im Experiment ein neuer Effekt beobachtet werden, für den die Theorie eine Erklärung liefert. Durch den Einsatz von Computern ist dieses Bild komplizierter geworden. In der folgenden Graphik sind die Bereiche farblich hinterlegt, in denen heutzutage Computer zum Einsatz kommen, die hellroten Bereiche werden in dieser Vorlesung behandelt:
Simulation
Theorie Experiment
Symbolische Mathematik
Numerische Lösung
Steuerung
Auswertung Vorhersage
Überprüfung
Eichung Vorhersage Vorhersage
Überprüfung
Zu den klassischen Säulen Theorie und Experiment ist die Simulation als Mittelding zwi- schen Theorie und Experiment gekommen. Computersimulationen stellen Experimente im Computer nach, ausgehend von bekannten theoretischen Grundlagen. Alles, für das es Wechselwirkungstheorien gibt, kann simuliert werden, von Galaxien bis hin zu Elek- tronen und Quarks. Dazu gibt es eine Vielzahl an unterschiedlichen Methoden, deren Grundlagen in dieser Vorlesung vorgestellt werden.
Simulationen erfüllen zwei Hauptaufgaben: Simulationen können einerseits genutzt werden, um Experimente möglichst genau zu reproduzieren, andererseits kann man auch abstrakte theoretische Modelle in ihrer vollen Komplexität untersuchen.
Simulationen, die an ein Experiment angepasst (geeicht) sind, können zusätzliche In- formationen liefern, die experimentell nicht zugänglich sind. Zum Beispiel kann man dort Energiebeiträge getrennt messen oder sehr kurzlebige Zwischenprodukte beobach- ten. Außerdem erlauben Simulationen, Wechselwirkungen und andere Parameter gezielt zu verändern, und damit Vorhersagen über zukünftige Experimente zu machen.
Simulationen, die auf theoretischen Modellen basieren, sind oft ein gutes Mittel, um
notwendige Näherungen auf Plausibilität zu überprüfen oder um einen ersten Eindruck
vom Verhalten dieses Modells zu erhalten. Damit können Simulationen auch helfen, zu
entscheiden, ob notwendige Näherungen oder das Modell unvollständig ist, wenn Theorie und Experiment nicht zu einander passen. Schließlich lassen sich, anders als im Experi- ment, Wechselwirkungen einfach ausschalten, um deren Einfluss abschätzen zu können.
In der klassischen theoretischen Physik werden Papier und Bleistift zunehmend vom Computer verdrängt, denn Computeralgebra ist mittlerweile sehr leistungsfähig und kann zum Beispiel in wenigen Sekunden komplexe Integrale analytisch lösen. Und falls eine Gleichung doch einmal zu kompliziert ist für eine analytische Lösung, so kann der Com- puter mit numerischen Verfahren oft sehr gute Näherungen finden. Letztlich passiert dies auch in einer Computersimulation, allerdings hat sich dieses Feld soweit entwickelt, dass es mit Recht als eigenständig bezeichnet wird.
In der experimentellen Physik fallen immer größere Datenmengen an. Der LHC erzeugt zum Beispiel pro Jahr etwa 10 Petabyte an Daten, also etwa 200 Millionen DVDs, was über mehrere Rechenzentren verteilt gespeichert und ausgewertet werden muss. Klar ist, dass nur Computer diese gigantischen Datenmengen durchforsten können. Aber auch bei einfacheren Experimenten helfen Computer bei der Auswertung und Aufbereitung der Daten, zum Beispiel durch Filtern oder statistische Analysen. Viele Experimente, nicht nur der LHC, sind aber auch so komplex, dass Computer zur Steuerung der Experimente benötigt werden, was wir in dieser Vorlesung aber nicht behandeln können. Die Auswer- tung und Aufbereitung der Daten hingegen wird besprochen, auch weil dies genauso auch für Computersimulationen benutzt wird.
Neben diesen direkten Anwendungen in der Physik ist der Computer mittlerweile na- türlich auch ein wichtiges Mittel für den Wissensaustausch unter Physikern, sei es beim Schreiben wissenschaftlicher Arbeiten oder beim internationalen Austausch über E-mail und Videokonferenz. Auch stehen mittlerweile die meisten wissenschaftlichen Arbeiten weltweit in elektronischen Bibliotheken zur Verfügung. Leider hat das einfachere Pu- blizieren mit Hilfe des Computers auch zu einem starken Anstieg immer spezialisierter Arbeiten geführt, so dass man zur Recherche in diesen riesigen Datenmengen mittlerweile ebenfalls Computer benötigt.
Um den Computer für Simulationen, Auswertung von Daten oder auch Lösung kom- plexer Differenzialgleichungen nutzen zu können, sind neben physikalischen Kenntnissen auch solche in Programmierung, numerischer Mathematik und Informatik gefragt. In die- sem Skript geht es vor allem um die grundlegenden Methoden und wie diese angewandt werden, daher dominiert die numerische Mathematik etwas. Anders als in einer richtigen Vorlesung zur Numerik stehen hier aber die Methoden und Anwendungen anstatt der Herleitungen im Vordergrund.
1.1 Über dieses Skript
Im Folgenden wird eine in der numerischen Mathematik übliche Notation benutzt. Wie
auch in den meisten Programmiersprachen werden skalare und vektorielle Variablen nicht
durch ihre Schreibweise unterschieden, allerdings werden üblicherweise die Namen i–l
für (ganzzahlige) Schleifenindizes benutzt, n und m für Dimensionen. Da Schleifen sehr
häufig auftreten, wird hierfür die Kurznotation Anfang(Inkrement)Ende benutzt. Zum
1.1 Über dieses Skript
Beispiel bedeuten
1(1)n = 1,2, . . . , n n(−2)1 = n, n − 2, . . . , 3, 1.
Alle anderen Variablen sind reellwertige Skalare oder Vektoren, R n bezeichnet dabei den n-dimensionalen Vektorraum reller Zahlen. Mit e i wird dabei der Einheitsvektor der i-ten Spalte bezeichnet, mit e T i seine Transponierte, also der Einheitsvektor der i-ten Zeile. Bei komplexen Vektoren steht entsprechend der obere Index H für die Hermitesche eines Vektors, also die Transponierte des Vektors, bei der alle Komponenten komplex konjugiert sind. Für reelle Vektoren sind also H und T gleichbedeutend.
Integrale werden mit dem Volumenelement am Ende geschrieben, dessen Dimensiona- lität sich aus dem Integrationsbereich erschließt. Sehr häufig werden Abschätzungen mit Hilfe der Landau -Symbole verkürzt. Wie üblich heißt für zwei Funktionen f und g
f = O x→a (g) ⇐⇒ lim
x→a
|f (x)|
|g(x)| < ∞.
In den meisten Fällen ist a = 0 oder a = ∞ und aus dem Kontext klar, welcher Grenzwert gemeint ist. Dann wird die Angabe weggelassen. Oft wird auch die Notation f = g +O(h) benutzt, um f + g = O(h) auszudrücken. f (x) ˙ =g(x) schließlich bedeutet, dass f und g um Null herum in linearer Ordnung gleich sind, also f (x) − g(x) = O x→0 (x).
Numerische Algorithmen werden in diesem Skript in der Sprache Python 1 dargestellt.
Dabei werden die leistungsfähigen numerischen Erweiterungen NumPy und SciPy 2 inten- siv eingesetzt, und zur Visualisierung dient die hervorragende matplotlib 3 . Alle Graphen in dieser Vorlesung sind mit matplotlib erstellt worden. Zum Erlernen von Python sei auf die Materialien der Veranstaltung „Computergrundlagen“ verwiesen, die im Fachbereich Physik der Universität Stuttgart jährlich angeboten wird.
Im Bereich des Hochleistungsrechnens werden vor allem die Sprachen Fortran und C/C++ eingesetzt, weil diese in Verbindung mit guten Compilern sehr effizienten Code ergeben. Allerdings verlangen diese Sprachen die explizite Typisierung von Variablen, was Beispiele unnötig verkompliziert. Zudem sind Speicherzugriffe nur ungenügend ge- schützt, was die Fehlersuche sehr erschwert. Daher werden in dieser Vorlesung und den zugehörigen Übungen C/C++ nicht eingesetzt.
Die meisten der in diesem Skript vorgestellten numerischen Methoden werden von Sci- Py direkt unterstützt. Die Qualität dieser Implementationen ist mit eigenem Code nur schwierig zu überbieten. Wo immer möglich, wird daher auf die entsprechend SciPy- Befehle verwiesen. Zum Beispiel wird auf die Funktion „method“ im SciPy-Modul „libra- ry“ in der Form scipy.library.method(arg1, arg2,...) verwiesen. Trotzdem sind viele Methoden auch als expliziter Code gezeigt, da man natürlich eine Vorstellung davon haben sollte, was diese Methoden tun.
1
http://python.org
2
http://www.scipy.org
3
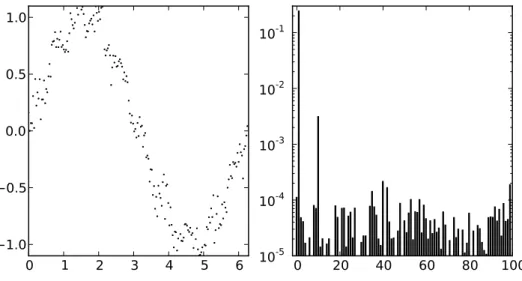
![Abbildung 3.6: Diskrete Fouriertransformation von 14 äquidistanten diskreten Daten- Daten-punkten (rote Punkte links) der Funktion sin(13t) (rote Kurve links) im Interval [0 : 2π].](https://thumb-eu.123doks.com/thumbv2/1library_info/3986654.1539582/41.892.139.658.148.435/abbildung-diskrete-fouriertransformation-äquidistanten-diskreten-punkten-funktion-interval.webp)