Path Integral Methods in Quantum Rate Theories

(1)

DISS. ETH NO. 27036

Path Integral Methods in Quantum Rate Theories

A thesis submitted to attain the degree of DOCTOR OF SCIENCES of ETH ZÜRICH

(Dr. sc. ETH Zürich)

presented by

MANISH JUNG THAPA

M.Sc. ETH in Physics born on 02.02.1991

citizen of Nepal

accepted on the recommendation of Prof. Dr. Jeremy O. Richardson, examiner Prof. Dr. Philippe H. Hünenberger, co-examiner

Prof. Dr. Jiri Vanicek, co-examiner

2020

(2)

(3)

Declaration of Authorship

I, Manish J.Thapa, declare that the work presented in this thesis titled “Path Integral Methods in Quantum Rate Theories” are my own. I confirm that:

• Where I have used the work of others, the source is clearly cited.

• Where the results are produced in collaboration with coworkers or external re- searchers, the credit is duly given.

A part of the work presented in this thesis has been published in:

• M. J. Thapa, W. Fang, and J. O. Richardson. "Nonadiabatic quantum transition- state theory in the golden-rule limit. I. Theory and application to model systems." J. Chem. Phys. 150, 104107 (2019).

• W. Fang, M. J. Thapa, and J. O. Richardson. "Nonadiabatic quantum transition- state theory in the golden-rule limit. II. Overcoming the pitfalls of the saddle- point and semiclassical approximations."J. Chem. Phys. 151, 214101 (2019).

• C. L. Vaillant, M. J. Thapa, J. Vanicek, and J. O. Richardson. "Semiclassi- cal analysis of the quantum instanton approximation." J. Chem. Phys. 151, 144111, (2019).

(4)

(5)

Acknowledgements

I am grateful for the support of my wife throughout the course of writing this thesis.

I am thankful for my family and friends for creating a positive atmosphere around me during my time at ETH Zürich. I acknowledge the guidance given by my super- visor Jeremy O. Richardson to successfully complete the projects presented here. My research at ETH Zürich was financially supported by an ETH Zürich Research Grant.

(6)

(7)

In this thesis, we propose path integral approaches to include nuclear quantum effects such as tunneling, delocalization and zero point energy in a chemical simulation. Our methods exhibit a strong connection to semiclassical instanton (SCI) theory, which has been rigorously derived from first principles. SCI theory relies on computing the quantum mechanical rate constant by making a steepest-descent approximation for the quantum Boltzmann operator. However, our methods go beyond the semiclassical approximation, and evaluate this operator exactly by sampling over instanton-like paths and other paths in its vicinity. This allows us to treat systems with strong anharmonicity where zero-frequency modes cause higher-order quantum fluctuations to dominate the reaction rates.

We present a set of methods to treat reactions characterized by asymmetric barriers at high and low temperatures for a challenging set of system parameters. Two of the methods are inspired by quantum transition-state theories, and include constraint functions in their formulations to enforce sampling of dominant tunneling paths. The final approach relies on evaluating the rate constant by the method of saddle-point approximation along the time variable. All these methods can be evaluated using path integral Monte Carlo or molecular dynamics techniques, and applied to compute the reaction rates in complex systems.

Our approach to treat chemical reactions in the nonadiabatic limit has the correct classical limit, and is exact for a system of many crossed linear potentials. The method is tested on a wide variety of model systems, and predicts excellent rates even deep in the tunneling regime. A particularly appealing feature of this approach is that it is able to accurately describe the inverted regime of the spin-boson model without resorting to numerical extrapolation techniques. The method has also been applied by coworkers to study electron-transfer reactions in the aqueous ferrous-ferric system, where its spin-boson nature was confirmed in the classical limit. Likewise, our methods developed to treat reactions in the Born-Oppenheimer regime show a similar level of accuracy in predicting rates where nuclear quantum effects are seen to play a significant role. We show that, for example, our quantum instanton approach outperforms SCI theory in computing accurate rates for an asymmetric Eckart barrier.

In presenting the theory and results for these methods, we also demonstrate that some of the other well-established methods that rely on the saddle-point approximation to evaluate the time correlation function break down in certain important regimes of chemical reactions. The deficiencies in these methods are explained and contrasted against our approaches.

(11)

Zusammenfassung

In dieser Doktorarbeit stellen wir Pfadintegralansätze vor, um nukleare Quanten- effekte wie Tunneleffekte, Delokalisierung und Nullpunktsenergie in eine chemische Simulation einzubeziehen. Unsere Methoden weisen eine enge Verbindung zur semik- lassischen Instanton-Theorie (SCI) auf, die strikt von ersten Prinzipien abgeleitet wurde. Die SCI-Theorie stützt sich auf die Berechnung der quantenmechanischen Geschwindigkeitskonstante, indem sie eine Näherung des steilsten Abstiegs für den Quanten-Boltzmann-Operator erstellt. Unsere Methoden gehen jedoch über die SCI- Näherung hinaus und beschreiben die exakte Auswertung dieses Operators durch Sampling von instanton-ähnlichen Pfaden sowie von anderen Pfaden in seiner Umge- bung. Dies erlaubt uns, Systeme mit starker Anharmonizität zu behandeln, bei denen Nullfrequenzmodi dazu führen, dass Quantenfluktuationen höherer Ordnung bei den Reaktionsraten vorherrschen.

Wir stellen eine Reihe von Methoden zur Behandlung von Reaktionen vor, die durch asymmetrische Barrieren bei hohen und niedrigen Temperaturen gekennzeich- net sind, und zwar für einen anspruchsvollen Satz von Systemparametern. Zwei der Methoden sind von Quanten-Übergangszustandstheorien inspiriert und enthal- ten in ihren Formulierungen Zwangsfunktionen, um das Sampling dominanter Tun- nelwege zu erzwingen. Der endgültige Ansatz beruht auf der Auswertung der Geschwindigkeitskonstante durch die Methode der Sattelpunktsnäherung in Zeitvari- ablen. Alle diese Methoden können unter Verwendung von Pfadintegral-Monte-Carlo- oder Molekulardynamik-Techniken ausgewertet werden und werden zur Berechnung der Reaktionsgeschwindigkeiten in komplexen Systemen herangezogen.

Unser Ansatz zur Behandlung chemischer Reaktionen im nichtadiabatischen Grenzbereich zeigt die korrekte klassische Grenze und ist genau für das mehrdimen- sionale System gekreuzter linearer Potentiale. Diese Methode wird an einer großen Anzahl von Modellsystemen getestet und sagt für diese Systeme selbst tief im Tunnel- bereich ausgezeichnete Raten voraus. Eine besonders ansprechende Eigenschaft dieses Ansatzes ist, dass er in der Lage ist, das invertierte Gebiet des Spin-Boson-Modells genau zu beschreiben, ohne auf numerische Extrapolationstechniken zurückgreifen zu müssen. Die Methode wurde von unseren Mitarbeitern auch zur Untersuchung von Elektronentransferreaktionen in einem wässrigen Eisen(II)-Eisen(III)-System ange- wandt, wo sie den Spin-Boson-Charakter dieses flüssigen Systems im klassischen Grenzbereich bestätigte. Ebenso zeigen unsere Methoden, die zur Behandlung von Reaktionen im Born-Oppenheimer-Bereich entwickelt wurden, ein ähnliches Maß an Genauigkeit für Reaktionen, bei denen nukleare Quanteneffekte eine bedeutende Rolle

(12)

asymmetrischen Eckart-Barriere übertrifft. Indem wir die Theorie und Ergebnisse für diese Methoden vorstellen, zeigen wir auch, dass einige der anderen gut etablierten Methoden, die sich auf die Sattelpunktsnäherung stützen, um die quantenmechanische Zeitkorrelationsfunktion zu bewerten, in bestimmten wichtigen Bereichen chemischer Reaktionen zusammenbrechen. Die Unzulänglichkeiten dieser Ansätze werden erklärt und unseren Ansätzen gegenübergestellt.

(13)

1

Chapter 1

Introduction

This work presents novel methods to include nuclear quantum effects in chemical reaction rate calculations. Some reactions proceed classically in which the classical statistical mechanics correctly captures the dominant reaction mechanisms. Other reactions require treating the reacting particles quantum mechanically, where quantum effects such as tunneling, delocalization and zero-point energy dominate the rates.

Chemical reactions in which the electronic and nuclear degrees of freedom are separated rely on the Born-Oppenheimer approximation to compute the rate constants.

On the other hand, reactions taking place in the Fermi’s golden rule regime assume that the electronic and nuclear motions are coupled, and hence a simulation requires inclusion of at least two electronic states.

Development of rate theories is instrumental in treating, for example, electron transfer (ET) reactions that govern many relevant physical and chemical processes.

For instance, important cellular activities such as respiration and photosynthesis rely on chains of electron-transfer reactions [1, 2]. Other areas of relevance for a unified theory of charge transfers include quantitative understanding of rust formation on metal surfaces, semiconductor technology in which the operation principles of new- generation electronics critically rely on the efficiency of charge transfers, or super- conducting quantum circuits where tunneling of Cooper pairs of electrons across a Josephson junction plays a key role in quantum information processing [3]. System- atic understanding of ET processes occurring over a range of time scales, from the Born-Oppenheimer to the golden rule regime, allows one to gain invaluable insights into the mechanisms underlying these useful reactions.

The Born-Oppenheimer approximation is one of the simplest approximations used to describe the internal states of atoms and molecules involved in a chemical reaction.

Under this approximation, the motion of nuclei is limited to a single ground adiabatic potential energy surface. This category of reactions requires that a position space dividing surface separates the reactants from the products. On the other hand, Fermi’s golden rule is based on the assumption that at least two electronic states partake in a given chemical reaction [4, 5]. These electronic states are weakly coupled such that it becomes sufficient to treat the reaction perturbatively up to second order in∆(x), the electronic coupling strength which generally depends on the nuclear position, x. In this limit, the electronic states naturally distinguish the reactants from the products.

(14)

In both the adiabatic and nonadiabatic limits, it is seen that nuclear quantum effects such as tunneling and delocalization play a key role. For light atoms at low temperatures, the nuclei rearrange via tunneling, speeding up the reactions by several orders of magnitude. Hence there is a need for a rate theory that is able to accurately account for nuclear quantum effects in the calculations of the rate constants in these two limits. This chapter reviews a variety of classical, quantum and semiclassical methods used to study chemical reactions in both the adiabatic (Born-Oppenheimer) and nonadiabatic (Fermi’s golden rule) limits. In doing so, a particular emphasis is placed on similarities and differences of the rate expressions obtained in these two regimes.

1.1 Classical rate theory

One useful approach to study ET reactions is by use of theoretical tools that rely on classical mechanics. The famous Marcus theory (Nobel prize in chemistry in 1992) was the first of its kind to accurately describe ET reactions for classical systems in the golden rule regime [6, 7]. When the electrons transfer from a donor to an acceptor molecule, the solvent nuclei around these chemical species reorganize themselves as a result of thermal fluctuations. Marcus theory relies on the assumption that the motion of the solvent nuclei are dictated by classical statistical mechanics. In addition, the free-energy of the reaction is treated harmonically, in which the nuclei are assumed to obey Gaussian statistics. It is almost as if the nuclei were connected by harmonic springs, and move according to Hooke’s law. As such, the reactant and product free- energies are described by a set of parabolas, each having a fixed equilibrium position at their minima. The Marcus rate decays exponentially with the activation energy, and is given as ^∆²

~

qπβ

λ e^−β(λ−)²^/4λ, where λ and are the nuclear reorganization energy and the thermodynamic driving force of the system, respectively. One obtains the Marcus rate expression only for a harmonic system by taking the classical limit of the instanton rate, which is derived rigorously by using the method of steepest- descent integration to evaluate the exact rate of Eq. (1.1) [8]. For a more general anharmonic system, the classical rate in the golden rule limit is given by the Landau- Zener (LZ) formula [9]. On the other hand, Eyring’s transition-sate theory (TST) is employed to treat chemical reactions in the Born-Oppenheimer regime [10]. It gives a good approximation to the classical rate at high-temperatures. Like Marcus theory, TST also depends exponentially on the activation energy, V^‡, via a simple formula,

1 2πβ~

Z^‡

Zre^−βV^‡, where Z^‡ and Zr are the total partition functions of the transition- state and reactants, respectively. The theory assumes that the reactants turn into the products at the bottle-neck region, which is commonly known as the transition state. This is the point of maximum potential. It also assumes that the motion along the reaction coordinate can be separated from other orthogonal modes and is treated classically. It sets an upper-bound for the true classical rate, and relies on a number of other important assumptions. For instance, the recrossing of the classical trajectory

(15)

1.2. Quantum rate theory 3 through the dividing surface is neglected. In addition, just as in Marcus theory, the nuclear quantum effects such as tunneling are ignored [11].

Both the classical rate theories ignore nuclear quantum effects, and suffer from their reduced accuracy at low temperatures. Therefore, there is a need for a rate theory that accounts for nuclear quantum effects at this regime. We now turn to exact quantum methods used to include tunneling contributions in a chemical simulation.

1.2 Quantum rate theory

One uses the Miller-Schwarz-Tromp formula to calculate the quantum rate constants as [12],

kZ_r= 1 2

Z ∞

−∞

Tr

Fˆ₁e^{i ˆ}^H/~ ^−t+iτ

Fˆ₂e^{−i ˆ}^H/~ ^−t−i(β~^−τ) dt, (1.1) where Fˆ1 and Fˆ2 are the flux operators and τ is the imaginary-time length of a path. Note that the exact rate in Eq. (1.1) is independent of one’s choice ofτ, which typically falls in the strip[0, β~]in the normal regime [12]. In the adiabatic limit, the flux operator is given by

Fˆj = 1 2m

δˆjpˆ+ ˆpˆδj

, (1.2)

wherem is the mass of particle andδ_j =δ(ξ_j(ˆx)), whereξ_j is the dividing surface for j∈ {1,2}. In the nonadiabatic limit, these operators are projection operators defined by

Fˆ_j = i∆

~

(|0i h1| − |1i h0|), (1.3)

where∆is the coupling constant between the electronic states |0i and |1i. For sim- plicity, we assume that it is independent of nuclear coordinates, which is known as the Condon approximation.

Fermi’s golden rule is used to compute the rate of thermally activated population transfer from a quantum state|0ito another quantum state|1i by treating the exact rate in Eq. (1.1) perturbatively up to second-order in∆[4]. This is the nonadiabatic limit. On the other hand, in the adiabatic limit, one considers the motion of nuclei just on the ground adiabatic potential energy surface. In both cases, the reaction occurs when the transition from the reactant state to product state obeys the energy conservation principle. This can be clearly seen when one treats the exact rate equivalently in the time-independent picture using the relatione^{−i ˆ}^Ht^c^/^~=R∞

−∞e^−iEt^c^/^~δ(E−H)dEˆ in Eq. (1.1) wheretc=t−iτ. With this substitution one can identify a new quantity in our rate expression,P(E) = ¹₂(2π~)²trFˆ₁δ(E−H) ˆˆ F₂δ(E−H)ˆ

[12]. This is known as the reaction probability, which is the central quantity of interest in scattering theory. The rate can then be obtained exactly by Boltzmann-averaging this quantum

(16)

mechanical trace for all allowed energies, E, of the system. However this approach relies on the fact that the internal states of the reacting particles are knowna priori.

One can obtain the vibrational states of small systems by solving the Schrödinger equation, and hence a full quantum solution to the problem is available. Unfortu- nately the problem of rate calculation becomes immediately intractable for larger systems in the condensed phase as the number of basis sets required to converge the rate calculations grow exponentially with the degrees of freedom. Hence one resorts to approximate methods which has a better scaling with the system-size.

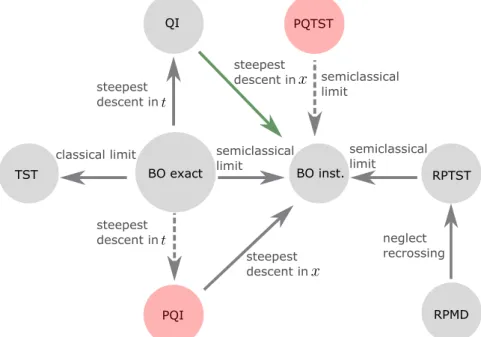
BO inst.

PQTST

RPMD RPTST BO exact

PQI QI

TST

steepest descent in

semiclassical limit

classical limit

neglect recrossing steepest

descent in steepest descent in steepest

descent in

semiclassical limit

Figure 1.1: Flow chart connecting various rate theories to each other in the Born-Oppenheimer (BO) regime. The solid-black arrows indicate that rigorous proofs connecting two given approaches are available; the dashed-black arrows indicate that there is still some room to obtain rigorous derivations connecting the two methods; and the solid-green arrow indicates that the connection between the two rate theories is true only in certain limits. Note that the rate theories cir- cled in red were discovered during the author’s doctoral studies, and

are the central topics of this thesis.

1.3 Approximate path integral rate theories

There are a number of approximate methods developed to compute rates that strive to demonstrate a good balance between computational complexity and accuracy. Some of these methods are inspired by the path integral formulation of quantum mechanics. Semiclassical instanton theory is a powerful path integral approach which can be rigorously derived by taking the asymptotic limit~→0 for the exact flux-flux correlation function, both in the adiabatic and nonadiabatic limits [13, 8]. The instanton approach to treat the problem of barrier penetration in quantum mechanics was first introduced by Sidney Coleman to tackle similar problems in quantum field theory [14,

(17)

1.3. Approximate path integral rate theories 5

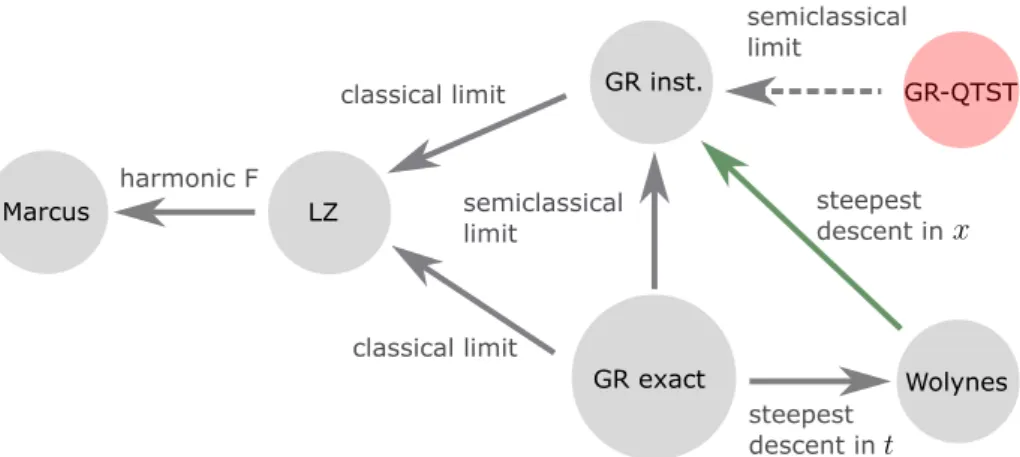
GR inst. GR-QTST

GR exact

Wolynes

LZ semiclassical

limit classical limit

steepest descent in

semiclassical limit

classical limit Marcus

harmonic F

Figure 1.2: Flow chart connecting various rate theories to each other in the golden rule (GR) regime. The colors represent the same meaning as in Fig. 1.1. GR-QTST was discovered during the author’s doctoral

studies.

15]¹. This approach relies on the optimization of a single tunneling pathway which dominates the rate expression in Eq. (1.1). One derives instanton rate theory by evaluating the exact rate integral by the method of steepest-descent in coordinate variables as well as in the time variable. In TST and Marcus theory, we noted that the rate formulae are proportional to e^−βV^‡. On the other hand, the resulting rate formula under the instanton formalism is proportional to the exponential of negative action, S[˜x(τ)], where x(τ˜ ) is a periodic orbit in imaginary-time,τ, known as an instanton.

The instanton method makes harmonic approximations for the quantum fluctuations, and has been successfully applied to compute the quantum mechanical rate constants for a variety of complex systems [16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26]. The Fermi’s golden rule instanton approach has also recently been extended to successfully treat reactions in the Marcus inverted regime, making it a viable approach to compute electron-transfer rates in a variety of molecular systems in this regime [27].

However, it is seen that the instanton approach breaks down in systems where the normal modes of the instanton exhibit frequencies close to zero. This is clearly a typical case for reactions demonstrating large anharmonicities in their potential energy surfaces. In addition, in the condensed phases, where many transition-states exist close to each other in position space, the instanton method fails as the individual steepest-descent curves overlap with each other, and does not resemble a Gaussian function of configuration variables, as is required by the instanton approximation.

Hence, new rate theories inspired by the path integral approaches are required in the two limits to accurately treat chemical reactions in solution.

A successful approach to treat reactions in the aqueous environment in the adiabatic limit is ring polymer molecular dynamics (RPMD) [28, 29]. It has been shown that this method is connected to the "ImF" approximation of semiclassical instanton theory, and hence predicts accurate rates for asymmetric barriers at low temperatures

1The nomenclature "instanton" is known to have been introduced by the Dutch theoretical physi- cist Gerard t’ Hooft [14].

(18)

[17]. RPMD relies on the solutions of classical equations of motion in the extended phase space to approximate the quantum mechanical flux-side correlation function, which defines the rate constants in its long-time limit. A TST version of RPMD has also been obtained, which is called RPTST [30]. RPTST is seen to give good approximation to the RPMD rate, but neglects recrossing effects. Harmonic RPTST (h-RPTST) is another approach related to the instanton method, and is obtained by evaluating RPTST expression by the method of steepest-descent integration. It is remarkable that the h-RPTST rate is seen to be equivalent to the instanton rate just below the cross-over temperature [17], demonstrating a deeper connection between these two approaches. A simple interpolation formula has also recently been proposed to successfully estimate rates for a general nonadiabatic reaction by interpolating the results from separately computed RPMD and Wolynes theory rates [31]. The formula has been shown to be accurate in the spin-boson model for challenging sets of system parameters. In the adiabatic limit, the interpolation formula is equivalent to Born- Oppenheimer RPMD, whereas in the nonadiabatic limit, it reduces to Wolynes theory, which has been demonstrated to predict accurate Fermi’s golden rule rates both in normal and inverted regime of multidimensional spin-boson model [32]. However, this approach does not provide mechanistic insights about chemical reactions occurring in the regime of intermediate coupling strengths, which is a desirable feature of a successful rate theory.

Other approaches exist that make use of path integral techniques to calculate rates for a general coupling strength, ∆, but have their drawbacks. For example, attempts have been made to use an isomorphic Hamiltonian with mixed quantum classical (MQC) method such as Tully’s surface-hopping to include nuclear quantum effects in a nonadiabatic simulation to extract the rates [33]. The resulting theory is called isomorphic RPMD, which is designed to treat general ET reactions and allows for an arbitrary coupling strength between reactant and product electronic states.

However, it has recently been shown that this approach fails to capture the Marcus turnover at low temperatures, underpredicting the rates in the symmetric case and overpredicting it in the activationless case for a spin-boson model [34]. The observed degraded accuracy is due to the fact that the isomorphic-RPMD rate formula fails to sample the dominant reactant and product paths which obey the energy conservation principle. Nonetheless, this method correctly recovers the Marcus rate in the classical limit, and is seen to be accurate for systems in the adiabatic limit as it reduces to the Born-Oppenheimer RPMD in the case of ∆ 1. A related method called KC- RPMD introduces a constraint functional in its rate expression to sample the dominant tunneling paths contributing to the rate [35]. The constraint is based on the centroid of a path, and as a result the KC-RPMD rate expression does not precisely capture tunneling mechanisms in asymmetric reactions. In addition, this approach is based on the sampling of real-time paths, and is thus a dynamical method. It is also worth noting that KC-RPMD is seen to perform poorly even for model systems exhibiting symmetric potential energy surfaces [36]. Approaches such as Wolynes theory in the

(19)

1.4. Summary 7 nonadiabatic limit [5] and quantum instanton (QI) approximation in the adiabatic limit [37] use a second-order cumulant expansion in time variable to approximate Eq. (1.1) to make it possible for the evaluation of the quantum rate expression using imaginary-time path integral approach. However, as shall be demonstrated in this thesis later, both these methods break down in certain regimes of ET reaction for a variety of reasons, predicting rates that are orders of magnitude different from the exact calculations.

A new approach called non-adiabatic quantum instanton (NAQI) has been recently proposed to calculate rates for systems with two electronic states, where the coupling constant between them is allowed to take an arbitrary value [38]. This new method utilizes a projection operator which is a linear combination of the projection operators employed by Wolynes theory and our projected quantum instanton (PQI) approach.

With the generalized projection operator, the rate is obtained via the second-order cumulant expansion of the NAQI correlation function, in a very similar manner to Wolynes theory and PQI approach. This method has been tested in an exponential curve crossing problem, and is found to perform excellently at a wide range of electronic coupling strengths at high and low temperatures. It clearly reduces to Wolynes theory in the nonadiabatic limit and to the PQI approach in the adiabatic limit by construction. However, like in Wolynes theory, there is a danger that this method will suffer in treating electron transfer reactions occurring at high temperatures or when the potential energy surfaces exhibit several nonadiabatic transitions. Similarly, in the adiabatic limit, due to its difficulty in locating the optimal dividing surfaces for higher dimensional systems, NAQI suffers as any conventional QTST-like approaches do in estimating the reaction rates.

We are therefore looking for rate theories that take inspiration from classical transition-state theory, and are simple to implement for atomistic potentials. The quantum version of transition-state theory we shall present in this thesis will not require sampling of real-time trajectories; will rely only on imaginary-time paths that resemble an instanton configuration; and include a generic form dividing surface in its formulation. We therefore propose a number of quantum transition-state theories (QTSTs) in the adiabatic and nonadiabatic limit that is applicable to treat reactions in solution. These methods are not based on a saddle-point approximation in either the coordinate variable or the time variable (or both), and are derived by connection to instanton theory, which itself is rigorously derivable from first principles.

1.4 Summary

As shown in Fig. 1.1 and Fig. 1.2, a variety of rate theories have been developed over the years to compute chemical reaction rate constants [39, 40, 41, 17, 42, 43, 44, 37, 45]. Some rely on semiclassical approximations to the exact rate expression, while others resort to path integral sampling techniques to account for anharmonicities in the potential energy surfaces, and take more of a quantum approach to calculating

(20)

the rate constants. One pressing challenge that chemists face today is to calculate the rates for reactions taking place in solution, where multiple transition states exist.

Approaches like RPMD are able to perform accurate rate calculations for a variety of reactions occurring in solution in the adiabatic limit. However, there is a hole in the currently available theoretical techniques to treat condensed-phase chemical reactions in the nonadiabatic limit. A new approach called the Linear Golden Rule (LGR) approximation has been recently discovered by Manolopolous and coworkers to treat ET reaction in condensed phases in the nonadiabatic limit. This approach shows excellent results in model potential surfaces such as spin-boson system and anharmonic system, and is designed to treat multidimensional ET reactions. However, the method is not derived by connection to the instanton theory and hence may suffer from reduced accuracy at very low temperatures and in complex systems where the instanton is curved. This work presents a set of quantum transition-state theories inspired by path integral approach to treat chemical reactions in aqueous environment in the adiabatic and nonadiabatic limits. All of the new methods derived in this work are done so by connection to the semiclassical instanton theory. Two quantum transition-state theories will be presented, both of which shall rely on imaginary-time path integral sampling approach, uses properties of only the quantum Boltzmann operator and share a lot of similarities in their formulation. In these approaches, the transition-state sampling will be made possible by introducing a specially-chosen constraint in their rate formulations which allows for the sampling of the instanton and relevant fluctuations around it. In addition, taking inspiration from Wolynes’

quantum instanton approach, we also present a variant of quantum instanton method (applicable in the adiabatic limit) called projected quantum instanton (PQI) which is found to be more accurate than the semiclassical instanton theory in treating reactions characterized by asymmetric barriers.

(21)

9

Chapter 2

Instanton Approach to Rate Theory

In this chapter, we will introduce path integral formalism of quantum mechanics, and demonstrate how it can be used effectively to compute chemical reaction rate constants. To motivate the formalism, we shall first discuss the Schrödinger equation which is a wave equation used to obtain the time-dynamics of Hamiltonian systems exhibiting quantum phenomena. These exact simulations rely on diagonalization of the system Hamiltonian which is difficult to perform for large systems. This difficulty has inspired path integral approaches, which offer a viable route to study complex reactions [46, 47, 48]. Some of these approaches can be obtained in the asymptotic limit

~→0 of quantum dynamics, which is determined by the corresponding Hamiltonian operator. In thinking about this, we will review instanton theory, which is a successful path integral approach used to treat chemical reactions in complex multidimensional systems with fewer computational resources [8, 13, 30]. In this section, we will demonstrate the accuracy of this theory with example calculations for rates performed on model systems, and motivate the development of novel quantum approaches which go beyond the semiclassical approximations employed by the instanton theory to describe complex reactions in condensed phases.

2.1 Quantum dynamics

We shall begin the discussion in this section by describing the exact approach to obtain the equations of the motion of a quantum system. Solutions of the Schrödinger equation exactly defines the dynamics of a quantum particle [49]. It is a linear partial differential equation, which is most generally written as,

i~∂ψ(x, t)

∂t = ˆHψ(x, t), (2.1)

where~is the reduced Planck’s constant,ψ(x, t) is the wavefunction of the system at a certain positionx and time tand Hˆ is the Hamiltonian operator defined by,

(22)

Hˆ = pˆ²

2m + ˆV , (2.2)

and where m is the mass of the particle, Vˆ is the potential energy operator, and ˆ

p = −i~_∂x^∂ the particle momentum. Hˆ is a Hermitian matrix, and hence has real eigenenergies. IfVˆ is time-independent, the solution of Eq. (2.1) is given by,

|ψ(t)i= ˆU(t)|ψ(0)i, (2.3) whereUˆ(t) = e^{−i ˆ}^Ht/^~ and hx

ψ(t)i =ψ(x, t). Note that if Vˆ is time-dependent, one replaces the unitaryUˆ(t)by a Dyson series, as Hamiltonians at different times do not generally commute with each other. Since all of the dynamics of the quantum system in this work are governed by time-independent potential, we shall not need to consider the Dyson series. For simple problems, such as those posed by a particle moving in the well-known model landscape of a two-dimensional Müller-Brown potential surface (as shown in Figure. 2.1) [50], the Schrödinger equation is solvable using easy numerical techniques such as the split-step Fourier approach. Using this approach, the time dynamics of the initial Gaussian wavepacket (shown in the left panel of Figure. 2.1) is obtained by alternately propagating it in real space and Fourier space.

Initially, at time t= 0, the wavepacket is near one of the local minima (reactant) of the Müller-Brown potential. At some later time, the wavepacket moves towards the global minimum (product) of the surface, and hence we say that at this point a chemical reaction has taken place. It should be remarked that since the evolution operator is a unitary matrix, it preserves the inner products, and hence the norm of the wavefunction at different times remain constant.

In general, though, one obtains the solution of Eq. (2.3) numerically by exact diagonalization of the system Hamiltonian. However, with each additional degrees of freedom, the size ofHˆ grows exponentially, and simulating time-independent Hamil- tonian dynamics by the method of exact-diagonalization becomes rapidly infeasible on a classical device. This motivates approximate approaches based on path integrals which have batter scaling with the system size, and can be generalized in a straightforward way to treat realistic multidimensional systems [47].

In path integral quantum mechanics, instead of working with states and wavefunction to describe the motion of a quantum system, one conveniently works with paths and trajectories the system takes in the course of the unitary evolution. This forms the basis of path integral formulation of quantum mechanics, which was introduced by Richard Feynman [47]. Under this formalism, one utilizes the quantum mechanical kernelK(x0, x, t) to obtain the quantum amplitude for a particle to travel from positionx₀ to x in time t. To this end, the solution of Eq. (2.1) can be equivalently written in terms ofK(x0, x, t) as,

(23)

2.1. Quantum dynamics 11

Figure 2.1: The figures show the dynamics of two dimensional wavepacket on a Müller-Brown potential energy surface. On the left, the wavepacket at t = 0is initialized as a two-dimensional Gaussian function. An initial momentum kick is given to this wavepacket, and it unitarily evolves in time, changing its amplitude and shape in a rather

complicated fashion, as can be seen in the right panel.

hx

ψ(t)i= Z

hx

Uˆ(t)|x₀ihx₀|ψ(0)idx₀ (2.4)

= Z

K(x₀, x, t)hx₀|ψ(0)idx₀, (2.5) where an identity operatorR

|x₀ihx₀|dx₀ = I has been inserted in Eq. (2.5). Rather than propagating the particle in one go for timet, one can also perform the propagation in tiny time steps of,N times such that t=N . After insertingN complete sets of orthonormal states into Eq. (2.4), and propagating the particle fromx0 to x in small steps ofrepeatedly, one receives the following for the quantum mechanical kernel,

K(x₀, x_N, t) =hx_N

Uˆ(t)|x₀i (2.6)

= Z

. . . Z

. . .hx_N

Uˆ()|x_N₋₁ihx_N−1

. . .|x₁ihx₁

Uˆ()|x₀idx1. . .dxN−1, (2.7) where we have slightly misused the notation, and changed x to xN. One then uses Lee-Trotter splitting to decouple the kinetic and potential term of the Hamiltonian, and the approximation for the time-evolution operator in the first time segment, , becomes

hx_n+1

Uˆ()|x_ni ≈ hx_n+1

e^{−i ˆ}^{V /2~}e⁻ⁱ^p^ˆ

2

2m/~e^{−i ˆ}^{V /2~}|x_ni (2.8) The potential term of Eq. (2.8) can be treated easily in position basis, as it diagonalizes Vˆ. However, one requires a small mathematical excursion to treat the kinetic term,

(24)

which can be done using the free particle result,

hx_n+1|e⁻ⁱ^p^ˆ

2

2m/~|x_ni= Z

hx_n+1|pie⁻ⁱ^p

2

2m/~hp|x_nidp (2.9)

= r m

2πi~e^im(xⁿ⁺¹^−xⁿ⁾²^/2^~, (2.10) where we have made use of the identity hx|pi= ^√¹

2π~

Re^ixp/^~dp. Using Eq. (2.6) and Eq. (2.8), one obtains a path integral discretization of the quantum mechanical kernel K(x₀, x_N, t) as,

K(x₀, x_N, t) = m 2πi~

N/2Z

· · · Z

e^{i ¯}^S^t^(x⁰^,x¹^,...,x^N−1^,x^N^)/^~dx₁. . .dxN−1, (2.11) whereS¯tis the action of a real-time path, which is defined as,

S¯t(x0, x1, . . . , xN−1, xN) =

N−1

X

i=0

m(xi+1−xi)²

2 −

2V(x0)−

N−1

X

i=1

V(xi)−

2V(xN).

(2.12) In the limit whenN → ∞,K(x0, xN, t)becomes a path integral, which is written as follows:

K(x₀, x, t) =

Z _x(t)=x_N

x(0)=x0

e^{i ¯}^S^t^[x(t)]/^~Dx(t). (2.13) ThereforeS¯t(x0, x1, . . . , xN−1, xN) is a finite-difference approximation toS¯t[x(t)], and the two are equivalent in the limit of N → ∞. The integral of Eq. (2.13) can be evaluated along an open path x(t), with boundary conditions x(0) = x0 and x(t) =x_N. The action along this path in the limit of→0 is given by,

S¯t[x(t)] = Z t

0

(1 2m

dx(t⁰) dt⁰

2

−V[x(t⁰)]

)

dt⁰. (2.14)

Eq. (2.14) is the time integral of the Lagrangian, and is well defined for paths which are bounded in the space of coordinate and time variables.

2.2 Quantum statistics

In quantum statistical mechanics, the Boltzmann distribution,e^−β^H^ˆ, gives the probability that a quantum system is in certain state in thermal equilibrium at a particular reciprocal temperatureβ = 1/k_BT [51]. e^−β^H^ˆ can be obtained following an identical derivation but by replacing t → −iβ~ in quantum propagator e^{−i ˆ}^Ht/^~. Therefore,

(25)

2.2. Quantum statistics 13 the Boltzmann operator is also known as the imaginary-time propagator. The matrix elements of this operator are,

ρ(x₀, x_N) = mN 2πβ~²

N/2Z

· · · Z

e^−S^β^~^(x⁰^,x¹^,...,x^N−1^,x^N^)/~dx₁. . .dxN−1, (2.15) where we have sett→ −iβ~and→ −iβ~/N in the quantum propagator [Eq. (2.11)].

The path contributing to the integral of Eq. (2.15) begins and ends at different points in the coordinate space, and is an open path. S_β_~ is also known as the Euclidean action, and is a function of spatial coordinates and imaginary timeβ~. This quantity is defined as,

Sβ~(x0, x1, . . . , xN−1, xN) =

N−1

X

i=0

mN(xi+1−xi)²

2β~ + β~

2NV(x0) +

N−1

X

i=1

β~

N V(xi) + β~

2NV(xN) (2.16) In Eq. (2.16), the imaginary-time action (or the Euclidean action) is notated by removing the bar from the real-time action. The sign in front of the potential in the expression of Euclidean action is negative, indicating that quantum mechanical propagation in imaginary-time is equivalent to real-time dynamics in an inverted potential,

−V(x). In the limit ofN → ∞, Eq. (2.16) becomes a functional of an imaginary-time path traveling in timeβ~, which is defined as,

S_β~[x(τ)] = Z β~

0

(1 2m

dx(τ) dτ

2

+V[x(τ)]

)

dτ (2.17)

Using imaginary-time path integrals, equilibrium averages of quantum systems can be computed efficiently even for complex molecular systems. Importantly, one can compute quantum partition function of a chemical and physical system using discretized quantum paths. The quantum partition function is defined as the trace of the quantum Boltzmann operator as follows,

Z_r(β) = tr e^−β^H^ˆ

, (2.18)

wheretrdenotes a trace over the nuclear degrees of freedom. Eq. (2.18) can be equivalently written using the path integral representation in the following manner,

Z_r(β) = Z ∞

−∞

hx₀

e^−β^H^ˆ|x₀idx₀ (2.19)

= mN

2πβ~² N/2Z

e^−S^β~^(x⁰^,x¹^{, ... ,x}^N−1^,x⁰^)/^~dx, (2.20)

(26)

where x = {x₁, . . . , xN} are coordinates of the so-called ring polymer and cyclic indices are implied such thatx₀ = x_N. Because the partition function is a trace of Boltzmann factor, the path starts and ends at the same point in the coordinate space.

Hence, such a path is termed as ring polymer. S_β_~(x₀, x₁... xN−1, x₀) can be written compactly as,

S_β_~(x) =

N

X

i=1

1 2

mN

β~ (x_i−xi−1)²+β~ N

N

X

i=1

V(x_i) (2.21)

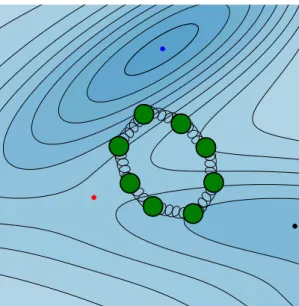
Fig. 2.2 shows one such ring polymer configuration. It is a closed polymer, which starts and ends at the same configuration point in the two-dimensional Müller-Brown potential energy surface. Each of the ring polymer bead, located atx_i, is connected to its two neighboring beads by harmonic springs [52]. The springs act in both x and y directions in this system. When mass m is large (or in the classical or high- temperature limit), the springs get stronger, and the ring polymer shrinks. However, for systems characterized by huge quantum effects, they loosen, and the ring polymer delocalizes, covering an extended space in the potential energy surface. This swelling of a ring polymer is a typical case seen in particles that tunnel through the potential barrier as is shown in Fig. 2.2, and characterizes the uncertainty in particle’s position.

Unlike Fig. 2.1 in which the probability distribution is shown to describe the quantum nature of a particle, here the coordinates of the delocalized ring polymer represents it.

A particularly remarkable feature of writing the quantum partition function in the form of Eq. (2.20) is that it can be easily evaluated in the limit of~→0. In this limit, one obtains the semiclassical approximation to Z_r. In the semiclassical limit, the multidimensional integral of Eq. (2.20) is going to be dominated by paths which are the stationary points ofS_β_~(x). Besides, in classical mechanics, it is well known that wavefunction and states do not exist, which makes it difficult to study how quantum theory reduces to the classical theory in some important limits. But when quantum expressions are written using the path integral notation, one can easily investigate its correspondence limit, a regime where action of a system is large in comparison to~.

To demonstrate the usefulness of the path integral approach to describe a system in thermodynamic equilibrium, we shall compute the partition function for a harmonic oscillator using a range of a number of ring polymer beads. We choose the frequency of the harmonic well to be ω/2πc = 500 cm⁻¹. The harmonic system is bounded from below, and one can easily use the ring polymer normal-mode transformation to obtain the exact partition function of the reactant well as Zr = [2 sinh (β~ω/2)]⁻¹ [30], which corresponds to evaluating Eq. (2.20) forN → ∞. However, for finite N, the partition function will be an approximation. The quantum Boltzmann operator is evaluated by performing Gaussian integrals over N normal modes [30]. For complex reactions in solution, this quantity can be sampled by employing the techniques which are routinely used in molecular simulations such as path integral molecular dynamics

(27)

2.2. Quantum statistics 15

Figure 2.2: Cartoon illustration of an imaginary-time path. It represents one of the quantum paths. This path is composed of many copies of a classical particle (in green). The classical beads are connected by harmonic springs. As the temperature is lowered, the necklace swells, and the quantum particle delocalizes. The potential energy landscape

is one of Müller-Brown surface.

[53, 54]. These techniques will be introduced in detail in the following chapters.

As shown in Table. 2.1, as the number of beads are increased, the partition function computed using a ring polymer gets ever-closer to the exact result. It should be noted that as the temperature is lowered, where quantum effects are conspicu- ously observed, one needs more number of ring polymer beads to converge the result to a desired accuracy. The classical partition function obtained using one bead in Eq. (2.20) overestimates the exact partition function for this system by 20 % at room temperature.

Table 2.1: Partition functions computed using Eq. (2.20) using different choices ofN for a harmonic system at room temperature.

N 1 2 4 8 16 32 ∞

Z_r 0.41702 0.35767 0.33861 0.33342 0.33209 0.33176 0.33176 The rate of a chemical reaction is proportional to the ratio of partition function at the transition state and reactant [10, 30]. Computing the partition function at the transition state is a nontrivial task. To calculate this quantity, we turn to a very powerful path integral approach inspired by the semiclassical formalism of quantum mechanics. This approach is called instanton theory, and offers insights into the tunneling mechanism of reaction at low temperature, and predicts accurate rates for a variety of systems both in the adiabatic and nonadiabatic limits. In all our approaches, we assume that forces have been made available to us by means of electronic structure calculations, and treat only the nuclear tunneling.

(28)

2.3 Rate coefficient

A plethora of approaches to treat nuclear quantum effects can be derived by employing the path integral description of quantum mechanics. One such successful method is instanton theory, which has been developed to efficiently treat reactions in both Born-Oppenheimer and Fermi’s gold rule regime [55, 8]. Instanton theory is derived by taking the semiclassical limit of the exact flux-flux correlation function in Eq. (1.1) [56]. In this method, no real-time propagation is necessary, which is extremely tedious to perform in reactions characterized by complex multidimensional potentials. The derivation of instanton expression relies on the evaluation of the multidimensional integral of Eq. (1.1) by the method of steepest-descent integration in both the coordinate and time variables. In what follows, we shall explore instanton theory in more rigor.

2.3.1 Adiabatic instantons

Instanton theory has been shown to give accurate estimates of the rate constants in multitude of symmetric and asymmetric systems characterized by atomistic potential energy surfaces. More important, it is seen to be a reliable method to elucidate the reaction mechanism. The rate constant under the instanton formalism is dominated by a single classical trajectory in imaginary-time known as the instanton. To obtain this classical trajectory, one searches for a saddle point of the Euclidean action in Eq. (2.16). The saddle point is a set of ring polymer coordinates that solves∇S_β_~(x)

= 0, where∇represents the derivative with respect to the bead positions. Such a saddle point defines an instanton configuration, and is denoted byx. Below the crossover˜ thresholdβ_c, the saddle point is delocalized¹. The ring polymer Hessian∇²S_β_~(x)˜ of the instanton configuration in the adiabatic limit has one negative eigenvalue corresponding to the reactive mode, one zero eigenvalue corresponding to the ring polymer permutation mode, and other positive eigenvalues [17, 57]. Instanton rate has been rigorously derived from first principles in Ref. [30, 55], and here we simply give the formula,

k_RPIZ_r = Λ⁻¹ β_N~

v u u t

N

X

i=1

|x_i−xi−1|²Y0 k

1 β_N~η_k

e^−S^β~^(˜^x)/^~, (2.22)

wheremη²_k are theN eigenvalues of the Hessian matrix. One of the normal modes of the ring polymer action has zero frequency, and henceη_k= 0, which has been omitted from the product in Eq. (2.22). This is signified by a prime in the formula.

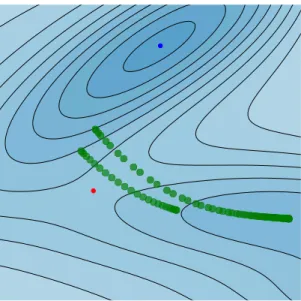
Fig. 2.3 shows two instanton trajectories overlayed onto the Müller-Brown surface at two different temperatures. At higher temperature, the instanton orbit gets shorter,

1Note thatβc= 2π/~ωb, whereiωbis the imaginary frequency of the potential energy barrier top, which can be calculated usingiωb=p

V⁰⁰(x^‡)/mandx^‡ is the location of the barrier top.

(29)

2.3. Rate coefficient 17

Figure 2.3: Two instanton trajectories (in green blobs) are shown for two different temperatures. The shorter one corresponds to high temperatureβ~ωb= 7obtained using 50 ring polymer beads, and the longer one corresponds toβ~ωb= 27obtained using 100 ring polymer beads. The quantum particle is chosen to be a Hydrogen atom of mass m = 1836me. The inverse crossover temperature for this system is βc= 143a.u. (or T = 2207 K). The system parameters were borrowed

from Ref. [50].

and the beads localize near the classical transition state (red dot). However, at lower temperature, the ring polymer stretches, and the trajectory gets longer. Note that since the ring polymer is made of copies of a classical bead, each of the bead of the instanton trajectory indicates a particular configuration of the chemical system. At the cross over inverse-temperatureβc, the ring polymer will collapse to a single bead at the transition state.

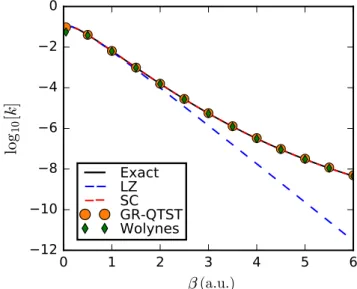
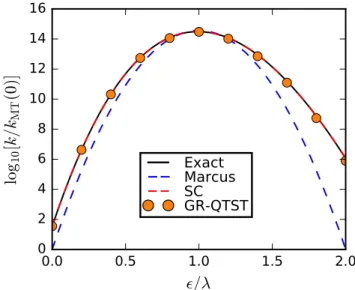
It is worth comparing the accuracy of instanton expression by computing the rates for a one-dimensional model system such as an Eckart barrier where exact rates are readily available for comparison. In this spirit, we consider the following asymmetric Eckart barrier defined by,

V(x) = (1−α)V₀

1 +e^−2ax +(1 +√ α)²V₀

4 cosh²(ax) . (2.23)

We choose the same system parameters as in Ref. [37]. The barrier height V₀ = 0.425 eV, a = 1.36 a⁻¹₀ and mass m = 1060 me (where a0 is the Bohr radius and m_e is the electronic mass). α is the asymmetry paremeter which defines the degree of exothermicity between the reactants and the products. When α = 1 the system is symmetric about x = 0. We chose an asymmetric system with α = 1.425. The reactant partition function for this system is given per unit length, and is Z_r/L = q _m

2πβ~².

Fig. 2.4 shows the Arrhenius plots of rate constants versus inverse temperature β. The exact thermal rates (indicated by black solid line) were obtained from the transmission probability defined by [58],

(30)

Figure 2.4: Arrhenius plots for various temperatures for an asymmetric Eckart system produced usingN = 200ring polymer beads. All quantities are given in atomic units. Below β = 776a.u. (crossover

inverse temperature), the instanton rate is not defined.

P(E) = 1−coshπ(δ−) + coshπζ

coshπ(δ+) + coshπζ. (2.24) whereν = 2m/a²,δ =√

νE, =p

ν(E−(1−α)V₀) and ζ =p (1 +√

α)²V₀ν−1.

One then performs the integration of this function after multiplying it by the Boltz- mann factor to give the exact rate,

kZ_r= 1 2π~

Z ∞ 0

P(E)e^−βEdE. (2.25)

As can be seen in Fig. 2.4, at lower temperatures, the instanton approximation predicts accurate rates for this system. On the contrary, the classical transition-state theory increasingly underestimates the rates for higher values ofβ, and this is due to its neglect of tunneling contributions. At the lowest temperature considered (β= 1600 a.u.), the instanton approximation shows a small error of 14 %, whereas the classical transition-state theory underpredicts the reaction rate by almost 4 orders of magnitude. It should be remarked that above the crossover temperature for this system (or β_c = 776 a.u.), the instanton theory fails to be applicable to treat the chemical reaction. This is because at high temperatures, there is only one classical path, which is over the barrier, and is not an imaginary-time trajectory anymore.

2.3.2 Nonadiabatic instantons

Instanton theory has been extended to treat reactions characterized by multiple electronic states in the golden rule regime [8, 59]. For the purpose of our discussion, we

(31)

2.3. Rate coefficient 19 consider two coupled electronic states with the associated diabatic nuclear Hamilto- nians,Hˆ₀ andHˆ₁. The total Hamiltonian of the system is therefore given by,

Hˆ = Hˆ₀

2 (I−σˆ_z) + Hˆ₁

2 (I+ ˆσ_z) + ∆ ˆσ_x, (2.26) where I is the identity and σˆx and σˆz are the Pauli spin matrices. The basis that diagonalizes σˆ_z is the electronic basis, |0i and |1i, with the corresponding nuclear Hamiltonian defined by,

Hˆn= ˆp²/2m+Vn(ˆx), (2.27) where n ∈ {0,1}, pˆis the momentum and V_n(ˆx) is the potential energy surface of then^th electronic state. In the golden rule regime, in which∆→0, the exact rate is defined as [60],

kZ_r= 2π

~ X

µν

|hν|∆|µi|²δ(E_µ−E_ν)e^−βE^µ, (2.28)

where|µiand |νi are the quantum states of nuclei with the corresponding energyEµ

andE_ν for the reactant and product states, respectively. Note that the delta function in Eq. (2.28) ensures that the reaction occurs when the reactant and product states have matching energies.

Because a nonadiabatic reaction is governed by the presence of at least two electronic states, the quantum system feels the force from both the reactant and product potential energy surfaces, and travels in these surfaces for different lengths of time.

The particle travels on the reactant surface in imaginary timeτ0 ≡τ =N0βN~ and on the product surface in imaginary timeτ₁ ≡β~−τ =N₁β_N~. The total length of this orbit isβ~. The total action along the combined pathway is given by,

Sτ(x) =Sτ0(xN, x1, . . . , xN0) +Sτ1(xN0, xN0+1, . . . , xN), (2.29) whereS_τ₀ and S_τ₁ are defined as in Eq. (2.16). For an instanton orbit, x, the paths˜ moving in the reactant and product surfaces combine at the diabatic hopping point, x^‡. At this point, the optimized locationsx˜_N₀ = ˜x_N =x^‡ andV₀(x^‡) =V₁(x^‡) in the N → ∞limit [59]. Fig. 2.5 shows a schematic of two paths that join together to form a ring polymer. Green path is on the reactant state (indicated by green contours), and the red path is on the product state (indicated by red contours). Beads 4 and 8 feel the average force of both the diabatic surfaces.

To obtain an instanton configuration for a system of crossed potential energy surfaces in the golden rule regime, one extremizesS_τ(x) simultaneously with respect to bead variables as well asτ. S_τ(x)is seen to be minimum with respect to the ring

(32)

Figure 2.5: Cartoon illustration of a ring polymer with 8 beads. 3 beads are on the reactant diabatic surface, other 3 beads are on the product diabatic surface and beads 4 and 8 are on the averages of the two diabatic surfaces. The potential energy surface (which was made by Wei Fang) has been borrowed from the model system used in Ref. [61] to test the accuracy of a novel path integral rate theory that

resulted from this thesis.

polymer bead positions, but a maximum along τ degree of freedom, making {˜x,τ˜} a saddle point of the Euclidean action. The ring polymer instanton rate in the nonadiabatic limit can be derived in the similar manner to the adiabatic case [8], and here we again just give the rate formula,

kZ_r=√ 2π~∆²

~²

β_N²~²

m ∇²S_τ(x)˜

−¹₂

− d²S_τ(˜x) dτ²

−¹₂

e^−S^τ^(˜^x)/~, (2.30) whereβN =β/N. We test the acuracy of the instanton theory in the nonadiabatic limit by considering an example system comprising of a pair of one-dimensional harmonic oscillators. The exact rate for this system can be obtained analytically as the Euclidean action is analytic for this system. The total action [Eq. (2.29)] of a classical trajectory which hops at the diabatic crossing seamx^‡ is therefore given by [8],

S(τ˜ ) =−τ+ 2mωξ²

h1−cosh (ωτ)

tanh (β~ω/2) + sinh (ωτ) i

(2.31) One can replaceτ by a complex argument τ−it, and perform the following integration numerically to obtain the exact rates for this particular system as [8],

k= ∆²

~² Z ∞

−∞

e⁻^S(τ−it)/^˜ ^~dt. (2.32)

Note that for this system, the partition function cancels exactly with the prefactor