PDDr.StephanA.B¨aurle WS2012/2013 f¨urStudierendederBiochemie,BiologieunddesLehramts(3.Semester) PhysikalischeChemieI SkriptzurVorlesung

(1)

Skript zur Vorlesung

Physikalische Chemie I

f¨ ur Studierende der Biochemie, Biologie und des Lehramts (3. Semester)

WS 2012/2013

von

PD Dr. Stephan A. B¨aurle

Skript erstellt von

M. Bernhardt, M. Hammer, M. Knorn

(2)

“Eine wirklich gute Idee erkennt man daran, dass ihre Verwirklichung von vorneherein ausgeschlossen erschien”,

Albert Einstein

(3)

Vorbemerkung

• Dieses Skript ist eine Abschrift des handschriftlichen Manuskripts “Aufschrieb PC1” der Vorlesung Physikalische Chemie I für Studierende der Biochemie, Biolo- gie und des Lehramts (3. Semester) von Priv.-Doz. Dr. Stephan A. Bäurle und dient als Begleitmaterial zu dieser Vorlesung. Es erhebt keinen Anspruch auf Vollständigkeit und kann Fehler enthalten, welche bei der Übertragung zustan- de kommen können.

• Es soll nicht als Ersatz zum Besuch der Vorlesung sowie der ¨Ubungen dienen.

• Fehler und Anregungen k¨onnen gerne unter folgenden E-mail-Adressen¹ gemeldet werden.

1stephan.baeurle@chemie.uni-regensburg.de, michaelhammer@hotmail.de

(4)

Inhaltsverzeichnis

1 Reaktionskinetik 5

1.1 Reaktionsgeschwindigkeit . . . 5

1.1.1 Konzentrationsabh¨angigkeit der Reaktionsgeschwindigkeit . . . . 6

1.1.2 Gesamt-Reaktionsordnung . . . 6

1.1.3 Umsatzvariable XA(t) . . . 6

1.2 Reaktionen 1. Ordnung in Bezug auf ein Edukt . . . 7

1.2.1 Allgemeine Formulierung . . . 7

1.2.2 Halbwertszeitt1/2 f¨ur Reaktionen 1. Ordnung . . . 8

1.2.3 Mittlere Lebensdauer τ eines Edukt-Teilchens . . . 9

1.3 Reaktionen 2. Ordnung in Bezug auf ein Edukt . . . 9

1.3.2 Halbwertszeitt_1/2 f¨ur Reaktionen 2. Ordnung in Bezug auf EduktA 10 1.4 Reaktionen der Gesamtordnung 2, jedoch jeweils 1. Ordnung in Bezug auf 2 Edukte . . . 11

1.4.2 Halbwertszeitt_1/2 (bez¨uglich Edukt A) f¨ur ungleiche Anfangskon- zentrationen . . . 13

1.5 Temperaturabh¨angigkeit der Reaktionsgeschwindigkeitskonstanten . . . . 13

1.5.1 Temperaturverhalten nach Arrhenius . . . 13

1.5.2 Moderne Gleichungen zur Beschreibung der Temperaturabh¨angigkeit der Geschwindigkeitskonstantenk . . . 16

1.6 Reaktionsmechanismus und Reaktionsordnung . . . 16

1.7 Hin- und R¨uckreaktionen 1. Ordnung (Gleichgewichtsreaktionen) . . . 17

1.8 Folgereaktionen . . . 19

1.9 Parallelreaktionen . . . 21

1.10 Folgereaktionen mit vorgelagertem Gleichgewicht und Quasistationarit¨at 23 1.11 Enzymreaktionen . . . 26

1.11.1 Michaelis-Menten-Kinetik . . . 27

1.11.2 Lineweaver-Burk-Gleichung . . . 29

1.12 Reaktionen an fester Katalysatoroberfl¨ache . . . 30

1.12.1 Fall 1: Adsorption/Desorption eines Gases A auf/von einer Kata- lysatoroberfl¨ache . . . 30

1.12.2 Fall 2: Unimolekulare Reaktion an der Katalysatoroberfl¨ache der adsorbierten Spezies . . . 33

1

(5)

Inhaltsverzeichnis 2

1.12.3 Fall 3: Bimolekulare Reaktion an der Katalysatoroberfl¨ache zwi-

schen adsorbierten Spezies . . . 34

2 Thermodynamik 39 2.1 Grundlagen und Wiederholung 1. Semester . . . 39

2.1.1 System und Umgebung . . . 39

2.1.2 Prozesse und Randbedingungen . . . 39

2.1.3 Innere und ¨außere Energie . . . 40

2.1.4 Nullter Hauptsatz . . . 41

2.1.5 Erster Hauptsatz . . . 41

2.1.6 Entropie . . . 42

2.1.7 Zweiter Hauptsatz . . . 45

2.1.8 Dritter Hauptsatz . . . 45

2.2 Gibbs’sche Fundamentalgleichungen und charakteristische Funktionen . . 47

2.2.1 Innere Energie U . . . 47

2.2.2 Enthalpie . . . 49

2.2.3 Helmholtz-Energie (freie Energie) F . . . 50

2.2.4 Gibbs’sche Energie (freie Enthalpie) G . . . 51

2.3 Thermodynamisches Gleichgewicht . . . 52

2.4 Gleichgewichte chemischer Reaktionen . . . 55

2.4.1 Gleichgewichtsbedingung und chemische Potentiale . . . 55

2.4.2 Gibbs’sche Reaktionsenergie . . . 57

2.4.3 Konzentrationsabh¨angigkeit des chemischen Potentials . . . 58

2.4.4 Thermodynamische Aktivit¨at verschiedener Stoffklassen . . . 59

2.4.5 Massenwirkungsgesetz . . . 60

2.5 Phasengleichgewichte . . . 63

2.5.1 Clausius-Clapeyron-Gleichung . . . 63

2.5.2 2-Phasen-Gleichgewichte . . . 66

2.5.3 Gibbs’sche Phasenregel . . . 70

2.5.4 Raoult’sches Gesetz . . . 71

2.5.5 Dampfdruckerniedrigung . . . 73

2.5.6 Siedepunktserh¨ohung und Schmelzpunktserniedrigung . . . 74

3 Elektrochemie 78 3.1 Elektrode (Halbzelle) . . . 78

3.2 Elektrochemische Zelle . . . 78

3.3 Galvanisches Element . . . 79

3.3.1 Physikalisch-chemische Prozesse an den Elektroden . . . 80

3.3.2 Zellspannung und elektromotorische Kraft . . . 81

3.3.3 Elektrodenpotential . . . 82

3.3.4 Elektrodenreaktion . . . 83

3.3.5 Zellreaktion . . . 85

3.4 Nernst-Gleichung . . . 86

3.5 Elektroden 2. Art . . . 88

(6)

Inhaltsverzeichnis 3

3.6 Elektrolyse-Zelle . . . 89

3.6.1 Faraday’sche Gesetze . . . 91

4 Leitf¨ahigkeit von Elektrolyten 92 4.1 Leitf¨ahigkeit . . . 92

4.1.1 Starke Elektrolyte . . . 93

4.1.2 Schwache Elektrolyte . . . 94

5 Transportvorg¨ange 96 5.1 W¨armeleitung . . . 96

5.2 Diffusion . . . 96

5.2.1 Fick’sche Gesetze . . . 96

5.2.2 Selbstdiffusion . . . 98 6 Physikalisch-chemische Konzepte in der Forschung 99

(7)

Empfohlene Literatur

1. Peter W. Atkins,

”Physikalische Chemie“, Wiley-VCH, ISBN-13:978-3527315468 2. Gerd Wedler,

”Lehrbuch der Physikalischen Chemie“, Wiley-VCH, ISBN-13:978- 3527310661

3. Wolfgang Bechmann, Joachim Schmidt,

”Einstieg in die physikalische Chemie f¨ur Nebenf¨achler“, Vieweg+Teubner, ISBN-13:978-3834806079

4. E. Zeidler,

”Teubner-Taschenbuch der Mathematik“, Vieweg+Teubner, ISBN-13:978- 3835101234

4

(8)

1 Reaktionskinetik

besch¨aftigt sich mit der Geschwindigkeit und dem Mechanismus einer Reaktion.

Aus kinetischen Messdaten werden ph¨anomenologische Geschwindigkeitsgesetze aufgestellt.

Chemische Reaktionsgleichung (allg. Form):

ν_AA+ν_BB+..→ν_PP +ν_QQ+..

mit A, B,.. = Ausgangsstoffe (Edukte)b

νA, νB..>0 = st¨b ochiometrische Koeffizienten der Edukte P,Q,.. = Endstoffe (Produkte)b

νP, νQ..>0 = st¨b ochiometrische Koeffizienten der Produkte

1.1 Reaktionsgeschwindigkeit

M¨ogliche Definition:

v^? =− 1

ν_A ·dn_A

dt =− 1

ν_B · dn_B

dt =..= 1 ν_P · dn_P

dt =..

mit dn_A = ¨b Anderung der Stoffmenge n_A des Edukts A im Zeitintervall dt (dn_i mit i=B,..,P,Q,.. entsprechend)

und v^? >0.

Nachteil dieser Definition ist, dass die Reaktionsgeschwindigkeit v^? von der Gr¨oße des betrachteten Reaktionssystems abh¨angt.

5

(9)

1.1. REAKTIONSGESCHWINDIGKEIT 6

Bessere Definition: f¨ur viele Anwendungen v = v^?

V =− 1 ν_A ·

dnA

V

dt =− 1 ν_A · dcA

dt =..

mit V als Volumen des Reaktionssystems.

Vereinbarung: im Folgenden werden alle st¨ochiometrischen Reaktionsgleichungen so formuliert, dass νA = 1, d.h.

v =−dc_A dt

1.1.1 Konzentrationsabh¨ angigkeit der Reaktionsgeschwindigkeit

Es gilt der allgemeine Ansatz (hier der Edukte):

v =k·c^α_A·c^β_B·...·c^σ_S ·...

mit k = Geschwindigkeitskonstante der betrachteten Reaktionb

α = Reaktionsordnung in Bezug auf Reaktionspartnerb A (entsprechend f¨urβ, σ)

Anmerkung: α = 0 bedeutet, dass v nicht von der Konzentration des Stoffes A abh¨angt.

1.1.2 Gesamt-Reaktionsordnung

m=α+β+...+σ+..

bildet sich aus der Summe der Reaktionsordnungen aller Reaktionspartner (Edukte).

1.1.3 Umsatzvariable X

_A

(t)

Definition: Stoffmenge des Edukts Apro Volumen V, die zwischen t= 0 (Beginn der Reaktion) undt umgesetzt wird, d.h.:

X_A(t) = n_A(t= 0)−n_A(t)

V =c_A(t= 0)−c_A(t) (1.1)

mit c_A(t = 0) = Anfangskonzentration vonb A.

(10)

1.2. REAKTIONEN 1. ORDNUNG IN BEZUG AUF EIN EDUKT 7

1.2 Reaktionen 1. Ordnung in Bezug auf ein Edukt

Bei diesem Reaktionstyp ist die Reaktionsgeschwindigkeit zum Zeitpunkttproportional zur Konzentration eines Reaktionspartners zum Zeitpunktt.

Beispiele:

1. radioaktiver Zerfall (→ siehe ¨Ubungen)

2. Zerfall vieler Molek¨ule, die mehr als drei Atome besitzen, wie z.B.:

N2O5 →N2O4+1

2O2 (1.2)

Geschwindigkeitsgesetz:

v =−dc_N₂_O₅

dt =k·c_N₂_O₅

1.2.1 Allgemeine Formulierung

f¨ur den Fall, dass ein StoffAin einer Reaktion 1. Ordnung bez¨uglichc_Averbraucht wird, d.h. entsprechend der Reaktionsgleichung

A−→^k P

v =−dc_A

dt =k·c_A Integration des obigen Geschwindigkeitsgesetzes:

dc_A

c_A = d lncA=−k·dt Z lncA(t)

lncA(t=0)

d lncA=−k Z t

t=0

dt lnc_A(t)−lnc_A(t = 0) =−k·t Mit Abk¨urzung c_A(t= 0) =a ergibt sich:

lnc_A(t) = lna−k·t

Graphische Darstellung: lnc_A(t) als Funktion von t ergibt eine Gerade mit der Steigung −k und dem Ordinatenabschnitt lna.

ln

cA(t) a

=−k·t

(11)

Abb. 1.1: Konzentration des Edukts A als Funktion der Zeit im Falle einer Reaktion 0., 1.

und 2. Ordnung

Graphische Darstellung: ln (cA(t)/a) als Funktion vont ergibt eine Gerade mit der Steigung −k und dem Ordinatenabschnitt Null.

Aufl¨osen nach cA(t) liefert:

c_A(t) =a·exp(−k·t) (1.3)

Das Abklingverhalten der Konzentration von A, ausgehend vom Startwertc_A(t= 0) =a wird durch die Abklingfunktion f(t) = exp(−k·t) beschrieben, welche allein durch den Parameterk bestimmt wird (siehe Abb. (1.1)).

Beispiel Reaktionsgleichung (1.2):

c_N₂_O₅(t) = c_N₂_O₅(t= 0)·exp(−k·t)

1.2.2 Halbwertszeit t

_1/2

f¨ ur Reaktionen 1. Ordnung

Die Halbwertszeit entspricht dem Zeitintervall t_1/2, in dem die Konzentration c_A(t) auf den halben Wert abgefallen ist, wie z.B. von c_A(t = 0) =a aufc_A(t=t_1/2) = ^a₂

Allgemeiner Zusammenhang zwischen c_A(t₁), c_A(t₂) und Zeitdifferenz (t₂ −t₁) f¨ur Re- aktionen 1. Ordnung (Substraktion von integralem Zeitgesetz):

lnc_A(t₁)

c_A(t₂) =k·(t₂−t₁)

(12)

Einsetzen vonc_A(t₂) = ^c^A^(t₂¹⁾ und t₂−t₁ =t_1/2 liefert:

t_1/2 = ln 2

k ≈ 0.7 k

Hieraus l¨asst sich ersehen, dass die Halbwertszeit t_1/2 bei Reaktionen 1. Ordnung kon- zentrationsunabh¨angig ist.

1.2.3 Mittlere Lebensdauer τ eines Edukt-Teilchens

Die mittlere Lebensdauer τ eines Edukt-Teilchens ergibt sich aus den individuellen Le- bensdauern der Edukt-Teilchen τ₁, τ₂, τ₃,..., gerechnet ab dem Zeitpunkt t = 0, wie folgt:

τ = τ₁+τ₂+τ₃+..

N(t= 0)

wobei N(t=0) der Anzahl der Edukt-Teilchen beit = 0 entspricht.

F¨ur Reaktionen 1. Ordnung gilt:

τ = 1

k (1.4)

Einsetzen von Gleichung (1.4) in Gleichung (1.3) ergibt, dass zum Zeitpunkt t = τ die Anzahl bzw. Konzentration der Edukt-Teilchen auf den Bruchteil ¹_e ≈ 0.37 abgefallen ist.

1.3 Reaktionen 2. Ordnung in Bezug auf ein Edukt

Beispiel:

N O₂ →N O+ 1 2O₂ Geschwindigkeitsgesetz:

v =−dc_{N O}₂

dt =k·c²_{N O}

2

1.3.1 Allgemeine Formulierung

f¨ur den Fall, dass ein StoffAin einer Reaktion 2. Ordnung bez¨uglichc_Averbraucht wird:

v =−dcA

dt =k·c²_A

(13)

Integration des Geschwindigkeitgesetzes:

−dc_A

c²_A =−c⁻²_A ·dc_A=k·dt

− Z cA(t)

cA(t=0)=a

c⁻²_A ·dc_A=k· Z t

t=0

dt 1

c_A(t)− 1

a =k·t 1

cA(t) = 1

a +k·t (1.5)

Graphische Darstellung: _c¹

A(t) als Funktion von t ergibt eine Gerade mit der Stei- gung k und dem Ordinatenabschnitt ¹_a.

Durch Aufl¨osen von Gleichung (1.5) nach c_A(t) ergibt sich:

c_A(t) =a· 1

1 +k·a·t (1.6)

Das Abklingverhalten der Konzentration von A, ausgehend vom Startwert cA(t= 0) = a, wird durch die Abklingfunktion f(t) = _1+k·a·t¹ beschrieben, welche durch k und a bestimmt wird (siehe Abb. (1.1)) .

1.3.2 Halbwertszeit t

_1/2

f¨ ur Reaktionen 2. Ordnung in Bezug auf Edukt A

Allgemeiner Zusammenhang zwischenc_A(t₁),c_A(t₂) und Zeitdifferenz (t₂−t₁) ergibt sich durch Subtraktion von Gleichung (1.5):

1

c_A(t₂) − 1

c_A(t₁) =k·(t₂−t₁)

Einsetzen vonc_A(t₁ = 0) =a und c_A(t₂) = ^a₂ sowiet₂−t₁ =t_1/2 liefert:

t_1/2 = 1 k·a

Hieraus ist ersichtlich, dass die Halbwertszeit t_1/2 bei Reaktionen 2. Ordnung abh¨angig von der Anfangskonzentrationa ist.

(14)

1.4. REAKTIONEN DER GESAMTORDNUNG 2, JEDOCH JEWEILS 1.

ORDNUNG IN BEZUG AUF 2 EDUKTE 11

1.4 Reaktionen der Gesamtordnung 2, jedoch jeweils 1.

Ordnung in Bezug auf 2 Edukte

Beispiel:

H2+I2 →2HI Geschwindigkeitsgesetz:

v =−dc_H₂

dt =k·c_H₂ ·c_I₂

1.4.1 Allgemeine Formulierung

f¨ur den Fall, dass ein Stoff A in einer Reaktion 2. Gesamtordnung, jedoch 1. Ordnung in Bezug auf Edukt A und B verbraucht wird, gem¨aß folgender Reaktionsgleichung:

A+B →P (1.7)

v =−dcA

dt =k·c_A·c_B (1.8)

L¨osung f¨ur gleiche Anfangskonzentrationen:

c_A(t= 0) =c_B(t = 0) Mitc_A(t= 0) =a und c_B(t= 0) =b folgt

a =b (1.9)

Aufgrund der St¨ochiometrie von Reaktion (1.7) gilt dann zu jedem Zeitpunkt t:

cA(t) = cB(t) (1.10)

Einsetzen in Gleichung (1.8) liefert:

v =−dcA

dt =k·c²_A Durch Integration ergibt sich¹:

c_A(t) =a· 1 1 +a·k·t

1Vergleich mit Fall Reaktion 2. Ordnung in Bezug auf Edukt A in Gleichung (1.6)

(15)

1.4. REAKTIONEN DER GESAMTORDNUNG 2, JEDOCH JEWEILS 1.

ORDNUNG IN BEZUG AUF 2 EDUKTE 12

und wegen Gleichung (1.9) und Gleichung (1.10) c_B(t) = b· 1

1 +b·k·t L¨osung f¨ur ungleiche Anfangskonzentrationen Es gilt:

c_A(t = 0)6=c_B(t= 0) d.h. a6=b

Aufgrund der St¨ochiometrie der Reaktion gilt hier zu jedem Zeitpunkt t:

c_B(t) = c_A(t) + (b−a) Einsetzen in Gleichung (1.8) liefert:

−dc_A

dt =k·c_A·[c_A(t) + (b−a)]

| {z }

=cB(t)

Integriertes Geschwindigkeitsgesetz:

ln c_A(t)

c_A(t) + (b−a) = lnc_A(t)

c_B(t) = lna

b −(b−a)·k·t (1.11) Durch Aufl¨osen von Gleichung (1.11) nach c_A(t) ergibt sich:

c_A(t) =a· (b−a)

b·exp((b−a)·k·t)−a =a·f(t)

Das Abklingverhalten der Konzentration vonA, ausgehend vom Startwertc_A(t= 0) =a, wird durch die Abklingfunktionf(t) beschrieben, welche sowohl durch k als auch durch a und b bestimmt wird.

N¨aherung f¨ur Fall b a:

lnc_B(t)≈lnb und (b−a)≈b Damit ergibt sich aus Gleichung (1.11):

lnc_A(t) = lna−b·k·t Daraus folgt:

cA(t) =a·exp(−b·k·t)

(16)

1.5. TEMPERATURABH ¨ANGIGKEIT DER

REAKTIONSGESCHWINDIGKEITSKONSTANTEN 13

In diesem Fall ergibt sich n¨aherungsweise eine Reaktion 1. Ordnung, welche als eine sogenannte Reaktion pseudo 1. Ordnung bezeichnet wird (Vergleiche mit Reaktion 1. Ordnung (Gleichung (1.3))).

1.4.2 Halbwertszeit t

_1/2

(bez¨ uglich Edukt A) f¨ ur ungleiche Anfangskonzentrationen

Allgemeiner Zusammenhang zwischenc_A(t₁), c_A(t₂), c_B(t₁), c_B(t₂) und (t₂−t₁):

1

b−a ·lnc_A(t₁)·c_B(t₂)

c_A(t₂)·c_B(t₁) =k·(t₂ −t₁) Einsetzen vonc_A(t₁) =a, c_B(t₁) =b, c_A(t₂) = ^a₂, c_B(t₂) = b− a

2

| {z }

=c_A(t₂)

| {z }

=a 2

+(b−a)

und (t₂−t₁) =

t^A_1/2 liefert:

t^A_1/2 = 1 k · 1

b−a ·ln(2− a b)

Hieraus ist erkennbar, dasst^A_1/2 von beiden Ausgangskonzentrationen a und b abh¨angig ist.

1.5 Temperaturabh¨ angigkeit der

Reaktionsgeschwindigkeitskonstanten

1.5.1 Temperaturverhalten nach Arrhenius

Temperaturverhalten von k(t) wird in vielen F¨allen durch die sogenannte Arrhenius- Gleichung wiedergegeben:

d lnk

dT = E_a

R·T² (1.12)

wobeiE_a der Aktivierungsenergie der betrachteten Reaktion (n¨aherungsweise temperaturunabh¨angig) entspricht.

Integration von Gleichung (1.12) liefert:

Z lnk(T)

lnk(T=∞)

d lnk = Ea

R Z T

T=∞

1 T²dT

(17)

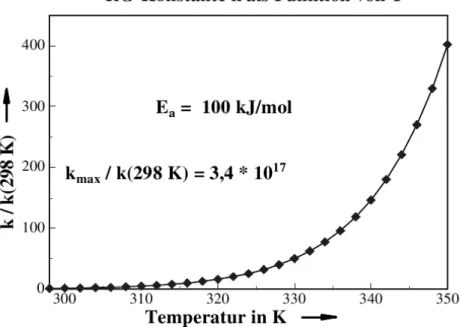
Abb. 1.2: Reaktionsgeschwindigkeitskonstante als Funktion der Temperatur unter der An- nahme, dass die AktivierungsenergieE_a temperaturunabh¨angig ist.

lnk= lnk(T =∞)− Ea

R·T

wobei k(T = ∞) = k_max dem maximalen Wert der Geschwindigkeitskonstanten entspricht. Es folgt:

k(T) =k_max·exp

− E_a R·T

Anmerkung:H¨aufig wirdk_max auch als pr¨aexponentieller Faktor oder als Frequenzfak- tor A bezeichnet.

Division obiger Gleichung durch k(T = 298K) und Logarithmieren liefert die Gera- dengleichung:

ln

k(T) k(T = 298K)

=− Ea

R·T + ln

kmax

k(T = 298K)

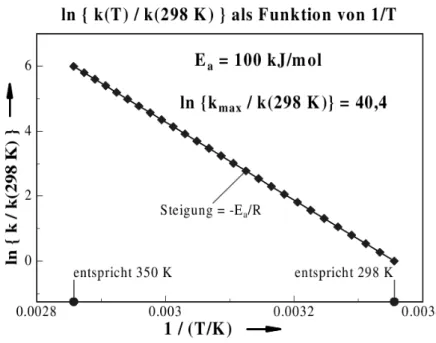
Arrhenius-Auftragung:

Auftragung von lnk gegen _T¹ zur graphischen Bestimmung der Aktivierungsenergie E_a (siehe Abb. 1.3 und 1.4 im Vergleich zu Abb. 1.2)

(18)

Abb. 1.3: Bestimmung der Aktivierungsenergie E_a mit Hilfe der Arrhenius-Auftragung lnk gegen 1/T.

Abb. 1.4: Bestimmung des pr¨aexponentiellen Faktors durch Extrapolation von ln(k(T)/k(T = 298K)) auf 1/T=0.

Steigung der Geraden:

d lnk

d(_T¹) =−E_a R

(19)

1.6. REAKTIONSMECHANISMUS UND REAKTIONSORDNUNG 16

Dieses Verfahren wurde von dem schwedi- schen Physikochemiker Svante August Arr- henius (*1837-†1923) entwickelt. Er erhielt den Nobelpreis 1903.

1.5.2 Moderne Gleichungen zur Beschreibung der

Temperaturabh¨ angigkeit der Geschwindigkeitskonstanten k

lnk(T) =α+ β

T +γ·lnT mit α, β und γ als Konstanten, oder:

lnk(T) =a+b·T^c mit a, b und c als Konstanten.

1.6 Reaktionsmechanismus und Reaktionsordnung

Elementarreaktion: Teilschritt einer Gesamtreaktion, der nicht mehr in weitere Teil- schritte unterteilt werden kann.

Molekularit¨at: einer chemischen Reaktion beschreibt die Anzahl der Molek¨ule, die am geschwindigkeitsbestimmenden Schritt der Reaktion beteiligt sind.

An einer Elementarreaktion k¨onnen beteiligt sein:

• Ein Teilchen (Molek¨ul, Ion, Radikal, . . . ) → unimolekulare Reaktion.

Bsp.:

(CH₂)₃

| {z }

Cyclopropan

→CH₃ −CH =CH₂

| {z }

P ropen

(20)

1.7. HIN- UND R ¨UCKREAKTIONEN 1. ORDNUNG

(GLEICHGEWICHTSREAKTIONEN) 17

• Zwei Teilchen (Molek¨ule, Ionen, Radikale, . . . ) → bimolekulare Reaktion.

Bsp.: Esterverseifung

CH₃COOCH₂CH₃

| {z }

Essigs¨aureethylester

+OH⁻ →CH₃COO⁻

| {z }

Acetation

+CH₃CH₂OH

| {z }

Ethanol

• Drei Teilchen (Molek¨ule, Ionen, Radikale, . . . ) → trimolekulare Reaktion.

Dieser Typ von Elementarreaktionen kommt nur sehr selten vor, da die Wahr- scheinlichkeit f¨ur den Zusammenstoß dreier Teilchen w¨ahrend der Reaktion sehr gering ist.

Anmerkung: Die Molekularit¨at einer Reaktion kann nur die Werte 1-3 annehmen.

H¨ohere Werte sind nicht bekannt. Besteht die Gesamtreaktion nur aus einem Elemen- tarschritt, so ist die Ordnung der Gesamtreaktion gleich der Molekularit¨at der Elemen- tarreaktion. Komplexe Reaktionen bestehen aus mehreren Elementarschritten. Sind alle Teilschritte einer komplexen Reaktion bekannt, kann die Gesamtkinetik aus der Kinetik der Elementarreaktionen abgeleitet werden.

1.7 Hin- und R¨ uckreaktionen 1. Ordnung (Gleichgewichtsreaktionen)

Schema:

A−_←−−^k₋₋^hin→₋

kr¨uck

P

F¨ur die Geschwindigkeit der Gesamtreaktion gilt:

−dcA

dt

| {z }

RGGesamt

=khin·cA(t)

| {z }

RGhin

−kr¨uck·cP(t)

| {z }

RGr¨uck

(1.13)

bzw.:

RGgesamt=RGhin−RGr¨uck (1.14)

wobei RG= Reaktionsgeschwindigkeit.b

F¨ur die Konzentrationen der Reaktionsteilnehmer gilt:

c_P(t) =c_P(t = 0) + [c_A(t = 0)−c_A(t)]

| {z }

Anteil von A, der zu P wegreagiert ist

=p+ [a−c_A(t)] (1.15)

mit p=c_P(t = 0). F¨ur die Anfangsbedingung p= 0 ergibt sich aus Gleichung (1.15):

c_P(t) = a−c_A(t) (1.16)

(21)

1.7. HIN- UND R ¨UCKREAKTIONEN 1. ORDNUNG

(GLEICHGEWICHTSREAKTIONEN) 18

Mit Gleichung (1.16) nimmt Gleichung (1.13) folgende Form an:

−dc_A

dt =k_hin·c_A(t)−k_r¨_uck·[a−c_A(t)]

= [k_hin+k_r¨_uck]·c_A(t)−k_r¨_uck·a

(1.17)

Grenzf¨alle von Gleichung (1.17):

1. Beginn der Reaktiont = 0: c_A(t) = a

− dc_A dt

t=0

=khin·a

F¨ur diesen Fall ergibt sich ein einfaches Geschwindigkeitsgesetz f¨ur eine Reaktion 1.

Ordnung ohne R¨uckreaktion.

2. Im chemischen Gleichgewicht gilt:

RG_Gesamt = 0 Aus Gleichung (1.14) folgt somit:

RG_hin = RG_r¨_uck (1.18)

k_hin·[c_A]Gleichgewicht = k_r¨_uck·[c_P]Gleichgewicht

c_P c_A

Gleichgewicht

= k_hin

k_r¨_uck =K (1.19)

wobei K die kinetische Gleichgewichtskonstante der Reaktion darstellt.

Aus Gleichung (1.19) erhalten wir durch Logarithmieren und Differentiation:

d lnK = d ln k_hin

k_r¨_uck

Einsetzen der integralen Form der Arrhenius-Gleichung (1.12) f¨ur die Temperaturabh¨angigkeit von k:

k_hin(T₎ =k_max·exp

− E_a^hin R·T

k_r¨_uck(T₎ =k_max·exp

−E_a^r¨^uck R·T

(22)

1.8. FOLGEREAKTIONEN 19

liefert:

d lnK

d(_T¹) =−E_a^hin−E_a^r¨^uck R

Diese Gleichung beschreibt die Temperaturabh¨angigkeit der Gleichgewichtskonstanten K.

Auftragung von lnK gegen _T¹ liefert die Steigung _d(1/T^{d ln}^K₎. Hieraus kann man die Dif- ferenz der AktivierungsenergienE_a^hin−E_a^r¨^uck der Gleichgewichtsreaktion bestimmen.

Durch Integration von Gleichung (1.17) ergibt sich:

c_A(t) =a·

=0 f¨urt→∞

z }| {

k_hin

k_hin+k_r¨_uck ·exp [−(k_hin+k_r¨_uck)·t] + k_r¨_uck k_hin+k_r¨_uck

Nach langer Zeitt→ ∞wird das chemische Gleichgewicht der Reaktion erreicht und es folgt aus obiger Gleichung:

[c_A]Gleichgewicht =a· k_r¨_uck k_r¨_uck+k_hin Mit Gleichung (1.16) ergibt sich:

[c_P]Gleichgewicht=a−[c_A]Gleichgewicht=a·

1− k_r¨_uck kr¨uck+khin

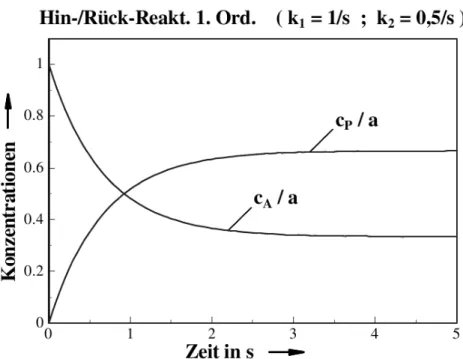
Das Zeitverhalten des Edukts A und Produkts P f¨ur eine Hin- und R¨uckreaktion 1.

Ordnung ist in Abb. (1.5) aufgetragen. Hieraus ist ersichtlich, dass sich nach langer Re- aktionsdauer ein Gleichgewicht der Konzentrationen der Reaktionsteilnehmer einstellt.

F¨ur den Quotienten der Konzentration von Produkt und Edukt im Gleichgewicht folgt somit:

c_P c_A

Gleichgewicht

= a·

1− _k ^k^r¨^uck

r¨uck+khin

a· _k ^k^r¨^uck

r¨uck+khin

= k_hin k_r¨_uck =K

Der Quotient der Konzentrationen im Gleichgewicht ist identisch mit der Gleichgewichts- konstanten bzw. dem Quotienten der Geschwindigkeitskonstanten der Reaktion.

1.8 Folgereaktionen

Schema:

A −^k→¹ P −^k→² Q

(23)

1.8. FOLGEREAKTIONEN 20

Abb. 1.5: Konzentration des Edukts A und Produkts P als Funktion der Zeit im Falle einer Hin- und R¨uckreaktion 1. Ordnung.

F¨ur den Fall, dass beide Teilschritte unimolekular ablaufen, gilt:

−dc_A

dt =k₁ ·c_A mit der L¨osung:

c_A(t) = a·exp (−k₁·t) (1.20) F¨ur das Zwischenprodukt P gilt hingegen:

dc_P

dt = k₁·c_A

| {z }

Bildung aus A

− k₂ ·c_P

| {z }

Reaktion zu Q

Einsetzen von Gleichung (1.20) ergibt:

dc_P

dt +k₂·c_P =k₁ ·a·exp (−k₁·t) (1.21) (inhomogene Differentialgleichung 1. Ordnung)

L¨osen der Differentialgleichung (1.21) f¨urk₁ 6=k₂ liefert:

c_P(t) = a· k₁ k₂−k₁ ·

exp (−k₁·t)−exp (−k₂·t)

(24)

1.9. PARALLELREAKTIONEN 21

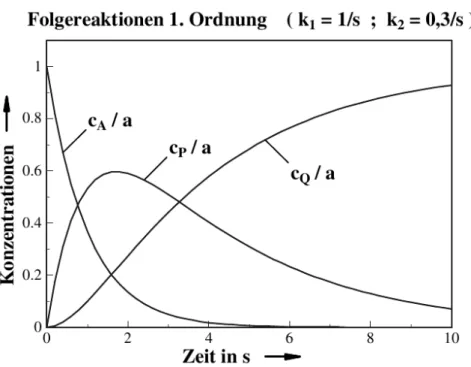
Abb. 1.6: Konzentration des Edukts A, Zwischenprodukts P und Folgeprodukts Q als Funk- tion der Zeit im Falle einer Folgereaktion 1. Ordnung.

F¨ur die Konzentration des Endprodukts Q gilt:

c_Q(t) =a−[c_A(t) +c_P(t)]

Eine Auftragung des Zeitverhaltens der Konzentration f¨ur eine Folgereaktion 1. Ordnung in Bezug auf alle Reaktionsteilnehmer ist in Abb. (1.6) dargestellt.

1.9 Parallelreaktionen

Schema:

A−^k→¹ P A−^k→² Q

F¨ur den Fall, dass beide Elementarreaktionen unimolekular ablaufen, gilt:

dc_P

dt =k₁·c_A (1.22)

dc_Q

dt =k₂·c_A (1.23)

(25)

1.9. PARALLELREAKTIONEN 22

Abb. 1.7: Konzentration des Edukts A, Produkts P und des parallelentstehenden Produkts Q als Funktion der Zeit im Falle einer Parallelreaktion 1. Ordnung

sowie:

−dc_A

dt = dc_P

dt +dc_Q

dt = (k₁+k₂)·c_A Durch Integration ergibt sich die L¨osung:

c_A(t) =a·exp

−(k₁+k₂)·t

(1.24) Verkn¨upfung von Gleichung (1.22) und Gleichung (1.23) ¨uberc_A(t) liefert:

dcP = k₁ k₂ ·dcQ

Durch Integration erhalten wir:

c_P(t) = k₁

k₂ ·c_Q(t) (1.25)

Aufgrund der St¨ochiometrie gilt:

a=c_A(t) +c_P(t) +c_Q(t) (1.26)

(26)

1.10. FOLGEREAKTIONEN MIT VORGELAGERTEM

GLEICHGEWICHT UND QUASISTATIONARIT ¨AT 23

Aus den Gleichungen (1.24), (1.25) und (1.26) folgt schließlich:

cP(t) = k1

k₁+k₂ ·a·

1−exp (−(k1+k2)·t)

c_Q(t) = k₂

k₁+k₂ ·a·

1−exp (−(k₁ +k₂)·t)

Eine Auftragung des Zeitverhaltens der Konzentrationen f¨ur eine Parallelreaktion 1.

Ordnung ist in Abb. (1.7) dargestellt.

1.10 Folgereaktionen mit vorgelagertem Gleichgewicht und Quasistationarit¨ at

Chemische Reaktionen in der Biologie und Biochemie bestehen in der Regel aus mehreren Teilreaktionen. Ein typisches Reaktionsschema lautet:

A −−→_←−−^k¹

k−1

B −^k→² C

Unter der Annahme, dass alle Teilreaktionen Zeitgesetzen 1. Ordnung folgen, ergeben sich folgende differentielle Zeitgesetze:

dcA

dt =−k1·cA+k−1·cB (1.27) dc_B

dt =k₁·c_A−k−1·c_B−k₂·c_B dc_C

dt =k₂·c_B Aufgrund der Stoffmengenerhaltung gilt außerdem:

cA+cB+cC =c⁰_A

wobeic⁰_A=c_A(t= 0) =adie Anfangskonzentration von A darstellt (Schreibweise in der Biochemie gebr¨auchlich). Hieraus folgt:

dc_A+ dc_B+ dc_C = 0

Obiges Gleichungssystem ist mit herkömmlichen analytischen Integrationsverfahren für den allgemeinen Fall nicht lösbar. Mit Hilfe numerischer Integrationsverfahren können jedoch die Konzentrationsverläufe der Reaktionsteilnehmer ermittelt werden (siehe hierzu Abb. (1.8)).

(27)

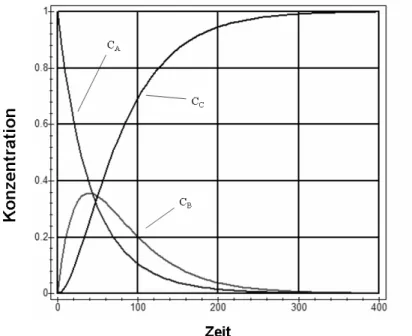
Abb. 1.8: Konzentrationsverlauf des Edukts A, Zwischenprodukts B und des Endprodukts C als Funktion der Zeit bei einer Folgereaktion 1. Ordnung mit vorgelagertem Gleichgewicht (allgemeiner Fall).

Allgemeiner Fall: in Abb. (1.8) beobachtet man, dass c_A exponentiell abnimmt und c_B ein Maximum durchl¨auft. Dagegen c_C zuerst langsamer als c_B und nach dem Wen- depunkt exponentiell bis zum maximalen Wert ansteigt.

Wichtiger Spezialfall: wird in Abb. (1.9) gezeigt. Hier erfolgt Bildung von B aus A langsam. Dies stellt den geschwindigkeitsbestimmenden Schritt der Gesamtreaktion dar. Dann reagiert reaktives Zwischenprodukt B schnell entweder zu A zurück oder zu C weiter, d.h.k−1, k₂ k₁. Dies hat zur Folge, dass die Konzentration von B auf sehr klei- nem Niveau gegenüber den anderen Konzentrationen bleibt. Hieraus resultiert eine sehr flache Kurve. In diesem Fall kann für Zwischenprodukt B ein quasistationärer Zustand angenommen werden:

dc_B

dt =k₁·c_A−k₋₁·c_B−k₂·c_B ≈0 (1.28) Durch Aufl¨osen obiger Gleichung nach c_B ergibt sich:

c_B =c_A· k₁ k₋₁+k₂

(28)

Abb. 1.9: Konzentrationsverlauf des Edukts A, Zwischenprodukts B und Endprodukts C bei einer Folgereaktion 1. Ordnung mit vorgelagertem Gleichgewicht. Spezialfall: Bil- dung von B aus A erfolgt langsam und B reagiert schnell entweder zu A zurück oder zu C weiter. Konzentration von B bleibt sehr klein gegenüber den anderen Konzen- trationen. In diesem Fall kann ein quasistationärer Zustand für Zwischenprodukt B angenommen werden.

Einsetzen in Gleichung (1.27) liefert schließlich:

dc_A

dt =−k₁·c_A+ k₁·k−1

k−1+k₂ ·c_A=−

=k

z }| { k₁·k₂ k−1+k₂·c_A dc_C

dt = k₁·k₂ k−1+k2

| {z }

=k

·c_A

Durch Einf¨uhrung der Konstanten k = _k^k¹^·k²

−1+k2 ergibt sich n¨aherungsweise eine Differen- tialgleichung 1. Ordnung f¨ur Edukt A:

dc_A

dt =−k·cA

mit integralem Zeitgesetz:

ln cA

c⁰_A

=−k·t

(29)

1.11. ENZYMREAKTIONEN 26

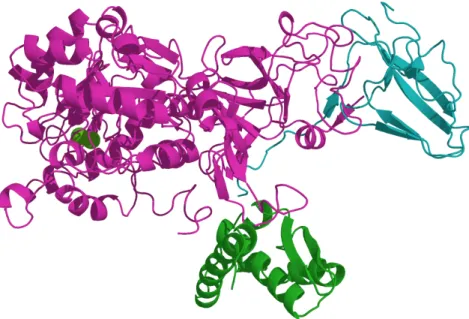
Abb. 1.10: Enzym Urease isoliert aus dem BakteriumKlebsellia Aerogenes. Es katalysiert die Hydrolysereaktion von Harnstoff zu Kohlenstoffdioxid und Ammoniak.

Dies entspricht n¨aherungsweise einer Reaktion 1. Ordnung folgenden Typs:

A−→^k C

Obige Herleitung zeigt, dass eine Folge von Reaktionen, in der nur der langsamste Re- aktionsschritt für die Gesamtreaktion maßgeblich ist, näherungsweise als eine Reaktion 1. Ordnung angesehen werden kann. Die quasi-stationäre Näherung kann in der Regel zur Behandlung von Reaktionen mit reaktivem Zwischenprodukt, wie z.B. von Enzym- und Radikalreaktionen, herangezogen werden.

1.11 Enzymreaktionen

Katalysatoren: sind Moleküle, die die Geschwindigkeit einer Reaktion erhöhen, jedoch aus der Reaktion unverändert hervorgehen.

Enzyme: sind biologische Katalysatoren auf Basis von Aminos¨auren (Proteine), welche bei der Steuerung des Stoffwechselgeschehens eine wichtige Rolle spielen.

Beispiel: Urease kommt besonders in Pflanzensamen und Bakterien vor (siehe Abb.

(1.10)). Sie katalysiert die Hydrolyse-Reaktion von Harnstoff:

H₂N CON H₂+ 3H₂O −−−−→^{U rease} 2N H₄⁺+OH⁻+HCO⁻₃

(30)

1.11.1 Michaelis-Menten-Kinetik

nach Leonor Michaelis und Maud Menten 1913.

TypischesReaktionsschema einer Enzymreaktion:

S+E −−→_←−−^k¹

k−1

ES −→^k^P P +E

wobei S = Substratb E = freies Enzymb

ES = Enzym-Substrat-Komplexb P = Produktb

Annahme: Hinreaktion sei 2. Gesamtordnung; die R¨uckreaktion sowie die Produkt- bildungsreaktion sei 1. Ordnung.

Differentielle Zeitgesetze f¨urES und P:

dcES

dt = k₊₁·c_S·c_E

| {z }

T1

−(k−1

|{z}

T2

+ k_p

|{z}

T3

)·c_ES (1.29)

dc_P

dt = k_P ·c_ES (1.30)

wobei T1 = Bildung von ES aus E und Sb T2 = R¨b uckbildung von E und S T3 = Weiterreaktion zu P und Eb

F¨ur die Gesamtkonzentration des Enzyms gilt:

c⁰_E =c_E+c_ES (1.31)

(31)

Mittels Gleichung (1.31) k¨onnen wir c_E aus Gleichung (1.29) eliminieren und wir erhalten:

dc_ES

dt =k₊₁·c_S·c⁰_E−(k₊₁·c_S+k−1+k_p)·c_ES (1.32) Bei Enzymreaktionen arbeitet man in der Regel mit sehr kleinen Enzymkonzentrationen, d.h. cS cES, und SubstratüberschußcS ≈c⁰_s. Für den Fall, daß der Enzym-Substrat- Komplex als reaktives Zwischenprodukt mit k−1, k_P k₊₁ angenommen werden kann, kann die quasi-stationäre Näherung auf Gleichung (1.32) angewendet werden:

dc_ES dt ≈0 Durch Aufl¨osen nach cES ergibt sich:

c_ES = c_S

c_S+K_M ·c⁰_E (1.33)

wobei

K_M = k−1+kP

k₊₁ (1.34)

die sog. Michaelis-Konstante darstellt. Einsetzen von Gl. (1.33) in Gleichung (1.30) liefert schließlich die Produktbildungsgeschwindigkeit:

v_P = dcP

dt =k_P ·c⁰_E · cS

c_S+K_M Mit Hilfe der Definition f¨ur denMaximalwert von vP:

v_P^max =k_P ·c⁰_E

welcher an der Substrat-S¨attigungsgrenze erreicht wird, ergibt sich schliesslich das sogenannte Michaelis-Menten-Gesetz:

v_P =v^max_P · c_S

c_S+K_M (1.35)

wobeic_S ≈c⁰_S. Es stellt eine grundlegende Beziehung der Enzym-Kinetik dar ! Die sogenannte Wechselrate (turn-over-rate) des Enzyms:

kcat = v^max_P c⁰_E

beschreibt wieviele Substratmoleküle von einem substratgesättigten Enzymmolekül pro Zeit umgesetzt werden.

(32)

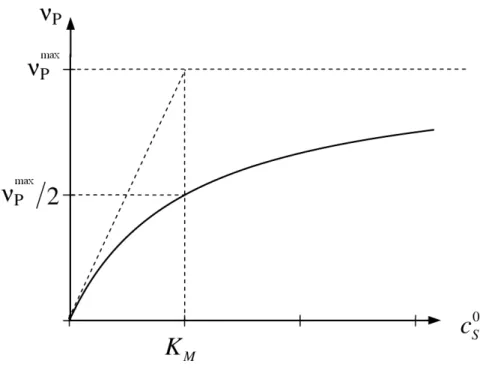
Abb. 1.11: Graphische Darstellung der Michaelis-Menten-Kinetik, in der die Produktbil- dungsgeschwindigkeit als Funktion der Gesamtkonzentration des Substrats aufgetragen wird.

Die ProduktbildungsgeschwindigkeitvP wird in enzymkinetischen Messungen als Funk- tion von c⁰_S gemessen. Da das exakte c_S w¨ahrend der Reaktion nur schwer bestimmbar ist, wird c_S ≈ c⁰_S angenommen und v_P(c⁰_S) aufgetragen (siehe Abb. (1.11)). Aus der Auftragung des Michaelis-Menten-Gesetzes ist erkennbar, dass bei c⁰_S = KM die Pro- duktbildungsgeschwindigkeit v_P = v^max_P /2 ist, daher wird die Michaelis-Konstante K_M auch als Halbs¨attigungskonzentration bezeichnet !

1.11.2 Lineweaver-Burk-Gleichung

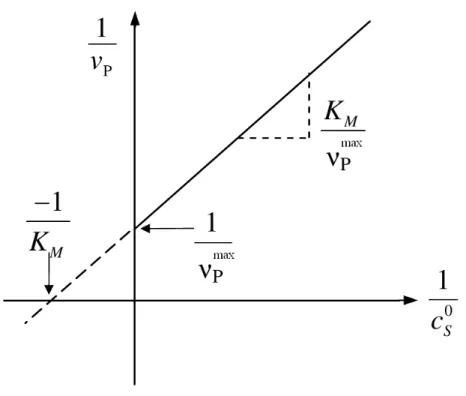
Um Meßwerte von v_P auf Verträglichkeit mit der Michaelis-Menten-Kinetik zu prüfen und gleichzeitig die Konstanten K_M und v_P^max zu bestimmen, formt man das Michaelis- Menten-Gesetz Gl. (1.35) so um, dass man eine Geradengleichung, die sog. Lineweaver- Burk-Gleichung, erhält:

1

v_P = K_M v^max_P · 1

c_S + 1 v_P^max

mit c_S ≈c⁰_S. Auftragung von 1/v_P gegen 1/c⁰_S liefert eine doppelt-reziproke Auftragung (siehe Abb. (1.12)). Wenn experimentell ermittelte Wertepaare f¨ur v⁻¹_P und (c⁰_S)⁻¹ eine Gerade ergeben, dann gehorcht die Enzymreaktion einer Michaelis-Menten-Kinetik. Aus den Achsenabschnitten der Lineweaver-Burk-Auftragung lassen sich die Werte f¨ur die

(33)

1.12. REAKTIONEN AN FESTER KATALYSATOROBERFL ¨ACHE 30

Abb. 1.12: Doppelt-reziproke Auftragung nach Lineweaver-Burk zur Bestimmung der Michaelis-Konstanten K_M und des Maximalwerts der Produktbildungsgeschwin- digkeit v^max_P .

Konstanten des Michaelis-Menten-GesetzesKM und v_P^max ablesen.

1.12 Reaktionen an fester Katalysatoroberfl¨ ache

1.12.1 Fall 1: Adsorption/Desorption eines Gases A auf/von einer Katalysatoroberfl¨ ache

Reaktionsschema:

Adsorption: A(g)+ad-Platz −−→^k^Ads A(ad) Desorption: A(ad) −−→^k^Des A(g)+ad-Platz

wobei ad-Platz ein Adsorptionsplatz an der Katalysatoroberfl¨ache darstellt.

Annahme: Die Teilreaktion der Adsorption sei bimolekular und die der Desorpti- on unimolekular. Zudem sind alle Adsorptionspl¨atze gleichwertig und besitzen daher die gleiche Besetzungswahrscheinlichkeit.

(34)

F¨ur die Geschwindigkeiten der Adsorptions- und Desorptionsteilreaktionen gilt dann:

RG_Adsorption = 1

A_Kat · dn_A(ad)

dt =k_Ads· p_A·(1−θ) (1.36)

RG_Desorption =− 1

A_Kat ·dn_A(ad)

dt =k_Des·θ (1.37)

wobei A_Kat = Oberfl¨b ache des Katalysators

dn_A(ad) = ¨b Anderung der Stoffmenge von A am Adsorptionsplatz im Zeitintervall dt

pA = Partialdruck von A in der Gasphaseb

θ = Bedeckungsgrad (Maß f¨b ur die Oberfl¨achenkonz. der mit A-Teilchen) besetzten Adsorptionspl¨atze

1−θ = Maß f¨b ur die Oberfl¨achenkonz. der unbesetzten Adsorptionspl¨atze

Definition des Bedeckungsgrades:

θ = Zahl der besetzten Adsorptionspl¨. atze Gesamtzahl der Adsorptionspl¨. atze F¨ur das Adsorptions-Desorptionsgleichgewicht gilt:

RGAdsorption =RGDesorption (1.38)

Mit Gleichung (1.36) und Gleichung (1.37) folgt f¨ur obige Gleichung:

k_Ads· p_A·(1−θ) =k_Des·θ welche umgeschrieben werden kann als

θ

1−θ = k_Ads

k_Des ·p_A=α·p_A (1.39)

mit

α= k_Ads k_Des = 1

p_A · θ 1−θ

Die Gr¨oße αentspricht dem Kehrwert des Partialdruckes p^∗_A, welcher bei Halbbesetzung der Adsorptionspl¨atze θ = ¹₂ im System herrscht, d.h. α= _p¹∗

A.

Aufl¨osen von Gleichung (1.39) nach θ liefert die sog. Langmuir-Isotherme:

θ= α·p_A 1 +α·p_A

(35)

Abb. 1.13: Bedeckungsgrad der Katalysator-Oberfl¨ache als Funktion des Partialdrucks einer SubstanzAin der Gasphase wird durch die sog. Langmuir-Isotherme wiedergegeben.

Graphische Auftragung von θ als Funktion von p_A wird in Abb. (1.13) gezeigt.

Zwei Grenzf¨alle:

1. Kleine Partialdr¨uckep_Ap^∗_A:

θ ≈α·p_A∝p_A

Bei kleinen Partialdr¨ucken ergibt sich ein lineares Verhalten f¨ur den Bedeckungsgrad (siehe Abb. (1.13)) !

2. Große Partialdr¨uckep_A p^∗_A:

1−θ ∝ 1 p_A

⇒θ ^p^A−→^→∞ 1

Bei großen Partialdr¨ucken tendiert der Bedeckungsgrad gegen die S¨attigungsgrenze (siehe Abb. (1.13)) !

(36)

Beweis:

1−θ = 1− α·p_A

1 +α·p_A = 1 1 + α

|{z}1 p∗

A

·p_A

= 1

1 + ^p_p^A∗ A

= p^∗_A p^∗_A+p_A

pAp^∗_A

≈ p^∗_A p_A

⇒1−θ∝ 1

p_A ⇒θ^p−→^A^→∞1

1.12.2 Fall 2: Unimolekulare Reaktion an der Katalysatoroberfl¨ ache der adsorbierten Spezies

Adsorptions-Desorptionsgleichgewicht:

A(g) +ad−P latz A(ad)

Folgereaktion:

A(ad)→^k P(g) F¨ur die Reaktionsgeschwindigkeit gilt:

1 Akat

· dn_P

dt =k·θ =k· α·p_A 1 +α·pA

Die Geschwindigkeit der Folgereaktion an der Oberfl¨ache ist proportional zum Be- deckungsgradθ.

Zwei Grenzf¨alle:

1. Schwache Adsorption, d.h.α·p_A1 bzw.p_Ap^∗_A: 1

A_kat ·dnP

dt ≈k·α·p_A

Bei schwacher Adsorption ergibt sich n¨aherungsweise ein Geschwindigkeitsgesetz 1. Ord- nung bzgl.p_A !

(37)

2. Starke Adsorption, d.h.α·p_A1 bzw. p_Ap^∗_A: 1

Akat

· dn_P dt ≈k

Bei starker Adsorption ergibt sich n¨aherungsweise ein Geschwindigkeitsgesetz nullter Ordnung !

1.12.3 Fall 3: Bimolekulare Reaktion an der Katalysatoroberfl¨ ache zwischen adsorbierten Spezies

Adsorption-Desorptionsgleichgewicht von Spezies A und B an der Katalysatoro- berfl¨ache:

A(g) + ad-PlatzA(ad) B(g) + ad-PlatzB(ad) Folgereaktion:

A(ad) +B(ad)→^k P(g)

Bei vielen Katalysereaktionen beruht der Mechanismus auf Stößen zwischen adsorbierten Spezies an der Katalysatoroberfläche, wobei die Spezies um die gleichen Adsorptions- plätze konkurrieren. Solche Reaktionen bezeichnet man als Langmuir-Hinshelwood- Reaktionen!

(38)

Aufgaben zur Kinetik:

1. Aufgabe: Reaktion erster Ordnung

14C ist ein radioaktives Kohlenstoffisotop, das nach einer Reaktion erster Ordnung mit einer Halbwertszeit von 5730a zerfällt (β^- Zerfall). Es entsteht in der oberen Atmosphäre aus Stickstoff unter Einwirkung von Höhenstrahlung. Durch Entstehung und Zerfall stellt sich ein Gleichgewicht ein. Solange ein Organismus lebt, führt er immer weiter ¹⁴C durch Nahrung / Assimilation zu. Nach dem Absterben zerfällt ¹⁴C jedoch nur noch. Dies macht es möglich, über die verbleibende Radioaktivität, die zu der Menge an verbleibenden ¹⁴C proportional ist, das Alter von archäologischen Funden abzuschätzen.

Die Eismumie aus den Ötztaler Alpen weist nur noch eine restliche Radioaktivität von 52,7 % eines lebenden Menschen auf. Wann ist der Mann gestorben?

2. Aufgabe: Reaktionsumsatz einer Reaktion 2. Ordnung

Die Esterhydrolyse verläuft unter basischen Bedingungen irreversibel, da das für die Rückreaktion nicht weiter reaktive Säureanion entsteht. Bei der hier betrachteten Hydrolyse von Essigsäureethylester beträgt die Geschwindigkeitskonstante 0,11 L mol^-1 s^-1.

CH3COOC2H5(aq) + OH^-(aq)  CH3COO^- (aq) + CH3CH2OH (aq)

Eingesetzt wurden die Edukte jeweils in einer Konzentration von 0,150 mol/l. Wie hoch sind die verbleibenden Esterkonzentrationen nach: 15 s, 15 min und 15 h ? Skizzieren Sie den Verlauf der Konzentrationen der Edukte und Produkte in der Reaktion in einem c über t Diagramm.

3. Aufgabe: Reaktionsordnung und Aktivierungsenergie

Das Molekül N2O5 zersetzt sich in einer Zerfallsreaktion zu N2O4 und O2. Bestimmen Sie die Ordnung der Reaktion durch eine geeignete Auftragung mit Hilfe der unten angegebenen Messdaten. Ermitteln Sie dann die Reaktionsgeschwindigkeitskonstante, die Halbwertszeit, sowie die Aktivierungsenergie der Reaktion.

45°C 65°C

t/s c(N2O5) / mol l^-1 c(N2O5) / mol l^-1

0 2,330 2,330

200 2,109 0,880

400 1,909 0,332

600 1,728 0,125

800 1,564 0,047

1000 1,416 0,018

(39)

4. Aufgabe: Hin- und Rückreaktion und Gleichgewicht

Bei der Bildung von HI in der Gasphase:

H2(g) + I2(g) 2HI(g)

wurde in einer Versuchsreihe bei einer Temperatur von 698,6K folgende Gleichgewichts- konzentrationen gemessen:

[H2] in Mol/l [I2]in Mol/l [HI] in Mol/l 4,5647 0,7378 13,5440

0,4789 0,4789 3,5341

1,1409 1,1409 8,4100

Dabei läuft die Reaktion in Form einer Elementarreaktion ab.

a) Bestimmen Sie die Gleichgewichtskonstante der Reaktion.

b) Wie verhalten sich bei Erreichen des Gleichgewichts die Reaktionsgeschwindigkeiten der Hin- und Rückreaktionen zueinander?

c) Wie verhalten sich die Geschwindigkeitskonstanten der Hin- und Rückreaktion zueinander?

5. Aufgabe: Folgereaktion erster Ordnung

Bei einem biotechnologischen Prozess entsteht aus der Substanz A das Produkt B, das selbst wieder zu dem Produkt C weiterreagiert. Die Reaktion soll nach folgendem Reaktionsschema ablaufen:

A  B  C

wobei kA und kB jeweils die Geschwindigkeitskonstanten der ersten und zweiten Teilreaktion darstellen. Jede Reaktionsstufe ist eine Reaktion erster Ordnung.

a) Geben Sie das differentielle Zeitgesetz für die Konzentration von B an, woraus sich folgendes integrales Zeitgesetz für c_B ergibt:

c_Bt= k_Ac⁰_A

k_B−k_A



e^−k^A^t−e^−k^B^t



wobei cA0 die Anfangskonzentration der Substanz A darstellt.

b) Leiten Sie einen Ausdruck für den Zeitpunkt her, bei dem die Konzentration von B ihr Maximum erreicht und berechnen Sie die maximale Konzentration von B.

c) Wie verhalten sich die beiden hergeleiteten Größen aus 5 a), wenn kB ansteigt während kA konstant gehalten wird ?

(40)

6. Aufgabe: Parallelreaktion erster Ordnung

131I ist ein radioaktives Iod-Isotop, das bei der Kernspaltung entstehen kann.¹³¹I ist ein β^- Strahler der mit einer Halbwertszeit von 8d zerfällt. Wird Iod vom Körper aufgenommen, lagert es sich hauptsächlich in der Schilddrüse ein. Die biologische Halbwertszeit beim Menschen in der Schilddrüse (durch Ausscheidung) beträgt 140d. Daraus folgt eine besonders starke Belastung der Schilddrüse bei Unfällen mit Radioaktivität, der man versucht mit Iod Tabletten entgegen zu wirken.

a) Berechnen Sie die effektive Halbwertszeit von ¹³¹I im menschlichen Körper.

b) Wie lange dauert es bis die mit ¹³¹I aufgenommene Radioaktivität in einem Menschen um 99 % abgenommen hat ?

7. Aufgabe: Konzentrationsverlauf und Quasistationärität

a) Geben Sie das Reaktionsschema an und skizzieren Sie die Konzentrationsverläufe der beteiligten Substanzen in Abhängigkeit der Reaktionsdauer für folgende Fälle:

i. Irreversible Parallelreaktion erster Ordnung ii. Hin-/Rückreaktion erster Ordnung

iii. Folgereaktion mit vorgelagertem Gleichgewicht

b) Welche Voraussetzungen müssen zur analytischen Lösung der differentiellen Zeitgesetze aus Aufgabe 7 a) iii. mit Hilfe der Quasistationaritätsbedingung erfüllt sein ?

8. Aufgabe: Folgereaktion und Quasistationärität

Aceton geht unter Säurekatalyse mit sich selbst eine Aldolkondensation ein. Dies geschieht nach folgendem vereinfachtem Reaktionschema:

O C H₃ CH₃

+ ^H⁺

k(+)

k(-)

OH C H₂ CH₃

+ ^H⁺

Aceton Enol

OH C H₂ CH₃

O C H₃ CH₃

+ ^k(p)

C H₃

O

CH₃ CH₃

+ ^H²^O

Enol Aceton Produkt (4-Methylpent-3-en-2on)

a) Leiten Sie unter Verwendung der Näherung des quasi-stationären Zustandes für das reaktive Zwischenprodukt (Enol) einen Ausdruck für die Konzentration des Enols her.

b) Leiten Sie daraus einen Ausdruck für die Produktbildungsgeschwindigkeit her.

(41)

9. Aufgabe: Michaelis-Menten-Kinetik

Das von Fleming entdeckte Antibiotikum Penicillin ist ein β-Lactam Antibiotikum, das bei gram-positiven Bakterien die Ausbildung der Zellwand verhindert. Manche Stämme von Staphylococcus aureus haben jedoch eine Gegenstrategie gegen das Penicillin entwickelt. Sie besitzen die β-Lactamase (auch als Penicillinase bekannt), die β-Lactam-Antibiotika, wie das Penicillin, hydrolysieren und somit unwirksam machen kann.

Im Rahmen einer Versuchsreihe sollte die Reaktionskinetik der Penicillinhydrolyse untersucht werden. Dazu wurde die von 1ng β-Lactamase (MW = 29,6 kDa) hydrolysierte Menge an Penicillin pro Minute in Abhängigkeit der Penicillinkonzentration in einem Reaktionsansatz von 1ml gemessen. Es wurden hierbei folgende Messdaten ermittelt:

Konzentration cPenicillin

[µM]

Produktbildungsgeschwindigkeit νP [nmol/min ml]

1 0,11

3 0,25

5 0,34

10 0,45

30 0,58

50 0,61

Nehmen Sie an, dass sich die Penicillinkonzentration während des Versuchs nicht merklich ändert.

a) Zeigen Sie anhand einer geeigneten Auftragung obiger Messwerte, ob die β-Lactamase der Michaelis-Menten-Kinetik gehorcht. Wenn ja, welchen Wert für die Michaelis- Menten-Konstante KM besitzt die β-Lactamase ?

b) Welchen Wert hat die maximale Produkbildungsgeschwindigkeit ?

c) Welche Wechselzahl hat das Enzym unter den angegebenen Bedingungen, wenn man davon ausgeht, dass das Enzym nur ein aktives Zentrum besitzt ?

(42)

2 Thermodynamik

2.1 Grundlagen und Wiederholung 1. Semester

2.1.1 System und Umgebung

System: Teil des Weltalls, der bei der Untersuchung betrachtet wird (siehe Abb. (2.1)).

Umgebung: Rest des Weltalls, der an das System angrenzt und gegebenfalls mit diesem in Wechselwirkung steht.

Ein Systembezeichnet man als:

• abgeschlossen bzw. isoliert, wenn weder Energie- noch Stoffaustausch mit der Umgebung stattfindet;

• geschlossen, wenn Energie- aber kein Stoffaustausch stattfindet;

• offen, wenn Energie- sowie Stoffaustausch stattfindet.

2.1.2 Prozesse und Randbedingungen

Prozesse, die an einem System ausgef¨uhrt werden, bezeichnet man je nach Randbedin- gungen als:

• isotherm: bei konstanter Temperatur;

• isobar: bei konstantem Druck;

• isochor: bei konstantem Volumen;

• adiabatisch: ohne W¨armeaustausch;

• reversibel: wenn sich, bei der Ausführung, das System bei jedem Prozessschritt im Gleichgewicht befindet (kann näherungsweise durch infinitesimale Änderun- gen der Zustandsvariablen erreicht werden) und der Prozess auf demselben Wege vollständig umkehrbarist;

• irreversibel: wenn die ¨Anderungen nichtumkehrbar sind.

39

(43)

2.1. GRUNDLAGEN UND WIEDERHOLUNG 1. SEMESTER 40

Abb. 2.1: Anschauliche Definition der Begriffe System, Umgebung und Weltall in der Ther- modynamik.

2.1.3 Innere und ¨ außere Energie

Innere Energie:

beschreibt die Gesamtenergie, die im System vorhanden ist, z.B. in Form kinetischer Energie (Bewegung) oder potentieller Energie (Anziehungs-/Abstoßungskräfte) der Mo- leküle. Generell ist jede Energie, die nicht durch Bewegung des Gesamtsystems verändert werden kann, zur inneren Energie zu zählen.

Außere Energie:¨

wird durch die Einwirkung äußerer Kräfte (z.B. Gravitationskraft) erzeugt und verändert die Bewegung des Gesamtsystems, wie z.B. Lageenergie.