FAKULT ¨AT F ¨UR INFORMATIK DER TECHNISCHEN UNIVERSIT ¨AT M ¨UNCHEN

FAKULT ¨ AT F ¨ UR INFORMATIK

DER TECHNISCHEN UNIVERSIT ¨ AT M ¨ UNCHEN

Interdisziplin¨ares Projekt

Glatte Kurven aus diskreten Punkten

Carlos Camino

FAKULT ¨ AT F ¨ UR INFORMATIK

DER TECHNISCHEN UNIVERSIT ¨ AT M ¨ UNCHEN

Interdisziplin¨ares Projekt

Glatte Kurven aus diskreten Punkten

Verfasser: Carlos Camino

Aufgabensteller: Prof. Dr. Dr. J ¨urgen Richter-Gebert Betreuer: Dipl.Inf. Martin von Gagern

Datum: 17. Oktober 2013

Inhaltsverzeichnis

1. Einleitung 1

1.1. WriteBird . . . . 1

1.2. Problemstellung . . . . 2

2. Mathematische Grundlagen 3 2.1. Parametrisierte Kurven . . . . 3

2.2. Bernsteinpolynome . . . . 5

2.3. B´ezierkurven . . . . 7

2.4. B-Spline-Basisfunktionen . . . . 9

2.5. B-Splines . . . . 13

3. Wichtige Eigenschaften von B-Splines 17 3.1. Mehrfachknoten und eingespannte B-Splines . . . . 17

3.2. Zusammenhang zwischen B´ezierkurven und B-Splines . . . . 20

3.3. Einf ¨ugen von B-Spline-Knoten . . . . 22

3.4. Konsequenzen der Lokalit¨atseigenschaft . . . . 23

4. Echtzeitbearbeitung der Daten 27 4.1. Hintergrund . . . . 27

4.1.1. Chord-Length-Parametrisierung . . . . 28

4.1.2. Event-Time-Parametrisierung. . . . 28

4.2. Implementierung mit win- und bsp-Variablen . . . . 28

4.2.1. Die Methode processControlPoint . . . . 29

4.2.2. Die Methode finishStroke . . . . 30

5. L ¨oschen von Kontrollpunkten 33 5.1. Hintergrund . . . . 33

5.1.1. Allgemeine L ¨osung . . . . 34

5.1.2. Hilfsvariablen . . . . 35

5.1.3. Diskrete Approximationen . . . . 36

5.2. Implementierung mit aux -Variablen . . . . 36

5.2.1. Die Methode computeAuxiliaryVariables . . . . 37

5.2.2. Die Methode removeKnots . . . . 38

6. Darstellung als B´ezierkurven 41 6.1. Hintergrund . . . . 41

6.1.1. Multiplizit¨atserh ¨ohung . . . . 41

6.1.2. Aufteilen von B-Splines . . . . 44

Inhaltsverzeichnis

6.1.3. Uberf ¨uhrung zu B´ezierkurven . . . . ¨ 45

6.2. Implementierung mit net- und rem-Variablen . . . . 46

6.2.1. Die Methode generateBezierControlPoints . . . . 47

6.2.2. Die Methode deBoor . . . . 48

6.2.3. Die Methode extractBezierControlPoints . . . . 48

6.2.4. Die Methode extractRemainingControlPoints . . . . 49

6.2.5. Die Methode extractLastBezierControlPoints . . . . 49

7. Ergebnisse und Ausblick 51 7.1. Bestimmung der Parameter . . . . 51

7.1.1. Die maximale ¨ Anderung der Kurve . . . . 51

7.1.2. Die Kapazit¨at des Fensters . . . . 52

7.1.3. Die Ordnung des B-Splines . . . . 52

7.1.4. Die Wahl der diskreten Norm . . . . 53

7.1.5. Parametrisierung der Knoten . . . . 54

7.2. M ¨ogliche Folgearbeiten . . . . 55

A. Log-Dateien 59 A.1. Einf ¨ugen von Knoten in das Fenster . . . . 61

A.2. Bewegen des Fensters . . . . 65

A.3. Einf ¨ugen des letzten Knoten . . . . 69

A.4. Berechnen von Hilfsvariablen im Fenster . . . . 72

A.5. L ¨oschen von Knoten . . . . 75

A.6. Generieren von B´ezierkurven . . . . 78

Literaturverzeichnis 81

1. Einleitung

D

zentrale Thema dieser Arbeit ist das effiziente Gl¨atten von handgezeichneten Kurven. Dies beinhaltet das Einlesen, die Bearbeitung und die graphische Dar- stellung von Daten, die mithilfe eines Eingabeger¨ats produziert werden. Dabei wird der Verlauf der Maus oder eines speziellen Stiftes ¨uber eine, mit Sensoren versehene, Zeichenfl¨ache verfolgt und in Form von Punkten gespeichert. Die gespeicherten Punk- te werden von der Software durch Kurven verbunden, so dass sie den Verlauf der Maus bzw. des Stiftes ¨ahneln. Beispiele f ¨ur solche Eingabeger¨ate sind Tablets, Zeichenpads und elektronische Tafeln.

Die Einsatzbereiche f ¨ur solche Verfahren sind sehr vielf¨altig. Einerseits sind sie in indus- triellen Softwares zu finden, die als Hilfsmittel f ¨ur das technische Zeichnen oder sogar f ¨ur das rechnerunterst ¨utzte Konstruieren von Bauteilen eingesetzt werden. Beispiele hierf ¨ur sind CAD-Programme. Der Fachbereich, in dem solche Verfahren studiert werden, ist un- ter dem Namen Computer Aided Geometric Design (CAGD) bekannt. Andererseits sind sie auch in Applikationen zu finden, die von Privatnutzern benutzt werden, meistens um No- tizen von Hand zu machen, die dann in elektronischer Form gespeichert werden k ¨onnen.

Gegenstand dieser Arbeit wird ein solches Programm sein, namens WriteBird.

1.1. WriteBird

WriteBird ist eine Software f ¨ur elektronische Tafeln, die es erlaubt Tafelinhalte im Portable Document Format (PDF) zu exportieren. Sie arbeitet vektororientiert und wurde von Mar- tin von Gagern in Java implementiert. Die aktuelle Version des Programms generiert die erw ¨unschten Kurven, indem sie benachbarte Punkte durch gerade Segmente, sogenannte Polygonz ¨uge, verbindet. Diese Methode kann aus folgenden Gr ¨unden vorteilhaft sein:

• Sie ist leicht zu implementieren.

• Der Rechenaufwand ist minimal, weil die eingelesenen Daten nicht ver¨andert wer- den.

• Die Abweichung zwischen der von dem Nutzer gezeichneten Kurve und der von der Software generierten Zeichnung kann minimiert, werden, wenn der Abstand zwischen den gespeicherten Punkten sehr klein ist.

Nat ¨urlich ist eine solche L ¨osung eng mit Nachteilen verbunden:

• Das entstehende Bild ist nicht immer glatt. In bestimmten F¨allen, beispielsweise bei

sehr schnell gezeichneten Linien, kann es dazu kommen, dass die Abst¨ande zwi-

1. Einleitung

schen den Punkten zu groß sind. Dadurch k ¨onnen unerw ¨unschte Ecken im Bild ent- stehen.

• Ist der Abstand zwischen den Punkten sehr klein, so sieht die Kurve zwar glatt aus, aber h¨atte eine erh ¨ohte Menge an ben ¨otigtem Speicherplatz zur Folge.

• Die Aufnahme der Punkte wird immer durch das Eingabeger¨at technisch bedingt sein. So kann es passieren, dass die Sensoren nicht akkurat sind und so ein verzerrtes Bild mit unerw ¨unschten Zacken entsteht.

1.2. Problemstellung

Im Rahmen dieses Projekts soll ein optimierter Ansatz f ¨ur die Darstellung von Kurven f ¨ur WriteBird implementiert werden. Insbesondere soll die Methode in Java implementiert und in das bestehende WriteBird-Projekt eingebaut werden.

Reduzierte Datenmenge. Die Ausgabe des Programms soll platzsparend sein. Das heißt, dass die Anzahl an gespeicherten Punkten minimiert werden soll. Dabei soll, nat ¨urlich, so wenig an Informationen ¨uber die urspr ¨ungliche Kurve verloren gehen. Die Abweichung zwischen der urspr ¨unglichen und der entstehenden Kurve soll also minimal sein.

Effiziente Berechnung. Zudem soll das Programm so implementiert sein, dass die Be- rechnung der neuen Kurve effizient ist. Der Rechenaufwand sollte also so verteilt werden, dass der Benutzer beim Zeichnen der Kurve keine Verz ¨ogerung erkennt. Das heißt insbe- sondere, dass das Programm jederzeit in der Lage sein soll neue Daten aufzunehmen und dass sich die Bearbeitung dieser nicht anstaut.

Asthetische Darstellung. ¨ Schließlich soll die entstehende Kurve glatt sein. So soll nat ¨urlich

aussehen und darf keine unerw ¨unschten Ecken oder Unstetigkeiten besitzen, selbst wenn

der Benutzer das entstehende Bild beliebig oft vergr ¨oßert.

2. Mathematische Grundlagen

D

Manipulation von Kurven und Fl¨achen ist ein Teil der geometrischen Datenver- arbeitung (von engl. Computer Aided Geometric Design, kurz CAGD). Die in dieser Disziplin entwickelten Methoden bilden die Grundlagen f ¨ur die graphische Da- tenverarbeitung und sind somit ein wichtiger Bestandteil dieser Arbeit. In diesem Kapitel werden parametrisierte Kurven diskutiert und wir werden insbesondere auf zwei Arten solcher Kurven eingehen: Die B´ezierkurven und die B-Splines. Diese werden sowohl for- mal als auch informal beschrieben werden und zum besseren Verst¨andnis werden diese Beschreibungen mit zahlreichen Beispielen und graphischen Darstellungen erg¨anzt. F ¨ur dieses Kapitel wurden folgende Quellen zu Rate gezogen: [3, 6, 11].

2.1. Parametrisierte Kurven

Parametrisierte Kurven liefern uns eine M ¨oglichkeit die (d-dimensionalen) Punkte X ∈ R

einer Kurve in Abh¨angigkeit eines Parameters t zu beschreiben.

Definition 2.1 (Parametrisierte Kurven)

Sei I ⊆ R ein Intervall (geschlossen, offen oder halboffen), t ∈ I und f

, . . . , f

: I → R Funktio- nen. Eine Punktemenge C = {X(t) | t ∈ I} ⊆ R

mit

X(t) =

Ö

f

(t) .. . f

(t)

è

nennt man parametrisierte Kurve.

Intuitiv beschreiben die Funktionen f

, . . . , f

den zeitlichen Verlauf der einzelnen Koor- dinaten der Kurve innerhalb des Zeitintervalls I . Man nennt zweidimensionale Kurven ebene Kurven und dreidimensionale Raumkurven.

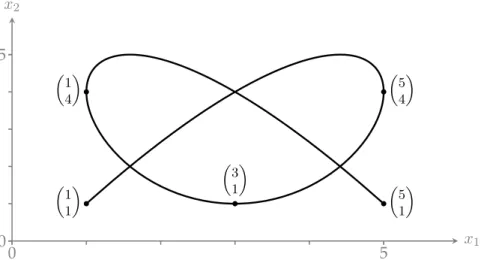
Beispiel 2.2 (Ebene Kurve)

Die Kurve C = {X(t) | t ∈ [0, 4]} mit

X(t) =

Ç

(t − 1)

(4 − t) + 1 t(t − 2)

(4 − t) + 1

å

stellt eine parametrisierte Kurve mit d = 2 dar. Ihr Verlauf ist in Abbildung 2.1 abgebildet.

2. Mathematische Grundlagen

x

x

0 5

0 5

Å5 1 ã Å1

4 ã

Å3 1 ã

Å5 4 ã

Å1 1 ã

Abbildung 2.1.: Kurvenverlauf der ebenen Kurve C aus Beispiel 2.2 mit eingezeichneten Punkten X(0) = (5, 1)

, X(1) = (1, 4)

, X(2) = (3, 1)

, X(3) = (5, 4)

und X(4) = (1, 1)

.

Man stelle sich vor, man w ¨urde die Kurve aus Beispiel 2.2 mit einem Bleistift auf ein Blatt Papier mithilfe eines x

, x

-Koordinatensystems zeichnen wollen. Man beginnt die Zeich- nung an dem Punkt X(0) = (5, 1)

. Zu jedem Zeitpunkt t ∈ [0, 4] befindet sich die Spitze des Bleistiftes auf dem Punkt X(t) des Koordinatensystems. Setzt man f ¨ur t beispielsweise die Werte 0, 1, 2, 3 und 4 ein, so erh¨alt man die Punkte

Ç

5 1

,

1

4

,

3

1

,

5

4

,

1

1

∈ C .

Diese findet man auf der Kurve in Abbildung 2.1 markiert. Nat ¨urlich ist hier der ¨ Ubergang von t = 0 zu t = 4 kontinuierlich, so das die Kurve nicht aus 5, sondern aus unendlich vielen Punkten besteht.

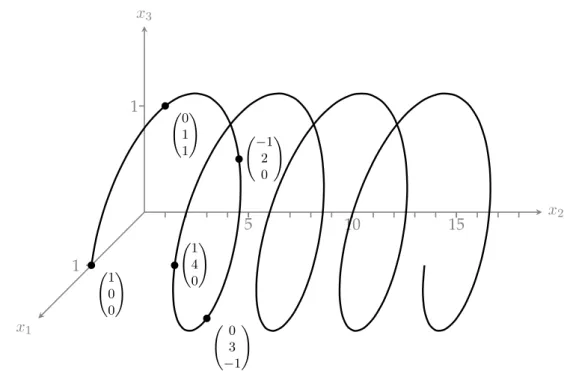
Beispiel 2.3 (Raumkurve)

Die Kurve C = {X(t) | t ∈ [0, 8π]} mit

X(t) =

Ö

cos(t) 2t/π sin(t)

è

stellt eine parametrisierte Kurve mit d = 3 dar. Ihr Verlauf ist in Abbildung 2.2 abgebildet.

Die Kurve aus 2.3 kann nicht mehr in eine Ebene gezeichnet werden. Sie muss im dreidi-

mensionalen euklidischen Raum eingebettet werden. Setzt man in diesem Fall die Werte

0,

π, π,

π, 2π f ¨ur t ein, so erh¨alt man folgende Punkte auf der Kurve:

2.2. Bernsteinpolynome

x

x

x

1

1

5 10 15

1 0 0

!

0 1 1

!

−1 2 0

!

0 3

−1

! 1

4 0

!

Abbildung 2.2.: Raumkurve C aus Beispiel 2.3 mit eingezeichneten Punkten X(0) = (1, 0, 0)

, X

= (0, 1, 1)

, X(π) = (−1, 2, 0)

, X

= (0, 3, −1)

und X(2π) = (1, 4, 0)

.

Ö

1 0 0

è

,

Ö

0 1 1

è

,

Ö

−1 2 0

è

,

Ö

0 3

−1

,

1

4 0

è

∈ C .

Diese sind ebenfalls in Abbildung 2.2 eingezeichnet worden.

Die in den folgenden Abschnitten beschriebenen Klassen parametrisierter Kurven und die entsprechenden Verfahren funktionieren f ¨ur beliebige Dimensionen. Nichtsdestotrotz werden wir uns in den folgenden Beispielen und Abbildungen im auf den Fall d = 2 ein- schr¨anken, da nur dieser f ¨ur unser Vornehmen von Bedeutung ist.

2.2. Bernsteinpolynome

B´ezierkurven geh ¨oren wohl zu den wichtigsten Klassen parametrisierter Kurven. Sie wur- den Anfang der 1960er Jahre, unabh¨angig voneinander, von Pierre B´ezier und Paul de Casteljau entwickelt. Um diese zu verstehen, m ¨ussen zuerst die sogenannten Bernsteinpo- lynome verstanden werden.

Definition 2.4 (Bernsteinpolynome)

Sei n ∈ N

und i ∈ {0, . . . , n}. Das i-te Bernsteinpolynom n-ten Grades hat die Gestalt

2. Mathematische Grundlagen

B

(t) :=

Ç

n i

· t

· (1 − t)

, wobei der Binomialkoeffizient

definiert ist als:

Ç

n i

:= n!

(n − i)! · i! = n · (n − 1) · . . . · (n − i + 1) i · (i − 1) · . . . · 1 . Wir zeigen diese Definition anhand eines Beispiels.

Beispiel 2.5 (Bernsteinpolynome)

Sei n = 5. Die sechs Bernsteinpolynome f ¨unften Grades lassen sich wie folgt berechnen:

B

(t) =

· t

· (1 − t)

= (1 − t)

B

(t) =

· t

· (1 − t)

= 5t(1 − t)

B

(t) =

· t

· (1 − t)

= 10t

(1 − t)

B

(t) =

· t

· (1 − t)

= 10t

(1 − t)

B

(t) =

· t

· (1 − t)

= 5t

(1 − t) B

(t) =

· t

· (1 − t)

= t

t

0 0, 2 0, 4 0, 6 0, 8 1

0 1

B5,0

B5,1

B5,2 B5,3

B5,4

B5,5

Abbildung 2.3.: Graphen der Bernsteinpolynome B

(t) f ¨ur i = 0, 1, 2, 3, 4, 5 im Intervall [0, 1].

Bernsteinpolynome k ¨onnen zwar ¨uber beliebige Intervalle definiert werden, aber sie sind sie sind im Intervall [0, 1] besonders interessant. Hier besitzen sie wichtige Eigenschaften, die eine entscheidende Rolle bei der Konstruktion von B´ezierkurven spielen werden. Im Folgenden werden diese erl¨autert.

Nichtnegativit¨at und Positivit¨at. Es gilt B

(t) ≥ 0 f ¨ur alle t ∈ [0, 1] und sogar B

(t) >

0 f ¨ur alle t ∈ (0, 1). Beide Eigenschaften folgen direkt aus der Definition.

2.3. B´ezierkurven

Randpunkte. Am linken Rand des Intervalls hat das erste Bernsteinpolynom den Funk- tionswert 1 und alle anderen 0. Am rechten Rand des Intervalls hat entsprechend das n-te Bernsteinpolynom den Funktionswert 1 und alle anderen 0. Diese Eigenschaft folgt eben- falls direkt aus der Definition.

Zerlegung der Eins. Diese Eigenschaft besagt, dass die Summe aller n + 1 Bernsteinpo- lynome n-ten Grades unabh¨angig von t genau 1 ergibt. Diese Eigenschaft l¨asst sich sehr schnell mithilfe des binomischen Lehrsatzes zeigen:

n

X

i=0

B

(t) =

n

X

i=0

Ç

n i

· t

· (1 − t)

= (t + (1 − t))

= 1

Hieraus folgt, mithilfe der Nichtnegativit¨at bzw. der Positivit¨at, dass B

(t) ≤ 1 f ¨ur alle t ∈ [0, 1] bzw. B

(t) < 1 f ¨ur alle t ∈ (0, 1) gilt.

Extrempunkte. Jedes Bernsteinpolynom besitzt im Intervall [0, 1] genau ein globales Ma- ximum. Dieses befindet sich an der Stelle t =

. F ¨ur die Bernsteinpolynome B

(t) und B

(t) ist dies trivialerweise erf ¨ullt. Es folgt n¨amlich, aus den oberen Eigenschaften, dass B

(t) = 1 falls t = 0 gilt und sonst B

(t) < 1. Analog gilt B

(t) = 1 falls t = 1 und sonst B

(t) < 1. F ¨ur die restlichen Polynome bildet man die erste Ableitung mithilfe der Produkt- und Kettenregel und setzt diese gleich Null. Man erh¨alt:

d

dt B

(t) =

n

i

· t

· (1 − t)

· (i − nt) = 0

⇐⇒ t = 0, t = 1 oder t = i n Aus den obigen Eigenschaften folgt, dass t = 0 und t = 1 Minima sind und t =

das Maximum bildet.

In Abbildung 2.3 k ¨onnen alle vier Eigenschaften f ¨ur den Fall n = 5 erkannt werden.

2.3. B´ezierkurven

F ¨ur die Konstruktion von B´ezierkurven brauchen wir zus¨atzlich noch sogenannte Kontroll- punkte P

, . . . , P

∈ R

. Diese werden mit den Bernsteinpolynomen B

(t), . . . , B

(t) gewichtet. Wir erhalten folgende Definition:

Definition 2.6 (B´ezierkurve)

Seien P

, . . . , P

∈ R

beliebige Punkte. Eine Kurve C = {X(t) | t ∈ [0, 1]} mit

X(t) =

n

X

i=0

B

(t) · P

2. Mathematische Grundlagen

heißt B´ezierkurve n-ten Grades.

Eine B´ezierkurve kann also eindeutig durch Kontrollpunkte bestimmt werden. Man nimmt in diesem Fall einfach die Anzahl der Punkte als n. Die Bernsteinpolynome werden dann eindeutig durch dieses n bestimmt.

B´ezierkurven gehen zwar nicht direkt durch die Kontrollpunkte, aber man kann mit die- sen sehr intuitiv den Verlauf der Kurve steuern. Hierzu kann man sich folgende Intuiti- on zu Hilfe nehmen: Man betrachtet die Kontrollpunkte als Magnete, die alle gleichzei- tig ein geladenes Teilchen anziehen. Die Anziehungskr¨afte dieser Magnete sind nicht alle gleich und jede einzelne variiert in Abh¨angigkeit von der Zeit t. Die Anziehungskraft des i-ten Magnets in Abh¨angigkeit von der Zeit t wird durch das Bernsteinpolynom B

(t) beschrieben und seine Position durch den Kontrollpunkt P

. Aufgrund der Maxima der Bernsteinpolynome ziehen die Magnete an unterschiedlichen Stellen des Intervalls [0, 1]

das Teilchen am st¨arksten: Der nullte Magnet zieht zum Zeitpunkt t = 0 am st¨arksten, der erste zum Zeitpunkt t =

, der zweite zum Zeitpunkt t =

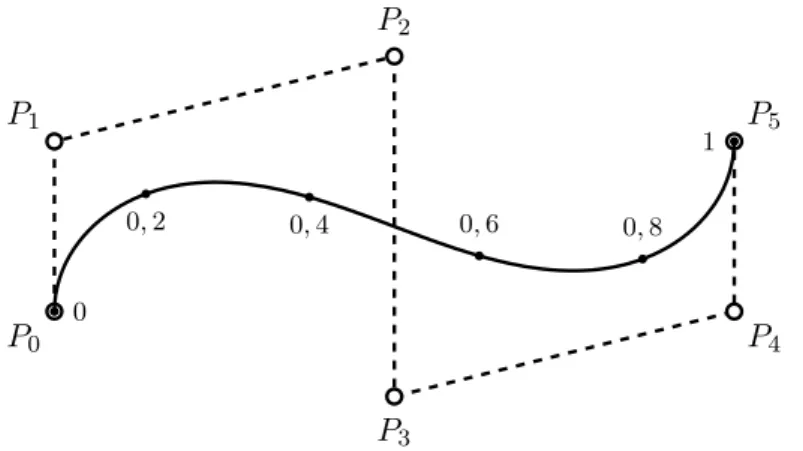
, usw. Betrachtet man nun die Bewegung des geladenen Teilchens im Zeitintervall [0, 1] so w ¨urde dieser den Verlauf der Kurve beschreiben. Abbildung 2.4 soll die Rolle der Kontrollpunkte und ihren Einfluss auf eine Beispielskurve veranschaulichen.

P

P

P

P

P

P

0

0,2 0,4 0,6 0,8

1

Abbildung 2.4.: Beispiel einer B´ezierkurve vom Grad n = 5 mit Kontrollpunkten P

, . . . , P

∈ R

und eingezeichneten Punkten X(0), X(0, 2), X(0, 4), X(0, 6), X(0, 8) und X(1).

Wir halten zwei wichtige Beobachtungen fest, die Folgerungen aus den Eigenschaften von Bernsteinpolynomen sind.

Endpunkte. Aufgrund des Verhaltens von Bernsteinpolynomen an den Randpunkten t = 0 und t = 1 gehen B´ezierkurven immer durch den ersten und den letzten Kontroll- punkt. In Abbildung 2.4 sind dies die Punkte P

und P

.

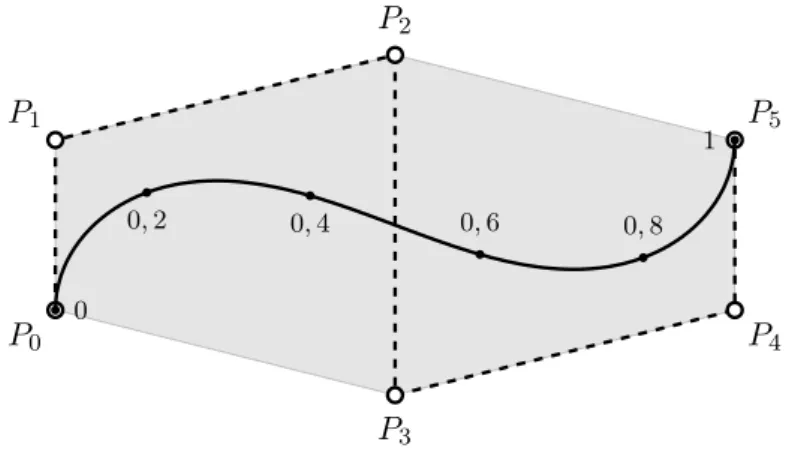
Konvexe H ¨ulle. Die Kurve liegt innerhalb der konvexen H ¨ulle des Kontrollpolygons. Die-

ses ist das kleinste Polygon, welches alle Kontrollpunkte beinhaltet (siehe Abbildung 2.5).

2.4. B-Spline-Basisfunktionen

Diese Eigenschaft besitzen alle B´ezierkurven. Sie folgt aus der Nichtnegativit¨at der Bern- steinpolynome und aus der Eigenschaft, dass diese eine Zerlegung der Eins bilden. Diese Eigenschaft wird f ¨ur uns eine wichtige Rolle spielen. Deshalb wird diese in Abschnitt 3.4 wieder aufgegriffen und ihre geometrische Bedeutung n¨aher betrachtet.

P

P

P

P

P

P

0

0,2 0,4 0,6 0,8

1

Abbildung 2.5.: B´ezierkurve aus Abbildung 2.4 mit eingezeichnetem Kontrollpolygon (grau).

2.4. B-Spline-Basisfunktionen

Bernsteinpolynome werden benutzt, um die Kontrollpunkte einer B´ezierkurve zu gewich- ten. B-Spline-Basisfunktionen erf ¨ullen bei den B-Splines dieselbe Aufgabe. Der Unterschied zu den Bernsteinpolynomen ist, dass das Intervall f ¨ur t die Form [t

, t

) f ¨ur beliebige t

und t

hat und in Subintervallen [t

, t

), [t

, t

), . . . , [t

, t

) aufgeteilt wird.

Definition 2.7 (B-Spline-Basisfunktionen)

F ¨ur einen gegebenen Vektor T = (t

, t

, . . . , t

) der L¨ange m sind die B-Spline-Basisfunktionen rekursiv definiert:

N

(t) =







I

(t) falls k = 1

t−t_i

ti+k−1−t_i

· N

(t) +

i+k−t_i+1

· N

(t) sonst I

ist hierbei die ¨ubliche Indikatorfunktion. Es gilt:

I

(t) =

(

1 falls t

≤ t ≤ t

0 sonst

Die Zahlen t

≤ t

≤ . . . ≤ t

werden Knoten genannt und T Knotenvektor. Die rekursi-

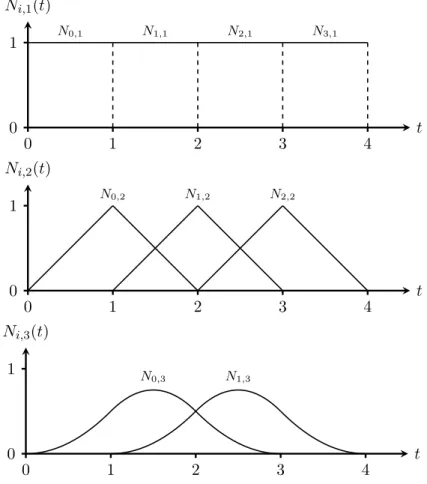
ve Definition von Basisfunktionen l¨asst sich sehr gut schematische als Netz darstellen. In

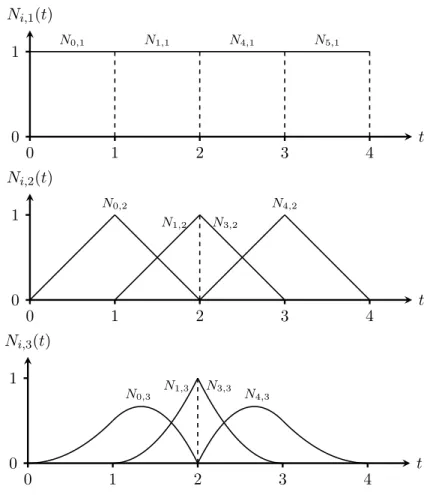
Abbildung 2.6 ist dieses Schema f ¨ur k = 1, . . . , 6 dargestellt.

2. Mathematische Grundlagen

[t

, t

) [t

, t

) [t

, t

) [t

, t

) [t

, t

) [t

, t

) N

N

N

N

N

N

N

N

N

N

N

N

N

N

N

N

N

N

N

N

N

Abbildung 2.6.: Schematische Darstellung f ¨ur die Berechnung aller Basisfunktionen mit k ≤ 6.

Wir wollen die Definition der B-Spline-Basisfunktionen an einem kleinen Beispiel sehen.

Wir rechnen hier die ersten drei Ebenen der Basisfunktionen per Hand.

Beispiel 2.8 (B-Spline-Basisfunktionen)

Sei T = (0, 1, 2, 3, 4) ein Knotenvektor. Wir berechnen alle Basisfunktionen f ¨ur k = 1, k = 2 und k = 3. F ¨ur k = 1 erhalten wir:

[0, 1) [1, 2) [2, 3) [3, 4)

N

(t) 1 0 0 0

N

(t) 0 1 0 0

N

(t) 0 0 1 0

N

(t) 0 0 0 1

F ¨ur den Fall k = 2 betrachten wir die Berechnung von N

(t). Wir erhalten:

N

(t) = t − t

t

− t

· N

(t) + t

− t t

− t

· N

(t)

= t · N

(t) + (2 − t) · N

(t)

=











t falls t ∈ [0, 1) 2 − t falls t ∈ [1, 2)

0 sonst

Die Berechnung von N

und N

verl¨auft analog. Wir erhalten f ¨ur k = 2:

2.4. B-Spline-Basisfunktionen

[0, 1) [1, 2) [2, 3) [3, 4)

N

(t) t 2 − t 0 0

N

(t) 0 t − 1 3 − t 0

N

(t) 0 0 t − 2 4 − t

F ¨ur den Fall k = 3 betrachten wir die Berechnung von N

(t). Wir erhalten:

N

(t) = t − t

t

− t

· N

(t) + t

− t

t

− t

· N

(t)

= t

2 · N

(t) + 3 − t

2 · N

(t)

=















1

2

t

falls t ∈ [0, 1)

−

(2t

− 6t + 3) falls t ∈ [1, 2)

1

2

(t − 3)

falls t ∈ [2, 3)

0 sonst

Analog erhalten wir f ¨ur N

(t):

N

(t) = t − t

t

− t

· N

(t) + t

− t t

− t

· N

(t)

= t − 1

2 · N

(t) + 4 − t

2 · N

(t)

=















1

2

(t − 1)

falls t ∈ [1, 2)

−

(2t

− 10t + 11) falls t ∈ [2, 3)

1

2

(4 − t)

falls t ∈ [3, 4)

0 sonst

Insgesamt erhalten wir f ¨ur k = 3:

[0, 1) [1, 2) [2, 3) [3, 4)

N

(t)

t

−

(2t

− 6t + 3)

(t − 3)

0 N

(t) 0

(t − 1)

−

(2t

− 10t + 11)

(4 − t)

In Abbildung 2.7 sind die Kurven zu allen im Beispiel berechneten Basisfunktionen abge- bildet. Man beachte im Fall k = 3, dass beide Kurven aus jeweils drei miteinander verbun- denen Polynomen zweiten Grades bestehen. Allgemein besitzt eine B-Spline-Basisfunktion h ¨ochstens den Grad k − 1.

B-Spline-Basisfunktionen besitzen ¨ahnliche Eigenschaften wie die Bernsteinpolynome. Wir

betrachten nur die zwei wichtigsten.

2. Mathematische Grundlagen

t N

(t)

0 1 2 3 4

0

1

t N

(t)

0 1 2 3 4

0

1

t N

(t)

0 1 2 3 4

0

1

0,3 N1,3

Abbildung 2.7.: Basisfunktionen N

aus Beispiel 2.8 f ¨ur k = 1, 2, 3.

Nichtnegativit¨at und Positivit¨at. Betrachtet man wieder Abbildung 2.6 auf Seite 10, so kann man zwei wichtige Beobachtungen machen:

• Die Basisfunktion N

(t) ist positiv im Intervall [t

, t

) und sonst Null.

• Im Intervall [t

, t

) sind h ¨ochstens k+1 Basisfunktionen auf der k-ten Ebene positiv.

Diese sind N

(t), N

(t), . . . , N

(t) (falls sie alle existieren).

Zerlegung der Eins. Diese Aussage besagt, dass die Summe aller Basisfunktionen auf der k-ten Ebene in jedem Intervall [t

, t

) f ¨ur i = k − 1, . . . , m − k genau Eins ist. Formal:

∀i ∈ {k, . . . , m − k}, t ∈ [t

, t

) :

i

X

j=i−k+1

N

(t) = 1 .

Der Beweis dieser Aussage wird vorgef ¨uhrt, weil der Leser von der G ¨ultigkeit der Aussage

¨uberzeugt sein sollte. Der Beweis erfolgt durch vollst¨andige Induktion ¨uber k. Weil der

Basisfall k = 1 trivial ist, wird nur der Induktionsschritt gezeigt:

2.5. B-Splines

i

X

j=i−(k+1)+1

N

(t)

=

i

X

j=i−k

Ç

t − t

t

− t

· N

(t) + t

− t t

− t

· N

(t)

=

i

X

j=i−k

Ç

t − t

t

− t

· N

(t)

+

i+1

X

j=i−k+1

Ç

t

− t

t

− t

· N

(t)

= t − t

t

− t

· N

(t)

| {z }

=0

+

i

X

j=i−k+1

Ç

t − t

t

− t

+ t

− t t

− t

å

| {z }

=1

·N

(t) + t

− t

t

− t

· N

(t)

| {z }

=0

=

i

X

j=i−k+1

N

(t) = 1

Man beachte, dass die Summe aller Basisfunktionen in der k-ten Ebene nur im Intervall [t

, t

) Eins ergibt. Im Allgemeinen ist dies in den Intervallen [t

, t

) und [t

, t

) nicht der Fall. Diese Aussage, zusammen mit der Nichtnegativit¨at und Positivit¨at von Ba- sisfunktionen, spielt eine sehr wichtige Rolle bei der Kontruktion von B-Splines.

2.5. B-Splines

Analog zu den B´ezierkurven benutzen wir B-Spline-Basisfunktionen als Gewichte f ¨ur Kon- trollpunkte.

Definition 2.9 (B-Spline)

Seien P

, P

, . . . , P

∈ R

beliebige Punkte und T = (t

, t

, . . . , t

) ein Knotenvektor der L¨ange m. Eine Kurve C = {X(t) | t ∈ [t

, t

)} mit

X(t) =

n−1

X

i=0

N

(t) · P

heißt B-Spline der Ordnung k.

Man beachte, dass B-Splines, im Gegensatz zu B´ezierkurven, durch die Kontrollpunkte nicht eindeutig bestimmt werden. B-Splines k ¨onnen n¨amlich auch durch die Wahl des Knotenvektors T beeinflusst werden.

Aufgrund der Eigenschaften von B-Spline-Basisfunktionen verhalten sich diese ¨ahnlich

wie die Bernsteinpolynome. Dies f ¨uhrt dazu, dass die Bedeutung der Kontrollpunkte f ¨ur

die entstehende Kurve dieselbe ist wie die f ¨ur B´ezierkurven. Abbildung 2.8 verdeutlicht

dies mit einem Beispiel.

2. Mathematische Grundlagen

P

P

P

P

P

P

P

P

P

P

P

P

P

P

t6

t7

t8

t9

t10

t11

t12

t13

t14

Abbildung 2.8.: Beispiel einer B-Spline-Kurve der Ordnung k = 7 mit n = 14 Kontroll- punkten P

, . . . , P

∈ R

und m = 21 Knoten t

, . . . , t

mit t

=

. Die Punkte X(t

), . . . , X(t

) sind auf der Kurve eingezeichnet worden.

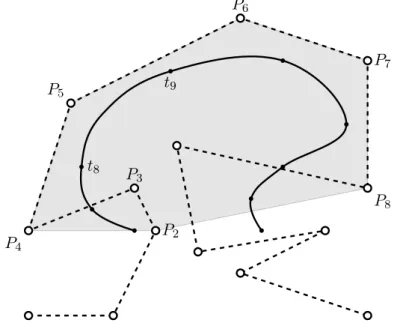
Analog zur schematischen Darstellung von B-Spline-Basisfunktionen lassen sich auch B- Splines schematisch darstellen. Diese Darstellung ist in Abbildung 2.9 zu finden. An ihr wird eine wichtige Beziehung zwischen der Anzahl n der Kontrollpunkten, der Anzahl m der Knoten und der Ordnung k erkannt. Es gilt n¨amlich f ¨ur jeden B-Spline die Gleichung

m = n + k .

P0 P1 P2 P3 P4 P5 P6 P7 P8 P9

[t0, t1) [t1, t2) [t2, t3) [t3, t4) [t4, t5) [t5, t6) [t6, t7) [t7, t8) [t8, t9) [t9, t10)[t10, t11[t)11, t12[t)12, t13) N10,3

N10,2 N11,2

N9,2 N9,3 N9,4

N0,1 N1,1 N2,1 N3,1 N4,1 N5,1 N6,1 N7,1 N8,1 N9,1

N0,2 N1,2 N2,2 N3,2 N4,2 N5,2 N6,2 N7,2 N8,2 N9,2

N0,3 N1,3 N2,3 N3,3 N4,3 N5,3 N6,3 N7,3 N8,3 N9,3

N0,4 N1,4 N2,4 N3,4 N4,4 N5,4 N6,4 N7,4 N8,4 N9,4

Abbildung 2.9.: Rekursives Berechnungsschema f ¨ur B-Splines am Beispiel einer B-Spline-

Kurve mit k = 4, n = 10 und m = n + k = 14.

2.5. B-Splines

Lokalit¨atseingenschaft. Eine sehr wichtige Eigenschaft von B-Spline-Kurven ist die so- genannte Lokalit¨atseigenschaft. Diese folgt aus dem rekursiven Berechnungsschema von Ba- sisfunktionen und besagt, dass jeder Kontrollpunkt P

die Kurve nur im Intervall [t

, t

) beeinflusst. Dies kann man ebenfalls an Abbildung 2.9 erkennen. Insbesondere besagt die- se Aussage, dass die Kurve im Intervall [t

, t

) nur durch die Kontrollpunkte P

, . . . , P

bestimmt wird.

Konvexe H ¨ullen einer B-Spline-Kurve. Aus der Lokalit¨atseigenschaft und den zwei vorgestellten Eigenschaften von Basisfunktionen folgt, dass die Kurve f ¨ur t ∈ [t

, t

) in der konvexen H ¨ulle des durch die Punkte P

, . . . , P

bestimmten Polygons liegt (siehe Abbildung 2.10). Aus diesem Grund wurde, in der Definition von B-Splines, nicht das ge- samte Intervall [t

, t

) f ¨ur t gew¨ahlt. Die Summe der Basisfunktionen ist n¨amlich nicht im gesamten Intervall Eins, sondern nur im Intervall [t

, t

). W ¨urde man das gesam- te Intervall w¨ahlen, so k ¨onnte die Kurve die konvexe H ¨ulle des Kontrollpunktepolygons verlassen, was f ¨ur den Zweck dieser Arbeit unerw ¨unscht w¨are. Diese Eigenschaft ist von besonderer Wichtigkeit. Im Abschnitt 3.4 werden wir diese der entsprechenden Aussage bei B´ezierkurven gegen ¨uberstellen.

P

P

P

P

P

P

P

t

t

Abbildung 2.10.: B-Spline-Kurve aus Abbildung 2.8 mit Ordnung k = 7, Kontrollpunkten

P

, . . . , P

∈ R

und Knotenvektor T = (t

, . . . , t

). Die Kurve ist f ¨ur t ∈

[t

, t

) vollst¨andig in der konvexen H ¨ulle der Punkte P

, . . . , P

enthalten.

2. Mathematische Grundlagen

3. Wichtige Eigenschaften von B-Splines

B ^-S

sind durch ihre Definition etwas komplizierter als B´ezierkurven. Sie be- sitzen jedoch Eigenschaften, die B´ezierkurven nicht besitzen aber f ¨ur diese Arbeit große Relevanz haben. Diese h¨angen n¨amlich sehr eng mit der Wahl der Knoten t

, . . . , t

zusammen. In diesem Kapitel wird dargestellt, wie man die Knoten eines B- Splines manipulieren kann und welche Effekte diese Ver¨anderungen haben k ¨onnen. An- schließend wird ein wichtiger Zusammenhang zwischen B´ezierkurven und B-Splines her- gestellt. Am Ende des Kapitels wird eine Methode diskutiert, mit der man einem B-Spline neue Knoten hinzuf ¨ugen kann.

3.1. Mehrfachknoten und eingespannte B-Splines

Dem aufmerksamen Leser wird nicht entgangen sein, dass die einzige Anforderung an den Knotenvektor T = (t

, . . . , t

), n¨amlich t

≤ t

≤ . . . ≤ t

, nicht ausschließt, dass zwei oder mehr Knoten denselben Wert haben. Ein Knoten darf mehrmals vorkommen.

Kommt ein Knoten s mal vor, so spricht man von einem s-fachen Knoten bzw. von einem Knoten mit Multiplizit¨at s. Die Tatsache, mehrere Kopien desselben Knotens benutzen zu d ¨urfen, erweitert die M ¨oglichkeiten beim Einsetzen von B-Splines, um Kurven darzustel- len. So k ¨onnen zum Beispiel Unstetigkeiten erzeugt werden wie spitze Ecken. Bei der Be- rechnung der Basisfunktionen ist allerdings etwas Vorsicht geboten. Kommt n¨amlich ein Knoten mehrmals vor, so begegnet man dem Fall, dass ein Bruch eine Null im Nenner stehen hat. Es wird gezeigt wie dieses Problem auf eine sehr einfache Art umgangen wer- den kann, ohne zu sehr auf technischen Details einzugehen. Voraussetzung daf ¨ur ist, dass alle bisher gezeigten Eigenschaften von B-Spline-Basisfunktionen und -Kurven auch bei Mehrfachknoten erhalten bleiben.

Wie Mehrfachknoten funktionieren und was sie f ¨ur Konsequenzen haben, wird an einem Beispiel illustriert.

Beispiel 3.1 (Mehrfachknoten)

Man betrachte den Knotenvektor T = (t

, t

, t

, t

, t

, t

, t

) = (0, 1, 2, 2, 2, 3, 4) mit dem Drei-

fachknoten 2. Auch hier werden alle Basisfunktionen f ¨ur die F¨alle k = 1, k = 2 und k = 3,

beginnend mit dem Fall k = 1.

3. Wichtige Eigenschaften von B-Splines

[0, 1) [1, 2) [2, 3) [3, 4)

N

(t) 1 0 0 0

N

(t) 0 1 0 0

N

(t) 0 0 0 0

N

(t) 0 0 0 0

N

(t) 0 0 1 0

N

(t) 0 0 0 1

Man erkennt, dass die Subintervalle [t

, t

) und [t

, t

) nicht existieren und die entsprechenden Basisfunktionen N

(t) und N

(t) beide konstant Null sind. Die Folgen hiervon begegnet man in der Berechnung von N

(t):

N

(t) = t − t

t

− t

· N

(t) + t

− t

t

− t

· N

(t)

= (t − 1) · N

(t) + 2 − t

0 · N

(t)

| {z }

:=0

= (t − 1) · N

(t)

=

(

t falls t − 1 ∈ [0, 1) 0 sonst

Nach mehreren Rechnungen erh¨alt man f ¨ur k = 2 und k = 3 folgende Ergebnisse:

[0, 1) [1, 2) [2, 3) [3, 4)

N

(t) t 2 − t 0 0

N

(t) 0 t − 1 0 0

N

(t) 0 0 0 0

N

(t) 0 0 3 − t 0

N

(t) 0 0 t − 2 4 − t

[0, 1) [1, 2) [2, 3) [3, 4)

N

(t)

t

−

(3t

− 16t + 20) 0 0

N

(t) 0 (t − 1)

0 0

N

(t) 0 0 (3 − t)

0

N

(t) 0 0 −

(3t

− 4t + 5)

(4 − t)

In Abbildung 3.1 sind die Graphen aller berechneten Basisfunktionen abgebildet.

Der Grund wieso in der Rechnung der Term

· N

(t) als Null definiert wurde ist, dass obwohl der Bruch nicht definiert ist, dieser trotzdem nur auf das Intervall [t

, t

) Einfluss h¨atte. Da aber [t

, t

) = [1, 1) = ∅ gilt konnte der Term ohne Weiteres ignoriert werden.

Betrachtet man wieder die Definition der Basisfunktionen, so stellt man fest, dass solche

3.1. Mehrfachknoten und eingespannte B-Splines

t N

(t)

0 1 2 3 4

0

1

t N

(t)

0 1 2 3 4

0

1

1,2 N3,2

N4,2

t N

(t)

0 1 2 3 4

0 1

N0,3

N1,3 N3,3

N4,3

Abbildung 3.1.: Basisfunktionen N

aus Beispiel 2.8 f ¨ur k = 1, 2, 3.

Situationen immer bei Termen der Form

b−ta

· N

(t) vorkommen. Da bekannt ist, dass N

(t) nur im Intervall [a, b) positiv ist, so kann der Term stets vernachl¨assigt werden.

Man vergleiche die Kurven f ¨ur k = 3 mit den Kurven in Abbildung 2.7 auf Seite 12. Diese entstandene Unstetigkeit an der Stelle t = 2 ist charakteristisch f ¨ur Mehrfachknoten. Diese

¨ubertr¨agt sich nat ¨urlich auf den jeweiligen B-Spline.

Mehrfachknoten eignen sich nicht nur gut, um Kurven mit Ecken und spitzen Winkeln darzustellen, sondern auch um zu erzwingen, dass die Kurve durch bestimmte Punk- te verl¨auft. Der in Abbildung 2.8 auf Seite 14 dargestellte B-Spline ist aus genau diesem Grund nicht zufriedenstellend. Ihm fehlt die Eigenschaft beide Endpunkte zu ber ¨uhren.

Man kann zwar den Verlauf der Kurve intuitiv mithilfe der Kontrollpunkte beeinflussen, jedoch nicht wo diese anf¨angt oder aufh ¨ort. Aus diesem Grund nimmt man sich Mehr- fachknoten zu Hilfe um die B-Spline-Kurve an den zwei ¨außeren Knotrollpunkten P

und P

einspannen.

Aus Abschnitt 2.4 wissen wir, dass die Summe der Basisfunktionen in der k-ten Ebene im

Intervall [t

, t

) Eins ergibt. W¨ahlt man dazu den Knotenvektor wie folgt:

3. Wichtige Eigenschaften von B-Splines

T = (t

, . . . , t

| {z }

gleiche Knoten

, t

, . . . , t

| {z }

innere Knoten

, t

, . . . , t

| {z }

gleiche Knoten

) ,

dann erh¨alt man: N

(t

) = 1 und N

(t

) = 1. Das bedeutet, dass die Kurve, analog zu den B´ezierkurven, durch die Endpunkte P

und P

gehen w ¨urde. Ein Beispiel f ¨ur eine solche eingespannte Kurve wird in Abbildung 3.2 dargestellt.

P

P

P

P

P

P

P

P

0

1

2

3 4

Abbildung 3.2.: Eingespannter B-Spline der Ordnung k = 5 mit Kontrollpunkten P

, . . . , P

∈ R

und Knotenvektor T = (0, 0, 0, 0, 0, 1, 2, 3, 4, 4, 4, 4, 4).

3.2. Zusammenhang zwischen B´ezierkurven und B-Splines

B´ezierkurven bilden eine Teilklasse der B-Splines. Bestimmte B-Splines lassen sich n¨amlich in B´ezierkurven ¨uberf ¨uhren, ohne dass sich die jeweilige Kurve ver¨andert. Diese m ¨ussen eingespannt sein und d ¨urfen keine innere Knoten besitzen. Das heißt, dass sie einen Kno- tenvektor der Form

T = (t

, . . . , t

| {z }

gleiche Knoten

, t

, . . . , t

| {z }

gleiche Knoten

)

besitzen m ¨ussen. Ed folgt eine Veranschaulichung durch ein Beispiel.

Beispiel 3.2 (B-Spline-Basisfunktionen als Bernsteinpolynome.)

Gegeben seien die Kontrollpunkte P

, . . . , P

∈ R

und der Knotenvektor T = (0, 0, 0, 0, 0, 1, 1, 1, 1, 1).

Gesucht ist eine B-Spline-Kurve

X(t) =

4

X

i=0

N

(t) · P

f ¨ur t ∈ [0, 1)

3.2. Zusammenhang zwischen B´ezierkurven und B-Splines

der Ordnung k = 5 ¨uber T. Da nur ein Subintervall zu betrachten ist, n¨amlich [0, 1), fallen viele Basisfunktionen weg. Die ¨ubriggebliebenen werden sukzessiv f ¨ur genau dieses Subintervall berechnet. Man erh¨alt folgende Basisfunktionen:

N

(t) = 1

N

(t) = (1 − t) · N

(t) = 1 − t

N

(t) = t · N

(t) = t

N

(t) = (1 − t) · N

(t) = (1 − t)

N

(t) = t · N

(t) + (1 − t) · N

(t) = 2 · t · (1 − t)

N

(t) = t · N

(t) = t

N

(t) = (1 − t) · N

(t) = (1 − t)

N

(t) = t · N

(t) + (1 − t) · N

(t) = 3 · t · (1 − t)

N

(t) = t · N

(t) + (1 − t) · N

(t) = 3 · t

· (1 − t)

N

(t) = t · N

(t) = t

N

(t) = (1 − t) · N

(t) = (1 − t)

N

(t) = t · N

(t) + (1 − t) · N

(t) = 4 · t · (1 − t)

N

(t) = t · N

(t) + (1 − t) · N

(t) = 6 · t

· (1 − t)

N

(t) = t · N

(t) + (1 − t) · N

(t) = 4 · t

· (1 − t)

N

(t) = t · N

(t) = t

Vergleicht man nun die Basisfunktionen aus diesem Beispiel mit den Bernsteinpolynomen aus dem Beispiel aus Abschnitt 2.2, so erkennt man Beziehung

N

(t) =

4

i

· t

· (1 − t)

= B

(t)

f ¨ur i = 0, 1, 2, 3. Insbesondere entspricht die B-Spline-Kurve

N

(t) · P

genau der B´ezierkurve

B

(t) · P

. Diesen Sachverhalt l¨asst sich f ¨ur beliebige Knotenvektoren T = (a, . . . , a, b, . . . , b), bestehend aus k as und k bs, verallgemeinern. Man erh¨alt in diesem Fall f ¨ur i = 0, . . . , k − 1 die Basisfunktionen

N

(t) =

Ç

k − 1 i

å

·

Å

t − a b − a

ã_i

·

b − t

b − a

,

welche sich durch die Projektion des Intervalls [a, b) auf das Intervall [0, 1) wieder in Bern-

steinpolynome ¨uberf ¨uhren lassen. Man setze t := (b − a)u + a f ¨ur ein u ∈ [0, 1) und erh¨alt:

3. Wichtige Eigenschaften von B-Splines

N

(t) =

Ç

k − 1 i

å

·

Å

t − a b − a

ã_i

·

b − t

b − a

=

Ç

k − 1 i

å

·

Ç

((b − a)u + a) − a b − a

å_i

·

Ç

b − ((b − a)u + a) b − a

å_k−i−1

=

Ç

k − 1 i

å

· u

· (1 − u)

= B

(u)

Aus diesem Grund k ¨onnen die Kontrollpunkte einer solchen B-Spline-Kurve direkt als Kontrollpunkte f ¨ur eine B´ezierkurve desselben Grades ¨ubernommen werden. Die Kurve bleibt dabei unver¨andert.

3.3. Einf ¨ugen von B-Spline-Knoten

Die f ¨ur diese Arbeit wichtigste Eigenschaft von B-Splines ist, dass beliebige Knoten in den Knotenvektor hinzugef ¨ugt werden k ¨onnen, ohne die Form der Kurve zu ver¨andern. Er- innert man sich an die Gleichung m = n + k, welche die Anzahl an Knoten eindeutig durch die Anzahl der Kontrollpunkte und die Ordnung der Kurve bestimmt, so stellt man Folgendes fest: Beim Hinzuf ¨ugen eines Knotens, m ¨usste man, entweder die Ordnung der Kurve erh ¨ohen oder einen weiteren Kontrollpunkt hinzuf ¨ugen, damit das Verh¨altnis nicht zerst ¨ort wird. Die Technik hierf ¨ur bestimmt die Koordinaten eines neuen Kontrollpunktes welcher problemlos hinzugef ¨ugt werden kann, ohne die Gestalt der Kurve zu ver¨andern.

Diese wurde 1980 von Wolfgang Boehm entwickelt. In diesem Abschnitt wird diese Me- thode erkl¨art. F ¨ur eine detailliertere Beschreibung sei der Leser auf [2] verwiesen.

Gegeben seien Kontrollpunkte P

, . . . , P

, einen Knotenvektor T = (t

, . . . , t

, t

, . . . , t

) und ein Knoten t

∈ [t

, t

), welcher in T hinzuf ¨ugt werden soll. Ziel dieser Methode ist es, k der Kontrollpunkte durch k + 1 weiter so zu ersetzen, dass die Kurve dadurch nicht ver¨andert wird. Aus Abschnitt 2.5 ist bekannt, dass nur die Punkte P

, . . . , P

betrachtet werden m ¨ussen. Die Vorgehensweise ist Folgende:

1. Berechnung der Hilfsvariablen l

, . . . , l

mithilfe der Formel:

l

= t

− t

t

− t

(j = 0, . . . , k) .

2. Zuhilfenahme dieser Hilfsvariablen f ¨ur die Berechnung von Hilfspunkten P

, . . . , P

. Es gilt:

P

= (1 − l

) · P

+ l

· P

(j = 0, . . . , k) .

3. Ersetzen der Punkte P

, . . . , P

durch die Hilfspunkte P

, . . . , P

. Die nicht be-

troffenen Punkte bleiben erhalten.

3.4. Konsequenzen der Lokalit¨atseigenschaft

Wir illustrieren dies Anhand eines Beispiels.

Beispiel 3.3 (Einf ¨ugen eines B-Spline-Knotens)

Sei k = 4 die Ordnung eines B-Splines mit Knotenvektor T = (0, 1, 2, 3, 4, 6, 7, 8, 9, 10) und Kontrollpunkten

P

=

0

0

, P

=

0

1

, P

=

1

2

, P

=

3

2

, P

=

4

1

, P

=

4

0

. Der Knoten t

= 5 ∈ [4, 6) soll nach obigem Schema als neuer Knoten hinzugef ¨ugt werden.

1. F ¨ur die Hilfsvariablen l

, l

, l

, l

, l

erh¨alt man:

l

= 5 − 1

5 − 1 = 1 , l

= 5 − 2 6 − 2 = 3

4 , l

= 5 − 3 7 − 3 = 1

2 , l

= 5 − 4 8 − 4 = 1

4 , l

= 5 − 5 9 − 5 = 0 . 2. Daraus ergeben sich folgende Hilfspunkte:

P

= (1 − 1) ·

0

0

+ 1 ·

0

1

=

0

1

, P

=

Å

1 − 3

4

·

0

1

+ 3 4 ·

Ç

1 2

=

47 4

å

, P

=

Å

1 − 1

2

·

1

2

+ 1 2 ·

Ç

3 2

=

2

2

, P

=

Å

1 − 1

4

·

3

2

+ 1 4 ·

Ç

4 1

=

47 4

å

, P

= (1 − 0) ·

Ç

4 1

+ 0 ·

4

0

=

4

1

.

3. Die Punkte P

, P

, P

, P

werden durch die Punkte P

, P

, P

, P

, P

ersetzt. Die neuen Kontrollpunkte der Kurve sind dann P

, P

, P

, P

, P

, P

und P

.

In dem Beispiel werden die Segmente P

P

, P

P

, P

P

, P

P

und P

P

durch die Hilfs- punkte zweigeteilt. Die Hilsvariablen l

, l

, l

, l

, l

stellen die L¨angenverh¨altnisse dieser Zweiteilungen dar. In Abbildung 3.3 ist dieser Zusammenhang zu erkennen.

3.4. Konsequenzen der Lokalit¨atseigenschaft

Obwohl in der Regel weder bei B´ezierkurven noch bei B-Splines die Kontrollpunkte di-

rekt auf der Kurve liegen, eignen sich beide Modelle sehr gut f ¨ur die Darstellung von

handgezeichneten Kurven. Der Grund hierf ¨ur ist, dass es in der Praxis viele Punkte ge-

ben wird, die sehr nah aneinander liegen. In der Regel betr¨agt der Abstand zwischen

zwei benachbarten Punkten in WriteBird nicht mehr als 5 Pixel. Jedoch, wie im Kapitel