Eine Kreispyramide im Dreieck
San-Gaku R¨atsel 30. August 2014
c b
A B
C
c
r3
r2
b
r1
k
D E
M
F G
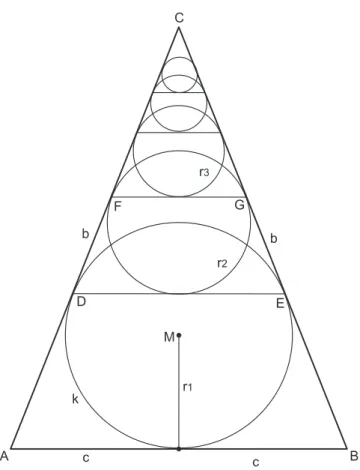
Abbildung 1: Skizze zur Aufgabe
Gegeben sei das gleichschenklige Dreieck A, B, C mit den Seitenl¨angen b =AC =BC und 2c = AB. Dem Dreick ist der Inkreis k mit Radius r1 einbeschrieben. Der Inkreis ber¨uhrt die Dreieckseiten AC, BCin den PunktenD, E. Dem DreieckD, E, C ist ebenfalls der Inkreis mit Radius r2 einbeschrieben (Abb. 1). Er ber¨uhrt die Dreieckseiten in den Punkten F, G. Dem Dreieck C, F, Gwird der Inkreis mit Radius r3 einbeschrieben. Nach gleichem Schema werden weitere Dreiecke und Inkreise dem Dreieck A, B, C einbeschrie- ben. Bestimme die Radien der Kreiser1, r2, r3. . . ri in Abh¨angigkeit von b, c. Berechne die unendliche Summe der Kreisfl¨acheninhalte aller dieser Inkreise.
1
Eine Kreispyramide im Dreieck
L¨ osungsvorschlag
c r1
m
c b-c-a
b-c
A B
C
r1
a r2
a
c
D E
M
F K
L
G
c
a
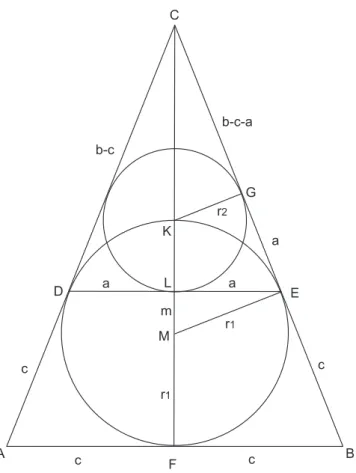
Abbildung 2: Skizze zur L¨osung
Die Punkte- und Streckenbezeichner seien nach Abbildung 2 gew¨ahlt. Vom Punkt B sind die Tangentenabschnitte an den Inkreis k gleich lang:
c=BD=BE (1)
ebenso die Tangentenabschnitte vom Punkt E and den Inkreis von Dreieck DEC:
a=EL=EG (2)
und vom Punkt C an den Inkreis k:
b−c=CD =CE (3)
Alle in Zeichnung 2 erkennbaren rechtwinkligen Dreicke sind einander ¨ahnlich. Wir k¨onnen folgende Verh¨altnisse aufstellen:
b−c a = b
c → a= (b−c)·c
b (4)
2
Eine Kreispyramide im Dreieck
c r1
m
c b-c-a
b-c
A B
C
r1
a r2
a
c
D E
M
F K
L
G
c
a
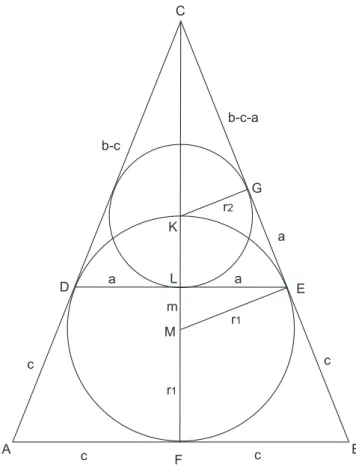
Abbildung 3: Skizze zur L¨osung
b−c−a
r2 = b−c
r1 → r2 = (b−c−a)·r1
b−c (5)
Wir ersetzen a mit dem Ergebnis aus (4) und erhalten:
r2 = (b−c− (b−bc)·c)·r1
b−c =r1 −r1·c b =r1·
1−c b
(6) Der n¨achst kleinere Radius kann also aus dem vorhergenden Radius und dem Verh¨altnis der anliegenden Seiten berechnet werden. Das Verh¨altnis der anliegenden Seiten bleibt aber immer gleich c÷b, wie die folgenden Rechnung zeigt:
r3 =r2 ·
1− a b−c
=r2·
1−(b−c)·c b·(b−c)
=r2·
1−c b
(7)
Wenn wir r2 in der letzten Gleichung durchr1 ersetzen, erhalten wir:
r3 =r2 ·
1− c b
=r1·
1− c b
2
→ ri =r1·
1− c b
i−1
(8) 3
Eine Kreispyramide im Dreieck
Die Summe der Kreisfl¨acheninhalte betr¨agt dann:
F =π·(r1)2·
∞
X
i=1
1− c b
2 (i−1)
= π b2r12
2b c−c2 (9)
Der Inkreisadius r1 kann im gleichschenkligen Dreieck ABC aus der H¨ohe h = √ b2−c2 und der Verh¨altnisgleichung
h−r1 r1 = b
c → r1 = c√ b2−c2
b+c (10)
bestimmt werden. F¨ur den Fl¨acheninhalt aller Kreise erhalten wir schließlich:
F =
π b2
c√ b2−c2
b+c
2
2b c−c2 = π b2c(b−c)
(2b−c) (b+c) (11)
Eine N¨ aherungsformel f¨ ur π
5 10 15
b 0.8
1.0 1.2 1.4 1.6 1.8 2.0 v
H1+bL H-1+2 bL -1+b2 H-1+bLb2Π
H2+bL H-2+2 bL -4+b2 H-2+bLb2Π
H3+bL H-3+2 bL -9+b2 H-3+bLb2Π
H4+bL H-4+2 bL -16+b2 H-4+bLb2Π
H5+bL H-5+2 bL -25+b2 H-5+bLb2Π
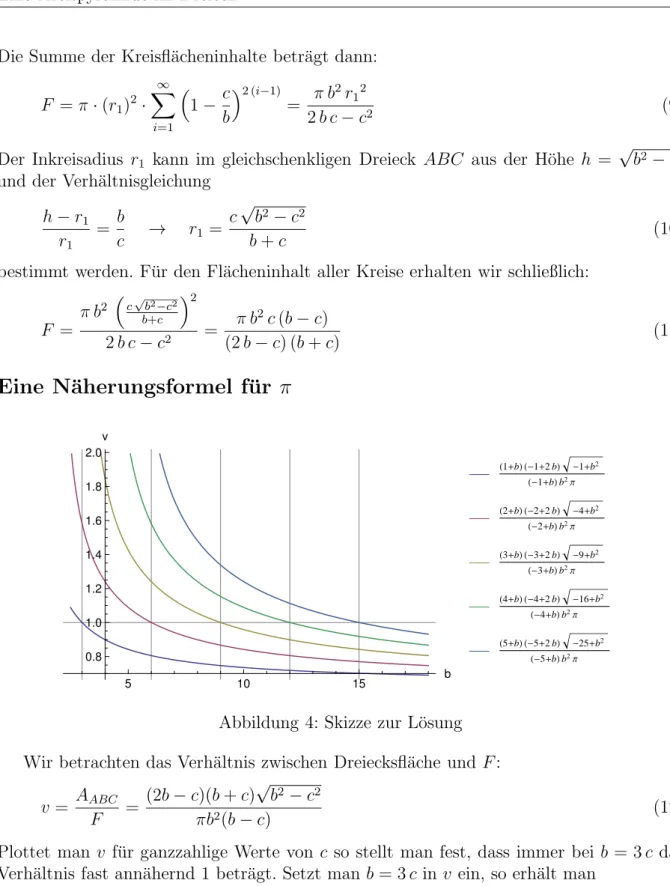
Abbildung 4: Skizze zur L¨osung Wir betrachten das Verh¨altnis zwischen Dreiecksfl¨ache und F:
v = AABC
F = (2b−c)(b+c)√ b2−c2
πb2(b−c) (12)
Plottet man v f¨ur ganzzahlige Werte von c so stellt man fest, dass immer bei b = 3c das Verh¨altnis fast ann¨ahernd 1 betr¨agt. Setzt man b= 3cin v ein, so erh¨alt man
b= 3c → v = 20√ 2
9π ≈1.000351462 → π≈ 20√ 2
9 (13)
eine N¨aherungsformel f¨ur π.
4