Theoretische Physik in zwei Semestern II Teil B: Thermodynamik und statistische Physik Joachim Krug

Teil B: Thermodynamik und statistische Physik

Joachim Krug

Institut f¨ur Theoretische Physik, Universit¨at zu K¨oln E-mail: krug@thp.uni-koeln.de

Thermodynamik und statistische Physik befassen sich mit makroskopischen Systemen mit vielen mikroskopischen Freiheitsgraden. Zur Erl¨auterung dieser Begriffe betrachten wir eine makroskopische Menge (z.B. 1 Mol) eines (einatomigen) Gases.

• Mikroskopische Beschreibung:

Im Rahmen der klassischen Mechanik wird das System beschrieben durch die Orte { ~r

}

und Impulse { ~p

}

der N Atome, wobei N von der Gr¨ossenordnung der Avogadro-Zahl N

≈ 6 × 10

ist. Das System hat somit 6N mikroskopische Freiheitsgrade. In der Quantenmechanik beschreibt man das System durch einen N -Teilchen-Zustand ψ(~r

, ~r

, ..., ~r

, t).

• Makroskopische (thermodynamische) Beschreibung:

Das System wird beschrieben durch wenige makroskopische Zustandsgr¨ossen wie z.B. Druck P , Temperatur T , Volumen V und Teilchenzahl N . Diese sind durch Zustandsgleichungen verkn¨ upft, wie z.B. durch die thermische Zustandsgleichung des klassischen idealen Gases

P V = N k

T. (0.1)

Hier bezeichnet k

≈ 1.3803 × 10

J/K die Boltzmann-Konstante, die durch R = N

k

mit der universellen Gaskonstante R zusammenh¨angt.

Die Thermodynamik (TD) im engeren Sinne ist die makroskopische Theorie der W¨arme. Zwei ihrer zentrale Themen sind

• W¨arme und Arbeit als Formen von Energie (1. Hauptsatz der TD)

• Bedingungen der Umwandlungen von Arbeit und W¨arme (2. Hauptsatz der TD, Begriff der Entropie).

Die statistische Physik dient einerseits der Begr¨ undung thermodynamischer Begriffe

und Zusammenh¨ange auf der Grundlage von mikroskopischen Modellen, andererseits

stellt sie Methoden zur Berechnung thermodynamischer Gr¨ossen f¨ ur spezifische

Substanzen bereit.

Ein wichtiger Grund f¨ ur den Erfolg der thermodynamischen Betrachtungsweise ist ihre Universalit¨at ; damit ist der Umstand gemeint, dass die Begriffe und Vorhersagen der Thermodynamik oft nur wenig von den zugrundegelegten mikroskopischen Modellen abh¨angen. Nur so ist zu verstehen, dass die Thermodynamik bereits Mitte des neunzehnten Jahrhunderts in ihrer bis heute g¨ ultigen Form entwickelt werden konnte, zu einem Zeitpunkt also, als ¨ uber den mikroskopischen Aufbau der Materie noch keine Klarheit herrschte, und dass sie die Revolutionen der Physik im zwanzigsten Jahrhunder unbeschadet ¨ uberstanden hat. Albert Einstein formulierte das wie folgt:

“Eine Theorie ist desto eindrucksvoller, je gr¨oßer die Einfachheit ihrer Pr¨amissen ist, je verschiedenartigere Dinge sie verkn¨ upft und je weiter ihr Anwendungsbereich ist.

Deshalb der tiefe Eindruck, den die klassische Thermodynamik auf mich machte.

Es ist die einzige physikalische Theorie allgemeinen Inhaltes, von der ich ¨ uberzeugt bin, daß sie im Rahmen der Anwendbarkeit ihrer Grundbegriffe niemals umgestoßen werden wird.”

1. Grundz¨ uge der Thermodynamik

Vorbemerkung: Zentrale thermodynamische Begriffe wie Temperatur und W¨arme werden im folgenden zun¨achst in einem relativ unscharfen, ph¨anomenologischen Sinn benutzt. Die pr¨azise mathematische Formulierung der Theorie werden wir nach und nach entwickeln.

1.1. Thermische Gleichgewichtszust¨ande

Wir gehen aus von der Existenz von Gleichgewichtszust¨anden als Erfahrungstatsache:

Von ihrer Umgebung abgeschlossene makroskopische Systeme streben Gleich- gewichtszust¨anden (GWZ) zu, deren Eigenschaften r¨aumlich homogen † und zeitunabh¨angig sind, und die sich durch wenige makroskopische Zustandsgr¨ossen beschreiben lassen. Der GWZ ist unabh¨angig von der Vorgeschichte des Systems.

In der Beschreibung von GWZ kommen zwei Typen von Zustandsgr¨ossen vor:

• extensive Zustandsgr¨ossen sind (unter ansonsten identischen Bedingungen) proportional zur Stoffmenge, z.B. das Volumen V und die Teilchenzahl N .

• intensive Zustandsgr¨ossen sind (unter ansonsten identischen Bedingungen) unabh¨angig von der Stoffmenge, z.B. der Druck P und die Temperatur T .

Wir k¨onnen diese Begriffe an der Zustandgleichung (0.1) des idealen Gases illustrieren:

Verdoppelt man die Stoffmenge, also N → 2N und V → 2V , so bleibt die Gleichung g¨ ultig, wenn P und T sich nicht ¨andern.

† Eine Ausnahme bilden Systeme, in denen mehrere Phasen koexistieren, z.B. Eis und Wasser am Schmelzpunkt.

Intensive Zustandsgr¨ossen bestimmen insbesondere die Gleichgewichtsbedin- gungen, die sich einstellen, wenn zwei Systeme miteinander in Kontakt gebracht wer- den. Wir betrachten zwei F¨alle:

• Mechanischer Kontakt/Volumenaustausch: Ein Gef¨ass mit Volumen V = V

+ V

wird durch eine bewegliche, aber w¨arme- und materieundurchl¨assige Wand in zwei Teilvolumina V

und V

unterteilt. Mechanisches Gleichgewicht stellt sich ein, wenn die Dr¨ ucke in beiden Teilvolumina gleich sind, also

P

= P

(mechanisches Gleichgewicht). (1.1)

• Thermischer Kontakt/W¨ armeaustausch: Hier wird das Gef¨ass durch eine unbewegliche, aber w¨armedurchl¨assige Wand geteilt. Wenn das thermische Gleichgewicht sich eingestellt hat, sind die Temperaturen in beiden Teilen gleich, also

T

= T

(thermisches Gleichgewicht). (1.2) Es wurde W¨arme zwischen den beiden Teilsystemen ausgetauscht. Zur Beschreibung dieses Vorgangs m¨ ussen wir die innere Energie E als weitere Zustandsgr¨osse einf¨ uhren. Beim W¨armeaustausch ist die Gesamtenergie E = E

+ E

erhalten.

Mikroskopisch gesehen ist die innere Energie die Summe der kinetischen und potentiellen Energien der Atome, also in einem klassischen Modell

E =

N

X

i=1

| ~p

|

2m

+ V (~r

, ..., ~ r

). (1.3) Geschwindigkeiten und Impulse sind hier bzgl. des Schwerpunktsystems zu messen, eine kollektive Bewegung des Gesamtsystems tr¨agt zur inneren Energie nicht bei. Im idealen Gas werden die Wechselwirkungen zwischen den Atomen vernachl¨assigt. Die potentielle Energie enth¨alt dann nur den Beitrag des einschliessenden Kastenpotentials U (~r), V (~r

, ..., ~ r

) = P

i=1

U (~r

). Die zentrale Bedeutung der Energie in der Thermodynamik ergibt sich aus der Tatsache, dass sie als einzige der mechanischen Erhaltungsgr¨ossen mit den typischen Randbedingungen thermodynamischer Systeme kompatibel ist: Der Gesamtimpuls eines in einem Kasten eingeschlossenen Gases ist wegen der St¨oße mit den W¨anden nicht erhalten, und Drehimpulserhaltung gilt nur f¨ ur rotationsymmetrische K¨asten.

Die innere Energie ist eine extensive Zustandsgr¨osse. F¨ ur das einatomige ideale Gas gilt die kalorische Zustandsgleichung

E = 3

2 N k

T. (1.4)

Die innere Energie eines idealen Gases ist unabh¨angig vom Volumen.

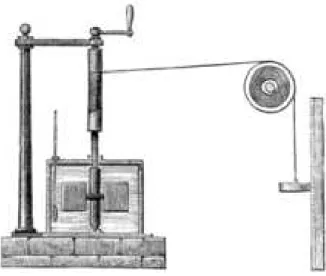
Abbildung 1. Skizze der Vorrichtung, mit der James Prescott Joule 1845 das mechanische W¨arme¨aquivalent bestimmte (aus Wikipedia).

1.2. Arbeit, W¨arme und Energie

Wir beginnen in diesem Abschnitt mit der systematischen Untersuchung von thermodynamischen Prozessen. Hier und im folgenden nehmen wir an, dass alle Zustands¨anderungen beliebig langsam (quasistatisch) ablaufen. Dadurch ist gesichert, daß sich das System zu jedem Zeitpunkt im Gleichgewicht befindet, und die Beschreibung durch makroskopische Zustandsgr¨ossen sinnvoll und ausreichend ist. Wir betrachten zun¨achst drei verschiedene M¨oglichkeiten, einem Gas auf mechanischem Wege Energie zuzuf¨ uhren.

(i) adiabatische Kompression/Expansion: Das Gas ist von seiner Umgebung durch adiabatische (=w¨armeundurchl¨assige) W¨ande isoliert. Uber einen ¨ beweglichen Kolben wird das Gas um ein kleines Volumen ∆V komprimiert. Dabei leistet der Kolben die Arbeit ‡

∆W = − P ∆V, (1.5)

die bei Kompression (∆V < 0) positiv ist. Da das System abgeschlossen ist, muss diese Arbeit zu einer entsprechenden Erh¨ohung der inneren Energie f¨ uhren, d.h.

∆E = ∆W = − P ∆V. (1.6)

Der Vorgang ist offensichtlich reversibel (umkehrbar): Expandiert das Gas, leistet es die gleiche Arbeit +P ∆V am Kolben.

(ii) adiabatisches R¨ uhren: ¨ Uber eine Welle wird im adiabatisch isolierten Gas ein Propeller angetrieben, indem ausserhalb des Systems ein Gewicht m uber eine ¨

‡ BezeichnetA die Fl¨ache des Kolbens, so ist die KraftF =P Amit dem Weg ∆xzu multiplizieren, wobei ∆V =A∆x.

H¨ohendifferenz ∆h abgesenkt wird (Abb. 1). Dem Gas wird damit die potentielle Energie des Gewichts zugef¨ uhrt, und es gilt, analog zu (1.6),

∆E = ∆W = mg∆h. (1.7)

Dieser Vorgang ist offensichtlich irreversibel : Es ist m¨ ussig, darauf zu warten, dass das Gas sich spontan abk¨ uhlt und seine Energie zum Heben des Gewichts bereitstellt.

(iii) isotherme Kompression: Hier wird das Gas wie unter (i) durch einen Kolben komprimiert, es steht aber zus¨atzlich ¨ uber eine w¨armedurchl¨assige Wand mit der Umgebung (einem W¨armereservoir ) in Kontakt, sodass seine Temperatur T bei der Volumen¨anderung konstant bleibt S . Damit wird jetzt zumindest ein Teil der durch den Kolben geleisteten Arbeit als W¨arme der Umgebung zugef¨ uhrt. Bezeichnen wir die dem System zugef¨ uhrte W¨armemenge mit ∆Q, so ist die an die Umgebung abgef¨ uhrte W¨arme − ∆Q, und es gilt die Energiebilanz

∆E = ∆W + ∆Q = − P ∆V + ∆Q. (1.8)

Da die innere Energie des idealen Gases nur von der Temperatur abh¨angt, gilt in diesem Fall sogar ∆E = 0, also ∆Q = − ∆W = P ∆V , und die geleistete Arbeit wird vollst¨andig als W¨arme an die Umgebung abgef¨ uhrt. Der Vorgang ist trotzdem reversibel : Expandiert das Gas, nimmt es von der Umgebung die entsprechende W¨armemenge wieder auf.

Die Gleichungen (1.6,1.7,1.8) sind Beispiele f¨ ur den 1. Hauptsatz der Thermodynamik. Er lautet, in Worten formuliert:

Die Summe der einem System zugef¨ uhrten W¨arme und der am System geleisteten Arbeit ist gleich der ¨ Anderung der inneren Energie des Systems.

Die Arbeit kann dabei (wie in den genannten Beispielen) in mechanischer Form geleistet werden, es k¨onnte sich aber auch um elektrische, magnetische, oder eine andere Form von Arbeit handeln. Als Arbeit bezeichnen wir jede Energieform, die in Form eines makroskopisch kontrollierbaren Freiheitsgrades zur Verf¨ ugung steht.

Wir m¨ ussen noch kl¨aren, worin sich die Gr¨ossen auf der linken (∆E) und der rechten (∆W, ∆Q) Seite von (1.8) unterscheiden. Dazu ist es n¨ utzlich, sich die Prozesse (i), (ii) und (iii) in einem P V -Diagramm zu veranschaulichen. Die adiabatische Kompression und Expansion (i) verl¨auft entlang einer Linie, die durch die Adiabatengleichung k

P V

= const. ⇒ P ∼ V

(1.9)

beschrieben wird. Hier ist γ = c

/c

das Verh¨altnis der spezifischen W¨armen bei konstantem Druck und konstantem Volumen, γ = 5/3 f¨ ur das einatomige ideale Gas.

S

k Die Herleitung dieser Gleichung erfolgt in den ¨Ubungen.

Der Prozess (iii) verl¨auft hingegen entlang einer Isothermen, die gem¨ass (0.1) von der Form

P V = const. ⇒ P ∼ V

(1.10)

ist. Wegen γ > 1 sind die Adiabaten steiler als die Isothermen.

Wir starten unser System in einem Zustand A mit Zustandsgr¨ossen P

, V

, T

. Durch adiabatische Kompression erreichen wir einen Zustand B mit Druck P

> P

, Temperatur T

> T

und Volumen V

< V

. Alternativ k¨onnen wir das System durch adiabatisches R¨ uhren bei gleichbleibendem Volumen V

auf die Temperatur T

erhitzen.

Den so erreichten Zustand nennen wir C. Eine weitere isotherme Kompression auf das Volumen V

f¨ uhrt dann in den Zustand B. Es gibt also zwei Wege von A nach B:

Weg 1: A → B (adiabatische Kompression); geleistete Arbeit ∆W

.

Weg 2: A → C (R¨ uhren), C → B (isotherme Kompression); geleistete Arbeit

∆W

.

Bei der adiabatischen Kompression (A → B) wie beim adiabatischen R¨ uhren (A → C) muss zur Erw¨armung des Gases von T

auf T

die gleiche Arbeit aufgewendet werden.

Um isotherm das Gas von C nach B zu komprimieren, ist zus¨atzliche Arbeit n¨otig, die an die Umgebung abgef¨ uhrt wird. Es gilt also ∆W

> ∆W

, und wir schliessen:

Die bei einer Zustands¨anderung geleistete Arbeit und zugef¨ uhrte W¨arme h¨angt nicht nur von den Anfangs- und Endzust¨anden ab, sondern auch vom Weg im Zustandsraum.

Wegen dieser Wegabh¨angigkeit sind Arbeit und W¨arme keine Zustandsgr¨ossen, sondern Prozessgr¨ossen.

1.3. Differentiale

Um die in der Thermodynamik ¨ ubliche differentielle Formulierung des ersten Hauptsatzes zu motivieren, teilen wir die beiden Seiten der Energiebilanz (1.8) durch die Verschiebung des Kolbens ∆x und f¨ uhren den Grenz¨ ubergang ∆x → 0 durch. Damit erhalten wir P

dE

dx = dW dx + dQ

dx = − P dV

dx + dQ

dx . (1.11)

Da die G¨ ultigkeit des 1. Hauptsatzes nicht von der spezifischen Prozessf¨ uhrung abh¨angt, eliminieren wir nun den Kontrollparameter x und verallgemeinern (1.11) zu einer Beziehung zwischen Differentialen,

dE = dW + dQ = − P dV + dQ. (1.12)

Zur Interpretation dieser und ¨ahnlicher Gleichungen ist es hilfreich, das Differential

einer allgemeinen Funktion f (x, y, z) zu betrachten. Wir stellen uns vor, daß die drei

unabh¨angigen Variablen x, y, z durch einen gemeinsamen Parameter λ ver¨andert werden,

P

also x = x(λ), y = y(λ), z = z(λ). Damit wird auch f eine Funktion von λ, deren totale Ableitung gem¨aß der mehrdimensionalen Kettenregel durch

d

dλ f(x(λ), y(λ), z(λ)) = ∂f

∂x dx dλ + ∂f

∂y dy dλ + ∂f

∂z dz

dλ (1.13)

gegeben ist. Wir k¨onnen wieder den (beliebigen) Parameter λ eliminieren und erhalten das Differential von f

df = ∂f

∂x dx + ∂f

∂y dy + ∂f

∂z dz (1.14)

als Linearkombination der Differentiale dx, dy und dz der unabh¨angigen Variablen. Die Koeffizienten der verschiedenen Terme sind die entsprechenden partiellen Ableitungen von f .

Als erste Anwendung betrachten wir den differentiellen 1. Hauptsatz (1.12) im Fall einer adiabatischen Zustands¨anderung, dQ = 0. Dann gilt dE = − P dV , und durch Vergleich mit der allgemeinen Relation (1.14) erhalten wir

P = − ∂E

∂V

ad

(1.15) als thermodynamische Definition des Drucks: − P ist die partielle Ableitung der inneren Energie nach dem Volumen unter adiabatischen Bedingungen.

Eine entsprechende Darstellung von dQ durch Zustandsgr¨ossen wird uns erst in Abschnitt 1.5 zur Verf¨ ugung stehen, aber wir k¨onnen dQ ¨ uber die W¨armekapazit¨at C mit einer Temperatur¨anderung in Verbindung bringen ∗ . Allgemein definiert dQ = CdT die W¨armemenge, die ben¨otigt wird um die Temperatur T eines Systems um dT zu erh¨ohen. Bei konstantem Volumen (dV = 0) gilt deshalb gem¨ass (1.12)

dE = dQ = C

dT, (1.16)

und die W¨armekapazit¨at bei konstantem Volumen C

ist gegeben durch C

=

∂E

∂T

V

. (1.17)

Wir benutzen hier erstmals die “thermodynamische Notation”

y,z

f¨ ur die Ableitung einer Funktion f (x, y, z) nach x bei konstanten y und z. In Abschnitt 1.6 werden wir sehen, daß adiabatische Prozesse bei konstanter Entropie S ablaufen, d.h. die Beziehung (1.15) f¨ ur den Druck kann zu P = −

S

pr¨azisiert werden. Wir notieren noch den Ausdruck

C

= 3

2 N k

T (1.18)

f¨ ur die W¨armekapazit¨at eines idealen Gases bei konstantem Volumen, die unmittelbar aus (1.4) folgt.

+ Analoge Rechnungen kennen Sie aus der Mechanik, wo der Parameterλmeist die Zeittdarstellt.

∗ S. dazu auch Aufgabe 30.

1.4. Kreisprozesse

“In Carnot’s treatise we encounter that fuzziness which was to become and remain a distinguishing feature of thermodynamics for bewildered outsiders. He rivals Herakleitos the obscure.” C. Truesdell, The Tragicomical History of Thermodynamics 1822-1854 Wegen der Wegabh¨angigkeit von Arbeit und W¨arme ist es m¨oglich, diese beiden Energieformen durch einen zyklischen Prozess ineinander umzuwandeln, indem ein geschlossener Weg im Zustandsraum wiederholt durchlaufen wird. Dieses Prinzip liegt allen W¨armekraftmaschinen (Dampfmaschine, Otto-Motor, W¨armepumpe etc.) zugrunde.

Betrachten wir zwei Zust¨ande A und B in der P V -Ebene, mit Volumina V

und V

, V

< V

, die durch zwei Wege 1 und 2 verbunden sind. Die beiden Wege seien durch Funktionen P = P

(V ) und P = P

(V ) parametrisiert. Die am System zu leistende Arbeit, um auf dem Weg 1 von A nach B und auf dem Weg 2 zur¨ uck von B nach A zu gelangen, ist jeweils

∆W

= − Z

VA

P

(V ) dV, ∆W

= − Z

VB

P

(V ) dV = Z

VA

P

(V ) dV.

Die am System in einem Umlauf geleistete Arbeit ist dann das Kreisintegral

− I

P dV = ∆W

+ ∆W

. (1.19)

Ist H

P dV > 0, so wandelt das System W¨arme in Arbeit um.

Das wichtigste Beispiel ist der Carnot’sche Kreisprozess, der ausschliesslich reversible Schritte benutzt † (Abb. 2). Der Prozess verl¨auft auf zwei Isothermen bei Temperaturen T

und T

, T

> T

, und auf zwei diese Isothermen kreuzenden Adiabaten.

Zur Realisierung des Prozesses werden also zwei Temperaturreservoire ben¨otigt, die nach Bedarf von dem System isoliert bzw. mit ihm in thermischen Kontakt gebracht werden k¨onnen.

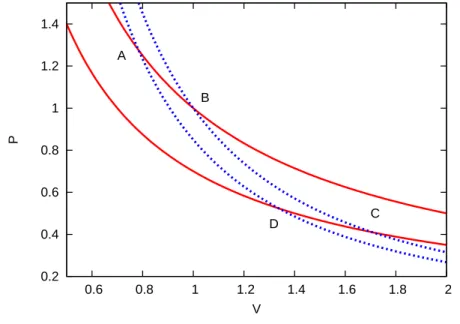
Die Zust¨ande an den vier Kreuzungspunkten der Isothermen und Adiabaten seien mit A, B, C und D bezeichnet. Der Prozess umfasst die folgenden vier Schritte:

• A → B: Isotherme Expansion bei Temperatur T

; dem System wird dabei die W¨armemenge ∆Q

zugef¨ uhrt.

• B → C: Adiabatische Expansion; Abk¨ uhlung auf T

.

• C → D: Isotherme Kompression bei T

; Abgabe der W¨armemenge ∆Q

an das Reservoir ‡ .

• D → A: Adiabatische Kompression, Erw¨armung auf T

.

† Sadi Carnot: Reflexions sur la Puissance Motrice du Feu et sur les Machines Propres `a d´evelopper cette Puissance (Paris, 1824).

‡ In dieser Betrachtung werden, entgegen unserer Konvention aus Abschnitt 1.2, ∆Q1und ∆Q2positiv gez¨ahlt.

0.2 0.4 0.6 0.8 1 1.2 1.4

0.6 0.8 1 1.2 1.4 1.6 1.8 2

P

V

D C

A

B

Abbildung 2. Der Carnot-Prozess ist ein Kreisprozess zwischen vier Zust¨anden A, B, C, D, die an den Kreuzungspunkten von zwei Isothermen (durchgezogene rote Linien,P∼V⁻¹) und zwei Adiabaten (gepunktete blaue Linien,P ∼V^−5/3) liegen.

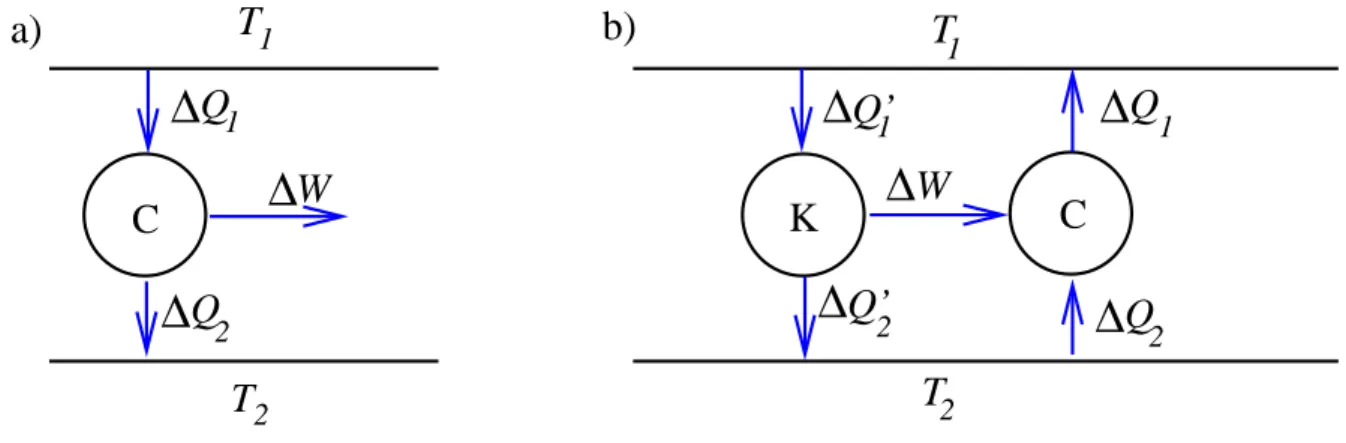
Das System entnimmt dem heisseren Reservoir die W¨armemenge ∆Q

und gibt die W¨armemenge ∆Q

an das k¨altere Reservoir ab. Da sich das System nach einem Umlauf in dem gleichen Zustand wie zu Beginn befindet, hat sich seine Energie nicht ge¨andert.

Die Differenz der beiden W¨armemengen steht also als vom System geleistete Arbeit

∆W = ∆Q

− ∆Q

zur Verf¨ ugung. Einer Vorstellung von Carnot folgend, die vermutlich von der Besch¨aftigung mit Wasserkraftwerken beeinflusst war, “f¨allt” die W¨arme vom heisseren in das k¨altere Reservoir und wird dabei teilweise in Arbeit umgewandelt S (s.

Abb.3 a)).

Wir analysieren jetzt den Prozess quantitativ, und nehmen dazu an, dass die Arbeitssubstanz ein ideales Gas ist. Entlang der Isothermen ist der Druck gem¨ass (0.1) gegeben durch P

(V ) = N k

T

/V , sodass die beiden W¨armemengen sich zu

∆Q

= Z

VA

P

(V ) dV = N k

T

Z

VA

dV

V = N k

T

ln(V

/V

), ∆Q

= N k

T

ln(V

/V

) berechnen lassen. Da die Zust¨ande B, C und A, D jeweils auf einer Adiabaten liegen, gilt ausserdem

P

(V

)V

= N k

T

V

= P

(V

)V

= N k

T

V

⇒ T

V

= T

V

,

und genauso T

V

= T

V

. Daraus folgt zun¨achst V

/V

= V

/V

= (T

/T

)

,

S

T

T

W W

C K C

a) b) T

T

∆

Q

Q

∆

∆

∆

Q’

Q’

Q

Q

∆

∆

∆

∆

Abbildung 3. Schematische Darstellung des Carnot-Prozesses. a) Der Carnot- Prozess C entzieht dem heisseren Reservoir die W¨armemenge ∆Q1, wandelt einen Teil ∆W in Arbeit um und f¨uhrt die W¨armemenge ∆Q2 dem k¨alteren Reservoir zu.

b) Illustration zum Beweis der Optimalit¨at des Carnot-Prozesses. Der Carnot-Prozess wird mit einem anderen Prozess K in Serie geschaltet.

und deshalb auch V

/V

= V

/V

. Einsetzen in die Ausdr¨ ucke f¨ ur ∆Q

und ∆Q

liefert damit als zentrales Ergebnis

∆Q

∆Q

= T

T

. (1.20)

Der Wirkungsgrad des Prozesses, definiert als der in Arbeit umgewandelte Bruchteil der zugef¨ uhrten W¨armemenge ∆Q

, ist somit

η

= ∆W

∆Q

= ∆Q

− ∆Q

∆Q

= 1 − ∆Q

∆Q

= 1 − T

T

. (1.21)

Betreibt man den Prozess im umgekehrten Umlaufsinn (A → D → C → B), so erh¨alt man eine W¨armepumpe, die W¨arme unter Aufwand von Arbeit vom k¨alteren in das heissere Reservoir transportiert.

Die grosse Bedeutung des Carnot-Prozesses leitet sich aus den folgenden beiden Eigenschaften her:

• Der Carnot-Prozess ist optimal: F¨ ur jeden anderen Kreisprozess K mit Wirkungs- grad η

gilt η

≤ η

.

Beweis: Wir schalten den Kreisprozess K in Serie mit einem Carnot-Prozess, der als W¨armepumpe betrieben wird (Abb. 3 b)). Der Prozess K entnimmt dem heissen Reservoir die W¨armemenge ∆Q

, produziert die Arbeit ∆W und gibt die W¨armemenge ∆Q

= ∆Q

− ∆W an das kalte Reservoir ab. Die Arbeit ∆W treibt den Carnot-Prozess, der somit die W¨armenge ∆Q

dem kalten Reservoir entzieht und die Menge ∆Q

= ∆Q

+ ∆W dem heissen Reservoir zuf¨ uhrt. Wenn der Wirkungsgrad von K gr¨osser ist als η

, also η

= ∆W/∆Q

> η

= ∆W/∆Q

, so folgt offensichtlich ∆Q

< ∆Q

, und wegen ∆W = ∆Q

− ∆Q

= ∆Q

− ∆Q

auch

∆Q

< ∆Q

. Das bedeutet, dass insgesamt dem kalten Reservoir die W¨armemenge

∆Q

− ∆Q

= ∆Q

− ∆Q

entzogen, und dem warmen Reservoir ohne ¨ausseren Arbeitsaufwand zugef¨ uhrt wird. Ein solcher Vorgang widerspricht der Erfahrung, die in der folgenden Formulierung des 2. Hauptsatzes der Thermodynamik (nach Rudolf Clausius) zusammengefasst wird:

Es ist nicht m¨oglich, durch einen Kreisprozess W¨arme von einem k¨alteren auf einen w¨armeren K¨orper zu ¨ ubertragen, ohne weitere Ver¨anderungen der Welt

zu verursachen. 2.HS/I

Damit ist die Behauptung bewiesen. Aus der Optimalit¨at des Carnot-Prozesses folgt insbesondere auch, dass es einen Arbeit leistenden Kreisprozess ohne Temperaturdifferenz nicht geben kann: Wenn T

= T

ist η

= 0. Eine Maschine, die zyklisch Arbeit leistet, und dabei lediglich einem Reservoir W¨arme entzieht, nennt man ein Perpetuum mobile zweiter Art k . Ein ¨aquivalente Formulierung des 2. Hauptsatzes ist deshalb

Es ist nicht m¨oglich, ein Perpetuum mobile 2. Art zu konstruieren. 2.HS/II

• Der Carnot-Prozess ist universell: Jeder andere reversible Kreisprozess hat den gleichen Wirkungsgrad η

.

Beweis: Ein Wirkungsgrad gr¨osser als η

ist durch die Optimalit¨at des Carnot- Prozesses bereits ausgeschlossen. W¨are der Wirkungsgrad des zweiten Prozesses kleiner als η

, so k¨onnten wir ihn r¨ uckw¨arts laufen lassen (er ist ja reversibel!) und k¨amen ebenfalls zu einer Verletzung des 2. Hauptsatzes.

Die praktische Aussagekraft des Carnot’schen Wirkungsgrades (1.21) ist allerdings eher gering, denn die Annahme einer quasistatischen Prozessf¨ uhrung bedeutet, daß die Leistung (=Arbeit/Zeit) des Carnot-Zyklus gleich Null ist.

1.5. Entropie und zweiter Hauptsatz

Die bisher entwickelte Theorie ist unvollst¨andig und l¨asst insbesondere die folgenden Fragen unbeantwortet:

a.) Beschreibung von W¨ armeaustausch durch eine Zustandsgr¨ osse: Was

¨andert sich am Zustand eines Systems (neben seiner Energie), wenn ihm W¨arme zugef¨ uhrt wird?

b.) Reversibilit¨ at/Irreversibilit¨ at: Welche Zust¨ande eines abgeschlossenen Systems lassen sich durch reversible Prozesse verbinden?

c.) Lassen sich die Gleichgewichtsbedingungen bei thermischem oder mechanischem Kontakt durch ein Extremalprinzip begr¨ unden?

k Ein Perpetuum mobile 1. Art ist eine Maschine, die Arbeit leistet, ohne W¨arme zu verbrauchen, in Verletzung des 1. Hauptsatzes.

Diese drei Fragen (und viele mehr) werden beantwortet durch eine neue, extensive Zustandsgr¨osse, die Entropie S. Das Wort wurde 1865 von Clausius eingef¨ uhrt † . Es leitet sich her vom griechischen τ ρoπη f¨ ur Umwandlung.

Zur Motivation der thermodynamischen Entropiedefinition erinnern wir an die Beziehung (1.20), die wir in die Form

∆Q

T

= ∆Q

T

(1.22) bringen. Die mit der inversen Temperatur

gewichteten W¨armemengen, die dem warmen Reservoir entzogen und dem kalten Reservoir zugef¨ uhrt werden, sind somit gleich. Das bedeutet, daß

als ¨ Anderung einer Zustandsgr¨osse – der Entropie – aufgefasst werden kann, die nach einem Zyklus des Carnotprozesses auf ihren Ursprungswert zur¨ uckkehrt.

Wir definieren deshalb die Entropiedifferenz zwischen zwei Zust¨anden A, B durch S(B ) − S(A) =

Z

A→B

dQ

T , (1.23)

wobei das Integral ¨ uber einen reversiblen Weg von A nach B auszuf¨ uhren ist. Damit S eine Zustandsgr¨osse ist, muss das Integral wegunabh¨angig sein, d.h. f¨ ur zwei beliebige Wege (1) und (2) von A nach B muss gelten

Z

A→B

dQ T =

Z

A→B

dQ

T . (1.24)

Benutzt man Weg (1) von A nach B und Weg (2) zur¨ uck von B nach A, erh¨alt man einen geschlossenen Weg. Das Kreisintegral ¨ uber den geschlossenen Weg ist dann gerade die Differenz der beiden Seiten von (1.24). Damit (1.24) f¨ ur beliebige zwei Wege gilt, muss also das Kreisintegral ¨ uber jeden geschlossenen reversiblen Weg verschwinden,

I dQ

T = 0. (1.25)

Diese Bedingung ist analog zur Bedingung der Wirbelfreiheit f¨ ur ein Vektorfeld, das sich als Gradient eines Potentials schreiben l¨asst.

F¨ ur den Spezialfall des Carnot’schen Kreisprozesses ist die Bedingung (1.25) wegen (1.22) erf¨ ullt. Nun k¨onnen wir aber jeden reversiblen Kreisprozess beliebig genau durch Carnot-Prozesse ann¨ahern, indem wir die P V -Ebene mit einem feinmaschigen Netz von Isothermen und Adiabaten ¨ uberziehen. Das Kreisintegral in (1.25) wird dann angen¨ahert durch eine Summe ¨ uber diese Carnot-Prozesse, wobei sich die Beitr¨age der isothermen Schritte wegen (1.20) paarweise wegheben. Damit ist gezeigt, dass (1.25) f¨ ur jeden reversiblen Kreisprozess gilt, und somit die Entropie durch (1.23) wohl definiert ist.

† R. Clausius: Uber verschiedene f¨¨ ur die Anwendung bequeme Formen der Hauptgleichungen der mechanischen W¨armetheorie. Ann. Phys. Chem. 125(1865), 353 – 400.

Zur Festlegung des absoluten Wertes von S nehmen wir den absoluten Nullpunkt T = 0 als Referenzpunkt. Dort gilt, gem¨ass dem 3. Hauptsatz der Thermodynamik ‡

S |

= 0. (1.26)

Zusammen legen (1.23) und (1.26) die Entropie als Zustandsgr¨osse fest, und beantworten die oben formulierte Frage a.). Die differentielle Form von (1.23) lautet

dS = dQ

T (reversible Prozesse). (1.27)

Dies liefert die gesuchte Darstellung des W¨armedifferentials durch Zustandsgr¨ossen, analog zur Beziehung dW = − P dV f¨ ur die mechanische Arbeit.

Es ist zu betonen, dass (1.23) und (1.27) f¨ ur reversible Zustands¨anderungen gelten.

Um zu sehen, was mit der Entropie bei irreversiblen Prozessen passiert, betrachten wir nochmals die Prozesse (i), (ii) und (iii) aus Abschnitt 1.2. Der irreversible Prozess (ii) (adiabatisches R¨ uhren) f¨ uhrt vom Zustand A zum Zustand C. Alternativ k¨onnen wir auf dem Umweg ¨ uber den Zustand B reversibel von A nach C gelangen. Entlang der Adiabaten von A nach B [Prozess (i)] wird dem System keine W¨arme zugef¨ uhrt, die Entropie bleibt also konstant. Bei der isothermen Expansion von B nach C hingegen [Prozess (iii)] wird eine W¨armemenge ∆Q

bei konstanter Temperatur T zugef¨ uhrt.

Somit gilt

S(C) − S(A) = (S(C) − S(B)) + (S(B) − S(A)) = S(C) − S(B) = ∆Q

T > 0.

Die Entropie steigt beim irreversiblen R¨ uhren an, obwohl dem System keine W¨arme hinzugef¨ ugt wurde. Wir schliessen daraus, dass f¨ ur irreversible Prozesse die Beziehung (1.27) zu

dS > dQ

T (irreversible Prozesse) (1.28)

abge¨andert werden muss. Zusammen stellen (1.27) und (1.28) den 2. Hauptsatz der Thermodynamik in allgemeiner, differentieller Form dar. Speziell f¨ ur abgeschlossene Systeme gilt dQ = 0, und aus (1.27) und (1.28) folgt, dass stets

dS ≥ 0 (abgeschlossene Systeme), (1.29)

in Worten:

Die Entropie eines abgeschlossenen Systems kann nur zunehmen. 2.HS/III Fasst man das gesamte Universum als abgeschlossenes System auf, so folgt die Formulierung

Die Entropie der Welt strebt einem Maximum zu. 2.HS/IV

‡ Der 3. Hauptsatz wurde 1906 von W. Nernst in einer etwas schw¨acheren Form aufgestellt: Er besagte nur, dass Entropie¨anderungen bei isothermen Prozessen f¨ur T →0 verschwinden. Die Formulierung (1.26) stammt von Max Planck.

die im 19. Jahrhundert erhebliche ¨ Angste vor dem drohenden W¨armetod weckte; damit ist der Zustand maximaler Entropie gemeint, eine traurige, strukturlose Suppe, die man sich als Endziel aller Entwicklung nur ungern vorstellen m¨ochte.

Die Eigenschaft der Entropie, bei irreversiblen Prozessen in einem abgeschlossenen System zuzunehmen, liefert uns die Antwort auf Frage b.):

Zwei Zust¨ande A, B eines abgeschlossenen Systems lassen sich durch einen reversiblen Prozess verbinden, falls S(A) = S(B). Falls S(A) > S(B ), so existiert ein irreversibler Prozess von B nach A, aber nicht von A nach B .

Die Entropie induziert in diesem Sinne eine Ordnungsrelation auf der Menge der Zust¨ande S Auch die Antwort auf Frage c.) deutet sich schon an: Wenn die Entropie eines abgeschlossenen Systems nur zunehmen kann, muss sie im Gleichgewichtszustand maximal sein. Darauf kommen wir in Abschnitt 1.7 zur¨ uck.

Vorher zeigen wir noch, wie aus der allgemeinen Formulierung des 2. Hauptsatzes folgt, dass W¨arme spontan stets vom heisseren zum k¨alteren System fliesst (Formulierung 2.HS/I). Wir betrachten zwei Systeme mit Temperaturen T

und T

, die in thermischen Kontakt gebracht werden. Wenn eine W¨armemenge dQ von dem System 1 an das System 2 abgegeben wird, so ¨andert sich die Entropie des Gesamtsystems gem¨ass

dS = dS

+ dS

= − dQ T

+ dQ T

= dQ 1

T

− 1 T

. (1.30)

Da das Gesamtsystem abgeschlossen ist, muss dS ≥ 0 gelten, und somit dQ > 0 wenn T

> T

und dQ < 0 wenn T

< T

.

1.6. Das Differential der Entropie

Wir kombinieren jetzt die Beziehung (1.27) mit dem 1. Hauptsatz in differentieller Form, Gl.(1.12), und erhalten

dS = 1

T (dE − dW ) = 1

T dE + P

T dV. (1.31)

Um zu verstehen, was das bedeutet, erinnern wir an die Definition des Differentials einer Funktion aus Abschnitt 1.3. Fassen wir die Entropie S = S(E, V, N ) als Funktion der extensiven Zustandsvariablen E, V und N auf, so ist das Differential dS gegeben durch

dS = ∂S

∂E

dE + ∂S

∂V

dV + ∂S

∂N

dN. (1.32)

Aus dem Vergleich von (1.31) und (1.32) k¨onnen wir somit die partiellen Ableitungen von S nach E und V ablesen,

∂S

∂E

V,N

= 1 T ,

∂S

∂V

E,N

= P

T . (1.33)

S

Die Teilchenzahl N wurde bei den bisherigen ¨ Uberlegungen konstant gehalten (dN = 0).

Wir definieren jetzt das chemische Potential µ uber die Beziehung ¨

∂S

∂N = − µ

T (1.34)

und erhalten damit dS = 1

T (dE + P dV − µdN ). (1.35)

Diese Beziehung kann nach dE aufgel¨ost werden, und liefert dann die Gibbs’sche Fundamentalform

dE = T dS − P dV + µdN. (1.36)

Hier wird die innere Energie E = E(S, V, N ) als Funktion von S, V und N aufgefasst.

Die Entropie S(E, V, N ) kann nach E aufgel¨ost werden, falls ∂S/∂E > 0, d.h. bei positiver absoluter Temperatur, was i.a. gegeben ist. Die Gibbs’sche Fundamentalform stellt die verschiedenen Beitr¨age zur ¨ Anderung der inneren Energie zusammen. W¨arme (dQ = T dS) und mechanische Arbeit (dW = − P dV ) wurden bereits ausf¨ uhrlich diskutiert; zus¨atzlich sehen wir, dass das chemische Potential µ ein Mass f¨ ur die Anderung der inneren Energie beim Hinzuf¨ ¨ ugen von Teilchen ist.

1.7. Das Gleichgewicht als Zustand maximaler Entropie

Der 2. Hauptsatz besagt, dass die Entropie in einem abgeschlossenen System zunimmt, bis alle m¨oglichen irreversiblen Prozesse abgelaufen sind. Wenn das System den GWZ erreicht hat, ist die Entropie also maximal; genauer:

Im Gleichgewicht nimmt die Entropie den mit allen vorhandenen Nebenbedingungen vertr¨aglichen maximalen Wert an.

Wir wollen nun zeigen, wie sich aus diesem Extremalprinzip die in Abschnitt 1.1 formulierten Gleichgewichtsbedingungen ableiten lassen.

(i) Thermischer Kontakt: Die beiden Teile des Gef¨asses tauschen Energie aus bei konstanter Gesamtenergie E = E

+ E

. Die Entropie ist additiv, d.h. die Entropie S des Gesamtsystems ist die Summe der Entropien S

und S

der Teilsysteme:

S = S

(E

, V

, N

) + S

(E − E

, V

, N

). (1.37) Hier wurde die Nebenbedingung E

= E − E

bereits eingebaut. Die Energie soll so auf die Teilsysteme verteilt werden, dass die Gesamtentropie maximal ist. Wir fordern also †

dS dE

= ∂S

∂E

+ ∂S

∂E

∂E

∂E

= ∂S

∂E

− ∂S

∂E

= 1 T

− 1

T

= 0 (1.38)

und somit T

= T

, wie erwartet.

† Wir schreiben hier _dE^dS

1 statt _∂E^∂S

1, weil E1der einzige Freiheitsgrad des Systems ist.

(ii) Volumenaustausch: Die beiden Teile des Gef¨asses sind durch eine bewegliche, aber w¨armeundurchl¨assige Wand getrennt. Da die Bewegung der Wand Arbeit leistet, tauschen die beiden Teilsystem sowohl Volumen als auch Energie aus, d.h.

wir haben die beiden Nebenbedingungen E = E

+ E

und V = V

+ V

zu ber¨ ucksichtigen. Energie und Volumen sind aber gekoppelt ¨ uber die Beziehungen dE

= − P

dV

, sodass

∂E

∂V

= − P

. (1.39)

Die Entropie des Gesamtsystems ist

S = S

(E

(V

), V

, N

) + S

(E − E

(V

), V − V

, N

). (1.40) Das Teilvolumen V

ist der einzige verf¨ ugbare Freiheitsgrad, d.h. die Bedingung maximal Entropie lautet dS/dV

= 0. Unter Benutzung der Kettenregel und von Gl.(1.39) erhalten wir

dS

dV

= ∂S

∂E

∂E

∂V

+ ∂S

∂V

− ∂S

∂E

∂E

∂V

− ∂S

∂V

= 1

T

(P

− P

), (1.41) sodass im Gleichgewicht in der Tat P

= P

gelten muss.

Wir haben bisher nur gefordert, dass die ersten Ableitungen von S im Gleichgewicht verschwinden m¨ ussen. Damit wirklich ein Maximum der Entropie vorliegt, muss ausserdem die zweite Ableitung negativ sein ‡ . F¨ ur den Fall des thermischen Kontakts heisst das

d

S dE

= d

dE

∂S

∂E

(E

, V

, N

) − ∂S

∂E

(E − E

, V

, N

)

= (1.42)

= ∂

S

∂E

+ ∂

S

∂E

< 0.

Zweimaliges Ableiten von S nach E ergibt allgemein

∂

S

∂E

= ∂

∂E

1

T (E, V, N ) = − 1 T

∂T

∂E

V,N

. (1.43)

Nach dem bekannten Satz ¨ uber die Ableitung von Umkehrfunktionen gilt ∂T

∂E

V,N

= ∂E

∂T

V,N

= 1 C

. (1.44)

Die Bedingung (1.42) bedeutet also, dass die W¨armekapazit¨aten der beteiligten K¨orper positiv sein m¨ ussen:

C

> 0. (1.45)

Dies l¨asst sich interpretieren als eine Stabilit¨ atsbedingung f¨ ur den thermischen GWZ.

Um das zu verstehen, betrachten wir zwei Teilsysteme mit Temperaturen T

und T

< T

im thermischen Kontakt. Der zweite Hauptsatz fordert, dass eine positive W¨armemenge von System 1 zu System 2 fliesst [vgl. (1.30)]. Wenn C

> 0, k¨ uhlt sich der heissere

‡ Eine pr¨azisere Bedingung wird in Abschnitt 1.8 formuliert.

K¨orper ab, da ihm W¨arme entzogen wird, w¨ahrend der k¨altere K¨orper aufgeheizt wird;

die Temperaturdifferenz baut sich somit ab, und das System strebt dem GWZ (T

= T

) zu. W¨are hingegen C

< 0, w¨ urde die Temperaturdifferenz weiter zunehmen und das System k¨ame nie ins Gleichgewicht.

Ahnliche ¨ ¨ Uberlegungen f¨ ur den Fall des mechanischen Kontakts f¨ uhren auf die Stabilit¨atbedingung

κ

= − 1 V

∂V

∂P

T

> 0 (1.46)

f¨ ur die isotherme Kompressibilit¨at κ

. Auch diese Bedingung ist anschaulich leicht einzusehen. Wir betrachten ein durch eine bewegliche Wand in zwei Teile getrenntes Gef¨ass. Im GWZ herrscht in beiden Teilsystemen der gleiche Druck, P

= P

. Komprimiert man nun das eine Teilsystem, so steigt der Druck dort an, falls κ

> 0, und die Wand wird in die Gleichgewichtslage zur¨ uckgeschoben. W¨are hingegen κ

< 0, so w¨ urde das komprimierte Volumen weiter abnehmen und das Teilsystem vollst¨andig kollabieren.

1.8. Zusammenfassung: Die Struktur der Thermodynamik

Im R¨ uckblick l¨asst sich die gesamte Thermodynamik zusammenfassen in einigen Aussagen ¨ uber die Eigenschaften der Entropie S(E, V, N ).

(i) Die Entropie ist extensiv, und sie ist eine Funktion der extensiven Zustandsgr¨ ossen. Daraus folgt, dass S(E, V, N ) homogen ersten Grades ist, d.h.

S(λE, λV, λN ) = λS (E, V, N ) (1.47) f¨ ur jeden beliebigen Faktor λ. Dies ist der mathematische Ausdruck daf¨ ur, dass die Entropie bei Vergr¨osserung oder Verkleinerung der Stoffmenge um den Faktor λ sich um den gleichen Faktor ¨andert.

(ii) Gleichgewichtszust¨ ande maximieren S.

(iii) Die intensiven Zustandsgr¨ ossen sind partielle Ableitungen von S:

∂S

∂E = 1

T , ∂S

∂V = P

T , ∂S

∂N = − µ

T . (1.48)

(iv) Die zweiten Ableitungen von S definieren thermodynamische Respon- segr¨ ossen, wie z.B. die W¨armekapazit¨at C

und die isotherme Kompressibilit¨at κ

∂

S

∂E

V

= − 1 T

C

,

∂

S

∂V

T

= − 1 T V κ

, (1.49)

deren Vorzeichen die Stabilit¨ at der thermodynamischen Gleichgewicht- szust¨ ande bestimmen.

(v) S verschwindet bei T = (∂S/∂E)

= 0.

2. Die Boltzmann’sche Entropie

Die Beschreibung eines Vielteilchensystems durch wenige makroskopische Freiheitsgrade ist hochgradig entartet, denn es gibt i.a. sehr viele Konfigurationen der mikroskopischen Freiheitsgrade (Mikrozust¨ ande, im folgenden auch MiZ), die mit einer Konfiguration makroskopischer Freiheitsgrade (einem Makrozustand, MaZ) vertr¨aglich sind. So gibt es z.B. sehr viele M¨oglichkeiten, die Positionen { ~r

} von N klassischen Teilchen auf ein Volumen V , oder die Gesamtenergie E auf die kinetischen und potentiellen Energien der Teilchen zu verteilen. Um diese Entartung zu quantifizieren, definieren wir den Entartungsgrad eines MaZ durch

Ω(E, V, N ) = Zahl der MiZ von N Teilchen im Volumen V mit Gesamtenergie E Die Boltzmann’sche Entropie ist dann einfach definiert durch

S(E, V, N ) = k

ln Ω(E, V, N ). (2.1) Es stellen sich zwei Fragen:

• Wie z¨ ahlt man Mikrozust¨ ande?

Das Z¨ahlen ist f¨ ur diskrete Quantenzust¨ande einfacher zu realisieren als f¨ ur klassische MiZ, die durch kontinuierliche Orts- und Impulsvariablen beschrieben werden. Insofern l¨asst sich die statistische Mechanik etwas nat¨ urlicher auf der Quantentheorie als auf der klassischen Mechanik aufbauen.

• Warum ist die Definition (2.1) sinnvoll, d.h. was hat sie mit der thermodynamischen Entropie zu tun?

Zur Beantwortung dieser beiden Fragen berechnen wir im folgenden Abschnitt die Boltzmann-Entropie des idealen Gases. Wir benutzen dabei weitgehend die Begriffe der klassischen Physik, bis auf eine minimale Anleihe bei der Quantenmechanik am Ende der Rechnung.

2.1. Die Boltzmann-Entropie des klassischen idealen Gases

Beim idealen Gas tragen die r¨aumlichen Freiheitsgrade { ~r

} und die Impulsfreiheitsgrade { ~p

} unabh¨angig voneinander zur Entropie bei, und wir k¨onnen schreiben

Ω(E, V, N ) = Ω

(V, N )Ω

(E, N ). (2.2)

Hier steht Ω

f¨ ur die Zahl der M¨oglichkeiten, N Teilchen im Volumen V zu platzieren, und Ω

beschreibt die m¨oglichen Verteilungen der Gesamtenergie

E =

N

X

i=1

| ~p

|

2m (2.3)

auf die Impulse der Teilchen. Wir beginnen mit dem Abz¨ahlen der r¨aumlichen MiZ.

2.1.1. R¨aumliche Freiheitsgrade. Um die r¨aumlichen MiZ abz¨ahlen zu k¨onnen, denken wir uns das Volumen in M Zellen mit Volumen v

= V /M unterteilt. Das Zellenvolumen wird im folgenden als beliebiger (kleiner) Parameter behandelt und am Ende der Rechnung spezifiziert. Die Kantenl¨ange einer Zelle sei ∆x, sodaß v

= (∆x)

. Der MiZ des Systems ist festgelegt, wenn von jedem Teilchen bekannt ist, in welcher Zelle es sich befindet. Jedes Teilchen hat M = V /v

MiZ und das System insgesamt somit (V /v

)

MiZ.

Indem wir jedem Teilchen eine bestimmte Zelle zuweisen, behandeln wir die Teilchen als unterscheidbar, was aus Sicht der Quantenmechanik f¨ ur identische Teilchen nicht korrekt ist. Tats¨achlich f¨ uhrt die Annahme unterscheidbarer Teilchen aber auch in der klassischen statistischen Physik zu Problemen, wie das folgende Argument zeigt:

Einsetzen des Ausdrucks † Ω

= (V /v

)

in die Boltzmann’sche Entropiedefinition (2.1) ergibt f¨ ur den r¨aumlichen Beitrag zur Entropie

S

(V, N ) = k

ln Ω

= k

N [ln V − ln v

]. (2.4) Ver¨andern wir nun die Stoffmenge um einen Faktor λ, so folgt

S

(λV, λN ) = k

λN [ln V + ln λ − ln v

] 6 = λS

(V, N ). (2.5) Der Ausdruck (2.4) verletzt die Homogenit¨atsrelation (1.47) und ist somit nicht extensiv.

Um dies zu korrigieren und die Konsistenz mit der quantenmechanischen Rechnung herzustellen m¨ ussen wir die Ununterscheidbarkeit der Teilchen bei Abz¨ahlen der MiZ ber¨ ucksichtigen. Die Korrektur ist einfach, wenn die Zahl der Zellen viel gr¨osser ist als die Zahl der Teilchen ‡ , M ≫ N . Dann befindet sich in jeder Zelle maximal ein Teilchen, und alle N ! “unterscheidbaren” MiZ, die durch eine Permutation der Teilchenindizes miteinander verkn¨ upft sind, geh¨oren zum gleichen “ununterscheidbaren” MiZ. Die Zahl der ununterscheidbaren MiZ ergibt sich damit zu

Ω

= 1

N! Ω

= 1 N !

V v

. (2.6)

Zur Auswertung der Fakult¨at f¨ ur grosse N benutzen wir die Stirling’sche Formel in der einfachen Form S

N ! ≈ (N/e)

(2.7)

und erhalten Ω

≈

e v

V N

. (2.8)

Die zugeh¨orige Entropie S

= k

ln Ω

ist extensiv, wie man durch Einsetzen in (1.47) nachpr¨ ufen kann.

† Hier steht “us” f¨ur “unterscheidbar”.

‡ Der Fall allgemeinerM undN wird in den ¨Ubungen behandelt.

S

2.1.2. Impulsfreiheitsgrade. Da jeder Impulsvektor drei Komponenten hat, k¨onnen wir (2.3) als Definitionsgleichung einer 3N -dimensionalen Kugelschale im Raum der Impulskomponenten interpretieren. Die Oberfl¨ache dieser Kugelschale ist ein Maß f¨ ur die Zahl der Impulszust¨ande mit Energie E. Um diese Zahl zu bestimmen m¨ ussen wir, analog zum r¨aumlichen Fall, eine kleine Zellengr¨osse ∆p einf¨ uhren. Zwei Impulszust¨ande werden als unterschiedlich betrachtet wenn sich die Impulse um ∆p unterscheiden. Wir dividieren beide Seiten von (2.3) durch ∆p

/2m und erhalten

N

X

i=1

| ~p

|

(∆p)

= 2mE

(∆p)

≡ R

(2.9)

als Gleichung f¨ ur eine 3N -dimensionale Kugelschale vom (dimensionslosen) Radius R.

Die gesuchte Zahl der Impulszust¨ande, Ω

, ist die Oberfl¨ache dieser Kugelschale.

In den ¨ Ubungen wird der Ausdruck V

= π

Γ(1 + d/2) R

(2.10)

f¨ ur das Volumen einer d-dimensionalen Kugel vom Radius R hergeleitet, wobei Γ(x) =

Z

0

t

e

dt. (2.11)

Die Gamma-Funktion (2.11) kann als Verallgemeinerung der Fakult¨at aufgefasst werden.

F¨ ur nat¨ urliche Zahlen n ist Γ(n + 1) = n!, und f¨ ur allgemeine x gilt Γ(x + 1) = xΓ(x).

Spezielle Werte sind Γ(1) = Γ(2) = 1 und Γ(1/2) = √

π. Die Oberfl¨ache O

der Kugelschale ergibt sich aus (2.10) durch Ableitung nach R zu O

= (d/R)V

. In diesem Ausdruck setzen wir nun d = 3N und R = ∆p

√

2mE und erhalten Ω

= 3N π

(3N/2)!

2mE (∆p)

. (2.12)

Dabei wurde angenommen daß 3N gerade ist, um Γ(1 + 3N/2) durch die Fakult¨at ersetzen zu k¨onnen. Mittels der Stirling’schen Formel (2.7) erhalten wir schließlich f¨ ur große N

Ω

≈

4πem 3

1

∆p

E N

. (2.13)

2.1.3. Entropie und Zustandsgleichungen. Wir multiplizieren nun die Ausdr¨ ucke (2.8) und (2.13) und schreiben f¨ ur das Zellvolumen v

= ∆x

. Damit folgt

Ω = Ω

Ω

= e

(∆x∆p)

4πm 3

E N

V N

. (2.14)

Aus Sicht der Quantenmechanik ist es naheliegend, die Zellengr¨oße ∆x∆p im Phasenraum von der Gr¨ossenordnung des Planck’schen Wirkungsquantums zu w¨ahlen, da dies die maximale Genauigkeit beschreibt, mit der sich der Zustand eines Teilchens festlegen l¨asst. Wir setzen deshalb ∆x∆p = h und erhalten

Ω = e

m 3π ~

E N

V N

. (2.15)

Daraus folgt f¨ ur die Entropie schließlich der Ausdruck S(E, V, N ) = k

N

ln

V N

+ 3

2 ln E

N

+ 3

2 ln m 3π ~

+ 5 2

, (2.16) der exakt mit dem Ergebnis der vollen quantenmechanichen Rechnung (im klassischen Grenzfall ~ → 0) ¨ ubereinstimmt.

Durch Ableiten von (2.16) nach V und E erhalten wir die vertrauten Zustandsgleichungen,

∂S

∂V = N k

V = P

T ⇒ P V = N k

T, (2.17)

∂S

∂E = 3N k

2E = 1

T ⇒ E = 3

2 N k

T. (2.18)

Damit haben wir die ¨ Aquivalenz der Boltzmann’schen Entropie mit der thermodynamis- chen Definition (zumindest f¨ ur dieses Beispiel) nachgewiesen.

2.2. Eigenschaften der Boltzmann’schen Entropie

In diesem Abschnitt sollen die wichtigsten Eigenschaften der thermodynamischen Entropie aus der Boltzmann’schen Definition (2.1) f¨ ur allgemeine Systeme begr¨ undet werden.

2.2.1. Additivit¨at. Wir betrachten zwei Systeme 1 und 2 mit jeweils Ω

und Ω

MiZ.

Werden diese Systeme formal zu einem System zusammengefasst, ohne dass sie die M¨oglichkeit haben, Energie, Volumen oder Teilchen auszutauschen (also ohne Kontakt), so ist die Anzahl der MiZ des Gesamtsystems einfach

Ω = Ω

× Ω

, (2.19)

denn zu jedem MiZ von 1 k¨onnen Ω

MiZ von 2 ausgew¨ahlt werden. Gem¨ass (2.1) addieren sich dann die Entropien, S = S

+ S

. Die Entropien unabh¨angiger System sind additiv, wie es sich f¨ ur eine extensive thermodynamische Zustandsgr¨osse geh¨ort.

Dieser Umstand ist der Grund f¨ ur die Verwendung des Logarithmus in der Definition (2.1).

2.2.2. Extremaleigenschaft. Wird nun der thermische Kontakt (Energieaustausch bei konstanter Gesamtenergie E = E

+ E

) zwischen den beiden Systemen zugelassen, so ist die thermodynamische Entropie im neuen GWZ

S(E) = max

E1

[S

(E

) + S

(E − E

)] (2.20)

(vgl. Abschnitt 1.7). Zur Bestimmung der Anzahl der MiZ des Gesamtsystems m¨ ussen wir in diesem Fall ¨ uber alle m¨oglichen Werte von E

integrieren,

Ω(E) = Z

0

dE

Ω

(E

)Ω

(E − E

), (2.21)

denn auf dem Niveau der mikroskopischen Freiheitsgrade sind beliebige Verteilungen der Energie auf die beiden Systeme m¨oglich. Es ist zun¨achst nicht offensichtlich, dass (2.21) mit (2.20) ¨ uber die Beziehung S(E) = k

ln Ω(E) vertr¨aglich ist: In (2.20) wird nur ein einziger MaZ ber¨ ucksichtigt, n¨amlich derjenige, der die Summe der beiden Entropien maximiert, w¨ahrend unter dem Integral (2.21) MaZ mit beliebigen Werten von E

auftreten. Eine genauere Rechnung zeigt, daß der Integrand in (2.21) f¨ ur grosse N ein scharfes Maximum bei der Energie E

des GWZ besitzt, und das Integral deshalb durch den GWZ praktisch vollst¨andig ausgesch¨opft wird.

2.2.3. Irreversibilit¨at. Eines der zentralen Probleme der statistischen Physik ist die Begr¨ undung von irreversiblem Verhalten makroskopischer Systeme aus mikroskopischen Gesetzen, die (wie die Gesetze der klassischen Mechanik und der Quantenmechanik) zeitumkehrinvariant sind, unter denen also alle Vorg¨ange gleichermassen vorw¨arts wie r¨ uckw¨arts in der Zeit ablaufen k¨onnen. Obwohl die L¨osung dieses Problems auf der Grundlage der Boltzmann’schen Entropiedefinition naheliegend und plausibel ist k , wird der Ursprung des (thermodynamischen) “Zeitpfeils” bis heute kontrovers diskutiert.

In der Thermodynamik gehen irreversible Vorg¨ange mit einer Erh¨ohung der Entropie einher, und die Irreversibilit¨at wird mit dem zweiten Hauptsatz begr¨ undet, der besagt, dass die Entropie (in einem abgeschlossenen System) nicht abnehmen kann.

Um zu verstehen, warum das so ist, ist es n¨ utzlich, typische Zahlenwerte zu betrachten.

Bei einer Erh¨ohung der Entropie um ∆S erh¨oht sich die Zahl der dem System zur Verf¨ ugung stehenden MiZ um den Faktor e

. Betrachten wir als Beispiel zwei Wassertropfen von je einen Gramm Gewicht, die sich zun¨achst bei Temperaturen T

und T

befinden. Werden die beiden Tropfen in thermischen Kontakt gebracht, so stellt sich die gemeinsame Temperatur T = (T

+ T

)/2 ein und die Entropie des Gesamtsystems erh¨oht sich um P

∆S = C

ln

(T

+ T

)

4T

T

. (2.22)

F¨ ur T

= 299.9 K und T

= 300.1 K ergibt dies eine Entropieerh¨ohung um ∆S = 4.2 × 10

J/K, und die Zahl der MiZ erh¨oht sich um den Faktor

e

= e

= 10

. (2.23)

Das ist eine unvorstellbar grosse Zahl. Selbst moderate Entropieerh¨ohungen entsprechen bei makroskopischen Systemen einer enormen Zunahme der Anzahl der verf¨ ugbaren MiZ. Daraus folgt unmittelbar die Irreversibilit¨at solcher Vorg¨ange: Die MiZ des Anfangszustands machen einen verschwindend kleinen Bruchteil der im neuen GWZ verf¨ ugbaren MiZ aus, sodass das System praktisch keine Chance hat, jemals in den

k S. z.B. J.L. Lebowitz: Boltzmann’s entropy and time’s arrow. Physics Today, September 1993, S. 32, verf¨ugbar auf der Vorlesungs-Webseite.

P

Abbildung 4. Die W¨ustenanalogie von R. Baierlein.

Anfangszustand zur¨ uckzukehren. In einem Bild von Baierlein

ist der Anfangszustand eine Oase in der weiten W¨ uste der MiZ des Endzustands, in die das System wie ein orientierungsloser Wanderer niemals ∗ zur¨ uckfindet (Abb.4).

Dieses Argument ist weitgehend unabh¨angig von der tats¨achlichen Dynamik des Systems. Es zeigt aber auch, dass die Zunahme der Entropie (und damit der 2.

Hauptsatz) ein statistischer Effekt ist: Eine R¨ uckkehr in den Anfangszustand ist nicht unm¨oglich, aber sie ist extrem unwahrscheinlich. Die Umkehrung irreversibler Vorg¨ange wird umso wahrscheinlicher, je kleiner das System ist. Bei Systemen, die nur noch aus wenigen Molek¨ ulen bestehen, wie sie z.B. in der Zellbiologie und in der Nanophysik vorkommen, sind Abweichungen vom 2. Hauptsatz durchaus beobachtbar.

2.2.4. Dritter Hauptsatz. Die Formulierung (1.26) des dritten Hauptsatzes besagt in der Boltzmann’schen Interpretation, dass das System bei der tiefsten erreichbaren Energie E

, der Grundzustandsenergie, einen eindeutigen (Grund-)Zustand besitzt:

Ω(E

) = 1. Dies ist f¨ ur die meisten Quantensysteme der Fall, es gilt aber nicht f¨ ur das klassische ideale Gas, das den dritten Hauptsatz verletzt. Bei tiefen Temperaturen m¨ ussen genuine Quanteneffekte ber¨ ucksichtigt werden. Darauf kommen wir in Kapitel 4 zur¨ uck.

3. Die Verteilungen der statistischen Physik

In seiner bisher dargestellten Form ist der Formalismus der statistischen Physik anwendbar auf abgeschlossene Systeme, deren Energie zeitlich konstant ist. Tats¨achlich hat man es aber oft mit Systemen zu tun, die durch den Kontakt mit einem W¨armereservoir bei konstanter Temperatur gehalten werden. In den folgenden

+ R. Baierlein, Thermal Physics (Cambridge University Press, 1999); das Bild ist entnommen dem Artikel Entropy and the second law: A pedagogical alternative, American Journal of Physics 62, 15 (1994).

∗ Genauer: Die R¨uckkehrzeit ist so enorm gross, dass sie f¨ur alle praktischen Zwecke als unendlich angenommen werden kann.