Thermodynamik und Statistische Physik
Matthias Vojta
Institut f¨ ur Theoretische Physik
TU Dresden, WS 2012/13
1 Thermodynamik
Nullter Hauptsatz
F¨ ur jedes thermodynamische System existiert eine intensive Zustandsgr¨ oße Temperatur T .
Erster Hauptsatz
F¨ ur jedes thermodynamische System existiert eine extensive Zustandsgr¨ oße Energie U, deren ¨ Anderung gegeben ist durch:
dU = δQ − δW + μdN (1)
wobei die vom System aufgenommene W¨ armemenge δQ und die verrichtete Arbeit δW Prozessgr¨ oßen sind.
Zweiter Hauptsatz
F¨ ur jedes thermodynamische System existiert eine extensive Zustandgr¨ oße Entropie S.
F¨ ur reversible Zustands¨ anderungen gilt:
dS = δQ
revT . (2)
F¨ ur reale, d.h. irreversible, Prozesse gilt:
dS > δQ
T . (3)
Dritter Hauptsatz
Die Entropie jedes abgeschlossenen homogenen thermodynamischen Systems geht f¨ ur T → 0 gegen eine universelle Konstante pro Mol, die Null gesetzt werden kann,
T
lim
→0S(T )/N = 0 (4)
Thermodynamische Fundamentalbeziehung Aus den Haupts¨ atzen und der Extensivit¨ at von S folgt
T S = U + P V − μN (5)
Thermodynamische Potentiale
Unter einem thermodynamischen Potential versteht man eine extensive Zustandsgr¨ oße
in Abh¨ angigkeit ihrer nat¨ urlichen Variablen, so dass aus ihr durch Differentiation alle
thermodynamischen Gr¨ oßen eines Systems gewonnen werden k¨ onnen. Verschiedene Po-
tentiale sind durch Legendre-Transformation miteinander verkn¨ upft.
• Innere Energie:
U (S, V, N ) = T S − P V + μN (6)
dU = T dS − P dV + μdN (7)
• (Helmholtzsche) Freie Energie:
F (T, V, N ) = U − T S = − P V + μN (8)
dF = − SdT − P dV + μdN (9)
• Enthalpie:
H(S, P, N ) = U + P V = T S + μN (10)
dH = T dS + V dP + μdN (11)
• Freie Enthalpie (Gibbssche freie Energie):
G(T, P, N ) = U − T S + P V = μN (12) dG = − SdT + V dP + μdN (13)
• Großes (großkanonisches) Potential:
Ω(T, V, μ) = U − T S − μN = − P V (14) dΩ = − SdT − P dV − N dμ (15) F¨ ur festgehaltene nat¨ urliche Variablen nimmt das jeweilige Potential im thermodynami- schen Gleichgewicht seinen Minimalwert an.
Thermodynamische Response-Funktionen
Die ( lineare ) Antwort eines thermodynamischen Systems auf zeitunabh¨ angige
“thermodynamische Kr¨ afte“ wird durch Ableitungen der thermodynamischen Potentiale beschrieben. In allen F¨ allen muss angegeben werden, welche ¨ außeren Variablen festge- halten werden.
• W¨ armekapazit¨ at:
C = δQ
dT = T ∂S
∂T (16)
• Kompressibilit¨ at:
κ = − 1 V
∂V
∂P (17)
• Thermische Ausdehnung:
α = 1 V
∂V
∂T (18)
• Magnetische Suszeptibilit¨ at:
χ = ∂M
∂B (19)
Beziehungen zwischen den Response-Funktionen folgen u.a. aus Maxwell-Relationen.
2 Wahrscheinlichkeitstheorie
Stochastische Prozesse werden durch Wahrscheinlichkeitsverteilungen bzw. Wahrschein- lichkeitsdichten (als Funktionen von stochastischen Variablen) beschrieben. Diese lassen sich durch Momente bzw. Kumulanten charakterisieren.
F¨ ur Prozesse mit mehreren stochastischen Variablen bedeutet statische Unabh¨ angigkeit
(der Variablen), dass die Verteilungsfunktion faktorisiert.
3 Statistische Physik von Gleichgewichtssystemen
Gibbssches Ensemble
Zur Bildung von Mittelwerten betrachtet man ein Ensemble identischer Systeme, die sich durch ihre Anfangsbedingungen unterscheiden, aber identischen globalen Randbe- dingungen (z.B. vorgegebener Energie oder Temperatur) unterliegen.
Klassische Statistik: Phasenraumstatistik
Eine klassisches System ist i.a. durch eine Hamilton-Funktion beschrieben. F¨ ur feste Zeit t ist sein Zustand gegeben durch einen Punkt im 6N -dimensionalen Phasenraum, wobei N die Anzahl der Teilchen ist. Ein Gibbssches Ensemble ist charakterisiert durch die Wahrscheinlichkeitsdichte f (q
i, p
i, t) im Phasenraum.
Mittelwerte von Observablen werden berechnet als Phasenraummittel (Scharmittel):
A (t) =
d
nq d
np f (q, p, t) A(q, p)
d
np d
nq f (q, p, t) . (20) Die Zeitentwicklung von f folgt der Liouville-Gleichung:
d
dt f (q, p, t) = ∂
∂t + v · grad
f = ∂f
∂t + { H, f } = 0 (21) die sich aus den Hamiltonschen Gleichungen ergibt. Hierbei bezeichnet { H, f } die Poisson-Klammer und v die Geschwindigkeit im Phasenraum.
F¨ ur ein einzelnes System kann man ein Zeitmittel entlang der Phasenraumtrajektorie bilden,
A ¯
t= lim
T→∞
1 T
T 0dt A( q(t), p(t) ) (22) In sogenannten ergodischen Systemen kommt das System jedem Punkte im Phasenraum ( der mit den Erhaltungss¨ atzen vertr¨ aglich ist ) im Verlauf der Zeit beliebig nahe. Dann folgt die Ergoden-Hypothese:
A = ¯ A
t[ Zeitmittel = Scharmittel ] Quantenstatistik: Hilbert-Raum-Statistik
Ein quantenmechanisches System ist i.a. durch einen Hamilton-Operator ˆ H beschrieben.
Der Zustand des Systems ist gegeben durch den Zustandsoperator (bzw. Dichtematrix) ˆ
ρ. In einer Diagonalbasis hat ˆ ρ die Gestalt ˆ
ρ =
α
W
α| ψ
αψ
α| (23)
und beschreibt ein Gibbssches Ensemble aus Quantensystemen, von denen sich jedes
Einzelsystem mit Wahrscheinlichkeit W
αim Zustand | ψ
αbefindet.
Mittelwerte von Observablen sind jetzt quantenstatistische Mittelwerte:
O ˆ = Sp
ˆ ρ O ˆ
=
α
W
αψ
α| O ˆ | ψ
αAllgemeine Eigenschaften von ˆ ρ:
Sp ( ˆ ρ) = 1, ρ ˆ = ˆ ρ
†, ψ | ρ ˆ | ψ ≥ 0 ∀ | ψ (24) Im allgemeinen gilt ˆ ρ
2= ˆ ρ. F¨ ur ˆ ρ
2= ˆ ρ liegt ein reiner Zustand vor.
Die Zeitentwicklung von ˆ ρ folgt der von-Neumann-Gleichung:
i¯ h ∂
tρ(t) = ˆ H , ˆ ρ(t) ˆ
(25) Entropie
Als Entropie eines quantenstatistischen Systems wird definiert:
S = − k Sp ( ˆ ρ ln ˆ ρ) ≥ 0 (26)
S wird maximal f¨ ur die Dichtematrix ˆ ρ
th, die den thermodynamischen Gleichgewichts- zustand unter den gegebenen Nebenbedingungen beschreibt; S ist dann gleich der ther- modynamischen Entropie. k ist die Boltzmann-Konstante,
k := k
B≡ 1, 38 · 10
−23J
K (27)
In einem reinen Zustand gilt wegen ˆ ρ
2= ˆ ρ : S = 0.
Interessanterweise kann die durch
S = − k
μ
W
μln W
μdefinierte Entropie einer Wahrscheinlichkeitsverteilung W
μals Maß f¨ ur die Unbestimmt- heit aufgefasst werden.
Mikrokanonische Gesamtheit
Die (Gibbssche) Gesamtheit abgeschlossener Systeme wird als mikrokanonisch bezeich- net. Jedes System der Gesamtheit ist gekennzeichnet durch Energieerhaltung E = const, sowie V = const, N = const.
Es folgt, daß alle Wahrscheinlichkeiten W
naus ˆ ρ =
W
n| n n | mit E
n= E verschwin- den. Aus dem Prinzip der maximalen Entropie folgt:
ˆ ρ = 1
Ω(E) Δ( ˆ H − E) mit Δ(E
n− E) =
1 f¨ ur E
n= E
0 sonst (28)
und mit Ω(E) = Sp (Δ(E
n− E)) = Zahl der Zust¨ ande mit Energie E
1.
⇒ S = k ln Ω(E) (29)
Daraus folgt, daß man S als thermodynamisches Potential auffassen kann mit E, V, N = const ⇒ S = S(E, V, N ).
Kanonische Gesamtheit
Die (Gibbssche) Gesamtheit aller Systeme, die an ein W¨ armebad fester Temperatur T gekoppelt sind, heißt kanonische Gesamtheit. Das W¨ armebad bestimmt den Mittelwert der Energie, E = U = const, außerdem ist V = const und N = const.
Das Maximum der Entropie unter den Nebenbedingungen Sp ( ˆ ρ) = 1 ; Sp
ˆ ρ H ˆ
= E = U liefert
ˆ
ρ
K= 1
Z
Ke
−βHˆ(30)
Z
K= Sp
e
−βHˆ(31) Der Anschluss an die Thermodynamik liefert
β = 1
k
BT . (32)
.
Thermodynamische Funktionen ergeben sich aus der freien Energie F wie folgt:
F (T, V, N) = − k
BT ln Z
K(T, V, N) U (T, V, N ) = − ∂
∂β ln Z
K= k
BT
2∂
∂T ln Z
KS(T, V, N) = −
∂F
∂T
V,N
= k
Bln Z
K+ k
BT ∂
∂T ln Z
KP (T, V, N) = −
∂F
∂V
T ,N
= k
BT ∂
∂V ln Z
K1
Ω( E ) wird manchmal auch als mikrokanonische Zustandssumme bezeichnet.
( Die Volumenabh¨ angigkeit in Z
Kkommt von der Volumenabh¨ angigkeit der Energieei- genwerte des Systems, siehe sp¨ ater )
μ(T, V, N ) =
∂F
∂N
T ,V
= − k
BT ∂
∂N ln Z
KG(T, V.N ) = F + P V = H − T S
= − k
BT ln Z
K+ k
BT V ∂
∂V ln Z
KGroßkanonische Gesamtheit
Die ( Gibbssche ) Gesamtheit aller Systeme, die sowohl an ein W¨ arme- als auch an ein Teilchenbad gekoppelt sind, wird als großkanonisch bezeichnet. Das W¨ armebad bestimmt wiederum T und damit U = E ; das Teilchenbad bestimmt das chemische Potential μ und damit die mittlere ( ! ) Teilchenzahl N ; außerdem ist V = const.
Das Maximum der Entropie unter den Nebenbedingungen Sp (ˆ ρ) = 1 ; Sp
ˆ ρ H ˆ
= E = U ; Sp
ˆ ρ N ˆ
= N = N , liefert nun:
ˆ
ρ
G= 1
Z
Ge
β( ˆH−μNˆ)(33) Z
G= Sp
e
β( ˆH−μNˆ)(34) (35) Der Zusammenhang mit der kanonischen Zustandssumme ist
Z
G=
∞ N=0Z
K(N)e
μN kBT
.
⇒ Das gilt nur f¨ ur [ ˆ N , H] = 0, was allerdings “fast immer“ erf¨ ˆ ullt ist!
exp(βμ) wird auch als Fugazit¨ at bezeichnet.
Thermodynamische Funktionen ergeben sich aus dem großkanonischen Potential Ω wie
folgt:
Ω(T, V, μ) = − k
BT ln Z
G= U − T S − μN = − P V U (T, V, μ) = k
BT
T ∂
∂T + μ ∂
∂μ
ln Z
GS(T, V, μ) = − ∂Ω
∂T
V,μ
= k
Bln Z
G+ k
BT ∂
∂T ln Z
GP (T, V, μ) = −
∂Ω
∂V
T ,μ
= k
BT ∂
∂V ln Z
G= − Ω V N (T, V, μ) = −
∂Ω
∂μ
T ,V
= k
BT ∂
∂μ ln Z
GF¨ ur die Kompressibilit¨ at gilt:
N
2V κ
T=
∂N
∂μ
T ,V
= − ∂
2Ω
∂μ
2T ,V
= 1
k
BT
( ˆ N − N ˆ
2≥ 0 Damit gilt f¨ ur Energie- und Teilchenzahlfluktuationen:
(ΔE)
2=
H ˆ − H ˆ
2= k
BT
2c
V(ΔN )
2=
N ˆ − N ˆ
2= k
BT N
2V κ
TEs folgt ΔE
E = 1
√ N , ΔN
N = 1
√ N ,
d.h. im thermodynamischen Limes ( N → ∞ ) verschwinden die relativen Fluktuationen.
⇒ Die verschiedenen thermodynamischen Ensembles sind f¨ ur große N ¨ aquivalent.
4 Ideale Systeme
Ideale Systeme sind Systeme nicht-wechselwirkender Teilchen im thermodynamischen Gleichgewicht. (Achtung: Damit ein Gleichgewichtszustand erreicht werden kann, muss eine schwache Rest-Wechselwirkung existieren!)
Zwei-Niveau-System
Wir betrachten ein System aus N ortsfesten (unterscheidbaren) Spins s =
12im Magnet- feld B (allgemein: Zwei-Niveau-Systeme). Das System besitzt 2
NSpinkonfigurationen (Mikrozust¨ ande). Das gesamte magnetische Moment ist
M = μ
0 Ni=1
σ
i, σ
i= ± 1 , μ
0= Moment eines Spins.
Ein Zustand mit gegebenem magnetischen Moment mμ
0, d.h.
12(N + m) Spins ↑ und
12
(N − m) Spins ↓ , wird als Makrozustand bezeichnet; ein Makrozustand wird i.a. durch viele Mikrozust¨ ande realisiert.
F¨ ur die Energie gilt:
E = − M B = − m μ
0B = − μ
0B
Ni=1
σ
i(m = − N, . . . , N ) .
Abgeschlossenes System (mikrokanonisch): Energie E (und damit Makrozustand) fest.
Anzahl der Mikrozust¨ ande:
Ω(N, m) =
N
12
(N + m)
= N !
(
N+2m)!(
N−2m)!
Im thermodynamischen Gleichgewicht gilt f¨ ur die Wahrscheinlichkeiten der m¨ oglichen Mikrozust¨ ande
W
N= 1
Ω(N, m) = const.
Mittelwert eines Spins:
σ
1= 1
Ω(N, m) ( N (σ
1= +1) − N (σ
1= − 1) ) ,
wobei N (σ
1= ±1) die Anzahl der Mikrozust¨ ande mit σ
1= ± 1 bezeichnet. Es gilt N ( σ
1= ± 1 ) = Ω( N − 1, m ∓ 1 )
und damit
σ
1= Ω( N − 1, m − 1 ) − Ω( N − 1, m + 1 )
Ω( N, m ) = m
N .
System im W¨ armebad (kanonisch): Dichteoperator ˆ
ρ
K=
n
W
n| n n | , wobei | n die Zust¨ ande | n = | σ
1σ
2. . . σ
Nsind. Es folgt:
W
N= 1 Z
Kexp
− E
Nk
BT
= 1 Z
Kexp
μ
0B k
BT
N i=1σ
iZ
K= ( Z
1)
N, Z
1=
σ=±1
exp μ
0B
k
BT σ
= 2 cosh μ
0B
k
BT
Beachte: Z
K= (Z
1)
Ngilt f¨ ur generell wechselwirkungsfreie, unterscheidbare Objekte.
Thermodynamik: In der mikrokanonischen Gesamtheit erh¨ alt man die Entropie S( E ) = k
Bln Ω( N, m )= − k
BN + m 2 ln
N + m 2N
+ N − m 2 ln
N − m 2N
mit E = − m μ
0B und − N < m < N.
Nun folgt aus dU = T dS:
dS dE = 1
T
> 0 f¨ ur E < 0
< 0 f¨ ur E > 0 ( ! )
T > 0 T < 0 S(E)
E N B μ
o−N B μ
oAbbildung 1: S(E) f¨ ur ein System wechselwirkungsfreier Spins im Magnetfeld
1
T = ∂S
∂E = 1
− μ
0B
∂S
∂m = k
B2μ
0B ln
1 −
mN1 +
mN= k
2μ
0B ln
1 −
μE0B1 +
μE0B
=
> 0 f¨ ur E < 0,
< 0 f¨ ur E > 0.
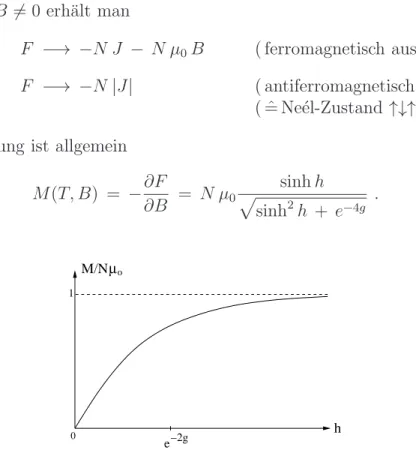
In der kanonischen Gesamtheit ergibt sich f¨ ur gegebenes T : E = − N μ
0B σ
1= − N μ
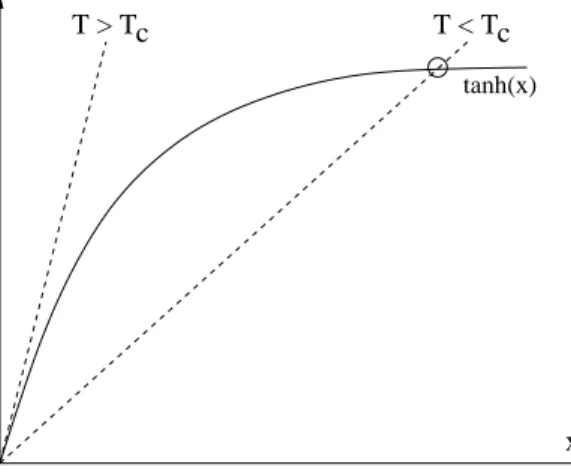
0B tanh
μ
0B k
BT
,
in ¨ Ubereinstimmung mit dem mikrokanonischen Resultat.
Offenbar ist es m¨ oglich ( und sinnvoll! ), negative thermodynamische Temperaturen ein- zuf¨ uhren; dies bedeutet, daß h¨ oherenergetische Niveaus st¨ arker besetzt sind als niede- renergetische (Besetzungsinversion).
In der kanonischen Gesamtheit erh¨ alt man weiter die freie Energie:
F = − k
BT ln Z
K= − N k
BT ln
2 cosh μ
0B k
BT
⇒ S(T ) = − ∂F
∂T = N k
Bln
2 cosh μ
0B k
bT
− μ
0B k
BT tanh
μ
0B k
BT
⇒ S( T ) = N ×
μ0B T
exp
−
μkB0BTf¨ ur k
BT μ
0B k
Bln 2 f¨ ur k
BT μ
0B
ln 2
S/N
T
Abbildung 4.2 a: S(T )
f¨ ur das 2-Niveau-System in der kanonischen Gesamtheit
T
μoB
~exp( −2 B/kT)
~T−2
C
μo
Abbildung 4.2 b: C(T )
F¨ ur die Spezifische W¨ arme folgt:
C(T ) = T ∂S
∂T
B
= N k
Bμ
0B k
BT
21 cosh
2 μ0B kBTDas charakteristische Maximum in Abbildung 4.2 b wird als Schottky-Anomalie ( Schottky-Peak ) bezeichnet. Das exponentielle Verhalten bei tiefen Temperaturen ist eine Folge der Energiel¨ ucke μ
0B, der quadratische Abfall ist charakteristisch f¨ ur ein System mit nach oben beschr¨ anktem Energiespektrum:
C( T ) = N k
B×
⎧ ⎪
⎨
⎪ ⎩
μ0BkBT
2exp
−
kμB0BTf¨ ur k
BT μ
0B
14
μ0B kBT 2f¨ ur k
BT μ
0B
F¨ ur die Magnetisierung gilt M = − ∂F
∂B = N
0μ
0tanh μ
0B
k
BT
= N μ
0σ
1. Die innere Energie folgt aus
U = F + T S = − N μ
0B tanh μ
0B
k
BT
.
Erweiterung auf N -Niveau-Systeme: F¨ ur ein System von N unabh¨ angigen unterscheidbaren Teilchen, von denen jedes einen von unendlich vielen Zust¨ anden mit Energien
1,
2, . . . annehmen kann, folgt also:
Z
K= ( Z
1)
Nmit Z
1=
i
exp −
ik
BT
Die Wahrscheinlichkeit, ein individuelles Teilchen im Zustand i zu finden, ist p
i= 1
Z
iexp −
ik
BT
( “Boltzmann-Verteilung“ ) . (36) Falls die Teilchen ununterscheidbar sind, gilt
Z
K= 1
N! ( Z
1)
N.
Dann kann man auch ein großkanonisches Ensemble betrachten:
Z
G=
N
1
N ! (Z
1)
Ne
Nμ
kBT
= exp Z
1e
μ kBT
Dann kann man schreiben unter Verwendung der Besetzungszahlen n
ider Einteilchen- niveaus i:
Z
G=
∞ n1=0 ∞ n2=0· · · 1
n
1!n
2! . . . exp
−
i
n
ii
− μ k
BT
Daraus l¨ asst sich die mittlere Besetzungszahl eines Niveaus ableiten:
n
i=
ni
n
i1 Z
i1 n
i! exp
− n
i(
i− μ) k
BT
Wni=
Wahrsch.keit, daß Niveau i mit n
iTeilchen besetzt ist
mit Z
i=
∞ ni=01 n
i! exp
− n
i(
i− μ) k
BT
n
i= exp
−
i− μ k
BT
(37)
Mittlere Besetzungszahl der Einteilchen-Niveaus in der Boltzmann-Statistik ( manchmal auch “Boltzmann-Verteilung“ genannt )
Quantenoszillatoren
Wir betrachten ein System aus N identischen, wechselwirkungsfreien ( unterscheidbaren ) eindimensionalen harmonischen Oszillatoren. Die Energieeigenwerte eines Oszillators sind:
n
= ¯ hω( n + 1 2 )
Die Systemzust¨ ande sind gegeben durch | n
1, . . . , n
N. Die Gesamtenergie ist E =
N i=1ni
. Damit faktorisiert die Zustandssumme f¨ ur ein kanonisches Ensemble:
Z
K= (Z
1)
NF¨ ur einen einzelnen Oszillator gilt:
Z
1=
∞ n=0e
−¯hω
2kBT
·
e
− ¯hω kBT
n= exp
−
2k¯hωBT1 − exp
−
k¯hωBT= 1 2 sinh
¯hω 2kBTThermodynamik
F (T ) = − k
BT ln Z
K= N k
BT ln
1 − e
−kBT¯hω+ N ¯ hω 2 S(T ) = − ∂F
∂T = N k
B− ln
1 − e
−kBThω¯+
¯ hω kBT
e
kBThω¯− 1
=
⎧ ⎨
⎩
N k
Bln
k¯hωBTf¨ ur k
BT ¯ hω : Hochtemperaturlimes N k
Bk¯hωBT
· e
− ¯hω
kBT
f¨ ur k
BT ¯ hω : Tieftemperaturlimes Innere Energie U = F + T S = N ¯ hω
2 + N hω ¯ exp
¯hω kBT− 1
= N ¯ h ω 1
2 + n
, wobei n die mittlere Zahl von Oszillatorquanten ( pro Oszillator ) ist. Die mittlere Besetzungszahl n =
exp
k¯hωBT
− 1
−1ist gerade die Bose-Einstein-Verteilung f¨ ur Sy- steme ohne Teilchenzahlerhaltung.
F¨ ur die W¨ armekapazit¨ at gilt:
C = T ∂S
∂T = ∂U
∂T = N ¯ h ω ∂ n
∂T = N k
B¯ hω
2k
BT
21 sinh
2 ¯hω kBT=
N k
Bf¨ ur k
BT ¯ hω N k
B ¯hω kBT 2exp
−
k¯hωBTf¨ ur k
BT ¯ hω
Das Hochtemperaturverhalten ist wiederum das eines klassischen Systems C( T ) →
T C
Nk
Abbildung 3: Spezifische W¨ arme von Quantenoszillatoren
const, insbesondere ist der sogenannte Gleichverteilungssatz erf¨ ullt. Das Tieftempera- turverhalten ist wegen der Anregungsl¨ ucke ¯ hω zwischen Grundzustand und erstem an- geregten Zustand durch den Boltzmannfaktor exp
−
k¯hωBTbestimmt - man nennt dies thermisch aktiviertes Verhalten.
Ideales Boltzmann-Gas
Wir betrachten ein ( klassisches ) ideales Gas aus N punktf¨ ormigen Teilchen im Kasten mit Volumen L
3und der Hamilton-Funktion
H( q, p ) = 1 2m
N i=1p
2i,x+ p
2i,y+ p
2i,z. (38)
Bei Verwendung periodischer Randbedingungen folgt p
i,x=
2πL¯h· n
i,x, . . . In der kanonischen Gesamtheit folgt wegen der Unabh¨ angigkeit der Teilchen
Z
K= 1
N ! ( Z
1)
N. (39)
( 1/N! wegen Ununterscheidbarkeit. ) F¨ ur Z
1folgt im Limes L → ∞ : Z
1=
{p}
exp
− 1 k
BT
p
22m
= L
3( 2π¯ h )
3d
3p exp
− p
22mk
BT
= Z
13,xZ
1,x= L 2π¯ h
∞−∞
dp
xexp
− p
2x2mk
BT
=: L λ
Tmit der thermischen de-Broglie-Wellenl¨ ange
λ
T=
2π¯ h
2mk
BT
12( λ
T T−→ ∞
→0! ) (40)
und es gilt
Z
K= 1 N !
L λ
T N·D∝ T
ND2· V
N, (41) wobei D = 3 die Anzahl der Raumdimensionen ist.
Thermodynamik:
F ( T, V, N ) = − N k
BT ln eV
N λ
DT; V = L
DS = −
∂F
∂T
= N k
Bln eV
N λ
DT+ D 2 N k
BU = F + T S = D
2 N k
BT ( kalorische Zustandsgleichung ) C
V=
∂U
∂T
V
= N k
BD
2 ( Gleichverteilungssatz ) P = −
∂F
∂V
T ,N
= k
BT N
V ( Thermische Zustandsgleichung ) μ =
∂F
∂N
T,V
= − k
BT ln V
N λ
DTAchtung: Wenn der mittlere Teilchenabstand a = ( V /N )
1/Dkleiner wird als die ther- mische de-Broglie-Wellenl¨ ange, a λ
T( dies passiert bei tiefen Temperaturen ! ), dann wird die Entropie nach den obigen Gleichungen negativ! Dies demonstriert das Versagen der klassischen Beschreibung, d.h. die Quantisierung der Energieniveaus wird wichtig.
Es ist n¨ utzlich, das Boltzmann-Gas in der großkanonischen Gesamtheit zu betrachten:
Z
G=
∞ N=0e
μN
kBT
Z
K(N)=
∞ N=0(Z
1)
NN! e
μN
kBT
= exp
Z
1e
μ kBT
Daraus folgt das großkanonische Potential:
Ω( T, V, μ ) = − k
BT ln Z
G= − k
BT Z
1e
μ
kBT
= − k
BT V λ
DTe
μ kBT
und daraus die Thermodynamik:
N = − ∂Ω
∂μ
T ,V
= V λ
DTe
μ
kBT
bzw. μ = − k
BT ln V
N λ
DTS = − ∂Ω
∂T
V,μ
=
D + 2
2 k
B− μ T
V λ
DTe
μ
kBT
= D + 2
2 k
BN + k
BN ln V N λ
DTP = − ∂Ω
∂V
T,μ
=
k
BT exp
μkBT
λ
DT= N k
BT
V bzw. P V = N k
BT U = Ω + T S + μN = D
2 N k
BT
In beiden Ensembles finden wir dieselben Zustandsgleichungen, P V = N kT und U =
D2N kT , wobei jeweils N und E durch Mittelwerte N und U = E zu er- setzen sind ( gleiches gilt f¨ ur das mikrokanonische Ensemble ).
Wir leiten noch die Maxwellsche Geschwindigkeitsverteilung ab. Die Wahrscheinlichkeits- dichte der Impulsverteilung f( p ) ( d.h. die Zahl der Teilchen mit Impuls p im Impuls- raumvolumenelement d
3p pro d
3p ) ist
f( p ) = L
3( 2π¯ h )
31 Z
1exp
− p
22mk
BT
= (2πmk
BT )
−32exp
− p
22mk
BT
. Daraus die Wahrscheinlichkeitsdichte f¨ ur die Geschwindigkeitsverteilung ( v =
mp)
f ( v ) =
m 2πk
BT
32
exp
− m v
22k
BT
( aus f ( p) d
3p = f ( v) d
3v ) F¨ ur den Geschwindigkeitsbetrag | v | = v folgt mit d
3v = 4πv
2dv:
F ( v ) = 4π v
2m 2πk
BT
32exp
− mv
22k
BT
(42) Dies ist die Maxwellsche Geschwindigkeitsverteilung.
Gleichverteilungssatz
Wir betrachten ein klassisches System im thermodynamischen Gleichgewicht. F¨ ur einen beliebigen Freiheitsgrad, der einen quadratischen Term additiv zur Hamiltonfunktion beitr¨ agt,
H( q; p
1, . . . , p
f) =
1(p
1) + H
( q; p
2, . . . , p
f) ,
1(p
1) = αp
21,
folgt:
ε
1= 1
2 k
BT (43)
Quantenstatistiken idealer Gase
Wir betrachten ein System aus N identischen nichtwechselwirkenden quantenmechani- schen Teilchen, beschrieben durch den Hamiltonoperator
H( 1, . . . , N ) =
N j=1h( j ) ,
wobei j = ( r
j, σ
j) f¨ ur die Orts- und Spinvariable eines Teilchens steht. Der Einteilchen- Hamiltonoperator h besitze ( Einteilchen- ) Eigenzust¨ ande
h | λ = ε
λ| λ .
Der Hilbertraum des N -Teilchen-Systems l¨ asst sich aus Zustandsvektoren aufbauen, die ein direktes Produkt von Einteilchenzust¨ anden sind,
Φ
P( 1, . . . , N ) = ϕ
λ1(1) ϕ
λ2(2) · · · ϕ
λN(N) ,
wobei ϕ
λ(j ) = j | λ die Einteilchenwellenfunktion in der Ortsdarstellung bezeichnet.
Die Ununterscheidbarkeit der Teilchen erfordert, dass sich beobachtbare Eigenschaften eines quantenmechanischen Zustands bei Vertauschung zweier Teilchen nicht ¨ andern d¨ urfen.
In D = 3 Dimensionen ergeben sich zwei Klassen von Vielteilchenzust¨ anden.
Bosonen besitzen Wellenfunktionen, die symmetrisch unter Teilchenaustausch sind. Diese k¨ onnen durch Summation ¨ uber alle Permutationen erzeugt werden:
| Φ
s= K
sP(P)
P ˆ
(P)| Φ ( K
s: Normierung ) ,
In | Φ
ssteckt nicht mehr die Information, welches Teilchen in welchem Einteilchen- zustand ϕ
λvorkommt, sondern nur, wie oft jeder Einteilchenzustand besetzt ist. D.h.
| Φ
sist eindeutig charakterisiert durch die Besetzungszahlen n
λund die Angabe der Symmetrie ( s ):
| Φ
s= | n
1n
2. . .
s= | { n
λ}
sDie | { n
λ} bilden ein vollst¨ andiges orthonormales Basissystem im Hilbertraum der Bo- sonensysteme mit beliebiger Teilchenzahl (Fock-Raum).
Die Zust¨ ande | { n
λ} sind Eigenzust¨ ande des Teilchenzahloperators ˆ N , N ˆ | { n
λ} =
λ
n
λ| { n
λ} f¨ ur Bosonen sind die n
λ= 0, 1, 2, . . . beliebig.
F¨ ur nichtwechselwirkende Systeme und eine Einteilchenbasis ϕ
λaus Eigenzust¨ anden des Einteilchen-Hamilton-Operators sind die | { n
λ} auch Energieeigenzust¨ ande:
H ˆ | { n
λ} =
λ
n
λε
λ| { n
λ}
Fermionen besitzen total antisymmetrische Zust¨ ande:
| Φ
a= K
aP(P)
( − 1)
PP ˆ
(P)| Φ F¨ ur Fermionen sind nur n
λ= 0, 1 zul¨ assig (Pauli-Prinzip).
Die Zustandssumme nichtwechselwirkender Bosonen oder Fermionen mit H ˆ =
h(j) , h | λ = ε
λ| λ . im großkanonischen Ensemble faktorisiert:
Z
G=
N
nλ
nλ=N
exp ( − β(E − μN)) =
λ1
λ2
. . . exp ( − βn
λ(ε
λ− μ)) =
λ
Z
λmit
Z
λ=
nλ
exp
− n
λε
λ− μ k
BT
. F¨ ur Bosonen gilt:
Z
λB=
∞ nλ=0exp ( − βn
λ(ε
λ− μ)) = 1+e
−β(ελ−μ)+
e
−β(ελ−μ)2+. . . = 1
1 − exp ( − β(ε
λ− μ)) F¨ ur Fermionen gilt:
Z
λF=
nλ=0,1
exp ( − βn
λ(ε
λ− μ)) = 1 + exp ( − β(
λ− μ)) .
Die mittleren Besetzungszahlen der Einteilchenniveaus ergeben f¨ ur Bosonen die Bose- Einstein-Verteilung,
n
λB
= 1
e
β(ελ−μ)− 1 ≡ n
B( ε
λ− μ ) (44) und f¨ ur Fermionen die Fermi-Dirac-Verteilung
n
λF
= 1
e
β(ελ−μ)+ 1 ≡ n
F( ε
λ− μ ) . (45) F¨ ur Bosonen mit ε
λ≥ 0 muss wegen n
λ≥ 0 notwendig μ ≤ 0 gelten!
F¨ ur hohe Energien ε
λgilt in beiden F¨ allen n
λ≈ exp ( − β(ε
λ− μ)), dies ist wiederum die Maxwell-Boltzmann-Verteilung.
( Dies gilt auch im Hochtemperatur-Limes wegen μ/kT 1, siehe sp¨ ater. )
Ideales Fermi-Gas
Wir betrachten ein Gas nichtwechselwirkender Fermionen im Kontakt mit einem W¨ arme- und Teilchenreservoir. Die großkanonische Zustandssumme ist
Z
G= Sp
e
−β( ˆH−μNˆ)=
λ
! 1 + e
−β(ελ−μ)"
Die Thermodynamik folgt aus dem großkanonischen Potential:
Ω( T, V, μ ) = − k
BT ln Z
G= − k
BT
λ
ln
1 + e
−ελ−μ kBT
N = N = − ∂Ω
∂μ =
λ
n
F( ε
λ− μ ) S = − ∂Ω
∂T = − Ω T +
λ
ε
λ− μ
T n
F(ε
λ− μ) P = − ∂Ω
∂V = − Ω
V ( es war Ω = − P V ) Grenzfall T = 0
n
λ=
1 f¨ ur ε
λ< μ ( besetzt ) 0 f¨ ur ε
λ> μ ( leer ) Dann ist:
Ω =
λ
(ε
λ− μ)θ(μ − ε
λ) , dies ist ( nat¨ urlich ) die Grundzustandsenergie ( bezogen auf μ ).
Man definiert die Fermi-Energie ε
F:= μ(T = 0).
Achtung: F¨ ur festes N ist μ(T ) temperaturabh¨ angig, ε
Fist konstant ( per Definition ).
In Metallen ist typischerweise ε
F5 . . . 10 eV. Dies definiert die Fermi-Temperatur nach ε
F= k
BT
F−→ T
F∼ 10
5K ( ! ).
Tieftemperaturbereich k
BT ε
FDie scharfe Fermikante ( T = 0 ) wird f¨ ur T > 0 auf einer Skala k
BT verbreitert. Die Ableitung
− ∂n
F(ε
λ− μ)
∂ε
λ= 1
4k
BT cosh
2 ελ−μ2kBT
bildet ein scharfes Maximum bei ε
λ= μ.
Dies erlaubt, die thermodynamischen Eigenschaften im Bereich k
BT ε
F⇔ T T
Fε
λn
FFermi−See 1
μ kT
T > 0 T = 0
Abbildung 4: Fermi-Verteilung n
F( sog. entartetes Fermigas ) durch eine Tieftemperaturentwicklung berechnen. Ausgangs- punkt ist
Ω = − k
BT V (2s + 1)
∞−∞
dε D(ε) ln [ 1 + e − β(ε
λ− μ) ] mit der Zustandsdichte ( s ist der Spin der Fermionen )
D( ε ) = 1 V (2s + 1)
λ
δ( ε − ε
λ) . (46)
Die Sommerfeld-Entwicklung liefert:
Ω
V = (2s + 1)
− b(μ) − π
26 D(μ)(k
BT )
2+ O
(k
BT )
4= − P (47) Die thermodynamischen Gr¨ oßen ergeben sich zu:
N (T ) = −
∂∂μΩ= V (2s + 1)
∂μ∂b+
π62∂D∂μ(μ)(k
BT )
2+ . . .
mit
∂μ∂b= a(μ) = a(ε
F) + (μ − ε
F) a
(ε
F) + . . . , a(ε
F) =
εF
−∞
dε
D(ε
) =
NV((2Ts=0 )+1), a
(ε
F) = D(ε) Chemisches Potential μ(T ) = ε
F−
π62D(ε1F)∂D(εF)
∂εF
(k
BT )
2+ O (k
BT )
4Entropie S = −
∂∂TΩ= (2s + 1) V
π32D(ε
F) k
B2T + . . . Spez. W¨ arme C
V= T
∂S∂T
V
= S + . . . Kompressibilit¨ at κ
T=
n12 ∂n∂μ
T
=
n12(2s + 1) D(ε
F) + O (T
2)
Suszeptibilit¨ at χ
Pauli=
V1∂M∂B= 2 μ
20D(ε
F) + O (T
2)
Bemerkungen zu S(T ) und C
V(T )
1. S(T ) → 0 f¨ ur T → 0 in ¨ Ubereinstimmung mit dem 3.Hauptsatz.
2. C
V= γT mit γ ∝ D(ε
F) - dies ist der dominierende Beitrag zur W¨ armekapazit¨ at von Metallen bei tiefen Temperaturen !
3. Lineare Abh¨ angigkeit S ∝ T , C
V∝ T f¨ ur tiefe Temperaturen ist Folge der endli- chen Zustandsdichte an der Fermi-Kante, D(ε
F) > 0, d.h. es existieren Anregungen mit beliebig kleiner Anregungsenergie.
( Dies gilt nicht in Isolatoren, Supraleitern, Halbleitern, Semimetallen, . . . )
Offensichtlich sind viele Tieftemperatur-Eigenschaften des Fermi-Gases nur durch die Zustandsdichte an der Fermi-Kante, D(ε
F), bestimmt.
Zustandsdichte f¨ ur freie nichtrelativistische Teilchen mit periodischen Randbedingungen in einem Kasten mit Volumen V = L
D. Die Eigenzust¨ ande sind ebene Wellen mit Im- pulseigenwerten
p
i= 2π¯ h
L n
i, p = (p
x, p
y, p
z) f¨ ur D = 3 , n
iganzzahlig.
Die Einteilchenzust¨ ande λ besitzen Quantenzahlen pσ ( σ = Spin ) mit Energien:
ε
λ= ε
p σ= p
22m = 1
2m 2π¯ h
L
2 D i=1n
2iDie Zustandsdichte D(ε) pro Spinrichtung ist dann D(ε) = 1
V
p
δ(ε − ε
p) = 1 V
V (2π¯ h)
Dd
Dp δ(ε − ε
p)
= Ω
D(2π¯ h)
D ∞0
dp p
D−1δ(ε − ε
p) = Ω
D(2π¯ h)
Dm
√ 2mε
p(ε)
D−2,
dabei ist Ω
Ddie Ober߬ ache der Einheitskugel in D Dimensionen.
Wir definieren den Fermi-Impuls p
F: p
F:= p(ε
F) = √
2mε
F=: ¯ hk
F( k
F: Fermi-Wellenzahl ) (48) Bei T = 0 sind alle Zust¨ ande mit ε < ε
Fbesestzt, d.h. | p | = p
Fdefiniert die Fermi- Fl¨ ache im Impusraum, welche die besetzten von den unbesetzten Zust¨ anden trennt.
( F¨ ur kompliziertere Dispersionsrelationen definiert allgemein ε
p= ε
Fdie Fermi-Fl¨ ache. )
F¨ ur die Gesamtteilchenzahl folgt bei T = 0:
N = V (2s + 1)
εF
−∞
dε
D(ε
) = V (2s + 1) (2π¯ h)
DΩ
DD p
DFVolumen d.
Fermikugel
(49)
damit N ∝ V ε
D/F 2und ε
F∝ n
2/D. Analog folgt f¨ ur die Energie bei T = 0:
U = E = V (2s + 1)
εF−∞