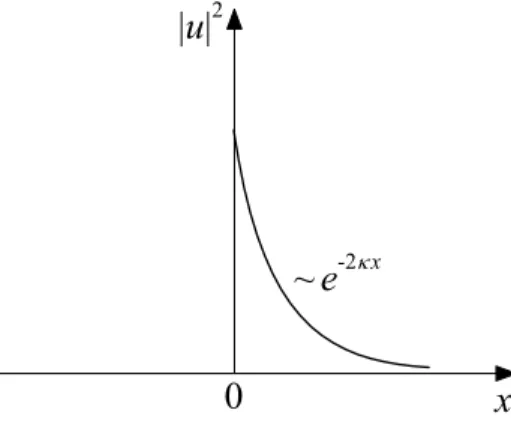
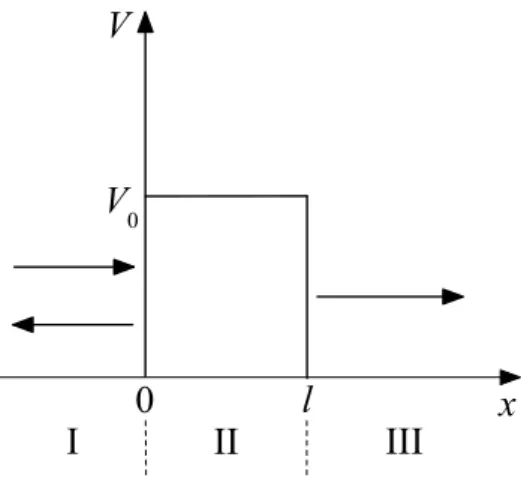
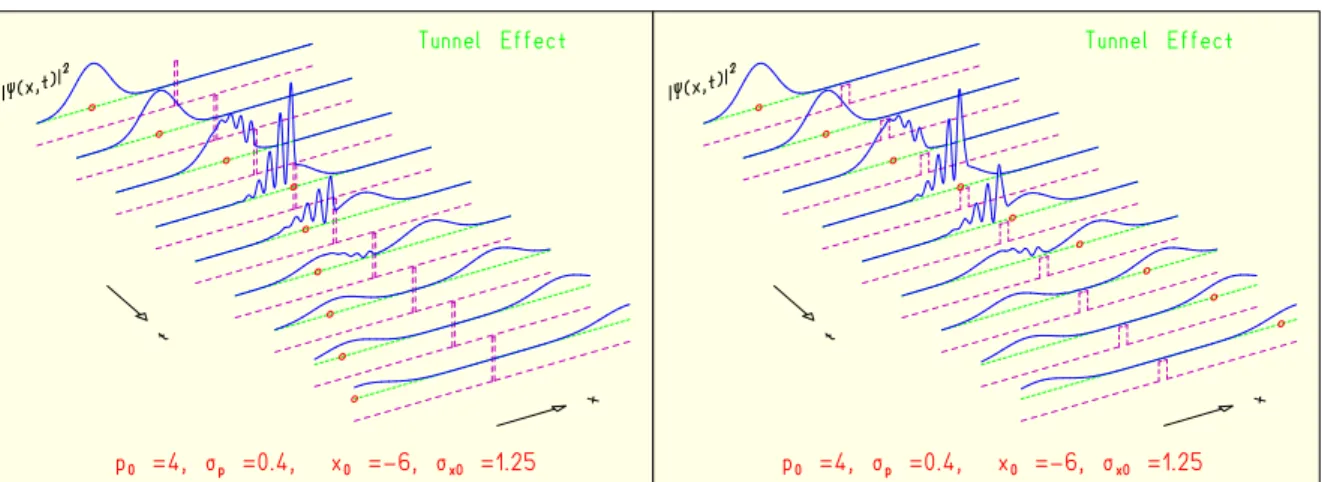
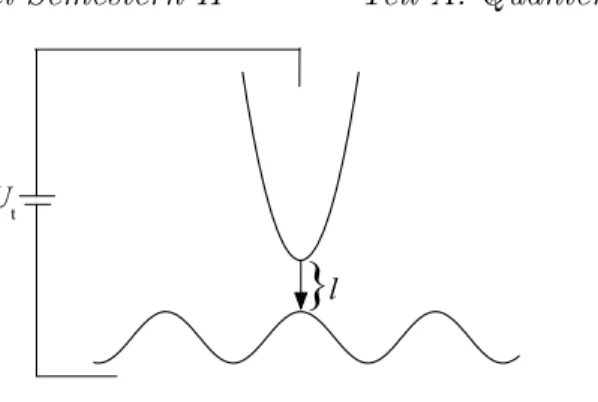
Theoretische Physik in zwei Semestern II Teil A: Quantenmechanik Joachim Krug
Volltext
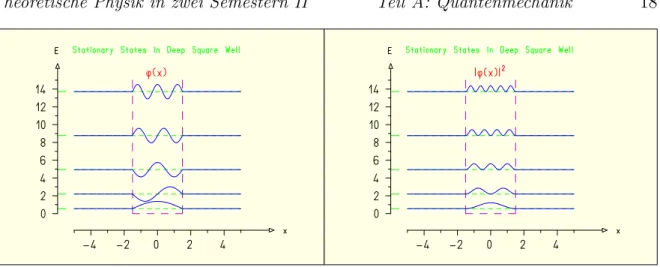
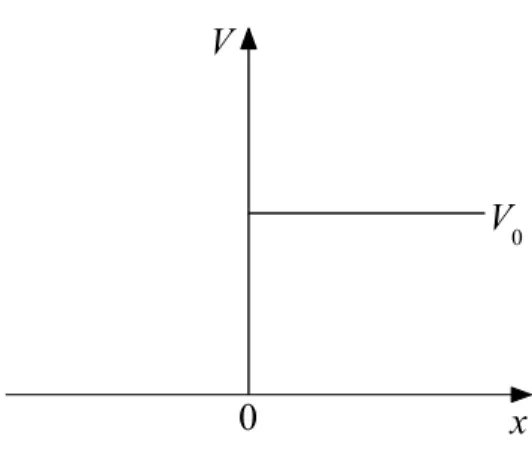
Abbildung
ÄHNLICHE DOKUMENTE
auf der Innenfl¨ ache eines Kegels mit dem halben ¨ Offnungswinkel α, dessen Symmetriachse die
Um die Paketrutsche stabil zu konstruieren, ben¨ otigt man das Maximum von
Finden Sie also zun¨ achst einen Ausdruck f¨ ur die Kraft im Inneren der Kugel und bestimmen Sie anschließend auch das Potential (inklusiver der ben¨ otigten Konstanten) so, dass
(g) Die Gleichungen (3,4) kann man verwenden, um verschiedene Identit¨ aten f¨ ur Vektorprodukte
Das Gef¨ alle hat einen Steigungswinkel θ und befindet sich auf einer horizontalen Ebene, auf der es sich ohne Reibung frei bewegen kann.. Die Schachtel f¨ angt aus der Ruhe an,
(a) Ein Teilchen (der Masse m) bewegt sich in einer Ebene, die durch Polarkoor- dinaten r und θ beschrieben wird, in Gegenwart von einem Zentralpotential U(r). Skizzieren Sie
(a) Leiten Sie eine Gleichung f¨ur die Zeit her, die die T¨ur bis zum Schließen ben¨otigt, wenn das Fahrzeug mit einer konstanten Beschleunigung a losf¨ahrt. (5 P.) Hinweis: Stellen
Wir betrachten ein Modell f¨ur eine skatende Person, die ungl¨ucklicherweise einen Sturz in einer Halfpipe erleidet. Auf der Innenfl¨ache eines raumfesten Zylin- dermantels