5.1 Quantenmechanische Theorie des Drehimpulses

Theorie des Drehimpulses. Bewegung im Zentralfeld. Wasserstoffatom

Nachdem wir uns bisher mit eindimensionalen Problemen besch¨aftigt hatten (Kastenpostential, harmonischer Oszillator etc.), wenden wir uns jetzt mehrdimensionalen Bewegungen zu. Wie in der klassischen Mechanik erfordert die Beschreibung der Dynamik gekr¨ummter Bahnen die Einf¨uhrung des Drehimpulses. In der Quantenphysik ist dies essentiell f¨ur die korrekte Beschrei- bung von Mikro-Teilchen in Atomen, Molek¨ulen, im Atomkern sowie in realen Materialien.

5.1 Quantenmechanische Theorie des Drehimpulses

Der Drehimpuls der Quantenmechanik ist von fundamentaler Bedeutung f¨ur zentralsymmetri- sche Probleme, insbesondere f¨ur die Struktur der Atome. Wir besch¨aftigen uns daher zun¨achst mit seinen Eigenschaften und seinem Eigenwertproblem.

5.1.1 Bahndrehimpulsoperator

Der funktionale Zusammenhang des Bahn-Drehimpulses¹ der klassischen Mechanik mit dem Impuls ist gegeben durch:

L=r×p

Aufgrund des schon besprochenen Korrespondenzprinzips erwarten wir in der Quantenmechanik daher:

Lˆ = ˆr׈p

Der Drehimpulsoperator l¨asst sich also mit Hilfe der folgenden Determinante formulieren:

Lˆ =

e_i e_j e_k ˆ

x yˆ zˆ ˆ

px pˆy pˆz

Dies kann man noch k¨urzer mit dem anitsymmetrischen (Levi-Civita-)Tensor² schreiben:

Lˆi =ǫijkˆrjpˆk.

1“Bahn-Drehimpuls” bezeichnet den Drehimpuls, der mit dem Bewegungs-Impuls auf der Teilchenbahn ver- kn¨upft ist – im Unterschied zu anderen Drehimpulsen, wie dem Spin.

2Zur Erinnerung:ǫhat die Werte 0,1 oder−1 f¨ur die F¨alle wiederholter Indizes bzw. unterschiedlicher Indizes mit positiver oder negativer Reihenfolge.

133

Der Drehimpuls-Operator der Quantenmechanik besitzt eine Reihe besonderer Eigenschaften, die sich fundamental vom Drehimpuls der klassischen Mechanik unterscheiden. Diese Eigen- schaften folgen aus der algebraischen Struktur und k¨onnen bereits in darstellungsunabh¨angiger Form abgeleitet werden.

Eigenschaften von L:ˆ 1. Es gilt ˆL⁺ = ˆL.

Beweis:

Lˆ⁺_i =ǫijkpˆ⁺_krˆ⁺_j

=ǫijkpˆkrˆj

=ǫijkrˆjpˆk= ˆLi. Dies gilt, da [ˆri,pˆj]∝δij ist.

2. Es gilt:

[ ˆLi,Lˆj] = i~ǫijkLˆk (5.1) Beweis:

[ ˆLx,Lˆy] = [ˆypˆz,zˆpˆx]−[ˆypˆz,xˆpˆz]−[ˆzpˆy,zˆpˆx] + [ˆzpˆy,xˆˆpz]

= ˆypˆx[ˆpz,z] + ˆˆ xˆpy[ˆz,pˆz]

=i~Lˆz

und analog f¨ur zyklische Vertauschungen der Indizes. Hierbei wurde [ ˆAB,ˆ C] = ˆˆ A[ ˆB,C] + [ ˆˆ A,C] ˆˆ B,

benutzt. Daraus folgt sofort: Zwei Komponenten des Drehimpulses sind nicht gleichzeitig messbar, in fundamentalem Gegensatz zur klassischen Mechanik.

Die Eigenschaft 2, zusammen mit der Linearit¨at, bedeutet, dass ˆLx,Lˆy und ˆLz eine Kom- mutator (Li-)Algebra bilden. Das heißt Addition und Multiplikation f¨uhren nicht aus der Algebra heraus.

3. Es ist f¨ur alle i=x, y, z mit ˆL² = ˆL²_x+ ˆL²_y+ ˆL²_z:

[ ˆL²,Lˆi] = 0. (5.2)

Beweis:

[ ˆL²,Lˆx] = [ ˆL²_y,Lˆx] + [ ˆL²_z,Lˆx]

= ˆLy[ ˆLy,Lˆx] + [ ˆLy,Lˆx] ˆLy+ ˆLz[ ˆLz,Lˆx] + [ ˆLz,Lˆx] ˆLz

=i~(−LˆyLˆz−LˆzLˆy + ˆLzLˆy + ˆLyLˆz) = 0

Also ist f¨ur alle idie Drehimpulskomponente Lˆi mit Lˆ² gleichzeitig messbar.

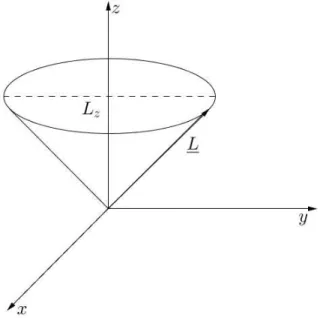
Daraus k¨onnen wir zusammenfassen, welche Eigenschaften des Drehimpulses in der Quanten- mechanik prinzipiell messbar sind und welche Information nicht zug¨anglich ist: Messbar sind z.B. der Betrag, |L| (kennt man durch ˆL²) und die Komponente Lz, aber keine weiteren Kom- ponenten. Graphisch bedeutet das, dass der Vektor L der Eigenwerte des Drehimpulses nur unvollst¨andig bestimmt werden kann: mit fixiertem Betrag und z-Komponente vereinbar sind dann alle Vektoren, die auf dem sogenannten Drehimpuls-Kegel liegen, s. Abbildung. Die ˆLx- und ˆLy-Komponenten bleiben unbestimmt bzw. alle Orientierungen sind gleich wahrscheinlich.

Abbildung 5.1: Drehimpuls-Kegel der Eigenwerte von ˆL (schematisch). L¨ange (Betrag von L) und z-Komponente sind fixiert. Damit sind alle Vektoren vereinbar, die auf diesem Kegel liegen.

Welche Einschr¨ankungen es f¨ur Betrag und z-Komponente gibt, bleibt hier noch offen.

Die Operatoren ˆLz und ˆL² besitzen also gemeinsame Eigenfunktionen. Die zentrale Frage ist nun, ebendiese Eigenfunktionen sowie die damit vereinbaren Eigenwerte der beiden Operatoren zu finden. Dies ist vor allem relevant f¨ur Teilchen im zentralsymmetrischen PotentialV =V(|r|).

Die Eigenschaften von ˆL charakterisieren den Bahndrehimpuls ˆL. Es existieren aber im Ge- gensatz zur klassischen Mechanik auch andere Drehimpulse mit denselben algebraischen Ei- genschaften. So sind zum Beispiel der Spin oder Isospin zu nennen. Wir untersuchen daher zun¨achst das Eigenwertproblem des allgemeinen Drehimpulses und kehren erst im Anschluss zum Bahndrehimpuls zur¨uck.

5.1.2 Eigenwert-Problem des allgemeinen Drehimpulsoperators

Wir ersetzen nun unseren mit ˆLbezeichneten Bahndrehimpuls durch einen allgemeinen dimen- sionslosen Drehimpuls ˆJ.

Lˆ →~Jˆ

Dieser Drehimpuls soll die Eigenschaften 2. und 3. aus dem vorigen Abschnitt besitzen:

[ ˆJi,Jˆj] =iǫijkJˆk, [ ˆJ²,Jˆi] = 0.

Die Operatoren ˆJ3 und ˆJ² besitzen also gemeinsame Eigenfunktionen. Setzen wir a als Eigen- wert von ˆJ² und m als Eigenwert von ˆJ3, so sind beiden Eigenwerte reell, a ≥ 0, und unsere

Eigenwertgleichungen lauten:

Jˆ²|ami=|ami (5.3)

Jˆ3|ami=m|ami (5.4)

Da ader Eigenwert des Drehimpulsoperators ˆJ² ist, so entspricht√

a dem Betrag des Drehim- pulsvektors. Ebenso entspricht m dem z-Anteil der Drehimpulses. Haben wir also ein fixiertes a, so existieren zun¨achst unendlich viele verschiedene M¨oglichkeiten f¨ur m.

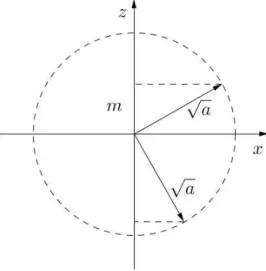
Abbildung 5.2: Projektion der Drehimpulskegel auf diez−x-Ebene. Die Abbildung ist analog zu Abb. 5.1, hier sind allerdings die Eigenwerte der quantenmechanischen Drehimplusoperatoren dargestellt. Nach Gleichung (5.5) ist die vertikale Projektion (m) immer streng kleiner als die L¨ange des Vektors √

a.

Man erkennt aber gleichzeitig (s. auch Abb. 5.2), dass a und m nicht unabh¨angig sind. Zum Beispiel erkennt man, dass diez-Projektionm nicht gr¨oßer als der Betrag√

a sein kann. In der Tat sieht man leicht, dass ein strengerer Zusammenhang existiert:

Satz: Es gilt immer

−√

a < m <√

a (5.5)

Beweis: Wir betrachten einen beliebigen Zustand |ψi und berechnen den Erwartungswert des Operators ˆJ²:

hJˆ²iψ =hψ|Jˆ²|ψi

=hψ|Jˆ1²+ ˆJ2²+ ˆJ3²|ψi

=hψ|Jˆ3²|ψi+hψ|Jˆ1²+ ˆJ2²|ψi

Nun gilt aberhψ|Jˆ1² + ˆJ2²|ψi>0, da sonst ˆJ1, ˆJ2 und ˆJ3 gleichzeitig messbar w¨aren (es m¨ussten gleichzeitig die Erwartungswerte von ˆJ1² und ˆJ2² verschwinden). Es gilt somit

hψ|Jˆ²|ψi>h|ψ|Jˆ3²|ψi

W¨ahlen wir nun als Zustand |ψi einen gemeinsamen Eigenzustand |ami, so folgt daraus und unter Verwendung des Eigenwertproblems von ˆJ und ˆJ3:

ham|Jˆ²|ami>ham|Jˆ3²|ami ham|a|ami>ham|m²|ami

aham|ami> m²ham|ami a > m².

Dies war zu zeigen.

Wir finden als n¨achstes die m¨oglichen Eigenwerte m des Operators ˆJ3, bei einem fixierten Eigenwert von ˆJ², alsoa∈Rfixiert. Dies geschieht am einfachsten durch Verwendung von zwei Hilfsoperatoren:

Definition: Wir definieren zwei Leiteroperatoren f¨ur das Drehimpuls-Problem:

Jˆ+ = ˆJ1+iJˆ2, (5.6)

Jˆ₋ = ˆJ1−iJˆ2, (5.7)

Die Motivation hierf¨ur ist, dass das Drehimpuls-Problem dieselbe algebraische Struktur wie der Harmonische Oszillator hat, insbesondere gelten die Analogien zwischen folgenden Operatoren:

Hˆ →Jˆ² ˆ x→Jˆ1

ˆ px →Jˆ2

ˆ a→Jˆ₋ ˆ

a^†→Jˆ+

Wir zeigen nun zun¨achst, dass identische Kommutator-Relationen gelten. Hieraus folgt dann, dass ˆJ_± in der Tat eine Leiterwirkung haben.

Eigenschaften von Jˆ_±:

1. Aus den Definitionen (5.6) und (5.7) folgt:

Jˆ+ = ( ˆJ₋)⁺ (5.8)

2. Die z-Komponente des Drehimpulses kommutiert nicht mit den Leiteroperatoren. Es gilt [ ˆJ3,Jˆ+] = + ˆJ+ (5.9) und

[ ˆJ3,Jˆ₋] = −Jˆ₋ (5.10) 3. Es gilt außerdem

Jˆ+·Jˆ₋= ˆJ² −Jˆ3( ˆJ3−1) (5.11) und

Jˆ₋·Jˆ+ = ˆJ²−Jˆ3( ˆJ3+ 1) (5.12)

4. Die Operatoren ˆJ_± und ˆJ² besitzen gemeinsame Eigenzust¨ande |ami, d.h.

[ ˆJ²,Jˆ_±] = 0 (5.13)

Das bedeutet auch, dass die Operatoren ˆJ²,Jˆ3 und ˆJ_± gemeinsame Eigenzust¨ande besitzen.

Aus Gleichung (5.13) schlussfolgern wir, dass die Wirkung von ˆJ_± auf einen Eigenzustand die Quantenzahla nicht ¨andert. Die Wirkung auf die Quantenzahl m bleibt dabei aber offen. Dies kl¨art der folgende Satz.

5. Satz: Es gelten die Eigenwertprobleme

Jˆ²|ami=a|ami , Jˆ3|ami=m|ami .

Weiter sei ˆJ_± gegeben durch Glg. (5.6). Es gelten dann folgende Relationen:

Jˆ+|ami=c+|a, m+ 1i (5.14) und

Jˆ₋|ami=c₋|a, m−1i (5.15) mit c_±∈C.

Beweis: Zun¨achst gilt, wegen (5.8), c₋ =c^∗+ :=c^∗. Da hier der Eigenwert aimmer fixiert ist, verwenden wir die Kurzbezeichnung |ami → |mi. Betrachten wir nun die Wirkung von ˆJ3·Jˆ+. Hierf¨ur benutzen wir Gleichung (5.9):

Jˆ3Jˆ+|mi

| {z }

|m^′i

= ( ˆJ+Jˆ3+ ˆJ+)|mi Jˆ3|m^′i= ˆJ+m|mi+ ˆJ+|mi

= (m+ 1) ˆJ+|mi Jˆ3|m^′i= (m+ 1)|m^′i

Aus dem Eigenwert-Problem von ˆJ3 folgtm^′ =m+ 1. Das heißt:

Jˆ3|m^′i= (m+ 1)|m^′i= (m+ 1)|m+ 1i Analog gilt dies f¨ur ˆJ₋, Glg. (5.15).

6. Satz: F¨ur jedes fixierte a existieren j und ˜j mit ˜j ≤ m ≤ j. Im Unterschied zu den bisherigen Ungleichungen existieren also ein exaktes Minimum und Maximum. Dabei gilt a = j(j+ 1) sowie ˜j =−j.

Beweis: Wir finden zun¨achst den Wert von j. Die Bedingung f¨ur die Existenz eines solchen Maximums ist:

Jˆ+|aji= 0

Wir verwenden nun Glg. (5.12):

Jˆ₋Jˆ+|aji

| {z }

=0

= 0 = ˆJ²|aji −Jˆ3²|aji −Jˆ3|aji Jˆ²|aji= ( ˆJ3²+ ˆJ3)|aji

= ˆJ3( ˆJ3+ 1)|aji a|aji=j(j + 1)|aji Daraus folgt:

a=j(j+ 1)

√a=p

j(j + 1)> j.

Es ist also Beziehung (5.5) erf¨ullt.

Analog finden wir nun ˜j. Hier ist die zu erf¨ullende Bedingung:

Jˆ₋|a˜ji= 0, so dass gilt:

Jˆ+Jˆ₋|a˜ji= 0 = ( ˆJ²−Jˆ3²+ ˆJ3)|a˜ji Jˆ²|a˜ji= ˆJ3( ˆJ3−1)|a˜ji

a|a˜ji= ˜j(˜j−1)|a˜ji. Hieraus folgt dann:

a = ˜j(˜j −1).

Diese beiden Ergebnisse sind simultan, f¨ur das selbe a, zu erf¨ullen. Hierf¨ur gibt es nur eine M¨oglichkeit im Rahmen unserer Bedingungen:

˜j =−j, also erhalten wir den Zusammenhang

mmin =−mmax (5.16)

7. Eigenwertspektrum der z-Komponente des Drehimpulses Aus dem Satz 6. folgte

−j ≤m≤j,

und wir wissen, dass ˆJ+ f¨ur jedes m den Zustand |ami in den Zustand |a, m+ 1i ¨uberf¨uhrt.

Dies ist nur m¨oglich f¨ur diskrete ¨aquidistante Eigenwerte. Die Menge aller m¨oglichen m ist dann:

m∈ {−j,−j+ 1, ..., j−1, j}.

Dies sind 2j+ 1 m¨ogliche Eigenwerte. Starten wir beim Zustand|a,−ji so ¨uberf¨uhrt ˆJ+ ihn in n Schritten in den Zustand |aji, wobein eine nat¨urliche Zahl ist:

n = 0,1,2, ...

Daraus folgt f¨ur den Maximalwert

j =−j+n

⇒j = n 2

F¨ur den allgemeinen Drehimpulsoperator ist mmax entweder ganzzahlig oder halbzahlig.

Es gilt also:

j = n 2 =







j = 0,1,2, ... n gerade, j = ¹₂,³₂, ... n ungerade.

8. Gemeinsames Eigenwert-Problem von Jˆ² undJˆ3, Zusammenfassung: Wir wissen, dass diese beiden Operatoren gemeinsame Eigenfunktionen mit den Quantenzahlen a bzw. m haben. Es ist alternativ ¨ublich die Quantenzahl a durch mmax=j zu ersetzen. Wir behandeln also im Folgenden Zust¨ande, die wir mit |jmi bezeichnen. Zwischen a und j besteht nach a=j(j+ 1) ein eindeutiger Zusammenhang.

Jˆ²|jmi=j(j+ 1)|jmi, (5.17) mit j = ⁿ₂ und n = 0,1,2, ....

Jˆ3|jmi=m|jmi, (5.18)

mit |m| ≤j.

Bemerkung: Der physikalische Drehimpuls folgt durch ˆJ →~·J. Die Eigenwerte von ˆˆ J² sind dann j(j+ 1)~², und die von ˆJ3 sind m·~.

9. Normierung der Eigenfunktionen: Aus der Beziehung Jˆ+|jmi=cjm|j, m+ 1i folgt, nach hermitescher Adjungation und Eigenschaft (5.8):

hjm|Jˆ₋=c^∗_jmhj, m+ 1| . Hieraus folgt, unter Benutzung von (5.12):

hjm|Jˆ₋Jˆ+|jmi=|cjm|²hj, m+ 1|j, m+ 1i j(j+ 1)−m(m+ 1) =|cjm|²

Wir w¨ahlen c wieder reell, da die Phase irrelevant ist. Analog funktioniert dies wieder f¨ur Jˆ₋|jmi. Das Resultat f¨ur die Eigenfunktionen ist dann:

Jˆ_±|jmi=p

j(j+ 1)−m(m±1)|j, m±1i . (5.19)

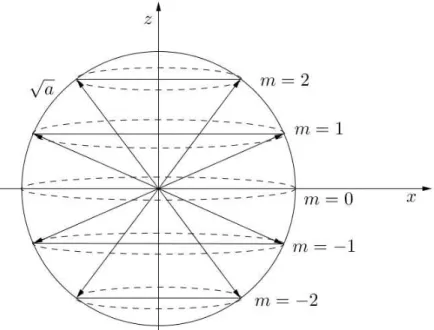
Illustration: die gefundenen Zusammh¨ange zwischen den Eigenwerten k¨onnen wir uns an einem Beispiel veranschaulichen und kehren dazu noch einmal zum Drehimpulskegel zur¨uck.

W¨ahlen wir j = 2. Dann ist der Eigenwert von ˆJ²: a=j(j+ 1) = 6. Die “L¨ange” des Vektors ist dann √

6, und die m¨oglichen Eigenwertem von ˆJ3 sind:

m={−2,−1,0,1,2}.

Wir haben hier also 2j + 1 = 5 m¨ogliche z-Projektionen des Drehimpulses. Jeder Eigenwert entspricht nun einem eigenen Kegel. Beachte hierbei, dass m = √

a nicht m¨oglich ist. Das Maximum der z-Komponente ist mmax = j = 2. Unten ist ein Schnitt durch eine Kugel mit Radius √

a dargestellt. Dies sind zun¨achst alle Endpunkte der m¨oglichen Vektoren mit dieser L¨ange. Da aber nur bestimmte z-Werte erlaubt sind, treten nun nur noch ganz bestimmte Drehimpulskegel (hier f¨unf) auf.

Abbildung 5.3: M¨ogliche Eigenwerte des Drehimpulses ˆJ3 und die zugeh¨origen Drehimpulskegel, bei vorgegebenem mmax =j = 2, d.h. Betrag des Drehimpulses, a=p

2(2 + 1) =√ 6.

5.1.3 Das Eigenwertproblem des Bahndrehimpulsoperators der Quantenmechanik

Wir wenden nun die zuvor gewonnenen Resultate auf den Bahndrehimpuls ˆL an und gehen zur Ortsdarstellung ¨uber. Das heißt, die Eigenzust¨ande werden zu Funktionen des Ortsvektors,

|lmi → h~r| |lmi)≡ψlm(~r). Hier haben wir die gebr¨auchliche Bezeichnung l f¨ur den maximalen Eigenwert des Drehimpulses ˆLz eingef¨uhrt, die den bisherigen Wert j ersetzt. Das Eigenwert- problem des Bahndrehimpulses wird also zu:

Lˆ²ψlm(r) = ~²l(l+ 1)ψlm(r), (5.20) mit l = 0,1,2, ... und

Lˆzψlm(r) =~mψlm(r), (5.21)

mit |m| ≤ l. Hier kann l nur ganzzahlige Werte annehmen, was aber noch zu zeigen ist. Wir beweisen zun¨achst jedoch:

Satz: Die Eigenfunktionen des Drehimpulses ψlm(r) sind unabh¨angig von |r|. Beweis: Wir wenden den Operator ˆL auf eine Funktionf(r²) an:

Lfˆ (r²) = ~

i(r× ∇)f(r²)

= ~

i(r× ∇r²) d dr²f(r²)

= 2~

i (r×r)df(r²) dr² = 0

Wir k¨onnen also in Kugelkoordinaten die Eigenfunktionen des Drehimpulses schreiben als:

ψlm(r) =ψlm(ϕ, θ), (5.22)

so dass sich die Kugelkoordinatenbeschreibung als g¨unstig erweist. Wir ben¨otigen nun noch den Lˆz-Operator in Kugelkoordinaten. Wir wissen:

x=rsinθcosϕ , y=rsinθsinϕ , z =rcosθ . Es gilt außerdem:

∂

∂ϕ =−y ∂

∂x +x ∂

∂y, woraus f¨ur die z-Komponente des Drehimpuls-Operators folgt:

Lˆz = ~ i

∂

∂ϕ. (5.23)

Da ˆLz und ˆL² kommutieren, finden wir ihre gemeinsamen Eigenfunktionen durch folgenden Produktansatz:

ψlm = ˜flm(θ)·Φm(ϕ) (5.24)

Dass dieser Ansatz gerechtfertigt ist (insbesondere die Wahl der Argumente und der Quanten- zahlen), muss durch die Rechnung best¨atigt werden.

Eigenfunktionen von Lˆz: Es ist also folgende Gleichung zu l¨osen:

~ i

∂

∂ϕ[ ˜flm(θ)Φm(ϕ)] =~mf˜lm(θ)Φm(ϕ)

∂ϕΦm(ϕ) =imΦm(ϕ)

Durch unseren Produktansatz sind die Eigenfunktionen von ˆLz also tats¨achlich nicht von θ abh¨angig. Macht man f¨ur obige Differentialgleichung einene-Ansatz, so erh¨alt man:

Φm(ϕ) = c·e^imϕ

mit ϕ∈[0,2π]. Die Eindeutigkeit von Φ als Wahrscheinlichkeitsamplitude erfordert:

Φm(ϕ) = Φm(ϕ+k·2π),

so dass wir die Bedingung erhalten (wir betrachten k= 1):

1 =e^i2πm,

und m (und damit auchl =mmax) muss also ganzzahlig sein, was wir bei unseren Eigenfunk- tionen oben schon vermerkt hatten. Durch Normierung erhalten wir die

Eigenfunktionen von ˆLz:

Φm(ϕ) = 1

√2πe^imϕ, m= 0,±1,±2, . . . (5.25)

Eigenfunktionen von Lˆ²: Als n¨achstes bestimmen wir die Eigenfunktionen von ˆL². Hier wird sich erst zeigen, ob der Produktansatz in der obigen Form gerechtfertigt war,

ψlm(θ, ϕ) = ˜flm(θ)Φm(ϕ).

Zun¨achst m¨ussen wir uns die zu l¨osende Eigenwert-Gleichung f¨ur ˆL² in der Ortsdarstellung in Kugelkoordinaten beschaffen. F¨ur den ¨Ubergang von kartesischen (x, y, z)-Koordinaten zu Kugelkoordinaten (r, θ, ϕ) gilt:

x=rsinθcosϕ y =rsinθsinϕ z =rcosθ r =p

x²+y²+z²

θ = arccos z

px²+y²+z²

!

ϕ = arctany x

Aus dem Korrespondenzprinzip hatten wir bereits ˆL = ˆr×pˆ gefunden, und in der Ortsdar- stellung hatten wir die Komponenten des Drehimpulses bereits in kartesischen Koordinaten angegeben:

Lˆx= ~ i

y ∂

∂z −z ∂

∂y

,

Lˆy = ~ i

z ∂

∂x −x ∂

∂z

,

Lˆz = h i

x ∂

∂y −y ∂

∂x

.

Um von hier zu Kugelkoordinaten ¨uberzugehen, ben¨otigen wir nun noch die Transformations- Vorschriften f¨ur die partiellen Ableitungen. Wenden wir zum Beispiel ∂x auf eine Funktion f[r(x, y, z), θ(x, y, z), ϕ(x, y, z)] in Kugelkoordinaten an, so gilt nach der Kettenregel:

∂

∂x = ∂r

∂x

∂

∂r + ∂θ

∂x

∂

∂θ + ∂ϕ

∂x

∂

∂ϕ,

und analog f¨ur ∂y und ∂z. Aus den obigen Transformations-Vorschriften erhalten wir die ge- suchten partiellen Ableitungen ∂ir, ∂iθ und ∂iϕ, f¨ur i = x, y, z. Hat man nun die partiellen Ableitungen bestimmt, k¨onnen wir die Drehimpulsoperator-Komponenten in Kugelkoordina- ten wie folgt aufschreiben:

Lˆx = ~ i

−sinϕ ∂

∂θ −cotθcosϕ ∂

∂ϕ

Lˆy = ~ i

cosϕ ∂

∂θ −cotθsinϕ ∂

∂ϕ

Lˆz = ~ i

∂

∂ϕ

Hierbei f¨allt die r-Unabh¨angigkeit in jeder Komponente auf. Durch Quadrieren und Addieren der Komponenten erhalten wir unseren gesuchten Operator:

Lˆ² =− ~² sin²θ

sinθ ∂

∂θ

sinθ ∂

∂θ

+ ∂²

∂ϕ²

. (5.26)

Vergleichen wir dies mit dem Laplace Operator in Kugelkoordinaten (man kann diesen auf die selbe Art und Weise erhalten),

∆ = 1 r²

∂

∂r

r² ∂

∂r

+ 1

r²sin²θ

sinθ ∂

∂θ

sinθ ∂

∂θ

+ ∂²

∂ϕ²

, (5.27)

so stellen wir fest, dass der Drehimpulsoperator ˆL² genau dem Winkelanteil ∆θ,ϕ des Laplace- Operators entspricht.

Lˆ² =−~²∆θ,ϕ (5.28)

Betrachten wir dies noch einmal etwas anders. In der klassischen Mechanik gilt:

p² =p²_r + 1 r²L² Außerdem gilt f¨ur den Impulsquadratoperator:

ˆ

p² =−~²∆

=−~² 1 r²

∂

∂rr² ∂

∂r − ~²

r²∆θ,ϕ (5.29)

Aus dem Korrespondenzprinzip kann man nun den Radialteil des Impulsquadratoperators ab- lesen (die Punkte symbolisieren die Wirkung auf eine Wellenfunktion):

ˆ

p²_r· · ·=−~² 1 r²

∂

∂rr² ∂

∂r· · ·=−~² r

d²

dr²r . . . . (5.30) Schreiben wir nun noch einmal die Eigenwertprobleme f¨ur die kommutierenden Operatoren ˆLz

und ˆL² mit ihren gemeinsamen Eigenfunktionen ψlm(θ, ϕ) in der Ortsdarstellung auf:

−~²∆θ,ϕψlm(θ, ϕ) =~²l(l+ 1)ψlm(θ, ϕ), (5.31)

−i~ ∂

∂ϕψlm(θ, ϕ) =~mψlm(θ, ϕ). (5.32)

Als Ansatz hatten wir einen Produktansatz gew¨ahlt, und wir kennen bereits den ϕ-abh¨angigen Teil der L¨osung. Wenn wir die Konstante zun¨achst wieder weglassen (wir bestimmen sie am Ende), erhalten wir:

ψlm(θ, ϕ) = ˜flm(θ)e^imϕ. (5.33) Wir setzen dies nun in (5.31) ein, benutzen (5.27) und erhalten:

−~² 1

sinθ

∂

∂θ

sinθ ∂

∂θ

+ 1

sin²θ

∂²

∂ϕ²

f˜lm(θ)e^imϕ=~²l(l+ 1) ˜flm(θ)e^imϕ, e^imϕ 1

sinθ

∂

∂θ sinθ∂f˜lm(θ)

∂θ

!

− f˜lm(θ)

sin²θ m²e^imϕ=l(l+ 1) ˜flm(θ)e^imϕ, 1

sinθ

∂

∂θ − m²

sin²θ +l(l+ 1)

f˜lm(θ) = 0,

wo wir den Faktor e^imφ k¨urzen konnten, so dass tats¨achlich keine Abh¨angigkeit von ϕ in die- ser Gleichung verbleibt. Unser Produktansatz ist also korrekt und f¨uhrt auf eine geschlossene Gleichung f¨ur ˜flm(θ).

Wir substituieren nunz = cosθ und nennen die Funktion, die nun von z abh¨angt, f, f˜lm(θ)→flm(cosθ) =flm(z),

wobei folgende Transformationen gelten:

sin²θ = 1−z², dz =−sinθdθ, df˜lm

dθ =−sinθdf dz. Formen wir hiermit unser Eigenwert-Problem weiter um:

1 sinθ

∂

∂θ −sin²θdflm

dz − m²

1−z²flm+l(l+ 1)flm = 0

− 1 sinθ

d

dθ(1−z²)dflm

dz − m²

1−z²flm+l(l+ 1)flm = 0 d

dz(1−z²) d

dz − m

1−z² +l(l+ 1)

flm(z) = 0, so erhalten wir das Endergebnis:

Die Gleichung

d

dz(1−z²) d

dz − m

1−z² +l(l+ 1)

flm(z) = 0 (5.34)

mit l, m= 0,±1,±2, ... und |m| ≤ l wird gel¨ost durch die assoziierten Legendrefunktionen P_l^m(z). F¨ur ganzzahlige m ist P_l^m(±1) regul¨ar.

Diese Legendrefunktionen untersuchen wir etwas sp¨ater. Die Gesamtl¨osung nennen wir nun nicht mehr ψlm, sondern wir verwenden hierf¨ur die ¨ubliche BezeichnungY_l^m(θ, ϕ). Das sind die Kugelfl¨achenfunktionen (Englisch: spherical harmonics)³.

3Man beachte, dass in der Literatur in verschiedenen Fachgebieten sehr viele unterschiedliche Notationen verwendet werden. Unsere Notation verwendet die komplexe Darstellung derφ-Abh¨angigkeit.

Die gemeinsamen Eigenfunktionen der Operatoren ˆL² und ˆLz sind f¨ur θ ∈ [0, π] und ϕ ∈ [0,2π]:

Y_l^m(θ, ϕ) = ClmP_l^m(cosθ)e^imϕ (5.35) mit

Clm =am

s2l+ 1 4π

(l− |m|)!

(l+|m|)!

und

am =

(1 , m≥0 (−1)^m , m <0

Eigenschaften:

1. Erzeugendes Funktional: Wir wollen an dieser Stelle eine n¨utzliche Darstellung der Legendre-Funktionen f¨ur m≥0 angeben:

P_l^m(x) = (1−x²)^m2 d^l+m dx^l+m

(x²−1)^l 2^ll!

2. Symmetrie der Legendre-Polynome f¨ur m≥0;

P_l^−m = (−1)^m(l−m)!

(l+m)!P_l^m (5.36)

3. Orthonormierung der Kugelfl¨achenfunktionen:Man zeigt durch direkte Rechnung⁴, dass die so definierten Kugelfl¨achenfunktionenY_l^morthogonalisiert und normiert sind, d.h.

das Integral ¨uber den gesamten Raumwinkel,dΩ = sinθdθdϕ, ergibt:

Z

Y_l^m′ ^′∗·Y_l^mdΩ =δm,m^′ ·δl,l^′.

4. Vollst¨andigkeit:Eine beliebige quadratisch integrable Funktion,f(θ, φ), kann nach Ku- gelfl¨achenfunktionen entwickelt werden

f(θ, φ) = X∞

l=0

Xl

m=−l

f_l^mY_l^m(θ, φ) (5.37)

mit den Entwicklungskoeffizienten (analog zur Fourier-Entwicklung) f_l^m =

Z

dΩf_l^mY_l^m∗(θ, φ) (5.38)

4Dies folgt bereits aus der allgemeinen Eigenschaft hermitescher Operatoren (hier ˆL² und ˆLz), da Eigen- funktionen zu verschiedenen Eigenwerten (hierl undm) orthogonal sind, vgl. Kapitel 5.

5. Uns¨old’s Theorem:

Xl

m=−l

Y_l^m∗(θ, φ)Y_l^m(θ, φ) = 2l+ 1

4π (5.39)

6. F¨ur m= 0 gilt

Y_l⁰(θ, φ) =

r2l+ 1

4π Pl(cosθ) (5.40)

7. F¨ur m=±l folgt

Y_l^±l(θ, φ) = (±1)^l 2^ll!

r(2l+ 1)!

4π sin^lθ e^±ilφ (5.41)

Wichtige F¨alle der Kugelfl¨achenfunktionen

1. Sei zun¨achst l = 0. Aus obiger Darstellung der Legendre-Funktionen folgt dann sofort P0⁰(z) = 1. Hieraus folgt f¨ur die Kugelfl¨achenfunktion Y0⁰ = ^√1_4π. Hier ist die Kugel- fl¨achenfunktion also winkelunabh¨angig. Die Wellenfunktion ist isotrop und sph¨arisch sym- metrisch. Solche Zust¨ande nennt man s-Zust¨ande.

2. Sei nunl = 1. Es gibt nun die dreip-Zust¨andemitm=−1,m= 0 undm= 1. Betrachten wir zun¨achst den Fall mitm= 0. Die Legendre-Funktion ist nun

P1⁰(z) =z, und wir erhalten die folgende Kugelfl¨achenfunktion:

Y1⁰(θ, ϕ) =C10cosθ = r 3

4π cosθ. (5.42)

Die Normierungskonstante haben wir aus 1 =

2π

Z

0

dϕ Z1

−1

dz|C10|²z² =|C10|²· 4π 3

erhalten. Die Funktionen Y1^±1 folgen nun aus Y1⁰ z.B. durch die Anwendung der Leiter- operatoren ˆL_±. Das Resultat ist:

Y1^±1(θ, ϕ) = ∓ r 3

8πsinθ e^±iϕ, (5.43)

3. Analog folgt f¨ur die d-Zust¨ande⁵, mit l = 2 und m={0,±1,±2}: Y2⁰(θ, ϕ) =

r 5

16π(3 cos²θ−1), (5.44)

Y2^±1(θ, ϕ) = ∓ r15

8πsinθcosθ e^±iϕ, (5.45) Y2^±2(θ, ϕ) =

r 15

32πsin²θ e^±2iϕ. (5.46)

5Dieser Fall entspricht dem Beispiel des Drehimpulskegels in Abbildung 5.3.

In analoger Weise findet man die Kugelfl¨achenfunktionen h¨oherer Ordnung, die zu h¨oheren Drehimpulsquantenzahlen l = 3,4, . . . korrespondieren.

Abbildung 5.4: R¨aumliche Struktur der s-, p-, d- und f-Orbitale (Kugelfl¨achenfunktionen mit l= 0,1,2,3. In jeder Zeile istlfixiert, undmwird variiert. Die s-Orbitale sind isotrop, w¨ahrend die p-Orbitale die charakteristische “Hantel”-Form besitzen. Rote (gr¨une) Bereiche entsprechen positiven (negativen) Werten. Die φ-Abh¨angigkeit wird nicht gezeigt. Quelle: Wikipedia

5.2 Bewegung im Zentralpotential

Wir untersuchen nun das Verhalten eines Quantenteilchens im dreidimensionalen Potential V(r). Hierbei machen wir eine weitere vereinfachende Annahme: das Potential sei radialsym- metrisch (isotrop). Es gilt also, mit r=|r|:

V(r) = V(r). Prominente Beispiele hierf¨ur sind:

• Das Elektron im Coulomb-Feld des Protons (Wasserstoffatom und wasserstoff-¨ahnliche Ionen)

• andere Atome oder Molek¨ule

• Baryonen im Atomkern

• Gravitationspotential

Durch die Isotropie behandeln wir also effektiv doch wieder ein eindimensionales Problem (in radialer Richtung bez¨uglich des Kraftzentrums). Der Hamiltonoperator lautet:

Hˆ = pˆ²

2m +V(r) Die allgemeine Schr¨odinger-Gleichung lautet dann:

i~∂

∂tΨ(r, t) = ˆHΨ(r, t)

Wie bereits bekannt, k¨onnen wir die zeitabh¨angige L¨osung wie folgt schreiben:

Ψ(r, t) =e^−~iEtψ(r)

Hierbei sind die {ψ(r, E)} die L¨osungen der station¨aren Schr¨odinger-Gleichung:

Hψ(r) =ˆ Eψ(r) Diskutieren wir nun Erhaltungsgr¨oßen. Es gilt:

∂Hˆ

∂t = 0⇒ hHˆi=E . (5.47)

Die EnergieE ist dann eine Erhaltungsgr¨oße.

Wir wollen nun die vollst¨andigen Observablen f¨ur unser System finden. Also suchen wir alle Observablen mit gemeinsamen Eigenfunktionen. Dies ist gleichbedeutend damit, dass wir alle kommutierenden Operatoren finden. Wir kennen bereits:

[ˆL,H] = 0ˆ , [ˆL²,Lˆz] = 0.

Das Resultat der ersten Zeile ergibt sich aus [V(r),L] = 0 und wegen [ˆˆ p²/2m,L] = 0. Daherˆ schlussfolgern wir:

Die Operatoren ˆL², ˆLz und ˆH haben gemeinsame Eigenfunktionen.

Zu l¨osen ist also das folgende Differentialgleichungssystem:

Hψ(r) =ˆ E ψ(r), (5.48)

Lˆ²ψ(r) = ~²l(l+ 1)ψ(r), (5.49)

Lˆzψ(r) = ~m ψ(r), (5.50)

wobeiE ∈Rundl = 0,1, ...mit|m| ≤lgilt. Da wir die L¨osungen des Winkelanteils schon zuvor als die Kugelfl¨achenfunktionen Y_l^m identifiziert haben, machen wir folgenden Produktansatz:

ψ(r) = R(r)·Y_l^m(θ, ϕ). (5.51) Hierbei ist R(r) der Radialanteil der Wellenfunktion. Bevor wir die Gleichung f¨ur den Radial- anteil l¨osen, pr¨ufen wir, dass dieser Ansatz zu keinem Widerspruch f¨uhrt, wenn wir ihn in die Lˆ²-Eigenwertgleichung einsetzen, deren L¨osung wir ja bereits kennen:

Lˆ²R(r)Y_l^m(θ, ϕ) = ~²l(l+ 1)R(r)Y_l^m(θ, ϕ), R(r) ˆL²Y_l^m(θ, ϕ) = ~²l(l+ 1)R(r)Y_l^m(θ, ϕ),

Lˆ²Y_l^m(θ, ϕ) = ~²l(l+ 1)Y_l^m(θ, ϕ).

Unter der VoraussetzungR(r)6= 0 haben wir also die zuvor schon durch die Kugefl¨achenfunktionen gel¨oste Eigenwertgleichung reproduziert. Wir m¨ochten nun den obigen Produktansatz in die Schr¨odinger-Gleichung einsetzen. Aus (5.29) wissen wir bereits:

ˆ

p² = ˆp²_r+Lˆ² r²,