3. Lineare dynamische Systeme

(1)

3. Lineare dynamische Systeme

Im Kapitel 1.1 wurde bereits erwähnt, dass die Wahl der Zustandsgrößen keinesfalls ein- deutig ist (siehe auch Aufgabe 1.6). Mit Hilfe einer regulären Zustandstransformation der Form

x(t) =Vz(t) (3.1)

mit einer regul¨aren (n×n)-Matrix V l¨asst sich das lineare, zeitinvariante System (siehe auch (2.32) und (2.33))

˙

x = Ax+Bu , x(0) =x₀

y = Cx+Du (3.2)

mit dem Zustandx∈Rⁿ in die Form

˙z =V⁻¹AV

| {z }

A˜

z+V⁻¹B

| {z }

B˜

u , z(0) =z₀ =V⁻¹x₀

y = CV

|{z}

C˜

z+ D

|{z}

D˜

u (3.3)

mit dem neuen Zustand z∈Rⁿ uberf¨uhren.¨

Man sagt dann auch, die beiden mathematischen Beschreibungen (A,B,C,D) von (3.2) und

A,˜ B,˜ C,˜ D˜

von (3.3) sind ¨aquivalent.

Man könnte nun diese Transformation zu einem neuen Zustandzinsofern nutzen, als man die Lösung des Systems (3.2) gemäß Satz 2.4

x(t) = Φ(t)x₀+Rt

0 Φ(t−τ)Bu(τ) dτ

y(t) = Cx(t) +Du(t) , (3.4)

insbesondere die Berechnung der Transitionsmatrix Φ(t), unter Verwendung einer geeig- neten Transformation, auf einfache Art und Weise bestimmen kann. Dazu w¨ahlt man die Zustandstransformation (3.1) so, dass die Struktur von A˜ des transformierten Systems (3.3) eine einfache Berechnung der TransitionsmatrixΦ˜(t) von (3.3) zul¨asst. Dies ist zum Beispiel der Fall, wenn A˜ Diagonalstruktur aufweist.

Die L¨osung des transformierten Systems (3.3) lautet dann z(t) = Φ˜(t)z₀+Rt

0 Φ˜ (t−τ)Bu˜ (τ) dτ

y(t) = Cz˜ (t) +Du˜ (t) . (3.5)

Transformiert man (3.5) mit der Vorschrift (3.1) in den Zustand xunter Verwendung der Ausdrücke für B,˜ C˜ und D˜ von (3.3) zurück, erhält man

x(t) = V ˜Φ(t)V⁻¹x₀+Rt

0 V ˜Φ(t−τ)V⁻¹Bu(τ) dτ

y(t) = Cx(t) +Du(t) . (3.6)

(2)

3.1. Diagonalisierung Kapitel 3. Lineare dynamische Systeme

Durch Vergleich mit (3.4) ergibt sich der Zusammenhang zwischen Φ(t) und Φ˜(t) zu

Φ(t) =V ˜Φ(t)V⁻¹ . (3.7)

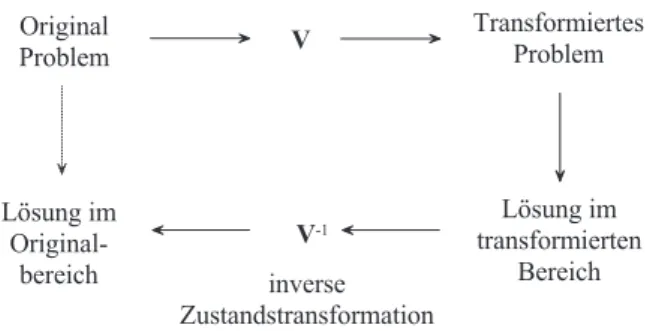
Abbildung 3.1 veranschaulicht grafisch diese Vorgangsweise.

T r a n s f o r m i e r t e s P r o b l e m

VV - 1

Z u s t a n d s t r a n s f o r m a t i o n

i n v e r s e Z u s t a n d s t r a n s f o r m a t i o n O r i g i n a l

P r o b l e m

L ö s u n g i m O r i g i n a l -

b e r e i c h

L ö s u n g i m t r a n s f o r m i e r t e n

B e r e i c h

Abbildung 3.1: Zur regul¨aren Zustandstransformation.

3.1. Diagonalisierung

Im vorigen Kapitel, Abschnitt 2.4, haben wir gesehen, dass sich die Transitionsmatrix Φ(t) des linearen, zeitinvarianten Systems (3.2) als Exponentialreihe

Φ(t) = X∞ k=0

A^kt^k

k! (3.8)

anschreiben l¨asst.

Die Anwendung der Beziehung (3.8) zur Berechnung der Transitionsmatrix ist dann be- sonders einfach, wenn die Dynamikmatrix A eine Diagonalstruktur aufweist. Setzt man n¨amlich f¨ur A eine DiagonalmatrixΛ der Form

Λ=







λ₁ 0 · · · 0 0 λ₂ · · · 0 ... ... . .. ...

0 0 · · · λ_n





 (3.9)

in (3.8) ein, erh¨alt man die Transitionsmatrix Φ(t) unmittelbar zu

Φ(t) =







exp (λ₁t) 0 · · · 0 0 exp (λ₂t) · · · 0 ... ... . .. ...

0 0 · · · exp (λ_nt)





 ^. (3.10)

Im Sinne der Vorgangsweise von Abbildung 3.1 zur Berechnung der Transitionsmatrix ist es daher naheliegend, folgende Frage zu stellen: Ist es möglich, für das lineare, zeitinvariante System (3.2) eine reguläre Zustandstransformation (3.1) so zu finden, dass

(3)

die Dynamikmatrix A˜ des Systems im neuen Zustand (3.3) Diagonalstruktur hat? D.h., gesucht ist eine regul¨are (n×n)-MatrixV so, dass gilt

V⁻¹AV=Λ . (3.11)

Schreibt man V in Form von Spaltenvektoren

V= [v₁,v₂, . . . ,v_n] (3.12)

an und setzt f¨ur Λ in (3.11) Gleichung (3.9) ein, erh¨alt man die Bedingung

[Av1,Av₂, . . . ,Av_n] = [λ1v₁, λ2v₂, . . . , λnv_n] . (3.13) Damit m¨ussen also Zahlen λi, i = 1, . . . , n und n linear unabh¨angige Vektoren v_i, i = 1, . . . , nso gefunden werden, dass die Gleichungen

(A−λiE)v_i =0 , i= 1, . . . , n (3.14) mit der (n×n)-Einheitsmatrix E erfüllt sind. Man beachte, dass das lineare Gleichungs- system (3.14) nur dann nichttriviale Lösungen v_i 6= 0 haben kann, wenn die Matrix (A−λiE) singulär bzw. det (A−λiE) = 0 ist. Damit müssen aber die Zahlen λi, i = 1, . . . , ndie Wurzeln des charakteristischen Polynoms der Matrix A

det (A−λE) =λⁿ+an−1λⁿ⁻¹+. . .+a1λ+a0 (3.15) und somit die Eigenwerte der Matrix A sein. Die nichttrivialen Vektoren v_i werden als die zu λi geh¨origen Eigenvektoren bezeichnet.

Dies erlaubt uns, die oben gestellte Frage im nachfolgenden Satz zu beantworten:

Satz 3.1. Die(n×n)-DynamikmatrixAdes linearen, zeitinvarianten Systems (3.2) kann mit einer regul¨aren (eventuell auch komplexwertigen) Zustandstransformation (3.1) genau dann auf Diagonalform transformiert werden, wenn zuA n linear unabh¨angige (eventuell auch komplexwertige) Eigenvektoren existieren.

Aufgabe 3.1. Beweisen Sie Satz 3.1.

Aus Satz 3.1 ist ersichtlich, dass die n Eigenwerte der Matrix A nicht notwendigerweise verschieden sein m¨ussen. Es gilt jedoch nachfolgender Satz:

Satz 3.2. Hat eine (n×n)-Matrix A n verschiedene Eigenwerte λ1, . . . , λn, dann sind die n zugeh¨origen Eigenvektorenv₁, . . . ,v_n linear unabh¨angig.

Beweis: (durch Widerspruch) Angenommen, es existieren zwei verschiedene Eigenwerte λj und λk, deren Eigenvektoren v_j und v_k linear abh¨angig sind. Dann existieren Zahlen cj, ck 6= 0 so, dass gilt

cjv_j +ckv_k =0 . (3.16)

Multipliziert man (3.16) von links mit A und benutzt die Definitionsgleichung f¨ur die Eigenwerte und Eigenvektoren (3.14), dann erh¨alt man

cjλjv_j+ckλkv_k=0 . (3.17)

(4)

Bezeichnet man den von Null verschiedenen Eigenwert mit λj, multipliziert damit (3.16) und subtrahiert diese Gleichung von (3.17), so folgt die Beziehung

(λj−λk)ckv_k=0 . (3.18)

Da aber ck 6= 0 und v_k 6= 0 ist, muss λj = λk sein, was ein Widerspruch zur Annahme ist.

Aufgabe 3.2. Zeigen Sie, dass die Matrizen A und A˜ =V⁻¹AV mit der regul¨aren (n×n)-Matrix V die gleichen Eigenwerte besitzen.

Hinweis: Es gelten die Beziehungen

det (AV) = det (A) det (V) und V⁻¹V=E .

Zeigen Sie weiters, dassV⁻¹v_k ein Eigenvektor vonA˜ =V⁻¹AV ist, wenn v_k ein Eigen- vektor von A ist.

Tafelbeispiel: Man transformiere das System

˙ x =

1 2 1 0

x+

1 0

u y =

0 1

x+ 2u

(3.19) auf Diagonalform.

Ergebnis: Diagonalisiertes System:

˙z = 2 0

0 −1

z+ 1/3

−1/3

u y =

1 1

z+ 2u

(3.20) Aufgabe 3.3. Berechnen Sie f¨ur die Dynamikmatrix

A=





1 0 0 3 −1 0 5 4 3



 die Transformationsmatrix V auf Diagonalform.

L¨osung: Abgesehen von Normierungsfaktoren erh¨alt man

V =





0 1 0

−3/2 3/2 0 3/2 −11/2 4





Man überzeugt sich leicht, dass eine (n×n)-Matrix A mit reellen Koeffizienten nur Ei- genwerte besitzen kann, die entweder reell oder konjugiert komplex auftreten. Man kann natürlich die besprochene Diagonalisierungsmethode auch für Systeme mit konjugiert komplexen Eigenwerten anwenden. Es sei aber an dieser Stelle angemerkt, dass in diesem Fall sowohl die Transformationsmatrix V als auch die Diagonalmatrix Λ von (3.9) komplexwertige Matrizen sind. Dies stört zwar nicht weiters, doch besteht oft der Wunsch, dass die Matrizen des transformierten Systems

A,˜ B,˜ C,˜ D˜

von (3.3) ebenfalls reellwer- tig sind. Wie diese Transformation dann im Detail aussieht, wird im n¨achsten Abschnitt besprochen.

(5)

3.2. Komplexe Eigenwerte Kapitel 3. Lineare dynamische Systeme

3.2. Komplexe Eigenwerte

F¨ur die nachfolgenden Betrachtungen setze man voraus, dass die Dynamikmatrix A des Systems (3.2) r = n/2 verschiedene konjugiert komplexe Eigenwerte der Form λj = αj +Iβj mit dem konjugiert Komplexen λ^∗_j = αj −Iβj, j = 1, . . . , r besitzt. Es gilt nun folgender Satz:

Satz 3.3. Hat eine MatrixA einen konjugiert komplexen Eigenwert, dann sind auch die zugeh¨origen Eigenvektoren konjugiert komplex.

Aufgabe 3.4. Beweisen Sie Satz 3.3.

W¨ahlt man nun als TransformationsmatrixV¯ die mit der regul¨aren MatrixT von rechts multiplizierte Matrix V der konjugiert komplexen Eigenvektoren

V¯ = [v₁,v^∗₁, . . . ,v_r,v^∗_r]

| {z }

V

T (3.21)

mit

T= 1 2







1 −I · · · 0 0 1 I · · · 0 0 ... ... . .. ... ...

0 0 · · · 1 −I 0 0 · · · 1 I







, T⁻¹ =







1 1 · · · 0 0

I −I · · · 0 0 ... ... . .. ... ...

0 0 · · · 1 1

0 0 · · · I −I







, (3.22)

dann errechnet sich die Dynamikmatrix A˜ des transformierten Systems zu A˜ =V¯⁻¹A ¯V =T⁻¹V⁻¹AV

| {z }

=Λ

T=Ω (3.23)

bzw.

Ω=T⁻¹







α₁+Iβ₁ 0 · · · 0 0

0 α₁−Iβ₁ · · · 0 0

... ... . .. ... ...

0 0 · · · αr+Iβr 0

0 0 · · · 0 α_r−Iβ_r







| {z }

Λ

T

=







α₁ β₁ · · · 0 0

−β₁ α₁ · · · 0 0

... ... . .. ... ...

0 0 · · · α_r β_r 0 0 · · · −βr α_r





 .

(3.24)

Eine genauere Berechnung der Transformationsmatrix V¯ von (3.21) zeigt, dass sich diese aus den Real- und Imagin¨arteilen der konjugiert komplexen Eigenvektoren zusammen- setzt, es gilt n¨amlich

V¯ = [v₁,v₁^∗, . . . ,v_r,v^∗_r]T= [v_1,Re,v_1,Im, . . . ,v_r,Re,v_r,Im] . (3.25)

(6)

3.3. Mehrfache Eigenwerte Kapitel 3. Lineare dynamische Systeme

Die Transitionsmatrix Φ˜(t) des transformierten Systems mit der Dynamikmatrix A˜ =Ω von (3.24) l¨asst sich sehr einfach in geschlossener Form

Φ˜(t) = exp (Ωt) =







e^α¹^tcos (β1t) e^α¹^tsin (β1t) · · · 0 0

−e^α¹^tsin (β₁t) e^α¹^tcos (β₁t) · · · 0 0

... ... . .. ... ...

0 0 · · · e^α^r^tcos (βrt) e^α^r^tsin (βrt)

0 0 · · · −e^α^r^tsin (β_rt) e^α^r^tcos (β_rt)







(3.26)

angeben.

Aufgabe 3.5. Berechnen Sie die Transitionsmatrix Φ(t) des Systems

˙ x=

1 1

−4 1

x

einmal ¨uber die Methode der Diagonalisierung nach Abschnitt 3.1 und einmal ¨uber die Methode mit reellen Transformationsmatrizen von Abschnitt 3.2.

L¨osung: Transitionsmatrix

Φ(t) =

exp (t) cos (2t) ¹₂exp(t) sin(2t)

−2 exp(t) sin(2t) exp (t) cos (2t)

3.3. Mehrfache Eigenwerte

Satz 3.2 besagt, dass die Eigenvektoren zu verschiedenen Eigenwerten linear unabh¨angig sind, was bei Mehrfacheigenwerten im Allgemeinen nicht mehr der Fall ist. Aus diesem Grund wird in diesem Abschnitt das Konzept des Eigenvektors verallgemeinert. Dazu wird im ersten Schritt der Begriff eines invarianten Unterraums definiert.

Definition 3.1. Es sei V ein linearer Unterraum des Rⁿ mit der Basis {r₁, . . . ,r_k}. Man nennt V invariant gegen¨uber einer (n×n)-Matrix A, wenn f¨ur alle x∈ V auchAx ∈ V gilt.

Aus der Definitionsgleichung f¨ur die Eigenwerte und Eigenvektoren (3.14) sieht man unmittelbar, dass ein Eigenvektor v_j von A einen Unterraum aufspannt, der invariant gegen¨uber A ist.

Nun ¨uberzeugt man sich leicht, dass f¨ur einenA-invarianten UnterraumV mit der Basis {r₁, . . . ,r_k} eine (k×k)-Matrix S^T = [s₁,s₂, . . . ,s_k] immer so existiert, dass gilt

A[r1, . . . ,r_k] = [r1, . . . ,r_k]S= Xk j=1

r_js^T_j . (3.27)

F¨ur das Weitere sei angenommen, dass die (n×n)-Dynamikmatrix A des Systems (3.2) einen n-fachen Eigenwert λ besitze.

(7)

3.3. Mehrfache Eigenwerte Kapitel 3. Lineare dynamische Systeme

Satz 3.4. Es sei λ ein n-facher Eigenwert der Matrix A, zu dem nur ein Eigenvektor v₁

(A−λE)v₁ =0 (3.28)

geh¨ore. Dann existieren zu v₁ weitere (n−1) Vektoren der Form

(A−λE)v_i+1 =v_i i= 1,2, . . . , n−1. (3.29) Man nennt v₁ auch den Haupteigenvektor und die Vektoren v₂,v₃, . . . ,v_n die Nebenei- genvektoren von A.

Nach Definition 3.1 ist der durch die Vektoren {v1,v₂, . . . ,v_n} aufgespannte Unterraum invariant gegen¨uber A, da nach (3.29) gilt

A[v1,v₂, . . . ,v_n] =λ[v1,v₂, . . . ,v_n] + [0,v₁,v₂, . . . ,v_n−1] (3.30) bzw.

AV = V(λE+N)

| {z }

=S

(3.31) mit der (n×n)-Matrix

N=







0 1 · · · 0 0 0 0 · · · 0 0 ... ... . .. ... ...

0 0 · · · 0 1 0 0 · · · 0 0







. (3.32)

Die Matrix Nhat nun eine ganz spezielle Struktur, sie ist n¨amlichnilpotent der Ordnung n. Dazu folgende Definition:

Definition 3.2. (Nilpotente Matrix) Man nennt eine(n×n)-MatrixNnilpotent der Ordnung k, wenn gilt N^k⁻¹ 6=0 und N^k=0.

W¨ahlt man nun als Spalten der Transformationsmatrix den Haupt- und die Nebeneigen- vektoren

V = [v1,v₂, . . . ,v_n], (3.33)

dann errechnet sich die Dynamikmatrix A˜ des transformierten Systems mit (3.31) zu

A˜ =V⁻¹AV=S=







λ 1 · · · 0 0 0 λ · · · 0 0 ... ... . .. ... ...

0 0 · · · λ 1 0 0 · · · 0 λ







. (3.34)

Die TransitionsmatrixΦ˜(t) des transformierten Systems mit der Dynamikmatrix A˜ =S von (3.34) l¨asst sich sehr einfach in geschlossener Form

Φ˜(t) =exp ((λE+N)t) = exp (λEt) exp (Nt)

| {z }

(∗)

= exp (λEt)

E+Nt+. . .+ Nⁿ⁻¹tⁿ⁻¹ (n−1)!

(3.35)

(8)

3.4. Jordan-Form Kapitel 3. Lineare dynamische Systeme

bzw.

Φ˜(t) = exp (λt)





 1 t t²

2! · · · tⁿ⁻¹ (n−1)!

0 1 t · · · tⁿ⁻² (n−2)!

... ... ... . .. ... 0 0 · · · t 0 0 · · · 1







(3.36)

anschreiben.Man beachte, dass die Gleichung (*) in (3.35) nur deshalb gilt, da die Matrizen E und N kommutieren, d.h., die BeziehungEN =NE erf¨ullen.

L¨osen Sie dazu folgende Aufgabe.

Aufgabe 3.6. Zeigen Sie, dass

exp ((A1+A₂)t) = exp (A1t) exp (A2t)

gilt, wenn die beiden Matrizen A₁ und A₂ die Bedingung A₁A₂ =A₂A₁ erf¨ullen.

L¨osung: Ausmultiplizieren und Koeffizientenvergleich Aufgabe 3.7. Transformieren Sie das System

˙ x=





0 −2 −1 1 2 1 0 1 1



x

auf die Form von (3.34).

L¨osung: Die Transformationsmatrix V und die Dynamikmatrix A˜ des transformierten Systems lauten

V=





−1 −2 −1

0 1 1

1 1 1



 und A˜ =



 1 1 0 0 1 1 0 0 1



 .

3.4. Jordan-Form

Die Ergebnisse der Abschnitte 3.1, 3.2 und 3.3 lassen sich nun wie folgt f¨ur ein allgemeines lineares, zeitinvariantes System (3.2) kombinieren.

Satz 3.5. (Kanonische Jordan-Form) Es sei die reellwertige (n×n)-Matrix A die Dynamikmatrix des linearen, zeitinvarianten Systems (3.2). Angenommen,Ahabekreelle Eigenwerte λj, j = 1, . . . , k und (n−k)/2 konjugiert komplexe Eigenwerte λj = αj + Iβj (λ^∗_j = αj −Iβj), j = k + 1, . . . , r mit r = (n+k)/2. Dann existiert eine regul¨are Zustandstransformation der Form (3.1) mit

V= [v1, . . . ,v_k,v_k+1,Re,v_k+1,Im, . . . ,v_r,Re,v_r,Im] (3.37) bestehend aus den Haupt- und Nebeneigenvektoren v_j, j = 1, . . . , r, v_i,Re =Re(vi) und v_i,Im=Im(vi),i=k+ 1, . . . , r so, dass die Dynamikmatrix des transformierten Systems folgende Form

(9)

A˜ =V⁻¹AV =







U₁ 0 · · · 0 0 U₂ · · · 0 ... ... . .. ...

0 0 · · · U_l







(3.38)

mit den so genannten Jordanbl¨ocken

U=







λ 1 · · · 0 0 0 λ · · · 0 0 ... ... . .. ... ...

0 0 · · · λ 1 0 0 · · · 0 λ







(3.39)

f¨ur die reellen Eigenwerte λ bzw.

U=







W E₂ · · · 0 0 0 W · · · 0 0 ... ... . .. ... ...

0 0 · · · W E₂ 0 0 · · · 0 W







(3.40)

mit

W=

α β

−β α

und E₂ = 1 0

0 1

(3.41) f¨ur konjugiert komplexe Eigenwerte α±Iβ besitzt.

Als Beispiel betrachte man das System

˙ x=







2 −2 −6 −8 −10

−3/2 4 8 12 15

6 4 1 0 0

−7/2 −4 −9/4 −3 0

0 0 0 0 −3







x (3.42)

mit dem einfachen reellen Eigenwert λ1 =−3 und dem zweifachen konjugiert komplexen Eigenwert λ2 = 1±I2. Der Eigenvektor zuλ1 =−3 lautet

v^T₁ =

0,0,0,−5 4,1

, (3.43)

und der einzige Haupteigenvektor zu λ2 = 1 +I2 ergibt sich zu v₂^T =

−2

3 ,1,0,−1 3 +I1

6,0

. (3.44)

Den Nebeneigenvektor erh¨alt man aus der Beziehung (3.29) mit

(A−λ2E)v₃ =v₂ (3.45)

(10)

zu

v^T₃ = −8

9 ,1, I2 3,−5

18 −I 5 18,0

. (3.46)

Damit lautet die Transformationsmatrix V

V= [v₁, Re(v₂), Im(v₂), Re(v₃), Im(v₃)] =







0 ⁻₃² 0 ⁻₉⁸ 0 0 1 0 1 0 0 0 0 0 ²₃

−5 4

−1 3

1 6

−5 18

−5

1 0 0 0 018







(3.47)

und die transformierte Dynamikmatrix in der Jordan-Form errechnet sich zu

A˜ =V⁻¹AV =





λ1 0 0 0 W E₂ 0 0 W





| {z } W =



 Re(λ2) Im(λ2)

−Im(λ₂) Re(λ₂)





=







−3 0 0 0 0 0 1 2 1 0 0 −2 1 0 1 0 0 0 1 2 0 0 0 −2 1







. (3.48)

Aus den ¨Uberlegungen der Abschnitte 3.1, 3.2 und 3.3 folgt die Transitionsmatrix des transformierten Systems zu

Φ˜ (t) =







e⁻^3t 0 0 0 0

0 e^tcos (2t) e^tsin (2t) te^tcos (2t) te^tsin (2t) 0 −e^tsin (2t) e^tcos (2t) −te^tsin (2t) te^tcos (2t) 0 0 0 e^tcos (2t) e^tsin (2t) 0 0 0 −e^tsin (2t) e^tcos (2t)







(3.49)

bzw. f¨ur das Originalsystem (3.42) nach (3.7)

Φ(t) =V ˜Φ(t)V⁻¹ (3.50)

mit V von (3.47).

Aufgabe 3.8. Berechnen Sie die Jordan-Form des Systems

˙ x=







2 1 4 0 0 2 1 −1 0 0 2 1 0 0 0 2





x .

L¨osung: Jordan-Form

A˜ =V⁻¹AV =







2 1 0 0 0 2 1 0 0 0 2 1 0 0 0 2







(11)

3.5. Allgemeines L¨osungsverhalten Kapitel 3. Lineare dynamische Systeme

Aufgabe 3.9. Berechnen Sie die Jordan-Form des Systems

˙ x=







2 1 4 0 0 2 1 0 0 0 2 0 0 0 0 2





x .

L¨osung: Jordan-Form

A˜ =V⁻¹AV =







2 1 0 0 0 2 1 0 0 0 2 0 0 0 0 2







3.5. Allgemeines L¨ osungsverhalten

Aus dem bisher Gesagten l¨asst sich auf einfache Art und Weise das L¨osungsverhalten eines linearen, zeitinvarianten autonomen Systems der Form

˙

x=Ax mit x(0) =x₀ (3.51)

angeben.

Satz 3.6. Jede L¨osungxj(t),j = 1, . . . , ndes Systems (3.51) ist eine Linearkombination der Funktionen

t^k¹e^λt, t^k²e^αtcos (βt) und t^k³e^αtsin (βt) (3.52) f¨ur die reellen Eigenwerte λ, die konjugiert komplexen Eigenwerte α ±Iβ und k1, k2, k3 = 0, . . . ,(r−1) mit r als der jeweiligen Dimension der Jordanbl¨ocke (entspricht der Vielfachheit des jeweiligen Eigenwertes mit nur einem Haupteigenvektor).

Aus Satz 3.6 kann man schließen, dass die Trajektorien eines linearen Systems der Form (3.51) weder in endlicher Zeit nach Null noch nach Unendlich streben können. Dies gilt natürlich nicht für nichtlineare Systeme.

Als direkte Konsequenz von Satz 3.6 l¨asst sich noch folgender Satz angeben:

Satz 3.7. (Globale asymptotische Stabilit¨at) F¨ur alle Anfangswerte x₀ ∈ Rⁿ gilt genau dann

tlim→∞

x(t) = lim

t→∞

Φ(t)x₀ =0, (3.53)

wenn alle Eigenwerte der MatrixA negativen Realteil besitzen. Man sagt dann auch, die Ruhelage x_R=0 ist global asymptotisch stabil.

Beweis:”⇒” F¨ur alle Anfangswertex₀ ∈Rⁿ gilt limt→∞x(t) =0⇒ alle Eigenwerte von A haben negativen Realteil. Angenommen, es existiert ein Eigenwert λ mit Re(λ) > 0, dann folgt nach Satz 3.6, im Speziellen (3.52), dass zumindest eine Komponente von limt→∞x(t) gegen Unendlich strebt.

”⇐” Alle Eigenwerte von A haben negativen Realteil ⇒ limt→∞x(t) = 0. Dies folgt unmittelbar aus Satz 3.6, im Speziellen (3.52), da gilt

|cos (βt)| ≤1, |sin (βt)| ≤1, lim

t→∞

t^k^2,3e^αt = 0 und lim

t→∞

t^k¹e^λt = 0 . (3.54)

(12)

Aufgabe 3.10. Ist die Ruhelage x_R =0 des Systems

˙ x=



 1 2 0 0 5 6 1 0 −1



x

global asymptotisch stabil?

L¨osung: Nein

Aufgabe 3.11. Ist die Ruhelage x_R =0 des Systems

˙ x=

1 −2

−2 4

x

global asymptotisch stabil?

L¨osung: Nein

Systeme 1-ter und 2-ter Ordnung

Tafelbeispiel: Es soll die L¨osung des Systems

˙

x=ax (3.55)

f¨ur verschiedene Parameter a diskutiert werden.

Ergebnis: Die allgemeine L¨osung lautet

x(t) =x0e^at . (3.56)

Man betrachte das System zweiter Ordnung

˙

x=Ax=

1.4 −1.2

−1.2 −0.4

x. (3.57)

Die Eigenwerte der Dynamikmatrix A errechnen sich zu λ1 =−1 undλ2 = 2, die Eigen- vektoren lauten

v₁ =

−0.447

−0.894

und v₂ =

−0.894 0.447

(3.58) und die zugeh¨orige Jordan-Form ergibt sich in der Form

A˜ =V⁻¹AV=

−1 0 0 2

. (3.59)

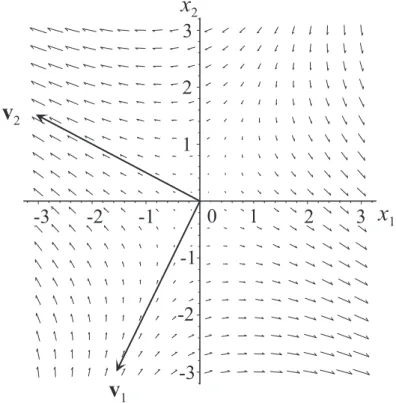
Abbildung 3.2 zeigt den Verlauf der Trajektorien zu diesem Beispiel. Wie bereits im Abschnitt 3.3 besprochen, sind die Eigenvektorenv₁ undv₂ invariant gegen¨uberAgem¨aß Definition 3.1. Mit anderen Worten heißt dies, dass wenn man mit einem Anfangswertx₀ auf einem Eigenvektor startet, also z.B.

x₀ =γ0v₁, γ0∈R (3.60)

(13)

321

- 1 - 2

- 3

0 1 2 3

- 1 - 2

- 3

v

1

v

2

x

2

x

1

Abbildung 3.2: Verlauf der Trajektorien f¨ur λ1 =−1 und λ2 = 2.

dann verbleibt die Trajektorie f¨ur alle Zeiten in dieser Richtung des Eigenvektors, d.h. die L¨osung hat die Form

x(t) =γ(t)v₁ . (3.61)

Um dies zu zeigen, setzt man (3.61) in das System (3.57) ein, und man erh¨alt

˙

γ(t)v₁ =γ(t)Av₁ =γ(t)λ1v₁ (3.62) bzw.

( ˙γ(t)−γ(t)λ1)v₁ =0 . (3.63) Da der Eigenvektor v₁ 6=0 ist, muss demnach gelten

˙

γ(t) = γ(t)λ1 (3.64)

bzw.

γ(t) =γ0exp (λ1t) . (3.65)

Dies bedeutet, dass sich das System entlang eines Eigenvektors durch eine gewöhnliche Differentialgleichung erster Ordnung beschreiben lässt. Die spezielle Lösung (3.61), (3.65)

x(t) =γ0exp (λ1t)v₁ (3.66)

wird auch als Eigenschwingung des Systems (3.57) bezeichnet. Wegen des charakteristischen Verlaufs der Trajektorien wird die Ruhelage x_R = 0 in diesem Fall auch als Sattelpunkt bezeichnet. Dies tritt f¨ur Systeme zweiter Ordnung immer dann auf, wenn

(14)

3.6. Literatur Kapitel 3. Lineare dynamische Systeme

zwei reelle Eigenwerte λ₁, λ₂ mit der Eigenschaft λ₁ < 0 < λ₂ existieren. Offensichtlich ist die Ruhelage nicht global asymptotisch stabil im Sinne des Satzes 3.7.

F¨ur Systeme zweiter Ordnung gibt es noch eine Reihe weiterer Klassifikationen der Ru- helage x_R=0 in Abh¨angigkeit der Lage der Eigenwerte. Dazu folgende Aufgabe:

Aufgabe 3.12. Zeichnen Sie die Trajektorien folgender Systeme:

• Eigenwerte reell λ₁, λ₂ <0: Ruhelage x_R =0 ist ein stabiler Knoten:

˙ x=

−1.4 0.4

0.4 −1.2

x

• Eigenwerte reell λ₁, λ₂ >0: Ruhelage x_R =0 ist ein instabiler Knoten:

˙ x=

1.8 −0.4

−0.4 1.2

x

• Eigenwerte konjugiert komplex λ1,2 = α±Iβ mit α < 0: Ruhelage x_R = 0 ist ein stabiler Strudelpunkt:

˙ x=

−5 10

−2 3

x

• Eigenwerte konjugiert komplex λ1,2 = α±Iβ mit α > 0: Ruhelage x_R = 0 ist ein instabiler Strudelpunkt:

˙ x=

−3 10

−2 5

x

• Eigenwerte konjugiert komplex λ1,2 = α±Iβ mit α = 0: Ruhelage x_R = 0 ist ein Wirbelpunkt:

˙ x=

−4 10

−2 4

x

• Wenn ein Eigenwert λ= 0 ist, liegt ein degenerierter Fallvor:

˙ x=

−0.4 0.2 0.8 −0.4

x

Hinweis: Verwenden Sie dazu in MAPLE den Befehl fieldplot.

3.6. Literatur

1. Director S.W., Rohrer R.A., Introduction to System Theory, McGraw-Hill, New York, (1972).

2. Hirsch M.W., Smale S., Differential Equations, Dynamical Systems and Linear Al- gebra, Academic Press, (1974).

3. Khalil H.K., Nonlinear Systems, Macmillan Pub. Company, New York, (1992).

(15)

3.6. Literatur Kapitel 3. Lineare dynamische Systeme

4. Ludyk G., Theoretische Regelungstechnik 1, Springer, Berlin Heidelberg, (1995).

5. Merz L., Jaschek H.,Grundkurs der Regelungstechnik, 13.Auflage, Oldenbourg, M¨un- chen, (1996).

6. Padulo L., Arbib M.A., System Theory, W.B. Saunders Company, Philadelphia, (1974).

7. Perko L.,Differential Equations and Dynamical Systems, Springer, New York, (1991).

8. Rugh W.J., Linear System Theory, Prentice Hall, New Jersey, (1993).