2. Elementare Gaskinetik

Zur Einf¨ uhrung in die kinetische Theorie von Gasen wird zun¨achst ein sehr simples, mikroskopisches Modell der Molek¨ ulbewegungen eingef¨ uhrt, das so- genannte ,,1/6” Modell. Hierbei bewegen sich alle Molek¨ ule mit einer mitt- leren Einheitsgeschwindigkeit jeweils in den sechs kartesischen Richtungen.

T rotz der Vereinfachungen erlaubt dieses Modell, alle wichtigen makroskopi- schen Eigenschaften eines Gases aus einer elementaren Betrachtung der mo- lekularen Bewegung abzusch¨atzen. Viele Begriffe und Definitionen aus der Thermodynamik und Gasdynamik, wie z.B. der Druck, die innere Energie, aber auch Transportgr¨ oßen, wie z.B. die Viskosit¨at, lassen sich sofort mittels bekannter Gesetze der Mechanik, auf die elementaren T eilchen angewendet, erkl¨aren und einsichtig interpretieren. Diese elementare Gaskinetik tr¨agt so- mit zum tieferen Verst¨andnis der Gesetze der klassischen Thermodynamik und Gasdynamik bei und ist gleichzeitig eine Einf¨ uhrung in die nachfolgen- den, detaillierten Betrachtungen der Gaskinetik.

2.1 Makroskopische Eigenschaften eines Gases in Ruhe

2.1.1

erteilung

Betrachtet wird ein abgeschlossenes Volumen V , indem sich eine große Zahl N Molek¨ ule (N

1) befinden. Makroskopisch sei das Gas in Ruhe, d.h. die Str¨ omungsgeschwindigkeit ist Null und die Temperatur und Dichte des Gases sind konstant. Die Molek¨ ule werden als kleine, starre Kugeln der Masse m und mit einem Durchmesser

betrachtet.

Ausgehend von einem beliebigen Anfangszustand w¨ urde sich in einem rea-

len Gas auf Grund von Kollisionen zwischen den Molek¨ ulen nach ausreichend

langer Zeit ein Gleichgewichtszustand mit irregul¨arer, chaotischer Bewegung

der Molek¨ ule einstellen. Statistisch gesehen ist dies ein ,,geordnetes Chaos”,

bei dem die Molek¨ ule im Mittel gleichm¨aßig im Raum verteilt sind und sich

ohne Vorzugsrichtung in alle Richtungen mit unterschiedlicher Geschwindig-

keit bewegen (Brownsche Bewegung). Dieser Zustand wird durch die Max-

wellsche Geschwindigkeitsverteilung beschrieben, die in Kapitel 4 behandelt

wird.

Anstelle der chaotischen Brownschen Bewegung wird jetzt vereinfachend angenommen, dass die Molek¨ ule sich lediglich auf sechs, kartesischen Vor- zugsrichtungen mit konstanter, mittlerer Geschwindigkeit c

bewegen. Der Ortsraum (x,

Geschwindigkeitsraum (c

, c

, c

) die- ses vereinfachten Modelles sind in Abb. 2.1 skizziert.

x

z y

c =c x 0

−c0

c =c c =c

0 0

−c 0 −c0 z

y

Abb. 2.1.Orts- und Geschwindigkeitsraumder molekularen,,1/6”-Verteilung

Die N Molek¨ ule im Volumen V werden dabei gleichm¨aßig auf jede Richtung aufgeteilt, so dass l¨angs jeder Richtung sich N/6 Molek¨ ule mit c

bewegen (,,1/6”-Verteilung). F¨ ur das elementare Molekularmodell gelten die in Tabel- le 2.1 zusammengefassten Definitionen und Beziehungen:

Tabelle 2.1.Grundgr¨oßendes elementarenModelles m Masse einesMolek¨ules

σ Durchmesser einesMolek¨ules c0 mittlere,thermischeGeschwindigkeit N GesamtzahlderMolek¨ule imVolumenV n=N/V Teilchendichte

#=n m Massendichte

N/6 AnzahlderMolek¨ule proRichtung, z.B.: N/6 mitcx=c0, cy= 0, cz= 0

N/6 mitcx=−c0, cy= 0, cz= 0 usw.

Anmerkung 2.1.1.

Das ,,1/6”-Modell ist im Prinzip unphysikalisch und in-

stabil. Selbst wenn man es schaffen k¨ onnte, eine solche ,,1/6”-Verteilung

anf¨anglich einzustellen, w¨ urden sich durch Molek¨ ulst¨ oße nach kurzer Zeit alle m¨ oglichen Richtungen und Betr¨age der Molek¨ ulgeschwindigkeiten einstellen.

Daneben verletzt dieses Modell auch die Isotropiebedingung des Druckes, der unabh¨angig von der Richtung einer Kontrollfl¨ache sein muss. Das Modell kann dennoch zur vereinfachten Darstellung der prinzipiellen Abh¨angigkei- ten der Zustands- und Stoffgr¨ oßen genutzt werden, da dieses vereinfachte, mikroskopische Modell wesentliche makroskopische Eigenschaften repr¨asen- tiert. In etwas erweiterter Form, jedoch immer noch stark vereinfachend, werden ¨ahnliche Modelle des Phasenraumes zur numerischen L¨ osung gaski- netischer Probleme formuliert. Beispiele hierzu sind die Lattice-Gas-Methode in Abschn. 8.2 und Lattice-Boltzmann-Methoden in Kap. 9.

2.1.2

kalorische

oßen

T

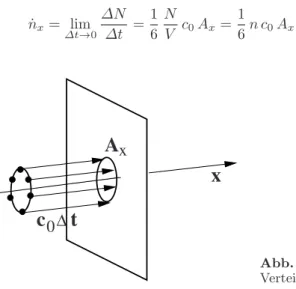
eilchenstrom ˙

Der Teilchenstrom ˙ n =

ist gleich der Anzahl von T eilchen, die pro Zeiteinheit ∆t durch eine Kontrollfl¨ache A treten. Zur Be- stimmung wird beispielhaft der Strom von T eilchen ˙ n

mit der Geschwindig- keit c

= c

durch eine Fl¨ache A

normal zur x-Richtung betrachtet. Alle T eilchen, die sich in einem Zylinder befinden mit dem Volumen

∆V = c

∆t A

,

gebildet mit der Grundfl¨ache A

und der Flugstrecke c

∆t, fliegen in positiver x-Richtung durch diese Fl¨ache. Die Anzahl dieser T eilchen ist ∆N = N/6

∆V

. Mit der Dichte n = N/V ergibt sich somit der Teilchenstrom in x-Richtung zu:

˙

n

= lim

∆t→0

∆N

∆t = 1 6 N

V c

A

= 1

6 n c

A

. (2.1)

A t

x c ₀

x

∆

Abb. 2.2. Teilchenstrom der ,,1/6”- VerteilungdurchFl¨acheAx

Der Massenstrom durch die entsprechende Fl¨ache ist

˙

m

= m

n ˙

.

Diese Beziehungen f¨ ur den T eilchenstrom bzw. den Massenstrom stellt ein vereinfachtes Ergebnis zur Absch¨atzung des Effusionsstromes durch eine klei- ne Lochblende ins Vakuum dar. Das Problem wird sp¨ater im Abschn. 4.2.1 genauer mittels Maxwell-Verteilung untersucht, wobei die Molek¨ ule aus al- len Richtungen des Halbraumes durch die Lochfl¨ache A

fliegen k¨ onnen. Das genauere Ergebnis ergibt ˙ n

=

n c

A

anstelle (2.1).

Druck p.

Der Druck p, bzw. die Druckkraft F

= p

A, die das Gas auf eine Wand der Fl¨ache A aus¨ ubt, kann als Reaktion auf die Impuls¨anderung bei elastischer Reflexion der Molek¨ ule an der Wand interpretiert werden. Die Reflexion eines elastischen Teilchens an einer Wand ist in Abb. 2.3 skizziert.

00 00 00 00 00 00

11 11 11 11 11 11

c

−c

x Fx =p A m

0

x

Abb. 2.3. ElastischeReflexion derMolek¨ule an einerWand

Die resultierende Druckkraft F

infolge Reflexion elastischer Teilchen der Masse m an einer Wand l¨asst sich mittels Impulssatz bestimmen. F¨ ur eine Kontrollfl¨ache unmittelbar an der Wand gilt:

I ˙

I ˙

= F

.

Die Impulsstr¨ ome der auftreffenden, bzw. reflektierten Molek¨ ule sind I ˙

= ˙ n

(m c

) und I ˙

= ˙ n

(−m c

). Die resultierende Kraft F

=

−p Ax

auf das Fluid ist gleich der Druckkraft. Damit folgt aus dem Impulssatz

˙

n

(−m c

)

n ˙

(m c

) =

(2.2) und somit mit (2.1) der Druck p zu:

p = 1

3

c

= 2 3 n

m

2 c

. (2.3)

Der Druck p steht somit in direkter Beziehung mit der Dichte und der kineti- schen Energie

c

der Molek¨ ule. Die Gleichung (2.3) kann als gaskinetische F ormulierung einer thermischen Zustandsgleichung interpretiert werden.

Gasgleichung.

Die Gasgleichung eines thermisch idealen Gases wird hier eingef¨ uhrt, um den Begriff der T emperatur T festzulegen. Die T emperatur ist eine in der Thermodynamik definierte Gr¨ oße, die aber in der kinetischen Theorie nicht als physikalische Gr¨ oße auftritt. Die Gasgleichung lautet:

p = n k T =

R T (2.4)

mit der Boltzmannkonstante k, bzw. der spezifischen Gaskonstante R = k/m.

Die Gasgleichung verkn¨ upft somit die Temperatur mit den kinetisch definier- baren Gr¨ oßen von Dichte und Druck.

Innere oder thermische Energie.

In der gaskinetischen Herleitung (2.3) des Druckes tritt als einzige Energieform translatorisch bewegter Molek¨ ule nur die kinetische Energie E

=

c

eines Molek¨ ules auf. Thermodyna- misch ist zum anderen die thermische oder innere Energie E

des Gases die einzige Energieform eines ruhenden Gases. Beide Energiebegriffe m¨ ussen somit ¨aquivalent sein.

Gleichsetzen der Beziehungen f¨ ur den Druck (2.3) aus der gaskinetischen Betrachtung und aus der Gasgleichung (2.4), liefert einen Zusammenhang zwischen der gaskinetischen und der thermodynamischen Deutung der ther- mischen Energie. Hieraus folgt f¨ ur die kinetische bzw. thermische Energie:

E

= m c

2 = 3

2 k T = E

. (2.5)

Diese Beziehung kann gleichzeitig auch als gaskinetische Definition der Tem- peratur betrachtet werden, da diese bis auf eine Konstante proportional der kinetischen Energie eines Molek¨ ules ist. F¨ ur ein Gas aus einatomigen Mo- lek¨ ulen gilt somit:

Die mittlere,

kinetische

ule entspricht

tur.

In der Thermodynamik wird die thermische Energie E

eines Gases im Allgemeinen auf die Masse bezogen, und ist f¨ ur kalorisch ideale Gase eine lineare F unktion der T emperatur:

e = E

m = ∂e

∂T

T = c

T.

Hierbei ist c

die spezifische W¨arme bei konstantem Volumen. F¨ ur die ther- mische Energie e pro Masse eines Gases folgt daraus mit (2.5):

e = 1 2 c

= 3

2 k

m

T = 3

2 R

T = c

T. (2.6)

Die spezifische W¨arme bei konstantem Volumen c

ergibt sich damit zu:

c

= 3 2

k m = 3

2 R.

Gleichverteilungssatz der Energien.

Ein beliebiger Geschwindigkeits- vektor

wird im Allgemeinen durch drei Komponenten

= (c

, c

, c

)

beschrieben. Jede Komponente tr¨agt einen Anteil zur kinetischen Energie bei, n¨amlich

E

= m

2 (c

+ c

+ c

).

Die kinetische Energie eines Teilchens in translatorischer Bewegung setzt sich somit aus den drei Anteilen der Komponenten in den einzelnen Richtungen (F reiheitsgraden) zusammen. Das Molek¨ ul besitzt somit drei

Die mittlere, thermische Energie eines Molek¨ ules in translatorischer Bewe- gung ist wiederum entsprechend der Beziehung (2.6) gleich 3/2 R T . Hieraus kann man schließen, dass jedem Freiheitsgrad eine Energie von 1/2 R T zu- geordnet werden kann. Dieses Ergebnis ist ein spezieller Fall des Gleichver- teilungssatzes der Energien in der gaskinetischen Theorie. Dieser besagt in etwas vereinfachter Form:

Jeder Anteil einer molekularen Energieform, der sich in einer Summe qua- dratischer T

erme

ucken l¨asst, tr¨agt zu

mit einen

R T

Als Energieformen in diesem Sinne kommen in Betracht:

•

die kinetische Energie translatorischer Bewegung,

•

die Rotationsenergie eines Systemes endlichen T r¨agheitsmomentes

•

oder die potentielle und kinetische Energie einer schwingenden F eder.

Das hier betrachtete ”1/6” Modell ist ein Sonderfall der T ranslation, bei dem jedes Molek¨ ul nur eine kartesische Gesamtgeschwindigkeit der Gr¨ oße c

besitzt. Zerlegt man z.B.

= c

= c

in einem gedrehten Koordinatensystem, so erh¨alt man wieder drei Freiheitsgrade und der Gleichverteilungssatz gilt auch f¨ ur dieses Modell.

Jeder Energieanteil wird durch einen Freiheitsgrad (abgek¨ urzt als F G) charakterisiert. Damit kann die innere Energie voll angeregter F reiheitsgrade in einer allgemeinen Form beschrieben werden zu:

e = F G 2 k

m

T = F G

2 R

T. (2.7)

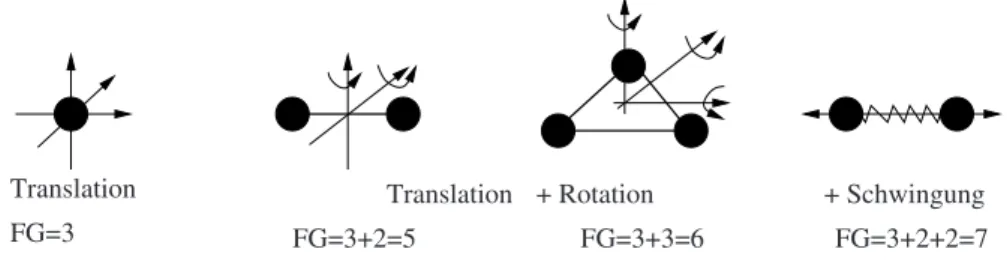
Bei der Bestimmung der Freiheitsgrade wird angenommen, dass ein Atom ein ausdehnungsloser Massepunkt ohne eigenes Tr¨agheitsmoment ist. Sind jedoch zwei oder mehrere Massepunkte in einem gewissen Abstand starr mit- einander verbunden, besitzen diese ein endliches T r¨agheitsmoment. M¨ ogliche F reiheitsgrade einfacher ein- und mehratomiger Molek¨ ule sind:

•

translatorische Freiheitsgrade der Bewegung in x-, y- und z-Richtung mit F G = 3,

•

rotatorische Freiheitsgrade einer Drehung um die kartesischen Achsen mit F G = 2 bis F G = 3, abh¨angig von der Anordnung der Molek¨ ule,

•

Schwingungsfreiheitsgrade einer gedachten Feder zwischen zwei Molek¨ ulen mit F G = 2 pro Verbindung f¨ ur potentielle und kinetische Energie.

Die einzelnen Molek¨ ulfreiheitsgrade gehen jedoch nur f¨ ur den Fall, dass sie

voll angeregt sind, mit dem Faktor 1/2 in die thermische Energie (2.7) ein. Bei

den meisten ein- bis dreiatomigen Molek¨ ulen ist das f¨ ur die translatorischen

und rotatorischen F reiheitsgrade bereits oberhalb einer Temperatur von 5 K der Fall, w¨ahrend die Schwingungsfreiheitsgrade i.Allg. erst bei hohen T em- peraturen voll angeregt sind. Zum Beispiel ist dies der Fall bei T

2270 K für O

oder bei T

3390 K f¨ ur N

.

FG=3

Translation Translation + Rotation + Schwingung FG=3+2+2=7 FG=3+3=6

FG=3+2=5

Abb. 2.4.Freiheitsgrade von einfachenMolek¨ulen

Spezifische W¨armen und Isentropenexponent.

Mit Hilfe der Glei- chung (2.7) f¨ ur die thermische Energie e als Funktion der Molek¨ ulfreiheits- grade lassen sich sehr einfach die spezifischen W¨armen c

und c

und der Isentropenexponent κ f¨ ur ein ideales Gas bestimmen. F¨ ur die thermische Energie eines idealen Gases gilt damit:

e = c

T = F G

2 R T mit c

= F G

2 R. (2.8)

F¨ ur die Enthalpie folgt entsprechend:

h = c

T = (c

+ R) T = ( F G

2 + 1) R T mit c

= F G + 2

2 R. (2.9) Der Isentropenexponent κ ist damit sofort bestimmt.

κ = h e = c

c

= F G + 2

F G . (2.10)

Einige Beispiele f¨ ur ideale Gase sind:

einatomige Molek¨ ule (He, Ar, Ne,

FG=3, κ =

= 1, 66, zweiatomige Molek¨ ule (O

, N

, CO,

FG=5, κ =

= 1, 4.

dreiatomige Molek¨ ule (CO

, NO

,

FG=6, κ =

1, 33.

Mittlere,

thermische

. Aus dem Zusammenhang zwischen kinetischer Energie der Molek¨ ule und thermischer Energie in (2.5) kann sofort die zun¨achst als Unbek annte angenommene Molek¨ ulgeschwindig- keit c

als F unktion der Temperatur festgelegt werden. F¨ ur die Molek¨ ulge- schwindigkeit c

ergibt sich aus (2.5):

c

=

3 k m T =

3 R T . (2.11)

Diese Geschwindigkeit wird als mittlere, thermische Geschwindigkeit c

be- zeichnet oder auch als quadratischer Mittelwert der molekularen Geschwin- digkeiten (4.19), wie in Kap: 4.1.3 allgemeiner definiert. Die Geschwindigkeit c

ist, wie obige Beziehung (2.11) zeigt, ein Maß f¨ ur die Temperatur eines ruhenden Gases. Ein Vergleich mit der Schallgeschwindigkeit a eines Gases

a =

d p

d

=

κ R T

zeigt, dass die mittlere Molek¨ ulgeschwindigkeit c

von der Gr¨ oßenordnung der Schallgeschwindigkeit a ist, da:

c

a =

3

κ = O(1).

F¨ ur ein einatomiges Gas mit einem Isentropenexponent κ = 5/3

1.66 folgt somit c

1.34 a, f¨ ur ein zweiatomiges Gas mit κ = 7/5 folgt c

1.46 a. Um eine Vorstellung von der Gr¨ oßenordnung der thermische Geschwindigkeit c

zu bekommen, vergleicht man diese zum Beispiel mit der Schallgeschwindig- keit in Luft a

. Die Schallgeschwindigkeit betr¨agt a

347 m/s bei 300 K und somit betr¨agt die mittlere thermische Geschwindigkeit c

500 m/s.

2.1.3

Betrachtet wird ein Gemisch idealer Gase, welches sich in einem abgeschlos- senen Volumen V im Gleichgewicht befindet. Gleichgewicht bedeutet hier, dass die einzelnen Spezies vollst¨andig durchmischt sind (keine Konzentra- tionsdifferenz) und die Temperatur der einzelnen Spezies sich angeglichen hat (konstante Temperatur T ). Das Gemisch besteht aus einer Anzahl

unterschiedlicher Spezies N

, N

, ..N

, die unterschiedliche Molek¨ ulmassen m

, m

, ..m

haben k¨ onnen.

DieErhaltung der Anzahl derMolek¨

ule im Gemisch fordert:

N = N

+ N

+

=

s

N

bzw.

n = N/V = n

+ n

+

=

s

n

. (2.12)

Die Erhaltung der Anzahl N, bzw. der Teilchendichte n gilt nur f¨ ur nichtrea- gierende Gase. In chemischen Reaktionen kann sich jedoch die Gesamtanzahl und die gesamte Teilchendichte n auf Grund von Entstehen und Vergehen einzelner Spezies ¨andern.

DieErhaltung der Masse

f¨ uhrt auf die Erhaltung der Gesamtdichte

M = N

m

+ N

m

+

=

s

m

N

bzw.

#

= M/V =

+

+

=

s

#s

. (2.13)

Im Gegensatz zur Teilchenzahl und Teilchendichte bleibt die Gesamtmasse M und damit die Gesamtdichte

auch in einem chemisch reagierenden Gemisch erhalten.

Daltonsches Gesetz.

Die Interpretation des Druckes als Reaktion auf die Impuls¨anderung reflektierter Molek¨ ule an einer Wand erlaubt sofort, den Ge- samtdruck p als Summe der Impuls¨anderungen aller Spezies anzusetzen. Un- ter Nutzung von (2.3) folgt f¨ ur den Gesamtdruck:

p = 1

3 V (N

m

c

+ N

m

c

+ ..) = 1 3 V

C

s

N

m

c

= n k T. (2.14) Jeder T erm dieser Gleichung hat die Form eines Partialdruckes der Spezies und somit repr¨asentiert die Beziehung (2.14) sofort das Daltonsches Gesetz, das aussagt, dass der Gesamtdruck gleich der Summe der Partialdr¨ ucke ist.

p = p

+ p

+ ... =

s

p

. (2.15)

Der Partialdruck einer Spezies ist z.B.:

p

= 1

3 n

m

c

= n

k T =

R

T.

Gleichverteilung der Energien in einem Gemisch.

F¨ ur die mittlere kinetische Energie eines Molek¨ ules einer Spezies gilt mit E

= E

nach (2.5) f¨ ur ein Gemisch im Gleichgewicht:

1

2 m

c

= 1

2 m

c

= 1

2 m

c

= 3

2 k T. (2.16)

Bei gleicher Temperatur jeder Spezies

besitzt jede Spezies somit auch glei- che kinetische Energie

m

c

. Die thermischen Geschwindigkeiten c

, c

, ..

der Spezies k¨ onnen jedoch auf Grund unterschiedlicher Massen, entsprechend obiger Gleichung, unterschiedlich sein.

c

=

3

2 k

m

T

1

m

. (2.17)

Gasdiffusion oder molekularerDiffusionseffekt.

Eine Konsequenz der Massenabh¨angigkeit der thermischen Geschwindigkeit ist die sogenannte Gas- diffusion oder molekulare Diffusion. Nimmt man an, dass z.B. m

< m

ist, dann folgt aus (2.17), dass sich leichte Molek¨ ule im Mittel schneller als schwe- rere bewegen.

c

c

=

m

m

> 1 falls m

< m

.

Dieser molekulare Diffusionseffekt wird industriell als Membrandiffusionsver-

fahren bzw. Gasdiffusionsverfahren zur Trennung von Isotopen in Gasgemi-

schen genutzt, siehe auch Abschn. 4.2.2.

Str¨

omungsgeschwindigkeit

Bewegt sich das Gasge- misch mit einer mittleren Str¨ omungsgeschwindigkeit

so kann prinzipiell jede Spezies

ihre eigene Str¨ omungsgeschwindigkeit

haben. F¨ ur den ge- samten Massenstrom pro Fl¨ache gilt:

#v

=

+

+

=

s

#svs

.

Hieraus folgt die massengemittelte

eines

zu:

v

=

+

+

#A

+

+

=

s#svs

#

. (2.18)

F¨ ur ein Gemisch im Gleichgewicht, d.h. ohne Gradienten der Geschwindigkei- ten

und ohne ¨außere Kr¨afte, gilt neben der Annahme gleicher T emperatur f¨ ur alle Spezies auch die Annahme gleicher Str¨ omungsgeschwindigkeit f¨ ur alle Spezies, d.h.

v

=

=

=

. (2.19)

Diese Bedingung erf¨ ullt Gleichung (2.18) exakt.

Der Nachweis, dass alle Spezies in Gemischen im Gleichgewicht glei- che Temperatur und Str¨ omungsgeschwindigkeit besitzen, wird sp¨ater in Ab- schn. 6.5 gebracht.

2.1.4

Obwohl in diesem ,,1/6” Modell bisher keine molekularen Kollisionen ange- nommen wurden, lassen sich hiermit dennoch Kollisionsparameter durch die Annahme fiktiver Kollisionen qualitativ absch¨atzen. Eine genaue Berechnung unter Ber¨ ucksichtigung der Relativgeschwindigkeiten zwischen den Molek¨ ulen erfolgt im Abschn. 4.4.3.

c 0

2 σ σ

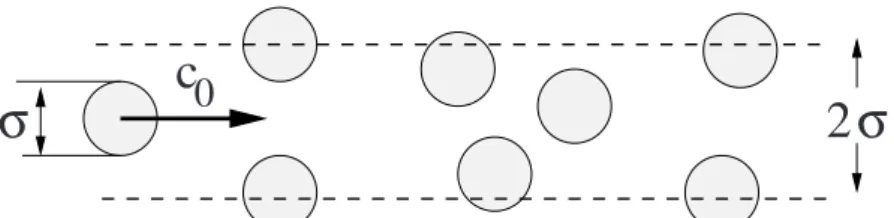
Abb. 2.5.Anordnung zurAbsch¨atzung vonKollisionsparametern.

Zur n¨aherungsweisen Absch¨atzung nimmt man, wie in Abb. 2.5 skizziert,

an, dass die Bewegung aller Molek¨ ule eingefroren ist, nur ein T estmolek¨ ul

bewegt sich mit c

. Alle Molek¨ ule werden als Kugeln mit dem Durchmesser

betrachtet. Das T estmolek¨ ul st¨ oßt bzw. ber¨ uhrt innerhalb einer Zeit ∆t

alle (ruhenden) Molek¨ ule, die sich in einem Zylinder mit dem Durchmesser

D =

+ 2

= 2

und der L¨ange c

∆t befinden. Das Volumen dieses Zylinders ist somit

∆V = πσ

c

∆t.

Stoßfrequenz.

Die Stoßfrequenz ν

ist gleich der Anzahl der Molek¨ ulst¨ oße pro Zeit. Die Anzahl der St¨ oße, gleich ν

∆t, ist proportional zu der Anzahl Molek¨ ule, die sich in dem betrachteten Zylinder mit Volumen ∆V befinden, bezogen auf die Gesamtzahl N der Molek¨ ule im gesamten Volumen V . Die Anzahl der St¨ oße ist somit:

ν

∆t = ∆V

V N = πσ

c

N V ∆t.

Hieraus ergibt sich die Stoßfrequenz ν

zu:

ν

= π

c

n. (2.20)

Die korrekte L¨ osung f¨ ur eine starre Kugel mittels Maxwell-Verteilung berech- net, (4.37), ist zum Vergleich

ν

= 4/

3π

πσ

c

n. (2.21)

Mittlere freie Wegl¨ange l^*

. Die mittlere freie Wegl¨ange l

ist die freie Flugstrecke eines Molek¨ ules, die es im Mittel zwischen zwei St ¨ oßen zur¨ ucklegt.

Sie ist eine wichtige Gr¨ oße zur Charakterisierung der Str¨ omungsbereiche. Die mittlere freie Wegl¨ange l

ergibt sich sofort aus der Kollisionsfrequenz ν

zu:

l

= c

ν

= 1

π

n = m π

1

#

. (2.22)

Die korrekte L¨ osung f¨ ur eine starre Kugel mittels Maxwell-Verteilung berech- net, (4.38), ist zum Vergleich

l

=

1 2

1

π

n . (2.23)

F¨ ur die mittlere freie Wegl¨ange l

folgt, dass sie im Wesentlichen umgekehrt proportional zur Dichte ist, bzw. dass das Produkt aus Dichte und Wegl¨ange nahezu eine Konstante f¨ ur eine Molek¨ ulsorte ist.:

l

=

m

2 π

const. (2.24)

Stoßzahlz²

. Die gesamte Anzahl

der St¨ oße pro Zeit und Volumen ist eine h¨aufig genutzte Gr¨ oße in der Reaktionskinetik. Die Gesamtzahl

ergibt sich aus:

zs

= n

ν

= π

c

n

.

Typisch f¨ ur die Kollisionszahl

ist, dass die beteiligten Gaskomponenten

mit dem Produkt ihrer Dichten eingehen, d.h. hier

n

.