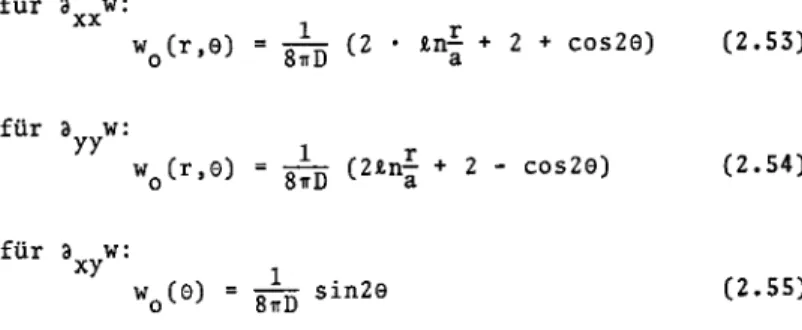Berechnung polygonaler Platten mit verbesserten Differenzgleichungen

Research Collection

Working Paper

Berechnung polygonaler Platten mit verbesserten Differenzgleichungen

Author(s):

Pfaffinger, Dieter Publication Date:

1970

Permanent Link:

https://doi.org/10.3929/ethz-a-000747218

Rights / License:

In Copyright - Non-Commercial Use Permitted

This page was generated automatically upon download from the ETH Zurich Research Collection. For more information please consult the Terms of use.

ETH Library

/ ^?

m

Berechnung polygonaler

Platten mit verbesserten

Differenzgleichungen

Dieter Pfaffinger

Januar 1970 Bericht Nr. 28

Institut für Baustatik ETH Zürich

Leer Vide Empty

Leer

Vide

Empty

mit verbesserten Differenzengleichungen

von

Dr. sc. techn. Dieter Pfaffinger

Institut für Baustatik

Eidgenössische Technische Hochschule Zürich

Zürich

Januar 1970

Leer

Vide

Empty

Die Lösung ^der Plattengleichung ^AAw

p/D ^{ist für} allgemein begrenzte, beliebig gelagerte und belastete Platten in den meisten praktischen ^{Fällen nur numerisch} möglich. ^{Bei Be¬}

nützung ^einer elektronischen Rechenmaschine stehen dabei das Differenzenverfahren und neuerdings die Methode der finiten Elemente im Vordergrund.

Die vorliegende Arbeit wurde von Herrn D. Pfaffinger ^im Rahmen eines Forschungsprojektes ^{des Instituts für Bau¬}

statik, Abteilung Massivbau, ^als Dissertation (Referent Prof. Dr. B. Thürlimann, Korreferent Dr. E. Anderheggen) ausgearbeitet. ^{Es ist ihm eine sehr} allgemeine ^Darstel¬

lung des_.J)ifferenzenverfahrens in Matrizenform gelungen, welches sich besonders für die Programmierung eignet. ^An Hand von typischen Beispielen zeigt ^{er auch die} prakti¬

sche Anwendung ^des ausgearbeiteten, weitgehend ^automati¬

sierten Programmes.

Eidgenössische ^{Technische Prof. Dr. Bruno Thürlimann} Hochschule

Zürich

Dezember 1969

Leer

Vide

Empty

Seite

1. Einleitung ⁹

2. Theorie der dünnen Platte konstanter Steifigkeit

2.1 Variationsproblem ¹¹

2.2 Differentialgleichung ^und Randbedingungen ¹⁶

2.3 Problemstellung ^und Lösungsmethode ²²

2.4 Inhomogene Lösungen ^und Singularitäten ²⁸

3. Basismatrizen des Differenzenverfahrens

3.1 Zweidimensionale Taylorentwicklung ³⁹

3.2 Entwicklungs- ^und Basismatrix 44

3.3 Spezielle Basismatrizen 53

3.4 Rechenerfahrungen ^und Anwendungen ⁵⁸

4. Berechnung polygonaler ^Platten

4.1 Geometrie 66

4.2 Sterngleichungen ⁷⁶

4.3 Gleichungssystem und Auflösung ⁸¹

4.4 Rechenerfahrungen ⁸⁷

5. Ergänzungen

5.1 Behandlung ^{von Stützen 104}

5.2 Energieansatz ^zur Berechnung polygonaler

Platten 110

6. Schlussbemerkungen ¹²²

Zusammenfassung ¹²⁴

Nomenklatur 129

Literatur 132

Leer

Vide

Empty

Die Bestimmung ^der Verformungen ^{und der inneren} Kräfte einer dünnen elastischen Platte konstanter Steifigkeit ^{unter ver¬}

tikalen Lasten gehört ^{zu dem Kreis von} Problemen, ^deren analytische Lösung ^{nur in} einigen Spezialfällen ^bekannt ist. Man ist daher auf Näherungslösungen angewiesen, ^welche in vielen Fällen durch Diskretisierung ^des Systems gewon¬

nen werden können. Dabei wird die in unendlich vielen Punk¬

ten gültige Aussage ^von Differentialausdrücken für die strenge Lösung ^ersetzt durch endlich viele Aussagen ^über die endlich vielen Bestimmungsstücke ^einer Näherungslösung.

So stellt beispielsweise ^die Auflösung ^einer elastischen Platte in einen Trägerrost ^eine physikalisch anschauliche wenn auch stark vereinfachende Diskretisierung ^{des konti¬}

nuierlichen Problems dar.

Bei der Behandlung ^der Plattenaufgabe ^{besteht eine charak¬}

teristische Schwierigkeit ^{in der} Tatsache, ^{dass die} grund¬

legenden Beziehungen ^{i.a. für die} Biegefläche aufgestellt

und gelöst werden, während aber für die Bemessung ^die Momente und Querkräfte ^{von Interesse sind. Da diese als} Linearkombinationen der zweiten und dritten partiellen Ableitungen ^der Biegefläche gewonnen werden, ^{müssen sich}

auch aus einer Näherungslösung ^{für die} Biegefläche ^alle benötigten ^höheren Ableitungen mit_guter Genauigkeit_.be- rechnen lassen. Die Erfüllung ^dieser Forderung ^{ist in} der Umgebung ^von Lastangriffspunkten, ^{Stützen oder} irgend¬

welchen Singularitäten ^{nur mit} grossen Schwierigkeiten möglich. ^{In vielen} wichtigen Fällen lassen sich aber ana¬

lytische ^Ausdrücke angeben, ^{welche die} Störungen ^exakt wiedergeben ^{und nur die} Randbedingungen der untersuchten Platte verletzen. Es soll daher die Lösung aufgespalten werden in analytische ^{Anteile zur} Erfassung ^der Störungen

sowie einen numerisch zu berechnenden Korrekturanteil zur

Erfüllung ^der Randbedingungen.

-

10

Zur Berechnung dieser nunmehr homogenen Zusatzlösung ^wird ein Differenzenverfahren verwendet, ^das durch die Verwen¬

dung ^von Mehrstellenbedingungen ^hohen Genauigkeitsanfor¬

derungen genügt. ^Die Funktion wird dabei in ihre Stützwer¬

te an endlich vielen Punkten diskretisiert. Die allgemeinen

Ansätze zu verbesserten Differenzengleichungen ^{sind vor}

allem in [l]* ^{angegeben und wurden von} verschiedenen Auto¬

ren (z.B. [2], [3], [4]) ausgebaut. ^{Der hier in} Kapitel ³ entwickelte Begriff ^der Basismatrix ermöglicht ^eine allge-

meine Diskussion des Differenzenverfahrens und bildet gleichzeitig ^die Grundlage ^{für die} automatische Durchfüh¬

rung aller weiteren Rechenprozesse ^{durch den} Computer. ^Es wird sich zeigen, ^{dass aus der} Erörterung der Differenzen¬

ansätze die Grundlagen ^zu einer Diskussion aller diskreti- sierenden Methoden gewonnen werden können, ^{welche wie etwa} in [5] ^und [6] ^auf polynomiale Ansatzfunktionen zurück¬

gehen.

Als mathematisches Hilfsmittel wird in dieser Arbeit die Matrizenrechnung verwendet, ^deren Grundzüge ^{als bekannt} vorausgesetzt ^{werden sollen} (vgl. [16], [17], [18]). ^Viele

Ueberlegungen ^{sind von den} Besonderheiten der programmier¬

ten Rechnung beeinflusst, ^{die dem} Leser generell geläufig

sein sollte. Obwohl alle beschriebenen Rechenabläufe _pro¬

grammiert ^und ausgetestet wurden, ^{werden die} eigentlichen Rechenprogranune ^nicht mitgeteilt, ^{da sie in der} gegenwär¬

tigen ^{Form für den} kommerziellen Einsatz noch nicht geeig¬

net sein dürften. Schliesslich ist Vertrautheit mit den Prinzipien der Elastizitätstheorie und der Theorie der dünnen Platte für das Verständnis wünschenswert.

*

Siehe Literaturnachweis am Ende der Arbeit.

2. THEORIE DER DUENNEN PLATTE KONSTANTER STEIFIGKEIT

2.1 Variationsproblem

An einem ruhenden, elastischen Körper ^{sind Lasten und Reak¬}

tionen im Gleichgewicht. ^Ebenso bilden die Kräfte ^an infi¬

nitesimalen Volumenelementen Gleichgewichtssysteme, ^deren Arbeit bei einer beliebigen ^virtuellen Verschiebung ^des Elementes verschwindet. Es verschwindet daher auch die Ge¬

samtarbeit aller Kräfte des Systems.

Betrachtet man nur virtuelle Verschiebungsfelder Su, ^wel¬

che die geometrischen Lagerbedingungen ^des Körpers ^nicht verletzen, ^so leisten die Reaktionen keine Arbeit. Die Arbeit der Lasten lässt sich also mit einem Potential V durch die Variation SV ausdrücken, während die Arbeit der inneren Kräfte _gegen die elastischen Bindungen ^{in den Ele¬}

menten der Aenderung ^der Formänderungsenergie ^U gleich

ist. Somit wird die Arbeit der elastischen Bindungskräfte

zu

SU und nach dem Prinzip der virtuellen Verschiebungen ist

SV

SU

0 (2.1)

Führt man mit

H

U

V (2.2)

die potentielle Energie ^des Systems ein, ^{so lässt sich die} Gl. (2.1) nach Wechseln des Vorzeichens auch in der Form

Sn

S(U

V) ⁼⁰ (2.3)

schreiben. Da n eine Funktion des Verschiebungsfeldes ^des

-

12

Körpers ^ist und weiterhin nur stabile Gleichgewichtslagen betrachtet werden sollen folgt, ^{dass unter} den wirklichen Verschiebungen ^die potentielle Energie ^des elastischen Körpers ^{minimal ist.}

In Fig. 2.1 ist eine dünne elastische Platte dargestellt, welche mit p(x, y) ^{im Feld sowie mit} Pr(s) ^und M^(s) ^am

Rande belastet sei. Die Randmomente sind durch Vektoren mit zweifacher Spitze dargestellt ^{und drehen nach der} Rechtsschraubenregel. ^{Die Platte sei an} Teilstücken des Randes ->©rart festgehalten, ^{dass sich} Gleichgewicht ^aus¬

bilden kann. Da die Plattendicke h verglichen ^{mit den} übrigen Abmessungen ^klein ist, ^darf vorausgesetzt werden, dass Punkte auf einer Normalen zur Mittelebene der Platte auch nach der Formänderung auf einer Normalen zur verform¬

ten Mittelfläche liegen. Weiterhin darf bei kleinen Durch¬

biegungen ^die Verzerrung ^der Plattenmittelebene vernach¬

lässigt werden, ^so dass die Verformungen ^{der Platte durch}

die vertikalen Durchbiegungen w(x, y) der Mittelebene be¬

stimmt sind.

j/l—'

M U

/

i

/'£•*••

$ ^_C_Ä

Fig. ^2.1 Fig. ^2.2

Unter den gemachten Voraussetzungen ^lassen sich die Ver¬

zerrungskomponenten des Plattenelementes der Fig. ^{2.2 durch} Ableitungen der Funktion w(x, y) ausdrücken. Mit dem

Hooke1sehen Gesetz sind damit auch die Spannungskomponen¬

ten bestimmt. Für isotrope ^{Platten erhält man durch} Integra¬

tion die bekannten Beziehungen ^{für die Momente} pro Längen¬

einheit:

h/2

32 32

D (r—r ^w

-—5- ^w)

v3xz

3y2

M

X

-h/2

•

z

dz

I

M

y

+

h/2

-h/2

•

z

dz

]

M xy

= -

M yx

+

h/2

"

i ^v

-

h/2

Die Plattenste:

n :

ifigkeit

E h3

D (Ifw

vfew) ^(2-4:)

-

z

dz

D (1

)

3x3y

12 (1

.vz) (2.5)

hängt neben der Plattendicke h vom Elastizitätsmodul E und der Querdehnungszahl

^{ab und wird als} konstant vorausge¬

setzt. Schliesslich liefert die Bedingung des Momenten¬

gleichgewichts ^{am Element auch die} Querkräfte pro Längen¬

einheit:

Qx

^D

fc ^Uw) _Qy

^D

fc ^{(Aw) (2.6)}

wobei

»2 »2

*

TT

TT

3xz

3yz

14

Für viele der folgenden Ueberlegungen ^{ist es} bequem, ^die Differentiationszeichen mit

r-

=3 =311

i j xx..xyy..y ^x yJ

9

i

j (2.7)

3x Sy

abzukürzen. Unter Vernachlässigung der Arbeit der Querkräf¬

te wird die Formänderungsenergie ^{des Elementes zu}

dU 1

M _xv ^(-3 _xx w)

^M (-3 w)

^{2 M 3 w}

y yy xy xy dxdy

Berücksichtigt ^{man die} Beziehungen (2.4) ^und integriert

über das Gebiet S, ^so ergibt sich für die Formänderungs¬

energie ^{der Platte} der Ausdruck

U

2 /T{(AW)2

^2C1

^VH3XXW

^3yyW

^{(3xyw)2]} dxdy}

S (2.8)

Das Potential der Lasten ist entsprechend Fig. ^{2.1 durch}

//'

V

// ^{p(x, y)}

^w

^dxdy

¹ PR(s)

^w

^ds

M_(s)

3 w

ds

R

n (2.9)

gegeben, ^{wobei n die äussere Normale} des Randes symboli¬

siert. Es ist also die potentielle Energie

n

§ ff ^JO)2

²⁽¹

^v)[3xxv»

^3yyw

Oxyw)*]j ^dxdy

S

ff _p

_wdxdy

j ^PR(s)wds

f ^MR

(2.10)

(s)

3 wds

n

und von allen möglichen Durchbiegungsfunktionen ^{w macht}

die wirkliche Funktion ⁿ zu einem Minimum. Die zur Konkur¬

renz zugelassenen Biegeflächen ^{müssen dabei am Rande der}

Platte den geometrischen Bedingungen genügen. ^{Setzt man}

voraus, dass keine Randlasten PR(S) und keine Randmomente M_(s) wirken, ^{so ist ein Randstück}

eingespannt, ^{falls w}

⁰ 3nw= ^{0 (2.11)}

aufliegend, ^{falls w}

⁰ M(s)

⁰ (2.12)

frei, ^falls M(s)= ⁰ p(s)

⁰ (2.13)

M(s) ^und p(s) ^stellen dabei die Randmomente bzw. Rand¬

lasten dar, ^{welche durch die} Biegefläche w(x, y) ^bestimmt werden.

Bei Beschränkung ^{auf diese drei} Randbedingungen gilt ^also für w

am eingespannten ^{Rand: w}

0;

am aufliegenden ^{Rand: w}

⁰

3 w

0

n (2.14)

(2.15)

Die Gesamtheit der möglichen Durchbiegungen ^{lässt sich}

auch erhalten, ^{indem man} der wirklichen Biegefläche w(x,y)

eine bis auf Stetigkeits- ^und Differenzierbarkeitseigen- schaften beliebige ^Funktion n(x,y) überlagert, ^welche

ebenfalls den geometrischen Bedingungen (2.14) ^bzw. (2.15) genügt. ^{Mit einem Parameter}

^ist daher die Minimalbedin¬

gung (2.3) der Forderung

lim d_

E+0 de ⁿ (w

n)

⁰ (2.16)

gleichwertig ^{und das} ursprüngliche Variationsproblem ^ist

damit auf eine Extremalaufgabe zurückgeführt.

-

16

2.2 Differentialgleichung ^.und Randbedingungen

Wendet man die Forderung (2.16) auf den Ausdruck (2.10) der potentiellen Energie an, ^so ergibt ^sich

D ff Taw

An

⁽¹

^{v) (3 w}

3 n

3 w

3 n

j ^L

^{xx yy yy xx}

2

3xyw3xyn^ ^dxdy

ffP

^ndxdy

^{a\ PR(s)nds}

MR(s)

3nn

^ds

^{0 (2.17)}

Dabei bedeuten w(x,y) ^{die wirkliche} Durchbiegungsfunktion

und n(x,y) eine stetige ^und stetig differenzierbare, ^sonst aber beliebige Zusatzfunktion, ^{welche ebenfalls} den geome¬

trischen Randbedingungen genügt. ^{Es soll} vorausgesetzt werden, ^{dass alle} benötigten Ableitungen ^{von w und n exi¬}

stieren. Weiterhin soll das Gebiet S (Fig. 2.3) ^{als ein¬}

fach zusammenhängend ^{und von} einer differenzierbaren Rand¬

kurve R(s) begrenzt angenommen werden.

Bezieht man den Punkt A einmal auf das System x, y und zum anderen auf das gedrehte System n, t, ^so ist mit der Transformations¬

matrix

[T]

-sma cosa

(2.18)

Fig. ^2.3

auch der Zusammenhang ^zwischen den Koordinaten gegeben:

=

[T] ^(2.19)

Es lässt sich sofort nachweisen, ^{dass die} transponierte Matrix [T] T ^die Eigenschaft

[T]X[T]

[I] ^(2.20)

besitzt, ^wobei [i] die Einheitsmatrix bezeichnet. Somit ist

[T] orthonormal, ^{d.h. ihre} inverse Matrix [T] ^ist gleich der transponierten ^Matrix [T] T ^:

[T]"1

[T]' ^(2.21)

Aus der Gleichung (2.19) ^{lässt sich mit Hilfe der Ketten¬}

regel ^{sofort die} Beziehung

t J

[T] (2.22)

für die ersten Ableitungen gewinnen ^{und daraus erhält man} auch die Transformationen

3 3

nn nt

3nt 3tt

[T]

3 3

xx xy

3 3

xy yy

[T]J

für die zweiten Ableitungen. ^{Die inversen Relationen wer¬}

den durch Vor- bzw. Nachmultiplikation ^mit der Kehrmatrix (2.21) gewonnen. Durch weiteres Differenzieren unter An¬

wendung ^der Kettenregel lassen sich auch die Transforma¬

tionsgleichungen ^{der höheren} Ableitungen ^{ermitteln. Formal}

-

18

ergibt ^sich

3

i,J

(cosa

³

^sina

)J1

(-sina

³

^cosa

³ )J

y

y

(2.23)

mit

«p

i

j

Entwickelt man die beiden Faktoren rechts mit der Binomial- formel wobei die Potenzen von x und _y in den Differentia¬

tionszeichen wie normale Potenzen behandelt werden dürfen,

so wird nach der Ausmultiplikation ^{3 i.} j ^zu einer Linear-

n t

kombination aller Ableitungen ^{nach x und} y der Ordnung <f>.

Ein analoges Ergebnis gilt ^{für die inversen} Beziehungen.

Mit Hilfe der Green'sehen Formel

(u

^av

^v

Au)dxdy

i _(u

3 v

v3 u)ds

S R

wobei

u

Aw v

n

zu setzen sind, ^{sowie durch} Anwendung ^des Gauss'sehen Satzes

II ^(3xu

3yv)dxdy

^{i (u dx}

^v

^dy)

und Transformation auf das System n, t lässt sich (vgl.

[7], [8]) ^die folgende grundlegende Umformung ^ableiten:

(1

v) (3 W-3 n+9 ^W

³ ti

v •"v

xx yy yy ^xx

ff Faw

Ar, S

-

23xyw

3xyn)l ^dxdy

^{ff n}

^AAwdxdy

f{"[-\ ^(AW)

⁽¹ -v)fI(3ntw) ^{3 n n(-3} nn ^w

V 3ttw)} ^{ds (2.24)}

Besteht der Rand R nur aus geradlinigen Teilstücken, ^{so ist}

h^nt^

3nttW

und Gl. (2.17) kann damit und mit (2.24) ^{in der Form}

ff _ri(D

^aäw

_p)dxdy

L n

S R

fcw

_PR(s)j

ds+

/

[-

D

3 w

D

⁽²

⁾

nnn

3nttw

Vs>

ds+

*

C"V>*

"

D

'

3nnw

^D

3ttw

MR(s)] ^ds

^{0 (2.25)}

geschrieben ^{werden. Da n im Gebiete S} beliebig angenommen werden darf, folgt ^{aus dem ersten} Integral ^{die Differen¬}

tialgleichung

AAw

ß

=

0 (2.26)

der dünnen elastischen Platte konstanter Steifigkeit. ^Für das Verschwinden der beiden Randintegrale genügt es, ^wenn in den Produkten jeweils ^{ein Faktor} verschwindet. Beach¬

tet man, dass n die geometrischen Randbedingungen (2.14)

-

20

und (2.15) ^ebenfalls erfüllt, ^{so erhält man} sämtliche Rand¬

bedingungen ^{für w:}

a) eingespannter ^Rand:

w

0; ³ _n ^w

⁰ (2.27)

b) aifliegender ^Rand:

w

0;

c) freier Rand:

D(3nnW

V3ttw)

MR(S>

(2.28)

D(3nnw

v,ttw) =MR(s); ³ nnn ^w

⁽²

^v)3

ntt

PR(s) ^(2.29)

Durch Nullsetzen von PR(s) ^und MR(s) ^{erhält man daraus die} Bedingungen (2.11), (2.12) ^und (2.13).

Die gesuchte Durchbiegungsfunktion w(x,y) ^{hat also neben}

der Differentialgleichung (2.26) ^{und den} geometrischen Randbedingungen ^noch zusätzliche statische Randbedingungen

zu erfüllen. Durch Transformation der Momente (2.4) ^und Querkräfte (2.6) ^{auf das} System n, t erkennt _man, dass

-

D(3

w

vj ^w)

M

nn tt

n

d.h. einem Randmoment M(s) entspricht, ^während

D 3 w

(2-v )3

[ ⁿⁿⁿ

^{ntt xn t nt}

eine Randbelastung p(s) darstellt, ^{welche durch die Scher¬}

kräfte und die in Kräfte aufgelösten Randdrillungsmomente

gebildet ^wird.

Macht man für w nun den Ansatz

w(x,y)

WQ(x,y)

wh(x,y) ^(2.30)

so folgt ^{zunächst aus} (2.26) ^die Gleichung

AAw

AAwh

^

^{0 (2.31)}

Da der inhomogene Lösungsanteil ^{w die} Belastung wiederge¬

ben soll, ^muss

AAwQ

£

^{0 (2.32)}

sein, während der homogene, lastfreie Anteil w, der Glei¬

chung

AAw,

0 (2.33)

genügen

^Ebenso lassen sich auch die Randgleichungen aufspalten. ^{Führt man mit}

Mo<s>

DC3nnwo

v3ttV> ^<2-34)

die Randmomente und mit

p„(s)

dH> w

(2

)9 .twl _(2.35)

o L ^{nnn o ntt ol}

die Randlasten des inhomogenen ^Zustandes ein, ^so erhält man:

a) eingespannter ^Rand:

w,

w^

0; ^{3 w,}

^{3 w}

0 (2.36)

honhno

-

22

b) aufliegender Rand:

wh

WQ

^0;

D(3nnwh

v3ttwh)

Mo(s)

⁰

(2.37)

c) freier Rand:

D<3nnwh

v3ttV

Vs>

^°>

-

D

¦J

3 w,

⁽²

^v)3

p (s)

0 _(2.38)

nnn h

ntt h *o

2.3 Problemstellung ^und Lösungsmethode

Bei der Herleitung ^der Randgleichungen ^{wurde in} Abschnitt 2.2 eine aus geradlinigen Teilstücken bestehende Randkurve vorausgesetzt. Darüber hinaus sollen folgende ^{weitere Ein¬}

schränkungen getroffen ^werden:

a) ^{Das Gebiet} S sei konvex. Die Platte hat damit die Form eines Polygons, ^bei dem das Plattengebiet ^{S stets} ganz auf einer Seite jedes Randstückes liegt.

b) Entlang einer Polygonseite sei die Randbedingung ^kon¬

stant. Dabei sollen nur die Bedingungen (2.11), (2.12) oder (2.13) möglich sein.

c) ^{Das Gebiet} S sei einfach zusammenhängend. ^{Dadurch wer¬}

den Aussparungen ^{in der Platte} ausgeschlossen.

d) ^{Im Gebiet S} seien keine geometrischen Bedingungen ^zu erfüllen. Damit werden Stützen im Plattengebiet ^aus¬

geschlossen.

Durch die gemachten Voraussetzungen ^{wird die automati¬}

sche Behandlung ^{durch den} Computer wesentlich vereinfacht.

Es soll aber ausdrücklich betont werden, ^dass die hier dar¬

gestellte Berechnungsmethode grundsätzlich ^von diesen Ein¬

schränkungen unabhängig ^{ist und mit} entsprechenden ^Rechen¬

programmen auch ^zur Lösung ^viel allgemeinerer Randwertauf¬

gaben verwendet werden kann.

In Fig. ^{2.4 ist eine} polygonale ^Platte dargestellt, ^welche obigen Forderungen genügt. ^{Die Platte ist auf ein recht¬}

winkliges Achsenkreuz _{x, y} bezogen ^{und mit l Lasten}

Pifx.y) ^1,.

belastet. Neben dem globalen x, y-System ^{sei für} jede Poly¬

gonseite ^{ein lokales} System n, t im Anfangseckpunkt einge¬

führt. Gesucht sind die Biegeflächen w.(x,y) ^{der Platte}

unter den i Belastungen sowie die Einflussflächen von be¬

stimmten partiellen Ableitungen ^der Biegefläche ^{für de.i} Einflusspunkt ^{A. Aus dem} Maxwell'sehen Satz über die Gegen¬

seitigkeit ^der Verschiebungen folgt, ^{dass die} Biegefläche

der Platte unter der Einzellast P

1 in A der Einflussfläche oder Green'sehen Funktion für die

Durchbiegungen ^im Einflusspunkt ^A gleich ^{ist. Durch} Differentiation nach dem Einflusspunkt erhält man aus die¬

ser Biegefläche ^auch die Einflussflächen der zweiten und drit¬

ten Ableitungen und durch Linearkombination nach (2.4) ^und (2.6) auch die Einflussflächen der Momente und Querkräfte.

Fig. ^2.4

24

Demnach erfüllen alle Green'sehen Funktionen der dünnen elastischen Platte die Gleichung

AAw

0

im Gebiet S mit Ausnahme des Einflusspunktes A, ^{sowie die} Randgleichungen ^{am Rande R. Da bereits unter} der Einzel¬

last P

1 in A bestimmte Spannungskomponenten ^unendlich

gross werden, ^{der Punkt} A somit ein singulärer ^Punkt ist, weist auch der Einflusspunkt ^A der Einflussflächen für die Ableitungen ^eine Singularität ^{auf. Diese} Singularitä¬

ten sind bekannt und damit lassen sich die Einflussflä¬

chen aich als Biegeflächen der mit den entsprechenden ^Sin¬

gularitäten ^im Einflusspunkt ^{belasteten Platte auffassen.}

Bei den Lastfällen 'Einflussflächen' stellen die Biege¬

flächen bereits das gesuchte Ergebnis dar, während bei den übrigen ^{Lastfällen aus den} Biegeflächen ^{noch die Mo¬}

mente und Querkräfte ^berechnet werden müssen.

Für verschiedene Lastformen p.(x,y) ^{sowie für die} Singu¬

laritäten der Einflussflächen lassen sich Gebiete S 0,1

(Fig. 2.4) ^{mit dem} Rand R _0,1

und der analytisch gegebe-

nen Biegefläche ^w

angeben, ^{für welche in einem} zuge- 0,1

ordneten Koordinatensystem ^{£., n• die} inhomogene ^Glei¬

chung

AAw ^{.(£., n-)} 0,lv l' l'

Viti*, ^1\AJ

erfüllt ist. Es soll ausdrücklich darauf hingewiesen ^wer¬

den, ^dass 5 und n hier dimensionsbehaftet sind. Das Gebiet S

hängt ^{von der Art der} Belastung p. ab und sein Bezugs¬

system £., n- soll um den Winkel 9. gegenüber ^dem x, y-Sy¬

stem gedreht ^{sein. Auch für S}

werden ^die Einschränkungen

0,1

c) und d) gemacht ^und weiterhin wird verlangt, dass die Polygonplatte ganz ^vom Rand R

umschlossen wird.

0,1

Ersetzt man in der Definitionsgleichung (2.18) ^{für die} Transformationsmatrix [T] ^{den Winkel}

^durch 9., ^so folgt mit dem Ortsvektor

{ci>

LyCi

durch sinngemässe Anwendung ^{von Gl.} (2.19) ^die Transforma¬

tion

[T] (2.39)

zwischen den Koordinatensystemen. ^Für den Randwinkel *

einer

Figur

einer

Polygonseite ^im System g., n- liest man aus der

(2.40)

ab und analog transformieren sich Winkelgrössen, ^welche beispielsweise ^zur Beschreibung der Last p. benötigt ^wer¬

den. Diese beiden Beziehungen gestatten ^die Beschreibung

der mit p. belasteten polygonalen ^{Platte im} System £., n••

Denkt man sich nun die Platte entlang ^{ihres Randes R aus} dem Gebiete S

herausgeschnitten, ^so sind Deformationen

0,1

und innere Kräfte durch die Funktion w .(£., n•) bestimmt.

o,x ^{1 1}

Insbesondere lassen sich auf R die Durchbiegungen, ^Normal¬

ableitungen, Randmomente (2.34) ^{und Randlasten} (2.35) ^aus

w

bestimmen, welche i.a. nicht mit den durch die Rand- 0,1

bedingungen ^{der Platte} vorgeschriebenen ^Werten übereinstim¬

men. Ueberlagert ^{man aber dem Zustand w}

^einen Eigen-

0,1

spannungszustand ^der Platte, ^welcher diese Randwerte auf ihre vorgeschriebenen ^Werte korrigiert, ^{so hat man damit} den wirklichen Zustand der Platte gefunden. ^Die Superposi-

tion beider Zustände entspricht genau dem Ansatz (2.30)

26

und da w

voraussetzungsgemäss ^die Gleichung (2.32) ^er-

0,1

füllt und bekannt ist, ^{muss nur noch} der Eigenspannungszu- stand ermittelt werden. Dieser ergibt ^{sich als} Lösung ^der homogenen Gleichung (2.33) ^{mit den} Randbedingungen (2.36), (2.37) ^oder (2.38) ^{wobei die} Randgrössen

w

3 w

M ^(s), p ^(s) o

ov

*ov

aus w

zu berechnen sind. Die Biegefläche w, des ^Eigen-

o,i

^h

spannungszustandes hängt ^{somit nur mehr von} den Randwerten ab und ist im Gebiet S frei von belastungsabhängigen ^Stö¬

rungen. Ihre numerische Berechnung ^{wird umso} einfacher, je weniger ^{die Randwerte des} inhomogenen ^{Zustandes von den} für das gegebene Plattenproblem vorgeschriebenen ^{Werten ab¬}

weichen. Sind die Lasten weit vom Rand entfernt, ^{so hat man} wenig oszillierende inhomogene ^{Randwerte. Das hier verwen¬}

dete Differenzenverfahren zur Lösung ^des homogenen ^Problems

erlaubt aber auch die Erfassung stark oszillierender Rand¬

funktionen mit einer gleichmässig ^hohen Genauigkeit. Spal¬

tet man auch die Schnittkräfte (2.4) ^und (2.6) gemäss (2.30) ^{in einen} inhomogenen ^{und einen} homogenen ^Anteil auf,

so zeigt ^sich der besondere Vorteil dieses Ansatzes: der inhomogene ^{Teil wird aus w}

^exakt berechnet und bestimmt

0,1

wesentlich die komplizierten Verhältnisse in Lastnähe, während der homogene ^Anteil durch numerische Differentia¬

tion der störungsfreien ^{Fläche w, ebenfalls mit hoher Ge¬}

nauigkeit gewonnen werden kann.

Jede Lösung ^der Plattendifferentialgleichung (2.26) ^für eine bestimmte Belastung ^{p. in einem} Gebiet S

der oben

1 0,1

definierten Beschaffenheit lässt sich als inhomogener ^Zu¬

stand der mit der gleichen ^Last p. belasteten polygonalen Platte auffassen. Dabei ist es bedeutungslos, ^{welche Bedin¬}

gungen ^von der Lösung ^w

^{am Rande R}

erfüllt werden.

Man erhält daher aus der Literatur einen ganzen Katalog

analytisch darstellbarer inhomogener Lösungen ^{für viele} praktisch wichtige Belastungen. ^{Für die} Abspaltbarkeit ^des Lastanteils soll dabei vorausgesetzt werden, ^{dass die Last-} grösse ^von Anfang ^an gegeben ^{ist. Ist die Platte} beispiels¬

weise auf Stützen aufgelagert ^so sind die Stützendrücke aus Verträglichkeitsbedingungen ^zu bestimmen und somit zu¬

nächst unbekannt. Diese Einschränkung ^ist aber ebenfalls nicht grundsätzlicher ^Natur.

INHOMOGENE LOSUNGEN UND SINGULARITÄTEN

LASTFALL GEBIET S0 ^{ART DER LOSUNG LITERATUR}

Gleichest p aufliegender Plattenstreifen geschlossener ^Ausdruck [9],S ¹⁸⁰

"

aufliegende Rechteckplatte einfache Reihen [9],S ²⁰⁰

"

aufliegende Kreisplatte geschlossener ^Ausdruck [9],S ²⁴⁰

"

eingespannte Kreisplatte geschlossener ^Ausdruck [9],S ^{24 1}

Hydrostatische ^Last aufliegender Plattenstreifen geschlossener ^Ausdruck [9],S ^{1 8 1}

'•

aufliegende Rechteckplatte einfache Reihen [10],S ¹²⁴

Dreieck

Streitenlast aufliegender Plattenstreifen einfache Reihen [11],S ^{5 5} Beliebige Streifenlast aufliegender Plattenstreifen einfache Reihen [9],S ^{18 1}

Rechtecklast p aufliegender Plattenstreifen einfache Reihen [9],S ¹⁸⁴

"

aufliegende Rechteckplatte einfache Reihen [9],S ¹⁹⁹

Linienlast p aufliegender Plattenstreifen einfache Reihen [9],S ¹⁸⁵ Beliebige ^Linienlast aufliegender Plattenstreifen einfache Reihen [11], ^{S 5 8}

Kreislast p aufliegende Kreisplatte geschlossener Ausdruck [9],S ^{24 2} Kreisringlast p aufliegende Kreisplatte geschlossener Ausdruck [9],S ^{24 5}

Einzellast P aufliegender Plattenstreifen einfache Reihen [9],S ¹⁸⁶

»

aufliegende Rechteckplatte ^{einfache Reihen} [9],S ²⁰⁰

"

aufliegende Kreisplatte geschlossener Ausdruck [9],S 244

»

Kreis

Einflusspunkt geschlossener ^Ausdruck [9],S ²⁶⁰

Einzelmoment M aufliegender Plattenstreifen einfache Reihen [9],S ¹⁸⁷

"

Kreis

Einflusspunkt geschlossener Ausdruck [10],S ^{32 6}

Singularitäten ^für

dxxw ^{ifn Feld Kreis}

Einflusspunkt geschlossener ^Ausdruck [9],S ²⁶² dXyW

^{Feld Kreis}

Einflusspunkt geschlossener ^Ausdruck [9],S ²⁶²

<3x(Aw)

^{Feld Kreis}

Einflusspunkt geschlossener ^Ausdruck [9],S ²⁶²

M über Querbalken durchlaufende Platte einfache Reihen [13], ^{S 121} dxxw ^am eingesp Rand Kragplatte geschlossener ^Ausdruck [14], ^{S 85}

<3„(Aw)am eingesp Rand Kragplatte geschlossener ^Ausdruck [14], ^{S 85}

Tabelle 2.1

-

28

In Tabelle 2.1 wurde eine Auswahl inhomogener Lösungen ^und Singularitäten zusammengestellt. ^Bestehen für eine bestimm¬

te Lastform mehrere Möglichkeiten, ^{so wählt} man diejenige

aus, für welche die inhomogenen Randwerte der aus S her¬

ausgeschnittenen Polygonplatte ^{am besten mit} den wirkli¬

chen Randbedingungen übereinstimmen. In diesem Falle sind mit der homogenen Lösung ^{nur kleine} Korrekturen ^zu berech¬

nen, wodurch die Genauigkeit ^der superponierten Gesamtlö¬

sung günstig beeinflusst wird.

2.4 Inhomogene Lösungen ^und Singularitäten

Von den zahlreichen bekannten inhomogenen Lösungen ^der Plattengleichung sollen in diesem Abschnitt einige ^wich¬

tige Funktionen genauer diskutiert werden. Bei den hier nicht behandelten inhomogenen Lösungen geht ^man analog ^vor.

Es wird sich bei der Berechnung ^des homogenen Lösungsan¬

teils zeigen, ^dass durch die verwendeten Gitterpunkte ^ein Rechteck der Seitenlängen ^l _x

l (Fig. 2.5) ^{bestimmt ist.}

y

Dieses Rechteck um- schliesst die poly¬

gonale ^Platte und bietet sich als na¬

türliche Begrenzung des Problems an.

Das Bezugssystem x, y der Platte soll daher in der nord¬

westlichen Ecke an¬

genommen und die Er¬

mittlung der Gebiete S auf dieses um-

o

schriebene Rechteck

Fig. ^2.5

abgestimmt ^werden.

Neben den Funktionswerten der inhomogenen Lösungen ^und Singularitäten ^{sind auch die} partiellen Ableitungen ^bis einschliesslich dritter Ordnung ^zur Berechnung ^der Schnittkräfte von Bedeutung. ^Es genügt, ^{alle Ausdrücke} für das System £, ⁿ anzugeben ^{und sie dann} gegebenenfalls mit den Beziehungen (2.23), (2.39) ^und (2.40) ^{zu trans¬}

formieren.

a) Gleichlast p

Als Gebiet S wird der unendlich lange, beidseitig drehbar aufgelegte Plattenstreifen (Fig. 2.6) gewählt.

Das System £, n der inhomogenen Lösung ^{soll mit dem} System x, y der polygonalen Platte zusammenfallen. Die zylindrische Biegefläche hängt ^{nur von} f, ab und wird mit

a

lx

w0CO

24D (5"

2a?3

a3c) (2'41)

Da

{c}

{0} und 9

0

ist, vereinfachen sich die Transformationen (2.39) ^und (2.40) ^zu

C=x; n=y; ^&

Die partiellen Ableitungen ^von (2.41) ^{sind in Tabelle 2.2}

zusammengestellt.

30

w0-10 per

Fig. ^2.6

b) Rechtecklast p Die Belastung ^sei durch den Ortsvek¬

tor

r ⁱ

{m} (2.42)

des Lastmittelpunk¬

tes (Fig. 2.7), ^den Winkel <P

die hal¬

ben Seitenlängen ^c und d sowie den Druck _p gegeben.

Der Winkel 9 lässt sich stets mit

o ± ^f ± ₂

angeben. ^{Auch hier} wird als Gebiet S

o der unendlich lange, beidseitig ^drehbar aufliegende ^Plat¬

tenstreifen gewählt, der nun aber um den Winkel 9 gegenüber ^der positiven

x-Achse gedreht ^{ist. Seine Ränder sollen} durch die Punkte (0, 0) ^und (sl _x

l ) ^{laufen und der} Nullpunkt ^{0 des} £, ^n-

y

Systems ^{wird durch die} Bedingung festgelegt, ^{dass der} Lastmittelpunkt ^{auf der} £-Achse liegen ^{soll. Aus der} Fig.

2.7 liest man für die Plattenbreite

a

l .cosip+ j -sin ?

x y (2.43)

ab und weiterhin gelten ^die Beziehungen

Fig. ^2.7

u

m

cos9>

m

sin 9

x y (2.44)

|{c}|

^m _x

^{sin 9}

^m

^cos

y (2.45)

Der Ortsvektor (c> hat damit die Komponenten

{c}

|{c}| ^sin<P

|{c}| ^{cos 9}

(2.46)

und da

.<

9

32

wo-10-^

Fig. ^2.8

ebenfalls bekannt ist, können alle Bestimmungsstücke ^der polygonalen ^{Platte im} System C, ⁿ dargestellt ^werden.

Mit der Abkürzung

nir

a (2.47)

lässt sich die Biegefläche des Plattenstreifens unter der Rechtecklast durch die folgenden einfachen Reihen darstel¬

len:

n

d:

w (5, n)

„

J ~5"

--n(ü) ^c)

^{sin(ci) u)}

^{sin(<- £)}

o

u^

n ' *• n ' *•

n

n n

=

-fc

i,

_, ^.

|

nn

(2.48.1)

•J2

^Ln

^Sh(unn)

⁽²

mnd)Ch((1)nd)|e"ulndl

n

1,2,...

n

d:

w0(5, ⁿ⁾

-^

^

sin(ü)nc)

sin(unu)

sin(<-nO

n n

(2.48.2)

|"(2

ri) Sh(u d)

^d Ch(_. d) 1 e"unn

L ⁿ

^{n n} vnJ

n

1,2,...

Für n

d stimmen die beiden Funktionen überein. Es ist zu

beachten, ^dass (2,48.1) ^und (2.48.2) ^{nur für}

r\->_ ⁰

definiert sind und daher mit | ^ri | gerechnet werden muss. Bei allen ungeraden Ableitungen ^{nach n} (Tab. 2.2) ^{ist aus die¬}

sem Grunde für n

0 das Vorzeichen zu ändern. Der Summen¬

index n wird für die praktische Rechnung ^{durch eine} gewähl¬

te obere Schranke N begrenzt. ^Diese Schranke bestimmt die numerische Genauigkeit ^der inhomogenen Lösung und wird für die Auswertung ^{durch den} Computer ^{etwa mit}

N

50

angenommen. ^Damit ist auch für kleine Belastungsflächen eine praktisch ausreichende Genauigkeit gesichert. ^In Fig. ^{2.8 ist die} Biegefläche ^des Plattenstreifens unter einer Rechtecklast in der Mittellinie mit den Abmessungen

_

a_

^a

10' ^a 20

dargestellt.

INHOMOGENE FUNKTIONEN FÜR GLEICHLAST UND RECHTECKLAST H

LASTFALL

Rechtecklast

i)

rj

FAKTOR

2P aD

2

D "„{(.¦n)

=

1^(f'

-

2-f

a"f ) £—l sin(wnc) sm(<jnu) sin(wn£) {-

[<-„

d) Ch(u)„^)]e","nd}

Z—; sin(cunc) sin(a>nu) sin(<u.£)

[(2

ai„_) Sh(wnd)-üi„d Ch(_.nd)]e~I"n'> -ä-w

df

±{4t>-6ae'

o>) 0

Zrr. sinlwnc) sin(wnu) cos(wn£)

{2*[«ni] Sh(üjn^)-(2*ü)„d) Ch(a)n^)]e""n<i} Zrr-; sin(wnc) sin(wnu) sm(uin£)

[a„v Ch((jn7,)-(1*ai„d) Sh(iun-)]e"a'"d

Z.-7-J sin(u»nc) sin(ü;nu) cos(a>n£)

[(2-<-„-> ShU-ndl-a^d Ch(la„d)]e-'un') Z—; sintwnc) sin(b>nu) sm(uJn£)

[u„d Ch(a)nd)-(1*(un7)) Sh(wnd)]e""'n,' af!"° af

w° _?iw

f-o f

-Zrr» sm(_inc) sin(ojnu) sin(a>n£)

{2*[a>„- Sh(cDn7j)-(2*<u„d) Ch(wn7,)]e-<Jnd } Z.-fi sin(_inc) sm(iunu) cos(<un{)

[a„v Ch(u>„7!)-(1*w„d) SMüi„-)]e'"a,nd r^4 smtwnc) smlainu) sm(cunf) [cun7j Shlwn-)-ii;nd Ch(aJ„^)]e"Wnd

-Z,~rs sin{wnc) sin(wnu} sin(cjnf)

[{2-i-wn-J Sh(cu„d)-<D„d Ch(_v1d)]e-"'i'''' Z77-; sin(<unc) sin(unu) cos(unf) [üj„d Ch&Jndl-d-UnT,) Sh(Wrd)]e-ü'"7' Zrr»

(«und sin(wnu) sin(u„{)

[io„

Shlo^dl-aind Ch(w„d)]e"u,n'' afäW° afdi,'

'

a-jW°

2f-0

0

"Z^-! sin(cii„c) sm(u)nu) cos(un{) {2

[cun- Sh(ur,^)-(2+aind) Ch(_in-)]e~<und} -Zm sin(ü)nc) sin(_.„u) sin(uinf)

[ajn

Ch(<K„_)- (1*_.nd) Sh(ü)„,)]e"und Z77-? sin(ui.c) sinlai.u) coslw.f)

[(jn7,Sh(i.n,)-üjnd Ch{ai„r,)]e'u''i') Z^p sin(u»nc) sin((jnu) sin(o;n£) [(1-a>nd) Sh(_.n~1*uini; Ch(wn7,)]e"wnd

-ZjJ-1 sin(u<nc) sm(cunu) cos(unf) [(2

iun-.) Sh(iii„d)-w„d Chlundlje-^n1) -Z-71 sin(ü)nc)vsin(üjnu) sm(u>„{)

[und Chlwndl-IH-Wni)) Sh(üind)]e-"''',> Z--; sin(c_„c) smlwnu) cos(unf) [_•„•, Sh(iurfJ)-wnd Ch(ü)nd)]e"'""'' Z^-; sm(<_nc) sin(iunu) sin(ainf) [l1-uin~0 Shtond)»cjnd Ch(w„d)]e""'"'''

c) Einzellast P

Im Punkte A der polygonalen ^{Platte der} Fig. 2.9 greife eine Einzellast P an. Das Gebiet S sei durch den Kreis

o

bestimmt, welcher durch die von A weitest entfernte Ecke des umschriebenen Rechtecks geht. ^Das System 5, ⁿ habe seinen Ursprung ^{in A und} gehe ^durch Parallelver¬

schiebung ^{aus dem} x, y-System ^{hervor. Mit 9}

^{0 und}

{c} (2.49)

gilt:

n

y-yA; ^*=_

In Polarkoordina¬

ten r und Q mit

U2

n2)^

(2.50)

are tan

j

hat die Singulari¬

tät einer Einzel¬

last die Form

wo-10

^8-7T-D Po2

— =10 OB Oß 04 02 0 02 04 06 Oß 10

Fig. 2.9

wQ(r) 8irD ^p

^r a

(2.51)

und ist somit rota¬

tions -symmetrisch.

Ihre Werte wurden in Fig. ^{2.9 für}

—

<_ ¹ wiedergegeben«

36

Aus den Beziehungen (2.50) lassen sich unter Beachtung der Kettenregel ^die Transformationsformeln

cose

sine

sine

cose

(2.52)

g'ewinnen und damit können die Ableitungen ^der Singula¬

rität (2.51) berechnet werden. Sie sind in Tabelle 2.3 zusammengestellt. ^Man sieht, dass die Funktion ^w von der zweiten Ableitung ^an im Punkt A singulär ^wird.

d) Singularitäten ^{für 3} _xx w, 3 w, yy

3 w xy

8-T7--D

Differenziert man die Singularität (2.51) ^{nach den Koor¬}

dinaten des Einflusspunktes ^{A und setzt man P}

1, ^so

erhält man die Singularitäten der Einfluss¬

flächen für die

entsprechende Ableitung ^der Biegefläche. ^Aus

den Einflussflä¬

chen für die zweiten Ableitun¬

gen im Punkte A lassen sich dann die Einflussflä¬

chen der Momente nach Gl. (2.4) ^su- perponieren.

Für einen Einfluss¬

punkt ^{A im Innern} polygonalen ^Platte wird das Kreisge¬

biet S wie o

Fig. ^2.10

in Fig. ^{2.9 gewonnen. In} Polarkoordinaten ergeben ^sich folgende Singularitäten (siehe ^{auch Tab.} 2.3):

für 3xxw:

wQ(r,e)

⁽²

tn|

²

^{cos2e) (2.53)}

für 3yyw:

wQ(r,e)

(2_nj

²

^{cos2e) (2.54)}

für 3 ^w:

xy

w0(e)

g^ ^{sin2e (2.55)}

Fig. ^{2.10 stellt die} Singularität (2.54) ^{für 3 w dar} und zeigt deutlich das singulare Verhalten im Einfluss¬

punkt. Obwohl die Ordinaten des Schlauches in A unend¬

lich _gross werden, ^ist sein Volumen endlich.

SPEZIELLE SINGULARITÄTEN LASTFALL Einzellost

Singulontot für

Singulontot für

axdy Singulontot

FAKTOR

8rO

1 4t

D

1

D

1

D «.(-.'¦)

,' l»i i(2ln-i-

2

cos29) ^ sin29 ^(2ln-5-*2-cos28) af w» (2

ln-£- +r)

9 Jj(3 cos9-cos39) l(sin9 -sm39) ^-(cos9*cos39) 2r di,

(2

r)

9 J-(sin9-sm39) J-(cos9_cos39) L{Z Sin9

sin39) d' _f*"»

"

2

2+cos29 4(2 cos29-cos49)

4(sin29-sin49)

49 afa~. "•

2 9 4(sin29-Sin49)

4

49

4(sm29*sin49)

d' di,'

2 ln-5"*2-cos29 4 C0S49

4lsin29-sm48) 4("2 cos29-cos49)

af*

-(3 cos9-cos39>

-V(5 cos39-3cos59) 4(sm39-sin59)

4-(-cos39»3cos59)

•I"(sin9-sin39)

-V(3 sin39-3 Sin59)

-V(-cos39»3cos59)

-T(sm3fl+

3sin59) df--'

—(cos9*cos39)

-1(-cos39+3cos59)

-Llsin39*3 sm58)

•1-1-3 cos39-3 cos58)

1(3 Sin9*sm39)

-y(sin39->-3sin58) ¦^¦(-cosse-cosse) -t(-5sin39-3 sm59)

3. BASISMATRIZEN DES DIFFERENZENVERFAHRENS

3.1 Zweidimensionale Taylorentwicklung

0

*-.h—H

\ /

VW

^s\ (-/

ip

"l

h

"•

1

t y

Fig. ^3.1

Von einer Funktion w(x,y) ^seien

im Punkte 0 (Fig. 3.1) ^{der Funk¬}

tionswert sowie die Werte aller benötigten partiellen Ableitungen bekannt. Macht man durch eine Koordinatentransformation ⁰ zum

Ursprung ^des kartesischen Systems

x, y und führt mit einer Bezugs- grösse ^{h die} nunmehr dimensions¬

losen Koordinaten

=

1 (3.1)

ein,so gilt ^{für den} Funktionswert an der Stelle P(£h; nh)

w(5h; nh)

w|o

^{^ (s}

^{\* 0}

ⁿ

3yw1{))

h2

+

_T («2

3xxw|o

²⁵ⁿ

Vlo

^"

N hn

2

3 W, ) yy \oJ

+ •••' +

RN+1

w|o

_n=l ^{U U}

^{äx M}

V w|o

+

R.

N+l (3.2)

Das Restglied RN+, ^{hat dabei die Form}

rn+i

WiTT <*-\

n-a/wV-h-e^h-n) ⁰

⁰

¹

(3.3) Die Entwicklung (3.2) entspricht ^einer Polynomdarstellung

in £ und n der Funktion ^w dergestalt, ^{dass die ersten N} Ordnungen ^der partiellen Ableitungen ^{von w und des} Poly¬

noms im Entwicklungspunkt ⁰ übereinstimmen. Ein beliebiger Differentialausdruck D (w), wobei D einen zunächst all-

opv op

gemeinen Differntialoperator bezeichnet, ^{lässt sich eben-}

-

40

falls nach (3.2) entwickeln, sofern seine partiellen ^Ab¬

leitungen ^im Nullpunkt ^{bekannt sind. Handelt es sich um} einen linearen Ausdruck mit dem Operator

L

al

Vx

Vy

^Vx*

^Vx(Vn

?V ^(3"4)

und sind zudem die Koeffizienten a. konstant, ^{dann wird} wegen der Linearität ^von (3.2) ^{auch die} Entwicklung ^von

Lw zu einer Linearkombination der Ableitungen ^{von w. Für} das Folgende ^{sollen D und L stets als lineare} Operato¬

ren mit konstanten Koeffizienten vorausgesetzt ^werden.

Während die Voraussetzung der Linearität wesentlich für die dargestellten ^Ansätze ist, kann die Forderung ^nach konstanten Koeffizienten gegebenenfalls fallengelassen werden.

In der Tabelle 3.1 wurde die Entwicklung (3.2) ^{der Funk¬}

tion w sowie des Ausdruckes AAw schematisch dargestellt.

Weiterhin sind in den letzten drei Kolonnen die Darstel¬

lungen ^von Lw,M

D(3 ^w

v3 w) ^{und AAw} jeweils ^für

den Nullpunkt wiedergegeben. ^{Die Terme} sind nach den Ab¬

leitungen ^{von w in 0} geordnet ^{und mit einer Nummer k ver¬}

sehen. Da diese Ableitungen ^{natürlich für alle} dargestell¬

ten Ausdrücke den gleichen ^Wert besitzen, ^{wurden sie in} Kolonne 3 aus dem Schema herausgezogen. ^{Zwischen der Ord¬}

nung ⁹ eines Termes und seiner Nummer k besteht die Be¬

ziehung

9

ent k/8

^k

⁷

1) (3.5)

wobei unter ent(a) ^die grösste ganze Zahl verstanden wird,

welche £ ^{a ist. Aus der} Ordnung ^{9 errechnet sich die Num¬}

mer k

des ersten und k _e des letzten zu 9 gehörenden ^Ter-

mes aus

9 k Faktor w(f h,i) ^hl AAw((

t; h) L« M«to AA«to

0 1 "lo ^{1 1 °1}

2 «x-lo ** ^{f °2}

3 ay"k> f" ^{V "5}

4 a«"lo 2Th' ^{C 04 -0}

2 5 a*y"io f* iv °s

6 dyy"io ihr ¹

⁰⁶

^D

7 ¦»>..*,„ ** ^{V <=7}

3 8

9

a«y "io d»y»"io

Vv ^oe

"s

10 ayyy"io -T*" ^{V °io}

11 ¦'»'"lo ^{€' 1 1 011 1}

12 d »sy"io fi

4 13 a »V",0 (7

-V ^{1 2}

²

14 a »y'"io

^0,

«V

15 d /»lo

4

1

1

16

io

f TT

f

17 a «V"l0 -'l TT

7

5 18

19

a «V«,,

a «V",o

8*

1=0, s

2 T7h

2 TTh f

1

20 a "/"lo fV ?V

^f

21 a/"io v' Tfh 1

22 a«*"io

• • • • • • • •

• • • • • • • • •

Tab. 3.1