Berechnung gewölbter Platten

Research Collection

Doctoral Thesis

Berechnung gewölbter Platten

Author(s):

Keller, Huldreich Publication Date:

1912

Permanent Link:

https://doi.org/10.3929/ethz-a-000091960

Rights / License:

In Copyright - Non-Commercial Use Permitted

This page was generated automatically upon download from the ETH Zurich Research Collection. For more information please consult the Terms of use.

ETH Library

Berechnung gewölbter ^Platten.

Von der

Eidgenössischen Technisehen Hochschule in Zürich

zur

Erlangung

^der

Würde eines Doktors der technischen Wissenschaften

genehmigte

Promotionsarbeit

vorgelegt

^von

Huldreich Keller, £ipl..3itg.

aus Arbon (Schweiz).

Referent: Herr Professor Dr. E. Meissner.

Korreferent: Herr Professor Dr. A. Stodola.

Berlin 1012.

Der Verfasser

vorliegender

Arbeit wurde

geboren

am 16. März 1868 in A^rbon amBodensee. Ich besuchte während sechs Jahren die Primär- und sodann während drei Jahren die Sekundärschule meines Geburtsortes und im Anschluss daran dreieinhalb Jahre hindurch die technische

Abteilung

der

thurgauischen Kantonsschule

ⁱⁿ Frauenfeld.

Alsdann machte ich drei Jahre

Werkstattpraxis

teils in den Werkstätten meines

Vaters,

teils in den Maschinen^-Fabriken von Baum und von S^{a u r}er in Arbon.

Vom Oktober 1889 bis März 1893 besuchte ich die mech. technische Ab¬

teilung

des

eidgenössischen Polytechnikums

^{in Zürich und erhielt daselbst}

zum Schluss das

Diplom

^eines

Maschineningenieurs.

Während des darauf¬

folgenden

^{Jahres war es mir} vergönnt, ^eine Assistentenstelle bei Herrn Pro¬

fessor Stodola einzunehmen. Sodann bekleidete ich die Stelle eines

Kon¬

struktionsingenieurs

ⁱⁿ der

Dampfmaschinen-Abteilung

^{von Escher}

^Wyss

^&

Cie. in Zürich. Im Sommer-Semester 1895 ^war ich aushilfsweise als Lehrer

am Technikum Winterthur

verpflichtet.

Vom Herbst 1896 bis Ende 1908 war ich bei der AEQ Berlin engagiert undzwar etwa sieben Jahre

lang

^{in der} Maschinenfabrik Brunnenstrasse und fünf Jahre

lang

ⁱⁿ der

neugegründeten

Turbinenfabrik Huttenstrasse. An beiden Orten ^war mir insbesondere das mechanische Laboratorium unter¬

stellt. Zu Ende 1908 kehrte ich wieder zu Escher

Wyss

& Cie. in Zürich

zurück,

^wo ich seither dem Literarischen und dem Patentbureau vorstehe.

Berechnung gewölbter ^Platten.

Von

Ingenieur

^Huldreich Keller in Zürich.

Durch

vorliegende

^{Arbeit soll der}

Weg gezeigt

^{werden für eine annähe¬}

rungsweise Berechnung

^von

gewölbten

^Platten. Er ist ähnlieh

demjenigen,

^den

icli einer früheren Arbeit über die

Berechnung

^von umlaufenden Radscheiben

zugrunde gelegt habe1).

^Das

Hauptkennzeichen

^dieses

Rechnungsverfahrens liegt darin,

^{daß man die}

Differentialgleichungen,

^{auf die man}

gelangt,

^durch

das

annäherungsweise

»Rechnen mit kleinen Differenzen« löst.

Unsere neue

Aufgabe

ist aber wesentlich

umfangreicher,

^als die Berech¬

nung ^von

Radscheiben,

^{weil zu den}

Normalspannungen

ⁱⁿ radialer und tangen¬

tialer

Richtung,

^{wie sie in}Radscheiben fast allein vorkommen, ^{in einer}

einseitig

belasteten,

gewölbten

^Platte noch Schub- und

Biegungsspannungen

hinzutreten.

Der Zweck

vorliegender

^Arbeit soll insbesondere auch darin

bestehen,

^die

teils ziemlich verwickelten Formelnin eine

möglichst

^{einfache Form zu}

^bringen,

wie sie für ein am Konstruktionstisch

gefordertes,

hinreichend

zuverlässiges

Rechnen brauchbar ist, ^das nicht allzusehr ermüdet.

Die

Berechnung

^{soll die}

Möglichkeit

schaffen, ^{in einer als}

Drehkörper durchgebildeten, gewölbten (oder ebenen)

^{Platte, welche von} einer Seite durch einen Gas- oder

Flüssigkeitsdruck

^belastet

^ist,

ⁱⁿ

^jedem

^{Punkt die Bean¬}

spruchung

^unddie

Formänderung

^{zuermitteln. Eskommen}also Platen in

Frage,

wie sie als Deckel undZwischenböden in

Dampfturbinen,

^{als Böden von}

Dampf¬

kesseln oder andern

Hochdruckgefäßen Verwendung

^linden.

Das Verfahren setzt voraus, daß die Dicke der Platte im Verhältnis zum

Krümmungshalbmesser

^{des Meridians}

klein,

^der Stoff durchaus

homogen

^und daß

jede

^schroffe

Querschnittänderung

vermieden sei. Ferner soll die Form¬

änderung entsprechend

der für den

gebogenen

^Balken

aufgestellten

^Bernoulli-

schen Annahme derart ^vor sich

gehen,

^{daß alle Punkte der}

Platte,

^{welche voi¬}

der

Biegung

^{auf einer zur}

Plattenwölbung

senkrechten Geraden

lagen,

^auch nach der

Durchbiegung

auf einer Geraden

liegen,

^die senkrecht steht zur Mittel¬

fläche2).

In die

Rechnung

^{führen wir}

folgende,

^aus

Fig.

ⁱ ersichtliche Bezeich¬

nungen ein:

') Siehe »Schweizerische Bauzeitung-< ^vom 27. ^November 1909 ^S. 307 ^{und »nie Turbine«}

vom 5. ^Dezember 1909 ^S. 88.

2) ^{Dies trifft für} gußeiserne gewölbte ^{Platten nur} annäherungsweise ^zu. Ver^I. Bach,

»Elastizität und Festigkeit« 1902 ^S. 5°4 ^{u.f. über} »gekrümmte, stahförmige Körper«.

Diss. Keller. 1

4 ^—

x in cm Abstand des auf der Meridian-Mittelfaser JA\

gelegenen

^{zu unter¬}

suchenden Punktes A von der

Symmetrieachse

^z—z der Platte.

h in cm Dicke der Platte beim Punkt A.

y in cm Abstand eines auf dem durch A

gehenden Krümmungshalbmesser

^des

Meridians

gelegenen

^{Punktes C von A.}

(* in cm

Krümmungshalbmesser

der Meridian-Mittelfaser im Punkt A.

<p Winkel zwischen diesem

Krümmungshalbmesser

^{und der}

Symmetrieachse.

Jcp

⁼V

Aenderung

^dieses Winkels _{cp bei} der

Durchbiegung.

J

(dq)

⁼dip

Aenderung

^des Winkelelementes dy.

m = ^- *-*

spezifische Aenderung

^des Winkelelementes.

dcp

p in

kg/qcm

^der

gleichmäßig verteilte, einseitige Ueberdruck,

winkelrecht auf die Platte wirkend. Für eine

Einzelbelastung

^{P wären}

diejenigen

^Glieder

der

Eechnung,

ⁱⁿ denen sonst p

vorkommt, sinngemäß

^{zu ändern. Ein}

Gleiches

gilt

^{für ein} Zusammenwirken einer

gleichmäßig

^{verteilten Be}

lastung

^{p und} einer Einzellast P.

ff, in

kg/qcm

^die

Normalspannung

in einem den Punkt C enthaltenden Flächen¬

element,

^{das auf} dem durch den Punkt A oder C senkrecht zur Platten¬

wölbung geführten Kegel liegt,

^dessen

Symmetrieachse

^mit

derjenigen

^der

Platte zusammenfällt. <yr ist

gleich gerichtet

wie die Meridian-Mittelfaser.

Der

Hauptsache

^nach verläuft sie

»radial«;

^ihr Wert sei deshalb abkür¬

zungshalber

^mit

»Radialspannung«

^bezeichnet —, dies in

Anlehnung

^an

die

Scheibenberechnung.

<rt in

kg/qcm

^die

Normalspannung (Hauptspannung)

^im

Meridianschnitt;

^{sie ver¬}

läuft

tangential

^zum Parallelkreis und soll deshalb

»Tangentialspannung«

heißen.

t in

kg/qcm

^die

Schubspannung

^{in dem}

Flächenelement,

auf welches <r, winkel¬

recht wirkt.

E in

kg/qcm

^der Elastizitätsmodul des Plattenstoffes.

In

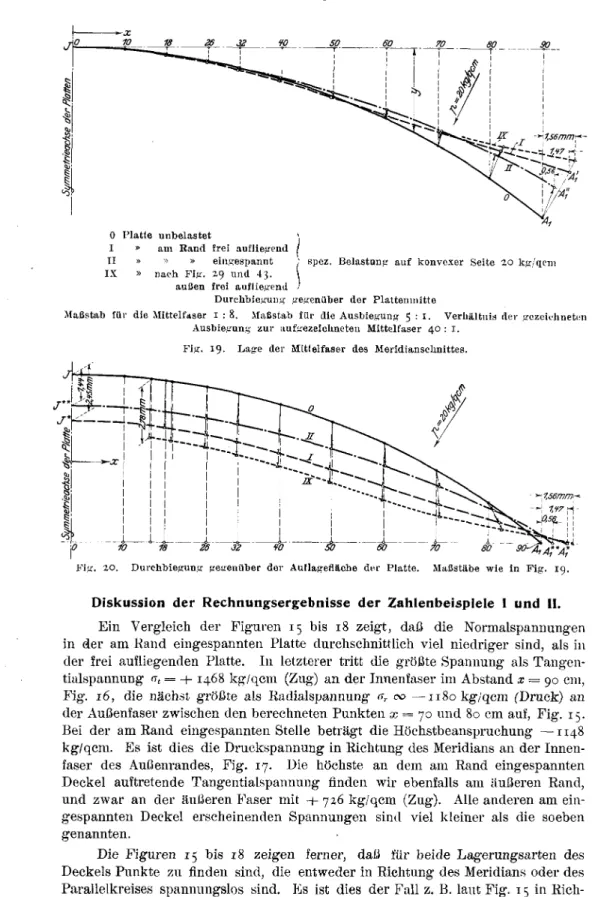
Fig.

ⁱ ist ein Meridianschnitt durch einen von der konkaven

Seite,

also im

positiven

^{Sinn mit der}

spezifischen Pressung

p belasteten Deckel

gezeichnet.

Durch diese

Belastung

p erfährt ein im Abstand ^xvon der

Symmetrieachse

^z—z

gelegenes

Element derimMeridianschnitt

liegenden

Mittelfaser in

Richtung

^dieser

Faser die

spezifische Verlängerung

fr0, ein im Abstand ₁₇ von der Mittelfaserlie¬

gendes, parallel

^{zu ersterem}

gerichtetes

Faserteilchen die

spezifische Verlänge¬

rung ^sr. Diese

Verlängerungen

^werden

bedingt

^{.durch die an diesen Stellen}

herrschenden

Radialspannungen

^{<s,ain der}Mittelfaser undarim Abstand_*/ hiervon und den

Tangentialspannungen

^{am und o,.}

1) Berechnung

^der

spezifischen Verlängerung

^sr.

Die oben

gemachte

Annahme, ^{daß die} Plattendicke

gering

sei im Verhältnis

zum

Krümmungshalbmesser

^des

Meridianschnittes,

^{hat zur}

Folge,

^daß die spe¬

zifischen

Dehnungen

der Meridianfasern in einem linearen Verhältnis ^zu ihrem Abstand _j? von der Mittelfaser angenommen ^werden

können, gleich

^{wie in einem}

gekrümmten

Balken1) ,

fr⁼iro -t-

(«I

^—

^tro)

^"

Um die

Rechnung

^zu vereinfachen und dadurch den

praktischen

^Bedürf¬

nissen anzupassen, wollen wir verschiedene

Annäherungen

^{zulassen. Weil die} Dicke h der Platte im Verhältnis ^zum

Krümmungshalbmesser

^<<

gering

^sein soll, dürfen wir setzen:

n ^~q;

(-7)

^{CO I.}

Hierdurch vereinfacht sich die

Gleichung

^{für fr auf}

m^•

?

(1).

2) Berechnung

^der

spezifischen

Verlängerung ^{e, im} Parallelkreis

vom Halbmesser

I

und dem Absfand // ^von der Mittelfaser.

In

Fig.

^{2 ist im}

vergrößerten

^Maße

dargestellt,

^{wie der} Meridianschnittaus seiner

anfänglichen Lage

^{AB bei der}

Belastung

^{in die}

Lage

AB' verschoben wird. Dabei

vergrößern

^{sich die Halbmesser der}

durch den

Mittenpunkt

^{A und den im Abstand} //

davon

gelegenen

^{Punkt C}

gehenden

Parallelkreise

von den

Anfangswerten

^{x und S auf die Endwerte}

(x

+

Jx)

^und

(I-4--/S).

^{Hierbei erfährt der durch}

den Punkt C

gehende

Parallelkreis eine

spezifische Dehnung

Nun ist

gemäß Fig.

²

?

⁼je+»/ sin ^<r.

Durch Differenzieren dieser

Gleichung

^erhält

man für die Zunahme von

|

den Ausdruck

^/|

⁼Ax-+-

Jq sing-)-//

^cos <>>

Jq>.

') Vergl. Bach, »Elastizitats- und Festigkeitslehre« 1902 ^s. 47a

— fi ^—

We^en

^{der Kleinheit von} ', und der daraus

folgenden

^{Kleinheit von}

-///

wird auf der rechten Seite der zweite Summand

gegenüber

^{den beiden ande¬}

ren Summanden

vernachlässigt,

^{und es} bleibt noch

à%

^=Jx-t- ;/

A<f

^cosq.

Diesen Wert

eingesetzt

^{in die}

Gleichung

^{«, = —*} ,

gibt

JX+7]/iwcosa x+7] sin(p

Mit hinreichender

Annäherung

^{kann man setzen x}-t-r/ sin q> ^oox; ferner ist -x=4(o, ^wo im die

spezifische Dehnung

des durch den Punkt A, d. h. im

X

Abstand _r\⁼o von derMittelfaser gezogenen Pararallelkreises ist. Dadurch ver¬

einfacht sich der Ausdruck für _e, auf die Form:

« e,⁼£,D+ ^v

Jcp

cosg;

(2).

X

Hierin ist aber

vorläufig

^weder e,a noch

Jq>

bekannt.

3) Berechnung

^{der im Punkt 0} herrschenden

Radialspannung

«t, und

Tangentialspannung

^at.

Die

Elastizitätslehre1) gibt

zwischen den

Spannungen

^{und den}

Dehnungen

die

Beziehungen

^:

mE _{|- -,} mE _{r -,}

<Tr⁼ -=_ma [m Sr+*lj ! «I⁼ -5 L*V + ^mS,],

—I m*^—I

wo m das Verhältnisder

spezifischen Längsdehnung

^{zur linearen}

Querzusanmien- ziehung

eines auf reinen

Zug beanspruchten

^Stabes

bedeutet'-').

Wir setzen

mE m'—\

Unter

Verwendung

^{der Gl.}

(1)

^und

(2)

^{erhalten wir}

ov⁼ c m fni + ^{m w—} + e, Jq>^cosqp

1 V 1 ~\

fr0 -+- « ^—+ wf«> + ^»*—^/q) ^{cos« .}

? ^» J

Setzen wir in diesen beiden

Gleichungen

rt ⁼ o, ^so erhalten wir als Sonderfälle die

Normalspannungen

^{im Abstand x von} der

Symmetrieachse

^und

in der

jeweiligen

Mittelfaser des Meridianschnittes und des Parallelkreis¬

schnittes:

Gm ⁼ c

[m

^{er0 -+-}

s»]

<r,o ⁼c

[sr(t

^-+-m

e,o]

^.

Berücksichtigt

^man

ferner,

^daß

Jdp ^{to Adir} A^dw

, dx . . .

w ^— ; ^{— = —' = r}; ^{ds =} ; /Jclcp ^~ dty ,

dep (t (i#95 ^{<is cos}y>

so

gehen

^die

Gleichungen

^{für cr und <r, über in die Form}

ar ⁼ 0,o +^c// ^cosi

ff< ⁼ o-10 + cj/^cosqp ^{—^} 4- ^w

<p\ ^m—21

(3).

(4)-

') ^s. Füppls »Festigkeitslehre« Band III 1909 ^S.246.

) /,. B. für Stahl in co ">l3; ^KU-Gußeisen: m⁼ 5 ^bis 9.

— 7 ^—

Setzen wir in diesen beiden

Gleichungen

^als Sonderwerte ïiir _// die Grenz¬

werte-

(± j ^ein,

^{so erhalten wir die}

^Spannungen

^{ar und <st in den Außen-}

und Innenfasern der Platte.

Um nun für

jeden

^{Punkt der Platte die Werte <sr und a, berechnen zu}

können,

^{wollen wir vorerst für Uro, da und \p}

Beziehungen

aufstellen.

4) ^Berechnung

^{von <r,fl unter}

Vermittlung

^der

Qleichgewichtsbedingung

der am Plattenelement

angreifenden

^Kräfte.

Wir denken uns

gemäß Fig.

3 im Abstand^{x von} der

Symmetrieachse

^aus

der Platte ihrer ganzen Höhe nach ein Element in

Eichtung

^desMeridians und des Parallelkreises von vorerst unendlich

kleinen

Grundriß-Abmessungen herausge¬

schnitten. Die vier Schnittflächen sollen alle senkrecht stehen zu den Meridian- und Parallelkreis-Mittelfasern ^des Elemen¬

tes. Zwei dieser Schnittflächen sollen Ebenen

sein,

^{durch die}

Symmetrieachse gehen

^{und unter sieh den Winkelda ein¬}

schließen. Winkelrecht auf dievonihnen

gebildeten

Seitenflächen GCDH und ^EFK1 des Plattenelementes ^wirken die

Tangen- tialspannnngen

^{<rt im Abstand 11 von der} mittleren Meridianfaser und ff,,, in der Mittelfaser selbst, ^{und diese haben die}

Pachtung

^der

Tangenten

^{an die}

bezüg¬

lichen Parallelkreise. Die auf diese bei¬

den Seitenflächen wirkenden Resultieren¬

den seien T, welche ebenfalls den Win¬

kel da miteinander einschließen.

Die beiden anderen Schnittflächen ^{für das} Plattenelement, ^{nämlich CDEF} und GHIK, ^sind

eigentlich Kegelflächen,

^dürfen ihrer Kleinheit wegen

jedoch

als Ebenen betrachtet werden. Sie schließen unter sich den Winkel dq> ^und mit der

Symmetrieachse

^{2—z die Winkel} <j> und

(qp

^{+dq>) ein. Die in diesen}

Flächen herrschenden

Normalspannungen

^seien a, und

(ff, +-dar)

im Abstand _r\

vom mittleren Parallelkreis sowie ar0 und

(<x„,

+-

da*,)

in den mittleren Parallel¬

kreisen selbst. Sie

ergeben

^{die auf die} ganzen Flächen wirkenden Resultieren¬

den S und

(S

+

dS).

In den beiden zuletztbetrachteten Schnittflächen wirkenaußer denNormal- spannungen noch

Schubspannangen

^{r und}

(r

⁺

dr).

welche die Resultierenden Seh und

(Seh

^-+-

dSch)

erzeugen. ^{Es sei}

gleich

^{an dieser Stelle}

hervorgehoben,

daß diese in

Richtung

^des

Krümmungshalbmessers

^wirkenden

Schubspannungen

in der Mitte der Flächen einen Höchstwert t0, am Rand der Flächen, ^{z. B. au} den Kanten CF und DE

jedoch

^{den Wert o haben. Ihr Mittelwert t„ tritt} also nicht in der

wagerechten

Mittellinie derSeitenfläche

CDEFnuî,

^{doch wollen}

wir dies nicht weiter

verfolgen,

^{da sieh dieser Wert aus der}

Rechnung

ganz eliminieren läßt.

Weil die Seitenflächen nicht

(Quadrate

^sondern

trapezähnliche

^Flächen

sind,

^{so sind die} in ihnen wirkenden mittleren

Normalspannungen

^{arm und <sim}

auch

nicht genau

gleich

^den

in den Mvttelîasern herrschenden Spannungen

^{a^}

— 8 ^-

und <rlf>; doch ist der Unterschied ^so

klein,

^{daß man} davon absehen

darf,

ohne einen

unzulässigen

^{Fehler zu}

begehen.

Die Größen der auf die Seitenflächen des Plattenelementes wirkenden Re¬

sultierenden

ergeben

^sich als Produkte aus den Flächen und den in ihnen wirkenden mittleren

Spannungen.

Wir können für sie

folgende Aufstellung

^machen:

FläÄie CDEF⁼xda h;

CDEF⁼x da h;

mittl. Spannung (Tr0

(normal);

rm

(Schub);

<rR1

(normal);

P

Resultierende S⁼

(xh)<Jro

^da Seh ⁼

(xh)Tm

^da

T=ds h<t,„ ^{= —} hc,o COSf

„ dx I dx\

P=» ^-- [x H I du, eosip ^{\ z}J

(5) (6) (7)

(8).

CDHG =FEIK⁼

dsh;

DEIH⁼

(x+ y) ^(Uds'>

I dx\ ^dx ,

= ceH 1 a a

\ 1 ' COSip

(Im

Ausdruck für P werden wir ^—_%

gegenüber

^{x nicht}

vernachlässigen

^mit

Rücksicht auf die später

durchgeführte Rechnung

^mit endlich kleinen Diffe¬

renzen statt unendlich kleinen

Differentialen,

weil sonst bei kleinem cc der Fehler zu

groß würde.)

An Hand von

Fig.

^{4, d. i. der} Seitenansicht des

Plattenelementes,

^kann

man für dieses Element

folgende Gleichgewichtsbedingung

^{für die an ihm wir¬}

kenden Kräfte aufstellen: Wir

vergleichen

^{die in}

Richtung

^der Normalkraft

iß

^-+-

dS)

^fallenden

Komponenten:

S-4-dS⁼Scosdq -+- Sehsindq 4-

Psin^

-+- 2 2"

cos(<f)

^-+-

dq).

Berücksichtigt

^{man wiederum, daß}

^dqp

^sehr klein, ^{so daß cos}dq ^{00 1}

sind'i

^os

dq, eos(<r

-f-

dq)

^oocosqr, ^so bleibt

dw

tf#⁼

Schdcp

+ P^-+² 7"cos7-

Fig. 4.

Hierin ist T' die in

Richtung

^des Halbmessers^x fallende

Komponente

^von T

Nach Gl.

(5)

^ist

folglich

T ⁼ Tsin

y ^°e T~;

(vergl. Fig. 5).

S⁼

(xh)n,o du,

dS⁼

[(xti)

^{ddr» -+- dm}

d(xh)1

^da.

— 9 ^—

Unter

Verwendung

^{der 61.}

(6)

^bis

(8)

^{erhält man nach}

Kürzung

^des

Faktors da:

dx\ dtp

a

/ a

h _ffiocos w .

(o).

cosy

(xh)

^d(Tr0 -+- <t,o

d(xh)

⁼

Tm(xh)dq

^-+-p^—-

(x

+- ^- ) cos; \

a /

Fig.

⁶

zeigt

^die

Möglichkeit,

^{die mittlere}

Schubspannung

^{rm durch die}

Normalspannung

^{al0 und die äußere}

Belastung

p ^,

auszudrücken und sie hierdurch ^aus der

Rechnung

zu eliminieren.

Um die

Rechnung

^nach

Möglichkeit

^{zu verall¬}

gemeinern,

wollen wir eine

gewölbte

^{Platte betrach¬}

ten, welche in der^{Mitte eine}

gleichachsige Bohrung

vom Halbmesserasä hat. Aus dieser Platte schneiden wir ein

Ringteil

^{mit dem äußeren Halbmesser x} und dem Zentriwinkel da heraus. Dieser

Ringaus¬

schnitt ist in

Fig.

^{6 in der} Seitenansicht

dargestellt.

Aus ihr lassen sich

folgende Beziehungen

^ablesen:

(cc2

^—

£C(2)

ⁿ

(—)

p^=xdu.

h(rm

cos'j + ara

sinqp)

/ i\ 2> /a-'2—

av\ / i\Slnœ

(xh)^{7m =J-} l ^— (xh) ar0

1 \ cos'/ ^' cosy

Die rechte Seite dieser

Gleichung

^{werde in 61.}

(9) eingesetzt:

(10).

(xh)

d^r0 -+ <Trt

d(xh)

Hieraus finden wir:

(as2

^—

xr)

^dx pcos'y

—

(xh)

^0,0

siny

(jcos-y P dx l dx\dx\ , »

, las -4- -) -H hdx(7I0.

a ocos'tf V ^a/

dOra⁼

— 0"k| d(xli)

xh dx

Slll(/' dx

dx

I.

,

Haupt- [ gleichung.

, p ¹ dx r ., , , /

i ^{—-- -} \x- ^—.v,- -+- dxla _

1 (xh)OQOS'cpL ^{\ a}

Diese I.

Hauptgleichung

^{hat die Form:}

d<rrU ^{= -} a,0

(15)

^-t-

r,0(i6)

+

(24) (ia),

wo die

Ziffern

ⁱⁿ

()

Zahlenwerte

bedeuten,

^die

abhängig

^{sind von der Form}

und der äußeren

Belastung

^{der Platte und der}

Lage

^des

augenblicklich

^zu

untersuchenden ^{Punktes A} auf der Mittelfaser des Meridianschnittes.

Würde man für den Halbmesser x die mittlere

Radialspannung

^{f!^,xkennen,}

so lieferte die

Hauptgleichung (I)

^{den Wert für die mittlere}

Radialspannung

ffro(x⁺d*) im Halbmesser

(x-\-dx)

O\0(x⁺dl) ^=OrlX-+-d(T,0

(11).

5) Berechnung

^von ^,0,

hergeleitet

^{aus der Dehnung} der Platte.

Der Parallelkreis mit dem Halbmesser x, der die

gestreckte Länge (%nx)

hat, ^{dehnt sich um das Stück}

J(znx),

^{wenn in}

Richtung

^der

Tangente

^die

spezifische Spannung

^{al0, senkrecht dazu die}

^Spannung

^a,0

wirkt,

^{und zwar ist;}

Or0\

., N 11XX I Oro\

— 10 ^—

danach

//as=^—I ffio

EE \ ml

Die

Differenzierung

^dieser

Gleichung

liefert die

Dehnung

^des Halbmesser- elementcs

(dx)

à

(dx)

^{= **-}

U0

^-

^-*»)

+

-

(dai0

^{_ ^>°}

)

. . . .

(I2).

.E \ mI E \ ml

Für diese

Dehnung

können wir noch einen zweiten Ausdruck aufstellen:

Wir denken uns

gemäß Fig.

7 ^aus der mittleren Meridianfaser im Abstand x von der

Symmetrieachse

^{bei A ein Element von der}

Länge

^{AD= ds}

herausgegriffen.

Weil

*

dx ⁼dscos<f,

so ist auch die durch die

Belastung erfolgte Aenderung

^von

dx,

^{das ist:}

J

(dx)

^{= J}

(ds

^cos

i))

= d

(ds)

^cos(ji^{-+- rf,v à}

(cos <j/).

J{d*)=d'U0- «*-) ^(13),

//(cosi/)^

^—

sin«j)^qp

⁼

—sinij-if (14),

à

(dx)

^{= *}

((T,o

^—

"'"-)

^cos<y ^—rf.v sina>.«j

£ V m /

J(dx)

⁼

a'(<fH)-"0)-tlxtgq.i(> _(15).

E \ m I

Die

Aenderung

^von

(dx)

^{ist das}

Ergebnis

^zweier

Formänderungen,

^näm¬

lich der

l.ängenänderung

^{und der}

Kichtungsänderung

des Meridian-Elementes ds.

Durcli Gleichsetzen der rechten Seiten der Gl.

(12)

^und

(15)

^{erhalten wir}

Nun ist

demnach

dj- / <7,o\ /• / dtr.o \ ^{dx /}

E \ ml E \ ml E \

«"10

dx V

tgrjr.

Es werden beide Seiten dieser

Gleichung

^{mit -}

multipliziert

^unddie Klam-

mern

aufgelöst:

dr dx <t,q da,a dj;

<Tio ^— +d_ff,o = ^—ff,o

Daraus finden wir

dal0⁼

(ff,o

^-

ff») (1

^+-1

)

^{"'' -K}tg<r^--xp+ d,r"' Diese

Gleichung

^{hat die Form:}

da«⁼

(ff,o

^-

«i») (17)

^- V

(27)

^{-+- -—}

— —K ^Wtg</.

x m x T ö '

II.

Haupl- gleichung

^'

(IIa).

Für die nur durch Fliehkräfte

beanspruchte

umlaufende Scheibe fand ich in meiner

diesbezüglichen, eingangs

erwähnten Arbeit die Ausdrücke

(in

^die

hier

gewählte Bezeichnungsweise übersetzt):

d(J,0^=-—(T,<)

(...)+

(T,o

(...)

+

( ),

7 / \ / ^I \ dx d(T,o

(l<f«,⁼(a,o—ffio) ¹ -+- +

\ ^m' T n

- 11 ^-

Der Aufbau der Formel ^für dar0 ist genau ^der

gleiche

^wie

derjenige

^der

hier

gefundenen

^Formel

(I)

^{für die}Platte, ^{nur daß natürlich für die}

(....)

^Aus¬

drücke andere Werte in

Frage

^{kommen. Zu der}

Gleichung

für da«, kommt laut Gl.

(IIa)

^{für die Platte}

gegenüber derjenigen

^{für die umlaufende Scheibe}

nur noch der Summand ^—y

(27)

^hinzu. Es ist also

möglich,

^beide

Rechnungen

miteinander zu

vereinigen,

wodurch das Mittel ^{an die}Hand

gegeben ^wird,

^eine

umlaufende Scheibe zu

berechnen,

die außer durch Fliehkräfte auch noch durch einen

einseitig wirkenden, gleichmäßig

^{verteilten Druck p} belastet wird. Der¬

artige

^{Fälle kommen vor in}

Eeaktions-,

^{seltener auch in}

Aktionsdampfturbinen.

Unter der

vorläufig

noch unzutreffenden

Annahme,

^{man kenne von der} Platte für den Halbmesserx die mittlere

Tangentialspannung

^{<r!(H, liefert}

^Haupt¬

gleichung (II)

^{den Wert für die mittlere}

Tangentialspannung

^{im Halbmesser}

(x-hdx),

^{indem man die}

Gleichung

^aufstellt:

x+ dr

GtO(x+dx) ^{= ö,oi -+-} d(7io

(l6).

6)

Berechnung ^{von v} und if> ^unter

Benutzung

der Momenten-

gleichung.

Wir stellen zu diesem Zwecke für das in

Fig.

3 axonometrisch

dargestellte Körperelement

^{CDEFGHIK die}

Momentengleichung

^{auf. Als} Momentenachse

greifen

^{wir die Achse 0—0 heraus, welche im Abstand (x-+-}

dx)

^{von der}

Sym¬

metrieachse z—z und senkrecht zu ihrer

Hichtung

mitten durch die äußere Be¬

grenzungsfläche

^{GHIK des} Plattenelementes läuft. Bei

Gleichgewicht

^{muß die}

Summe der Momente aller äußeren Kräfte,

bezogen

^{auf die Achse} 0—0,

gleich

null sein.

An dem Plattenelement wirken

folgende

^{äußere Kräfte auf}

^Verdrehung

um die Achse 0—0:

a)

^{auf die der}

Symmetrieachse zugekehrte Begrenzungsfläche

^CDEF:

Die

Normalspannungen,

^deren

Wirkung

^{ersetzt werden kann:}

1)

durch eine im

Mittelpunkt

^derFläche

angreifende

EinzelkraftS~x du hr>,0 wirkend am Hebelarm dasin

(dq).

2)

^{ein Moment} »3f,,_«, auf welches später

einzugehen

^ist.

3)

^{die Schubkraft Sch=xdahr,» am Hebelarm d.scos}

(dqp).

1))

^Auf die beiden Seitenflächen GCDH und EFK1 wirken

Normalspannungen,

deren Einfluß ersetzt werden kann:

1)

durch die Xormalkraft Too dsho„.

Von ihr kommt als drehend um die Achse o^—o nur die

Kompo¬

nente 2"⁼

TSin-"

^oa t^— in Betracht

(vergl. Fig. 5).

^{Die beiden anderen}

Komponenten

^{T''=Tcoa—— verlaufen}

parallel

^{zur Achse 0 — 0 und}

ergeben

daher kein Drehmoment

(vergl. Fig.

5 ^und

Fig. 3).

^{Die beiden}

Komponenten

^T wirken

je

^{am Hebelarm * sin}

(qr

^-+-

dqp)

^{ex> —}sin qp

(siehe Fig. 4).

2)

^{durch das} Moment »Jfj,« ^der

Spannungen

<r,, auf welches wir später zurückkommen.

c)

^{Normal zur unteren}

Begrenzungsfläche

^{HDVA und in die Mitte derselben}

konzentriert gedacht, wirkt die Kraft

^P=

(x

+^—

\da _dsp

am Hebelarm ^d*

— 12 ^—

[Auch

^{hier wollen}wir mit Rücksicht auf die

spätere Rechnung

mit kleinen Diffe¬

renzen statt Differentialen von einer

Vernachlässigung

^{des Wertes}

—absehen.]

Alle dieunter a, b und^cgenannten ^Momenteversuchen, ^dasPlattenelement im einen oder anderen Sinn um die _{Achse o—o,}

Fig.

3, ^zu drehen. Es kann in seiner

Lage,

^{d. h. im}

Gleichgewicht,

^{nur dadurch}

gehalten werden,

^{daß auf} die äußere

Begrenzungsfläche

^{GHIK das bisher noch nicht}

berücksichtigte

Moment

Ma<

+jar

wirkt,

^welches

gleich

^{ist der}

algebraischen

^Summe

jener

^vor¬

genannten Spannungsmomente

^und

entgegengesetztes

^{Vorzeichen hierzu hat.}

Wir wollen

jene

^{Momente zuerst nach der}

Größe,

^{sodann nach demVorzeichen} bestimmen:

dx

Zu a

1)

Nunist

Ms⁼S du sin

(d

(j

)

^{osS-^^} dw.

cosy

ds dx

(> QQOSCp

'

Ms⁼da

(xh)

^{<rrt das*}

(>cos"y>

Zu a

3)

^{Msch=Schdscos(d}

qp)

^{00Seh ds.}

Aus Gl.

(10)

finden wir für Sch⁼

(xJi)Tmda

p

(x-'-x,2)

(17).

Seh-.

MSch⁼du

cosy dx

n-j

^—

(xh)

^an

tg

cp

da(xh)OroSm

f

(18).

coa'9P cos"9"

Zu a

2)

^In

Fig.

^{8 ist das}Plattenelement in

gleicher

^Weise

dargestellt,

^wie in

Fig.

3, und ^{es sind an dem} einen Rand der inneren

Begrenzungsfläche

^CDEF

in einem

gewissen

Maßstab die

Spannungen

^<r, der Größe und

Richtung

^nach

aufgetragen.

^In

der Mitte derKanteEF herrscht die

Spannung

ovo, im Abstand_>] von derMitte die

Spannung

^or.

Sie darf über dem

gestrichelten

Flächenstreifen

von derHöhe

dy

^{und der}

angenäherten

^Breite

xdu als unveränderlich angenommen werden.

DasMoment der

Spannungsdifferenzen (nr

^—ovo), welchesauf die

Begrenzungsfläche

^{CD EF}

^wirkt,

und welches wir

abkürzungsweise

^{mit M,} die aus der

Fig. 8. _Cr

Multi- bezeichnen

wollen,

^ist

gleich

^{der Summe aller Produkte}

plikation

nachstehender drei Faktoren entstehen:

1)

^{dem in}

Fig.

⁸

gestrichelten

Flächenelement

df,

2)

^dem Unterschied der in diesem Flächenelement

df

herrschenden

Spannung

^aT

gegenüber

^{der in der} Mittelfaser herrschenden

Spannung

^{or0, also}

der Differenz

(t,

^—

o,0),

3)

dem Abstand _{// des} Flächenelementes von der Mittelfaser.

h H

Mar

⁼

-jdf(

^Cr

^O-r0)

^tj.

Hierin ist

df

⁼

(x-h

rjsin

cf) dadtj.

- 13 ^-

Für

(ff,

^—

ffro)

^{wollen wir an Hand von Gl}

(3)

^einsetzen

(<7r—ffr0)

⁼c'/^cosqpv,

wo u^-

h

r dip ¹ L ^dx

Mar

⁼

J

^{cijcos 7}

u(x

^-+-i, sin

q>)dadijij.

(19),

In diesem

Integral

^{ist nur tj als} Veränderliche, ^alle

übrigen

Größen sind als Konstante ^zu betrachten.

Ma

^{=da ccos}7 ^u

2. 2

x(i!2dii

+

smi]jrtsd)i\; jij'dii=^-z; j>/3dti

^=o.

M„ ^{= dac} cos7 ^{ux -}.

Setzen wir den Wert für u wieder ein aus Gl.

(19),

^{so erhalten wir:}

M„ ^{daex— cos}7 d<fi

dx

(20).

Wir werden später

sehen,

daß wir noch des Wertes

dM„r ^bedürfen,

^{d. h.}

des

Betrages,

^{um den sich}

M„t

ändert, ^{wenn wir vonx um} dx vorwärts

gehen.

Wir erhalten, indem wir die Gl.

(20)

^{nach x} differenzieren:

d-if> ^du>

c \

(mxh-*

^cos

7)

—-,das-f-

d(mxhz

^cos

7)

dM„ ^{=da ( dx- dx}

\+h3

cos

(fdip

^-+

c/(A3

^cos

^{7>)ip (21).}

Zu

bi)

^{2,MT-=%TV^r m>—dS sin}7 ^{=2mTsm. Öl— dS—sin. er.}

1 a 2 '

Statt ZMT wollen wir einfach setzen MT.

MT⁼

da(d.s h)

n,0—"- sin7,

,, ^, / h dx1 . \

MT⁼da ( sm7 ^I

\1 COS'f I

(22).

Zub

2)

^{Das Moment}

Mat

^der

Spannungen

^{ff,, oder was das Gleiche}

besagt,

der

Spannungsdifferenzen (<x,

^—

ff,0),

^wel¬

ches auf

jede

^{der beiden} Seitenflächen G H DC und KIEF von

Fig.

3

wirkt,

^ist

gleich

der Summe aller

Produkte,

^{die aus}

der

Multiplikation

nachstehenderdreiFak¬

toren entstehen:

(vergl. Fig. 9). ^$i

1)

^dem Flächenelement df ^{von der}

7 \ß".Jfcç/

\ dr„ welches im Abstand _?/ von der

"^^ ykf

Höhe

Mittel-MeridianfaserzurKante G C

parallel

verläuft.

2)

^{von dem} Unterschied der in die¬

sem Flächenelement herrschenden

Span¬

nung ^a,

gegenüber

^der

Spannung

<r,0 in der Mittelfaser die in die

Richtung

^senk-

— H ^—

recht zur

Symmetrieachse

entfallende

Komponente,

^also

/ \ ^. da , \du

(ff« ^— ffio)^{sm— co}(fft—(ji0)^{— .}

3)

dem Abstand _»7 des Fluchenelementes von der

Mittelfaser, multipliziert

mit cos</>

* +

M„.

fj,

⁼²

df(at

^—

ffio)

^d" )?^cos7.

Hierin ist nach

Fig.

9

,

df=(ds

+

ijdq)dij.

Gl.

(4) besagt:

(ffi

^—

ffio)

^=c//^cosij) ^—+ ^III—

]•

Setzen wir

vorübergehend

^als

Abkürzung

so ist

JH.

v ^—\ ^{-^}_-+-m ^-

\_dx x

(23),

= 2 I

(ds

+

qdq>)drj

^ctjcos2_<J>« ^—17.

cosqp ^....

(24).

Auch

hier,

^{wie bei der}

Ausrechnung

^von

M„r

^{sind bei der}

Integration

alle Größen _{außer 1/} als Konstante zu betrachten.

* 1,

+ ^— H

2 2

Mat

^=dacv

^cos-'qi Idslq'dij

⁺

dq) itj'dtj

^.

_A A

2 2

Durch

analogen Kechnung.-gang

^{wie für}

MBr

finden wir:

M„, ⁼daedx ^—+ⁱ

ZU ^C) 1/ Dds ;

Z'

, dœ\j

'

il/p=P—= ds Itc -\ Jdap

MP=da^-(x

₊

~)

^{-x„ (25).}

2, V 1I

cos3?"

^J

Nunmehr sind von diesen Momenten noch die Vorzeichen zu bestimmen.

Sie erhalten bei der

Summierung

^das

positive

^oder

negative Vorzeichen, je

nachdem sie verstärkend oder verschwächend auf die

Plattenkrüinmuug

^{in dem}

Querschnitt hinwirken,

^der die Drehachse 0^—0,

Fig.

3, enthält. Es wirken auf diese

Krümmung:

Ms

verstärkend,

also Vorzeichen _+, Mach

verschwächend,

^{also Vorzeichen} —,

MSr verstärkend,

^{wenn die}

Spannungsuntei^chiede (ar

^—

<r,„)

^{über der}

Mitte des

Querschnittes positiv sind,

^{somit dann}

M„r

^+,

MT

verstärkend,

^also -t-,

MGt analog Ma>,

^{also -4-,} Mp

verschwächend,

^{also —.}

M{„r

⁺d„r)=

M„r

^{+ Ms-MScH}

^+tf,+ M„t

^-

MF<

— 15

Nun kann auch

geschrieben

^werden:

M{ar+

,lo,)⁼

Mai

^{d U„}

und daraus

ergibt

^sich

dM„r

^{=Ms—M»,.-+-MT-}

Ma,

^-MP

^(26I

dx2

Hierin setzen wir die Werte ein aus den

Gl.

(21), (17), (18), (22), (24), (25).

Alle diese Werte enthalten

da,

welchen Wert wir besonders

vorangestellt haben,

als Hinweis darauf, daß ^man damit kürzen kann. Es bleibt:

c

\(mxh-c08 qp)—^dx

+

d(mxh

^cos

<j)'

^*-f-A cosqrdtf

4-r/(/i cosqp)^

^aus

(21)

12 [_ ^{dar rfj}

. . aus

(17)

. . aus

(18)

aus

(22)

. . aus

(24)

. aus

(25).

-

p

(cc2

+ ö"«>

2 cos2_y>

av

)

^— ,, -

cos-<f

sin qp

(iroixh)

sin qp ^dx

—

dtp

^coscp -t- ^c—dxm

12 ia

cosqi

» / dx\ dx2

a V 2 / cos-y>

Die

Multiplikation

^dieser

Gleichung

^{mit -}

gibt

edr dxp d(mxJi%^cos(f)

dx dx

d(H3cos</>)

dx

7«Xll CO«*f/

V

mit' COS(Ji

12 xä r<j* • ~1 fro —5- ^—-4-^sinqp

c cos^y|_p ^J

iz A «ix

ff«, .

c 2 cos^ç>

J> ¹² 2 c cos

sinqp

III.

ITaupt- gleichung

~ as2^—as,2+

(x

-+-

r'as

js^yL V ^a ' J .

Diese

Hauptgleichung

^{hat die} schematische Form:

!!"t

⁼

^,L l(32)(7^

+

(36)'T'o -(42)^+ (49)

V ^-

(51)!

^•

ax (40) ^{i dx )}

(III a),

wo die in den runden Klammern

( )

stehenden Ziffern Faktoren

bedeuten,

^welche

lediglich abhängig

^{sind von} der Form und der äußeren

Belastung^

^der

Platte,

nicht aber z.B. vonder

Randbedingung,

^{d. h.}

davon,

ob die Platteam Randein¬

gespannt ^{sei oder frei}

aufliege.

^{Ob die Platte in der Mitte eine}

Bohrung

^hat

oder

nicht,

^kommt

lediglich

^{im Summand}

(51)

^{zum Ausdruck, indem dort der}

Summand sc,2 einen von null verschiedenen Wert erhält oder nicht. Da ferner die Platte nicht eben zu sein

braucht,

^{sondern in}

jedem

Punkt der Meridian¬

mittelfaser eine andere

Krümmung

^{mit dem} veränderlichen Halbmesser _q und außerdem eine von Punkt zu Punkt etwas veränderliche Dicke h haben

kann,

so ist dieses

Kechnungsverfahren

anwendbar auf

gewölbte

^{wie ebene}

(ç=oo,

qp⁼

o) Platten,

volle und in der Mitte

gelochte,

^am Außenrand frei

aufliegende

^oder

eingespannte

^{Platten von} veränderlicher Dicke.

Nach

Ausrechnung

^{der Gl.}

(III)

^{erhalten wir:}