Arithmetische Schnittheorie R. Weissauer

Arithmetische Schnittheorie

R. Weissauer

Inhaltsverzeichnis

I Komplexe Mannigfaltigkeiten 6

1 Formen 7

1.1 Differentialformen . . . 7

1.2 Aussere Ableitungen . . . .¨ 7

1.3 Pullback . . . 8

1.4 Die GarbenAⁿ_X . . . 8

2 Str¨ome 9 2.1 Testformen . . . 9

2.2 Str¨ome aufX . . . 9

2.3 Erstes Beispiel: Zykel . . . 9

2.4 Funktorialit¨at . . . 10

2.5 Ableitung von Str¨omen . . . 10

2.6 Multiplikation . . . 10

2.7 Beispiel . . . 11

3 Gl¨attung 12 3.1 Das Poincar´e–Lemma . . . 12

3.2 Gl¨attungslemma . . . 12

4 Lineare Algebra 14 4.1 Komplexifizierung . . . 14

4.2 Hermitesche Formen aufV . . . 14

4.3 Die unit¨are Gruppe U . . . 15

4.4 Die Grassmann-Algebra . . . 15

4.5 Paarungen und∗ . . . 16

4.6 Hermitesche Form aufW^• . . . 17

5 Invariantentheorie 18 5.1 Verbindung zusl(2,C) . . . 18

5.2 Darstellungstheorie vonGl(2,C). . . 19

5.3 Beweis des Zerlegungslemmas . . . 19

5.4 Appendix . . . 20

6 K¨ahlersche Mannigfaltigkeiten 21 6.1 Der∗Operator . . . 21

6.2 Die globale Paarung . . . 21

6.3 K¨ahlermetriken . . . 22

1

INHALTSVERZEICHNIS 2

6.4 Infinitesimale Umgebungen . . . 22

7 K¨ahleridentit¨aten 25 7.1 Die 6 Operatoren . . . 25

7.2 Identit¨aten zweiter Ordnung . . . 26

8 Der Satz von Hodge 28 8.1 Harmonische Formen . . . 28

8.2 Der Satz von Hodge . . . 29

9 Der Satz von Lefschetz 30 10 10 Die Potentialgleichung 31 10.1 Der OperatorK . . . 31

10.2 Das Gl¨attungslemma . . . 32

11 ¨Ubungsaufgaben 34

II Arithmetische Chowgruppen 35

12 Greensche Str¨ome 36 13 Arithmetische Variet¨aten: 38 13.1 Erhaltungseigenschaften . . . 39

14 Chowgruppen 40 14.1 Die Chowgruppe . . . 40

14.2 Herbrandindex und Moduln endlicher L¨ange . . . 40

14.3 Multiplizit¨aten . . . 41

15 Arithmetische Chowgruppen 42 15.1 Arithmetische Zykel . . . 42

15.2 Arithmetische Chowgruppe . . . 43

16 Relative Sequenz: 44 16.1 Der Homomorphismusk . . . 45

16.2 Der Spezialfallp= 0 . . . 45

16.3 Der Spezialfallp= 1: . . . 45

16.4 Der Zahlringfall . . . 46

16.5 Der Spezialfallp=d+ 1: . . . 46

17 Eine h¨ohere arithmetische Chowgruppe 48

III Arithmetische K–Gruppen 50

18 Metrisierte Vektorraumb ¨undel 51 18.1 Antiholomorphe Ableitung . . . 51

18.2 Zusammenh¨ange . . . 51

18.3 Der metrische Zusammenhang . . . 52

18.4 Kr¨ummungstensor∇²=∇²(E, h). . . 53

INHALTSVERZEICHNIS 3

18.5 H¨ohere Chernformenci(E, h) . . . 54

19 Bott - Chern Klassen 55 20 Der Cherncharakter 59 21 Metrisierte K-Gruppen 61 22 Der Ringhomomorphismusk 63 22.1 H¨ohenpaarungen . . . 63

23 Metrisierte Picardgruppen 65 24 Metrisierte Determinanten 66 25 λ-Ringstruktur 68

IV Der Dirac Operator 72

26 K¨ahleridentit¨aten (Verallgemeinerung) 73 27 Cliffordalgebren 75 28 Derivationen 78 29 Einige Differentialoperatoren 80 29.1 Zusammenh¨ange . . . 80

29.2 Graßmann - Situation: . . . 81

29.3 Dirac-Situation . . . 81

30 Der Hesse-Laplace Operator 84 31 Lichnerowicz Formel 86 A Kr ¨ummungstensoren 88 B Lokale Rechnungen 89 B.1 Bezeichnungen . . . 89

B.2 Ein Vergleich . . . 89

B.3 Symbolterme 2.Ordnung . . . 90

B.4 Terme 1.Ordnung . . . 90

B.4.1 . . . 90

B.4.2 . . . 90

B.5 Normalkoordinaten . . . 91

B.6 Term nullter Ordnung . . . 91

B.6.1 . . . 91

B.6.2 . . . 92

B.7 Differenzterm nullter Ordnung . . . 92

B.8 Der Kr¨ummungstensor . . . 92

INHALTSVERZEICHNIS 4

V Elliptische Operatoren und W¨armekerne 94

Sobolev Theorie 95

.1 Sobolev-R¨aumeHs . . . 95

.2 Sobolev Einbettungssatz . . . 96

.3 Rellich-Theorem . . . 96

.4 Allgemeine MannigfaltigkeitenX . . . 97

.5 Differentialoperatoren . . . 97

Gardings’ Ungleichung 98 .1 Verallgemeinerte Garding-Ungleichungen . . . 99

Selbstadjungierte Operatoren 100 Der Greensche Operator 102 .1 Resolventen . . . 102

W¨armeleitungskerne (Definition) 104 .1 Elementare Eigenschaften . . . 105

.1.1 Eindeutigkeit . . . 105

.1.2 Funktionalgleichung . . . 106

.1.3 Tensorprodukt . . . 106

.1.4 Summierbarkeit . . . 106

Existenz von W¨armekernen I 107 .1 Die Existenz . . . 107

.2 Fundamentale Absch¨atzung . . . 108

.3 Versch¨arfung . . . 108

St¨orungstheorie (Streuformeln) 109 .1 St¨orungsintegrale . . . 109

.2 Charakterisierende Differentialgleichung . . . 110

.3 Inhomogene W¨armegleichung . . . 112

Lokalisation 113 .1 Vergleich von W¨armekernen . . . 113

Existenz von W¨armekernen II 115 Asymptotische Entwicklung 117 .1 Das Theorem . . . 117

.2 Beweis . . . 117

.2.1 Lokalisierung . . . 117

.2.2 Reskalierung . . . 118

.2.3 Pullback des W¨armekerns . . . 118

.2.4 Reihenentwicklung . . . 119

.2.5 Euklidische Kerne . . . 119

.2.6 Polynomiale Operatoren . . . 120

.2.7 Das letzte Integral . . . 121

.2.8 Schlußbetrachtung . . . 121

INHALTSVERZEICHNIS 5

Zetafunktionen 123

A 124

B Spektralsatz f ¨ur kompakte Operatoren 125

C Darstellungssatz f ¨ur glatte Kerne 126

D Berechnung von Integralen 128

D.1 Der Fallα >−1 . . . 128

VI Indexs¨atze 130

Normalkoordinaten 131 .1 Normalkoordinaten f¨ur Vektorb¨undel (der OrdnungN) . . . 131

.2 K¨ahlersche Normalkoordinaten (der OrdnungN) . . . 131

.3 Komplexe versus reelle Koordinaten . . . 132

Die Asymptotik des Dirac Operators 134 .1 “Phantastische K¨urzungen” . . . 134

Bestimmung der dominanten Terme 137 .1 Der vereinfachte Differentialoperator . . . 137

.2 Der Fall d=1 . . . 138

Hirzebruch-Riemann-Roch 139 Erweiterte Superspuren 141 .1 Verallgemeinerte Superspuren . . . 141

Formel f ¨ur den subdominanten Term 143 Der Konjugationstrick 144 .1 1.Parit¨atsannahme . . . 144

.2 2.Parit¨atsannahme . . . 144

.3 3.Parit¨atsannahme . . . 145

.4 Anwendung . . . 145

Bismut-Lichnerowicz Formel 147 .1 Zur Erinnerung . . . 147

.2 Neue Operatoren∇⁰ . . . 147

.3 Diskussion der Terme . . . 148

.4 Bismut-Lichnerowicz Formel . . . 149

Teil I

Komplexe Mannigfaltigkeiten

6

Kapitel 1

Formen

Eine MannigfaltigkeitX heißt komplexe oder analytische Mannigfaltigkeit, wenn alle Kartenabbil- dungenφi : Ui ⊂ X → φi(Ui) ⊂ C^d stetige Abbildungen zwischen offenen Untermengen der R¨aumeX undC^dsind, und die Kartenwechselφij =φj◦φ⁻¹_i holomorphe Funktionen aufφi(Ui) sind. IstXzusammenh¨angend, heißt die Zahld=d(X)Dimension vonX.

Eine Abbildungf :X →Cheißt holomorph, wenn alle Einschr¨ankungenf◦φ⁻¹_i holomorph auf φi(Ui)sind. Die holomorphen Funktionen aufX definieren eine UntergarbeOXder GarbeC_X^∞der unendlich oft differenzierbaren komplexwertigen Funktionen aufX.

Seif :X → Y eine Abbildung zwischen komplexen Mannigfaltigkeiten. Diese heißt holomorph, falls Pullbacksf^∗(h) =h◦fholomorpher Funktionenh∈OY(V)wieder holomorph sindf^∗(h)∈ OX(f⁻¹(V)).

1.1 Differentialformen

F¨urU ⊂C^dist derC^∞(U)-Modul derC^∞-Differentialformen definiert durch A¹(U) =C^∞(U)dz₁⊕...C^∞(U)dz_d⊕C^∞(U)d¯z₁⊕...C^∞(U)d¯z_d sowie derC^∞(U)-Modul der alternierendenn-Formen

Aⁿ(U) =

^n

A¹(U).

1.2 Aussere Ableitungen ¨

Sei∂i = ¹₂(∂/∂xi−i∂/∂yi)und∂i = ¹₂(∂/∂xi+i∂/∂yi)sowiedzi = dxi+idyirespdzi = dxi−idyi. Man definiert∂durch

∂(hdzI ∧dzJ) = Xd i=1

∂i(h)dzi∧dzI∧dzJ

und analog∂. Offensichtlich gilt∂²=∂²= 0sowie∂∂+∂∂= 0. Die ¨aussere Ableitung d:Aⁿ(X)→Aⁿ⁺¹(X)

7

KAPITEL 1. FORMEN 8

ist definiert durchd = ∂+∂und erf¨ulltd² = 0.A^•(U) =L_2d

n=0Aⁿ(U) =L

A^p,q(U)ist ein bigraduierter, superkommutativer Ring bez¨uglich des∧-Produktes. Diesbez¨uglich gilt

d(η∧ω) =dη∧ω+ (−1)ⁿη∧dω f¨urη∈Aⁿ(U)undω∈A^m(U).

1.3 Pullback

F¨ur holomorphe Abbildungenf :U →U⁰mitU⁰⊂C^d0 undU ⊂C^dhat man den Pullback f^∗:A^•,•(U⁰)→A^•,•(U).

Dies sind bigraduierte Ringhomomorphismenf^∗(η1∧η2) =f^∗(η1)∧f^∗(η2), vertr¨aglich mit der Ableitung

d(f^∗(η)) =f^∗(dη)

und funktoriell(f◦g)^∗=g^∗◦f^∗. Diese Eigenschaften charakterisieren die Pullbacks eindeutig.

Beispiel 1.3.1. AufA^1,0giltf^∗(h(z⁰)dz_i⁰) =P_d⁰

j=1h(f(z))(dfi/dzj)(z)dzj.

1.4 Die Garben A

ⁿ_X

F¨ur allgemeinesX und U ⊂ X offen definiert man dieC_X^∞-ModulgarbeAⁿ_X der alternierenden n-Formen aufX durch die Schnitte

Aⁿ_X(U) ={ηi∈Aⁿ(φi(U∩Ui))|φ^∗_ij(ηj) =ηi∈Aⁿ(φi(Ui∩Uj∩U))}.

Alle lokalen Aussagen verallgemeinern sich durch Verkleben. Insbesondere hat man die Pullbacks f^∗:Aⁿ(Y)→Aⁿ(X)

f¨ur holomorphe Abbildungenf :X →Y. Desgleichen hat man auch global Aⁿ_X= M

p+q=n

A^p,q_X

durch Sortieren der holomorphen und antiholomorphen Differentiale (wohldefiniert, da Kartenwech- sel holomorph!).

Kapitel 2

Str¨ome

2.1 Testformen

SeiA^2d−n_c (X)derC-Vektorraum der Schnitte der GarbeAⁿ_X mit kompaktem Tr¨ager aufX. Auf A^2d−n_c (X)hat man die Schwartztopologie. Die Nullfolgen dieser Topologie

φ_ν →0

sind Folgen mit der Tr¨agerbedingung∪νsupp(φν)⊂K,Kkompakt und der Eigenschaft supx∈K|D^r(φν)(x)| →0 (f¨ur alle r)

f¨ur aller-fachen Ableitungen der Koeffizienten derφν(dies ist wohldefiniert wegen der Tr¨agerbedingung!).

2.2 Str¨ome auf X

SeiD^p,q(X)der Raum der stetigenC-LinearformenT auf dem TestraumA^d−p,d−q_c (X)und ana- log Dⁿ(X) = L

p+q=nD^p+q(X). DieD^p,q(U)definieren f¨ur offene Teilmengen U ⊂ X (im Gegensatz zu denA^d−p,d−q_c (U)!)C_X^∞-Modulgarben (benutze Partition der 1) aufX

Dⁿ_X= M

p+q=n

D_X^p,q.

Man nennt sie die Garben derp, q-Str¨omeD^p,q_X odern-Str¨omeDⁿ_X. DieC^∞-Modulstruktur ergibt sich f¨urf ∈C^∞(X)durch

(f T)(η) =T(f η).

AlsC_X^∞-Modulgarben sind die GarbenA^p,q_X , D^p,q_X fein und haben somit verschwindende Garbenko- homologieHⁿ(X, A^p,q_X ) =Hⁿ(X, D_X^p,q) = 0f¨urn >0.

2.3 Erstes Beispiel: Zykel

Zykel sind formale endliche LinearkombinationenZ =P

jnjYjvon abgeschlossenen komplexen UntermannigfaltigkeitenYj (oder allgemeiner komplexen Unterr¨aumen) von X von einer festen

9

KAPITEL 2. STR ¨OME 10

komplexen Kodimensionk. Solchek-Zykel definieren Str¨omeδZ = P

njδYj mit Hilfe der Dirac DistributionenδYj. Hierbei ist

δY ∈D^{d−d(Y),d−d(Y)}(X) =D^k,k(X) δY(η) =

Z

Y^ns

i^∗(η) = Z

Y˜

π^∗i^∗(η)

definiert f¨ur abgeschlossene komplexe Unterr¨aume i : Y → X von X mit Desingularisierung π : ˜Y → Y. (Komplexe Mannigfaltigkeiten sind automatisch orientiert, somit sind die Integrale wohldefiniert. W¨ahle im folgenden immer die ¨ublichen kompatiblen Orientierungen.)

2.4 Funktorialit¨at

Eine Abbildung heißt eigentlich, wenn Urbilder kompakter Mengen kompakt sind. Seif :X →Y eine eigentliche holomorphe Abbildung zwischen zusammenh¨angenden komplexen Mannigfaltig- keiten. Der Pullback definiert eine Abbildung

A^p,q_c (Y)→A^p,q_c (X) sowie dual dazu

D^p,q(X)→D^p−r,q−r(Y). Hierbei bezeichener=d(X)−d(Y)die relative Dimension.

F¨ur glatte holomorphe Abbildungenf :X →Y erh¨alt man durch Integration ¨uber Fasern (!) eine Abbildung

A^p,q_c (X)→A^p−r,q−r_c (Y) und dual einen Pullback

f^∗:D^p,q(Y)→D^p,q(X).

2.5 Ableitung von Str¨omen

F¨urT ∈Dⁿ(X)definiert man die AbleitungdT ∈Dⁿ⁺¹(X)durch (dT)(η) = (−1)ⁿ⁺¹T(dη) , η∈A^2d−n−1_c (X). Analog definiert man∂und∂und zeigt die ¨ublichen Formelnd²=∂²=∂²= 0.

Beispiel 2.5.1. F¨ur Zykel giltdδY = 0. Dies folgt aus dem Satz von Stokes. Dieser besagtd(δY) =

±R

Y d(?) = 0f¨ur Formen mit kompaktem Tr¨ager auf Y. Reduziere dies mit Partition der 1 und Fubini aufR_∞

−∞φ⁰(x)dx= 0f¨urφ(x)∈C_c^∞(R).

2.6 Multiplikation

D_X^• ist eineA^•_X-Modulgarbe. F¨urT ∈ Dⁱ(X)undω ∈ A^j(X)definiert manω∧T ∈ D^i+j(X) durch

(ω∧T)(η) =T(ω∧η) , η∈A^2d−i−j_c (X). Dies machtD^•,•_X zu einer bigraduiertenA^•,•_X -Modulgarbe.

Achtung: Das∧-Produkt zweier Distributionen inDⁱ(X)undD^j(X)ist im allgemeinen aber nicht erkl¨art!

KAPITEL 2. STR ¨OME 11

2.7 Beispiel

Beispiel 2.7.1. F¨urω∈Dⁿ(X)seiTω=ω∧δX

Tω(η) = Z

X

ω∧η . Dies definiert injektive Garbenabbildungen

Aⁿ_X,→Aⁿ_X∧δX⊂D_Xⁿ

gegeben auf globalen Schnitten durchω 7→ Tω ∈ D_Xⁿ. Insbesondere geht die konstante Funktion 1∈A⁰(X)aufδX ∈D⁰(X).

Diese Injektionen sind kompatibel mit derA^•,•(X)-Modulstruktur sowie mit Ableitungen . . . −−−−→ Aⁿ_X −−−−→^d Aⁿ⁺¹_X −−−−→ . . .

 y

 y

. . . −−−−→ D_Xⁿ −−−−→^d Dⁿ⁺¹_X −−−−→ . . . Beweis:Tdω(η)ist

Z

X

(dω)∧η= Z

X

d(ω∧η)− Z

X

(−1)ⁿω∧dη= Z

X

d(ω∧η) +dTω(η) =dTω(η) wegen dem Satz von StokesR

Xd(?) = 0.

Bemerkung 2.7.2. Das Beispiel (2.7.1) zeigt, daß man sogar jeden Schnittω ∈ Aⁿ_L1,loc(X)als Strom inDⁿ(X)auffassen kann (viaω7→Tωdefiniert durch obige Formeln).

Seiω∈Aⁿ_L1,loc(X)und die Einschr¨ankung vonωsei glatt auf einer offenen dichten TeilmengeU. Die Ableitungdω∈Aⁿ⁺¹(U)lasse sich zu einem Schnitt inAⁿ⁺¹_L1,loc(X)fortsetzen. Dann sindTdω

unddT_ωwohldefiniert. Der Satz von Stokes ist nicht mehr direkt anwendbar. Der verbleibende Term R

Ud(ω∧η)liefert ein sogenanntes Residuumres=Tdω−dTω.

Beispiel 2.7.3. ω=_2πi¹ dz/z∈D^1,0(C),U =C^∗⊂X=Cmitdω= 0∈D^1,1(C^∗)und res(Tω) =−dTω=δ{0},

da sich f¨ur den St¨orterm inD²(C)mittels des Satzes von Stokes aus

− Z

U

d(ω∧η) =−lim

²→0

I

²

1

2πidz/z∧f(z) =f(0) ergibt.

Kapitel 3

Gl¨attung

3.1 Das Poincar´e–Lemma

Wir erinnern an das Poincare Lemma:

Lemma 3.1.1. Die Garbenkomplexe(A^p,•_X , ∂),(D^p,•_X , ∂) sowie(A^•_X, d),(D_X^•, d)sind exakt mit Ausnahme an der nullten Stelle.

Im folgenden betrachten wir nur die∂Komplexe, da derd-Fall einfacher ist.

Das Poincare Lemma liefert eine Komplexabbildung zwischen feinen Garbenaufl¨osungen

0 −−−−→ Kern(∂:D^p,0_X −−−−→ D_X^p,1) −−−−→ D_X^p,1 −−−−→ D_X^p,2 −−−−→ ... −−−−→ D_X^p,d −−−−→ 0 x



x



x



x



x



0 −−−−→ Kern(∂:A^p,0_X −−−−→ A^p,1_X ) −−−−→ A^p,1_X −−−−→ A^p,2_X −−−−→ ... −−−−→ A^p,d_X −−−−→ 0. Die Garbe

Ω^p_X :=Kern(∂:A^p,0_X →A^p,1_X )

ist die Garbe der holomorphen alternierenden p-Formen . Lokal f¨urU ⊂C^dund ω=X

I

hIdzI ∈Ω^p_X(U)

impliziert n¨amlich

∂ω=X

I,i

∂i(hI)dzi∧dzI = 0,

die Holomorphiebedingungen∂ihI = 0(f¨ur alleiundI) f¨ur die KoeffizientenhI ∈C^∞(U). Die KoeffizientenhI ∈OX(U)sind also notwendigerweise holomorph.

3.2 Gl¨attungslemma

Wir zeigen nun folgendes Gl¨attungslemma:

12

KAPITEL 3. GL ¨ATTUNG 13

Lemma 3.2.1. F¨urT ∈D^p,q(X)mit

∂T =η∈A^p,q+1(X) existiert einω∈A^p,q(X)und einS∈D^p,q−1(X)mit

T =ω+∂S .

Beweis: Wir nehmen an, wir h¨atten die Aussage im Fallq= 0undη= 0bewiesen. Dann folgt Ω^p_X:=Kern(∂:A^p,0_X →A^p,1_X ) =Kern(∂:D_X^p,0→D^p,1_X ).

Da Kohomologie von der Wahl einerΓ(X,)-azyklischen Aufl¨osung nicht abh¨angt, folgt H^q(X,Ω^p_X)∼=H^q(A^p,•_X , ∂)∼=H^q(D^p,•_X , ∂).

Der zweite Isomorphismus wird induziert von der obigen Komplexabbildung und liefert zwei Spe- zialf¨alle des Gl¨attungslemmas:

• i) Surjektivit¨at: Aus∂T˜ = 0folgt die Existenz einer glatten Formω˜ mitT˜ = ˜ω+∂S und insbesondere∂ω˜ = 0.

• ii) Injektivit¨at: Sei eine glatte Formηdurch einen Strom berandetη =∂T, dann existiert eine glatte Formωmitη =∂ω.

i) und ii) implizieren andererseits das Gl¨attungslemma:

Sei ∂T = η wie in der Formulierung des Gl¨attungslemmas. Nach ii) gibt es ein glattes ω⁰ mit

∂(T−ω⁰) = 0. Nach i) folgt daraus(T−ω⁰) =ω⁰⁰+∂Sf¨ur ein glattesω⁰⁰. F¨urω=ω⁰+ω⁰⁰folgt die Behauptung.

Es verbleibt der noch fehlende Nachweis des Gl¨attungslemmas im Fallη = 0undq = 0. F¨ur die KoeffizientenhI ∈D⁰(U)vonT =P

IhIdzI reduziert sich dies auf die Aussage: Seih∈D⁰(U) mit∂h= 0, dann isthglatt. Einen Beweis findet man in Teil V, Appendix A an der Seite 124.

Bemerkung 3.2.2. Analog zeigt manKern(d:A⁰_X→A¹_X) =CXund Hⁿ(X,CX) =Hⁿ(A^•(X), d)) =Hⁿ(D^•(X), d)).

F¨ur zwei Kohomologieklassen [zi] vonHⁿⁱ(A^•(X), d))mit geschlossenen Repr¨asentanten zi ∈ Aⁿⁱ(X),dzi= 0ist die Kohomologieklasse[z1][z2] = [z1∧z2]∈Hⁿ¹⁺ⁿ²(X,CX)wohldefiniert.

Sie h¨angt nicht ab von der Wahl der Repr¨asentantenziwegen(z1+dω1)∧(z2+dω2) =z1∧z2+dω3. Dies definiert das superkommutative Cup-Produkt∩auf der KohomologieH^•(X,CX).

Beispiel 3.2.3. IstXkompakt und zusammenh¨angend, dann definiert Integration ¨uberXeine nicht- triviale Abbildung# : H^2d(X,C_X) ∼= A^2d(X)/dA^2d−1(X) → C. F¨ur k-Zykel Z₁ undZ₂ mit Kodimensionk1+k2=derh¨alt man mittels des Gl¨attungslemmas das Schnittprodukt

(Z1, Z2) = #(δZ1∩δZ2).

Kapitel 4

Lineare Algebra

4.1 Komplexifizierung

Wir betrachten einen komplexen VektorraumV. Seiσdie komplexe Konjugation aufCund W =C⊗_RV ∼=V ⊕V

λ⊗Rv7→(λv, σ(λ)v)

der komplexwertige Tangentialraum”vonV. Auf W hat man zwei Vektorraumstrukturen, einmal via λ(v, w) = (λv, σ(λ)w)auf den Koeffizienten und zum anderen die induzierte geometrische Operationλ(v, w) = (λv, λw). Falls nicht anders gesagt betrachten wir die Koeffizienten- Struktur aufW. Die Abbildung(v, w)7→(v, w) = (w, v)ist antilinear bez¨uglich der Koeffizientenstruktur und heißt komplexe Konjugation auf W. Wir identifizieren im folgendenV mit dem C-linearen Unterraum aller Elemente(v,0) ∈ W. Dann ist der konjugierte RaumV derC-Unterraum aller Elementev:= (0, v)∈W. Man erh¨alt damit dieC-Vektorraumzerlegung

W =V ⊕V .

Hierbei sindV undV die Eigenr¨aume von der FortsetzungJ =id⊗RiaufW von der Multiplikation mit i aufV. Wir identifizieren dabeiV mit dem ersten Summanden viav:= (v,0) = ¹₂(1⊗v−i⊗iv) inC⊗RV. Dann istv= (v,0) = (0, v) = ¹₂(1⊗v+i⊗iv).

4.2 Hermitesche Formen auf V

Seiheine positive definite hermitesche Form aufV mith(λv1, µv2) = λµh(v1, v2). Die Formh aufV istR-linear. Das gleiche gilt f¨ur die beidenR-Bilinearformeng=Re(h)sowie

ω:=−Im(h) :V ×V →R.

Die Sesquilinearit¨at vonhistRe(h)eine symmetrische und−Im(h)eine symplektische Biline- arform aufv. Skalare Erweiterung induziert zwei entsprechendeC-Bilinearformen aufW. Wegen

−ω(Jv, w) = Im(h)(iv, w) = g(v, w)f¨urv, w ∈ V istg und damit auchhdurchω eindeutig bestimmt.

14

KAPITEL 4. LINEARE ALGEBRA 15

Seie1, .., edeine Orthonormalbasis vonVbez¨uglichh. Eine kurze Rechnung zeigt: DieC-Unterr¨aume V undV vonW sind maximal isotrop bez¨uglich der symmetrischen Formg=Re(h)und der sym- plektischen Formω. Desweiteren giltg(eν, eµ) = ¹₂ undω(eν, eµ) =−Im(h)((eν,0),(0, eµ)) =

i

2δν,µ= ⁱ₂(e^∗_ν⊗e^∗_ν−e^∗_ν⊗e^∗_ν). Anders formuliertω= ⁱ₂P_d

ν=1e^∗_ν∧e^∗_ν.

Normierung: Wir normieren die Dualbasise^∗_ν = dzν, e^∗_ν = dzν des KotangentialraumW^∗durch die Normierungvν = e^∗_ν/√

2 bzw.vν = e^∗_ν/√

2. Bez¨uglich der dualen Metrik aufW^∗gilt dann g(vν, vµ) =δνµ. Also

ω=i Xd

ν=1

vν∧vν ,

undi·vν∧vν =₂ⁱdzν∧dzν =dxν∧dyνist das Euklidsche Volumenelement. Der Faktorimacht ω=ωreell. Da dievν∧vνmiteinander kommutieren, sieht man leicht

ω^d

d! = (dx1∧dy1)∧...∧(dxd∧dyd).

4.3 Die unit¨are Gruppe U

SeiU = U(V, h)die zu hgeh¨orige unit¨are Gruppe. Diese operiertC-linear aufV mit der Stan- darddarstellung. Dies induziert eineC-lineare Operation vonU aufW durch skalare Erweiterung.

Bez¨uglich derC-linearen Ientifikation

H :W =V ⊕V →V ⊕V^∗ (v, w)7→(v, h(., w))

operiert dannU auf dem ersten SummandenV ⊂W mit der Standarddarstellung, und aufV^∗mit der kontragredienten Darstellungw7→(u⁰)⁻¹wwegen

u(v, w)←→(u(v), h(., u(w))) = (uv, h(u⁻¹(.), w))←→(uv,(u⁰)⁻¹w).

4.4 Die Grassmann-Algebra

Wir betrachten die Grassmann AlgebraW^• = L_2d

n=0Wⁿ des KotangentialraumesW ∼= W^∗ = TC(V)^∗

Wⁿ =

^n

W^∗= M

p+q=n

^p

V ∧

^q

V^∗= M

p+q=n

W^p,q. Die Operation vonU aufW setzt sich fort aufW^•mittelsu(V

ivi) =V

iu(vi). Die Aktion vonU vertauscht mit den ProjektionenΠ^p,q : W^• →W^p,qauf die Unterr¨aumeW^p,q. Der Raum(W²)^U derU-Invarianten inW²ist eindimensional

(W²)^U =C·ω , ω=i Xd

ν=1

vν∧vν

Die durchη7→η∧ωdefinierte Abbildung

L:W^•→W^• η7→η∧ω

hat Bigrad(1,1)und kommutiert mitUund der komplexen Konjugation.

KAPITEL 4. LINEARE ALGEBRA 16

4.5 Paarungen und ∗

Das∧-Produkt definiert eine nichtausgearteteC- undU-lineare Cup-Produkt Paarung h,i1:W^p,q⊗W^d−p,d−q −→^∧ W^d,d=

^d

V ∧

^d

V^∗−→^or C

durchhη, η⁰i1 = or(η1∧η2), wobei der Isomorphismusor : W^d,d ∼= Cnormiert sei durch die Vorschrifti^dv1∧v1...∧vd∧vd7→1. Weiterhin hat man

h,i2:W^p,q⊗W^q,p=

^p

V ∧

^q

V^∗⊗

^q

V ∧

^p

V^∗→C, und somit dieC- undU-lineare Auswertungspaarung

h,i₂:W^p,q⊗W^q,p→C

definiert¹durchhvI ∧vJ, vI⁰ ∧vJ⁰i2 = (−1)^|I||J| = (−1)^pq f¨urI⁰ = J, J⁰ =I und Null sonst.

Dies definiert viahη, .i1=h∗η, .i2 einen Isomorphismus

∗:W^•→W^•.

Aus dieser Definition folgt: DieC-lineare Abbildung∗ :W^p,q ∼= (W^d−p,d−q)^∗ ∼=W^d−q,d−pver- tauscht mit der Operation vonU. Ebenso mit komplexer Konjugation

∗η=∗η

wegenhv, wi=hv, wif¨ur beide Paarungen. Explizit berechnet²ergibt sich bis auf das Vorzeichen CIJ=i^d(−1)d(d−1)/2+pdsign(I, I^c)sign(J, J^c)

∗(v_I∧v_J^∗) =C_IJ·v_J^c∧v^∗_Ic

Hierbei seisign(I, I^c)das Vorzeichen der Permutation, welche(I, I^c)f¨ur aufsteigend geordneteI undI^cin(1,2,3..., d)umordnet.

Beispiel:∗1 =i^d(−1)^d(d−1)/2v_{1,..,d}∧v^∗_{1,..,d}= (iv1∧v₁^∗)· · ·(ivd∧v^∗_d) =ω^d/d!.

Aussign(I, I^c)sign(I^c, I) = (−1)^p(d−p)f¨ur|I|=petc. folgt dann mit einer kleinen Rechnung³

∗ ∗η= (−1)^p+qη , η∈W^p,q.

Im Diagramm (4.1) an der Seite 17 bedeutet∗spiegeln an der horizontalen Achse und⁻spiegeln an der vertikalen Achse.

1Beachte V_p V ∧V_q

V^∗

⊗ V_q V ∧V_p

V^∗

= V_p V ∧V_q

V^∗

⊗ V_p V^∗∧V_q

V .

2BenutzecIJ(−1)^{(d−p)(d−q)}= (−1)^d(−1)^d(d−1)/2(−1)^(d−p)qsign(I, I^c)sign(J, J^c)

3wegenCIJCJ^cI^c= (−1)d+pd+(d−q)d(−1)^p(d−p)(−1)^q(d−q)= (−1)^p+q

KAPITEL 4. LINEARE ALGEBRA 17

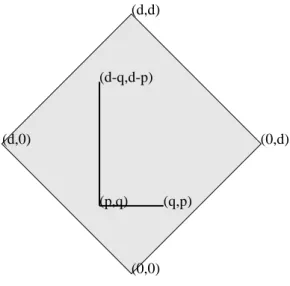
(0,d) (d,d)

(d,0)

(0,0) (p,q) (d-q,d-p)

(q,p)

Abbildung 4.1: Die Operatoren∗und⁻

4.6 Hermitesche Form auf W

^•

Man sieht soforthvI∧v_J^∗),∗(vI⁰∧v_J^∗0)i1=δII⁰δJJ⁰f¨ur alleI, J, I⁰, J⁰. Daher definiert f¨urη1, η2∈ W^p,q

η1∧ ∗η₂∈W^d,d=

^d

V ∧

^d

V^∗∼=C eine positiv definite hermitesche Paarung[η1, η2] =or(η1∧ ∗η₂)aufW^p,q. Ubungsaufgaben:¨

• List selbstadjungiert bez¨uglichh., .i1.

• Λ =∗⁻¹L∗ist das (hermitesch) adjungierte vonLbez¨uglich[., .]oderh., .i2.

Kapitel 5

Invariantentheorie

5.1 Verbindung zu sl(2, C)

Betrachte nunΛ = ∗⁻¹L∗. Dies ist einC-linearer Operator aufW^•, welcher mitU und der kom- plexen Konjugation vertauscht. Man zeigt durch Reduktion¹auf den offensichtlichen²Fall der Di- mensiond= 1die fundamentale Lefschetzidentit¨at

ΛL−LΛ =h:=X

p,q

(d−p−q)Π^p,q.

Unmittelbar klar sind ausserdem

hL−Lh=−2L hΛ−Λh= 2Λ.

Dies entspricht den Relationen der Liealgebrasl(2,C)verm¨oge der Zuordnung µ0 1

0 0

¶

→Λ, µ0 0

1 0

¶

→L ,

µ1 0 0 −1

¶

→h .

Die Aktion integriert sich zu einer Operation der einfach zusammenha¨ngenden GruppeSl(2,C).

Zusammen mit der damit kommutierenden Aktion von z ∈ C^∗ aufW^p,q viaz^d+p−q erh¨alt man eine Darstellung vonGL(2,C) = (Sl(2,C)×C^∗)/±1aufW^•, welche mit der Operation vonU kommutiert. Die UntergruppeGl(2,R)⁺vertauscht obendrein mit der komplexen Konjugation. Die Gruppe

Gl(2,R) =hGl(2,R)⁺,∗i vertauscht ebenfalls mitU und der komplexen Konjugation.

Lemma 5.1.1(Zerlegungslemma). Die(d+ 1)(d+ 2)/2irreduziblen Konstituenten vonW^•unter der Operation vonGl(2,C)×U haben Multiplizit¨at≤1.

1F¨ur(V, h) = (V1, h1)⊕(V2, h2)gilt(W^•,[., .]) = (W₁^•,[., .])⊗C(W₂^•,[., .])undL=L1⊗id+id⊗L2sowie h=h1⊗id+id⊗h2. EbensoΛ = Λ1⊗id+d⊗Λ2durch Adjunktion bzgl.[., .]. Kommutatoren von Tensorderivationen sind wieder Tensorderivationen. Somit folgt die Kommutatorrelation aus derjenigen f¨urV1resp.V2.

2[Λ, L]1 = ΛL(1) = Λ(ω) = (∗⁻¹L∗)∗1 =∗⁻¹L1 = 1wegen∗1 =L1 =ωundp+q= 0.

18

KAPITEL 5. INVARIANTENTHEORIE 19

5.2 Darstellungstheorie von Gl(2, C)

Vektorenwmit der EigenschaftΛw = 0heißen primitiv. Die Darstellungstheorie der Untergrup- peU(2) ⊂ Gl(2,C)zeigt, daß eine irreduzible UnterdarstellungWπ vonGl(2,C)inW^• einen eindeutig bestimmten primitiven Vektorwπbesitzt. Beachte, daß dies gerade der Eigenvektor unter dem Torus der Diagonalmatrizen (oder ¨aquivalent dazu der Eigenvektor vonh) mit dem h¨ochsten Gewicht ist. Insbesondere charakterisiert das Eigenwertsystemdiag(t1, t2)wπ=tⁿ₁¹tⁿ₂²wπdie Dar- stellungπ. Eine Basis des irreduziblen DarstellungsraumesWπerh¨alt man in der Form

wπ, L(wπ), L²(wπ), .., L^r(wπ).

Hierbei ist r gegeben durch diag(t, t⁻¹)(wπ) = t^rwπ oder h(wπ) = rwπ. Beachte weiterhin h(L^m(wπ)) = (r−2m)wπ. Insbesondere istLdamit a priori injektiv auf allen Eigenr¨aumen vonh vom Eigenwert>0. Schließlich folgtWπ=Wπ,prim⊕L(Wπ).

5.3 Beweis des Zerlegungslemmas

Die Eigenr¨aume inW^•unter den Matrizen{diag(t1, t2)}sind genau dieW^p,qmit den Eigenwert- systemendiag(t₁, t₂)7→t^d−q₁ t^p₂. Die Vektoren

vp,q=v1∧...∧vp∧v_d+1−q^∗ ∧...∧v^∗_d∈W^p,q , p+q≤d

inW^p,q sind offensichtlich (!) primitivΛ(vp,q) = 0. Es sind gleichzeitig (!) Vektoren vonU vom H¨ochstsgewicht

(1,1, ..,1

| {z }

pmal

,0, ..,0,−1, ..,−1

| {z }

qmal

).

Der davon erzeugte irreduzibleU-Modul besteht nur aus primitiven Elementen (U undΛkommu- tieren) und hat die Dimension³

µd p

¶µd q

¶

− µ d

p−1

¶µ d q−1

¶

Dies ist aber genau

dimC(W^p,q)−dimC(L(W^p−1,q−1)), dennList injektiv f¨urp+q≤d(Darstellungstheorie derGl(2,C)). Es folgt

W^p,q =W_prim^p,q ⊕L(W^p−1,q−1)

undW_prim^p,q ist ein irreduzibler primitiverU-Modul vom angegebenen H¨ochstgewicht. Andererseits gibt es f¨urp+q > dkeine primitiven Elemente (dasU(2)-Gewichtr=d−p−qeines primitiven Vektors ist immer positiv). Folglich erzeugen dievp,q unter der Operation vonGl(2,C)×U ganz W^•. Die Behauptung folgt.

bis auf einen Skalar

Korollar 5.3.1(Hodge-Riemann Bilinearrelationen). Je zweiU-invariante hermitesche Formen auf W_prim^p,q sind proportional (Schursches Lemma!) und damit bis auf einen Skalar definit.

3Benutze Induktion nach d. Sei obdA p > 0. Wegen Weyl’s Dimensionsformel nimmt dimC(W_prim^p,q ) beim Ubergang von¨ (d, p, q)zu (d−1, p−1, q)den Faktor _p(d+1−q)^(d+1)d auf. Dasselbe gilt f¨ur ^d_pd

q

− _p−1^d _d

q−1

=

d!(d+1)!

p!q!(d−p+1)!(d−q+1)!(d+ 1−p−q).

KAPITEL 5. INVARIANTENTHEORIE 20

Beispiel 5.3.2. η1∧η₂∧_(d−p−q)!^ωd−p−q ist aufW_prim^p,q das(−1)(p+q)(p+q−1)/2i^p−q-fache⁴der definiten Formη1∧ ∗η₂.

Daß die erste Paarung diese Eigenschaft besitzt ist direkt nicht einfach einzusehen (selbst im Fall d=p+q), und im allgemeinen auch nicht richtig auf ganzW^p,q.

5.4 Appendix

Wir erinnern in diesem Anhang an einige wohlbekannte Eigenschaften (stetiger endlich dimensio- naler) Darstellungenπ der unit¨aren Gruppe U = U(d) ⊂ Gl(d,C)auf endlich dimensionalen komplexen Vektorr¨aumenV. Solche Darstellungenπ:U →Gl(V)aufV heißen irreduzibel, falls V keinen nichttrivialenU-stabilen Teilraum besitzt.

Lemma 5.4.1 (Schursches Lemma). Zwischen irreduziblen Darstellungen gibt es bis auf skalare Vielfache h¨ochsten eineU-lineare Abbildung (Kern und Bild sindU-stabil).

Jede Darstellung ist isomorph zu einer direkten Summe von irreduziblen (man konstruiert mittels Integration eineU-invariante hermitesche Metrik und verwendet dann orthogonale Projektion).

Die Isomorphiklassen irreduzibler DarstellungenVπstehen in eineindeutiger Korrespondenz zu den d-Tupelnχ=χ(π)ganzer Zahlen

n1≥n2≥...≥nd.

Die Zuordnungπ7→χ(π)ist wie folgt definiert: Betrachte den TorusT =U(1)^dder Diagonalma- trizen inU. Der RaumVπzerf¨allt in Eigenr¨aume unterT mit den Eigenwertendiag(t1, .., td)v = t^m₁¹...t^m_d^dv. Die Permutationsmatrizen sind in U enthalten und operieren auf Vπ. Zu jedem ‘Ei- genwert’(m1, .., md)gibt es somit einen permutierten, welcher angeordnet istm1 ≥ ... ≥ md. Der bez¨uglich der lexikographischen Anordnung gr¨oßte dieser Eigenwerte ist das H¨ochstgewicht χ=χ(π)der DarstellungVπ. Schließlich hat man die Weyl’schen Dimensionsformeln:

dimC(Vπ) = ∆(n1+d−1, n2+d−2, .., nd−1+ 1, nd)

∆(d−1, d−2, ..,1,0) mit∆(x1, .., xd) =Q

i>j(xi−xj).

”Ubungsaufgabe 5.4.2. Die Darstellungendet^m⊗Symm^r(C²)ersch¨opfen alle Isomorphieklassen irreduzibler Darstellungen vonU(2)(undGl(2,C)). Zeige damit die Vorbemerkung zum Beweis des Zerlegungslemmas.

”Ubungsaufgabe 5.4.3. F¨urp >0istdim(W_prim^p,q;d)gleich _p(d+1−q)^(d+1)d ·dim(W_prim^{p−1,q;d−1})wegen der Gleichung ∆(d,d−1,..,(d−p)^∨,..,(q−1)^∨,..,0,−1)

∆(d−1,..,1,0) =_p(d+1−q)^(d+1)d ∆(d−1,..,(d−p)^∨,..,(q−1)^∨,..,0,−1)

∆(d−2,..,1,0) .

4(−1)^pq(−1)^qq(−1)^p(p−1)/2(−1)^q(q−1)/2i^−p−q= (−1)(p+q)(p+q−1)/2i^p−q

Kapitel 6

K¨ahlersche Mannigfaltigkeiten

Wir betrachten eine komplexe Mannigfaltigkeit, deren komplexes Tangentialb¨undel (assoziiert zum Dual der lokalfreien GarbeΩ¹_X) eine hermitesche Metrikhbesitzt. Seiφ1, ..φd eine lokale Basis vonA¹(X), welche in lokalen Koordinaten punktuell in jedem Punktxvon der Formv1, .., vd ∈ Tx(X,C)^∗gebildet zu einer Orthonormalbasise1, .., eddes TangentialraumsTx(X,C)bez¨uglichh.

6.1 Der ∗ Operator

Die hermitesche Metrik definiert nun den∗Operator aufA^•(X)wie im lokalen Fall. Benutze dazu die Basisφνund die expliziten Formeln im Abschnitt ¨uber lineare Algebra. Wie dort gezeigt wurde, ist die Definition intrinsisch und h¨angt nicht ab von der Wahl derφνab. Analog definiert man den LefschetzoperatorLwie im lokalen Fall.

6.2 Die globale Paarung

Auf einer komplexen MannigfaltigkeitXmit einer hermiteschen Metrik definiert nun (η1, η2)X=

Z

X

η1∧ ∗η₂

eine positiv definite hermitesche Form auf den A^p,q_c (X). Die globalen OperatorenL, ∂, ∂ und d definieren die hermitesch adjungierten globalen OperatorenΛ, ∂^∗,∂^∗undd^∗sind diesbez¨uglich der Paarung(., .)X. Es gilt dann wiederd^∗d^∗ =∂^∗∂^∗ = ∂^∗∂^∗ = 0. Es gilt auch globalΛ =∗⁻¹L∗.

Ausserdem gilt f¨urd^∗=∂^∗+∂^∗

∂^∗=− ∗∂∗

∂^∗=− ∗∂∗

nach dem Satz von Stokes¹.

1R

Xdη1∧ ∗η₂ =R

Xd(...)−(−1)^p−1R

Xη1∧d∗η2f¨ur diep−1-Formη1. F¨ur die2d−p+ 1-Form∗η2ist

∗∗= (−1)^2d−p+1= (−1)^p−1. Es folgt(dη1, η2)X=R

Xdη1∧ ∗η₂=R

Xη1∧ ∗(− ∗d∗)η2= (η1,(− ∗d∗)η2)X.

21

KAPITEL 6. K ¨AHLERSCHE MANNIGFALTIGKEITEN 22

6.3 K¨ahlermetriken

Eine hermitesche Metrikhauf einer komplexen Mannigfaltigkeit heißt K¨ahlermetrik, wenn die as- soziierte reelle (1,1)-Form

ω=iX

φν∧φ_ν ∈A^1,1(X) , ω=ω geschlossen ist

dω= 0.

Bemerkung 6.3.1. In den einzelnen Punkenx∈X entsprichtωaufTx(X)⊗RC∼=V ⊕V^∗der bereits betrachteten symplektischen Form−Im(h) =iP

vν∧vν. Somit istωintrinsisch definiert und h¨angt nur ab vonhund nicht ab von der Wahl derφν.

Bezeichne

L:A^•(X)→A^•(X) η7→η∧ω .

Die K¨ahlerbedingungdω= 0ist gleichbedeutend mit der K¨ahleridentit¨at

∂L=L∂ , ∂L=L∂ .

Es zeigt sich, daß die K¨ahlerbedingung eine Reihe anderer Identit¨aten von Operatoren nach sich zieht, z.B trivialerweise

∂^∗Λ = Λ∂^∗ , ∂^∗Λ = Λ∂^∗.

Zuerst zeigen wir, daß f¨ur jeden Punktx∈X bez¨uglich eines geeigneten Koordinatensystems (Ei- chung) die Formωinfinitesimal in erster Ordnung beixinvariant unter der lokalen Symmetriegruppe U(d)gemacht werden kann.

6.4 Infinitesimale Umgebungen

Sei (X, h)eine komplexe Mannigfaltigkeit der Dimension dmit hermitescher Metrik h. Fixiere x ∈ X. Wir betrachten Taylorentwicklungen im Nullpunkt bis zu Termen zweiter Ordnung. D.h.

formal ersetzen wirR =C^∞(X)nach Wahl lokaler holomorpher Koordinatenz1, .., zddurch den RestklassenringR=C^∞(X)/m²nach dem Quadrat des Idealsm= (z1, .., zd, z1, .., zd). Formen ausA^•(X)reduzieren sich dann auf Elemente inR⊗C W^•. Dazu ist obdA X offen in C^d und x = 0. Sei h = h0+h1 die Taylorentwicklung der hermiteschen Metrik im Punktx = 0, und U =U(V, h0)die zugeh¨orige unit¨are Gruppe aufV des konstanten Koeffizientenh0.Uoperiert auf Rin der nat¨urlichen Weise und mit der induzierten Operation aufR⊗CW^•. Sei

ω=ω₀+ω₁∈R⊗W^1,1

die Taylorentwicklung im Punktxder globalen(1,1)-Formω =−Im(h). Als Komplexifizierung der reellwertigen Funktion−Im(h)istω=ωreell. Daher giltω1=ω1.

Satz.Aquivalent sind¨

1. In jedem Punktx∈Xexistieren lokale holomorphe Koordinatenz₁, .., z_df¨ur die giltω₁= 0.

2. In jedem Punktx∈Xexistieren lokale holomorphe Koordinatenz1, .., zdf¨ur dieω1invariant unterU =U(Tx(X), hx)ist.