Institut f¨ ur Informatik
Sommersemester 2014
Implementierung von Algorithmen zum
Graph-Isomorphismus-Problem f¨ ur
Rooted Outgoing-Ordered Labeled Digraphs und andere Graphklassen
Bachelorarbeit
Rafael Franzke
rafael@cs.uni-frankfurt.de
26. Juni 2014
Eingereicht bei:
Prof. Dr. Manfred Schmidt-Schauß
1 Einleitung 4
2 Grundlagen 6
2.1 Elementare Begriffe . . . 6
2.1.1 Rooted Outgoing-Ordered Labeled Digraphs . . . 11
2.2 Komplexit¨ats¨uberblick . . . 14
3 Algorithmen 20 3.1 Uberpr¨¨ ufung der Rooted Outgoing-Ordered Eigenschaft . . . 20
3.2 Isomorphietest f¨urRooted Outgoing-Ordered Labeled Digraphs . . 24
3.3 Berechnung desOutgoing-Ordered Subgraphs . . . 27
4 Design und Verwendung 30 4.1 Die Datenstruktur f¨ur Graphen . . . 30
4.1.1 Die Klasse Node . . . 32
4.1.2 Die Klasse Edge . . . 33
4.1.3 Die Klasse Graph . . . 33
4.2 Der Interpreter . . . 35
4.3 Sonstiges . . . 40
5 Implementierungen 43 5.1 Graph.java . . . 43
5.2 MainProgram.java . . . 47
5.3 Algorithms.java . . . 50
5.3.1 Uberpr¨¨ ufung derRooted Outgoing-Ordered Eigenschaft . . 50
5.3.2 Isomorphietest f¨urRooted OOLDGs ([3], Proposition 2.9) . 52 5.3.3 Berechnung des Outgoing-Ordered Subgraphs . . . 55
6 Tests 58 6.1 Vorbemerkungen . . . 60
6.2 Testdaten zur ¨Uberpr¨ufung der Rooted-OO-Eigenschaft . . . 61
6.3 Testdaten zum Isomorphietest ([3], Proposition 2.9) . . . 65
6.4 Testdaten zur Berechnung des OO-Subgraphs . . . 70
7 Zusammenfassung und Ausblick 75
Literaturverzeichnis 77
Abbildungsverzeichnis 78
Selbstst¨andigkeitserkl¨arung 79
1 Einleitung
Das Graphisomorphie-Problem (Abk¨urzung: GI) geh¨ort wohl zu den ber¨uhmtes- ten, derzeit noch ungekl¨arten Problemen der theoretischen Informatik.
Im Moment ist die Komplexit¨at von GI v¨ollig unklar: Existiert ein in polyno- mieller Zeit laufender Algorithmus, der entscheidet, ob es einen Isomorphismus zwischen zwei Graphen gibt; in anderen Worten: Liegt GI in P? Erwiesen ist lediglich, dass GI in N P ist, denn ein (geratener) Isomorphismus kann in Po- lynomialzeit verifiziert werden. Nichtsdestotrotz fehlt bislang ein Nachweis f¨ur die N P-Vollst¨andigkeit des Problems. Aus diesem Grund besteht die Vermutung, dass GI zu N P-Intermediate geh¨ort, welche als
”zwischen“P und N P liegende Komplexit¨atsklasse aufgefasst wird. Mehr hierzu findet sich in Abschnitt 2.2.
Insbesondere aufgrund der vielen praxisrelevanten Einsatzgebiete der Graphiso- morphie ist die Forschung sehr interessiert daran, die Schwierigkeit des Pro- blems endg¨ultig zu determinieren. Beispielsweise geh¨oren hierzu Anwendungen aus der Bildverarbeitung, Chemie, Biologie oder auch dem Data- bzw. Textmining- Bereich. Bei genauerer Betrachtung stellt sich heraus, dass eine Vielzahl dieser Praxisprobleme mit speziellen Graphen beschrieben werden k¨onnen, f¨ur die die Frage nach Isomorphismen effizient beantwortbar ist.
Die in [3] eingef¨uhrte Klasse derRooted Outgoing-Ordered Labeled Digraphs(kurz:
Rooted OOLDGs) ist eine dieser gerade erw¨ahnten Spezialklassen, f¨ur die ein Poly- nomialzeitalgorithmus f¨ur das Isomorphieproblem existiert. Diese Klasse ist The- ma der vorliegenden Arbeit.
Das Hauptanwendungsgebiet dieser Graphen ist die Feststellung der erweiterten Alpha- ¨Aquivalenz zweier Ausdr¨ucke im Lambda-Kalk¨ul, in h¨oheren Programmier- sprachen, h¨oheren Programm-Kalk¨ulen sowie Prozess-Kalk¨ulen. In [3] zeigt sich, dass das Entscheiden dieser ¨Aquivalenz mindestens so schwer ist wie das GI- Problem. Erst nach Entfernen von ungenutzten Bindungen von let’s aus einem Ausdruck kann aus diesem im Anschluss einRooted OOLDG konstruiert werden, mit dem danach der Isomorphiealgorithmus aufgerufen werden kann.
Die Details hierzu sind f¨ur diese Arbeit zu weitreichend, weshalb auf [3] verwiesen sei. Im Folgenden wird der Schwerpunkt deswegen auf den Entwurf dieses Algo- rithmus gelegt, welcher im weiteren Verlauf dieser Arbeit auch real implementiert und getestet wird.
Kapitel 2 f¨uhrt in die grundlegenden Begriffe ein und liefert einen kurzen Kom- plexit¨ats¨uberblick f¨ur die eingef¨uhrte Spezialklasse und allgemeine Erkenntnisse bez¨uglich GI.
Anschließend werden in Kapitel 3 drei Algorithmen zuRooted OOLDGs vorgestellt und laufzeittechnisch analysiert, wobei der Isomorphiealgorithmus eine hervorge-
hobene Bedeutung hat.
Darauf folgend enth¨alt Kapitel 4 Informationen ¨uber die verwendete Program- miersprache und wissenswerte Details hierzu. Außerdem wird die entwickelte Da- tenstruktur pr¨asentiert und Einzelheiten zur Verwendung (der Interpreter) und zum Abfangen von Fehlern dargelegt.
Kapitel 5 besch¨aftigt sich dann schließlich mit der tats¨achlichen Implementierung und zeigt wichtige Code-Ausschnitte, bei denen ebenfalls bevorzugt Wert auf die vorher vorgestellten Algorithmen gelegt wird. Diese werden schlussendlich in Ka- pitel 6 ausf¨uhrlich getestet, wobei vier unterschiedliche Graphstrukturen f¨ur die Testf¨alle mittels eines eigens angepassten Graphgenerators erzeugt worden sind.
Ebenso findet sich hier eine jeweilige Analyse bzw. Auswertung der Testdaten f¨ur die einzelnen Algorithmen.
Abschließend wird eine Zusammenfassung der Ergebnisse gegeben, in der alle zen- trale Erkenntnisse dieser Arbeit erneut kurz dargestellt werden.
2 Grundlagen
In diesem Kapitel werden zun¨achst einige f¨ur die sp¨ater folgende Implementierung der Algorithmen notwendigen Begriffe und theoretischen Grundlagen definiert.
Dabei wird sich an einigen Stellen an [4] orientiert. Außerdem ist im zweiten Teil ein grober ¨Uberblick ¨uber die Komplexit¨atserkenntnisse von Graphen allgemein und auch von den eingef¨uhrten Graphklassen gegeben.
2.1 Elementare Begriffe
Definition 2.1.
Ein ungerichteter Graph G = (V, E) besteht aus einer Menge V von Knoten und aus einer MengeE ⊆ {{u, v} |u, v ∈V, u6=v}, welche Kantenmenge genannt wird.
SofernE ⊆ {(u, v)|u, v ∈V}ist, spricht man von einemgerichteten Graphen.
G heißt endlich, falls |V|endlich ist.
Beispiel 2.2.
Der Graph G1 := ({a, b, c, d, e},{{a, b},{a, c},{a, d},{b, e},{c, d},{d, e}}) ist ein endlicher, ungerichteter Graph mit der Knotenmenge V = {a, b, c, d, e} und der Kantenmenge E = {{a, b},{a, c},{a, d},{b, e},{c, d},{d, e}}. Abbildung 1 zeigt G1 in seiner graphischen Darstellung:
a
c
b
d e
Abbildung 1: G1 graphisch
Der GraphG2 := ({1,2,3,4},{(1,1),(1,2),(1,3),(2,4),(3,1),(4,3)}) ist ein endli- cher, gerichteter Graph, welcher in der folgenden Abbildung 2 graphisch repr¨asen- tiert ist:
1 2
3 4
Abbildung 2: G2 graphisch
Anmerkung: Im Folgenden ist immer die Rede von endlichen Graphen, da un- endliche Graphen mit Computern schwer handhabbar und somit, insbesondere f¨ur die in Kapitel 3 vorgestellten Algorithmen, unbrauchbar sind.
Notation 2.3.
Sei G= (V, E) ein Graph.
(a) Ein Knoten u ∈V heißt inzident zu einer Kante e∈ E, falls v ∈ e (unge- richtet) bzw. falls v im Tupel e vorkommt (gerichtet).
(b) Der Knoten u ∈ V heißt adjazent zu Knoten v ∈ V, falls {u, v} ∈ E (ungerichtet) bzw. falls (u, v)∈E oder (v, u)∈E (gerichtet).
(c) Falls zwei Knoten u, v ∈ V adjazent zueinander sind, so sind sie auch be- nachbart.
Definition 2.4.
Sei G= (V, E) ein Graph.
(a) Ein Weg in G ist ein Tupel (v1, . . . , vk)∈ Vk mit k ∈N>0, so dass f¨ur alle 1 6 i < k gilt: {vi, vi+1} ∈ E, falls G ungerichtet ist bzw. (vi, vi+1) ∈ E, falls Ggerichtet ist.
(b) Ein Weg (v1, . . . , vk) mit k ∈ N>0 wird Kreis genannt, falls v1 = vk und k >1.
(c) DerGradeines Knotensu∈V in einem ungerichteten GraphGist GradG(u) :=
|{{u, v} ∈E |v ∈V}|, also die Anzahl der Kanten, mit denen u in G inzi- dent ist.
In einem gerichteten Graphen G wird zwischen dem Ein- und dem Aus- grad unterschieden. Es ist EingradG(u) := |{(v, u) ∈ E | v ∈ V}| und AusgradG(u) := |{(u, v)∈E |v ∈V}|.
Beispiel 2.5.
In G1 aus Abbildung 1 sind beispielsweise die Knoten a und b benachbart (bzw.
adjazent) – genauso wie die Knotencund d. Der Grad von Knoten d ist 2, wobei Knoten a einen Grad von 3 hat. (a, c, d, e) ist ein Weg, w¨ahrend (a, c, d, e, b, a) einen Kreis darstellt.
Im gerichteten Graphen G2 (vgl. Abbildung 2) sind zum Beispiel die Knoten 1 und 3 benachbart. Knoten 4 ist inzident zu der Kante, die zu Knoten 3 f¨uhrt. Der Eingrad von Knoten 1 betr¨agt 1, w¨ahrend sein Ausgrad bei 3 liegt. (1,2,4,3) ist ein Weg; gleichzeitig ist (3,4,2,1) kein Weg in G2. Beispielsweise ist (1,3,1) ein Kreis.
Definition 2.6.
SeiG= (V, E) ein Graph.G0 = (V0, E0) mitV0 ⊆V und E0 ⊆E heißtTeilgraph von G.
Definition 2.7.
Sei G= (V1, E1) ein ungerichteter Graph.
(a) G heißt zusammenh¨angend, falls f¨ur je zwei Knoten u, v ∈ V1 ein Weg existiert, der inu beginnt und in v endet.
(b) Falls Gnicht zusammenh¨angend ist, so zerf¨allt Gin seine Zusammenhangs- komponenten. EineZusammenhangskomponentevonGist ein maximal zusammenh¨angender TeilgraphG0 von G.
Sei H = (V2, E2) ein gerichteter Graph.
(c) H heißt stark zusammenh¨angend, falls es f¨ur je zwei Knoten u, v ∈ V2
einen Weg von u nachv gibt.
(d) H heißt schwach zusammenh¨angend, falls der zugeh¨orige ungerichtete GraphHu = (V2, Eu) (inHusind alle Kanten (u, v)∈E2durch{u, v}ersetzt und Element von Eu) zusammenh¨angend ist.
(e) Eine starke Zusammenhangskomponente von H ist ein maximal stark zusammenh¨angender TeilgraphH0 von H.
a
c
b
d e
Abbildung 3: G01 (G1 modifiziert)
Beispiel 2.8.
G1 aus Abbildung 1 ist zusammenh¨angend. Entfernt man beispielsweise die Kan- ten {a, c},{a, d} und {d, e}, so entsteht G01 (siehe Abbildung 3):
G01 ist nicht zusammenh¨angend und zerf¨allt nach Definition 2.7 (b) in seine Zu- sammenhangskomponenten: In einer Komponente befinden sich die Knotencund d, in einer weiteren Komponente die Knotena, bund e. Insbesondere sind sowohl G01 als auch diese Komponenten Teilgraphen von G1.
G2 als gerichteter Graph aus Abbildung 2 ist stark zusammenh¨angend. Nach Ent- fernen der Kante (3,1) entsteht ein neuer Graph G02 (siehe Abbildung 4):
1 2
3 4
Abbildung 4: G02 (G2 modifiziert)
G02 ist nun nicht mehr stark zusammenh¨angend. Jeder der Knoten 1, 2, 3, 4 bil- det eine eigenst¨andige Zusammenhangskomponente, weil sich kein stark zusam- menh¨angender Teilgraph mit mindestens zwei Knoten finden l¨asst. G02 ist jedoch schwach zusammenh¨angend, weil der zugeh¨orige ungerichtete Graph G002 (siehe Abbildung 5) zusammenh¨angend ist:
1 2
3 4
Abbildung 5: G002 (zu G02 geh¨origer ungerichteter Graph)
Definition 2.9.
Sei G= (V, E) ein Graph. G heißt genau dann vollst¨andig, wenn E ={{u, v} | u, v ∈V, u6=v} bzw. E ={(u, v)|u, v ∈V} ist.
Anmerkung: In einem vollst¨andigen ungerichteten Graphen mit n Knoten hat jeder Knoten einen Grad von n−1 und n·(n−1)2 Kanten.
Definition 2.10.
Seien G1 = (V1, E1), G2 = (V2, E2) Graphen. G1 und G2 sind gleich (in Zeichen:
G1 =G2), falls V1 =V2 und E1 =E2.
Beispiel 2.11.
Folgende Graphen sind nach obiger Definition nicht gleich, aber
”sehr ¨ahnlich“:
G1 entsteht durch Umbenennen der Knoten von G2 und umgekehrt:
G
1:
1
2 3
4 5
G
2:
ab c
d e
Dieses Beispiel illustriert den Begriff der Isomorphie, welcher zentral f¨ur diese Arbeit ist und in folgender Definition verankert wird:
Definition 2.12.
Zwei Graphen G1 = (V1, E1), G2 = (V2, E2) heißen genau dann isomorph (in Zeichen: G1 ∼=G2), wenn es eine bijektive Funktionπ :V1 →V2 gibt, so dass
f.a. {v1, v2} ∈E1 : {v1, v2} ∈E1⇐⇒ {π(v1), π(v2)} ∈E2 (ungerichtet) bzw.
f.a. (v1, v2)∈E1 : (v1, v2)∈E1 ⇐⇒(π(v1), π(v2))∈E2 (gerichtet) gilt. In diesem Zusammenhang ist π ein Isomorphismus von G1 nachG2. Klar ist, dass die in Beispiel 2.11 dargestellten Graphen zwar nicht gleich, aber isomorph sind. Die Abbildungπ :V1 →V2 mit π={17→a, 27→b, 37→c, 47→d, 5 7→ e} ist ein Isomorphismus (nicht der Einzige) von G1 nach G2, weil nach
”Umbenennung“ der Knoten mittels π die Kantenstruktur in G2 erhalten bleibt und jetzt G1 =G2 gilt.
2.1.1 Rooted Outgoing-Ordered Labeled Digraphs
Die in Kapitel 3 vorgestellten und in Kapitel 5 implementierten Algorithmen be- handeln nicht die oben definierten gew¨ohnlichen Graphen, sondern verwenden In- stanzen der Klasse der Rooted Outgoing-Ordered Labeled Digraphs. Diese Graph- klasse hat einige weitreichend einschr¨ankende Bedingungen inne, wodurch das Isomorphie-Problem innerhalb dieser Klasse effizient gel¨ost werden kann. F¨ur De- tails hierzu sei auf Abschnitt 2.2 verwiesen; zun¨achst werden die formalen Grund- lagen vorgestellt.
Definition 2.13.
Ein beschrifteter gerichteter Graph (LDG) (Labeled Digraph) ist ein Tupel G= (V, E, L, lab), wobeiV eine endliche Menge von Knoten,E ⊆(V×V×L) eine Menge von Beschriftungen (labels) und lab :V → L eine Funktion ist, die jedem Knoten eine Beschriftung zuweist. Wenn|L|= 1 ist, dann heißtGunbeschriftet (unlabeled) und wenn (v1, v2, l)⇐⇒(v2, v1, l)∈E gilt, so ist Gungerichtet.
Beobachtung 2.14. In einem LDG hat nicht nur jeder Knoten durch die lab- Funktion eine Beschriftung, sondern durch die Wahl von E ⊆ (V ×V ×L) auch jede Kante.
Notation 2.15. In unbeschrifteten Graphen G = (V, E, L, lab) werden die Komponenten L und lab manchmal weggelassen.
An dieser Stelle ist weiterhin zu beachten, dass die obige Definition mehrere Kan- ten von Knotenv1zu Knotenv2 nur mit unterschiedlichen Beschriftungen erlaubt, wodurch mehrere Kanten von v1 nach v2 in unbeschrifteten Graphen implizit verboten sind.
Definition 2.16.
Zwei LDGs G1 = (V1, E1, L, lab1), G2 = (V2, E2, L, lab2) heißen genau dann iso- morph (in Zeichen: G1 ∼=G2), wenn es eine bijektive Funktion π:V1 →V2 gibt, so dass
f.a. (v1, v2, l)∈E1 : (v1, v2, l)∈E1 ⇐⇒(π(v1), π(v2), l)∈E2 und f.a. v ∈V1 : lab1(v) =lab2(π(v))
gilt. In diesem Zusammenhang ist π ein Isomorphismus von G1 nachG2. Beispiel 2.17.
Die folgenden Beispielgraphen sollen erneut den Begriff der Isomorphie festigen – hier allerdings bezogen auf LDGs, da diese die Bedingungen eines Isomorphismus an die Klasse anpasst.
G1 ist isomorph zu G2, da die Konditionen aus Definition 2.16 erf¨ullt sind.
Anmerkung: Es ist L={1,2, . . . ,6, a, b, . . . , f}. Die Knotenbeschriftungen von G1 sind nicht explizit eingezeichnet, aber wie folgt gew¨ahlt:
F¨urG1 istlab1 :V1 →L mit vi 7→i, i∈L.
F¨urG2 istlab2 :V2 →L mit vi 7→(7−i),i∈L.
G
1:
v1
v2 v3
v4 v5
v6
a b
c d
e f
G
2:
v5v6
v3
v4 v2
v1
a
c
b
d
e
f
Es gilt G1 ∼=G2 mit π : V1 → V2 und π ={v1 7→v6, v2 7→ v5, v3 7→ v4, v4 7→v3, v5 7→v2 und v6 7→v1}. Weiterhin ist die Bedingung f¨ur die Knotenmarkierungen
erf¨ullt, d.h. f.a. v ∈V1 gilt lab1(v) =lab2(π(v)).
Definition 2.18.
Ein LDG G = (V, E, L, lab) heißt genau dann Outgoing-Ordered (OOLDG), wenn f¨ur alle Knoten v ∈ V gilt: Falls (v, v1, l) ∈ E und (v, v2, l) ∈ E, so ist v1 =v2.
Umgangssprachlich formuliert besagt Definition 2.18, dass ein LDG genau dann dieOutgoing-Ordered-Eigenschaft besitzt, wenn f¨ur jeden Knoten die zugeh¨origen ausgehenden Kanten eindeutig beschriftet sind (also kein Knoten mehr als eine ausgehende Kante mit derselben Beschriftung hat).
Definition 2.19.
Sei G= (V, E, L, lab) ein gerichteter, beschrifteter oder unbeschrifteter Graph.
Ein Knoten v ∈ V heißt Wurzel (root), falls er keine eingehenden Kanten hat, also ¬∃(w, v, l)∈E.
Ein Knotenv ∈V heißtBlatt (leaf ), falls er keine ausgehenden Kanten hat, also
¬∃(v, w, l)∈E.
Weiterhin sei erreichbar(v, G) (f¨ur v ∈V aus G) die Menge der Knoten in G, die von v aus ¨uber gerichtete Kanten erreichbar sind, d.h. alle Knoten w, so dass es einen Weg (v, . . . , w) in G gibt.
Ein Knoten v heißt genau dann initial, wenn jeder andere Knoten w ∈ V\{v}
von v aus erreichbar ist (d.h. w∈erreichbar(v, G)).
Eine KnotenmengeS ⊆V heißt genau danninitial, wenn jeder Knotenw∈V\S von einem Knoten v ∈S aus erreichbar ist (d.h. w∈S
v∈Serreichbar(v, G)).
Gheißt genau dannk-initial, wenn es f¨ur jede schwache Zusammenhangskompo- nente G0 von Geine initiale MengeSG0 gibt, die h¨ochstens k Knoten enth¨alt (d.h.
|SG0|6k).
G heißt k-rooted, wenn jede schwache Zusammenhangskomponente G0 von G h¨ochstens k Wurzeln (roots) enth¨alt und wenn die Menge RG0 der Wurzeln in G0 eine initiale Menge ist.
Weiterhin heißt G rooted, fallsG 1-rooted und schwach zusammenh¨angend ist.
Die Gr¨oße |G|eines LDGs G= (V, E, L, lab) ist |G|=|V|+|E|.
Beispiel 2.20.
Sowohl G1 als auch G2 aus Beispiel 2.17 sind Rooted Outgoing-Ordered Labeled Digraphs. Beide sind gerichtet und erf¨ullen die Eigenschaften eines LDGs (jeder
Knoten und jede Kante tr¨agt eine Beschriftung). Außerdem wird das Outgoing- Ordered-Kriterium eingehalten (pro Knoten ist jede ausgehende Kante eindeutig beschriftet) und sie besitzen jeweils genau eine Wurzel (v1 bzw. v6). Weiterhin existiert jeweils nur eine schwache Zusammenhangskomponente und auch nur ge- nau eine Wurzel, von der aus alle anderen Knoten erreichbar sind.
Definition 2.21.
Der Outgoing-Ordered Subgraph OO(G) = (V, E0, L, lab) f¨ur einen LDG G = (V, E, L, lab) ist der Graph, der aus G durch Entfernen aller mehrdeuti- gen Beschriftungen konstruiert wird, d.h.:
Wenn e1, . . . , en ausgehende Kanten von Knoten v ∈ V mit Beschriftung l ∈ L sind, so werden – falls n > 2 – die Kanten e1, . . . , en entfernt. Die zugeh¨origen Knoten, auf die die Kanten zeigen, werden allerdings beibehalten.
2.2 Komplexit¨ ats¨ uberblick
Nachdem nun elementare Begriffe bekannt sind, soll eine komplexit¨atstechnische Einordnung vorgenommen werden. Dazu wird zun¨achst das Ausgangsproblem der vorliegenden Arbeit erl¨autert. Die Frage nach der Isomorphie zweier Graphen (Graphisomorphie (GI)) ist das wie folgt definierte Entscheidungsproblem:
Definition 2.22.
Graphisomorphie (GI)
Eingabe: Zwei (un)gerichtete Graphen G1 = (V1, E1), G2 = (V2, E2) Ausgabe: Ja, fallsG1 ∼=G2; Nein, sonst.
Um die Schwierigkeit des im Folgenden immer mit GI abgek¨urzten Problems bestimmen zu k¨onnen, sind zun¨achst Grundlagen zur Komplexit¨atseingliederung zu kl¨aren. Im Vordergrund steht hierbei die KlasseN P:
Definition 2.23.
In der Klasse N P sind alle Entscheidungsprobleme L, die mittels einesnichtde- terministischen und in polynomieller Zeit laufenden Algorithmus gel¨ost werden k¨onnen.
In der Klasse P hingegen sind alle Entscheidungsprobleme K, die mittels eines deterministischen und in polynomieller Zeit laufenden Algorithmus gel¨ost werden k¨onnen.
Definition 2.24.
Ein Entscheidungsproblem L1 l¨asst sich auf ein Entscheidungsproblem L2 poly- nomiell reduzieren (in Zeichen: L1 ≤P L2), wenn es eine deterministische und in polynomieller Zeit laufende Transformation T gibt, die f¨ur jede Eingabe w f¨ur L1 eine Eingabe T(w) f¨urL2 berechnet, so dass (w∈L1 ⇐⇒T(w)∈L2) gilt.
Zur Abgrenzung der
”h¨artesten“ von den ¨ubrigen Problemen in N P wird der Begriff der N P-Vollst¨andigkeit eingef¨uhrt:
Definition 2.25.
Ein Entscheidungsproblem L heißt genau dann N P-hart, wenn K ≤P L f¨ur alle Entscheidungsprobleme K ∈ N P. Falls zus¨atzlich L ∈ N P, so wird L N P- vollst¨andig genannt (kurz: L∈ N PV).
Ist GI N P-vollst¨andig, d.h. z¨ahlt GI zu den h¨artesten Problemen in N P, oder l¨asst sich das Problem effizient (d.h. in polynomieller Zeit mit deterministischen Berechnungen) l¨osen?
Es ist wohlbekannt, dass diese Fragen und somit die Komplexit¨at vonGI derzeit ungewiss sind, was das Problem insbesondere f¨ur die Forschung interessant macht (vgl. [1]). Trotz intensiver Suche ist es bisher weder gelungen einen Nachweis f¨ur die N P-Vollst¨andigkeit noch einen polynomiellen Algorithmus f¨ur GI zu finden.
Klar ist aktuell lediglich, dass GI ∈ N P, denn ein (geratener) Isomorphismus kann durch Abbildung der Knoten aufeinander und einem anschließenden Kan- tenvergleich in Polynomialzeit verifiziert werden. Diese Erkenntnis allein ist jedoch leider nicht wirklich richtungsweisend, weshalb es unterschiedliche Ans¨atze gibt, um der Entr¨atselung der Schwierigkeit des Problems n¨aher zu kommen.
Einer dieser Ans¨atze, die sich in der theoretischen Informatik durchgesetzt haben, ist ein im Jahr 1975 von Richard Ladner bewiesenes Theorem, welches sich mit der Struktur von N P besch¨aftigt.
Definition 2.26. (Ladner’s Theorem)
Unter der Voraussetzung vonP 6=N P muss es Probleme in einer
”Zwischenklas- se“ geben, welche N P-Intermediate genannt wird.
(Formal: P 6=N P =⇒ N P-Intermediate 6=∅)
Bislang geht man aufgrund der, trotz intensiver Forschung bescheidenen, Ergeb- nisse mutmaßend davon aus, dass GI Teil dieser Zwischenklasse ist.
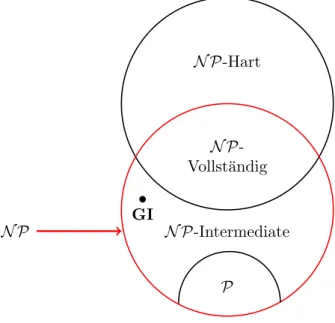
In der folgenden Abbildung 6 soll das Zusammenspiel zwischen den vorgestellten Klassen visualisiert werden.
N P-Hart
N P- Vollst¨andig
GI
N P-Intermediate N P
P
Abbildung 6: Struktur von N P
Die Vermutung zur Existenz vonN P-Intermediate wird zudem von der folgenden Beobachtung 2.27 verst¨arkt:
Beobachtung 2.27.
Alle inN Pans¨assigen Probleme k¨onnen in Polynomialzeit auf einN P-vollst¨andi- ges Problem reduziert werden.
Gerade f¨urGI, aber auch beispielsweise f¨ur das ProblemPrimfaktorzerlegung ist genau das – trotz zahlreicher Versuche – bisher nicht gelungen. Entsprechend verst¨arkt wird die Annahme, dass diese Klasse existiert und insbesondere, dass GI ∈ N P-Intermediate gilt.
Trotz allem l¨asst diese Vermutung zun¨achst keine weiterf¨uhrenden Erkenntnisse zu, weswegen es in Forschungskreisen weitere verschiedene Ans¨atze gibt, um die Komplexit¨at des Problems letztlich zu determinieren [1].
Einer dieser Ans¨atze widmet sich einer neuen Komplexit¨atsklasse,
”GI-vollst¨and- ig“, auf die nachfolgend weiter eingegangen wird.
Ein weiterer Versuch konzentriert sich auf spezielle Graphklassen, innerhalb derer
das Problem, einen Isomorphismus zu finden, effizient l¨osbar ist. Im Rahmen die- ser Arbeit ist es ausreichend, einige dieser Klassen beispielhaft aufzuz¨ahlen, aber nicht n¨aher zu diskutieren: Planare Graphen, Intervallgraphen, Permutationsgra- phen, Zuf¨allige Graphen, Graphen mit beschr¨anktem Grad, B¨aume und Rooted Outgoing-Ordered Labeled Digraphs. Lediglich auf die zuletzt genannte Klasse wird komplexit¨atstechnisch im weiteren Verlauf dieses Kapitels noch eingegangen.
Außerdem gibt es die Bem¨uhung, sich via einer neuen Interpretation der Klassen P undN Pder Aufdeckung der Komplexit¨at vonGIanzun¨ahern. Die Details hier- zu sind ebenfalls zu weitreichend und deshalb sei auf [1] verwiesen, aber letztlich f¨uhrt dieser Ansatz auf die sogenannte Polynomialzeithierarchie. Es stellte sich heraus, dass die N P-Vollst¨andigkeit von GI den Kollaps eben dieser Hierarchie auf zweiter Ebene zur Folge h¨atte, was eine weitere Versch¨arfung der Intuition ist, dassGraphisomorphievermutlich nichtN P-vollst¨andig ist (was nat¨urlich nicht zwangsl¨aufig bedeutet, dass es f¨ur das Problem einen polynomiellen Algorithmus gibt).
Um dieser Intuition etwas n¨aher zu kommen, bleibt also eine Betrachtung der Klasse GI-vollst¨andig (kurz: GIV), worauf jetzt der Fokus liegen soll. Auch hier wird sich zeigen, dass Erkenntnisse bzw. Beobachtungen anderer Probleme zur Komplexit¨atsbestimmung zwar nicht aufschlussreich, aber dennoch richtungswei- send sind.
Definition 2.28.
Ein Entscheidungsproblem L ist in der Klasse GI (oder auch: L ∈ GI), falls es eine in polynomieller Zeit berechenbare Transformation T gibt, die f¨ur jede Ein- gabewf¨urLeine EingabeT(w) f¨urGI erzeugt, so dass (w∈L⇐⇒T(w)∈GI) gilt (L ist also h¨ochstens so schwer wie GI).
Ein Entscheidungsproblem K istGI-hart, falls es eine polynomielle Transforma- tion U gibt, die f¨ur jede Eingabe x f¨ur GI eine Eingabe T(x) f¨ur K erzeugt, so dass (x∈GI⇐⇒U(x)∈K) gilt (K ist also mindestens so schwer wieGI).
Ein Entscheidungsproblem P ist genau dann GI-vollst¨andig (oder auch: P ∈ GIV), wenn P ∈ GI und P GI-hart ist.
Ein Beispiel f¨ur ein solches aus komplexit¨atstheoretischer Sicht zuGI¨aquivalentes – alsoGI-vollst¨andiges – Problem w¨are das Z¨ahlenallerIsomorphismen zwischen zwei Graphen. DieGI-H¨arte dieses Problems ist offensichtlich: Um die Anzahl aller Isomorphismen ¨uberhaupt z¨ahlen zu k¨onnen, muss mindestensGIgel¨ost werden – ansonsten k¨onnte man die Frage nach Isomorphismen ¨uberhaupt nicht entscheiden und erst recht nicht z¨ahlen, wie viele es gibt.
Zur¨uck zur oben erw¨ahnten Intuition, f¨ur deren Steigerung Beobachtung 2.29 wichtig ist.
Beobachtung 2.29.
Die ”Abz¨ahl-Version“ eines N P-vollst¨andigen Problems ist meistens viel h¨arter als die
”Entscheidungs-Version“ des Problems.
Wie bereits erw¨ahnt ist die Abz¨ahl-Version vonGI genauso schwer wie GI selbst (hier ohne Beweis), was die Vermutung f¨ur GI 6∈ N PV erh¨oht. Trotzdem reicht das bei Weitem nicht f¨ur einen tiefergehenden Aufschluss ¨uber die Komplexit¨at von GI, zeigt aber zumindest den Weg in die vermeintlich richtige Richtung auf.
Weitere Beispiele f¨urGI-vollst¨andige Probleme sind das Entscheiden nach einem Isomorphismus zwischen zwei bipartiten oder zwei beschrifteten Graphen, was nun zur Diskussion ¨uber die Komplexit¨at von Rooted Outgoing-Ordered Labeled Digraphs f¨uhrt.
In Definition 2.13 werden die beschrifteten Graphen eingef¨uhrt, mit denen im Folgenden gearbeitet wird. Wie bereits erw¨ahnt spielt es keine Rolle, ob ein Graph Beschriftungen an Knoten bzw. Kanten tr¨agt oder nicht – das Isomorphieproblem wird dadurch nicht leichter.
Behauptung 2.30.
Die Frage nach einem Isomorphismus zwischen zwei LDGs (beschriftet oder un- beschriftet) ist GI-vollst¨andig.
Beweisskizze. F¨ur die Transformation T von einem ungerichteten Graphen G= (V, E) zu einem LDG G0 = (V, E0, L, lab) mit L = {1,2} reicht es aus, f¨ur jede Kante {u, v} ∈E die Kanten (u, v,1)∈E0 und (v, u,1)∈E0 zu erzeugen. Außer- dem ist lab(v) = 1 f.a. v ∈V.
Man kann dann leicht zeigen, dass es f¨ur zwei gegebene ungerichtete GraphenG1, G2 genau dann einen Isomorphismus gibt, wenn T(G1)∼=T(G2).
Betrachtet man nun die Outgoing-Ordered-Eigenschaft etwas genauer wird man schnell zu der Erkenntnis gef¨uhrt, dass das GI-Problem ebenfalls nicht einfacher wird, wenn die Beschriftungen von ausgehenden Kanten pro Knoten eindeutig sind.
Behauptung 2.31.
Die Frage nach einem Isomorphismus zwischen zweiOOLDGs istGI-vollst¨andig.
Beweis. Der Beweis hierzu erfolgt anlehnend an [3], Proposition 2.6.
Aus Behauptung 2.30 folgt trivialerweise, dass das Problem in GI ist. Um zu zeigen, dass es GI-hart ist (und damit auch GI-vollst¨andig) transformiert man
einen beliebigen unbeschrifteten gerichteten GraphenG= (V, E) in einenOOLDG G0 = (V0, E0, L, lab) mit L={1,2} und lab(v) = 1 f¨ur alle v ∈V:
Jede Kante (v1, v2) ∈ E aus G wird durch zwei Kanten (v, v1,1) ∈ E0 und (v, v2,2) ∈ E0 in G0 ersetzt, wobei v ∈ V0 ein neuer Knoten ist. Sei T die eben gew¨ahlte Transformation. Als Beispiel ist Abbildung 7 zu betrachten:
−→
T1
1
1 1
2
2 2
2
Abbildung 7: Beispieltransformation
F¨ur zwei gegebene unbeschriftete gerichtete Graphen G1, G2 gilt: G1 ∼= G2 ⇐⇒
T(G1)∼=T(G2): Jeder Isomorphismus π von T(G1) und T(G2) bildet ausschließ- lich alte auf alte Knoten und neue auf neue Knoten ab, weil nur die neuen Knoten ausgehende Kanten und nur die alten Knoten eingehende Kanten haben. Auf- grund der Wahl der Beschriftungen 1, 2 bleiben die Kantenrichtungen erhalten.
Da die Transformation T die Gr¨oße des Graphen h¨ochstens verdoppelt und das Isomorphieproblem f¨ur unbeschriftete gerichtete Graphen GI-vollst¨andig ist, ist das Isomorphieproblem f¨ur OOLDGs GI-hart.
Letztlich bleibt noch die Untersuchung vonRooted OOLDGs hinsichtlich des Iso- morphieproblems. Aus Behauptung 2.31 ist bekannt, dass dieses f¨ur OOLDGs genauso schwer ist wie f¨ur gew¨ohnliche Graphen. Es stellt sich allerdings heraus, dass das Problem unter Hinzunahme der Anforderung an den Graphen, dass er schwach zusammenh¨angend ist und eine Wurzel existiert, von der aus alle anderen Knoten erreichbar sind, deutlich einfacher wird. Genauer: Es existiert ein in po- lynomieller Zeit laufender Algorithmus, der dasGI-Problem f¨urRooted OOLDGs l¨ost.
Dieser (aus [3], Proposition 2.9 stammend) wird in den folgenden Kapiteln vorge- stellt, implementiert und getestet.
3 Algorithmen
Nachdem im vorangehenden Kapitel die elementaren Begriffe gekl¨art und ei- ne knappe Einordnung der Komplexit¨at des GI-Problems zum einen allgemein, zum anderen aber auch auf die Rooted OOLDGs bezogen, vorgenommen wurden, k¨onnen jetzt die Algorithmen vorgestellt werden, die letztlich als Hauptbestand- teil dieser Arbeit implementiert und getestet werden sollen.
Die Vorstellung erfolgt dabei vorwiegend explanatorisch, wobei die Algorithmen selbst als Pseudocode bzw. sprachliche Berechnungsvorschriften aufgeschrieben sind. Implementierungstechnische Details finden sich anschließend in Kapitel 5.
Das Ziel ist nach wie vor die effiziente ¨Uberpr¨ufung der Isomorphie f¨ur zweiRooted OOLDGs und auch die Berechnung des entsprechenden Isomorphismus π.
Diese Graphklasse basiert allerdings prim¨ar auf LDGs, also Graphen, die nicht notwendigerweise Rooted sind bzw. der Outgoing-Ordered Eigenschaft nachkom- men. Dass Letztere f¨ur die polynomielle Untersuchung hinsichtlich eines Isomor- phismus zweier Rooted LDGs nicht unbedingt wesentlich ist, wird in Abschnitt 3.3 anhand der in Definition 2.21 eingef¨uhrten OO-Subgraphen erl¨autert. Trotz- dem ist dieOutgoing-Ordered Eigenschaft unabdingbar f¨ur den Hauptalgorithmus (OO-Subgraphen erf¨ullen diese Eigenschaft per Konstruktion nat¨urlich auch). Im praxisbezogenen Alltag wird, wie eingangs beschrieben, auch tats¨achlich mitRoo- ted OOLDGs gearbeitet.
3.1 ¨ Uberpr¨ ufung der Rooted Outgoing-Ordered Eigenschaft
Im Hinblick auf den Isomorphietest f¨ur zwei Rooted Outgoing-Ordered Labeled Di- graphs ist es also zun¨achst erforderlich, die Eingaben f¨ur den Algorithmus ([3], Proposition 2.9) hinsichtlich der Erf¨ullung dieser notwendigen Eigenschaften zu untersuchen. Schließlich m¨ussen die eingegebenen Graphen nicht direkt Rooted sein bzw. derOutgoing-Ordered Eigenschaft nachkommen (w¨aren wenigstens ihre OO-Subgraphen Rooted, dann k¨onnte man in diesem Fall den Umweg ¨uber diese gehen; siehe Abschnitt 3.3). Nichtsdestotrotz bedarf es demnach einer Subrouti- ne, die die genannten ¨uberpr¨ufenden Aufgaben ¨ubernimmt. Diese kann in mehrere Phasen unterteilt werden:
Phase 1: ¨Uberpr¨ufung der Outgoing-Ordered Eigenschaft
Damit ein LDG G= (V, E, L, lab) die Outgoing-Ordered Eigenschaft erf¨ullt, darf f¨ur jeden Knoten die Anzahl seiner ausgehenden Kanten mit gleicher Beschriftung h¨ochstens eins sein, also |{(v, w, l) ∈ E | w ∈ V}| 6 1 f¨ur jeden Knoten v ∈ V und jede Beschriftung l ∈L.
Um das letztlich zu verifizieren, reicht es aus alle Kanten (v1, v2, label) ∈ E zu durchlaufen und eine Kombination aus v1 und labelabzuspeichern. Trifft man bei einer weiteren Iteration erneut auf eine solche Kombination, so kann man direkt den Bool-Wert falsezur¨uck geben und terminieren, weil dann f¨urv1 mindestens zwei ausgehende Kanten mit der Beschriftung label existieren.
Der folgende Pseudo-Code soll diese Idee vermitteln. Die Eingabe ist ein beschrif- teter (oder unbeschrifteter) gerichteter Graph G und ausgegeben wird true, falls G die Outgoing-Ordered Eigenschaft erf¨ullt bzw. false, falls er sie nicht erf¨ullt:
Algorithmus 1 Uberpr¨¨ ufung derOutgoing-Ordered-Eigenschaft
1: function OOProperty(G)
2: List counting = new List();
3:
4: for all (v1, v2, label)∈E do
5: if counting.contains([v1, label]) then
6: return false;
7: else
8: counting.add([v1, label]);
9: end if
10: end for
11:
12: return true;
13: end function
Unterstellt man, dass counting.contains() in konstanter Zeit funktioniert, so veri- fiziert die FunktionOOProperty(G)inO(|E|) Zeit die Erf¨ullung derOutgoing- Ordered Eigenschaft.
Phase 2: ¨Uberpr¨ufung der 1-rooted (Rooted) Eigenschaft
Ein LDG GistRooted, fallsGschwach zusammenh¨angend ist und es genau einen Knoten gibt, der keine eingehenden Kanten hat und von dem aus alle anderen Knoten erreichbar sind.
Um schnell zu testen, dass es tats¨achlich nureine Wurzel gibt, kann man in der Datenstruktur f¨ur die Graphen direkt beim Einf¨ugen, Modifizieren und Entfernen von Knoten oder Kanten kontrollieren, ob f¨ur den bzw. die betroffenen Knoten die Anzahl seiner bzw. ihrer eingehenden Kanten null oder gr¨oßer ist. Alle Knoten, die keine eingehenden Kanten haben, werden in einer Liste Roots gespeichert, so dass nun nur noch abgefragt werden muss, ob die Gr¨oße dieser Liste eins ist oder nicht.
Algorithmus 2 Uberpr¨¨ ufung, obgenaueine Wurzel existiert
1: function OneRoot(G)
2: if G.Roots.size()6= 1 then
3: returnfalse;
4: else
5: returntrue;
6: end if
7: end function
Wird die Funktion OneRoot(G) zu true ausgewertet, kann nun f¨ur diese eine in G existierende Wurzel ¨uberpr¨uft werden, ob von ihr aus alle anderen Knoten erreichbar sind, woraus direkt der schwache Zusammenhang von G folgt. Diese Konsequenz wird in folgender Behauptung verdeutlicht:
Behauptung 3.1.
Wenn es in einem gerichteten Graphen G = (V, E) einen initialen Knoten gibt, dann istG schwach zusammenh¨angend.
Beweis. Sei G= (V, E) ein gerichteter Graph und sei r∈V ein initialer Knoten, d.h. f¨ur allev ∈V\{r} existiert ein Weg (r, v1, v2, . . . , v) in G.
Weiterhin sei Ge = (V, E0) der entsprechende ungerichtete Graph von G, d.h. f¨ur alle (a, b)∈E ist die Kante {a, b} ∈E0.
Seienu, v ∈V beliebige Knoten. Weil inGdie Wege (r, u1, . . . , u) und (r, v1, . . . , v) existieren, gibt es diese Wege auch inG. Insbesondere sind im ungerichteten Graphe Ge aber auch die Wege (u, . . . , u1, r) und (v, . . . , v1, r).
Damit existiert ebenso in Ge der Weg (u, . . . , u1, r, v1, . . . , v) von u nach v, womit Ge zusammenh¨angend und somitG schwach zusammenh¨angend ist.
Um das Vorhandensein der Rooted Eigenschaft also vollst¨andig zu untersuchen, reicht es, eine Tiefensuche von der Wurzelr des Graphen Gausgehend zu starten und am Ende zu ¨uberpr¨ufen, ob alle Knoten erreicht wurden.
Die eigentlich gew¨ohnliche Tiefensuche ist insofern modifiziert, dass dieAnzahl der insgesamt besuchten Knoten stets gespeichert und inkrementiert wird. Damit wird sich nach Beendigung der Suche das Durchlaufen desbesucht-Arrays gespart, um sicherzustellen, dass auch tats¨achlich alle Knoten besucht wurden. Es gen¨ugt, die gespeicherte Anzahl mit der tats¨achlichen Anzahl der Knoten zu vergleichen.
Im folgenden Algorithmus ist die beschriebene Idee pseudocodem¨aßig dargestellt:
Algorithmus 3 Uberpr¨¨ ufung derinitial-Eigenschaft der Wurzel
1: function WeaklyConnected(G)
2: Node root = G.getRoot();
3: Stack stack =new Stack();
4: int visitednodes = 0;
5:
6: for all Node v ∈V do
7: visited[v] = false;
8: end for
9:
10: stack.push(root);
11: while ¬stack.empty() do
12: Nodecurrentnode = stack.pop();
13: visitednodes++;
14:
15: if ¬visited[currentnode]then
16: visited[currentnode] = true;
17:
18: for all successor nodes w of currentnode do
19: if ¬visited[w] then
20: stack.push(w);
21: end if
22: end for
23: end if
24: end while
25:
26: if G.numberOfNodes() == visitednodes then
27: returntrue;
28: else
29: returnfalse;
30: end if
31: end function
Abh¨angig von der gew¨ahlten Datenstruktur erreicht dieser Algorithmus die tiefen- suche-typische Laufzeit von O(|V|+|E|).
Ein eingegebener LDG G hat also genau dann die Rooted Outgoing-Ordered Ei- genschaft, wenn die drei vorgestellten Algorithmen jeweils zutrueauswerten. Die Gesamtlaufzeit ergibt sich zuO(|E|+ 1 +|V|+|E|) =O(|V|+|E|) =O(|G|) und ist linear in der Gr¨oße des Graphen G.
3.2 Isomorphietest f¨ ur Rooted Outgoing-Ordered Labeled Digraphs
Nachdem ein eingegebener Graph mit den pr¨asentierten Methoden auf die Eig- nung zur Durchf¨uhrung des Isomorphietest gepr¨uft wurde, soll jetzt der eigentliche Algorithmus diskutiert werden, mit dem dieser Test realisiert wird. Wie schon an mehreren Stellen angef¨uhrt, stammt dieser aus [3], Proposition 2.9.
Behauptung 3.2.
Das Isomorphieproblem f¨ur Rooted OOLDGs ist effizient l¨osbar.
Bevor mit der eigentlichen Berechnung begonnen wird, sind vorl¨aufig einige, teils triviale Umst¨ande zu kontrollieren, um die in Definition 2.16 verankerten Iso- morphiebedingungen m¨oglicherweise direkt als verletzt zu erkennen und somit kostbare Rechenleistung zu sparen.
Es ist klar, dass man f¨ur zwei gegebene Rooted Outgoing-Ordered Labeled Digra- phs G1 = (V1, E1, L1, lab1), G2 = (V2, E2, L2, lab2) die Frage nach G1 ∼= G2 direkt verneinen kann, falls |V1| 6=|V2| oder|E1| 6=|E2| ist, denn die entstehende Abbildung π muss bijektiv sein. Außerdem muss zur Existenz eines Isomorphis- mus die Kantenstruktur beider Graphen gleich sein, was bei unterschiedlichen M¨achtigkeiten der Kantenmengen nicht m¨oglich ist.
Ein weiterer vorl¨aufiger Schritt ist die ¨Uberpr¨ufung auf Gleichheit der beiden Be- schriftungsmengen L1, L2. Die besagten Isomorphiebedingungen setzen L1 = L2 voraus, damitG1 ∼=G2gelten kann, weil die Knoten- und auch Kantenbeschriftun- gen konsistent bez¨uglich der Abbildung π sein m¨ussen. Entsprechend kann man annehmen, dass jede Beschriftung l ∈ L1 in G1 und k ∈ L2 in G2 benutzt wird (unbenutzte Beschriftungen werden schlichtweg tempor¨ar aus den Mengen ent- fernt). Mit dieser Annahme k¨onnte man L1 6=L2 so interpretieren, dass es in G1 oderG2 einen Knoten bzw. eine Kante gibt, die im jeweils anderen Graphen nicht existiert, womit die Isomorphiebedingungen direkt verletzt sind. Die zu testende Gleichheit kann schnell ausgef¨uhrt und f¨ur eine vorzeitige Entscheidung benutzt werden, falls sie mit nein beantwortet wird.
Stimmt also sowohl die Anzahl der Knoten und Kanten als auch die Menge der Beschriftungen ¨uberein, so kann der eigentliche Algorithmus durchgef¨uhrt werden.
Dieser ist im Folgenden zum einen in sprachlicher Form, zum anderen auch durch Pseudocode dargestellt.
Dabei bezeichne r1 die Wurzel (root) von G1 und r2 die Wurzel (root) von G2. Die folgenden Schritte wurden von der Beschreibung aus [3] in einer implementie- rungsn¨aheren Kurzfassung des Algorithmus verarbeitet.
Algorithmus 4 Uberpr¨¨ ufung, ob zwei gegebeneRooted OOLDGs isomorph sind.
(1) Speichere alle Kanten (w1, w2, l)∈ E2 mit Schl¨ussel (w1, l) und Wertw2 in einer Datenstrukturedges mit einer effizienten Lookup-Operation.
(2) Initialisiere ein visited-Array. Setze den Wert auf false f¨ur alle Knoten v ∈V1.
(3) Setzeπ(r1) :=r2, fallslab1(r1) =lab2(r2) – sonst terminiere. F¨uger1 in den Stack nodes ein.
(4) Solange der Stack nicht leer ist, tue Folgendes:
(a) Sei v1 der Knoten, der durch nodes.pop() zur¨uckgegeben wird.
Falls visited[v1] == true, ¨uberspringe diesen Durchlauf.
Setzevisited[v1] = true.
(b) Durchlaufe alle Kanten (v1, v2, l) ∈ E1 und setze π(v2) := w2, falls lab1(v2) = lab2(w2), wobei w2 der Wert zu dem Schl¨ussel (π(v1), l) in edges ist.
(i) Wurde π(v1) bereits anders definiert oder ist lab1(v2) 6= lab2(w2), dann terminiere, denn G1 6∼=G2.
(ii) F¨uge v2 zunodes hinzu, falls visited[v2] == false.
(5) π ist der eindeutige Isomorphismus von G1 und G2.
Prinzipiell wird auch hier eine gew¨ohnliche Tiefensuche benutzt, welche allerdings iterativ beschrieben und sp¨ater auch so implementiert ist. Bevor auf die Laufzeit und weitere Details eingegangen wird, ist die Beschreibung in Pseudocode vorzu- stellen, die sich an der eben vorgef¨uhrten sprachlichen Deskription orientiert.
Algorithmus 4 Uberpr¨¨ ufung, ob zwei gegebeneRooted OOLDGs isomorph sind.
1: function CheckIsomorphism(G1, G2)
2: Dictionary edges =new Dictionary();
3: Array visited = new Array();
4: Stack stack =new Stack();
5:
6: for all (w1, w2, l)∈E2 do .(1)
7: edges.add((w1, l),w2);
8: end for
9: for all nodes v ∈V1 do .(2)
10: visited[v] = false;
11: end for
12:
13: if lab1(r1) ==lab2(r2) then .(3)
14: π(r1) :=r2;
15: stack.push(r1);
16: else
17: returnfalse;
18: end if
19:
20: while ¬stack.empty() do .(4)
21: v1 = stack.pop();
22: if visited[v1] then .(4a)
23: continue;
24: else
25: visited[v1] = true;
26: end if
27:
28: for all (v1, v2, l)∈E do . (4b)
29: w2 = edges.get((π(v1), l));
30:
31: if lab1(v2) ==lab2(w2)and(π(v2) ==null orπ(v2) ==w2)then
32: π(v2) := w2;
33:
34: if ¬visited[v2] then .(4b(ii))
35: stack.push(v2);
36: end if
37: else .(4b(i))
38: return false;
39: end if
40: end for
41: end while
42:
43: return π; .(5)
44: end function
Bez¨uglich der Laufzeit des vorgestellten Algorithmus ist zu sagen, dass in den Ini- tialisierungsvorg¨angen zun¨achstO(|E2|log|E2|+|V1|log|V1|) Zeit ben¨otigt wird, um die Kanten zu speichern und dasbesucht-Array zu initialisieren. W¨ahrend der
Hauptschleife werden alle Knoten aus V1 und die zugeh¨origen Pfade, sprich |E1|, betrachtet, was wiederum zur tiefensuche-typischen Laufzeit von O(|V1|+|E1|) f¨uhrt. Dabei muss f¨ur jede Kante aus E1 die Lookup-Operation f¨ur die edges- Datenstruktur in O(log|E2|) Zeit angewendet werden.
Summiert man die angegebenen asymptotischen Schranken auf, gelangt man zu einer Gesamtzeit vonO(|E2|log|E2|+|V1|log|V1|+|V1|+|E1|log|E2|). Um diese al- lerdings etwas kompakter abzusch¨atzen und implementierungsabh¨angige Schwan- kungen mit einzuberechnen, wirdn:=|V1|+|E1|+|V2|+|E2|=|G1|+|G2|gesetzt, wodurch eine Gesamtlaufzeit von O(nlogn) resultiert.
Weiterhin ist klar, dass alle Knoten besucht werden, weil die Graphen per Voraus- setzung Rooted sind und damit von dem Startknoten, also der Wurzel, aus jeder andere Knoten erreichbar ist. Es entsteht außerdem eineindeutigerIsomorphis- mus π, falls es zwischendurch nicht zu einem Konflikt kommt, weil ein Knoten bereits anders inπ definiert war.
3.3 Berechnung des Outgoing-Ordered Subgraphs
Der Outgoing-Ordered Subgraph (kurz: OO-Subgraph) eines LDGs G ist der Graph, der entsteht, wenn man aus G alle mehrdeutigen Kantenbeschriftungen entfernt (vgl. Definition 2.21). Doch wozu ist er in Bezug auf den Isomorphietest n¨utzlich? Die folgende Behauptung kl¨art diese Frage:
Behauptung 3.3.
Seien G1 = (V1, E1), G2 = (V2, E2) zwei LDGs, so dass ihre OO-Subgraphen G0i :=OO(Gi) mit i= 1,2 die Rooted Eigenschaft besitzen.
Dann kann die Frage nach einem Isomorphismus zwischenG1 und G2 mittels Al- gorithmus 4 in ZeitO(nlogn) mitn=|G1|+|G2|beantwortet werden. Außerdem gibt es h¨ochstens einen solchen Isomorphismus.
Beweis. Eine bijektive Abbildung π:V1 →V2 ist genau dann ein Isomorphismus von G1 nachG2, wennπ ein Isomorphismus vonG01 nachG02 ist, da in G0i,i= 1,2 keine Knoten entfernt wurden.
Außerdem haben die Graphen G0i per Konstruktion die Outgoing-Ordered Eigen- schaft, so dass Algorithmus 4 mit den Eingaben G01 und G02 aufrufbar ist. Es ist bereits bekannt, dass die berechnete Abbildung πeindeutig ist, falls der Algorith- mus G01 ∼=G02 erfolgreich feststellt.
Damit ist es realisierbar, die eigentlich GI-vollst¨andige Frage nach der Isomor- phie zweier LDGs zu ¨uberpr¨ufen, welche weder Rooted sind noch die Outgoing- Ordered Eigenschaft besitzen. Die einzige Voraussetzung hierf¨ur ist, dass ihre OO- Subgraphen Rooted sind.
Wie man effizient ¨uberpr¨uft, ob ein eingegebener Graph diese Eigenschaft besitzt, wurde ausf¨uhrlich in Abschnitt 3.1 beschrieben. Zentral in diesem Teil der Arbeit soll der Algorithmus zur Berechnung des OO-Subgraphs sein.
Prinzipiell besteht die Hauptaufgabe dabei lediglich darin, die Menge der Kanten E zu durchlaufen und all diejenigen Kanten zu entfernen, die von demselben Kno- ten mit derselben Beschriftung ausgehen. Im nachfolgenden Pseudo-Code wird die- se Idee realisiert, indem zuerst die Kanten gez¨ahlt und anschließend nur diejenigen in den Subgraphen aufgenommen werden, die nicht ¨ofter als einmal vorkommen:
Algorithmus 5 Berechnung des OO-Subgraph eines gegebenen LDGs.
1: function CalculateOOSubgraph(G)
2: Graph oosubgraph = new Graph();
3: Dictionary counting = new Dictionary();
4:
5: oosubgraph.Labels = G.Labels; . copy all labels
6: oosubgraph.Nodes = G.Nodes; . copy all nodes
7:
8: for all (v1, v2, label)∈E do
9: if counting.contains((v1, label))then
10: counting.add((v1, label), counting.get((v1, label))+1);
11: else
12: counting.add((v1, label), 1);
13: end if
14: end for
15:
16: for all (v1, v2, label)∈E do
17: if counting.get((v1, label)) <2then
18: oosubgraph.addEdge(v1, v2, label); . add edge to subgraph
19: end if
20: end for
21:
22: return oosubgraph;
23: end function
Es ist direkt ablesbar, dass in O(|L|+|V|+ 2|E|) =O(|L|+|V|+|E|) Zeit der OO-Subgraph eines Graphen G berechenbar ist. Wie eingangs beschrieben, l¨asst sich mit diesem anschließend – sofern er die Rooted Eigenschaft besitzt – die Iso- morphie zweier LDGs testen.
In Kapitel 5 sind diese Algorithmen implementiert und vorgestellt. Außerdem fin- den sich im Anschluss Tests zur Laufzeit und Effizienz dieser.
Da die fundamentalen Algorithmen nun bekannt sind, kann sich den Rahmengege- benheiten f¨ur die zu entwickelnde Implementierung gewidmet werden. Haupts¨ach- lich werden hierbei im folgenden Kapitel die, im Sinne der Laufzeit nicht unerheb- liche, Datenstruktur f¨ur die Graphen und weitere Komponenten des Programms vorgestellt.
4 Design und Verwendung
Um die pr¨asentierten Algorithmen letztlich implementieren zu k¨onnen, ist es zun¨achst notwendig, sich f¨ur eine Programmiersprache zu entscheiden. Im Rah- men dieser Bachelorarbeit wird mit der, dem imperativen Programmierparadigma folgenden, SpracheJavagearbeitet, welche in ihrer Entwicklung stark vonC bzw.
C++ gepr¨agt wurde, aber dennoch weniger low-level Funktionalit¨aten als diese besitzen.
Java ist insbesondere deshalb so praktikabel, weil es, begr¨undet durch die soge- nannte Java Virtual Machine (JVM), unabh¨angig von dem jeweiligen Betriebs- system ist, auf dem ein Java-Programm ausgef¨uhrt werden soll. Das Programm wird, anders als bei anderen Programmiersprachen, zun¨achst in denJava Byteco- de ¨ubersetzt, welcher erst innerhalb der besagten JVM zu plattformspezifischem Maschinencode kompiliert wird. Bei
”herk¨ommlichen“ Programmiersprachen f¨allt dieser Zwischenschritt weg, weil das Programm direkt in den Maschinencode trans- formiert wird.
Trotzdem wird, wie in [2] beschrieben, Java-Programmen nachgesagt, dass sie langsamer sind und mehr Speicherplatz als C++ -Programme ben¨otigen. Seit der Einf¨uhrung des Just-In-Time Java Compilers von Symantec (vgl. [5]) ist die Ausf¨uhrungsgeschwindigkeit von Java Programmen jedoch rapide angestiegen, weil zahlreiche Optimierungen der JVM vorgenommen und zus¨atzliche Features f¨ur die Programmiersprache eingef¨uhrt wurden, womit ihr Code besser und vor allem schneller analysiert werden kann.
Grunds¨atzlich istJavaobjekt-orientiert, wird aber nicht als
”reine objekt-orientier- te Sprache“ angesehen, weil ihreprimitiven Datentypen selbst keine Objekte sind.
Im Gegensatz zu anderen Sprachen haben sich die Java-Designer daf¨ur entschie- den, die Werte von Variablen von primitiven Datentypen in Feldern oder auf dem Stack zu speichern anstatt, wie eigentlich ¨ublich, im Heap. Die Entscheidung hier- zu beruht auf Performanzgr¨unden.
Dieses Kapitel soll prim¨ar einen ¨Uberblick ¨uber die benutzte Datenstruktur f¨ur ge- richtete (un-)beschriftete Graphen geben und den Interpreter vorstellen, mit dem der Anwender flexibel Graphen erstellen und die Algorithmen auf ihnen ausf¨uhren kann.
4.1 Die Datenstruktur f¨ ur Graphen
Wie erw¨ahnt wird mit einer objekt-orientierten Programmiersprache gearbeitet, so dass es f¨ur die Implementierung naheliegend ist, auf eine Klassenstruktur zur¨uck- zugreifen. Zur Visualisierung der Idee der Klassenkonstruktionen wird zun¨achst
eine Darstellung in derUnified Modeling Language (UML) angegeben, welche un- ter anderem Klassendiagramme zur Verf¨ugung stellt und damit Klassenstrukturen und ihre Beziehungen untereinander anschaulich abbilden kann.
Graph
#NodeMapping: Map<String, Node>
#Labels: List<String>
#AdjacencyList: Map<Node, List<Edge>>
#CountEdges: Integer
#Roots: List<Node>
#NodeLabels: Map<String, String>
+Graph() +CheckRoot() +addLabel() +getLabelByIndex() +getLabelByName() +getLabelPosition() +removeLabel() +exportGraph()
+addNode() +existsNode() +changeNodeLabel() +getSuccessors() +removeNode() +addEdge() +existsEdge()
+changeEdgeLabel()
+removeEdge() +printGraph() +printLabels() +printNodes() +printEdges() +generateMap()
Node
-name: String -label: String -in degree: Integer -out degree: Integer +Node()
+getLabel() +getName() +getInDegree() +getOutDegree()
+setLabel() +incInDegree() +incOutDegree() +decInDegree() +decOutDegree()
Edge
-from: Node -to: Node -label: String +Edge()
#finalize() +setLabel() +getLabel()
+getNameFrom() +getNameTo() +getLabelFrom() +getLabelTo()
1
0. . .∗ hat
1
0. . .∗ hat
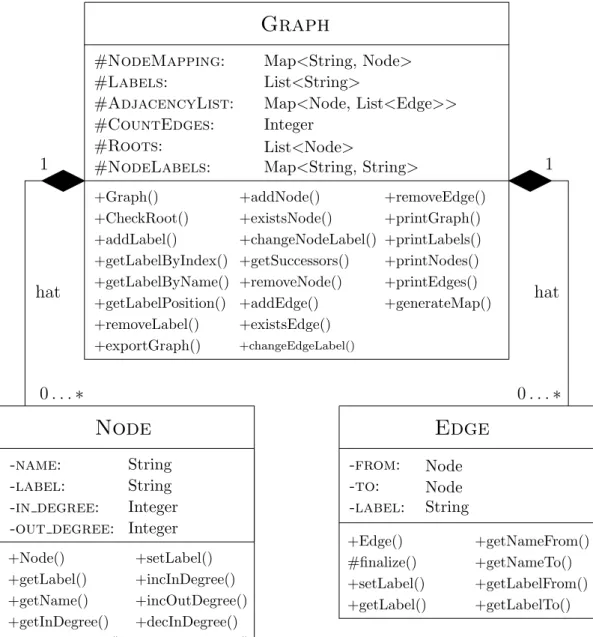
Abbildung 8: UML-Klassendiagramm f¨ur Graphen
Die HauptklasseGraphbesitzt zwei sogenannteInner Classes,NodeundEdge, welche durch Java unterst¨utzt und direkt im Code der Graph-Klasse definiert werden. Im obigen UML-Diagramm wurde diese Beziehung durch eine Komposi-
tion dargestellt (hat-Beziehung). Die Multiplizit¨aten geben hierbei an, dass eine Instanz der Klasse Graph beliebig viele (0. . .∗) Instanzen der Klasse Node bzw. Edge besitzen kann, wobei umgekehrt jede Instanz der Klasse Node bzw.
Edge zugenau einer (1) Instanz der KlasseGraph geh¨ort.
Es wird nun genauer auf die einzelnen Klassen eingegangen und ihre Funktions- weisen erl¨autert.
4.1.1 Die Klasse Node
In dieser Klasse werden die Knoten des Graphen verwaltet. Dabei hat jeder Kno- ten einen Namen name vom Typ String und eine Beschriftung label, eben- falls vom Typ String. Weiterhin werden der Eingangsgrad in degree und auch der Ausgangsgrad out degree, jeweils Integerzahlen, zu jedem Knoten gespei- chert und aktuell gehalten. Dies dient haupts¨achlich der Identifizierung alsWurzel (in degree = 0) bzw. als normaler Knoten (in degree 6= 0). Hierauf wird im sp¨ateren Verlauf dieser Arbeit erneut Bezug genommen.
Erw¨ahnenswert ist, dass der Name eines Knotens zur eindeutigen Identifizierung verwendet wird – soll heißen: Es darf keine zwei Knoten mit demselben Namen geben.
Die genannten Attribute der Klasse haben allesamt den Sichtbarkeitsmodifikator
”-“, sind alsoprivateund somit nur von der eigenen Klasse einseh-/modifizierbar.
Um die Attribute zu manipulieren bzw. auszulesen, sind aus diesem Grund Get- ter- und Setter-Methoden vorgesehen, die wiederum public (+) sind, das heißt auf die von außen zugegriffen werden kann.
Mittels getLabel(), getName(), getInDegree() und getOutDegree() k¨onnen die At- tribute ausgelesen werden, wobei lediglich der Wert zur¨uckgegeben wird und an- sonsten keine weiteren Befehle ausgef¨uhrt werden. Ferner ist es durch die Methode setLabel() m¨oglich, die Beschriftung des Knotens explizit zu setzen.
Bei der Instanziierung Node() der Objekte wird zwingend ein Knotenname ben¨o- tigt, aber nicht unbedingt eine Beschriftung. F¨ur unbeschriftete Graphen wird dann immer der einzige Eintrag l ∈L als Standardbeschriftung ausgew¨ahlt. Au- ßerdem ist die Absicht der eindeutigen Identifizierung ¨uber den Knotennamen der Grund daf¨ur, dass es keinesetName()-Methode in der Klasse Nodegibt. M¨ochte man einen Knoten umbenennen, so muss man ihn zun¨achst mit Hilfe von remo- veNode() entfernen und anschließend mit neuem Namen wieder hinzuf¨ugen.
Zur Anpassung des Ein- und Ausgrad-Wertes gibt es die MethodenincInDegree() und incOutDegree() bzw.decInDegree() und decOutDegree(), mit denen man den entsprechenden Wert entweder um eins erh¨ohen oder um eins vermindern kann.
Die Klasse Node braucht zudem Zugriff auf die Menge der Beschriftungen aus der Graph-Instanz, falls ein beschrifteter Graph angelegt wird und demnach alle
Knoten und Kanten gleich beschriftet sind. Aufgrund der Tatsache, dass Node eine Inner Class von Graph ist, wird dies allerdings direkt gew¨ahrleistet.
4.1.2 Die Klasse Edge
Die KlasseEdge soll die Menge der KantenE eines Graphen repr¨asentieren und funktioniert prinzipiell ¨ahnlich wie die eben vorgestellte KlasseNode. Sie besitzt drei Attribute: fromund to sind jeweils Objekte vom Typ Nodeund beschrei- ben den Knoten, von dem die Kante ausgeht (from) bzw. den Knoten, in den die Kante eingeht (to). Außerdem hat, per Definition eines LDGs, jede Kante eine Beschriftung, so dass auch hier ein Attributlabelvom Typ String ben¨otigt wird. Ebenso sind die Attribute aus den genannten Gr¨unden wieder private (-) und k¨onnen nur mittels Getter- & Setter-Methoden ausgelesen bzw. ver¨andert werden, die selbst wiederum public (+) sind.
Zur eindeutigen Identifizierung einer Kante wird jetzt die Kombination aus allen drei Attributen gew¨ahlt. Das ist notwendig, weil es mehrere Kanten von Kno- ten v zu Knotenu geben kann, falls die jeweiligen Beschriftungen unterschiedlich gew¨ahlt wurden.
Zum Lesen deslabel-Wertes gibt es die MethodegetLabel(), die den entsprechen- den String zur¨uckliefert. Um die Beschriftung zu setzen, istsetLabel() vorgesehen.
Die from- und to-Werte selbst k¨onnen direkt nicht ausgelesen werden, sondern nur der Name bzw. die Beschriftung des entsprechenden Knotens. Daf¨ur sind die Methoden getNameFrom(), getNameTo(), getLabelFrom() und getLabelTo() vor- gesehen, die ebenfalls direkt den zugeh¨origen String zur¨ucksenden. Es wird also nur indirekt mit den eigentlichen Instanzen der Klasse Node gearbeitet.
Weiterhin ist beim Anlegen einer Kante mittels des Konstruktors Edge() der Ein- Grad vom Knoten to und der Aus-Grad vom Knoten from zu inkrementieren.
Insbesondere sollte anschließend ¨uberpr¨uft werden, ob dadurch die beiden Kno- ten die Wurzel-Eigenschaft verlieren oder erhalten. Als Destruktor ist finalize() vorgesehen, der den Ein- bzw. Aus-Grad dekrementiert und erneut die Wurzel- Uberpr¨¨ ufungen aufrufen soll.
4.1.3 Die Klasse Graph
Wie bereits erw¨ahnt, besteht die Klasse Graph aus Instanzen von Node und Edge, die in einer Datenstruktur AdjacencyListvom Typ Map als Adjazenz- liste verwaltet werden. Diese Map bildet hierbei einen Knoten (Schl¨ussel) auf eine Liste von Kanten (Wert) ab. Ihre Gr¨oße gibt damit die Anzahl der Knoten im Graphen an. Um die Anzahl der Kanten abzufragen (was haupts¨achlich im Hin- blick auf Algorithmus 4 relevant ist), m¨usste man jede einzelne Kantenliste pro Knoten durchgehen und einen Z¨ahler inkrementieren. Aus Laufzeitgr¨unden soll
deshalb ein Attribut CountEdges stets die aktuelle Zahl der Kanten im Gra- phen speichern und direkt beim Erzeugen bzw. L¨oschen von Kanten modifiziert werden.
Weiterhin dient das Attribut NodeMapping dazu, den Name eines Knotens auf seine zugeh¨orige Node-Instanz abzubilden, um auch hier Laufzeit einzusparen und die jeweilige Instanz m¨oglichst schnell greifbar zu haben.
F¨ur die Menge der Beschriftungen L des Graphen ist eine Liste Labels von Strings vorgesehen. Weiterhin soll ebenfalls beim Erzeugen bzw. Entfernen von Knoten bzw. Kanten eine Liste Roots aktuell gehalten werden, in der alle Kno- ten eingespeichert sind, die die Wurzel-Eigenschaft besitzen. Zudem ist, ebenso im Hinblick auf Algorithmus 4, eine Zuordnung NodeLabels von Knotennamen auf Knotenbeschriftung vorgesehen, um diese schnell abfragen zu k¨onnen.
Alle genannten Attribute sind protected (#), um dem gesamtem package und somit auch den Inner Classes Node und Edge Zugriff auf sie zu gew¨ahren. Von außerhalb sind sie allerdings nicht aufruf-/modifizierbar. Die Methoden der Klasse sind trivialerweise hingegen public(+).
Um Beschriftungen, Knoten und Kanten anzulegen, sind die Methoden addLa- bel(), addNode() und addEdge() vorgesehen. Zum Entfernen soll removeLabel(), removeNode() und removeEdge() benutzt werden. Wichtig ist an einigen Stellen, dass die interne CheckRoot()-Methode aufgerufen wird, um nach Ver¨anderungen zu ¨uberpr¨ufen, ob ein Knoten die Wurzel-Eigenschaft hat oder nicht. Hierzu wird das Attribut in degree der Klasse Node verwendet.
Weiterhin ist es per changeNodeLabel() bzw. per changeEdgeLabel() m¨oglich, die Beschriftung eines Knotens bzw. einer Kante zu modifizieren. Hier (aber auch beim Entfernen von Beschriftungen) ist es beispielsweise anschließend notwendig, redundante Kanten zu entfernen, falls durch die Modifizierung denn solche entste- hen. Erw¨ahnenswert ist außerdem, dass beim Anlegen eines Knotens bzw. einer Kante keine Beschriftung explizit angegeben wird, sondern immer automatisch die erste Beschriftungbder MengeLausgew¨ahlt wird. Das Gleiche passiert, wenn eine Beschriftung l entfernt wird – alle Knoten/Kanten, die diese Beschriftung l getragen haben, werden nun auf b gesetzt.
F¨ur die Visualisierung eines Graphen bzw. dessen Komponenten sind die Metho- den printLabels(),printNodes(), printEdges() und printGraph() gedacht. Die drei Erstgenannten geben lediglich zeilenweise ihre Eintr¨age aus, w¨ahrend die Letzt- genannte den Graph als Adjazenzliste darstellt.
Ansonsten erzeugtgenerateMap() die in Schritt (1) von Algorithmus 4 beschriebe- ne Datenstruktur und getSuccessors() gibt explizit die Nachfolger eines bestimm- ten Knoten zur¨uck.
Abschließend sei noch angef¨uhrt, dass mittelsexportGraph()eine Graph-Instanz in eine Datei exportiert werden kann, um sie sp¨ater wieder flexibel mittels des