1 Harmonische Kette

Phononen

Mathematische Bissen zu Kursvorlesungen der theoretischen Physik Martin Wilkens, Universit¨at Potsdam

Phononen sind quantisierten Elementaranregungen eines schwingungsf¨ahigen Gitters. Das einfachste Gitter ist die harmonische Kette. Die harmonische Kette ist ein Standard-Tanz der Physik den eine jede Physikerin/ein jeder Physiker beherrschen sollte . . .

1 Harmonische Kette

Abbildung 1: Die harmonische Kette.

N Teilchen, beispielsweise Atome, sind auf ei- ner Kette aufgereiht. In der Ruhelage der Ket- te spezifiziert durch ¨aquidistante Positionen R⁽⁰⁾₁ . . . R⁽⁰⁾n , mit R⁽⁰⁾_i+1 − R⁽⁰⁾_i = a, die Gitter- konstante unserer Kette. Die Auslenkung des i-ten Atoms aus der Ruhelage bezeichnen wirξ_i. Die Atome m¨ogen nur mit ihren n¨achsten Nach- barn wechselwirken, beispielsweise ¨uber Federn – vgl. Abb. 1. Mit Federn der Ruhel¨ange aund Federkonstante κ lautet die Hamiltonfunktion

H =

N

X

j=1

p²_j 2m +κ

2

N

X

j=1

(ξ_j+1−ξ_j)² (1) wobei hier der Einfachheit halber periodische

Randbedingungen angenommen wurden, d.h. ξ_N+1 = ξ₁ und ξ₀ = ξ_N. Die Kette ist also, wie eine handels¨ubliche Halskette, geschlossen.

Die Newton’schen Bewegungsgleichungen zur Hamiltonfunktion (1) lauten

mξ¨_j =−κ(2ξ_j −ξj−1−ξ_j+1), j = 1, . . . , N . (2) Das System ist linear: mitξ⁽¹⁾_j ein bestimmte L¨osung, undξ_j⁽²⁾ eine weitere solche L¨osung ist auch jede Linearkombinationξ⁽¹⁾+ξ⁽²⁾ eine L¨osung. Insbeondere d¨urfen wir auch komplexe L¨osungen aufsuchen. Die eigentlich interessierenden relle L¨osung erh¨alt man dann aus dem Realteil der komplexen L¨osung.

Das System ist translationsinvariant – wederκnochmh¨angen vonjab. Die rechte Seite von Gl. (2) ist die Differenz zweier Differenzen – so etwas wie die diskrete Variante der zweiten Ableitung. Es ist dann naheliegend, dass die j-Abh¨angigkeit durch diskrete ebene Wellen

∝e^ikja beschrieben werden kann (bei fester Wellenzahl k istjahier als “Raumkoordinate”

anzusehen). Mit dem entsprechenden Ansatz ξ_j,k = ˜ξ_k(t) 1

√Ne^ikja (3)

1 Harmonische Kette Mathematische Bissen: Phononen

ergibt sich unter Ber¨ucksichtigung von 2e^ikaj−e^ika(j−1)−e^ika(j+1) = 2 (1−cos(ka))e^ikaj = 4 sin²(ka/2)e^ikaj eine Schwingungsgleichung f¨ur die komplexe Amplitude

¨˜

ξ_k =−ω_k²ξ˜_k, (4)

wobei ω_k die Frequenz der Schwingung, ω_k =

r4κ

m|sin(ka/2)|. (5)

Die k-Abh¨angigkeit der Schwingungsfrequenz ω_k definiert die Dispersionsrelation der li- nearen Kette. Weil e^ikja in k periodisch mit Periode 2π/a, also ei(k+2π/a)ja = e^ikja, darf der Wertebereich der Wellenzahlen in der Dispersionsrelation o.B.d.A. auf das Intervall

−π/a ≤ k < π/a eingeschr¨ankt werden, genannt die erste Brillouin-Zone. Das Intervall ist halboffen um eine Doppelz¨ahlung auszuschließen: schließlich gleichen sich die Moden- funktionen zu k =−π/aund k = +π/a – in beiden F¨allen gegeben (−1)^j.

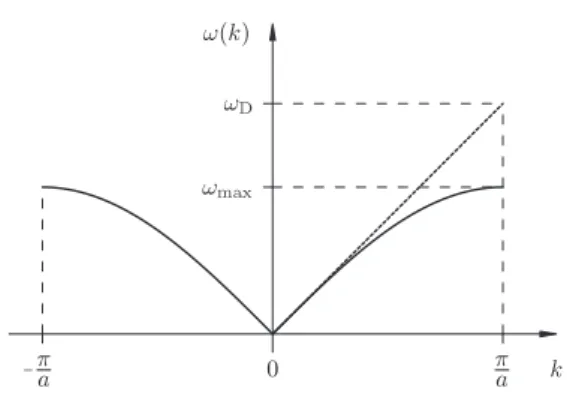
Abbildung 2:Dispersionsrelation der har- monischen Kette in der ersten Brillouin- zone.

Eine reelle L¨osung von (4) ist nun schnell hin- geschrieben: Ae^{i(kja−ωkt)}+c.c, wo A eine kom- plexe Konstanten die durch die Anfangsbedin- gung festgelegt wird. Die L¨osung ist vom Typ

“fortschreitende Welle”. Der Faktor ^√1

Ne^ikja definiert die Normalmode in der Zerlegung nach ebenen Wellen. Andere L¨osungen, etwa vom Typ “stehende Welle”, erh¨alt man aus Li- nearkombinationen gegenl¨aufig fortschreitender Wellen. Wir bleiben bei den fortschreitenden Wellen.

Wellenpakete werden durch ¨Uberlagerung von fortschreitenden Wellen leicht unterschiedli- cher Wellenzahlen gebildet. Solche Wellenpake- te propagieren mit der Gruppengeschwindigkeit v_k = ^dω_dk, auszuwerten f¨ur die Zentralwellenzahl des Pakets.

• An den Zonenr¨andern, also ka = ±π ist die Gruppengeschwindkeit gleich Null – die Wellenl¨ange ist minimal, λ= 2a, die Welle steht, benachbarte Atome schwingen gegenphasig mit Frequenz,

ωmax= r4κ

m . (6)

• Im Grenzfall großer Wellenl¨angen, also ka1, liest man aus der Dispersionrelation (5) ab ωk=csk, mit

c_s= rκa²

m (7)

die Schallgeschwindigkeit. In diesem Grenzfall fallen Phasengeschwindigkeit und Gruppengeschwindigkeit mit der Schallgeschwindigkeit zusammen, und Wellenpake- te propagieren ohne auseinanderzulaufen (sie behalten ihre Form). Im Debyschen

2 1D Phononen Mathematische Bissen: Phononen

Modell der harmonischen Kette wird eine lineare Dispersionsrelation ¨uber die ganze Brillouinzone angenommen – vgl. Abb. 2. Die Maximal-Frequenz ist dann nicht wie in (6) angegeben, sondern vielmehr ω_D =c_sk_max, mit k_max =π/a also

ωD =csπ/a , (8)

sog. Debye-Frequenz der harmonischen Kette.

Hat man es mit einer großen Zahl von Atomen zu tun,N 1, und sind die interessierenden Wellenl¨angen groß gegen die Gitterkonstante, ka1, greift man h¨aufig zur Kontinuums- beschreibung, bei der die Auslenkung ξ_j durch ein Feldξ(x) beschrieben wird,

ξ_j(t)→ξ(x, t), ξ_j±1 →ξ(x±a, t). (9) Taylorentwicklung zeitigt

ξj±1(t)≡ξ(x±a, t) =ξ(x, t)±a∂ξ(x, t)

∂x +a² 2

∂²ξ(x, t)

∂x² +. . . (10) und aus dem Satz diskreter Bewegungsgleichungen (2) wird die eindimensionale Wellen- gleichung

∂²ξ(x, t)

∂t² =c²_s∂²ξ(x, t)

∂x² . (11)

2 1D Phononen

In der Festk¨orperphysik trifft man selten auf Bewegungsgleichungen a la (2). Bezugspunkt ist vielmehr die Hamiltonfunktion bzw der daraus abgeleitete Hamiltonoperator. Den Ha- miltonoperator erh¨alt man kanonisch – d.h. H¨ute auf dieq_j, p_j, und Ersetzung der Poisson- klammern durch Kommutatoren,

[ˆq_j,pˆ_j⁰] =i~δ_jj⁰. (12) Vor dem Hintergrund der Translationsinvarianz empfiehlt sich f¨ur die harmonische Kette zun¨achst eine Koordinatentransformation auf Fourierkoordinaten,

ˆ qj = 1

√N X

k

e^ikajq˜k ; q˜k= 1

√N

N

X

j=1

ˆ

qje^−ikaj (13) ˆ

p_j = 1

√N X

k

e^−ikajp˜_k ; p˜_k= 1

√N X

j

ˆ

p_je^ikaj (14)

Die periodischen Randbedingungen ˆq₀ = ˆq_N implizieren eine Diskretisierung der Wellen- zahl,k =n^2π_a mitn ganze Zahl,n =n_min, n_min+ 1, . . . , n_max. Wir w¨ahlen hiern_min =−N/2 fallsN geradzahlig, undn_min =−(N−1)/2 fallsN ungeradzahlig. Der Wert vonn_maxergibt sich dann aus der Tatsache, dass eine Konfiguration derN-atomigen Kette wahlweise durch N Auslenkungenq_j oder ebenN Fourieramplituden ˜q_k spezifiziert ist,n_max=n_min+N−1.

Die Fourieramplituden sind komplex. Aus der Tatsache, dass die q_j reell sind folgt unmit- telbar ˜q^∗_k= ˜q−k, insbesondere ˜q₀ reell.¹

1Im FallN geradzahlig ist auch ˜qk_min reell, ˜qk_min= ^√1

N

P

j(−1)^jqj.

2 1D Phononen Mathematische Bissen: Phononen

Die Trafo () ist kanonisch, denn

[˜q_k,p˜_k⁰] = 1 N

X

jj⁰

[ˆq_j,pˆ_j⁰]

| {z }

=i~δ_jj0

e^{−i(jk−k0j0)a} (15)

= i~1 N

X

j

e^{−ij(k−k0)a} =i~δ_kk⁰ (16)

Eingesetzt in () lautet der Hamiltonoperator der harmonischen Kette zun¨achst ˆH =P

k

˜ pkp˜−k

2m +

m

2ω_k²q˜_kq˜−k F¨uhrt man an dieser Stelle Leiteroperatoren ein ˆ

a_k =

rmω_k 2~

˜ q_k+ i

mωk

˜ p−k

(17) ˆ

a^†_k =

rmω_k 2~

˜

q−k− i mω_kp˜_k

(18) nimmte der Hamiltonoperator die vertraute Form an,

Hˆ =X

k

~ω_k

ˆ

a^†_kˆa_k+1 2

. (19)

Die Leiteroperatoren gen¨ugen den bekannten Vertauschungsrelationen des harmonischen Oszillators,

h ˆ a_k,ˆa^†_k0

i

=δ_kk⁰ (20)

alle anderen Kommutatoren gleich Null. Kurz: die harmonische Kette ist aus dynamischer Sicht eine Menge ungekoppelter Oszillatoren, f¨ur jede Normalmode ein Oszillator, wobei der “Auslenkung” des Oszillators die Amplitude der Normalmode beschreibt. Anregungs- quanten heißen hier Phononen.

Hilbertraum ist das Produkt der Hilbertr¨aume der einzelnen Oszillatoren. Ein Basiszustand wird hier notiert

|Ψi=|n_k1, n_k2, . . . , n_ki, . . .i (21) mit Bedeutung

ˆ a^†_k

iˆa_ki|Ψi=n_ki|Ψi, (22)

lies: n_ki Phononen in Normalmode der Wellenzahl k_i. Im Heisenbergbild bewegen sich die Operatoren,

˜ q_k(t) =

r ~ 2mωk

ˆ

a_ke^−iωkt+ ˆa^†_−ke^iωkt

(23) bzw

ˆ

q_j(t) = X

k

r ~ 2mN ωk

ˆ

a_ke^−iωkt+ ˆa^†_−ke^iωkt

e^ikja (24)

F¨ur den besonderen Fall, dass nur eine Mode k koh¨arent angeregt ist, also ˆa_k|ψi=α|ψi,

hqˆji ∝αke^{i(kja−ωkt)}+c.c (25)

3 Harmonische zweiatomige Kette Mathematische Bissen: Phononen

Lies: eine mit zunehmeder Zeit t nach rechts (zunehmendem j) laufende Welle der Wel- lenl¨ange 2π/k, Frequenz ω_k, und Amplitude ∝ |α|.

Im kanonischen Ensemble ist die mittlere thermische Besetzungszahl einer Mode zur Wel- lenzahl k leicht berechnet,

hˆn_ki= 1

e^β~ωk−1. (26)

F¨ur hohe Temperaturenβ~ω_k1 erh¨alt manhn_ki ≈k_bT /(~ω)1, und also eine mittlere Energie k_BT in ¨Ubereinstimmung mit dem Gesetz von Dulong-Petit.

Hat man es mit einer großen Zahl von Atomen zu tun, N 1, liegen die Wellenzahlen in der Brillouinzone dicht, ∆k = 2π/(N a). Summen der Provinienz P

kf(k) lassen sich dann durch Integrale approximieren, P

kf(k) →R

1. BZf(k)Z(k)dk wo Z(k) die Zustandsdichte im k-Raum, Z(k) = ^{N a}_2π. Sind Funktionen der Frequenz zu summieren, empfiehlt sich ein Umschreiben auf ein Frequenzintertgral, P

kF(ωk) → R

F(ω)D(ω)dω mit D(ω) die Zu- standsdichte im Frequenzraum, kurz Zustandsdichte (engl. density of states, abgek¨urzt DOS). Im vorliegenden Fall, wegen dk = _dω^dkdω, ist

D(ω)≡2N a 2π

1

|dω_k/dk| = 2N πω_max

1

p1−ω²/ω²_max (27) wobei der Faktor 2 dem Umstand geschuldet, dassω_k eine gerade Funktion der Wellenzahl, ω_−k =ω_k. In den ¨Ubungen ¨uberzeugen Sie sich, dassRωmax

0 D(ω)dω =N, also Gesamtzahl der Freiheitsgrade.

3 Harmonische zweiatomige Kette

N Atome der Sorten A, B, alternierend linear angeordent, also Gitter mit zweiatomiger Basis. Gitterkonstante, also Abstand der A-Atome in Ruhelage, bezeichnet a. Masse der A-Atome m, der B-Atome M. Auslenkung der A-Atome bezeichnet ξ_j, der B-Atome be- zeichnet ζ_j. Harmonische N¨achst-Nachbar-Wechselwirkung, A−B mit Federkonstante κ, B−A mit Federkonstante γ. Hamiltonfunktion

H =X

j

p²_j

2m + P_j² 2M +κ

2

N

X

j=1

(ξ_j −ζ_j)²+γ 2

X

j

(ζ_j−ξ_j+1)² (28) und also Bewegungsgleichungen

mξ¨_j = −κ(ξ_j−ζ_j)−γ(ξ_j−ζj−1), (29) Mζ¨_j = −κ(ζ_j−ξ_j)−γ(ζ_j−ξ_j+1). (30) Ansatz ebene Welle der Frequenz ω und Wellenzahl k,

ξ_j,k = ˜ξe^i(kja−ωt), ζ_j,k = ˜ζe^i(kja−ωt), (31) Einsetzen, gemeinsamen Faktor e^i(kja−ωt) k¨urzen, f¨uhrt auf homogenes Gleichungssystem zweier gekoppelter Gleichungen f¨ur die Amplituden

mω²−(κ+γ)ξ˜+ κ+γe^−ikaζ˜ = 0, (32) κ+γe^ikaξ˜+

M ω²−(κ+γ)ζ˜ = 0. (33)

4 3D Phononen Mathematische Bissen: Phononen

Eine L¨osung (f¨ur das Verh¨altnis der Amplituden) existiert, falls die Koeffizienten-Determinante gleich Null,

mω²−(κ+γ) M ω²−(κ+γ)

− κ+γe^−ika

κ+γe^ika

= 0, (34) bzw.

ω² = (m+M)(κ+γ)±p

(m+M)²(κ+γ)²−8κγmM(1−cos(ka))

2mM (35)

F¨ur jeden der N Werte von k gibt es zwei L¨osungen. d.h. insgesamt 2N Normalmoden, entsprechend den 2N Freiheitsgraden eines N-zelligen Gitters mit zwei Atomen in der Einheitszelle. Zwei Zweige – einen akustischen Zweig, einen optischen Zweig.

F¨ur große Wellenl¨angenka1 ist die Frequenz im optischen Zweig nahezuk-unabh¨angig, ω'

r(m+M)(κ+γ)

mM (36)

wohingegen die Dispersionsrelation im akustischen Zweig linear ω 'csk , cs=

s κγ κ+γ

a²

M +m (37)

F¨ur das Amplitudenverh¨altnis erh¨alt man im optischen Zweig ξ˜

ζ˜' −M

m (38)

wohingegen im akustischen Zweig

ξ˜

ζ˜ '1. (39)

Im optischen Zweig schwingen die A-Atome und B-Atome gegenphasig, im akustischen Zweig in Phase.

4 3D Phononen

Die Auslenkung des j-ten Atoms ξ_j = (ξ^X_j , ξ_j^Y, ξ_j^Z).

1 2

∂²V(R~_i, ~R_j)

∂R^A_i ∂R^B_{j ~}

R⁽⁰⁾

ξ_i^Aξ_j^B (40)

Anmerkungen