NathanaelSkrepek Ao.Univ.Prof.Dr.MichaelKaltenb¨ack AnalysisundScientificComputing BaseninBanachr¨aumen Bachelorarbeit

Basen in Banachr¨ aumen

ausgef¨ uhrt am Institut f¨ ur

Analysis und Scientific Computing

der Technischen Universit¨ at Wien

unter der Anleitung von

Ao. Univ. Prof. Dr. Michael Kaltenb¨ ack

durch

Nathanael Skrepek

2. Juni 2015

1 Motivation/Einleitung 1

2 Schauderbasis 2

2.1 Grundlegendes ¨uber Schauderbasen . . . 2 2.2 Der Raumc(N, X) . . . 5 2.3 Basisfolgen . . . 8

3 Das Basisproblem 10

4 Schwache Schauderbasen 11

5 Duale Schauderbasis 13

6 Beispiele 16

7 Unbedingte Schauderbasen 19

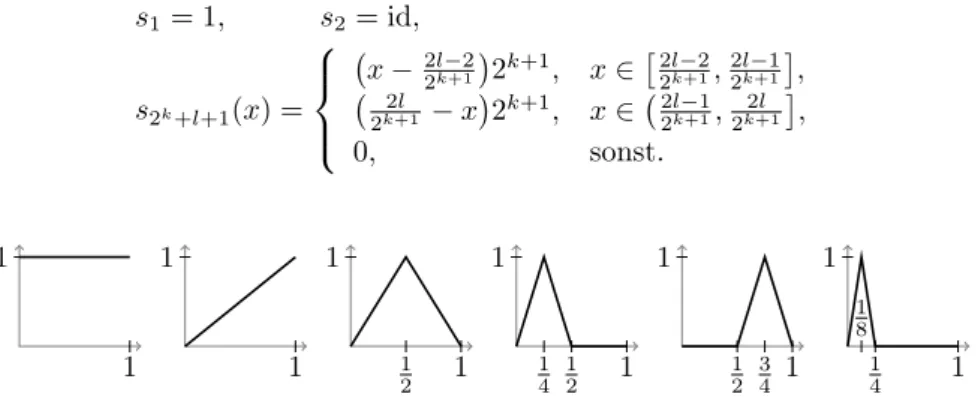
Notation

Symbol Bedeutung

N≤n {k∈N|k≤n}

N<n {k∈N|k < n}

[n, m]_N {k∈N|n≤k≤m}

X meistens normierter Vektorraum oder Banachraum

X⁰ topologischer Dualraum zuX

X^∗ algebraischer Dualraum zuX

B(M, X) Menge der beschr¨ankten Funktionenf :M →X +˙ direkte Summe zweier Unterr¨aume

B^X_r (x) offene Kugel umxmit RadiusrinX lim^w_i∈I Grenzwert in der schwachen Topologie

clsM Abschluss der linearen H¨ulle vonM (clsM = spanM) ι kanonische isomorphe Isometrie vonX nachX⁰⁰ δi,j Kronecker-Delta (δi,j= 1 wenni=j und 0 sonst)

1 Motivation/Einleitung

Der klassische Basisbegriff in einem Vektorraum ist der der Hamelbasis. Dabei l¨asst sich jedes Element des Vektorraumes eindeutig als Linearkombination von Basisvektoren darstellen. Hier sei angemerkt, dass Linearkombinationen immer endliche Summen sind. Das heißt konkret f¨ur einen VektorraumV ist B ⊆V genau dann eine Basis, wenn sich jedesx∈V eindeutig darstellen l¨asst als

x=

n

X

k=1

xkbk

f¨ur gewissebk ausB. Die M¨achtigkeit der Basis wird als Dimension des Vektor- raum bezeichnet.

In einem unendlichdimensionalen Banachraum sind Hamelbasen immer ¨uber- abz¨ahlbar groß, wie das folgende Beispiel zeigen wird.

1.1 Beispiel. Sei X ein unendlichdimensionaler Banachraum und B seine normierte Hamelbasis, das heißt kbk_X = 1 f¨ur alle b∈B. Betrachte nun einen echten Teilraum Y von X, sodass M mit M (B eine Basis von Y ist. Da in jeder -UmgebungB(y) einesy ∈Y das Element y+₂b f¨ur b /∈M enthalten ist, gilt

B(y)*Y f¨ur alle >0.

Also ist keine offene Menge inY enthalten. Daher ist das Innere vonY leer und infolge istX\Y dicht inX.

W¨are B nun abz¨ahlbar, dann g¨abe es eine Bijektion von N auf B. Daher l¨asst sich B auch als {bn|n ∈N} schreiben. Nun erf¨ullt jedes Folgenglied von

span{bi|i ∈ N≤n}

n∈N die gleichen Vorraussetzungen wie Y zuvor. Außer- dem ist jedes Folgenglied ein endlichdimensionaler Unterraum vonX und daher

abgeschlossen. Nach dem Satz von Baire [2, Satz 4.1.1] ist

\

n∈N

X\span{bi|i∈N≤n}

dicht inX. Andererseits ist jedesx∈X ein Element aus span{bi|i∈N≤n}f¨ur einn∈N. Somit erh¨alt man den Widerspruch

\

n∈N

X\span{bi|i∈N≤n}=∅.

Im Falle eines unendlichdimensionalen Banachraumes hat man also immer eine ¨uberabz¨ahlbar große Hamel-Basis. Nachdem der Existenzbeweis f¨ur solche Basen das Lemma von Zorn verwendet, ist es schwierig so eine anzugeben. Daher ist es naheliegend, einen anderen Basisbegriff f¨ur Banachr¨aume zu verwenden.

2 Schauderbasis

Im weiteren Verlauf werden normierte Vektorr¨aume und Banachr¨aume ¨uber dem Skalark¨orperRoderCbetrachtet, da es selten einen Unterschied macht, welcher der beiden Skalark¨orper konkret verwendet wird, wirdKden Skalark¨orper der Vektorr¨aume bezeichnen.

2.1 Grundlegendes ¨ uber Schauderbasen

2.1 Definition. Eine Folge (e_i)_i∈N in einem normierten Vektorraum X wird Schauderbasis von X genannt, falls es f¨ur jedes x ∈ X eine eindeutige Folge (a_i)_i∈Naus dem Skalark¨orperKgibt, sodass

x=

∞

X

i=1

aiei.

2.2 Beispiel.

• Jede Orthonormalbasis in einem seperablen Hilbertraum ist klarerweise auch eine Schauderbasis.

• Die R¨aume`<sup>p</sup> mit p∈[1,+∞) habenei = (δi,j)<sub>j∈N</sub> f¨uri∈Nals Schau- derbasis. Denn ist (ai)<sub>i∈N</sub>∈`^p, so gilt

(ai)i∈N−

n

X

i=1

aiei

_p=

∞

X

i=n+1

|ai|^{p 1}_p

<

f¨urn∈Ngroß genug.

• Der Raum der Nullfolgenc₀versehen mit der Supremumsnorm hat eben- falls die Schauderbasis (e_i)_i∈N aus dem vorherigen Beispiel. Da f¨ur eine Nullfolge (a_i)_i∈N

(ai)_i∈N−

n

X

i=1

aiei

_∞= sup

i>n

|ai|<

f¨urn∈Ngroß genug gilt.

2.3 Fakta.Aus Definition 2.1 folgen unmittelbar einige Eigenschaften:

• Wegen der Eindeutigkeit der Folge (a_i)_i∈Nsind die Vektoren (e_i)_i∈Nlinear unabh¨angig.

• Besitzt der RaumX eine Schauerbasis, so ist dieser automatisch sepera- bel, da die Menge aller rationalen Linearkombinationen von Basisvektoren (ei)_i∈N abz¨ahlbar ist und dicht inX liegt.

• Die Abbildungen e⁰_i :X →K, x7→ai sind wohldefiniert und linear. Die Wohldefiniertheit der Abbildung folgt aus der Eindeutigkeit der Koeffizi- entenfolge zu jedem x. Die Abbildung ist linear, da es f¨ur alle x, y∈ X eine eindeutige Koeffizientenfolgen (ai)i∈N,(bi)i∈Ngibt, sodass

x=

∞

X

i=1

a_ie_i und y=

∞

X

i=1

b_ie_i

und somit f¨ur jedesλ∈K e⁰_i(x+λy) =e⁰_iX^∞

i=1

(a_i+λb_i)e_i

=a_i+λb_i=e⁰_i(x) +λe⁰_i(y) gilt

• Durch die Basisdarstellung sind in nat¨urlicher Weise Projektionen P_n: X → span{ei|i∈N≤n}

P∞

i=1aiei 7→ Pn i=1aiei

definiert. F¨ur diese gilt dim ranP_n =n,P_nP_m=P_mP_n=P_min{n,m} und lim_n∈NPnx=xf¨ur allex∈X.

Wenn man umgekehrt eine Folge von Projektionen (Pn)n∈N gegeben hat, dann gibt uns der folgende Satz Auskunft, wann man daraus wieder eine Schau- derbasis erh¨alt.

2.4 Satz. Sei (P_n)_n∈N eine Folge von beschr¨ankten linearen Selbstabbildungen in einem normierten RaumX mit folgenden Eigenschaften:

(i) dim ranPn =n, (ii) PnPm=P_min{n,m},

(iii) lim_n∈NPnx=xf¨ur allex∈X.

Dann erh¨alt man eine Schauderbasis indem man06=ei ∈ranPi∩kerP_i−1 f¨uri∈Nbeliebig w¨ahlt, wobeiP0= 0. Dabei sind die(Pn)n∈N wiederum genau die Projektionen zur Schauderbasis (ei)i∈N.

Beweis. AusPnPm=P_min{n,m}folgt f¨urm=n, dass es sich um Projektionen handelt und damitX = ranP_n+ ker˙ P_n.

Wegen (i) und (ii) gilt ranP_n−1(ranP_n. Nachdem immer eine Dimension unterschied zwischen ranP_n und ranP_n−1 ist, muss ranP_n ∩kerP_n−1 eindi- mensional sein. Die Abbildung Pn−P_n−1 ist genau die Projektion auf diesen eindimensionalen Unterraum.Pnxl¨asst sich als Teleskopsumme

Pnx=

n

X

i=1

(Pi−P_i−1)x.

schreiben. Gem¨aß der Wahl der (ei)i∈N l¨asst sich so eine eindimensionale Pro- jektion (Pi−Pi−1)xauch schreiben alsαi(x)ei mit einem linearen Funktional αi. Wegen (iii) gilt

x= lim

n∈NP_nx=

∞

X

i=1

α_i(x)e_i f¨ur allex∈X.

Gem¨aß der Wahl der (ei)_i∈NgiltPnei =ei falls n≥i undPnei = 0 sonst.

Gilt f¨ur einx∈X,x=P∞

i=1βiei, dann folgt aus der Stetigkeit der Projektionen Pn

α_n(x)e_n= (P_n−P_n−1)

∞

X

i=1

β_ie_i^Pjstetig=

∞

X

i=1

β_i(P_n−P_n−1)e_i=β_ne_n, womit auch die Eindeutigkeit der Koeffizientenfolge gezeigt wurde.

q 2.5 Lemma. Sei X ein normierter Vektorraum, (I,) eine gerichtete Menge und (P_i)_i∈I ein Netz von beschr¨ankten linearen Selbstabbildungen inX.

Wenn das Netz (P_i)_i∈I gleichm¨aßig beschr¨ankt ist, d.h. sup_i∈IkPik <+∞, und gilt lim_i∈IP_ix = x f¨ur alle x ∈ D f¨ur ein dichtes D ⊆ X, dann folgt lim_i∈IP_ix=xf¨ur allex∈X.

Beweis. Seiy∈X beliebig. Wegen der Dichtheit vonD gibt es f¨ur jedes >0 einx∈D, sodasskx−yk< . Nun ergibt sich

kPiy−yk=kPiy−y+Pix−Pix+x−xk

≤ kx−yk+kPi(y−x)k+kPix−xk

≤(C+ 1)+kPix−xk,

wobeiCeine obere Schranke f¨ur allekP_ikist. Somit gilt lim sup_i∈IkP_iy−yk ≤ (C+ 1), und wegen der Beliebigkeit von >0 folgt lim_i∈IP_iy=y und damit die Aussage.

q 2.6 Korollar. Sei (Pn)n∈N eine gleichm¨aßig beschr¨ankte Folge von linearen Selbstabbildungen in einem normierten VektorraumX, sodassP_mP_n=P_min{n,m}

und dim ranP_n =n. W¨ahlt man f¨ur jedesi∈Nein06=e_i ∈ranP_i∩kerP_i−1, wobei P₀= 0, so ist(e_i)_i∈N eine Schauderbasis f¨ur Z:=S

n∈NranP_n.

Beweis. Wegen der Wahl der (ei)_i∈Ngilt ranPn= span{ei|i= 1, . . . , n}, womit [

n∈N

ranPn= span{ei|i∈N} und Z= cls{ei|i∈N}

gilt. Offensichtlich liegt span{e_i|i∈N}dicht inZ. F¨ur jedesx∈span{e_i|i∈N} gibt es eink_x∈Nund Koeffizienten (a_i)^k_i=1^x , sodassx=Pkx

i=1a_ie_i. Daher folgt Pnx=Pn

k_x

X

i=1

aiei=

k_x

X

i=1

aiPnei=

min{n,kx}

X

i=1

aiei.

Also giltPnx=x, wennn≥kx, weswegen lim_n∈NPnx=xerf¨ullt ist. Nun sind wegen Lemma 2.5 die Voraussetzungen von Satz 2.4 erf¨ullt, womit (ei)_i∈Neine Schauderbasis von Z ist.

q 2.7 Proposition. Sei (ei)_i∈N eine Schauderbasis eines dichten Unterraumes Y von X, dessen Projektionen (Pn)_n∈N gleichm¨aßig beschr¨ankt sind, dann ist (ei)_i∈N bereits eine Schauderbasis f¨ur X.

Beweis. Die Projektionen lassen sich wegen der Dichtheit von Y in X stetig aufX fortsetzen. DaPn(Y) bereits abgeschlossen ist, giltPn(X) =Pn(Y). Die Abbildungsnorm bleibt ebenfalls erhalten. Die Fortsetzungen erf¨ullen daher alle Voraussetzungen von Korollar 2.6, womitX eine Schauderbasis hat. Nachdem 06=ei∈ranPi∩kerP_i−1f¨ur allei∈N, ist (ei)_i∈N eine m¨ogliche Wahl f¨ur eine Schauderbasis von X.

q Um zu zeigen, dass die Projektionen (Pn)n∈Nzu einer Schauderbasis (en)n∈N

in einem Banachraum beschr¨ankt sind, wird ein Umweg ¨uber einen Funktionen- raum gemacht.

2.2 Der Raum c( N , X )

F¨ur einen Banachraum X sei daran erinnert, dass der Raum B(I, X) der be- schr¨ankten Funktionen von einer MengeInachXversehen mit der Supremums- normk.k_∞ einen Banachraum abgibt.

2.8 Definition. F¨ur einen Banachraum X und eine gerichtete Menge I be- zeichne c(I, X) die Menge aller f ∈ B(I, X), f¨ur die limi∈If(i) in X existiert.

Wegen der Linearit¨at des Grenzwerts istc(I, X) ein Unterraum vonB(I, X).

c(I, X) ist nicht leer, da alle konstanten Funktionen darin enthalten sind. Mit der Hilfe des folgenden Resultats aus der Analysis [6, Lemma 8.7.1] erh¨alt man sogar mehr.

2.9 Satz.Seien(I,I)und (J,J)zwei gerichtete Mengen und sei hX, diein vollst¨andig metrischer Raum.

Weiters seien H : I×J → X und h: I →Y Funktionen, sodass f¨ur alle j∈J die FunktionH_j :I→X, i7→H(i, j)beschr¨ankt ist und sodass

h(i) = lim

j∈JH(i, j) gleichm¨aßig auf I, das heißt

∀ >0∃j0:∀jj0∀i∈I:d(H(i, j), h(i))≤, bzw. ¨aquivalent dazu h= lim_j∈JHj inhB(I, X), d_∞i.

Schließlich existiere f¨ur alle j ∈ J der Limes A_j := lim_i∈IH(i, j). Unter diesen Voraussetzungen ist sowohl(A_j)_j∈J als auch(h(i))_i∈I inX konvergent, wobei

limi∈JAj= lim

i∈Ih(i).

Also gilt

limj∈Jlim

i∈IH(i, j) = lim

i∈Ilim

j∈JH(i, j).

2.10 Korollar. Der Vektorraum c(I,X) ist ein Banachraum. Die FunktionL: c(I, X)→X,f 7→limi∈If(i) ist linear und beschr¨ankt mitkLk= 1.

Beweis. W¨ahlt manJ =N,H(i, n) =fn(i) undh(i) =f(i) f¨ur eine inB(I, X) gegen einf ∈ B(I, X) konvergente Folge (fn)_n∈N ausc(I, X), so folgt aus Satz 2.9, dass auch f ∈ c(I, X). Damit ist c(I, X) ein abgeschlossener Unterraum vonB(I, X) und infolge vollst¨andig. F¨ur den OperatorLgilt

kL(f)k=klim

i∈If(i)k ≤sup

i∈I

kf(i)k=kfk_∞. Da f¨ur konstante Funktionen sogar Gleichheit gilt, folgtkLk = 1.

q 2.11 Definition.SeiX ein Banachraum undIeine gerichtete Menge. Weiters seiZif¨ur jedesi∈Iein abgeschlossener Teilraum vonX undAi,j :Zj →Zif¨ur i, j ∈I mitij ein linearer beschr¨ankter Operator, sodassAi,k=Ai,j◦Aj,k

f¨urijk. Dann setzen wir

B(I,(Ai,j), X) :={f ∈ B(I, X)| ∀i∈I f(i)∈Zi,∀ij f(i) =Ai,jf(j)}

c(I,(A_i,j), X) :=B(I,(A_i,j), X)∩c(I, X).

Da die (Zi)_i∈I lineare Teilr¨aume vonXund die (Ai,j)_ijlineare Abbildungen sind, gilt f¨urf, g∈ B(I,(Ai,j), X) undλ∈K

f +λg∈ B(I,(Ai,j), X).

Außerdem istB(I,(Ai,j), X) nicht leer, da die konstante 0 Funktion alle Forde- rungen erf¨ullt, womitB(I,(Ai,j), X) ein linearer Teilraum vonB(I, X) ist.

Die Teilr¨aume (Z_i)_i∈I werden in der Schreibweise B(I,(A_i,j), X) weggelas- sen, da sie implizit durch die Definitionsbereiche der (A_i,j)_ij gegeben sind:

Z_i= domA_i,i.

2.12 Lemma.B(I,(Ai,j), X) ist abgeschlossen inB(I, X) und damit selbst ein Banachraum. Insbesondere ist c(I,(A_i,j), X) ebenfalls ein Banachraum.

Beweis. Die Abbildungen πi : B(I, X) → X, f 7→ f(i) sind linear und be- schr¨ankt, womit

Y :={f ∈ B(I, X)| ∀i∈I f(i)∈Zi }=\

i∈I

π_i⁻¹(Zi)

abgeschlossen ist. Die Abbildungen φ_i,j = π_i−A_i,j◦ π_j : Y → Z_i sind als Zusammensetzung stetiger Abbildungen selbst stetig. Daher ist

B(I,(A_i,j), X) ={f ∈Y |φ_i,j(f) = 0∀ij}=\

ij

kerφ_i,j

abgeschlossen. Der Raumc(I,(A_i,j), X) =B(I,(A_i,j), X)∩c(I, X) ist als Schnitt zweier abgeschlossener Teilr¨aume selbst abgeschlossen.

q 2.13 Satz.SeiX ein Banachraum, (ei)i∈N eine Schauderbasis vonX,(Pn)n∈N

die dazugeh¨origen Projektionen und f¨ur n≤mseiP_n,m: ranP_m→ranP_n die Einschr¨ankung P_n|ranPm.

Dann istL:c(N,(P_n,m), X)→X,f 7→lim_n∈Nf(n) eine in beide Richtun- gen beschr¨ankte lineare Bijektion.

Beweis. ranP_mist endlichdimensional, womitP_n,mbeschr¨ankt und ranP_mab- geschlossen ist. Also l¨asst sichc(N,(Pn,m), X) definieren und gibt wegen Lemma 2.12 einen Banachraum ab. F¨ur einf ∈c(N,(Pn,m), X) giltf(n)∈ranPnf¨ur je- desn∈N. Wegen der linearen Unabh¨angigkeit der (ei)_i∈Ngiltf(n) =Pn

i=1aiei

f¨ur eindeutige Koeffizienten (ai)ⁿ_i=1. NachdemPk,mf(m) =f(k) f¨urk≤moder gleichbedeutend

Pk m

X

i=1

aiei=

k

X

i=1

aiei,

gilt, gibt es f¨ur jedes f ∈ c(N,(P_n,m), X) eine eindeutige Koeffizientenfolge (a_i)_i∈N, sodass f = (Pn

i=1a_ie_i)_n∈N. Somit giltL(f) =P∞

i=1a_ie_i. Nun muss L injektiv sein, nachdem (e_i)_i∈N eine Schauderbasis ist und damit nur die kon- stante 0-Folge unterLauf 0 abgebildet wird.

Außerdem ist f¨ur jedes x∈ X die Folge (Pnx)_n∈N beschr¨ankt, da sie kon- vergent gegenxist. Daher istf := (Pn(x))_n∈Nein Element vonc(N,(Pn,m), X) mit L(f) =x.

Schließlich istLeine beschr¨ankte lineare bijektive Abbildung zwischen zwei Banachr¨aumen und wegen des Satzes der offenen Abbildung [2, Satz 4.3.1] ist auchL⁻¹ beschr¨ankt.

q 2.14 Korollar.Die Projektionen(Pn)_n∈Neiner Schauderbasis(ei)_i∈Nin einem Banachraum X sind stetig und sogar gleichm¨aßig beschr¨ankt. Die Koeffizien- tenabbildungen (e⁰_i)_i∈Nsind ebenfalls stetig.

Beweis. Nachdem die Inverse L⁻¹ :X →c(N,(Pn,m), X) von L aus Satz 2.13 beschr¨ankt ist, wobeiL⁻¹x= (Pnx)_n∈N, erhalten wir

L⁻¹ = sup

kxk=1

k(Pnx)n∈Nk_∞= sup

kxk=1

sup

n∈N

kPnxk = sup

n∈N

sup

kxk=1

kPnxk= sup

n∈N

kPnk.

Insbesondere gilt sup_n∈NkPnk<+∞und f¨ur die Koeffizientenabbildungen folgt

|e⁰_n(x)| ke_nk=ke⁰_n(x)e_nk=k(P_n−P_n−1)xk ≤2 sup

n∈N

kP_nk kxk ke_nk,

womitke⁰_nk ≤ ^{2 sup}_ke^n∈NkPnk

nk .

q 2.15 Definition. Der Wert bc(e_i) := sup_n∈NkP_nk wird Basiskonstante ge- nannt. Gilt bc(e_i) = 1, so wird die Schauderbasis (e_i)_i∈N monoton genannt.

2.16 Bemerkung. Normiert man die Schauderbasis (ei)_i∈N, so erh¨alt man, dass (˜ei)i∈N= _ke^ei

ik

i∈N ebenfalls eine Schauderbasis ist, dessen Koeffizientenabbil- dungen (˜e⁰_i)_i∈N= (keike⁰_i)_i∈Ngleichm¨aßig mit

k˜e⁰_ik =keik ke⁰_ik ≤2bc(e_n) beschr¨ankt sind.

2.3 Basisfolgen

2.17 Definition. Eine Folge (ei)i∈Nin einem Banachraum X wirdBasisfolge genannt, falls diese eine Schauderbasis von cls{ei|i∈N}ist.

2.18 Bemerkung. Auch f¨ur eine Basisfolge (e_i)_i∈N sind die Koordinatenabbil- dungen e⁰_i : cls{ei|i ∈ N} → K stetige Funktionale und die Projektionen Pn : cls{ei|i ∈ N} → span{ei|i ∈ N≤n}, x 7→ Pn

i=1e⁰_i(x)ei gleichm¨aßig be- schr¨ankt mitbc(ei).

2.19 Korollar. Eine Folge (ei)i∈N in einem Banachraum X ist genau dann eine Basisfolgen, wenn e_i 6= 0 f¨ur allei ∈ N und es eine Konstante K ∈ R⁺ f¨ur alle Folgen(a_i)_i∈Naus dem Skalark¨orper und allen, m∈Nmitn≤mgibt, sodass

n

X

i=1

aiei

≤K

m

X

i=1

aiei

. (1)

Die kleinste derartige Konstante K stimmt mitbc(e_i)¨uberein.

Beweis. Wenn (ei)_i∈Neine Basisfolge ist, so gilt

n

X

i=1

a_ie_i

=

P_n

m

X

i=1

a_ie_i

≤bc(e_i)

m

X

i=1

a_ie_i

f¨ur allen≤mund alle (ai)i∈N, wobei diePn die Projektionen aus Bemerkung 2.18 sind.

W¨aren die (ei)i∈Nlinear abh¨angig, so g¨abe es einn∈Nund Skalare (ai)ⁿ_i=1, sodassPn

i=1a_ie_i= 0 undPn−1

i=1 a_ie_i 6= 0 gilt. Das widerspr¨ache aber Bedingung (1). Somit gilt dim span{ei|i ∈ N≤n} = n. Definiert man nun Projektionen durch

P_n: span{ei|i∈N} → span{ei|i∈N} Pm

i=1a_ie_i 7→ Pmin{n,m}

i=1 a_ie_i ,

so ist die Folge (Pn)_n∈N, wegen (1) gleichm¨aßig beschr¨ankt und erf¨ullt alle Voraussetzungen von Satz 2.4. Die Bedingung (iii) ist erf¨ullt, da Pnx f¨ur ein

x ∈ span{e_i|i ∈ N} ab einem hinreichend großen n₀ konstant x ist. Also ist (e_i)_i∈Neine Schauderbasis von span{e_i|i∈N}und wegen Proposition 2.7 auch eine Schauderbasis von cls{ei|i∈N}.

Aus der Definition von bc(ei) folgt unmittelbar bc(ei) ≤ K f¨ur jedes K, welches (2.19) erf¨ullt. Dabc(ei) eine m¨ogliche Wahl f¨ur ein solchesK ist, folgt die Behauptung.

q 2.20 Definition. Sei (e_i)_i∈N eine Basisfolge in einem Banachraum X und (b_i)_i∈Neine Basisfolge in einem BanachraumY. Dann heißt (e_i)_i∈N¨aquivalentzu (b_i)_i∈N, wenn f¨ur jede Koeffizientenfolge (a_i)_i∈Ndie Konvergenz ReiheP∞

i=1a_ie_i

¨aquivalent zu der vonP∞

i=1a_ib_i ist.

2.21 Satz.Sei(ei)i∈Neine Basisfolge in einem BanachraumX und(bi)i∈Neine Folge in einem BanachraumY. Dann sind die folgenden Aussagen ¨aquivalent.

(i) (b_i)_i∈Nist eine zu (e_i)_i∈N¨aquivalente Basisfolge.

(ii) Es gibt eine in beide Richtungen beschr¨ankte lineare Bijektion Φ : cls{ei|i∈N} →cls{bi|i∈N}, sodass Φ(ei) =bi f¨ur allei∈N. (iii) Es gibt zwei KonstanteC1, C2>0, sodass f¨ur alle Skalare(ai)ⁿ_i=1

1 C1

n

X

i=1

aiei

_X

≤

n

X

i=1

aibi

_Y

≤C2

n

X

i=1

aiei

_X gilt.

Beweis. (i)⇒(ii): Definiere die Abbildung

Φ : cls{ei|i∈N} → cls{bi|i∈N} x=P∞

i=1e⁰_i(x)ei 7→ P∞

i=1e⁰_i(x)bi

.

Diese Abbildung ist wohldefiniert, linear, injektiv und surjektiv, da es sich laut Voraussetzung um ¨aquivalente Basisfolgen handelt. Ist (x_k,Φ(x_k))

k∈N eine gegen (x, y) konvergente Folge aus cls{ei|i ∈N} ×cls{bi|i ∈N}, so folgt aus der Stetigkeit der Koeffizientenabbildungen, dass

k∈limN

e⁰_i(xk) =e⁰_i(x) und lim

k∈N

e⁰_i(xk) = lim

k∈N

b⁰_i(Φ(xk)) =b⁰_i(y)

f¨ur alle i ∈ N. Daher gilt e⁰_i(x) = b⁰_i(y) und damit Φ(x) = y. Aus dem Satz des abgeschlossenen Graphen [2, Satz 4.4.2] folgt, dass Φ stetig ist und aus dem Satz der offenen Abbildung [2, Korollar 4.3.4], dass Φ⁻¹ stetig ist.

(ii)⇒(iii): (iii) gilt f¨urC₁:=

Φ⁻¹

undC₂:=kΦk.

(iii)⇒(i): F¨ur beliebigesm≤nund beliebige Skalare (a_i)ⁿ_i=1 gilt

n

X

i=1

aibi

_Y

≤C2

n

X

i=1

aiei

_X

≤C2bc(ei)

m

X

i=1

aiei

_X

≤C1C2bc(ei)

m

X

i=1

aibi

_Y

,

womit (bi)_i∈Nlaut Korollar 2.19 eine Basisfolge ist.

Sei nun (ai)_i∈N eine Folge aus dem Skalark¨orper, sodass P∞

i=1aiei kon- vergiert. Dann gilt nachdem Cauchy-Kriterium kPn

i=maieik_X < _C

2, wenn

n, m > n₀ f¨ur ein gewisses n₀∈N. W¨ahle nun diesen₀ und definiere f¨ur gege- benesmdie Folge (˜a_i)_i∈Ndurch

˜ ai=

ai, i≤m, 0, sonst.

Dann gilt

n

X

i=1

aibi−

m

X

i=1

aibi

_Y

=

n

X

i=1

(ai−˜ai)bi

_Y

≤C2

n

X

i=m+1

aiei

_X

< ,

womit Pn i=1aibi

n∈Neine Cauchy-Folge ist und konvergiert. Umgekehrt verl¨auft der Beweis analog. Also sind (ei)_i∈Nund (bi)_i∈N ¨aquivalent.

q

3 Das Basisproblem

Wie schon am Anfang in Fakta 2.3 angemerkt, ist jeder Banachraum mit Schau- derbasis seperabel, wodurch sich die Frage aufdr¨angt, ob auch jeder seperable Banachraum eine Schauderbasis besitzt. Diese Fragestellung wird dasBasispro- blem genannt. Lange Zeit war diese Fragestellung ein offenes Problem bis 1972 Per Enflo das Problem negativ l¨oste [3].

3.1 Definition.Ein BanachraumX hat diebeschr¨ankte Approximationseigen- schaft (BAP), wenn es eine Folge (A_n)_n∈Nvon beschr¨ankten linearen Selbstab- bildungen endlichen Ranges gibt, sodass

n∈limN

kAnx−xk = 0 f¨ur alle x∈X. (2)

3.2 Bemerkung. Die Projektionen (P_n)_n∈N zu einer Schauderbasis erf¨ullen die Forderung (2), womit jeder Banachraum, der eine Schauderbasis besitzt, die beschr¨ankte Approximationseigenschaft hat.

3.3 Definition. Ein Banachraum X hat die Approximationseigenschaft, wenn es f¨ur jeden BanachraumY und zu jedem kompakten OperatorT :Y →X eine Folge von Operatoren endlichen Ranges (T_n)_n∈Ngibt, sodass

n∈limN

kT−T_nk= 0.

3.4 Lemma.Ein BanachraumX hat die Approximationseigenschaft, wenn f¨ur jede kompakte Menge K und alle > 0 ein Operator A : X → X endlichen Ranges existiert, sodass

sup

x∈K

kAx−xk< .

Beweis. Ist Y ein Banachraum und T : Y → X ein kompakter Operator, so ist K := T(B₁(0)) kompakt. W¨ahle nun f¨ur jedes n ∈ N einen Operator An :X →X, sodass sup_x∈KkAnx−xk <_n¹. Dann gilt

kT−A_nTk= sup

y∈B1(0)

kT y−A_nT yk= sup

x∈K

kx−A_nxk< 1 n. Also hat (Tn)_n∈N:= (AnT)_n∈Ndie in Definition 3.3 geforderte Eigenschaft.

q 3.5 Satz.Aus der beschr¨ankten Approximationseigenschaftfolgt die Approxi- mationseigenschaft.

Beweis. Nachdem die Folge (An)_n∈N aus Definition 3.1 punktweise gegen die Identit¨at konvergiert gilt sup_n∈NkAnxk <∞. Nach dem Principle of Uniform Boundedness [2, Korollar 4.2.2] folgtC:= sup_n∈NkAnk <∞.

SeiK ⊆X kompakt. Klarerweise l¨asst sich K von S

x∈KB

2(C+1)(x) ¨uber- decken. Nachdem K kompakt ist, gilt bereits K ⊆ Sk

i=1B

2(C+1)(xi) f¨ur be- stimmte (xi)^k_i=1 aus K. F¨ur jedes x ∈ K gibt es demnach ein xi, sodass kx−xik< _2(C+1) . Daher gilt

kA_nx−xk ≤ kA_nx−A_nx_i+x_i−xk+kA_nx_i−x_ik

≤(kAnk+ 1)kx−xik+kAnxi−xik.

W¨ahlt man nunnso groß, dass max_i=1...kkA_nx_i−x_ik ≤ ₂, so erh¨alt man kA_nx−xk<(C+ 1)

2(C+ 1)+ 2 < ,

wenn nur x∈K. Also gilt auch sup_x∈KkAnx−xk < f¨ur ngroß genug. Aus Lemma 3.4 folgt schließlich die Behauptung.

q Aus Bemerkung 3.2 und Satz 3.5 folgt, dass jeder Banachraum mit Schau- derbasis die Approximationseigenschaft hat.

Das heißt, um das Basisproblem negativ zu l¨osen, reicht es einen seperablen Banachraum zu finden, der die Approximationseigenschaft nicht erf¨ullt, da diese aus der Existenz einer Schauderbasis folgen m¨usste. In der Tat ging Per Enflo bei seiner L¨osung des Basisproblems derart vor [3].

4 Schwache Schauderbasen

4.1 Definition. Eine Folge (e_i)_i∈N in einem normierten VektorraumX wird schwache Schauderbasis vonX genannt, falls es f¨ur jedesx∈X eine eindeutige Folge (a_i)_i∈Naus dem Skalark¨orperKgibt, sodass die ReiheP∞

i=1a_ie_ischwach gegenxkonvergiert, d.h.

Nlim→∞φX^N

i=1

aiei

=φ(x) f¨ur alle φ∈X⁰.

4.2 Bemerkung. Auch f¨ur eine schwache Schauderbasis ist in nat¨urlicher Weise eine Folge von Projektionen (P_n)_n∈N definiert

P_n: X → span{e_i|i∈N≤n} x 7→ Pn

i=1aiei

,

wobei (a_i)_i∈N die eindeutige Koeffizietenfolge zuxist.

4.3 Lemma. Sei X ein Banachraum und (x_n)_n∈N eine gegen xschwach kon- vergente Folge, d.h. lim_n∈Nφ(xn) = φ(x) f¨ur alle φ ∈ X⁰. Dann ist die Folge beschr¨ankt.

Beweis. Im Folgenden bezeichnetι: X →X⁰⁰ die kanonische Einbettung von X in dessen topologischen BidualraumX⁰⁰.

Wegen φ(xn) ^n→∞→ φ(x) gibt es einn0 sodass |φ(xn)| < |φ(x)|+ 1 f¨ur alle n≥n0. Nachdemι(xn)(φ) =φ(xn) gilt

sup

n∈N

kι(xn)(φ)k= sup

n∈N

kφ(xn)k ≤max

n≤no

{|φ(xn)|,|φ(x) + 1|}

| {z }

:=C_φ

<∞.

Wegen des Principle of Uniform Boundedness [2, Korollar 4.2.2] istι(xn) gleich- m¨aßig beschr¨ankt. Daι eine Isometrie ist, folgt die Aussage.

q 4.4 Definition. F¨ur einen BanachraumX und eine gerichtete Menge (I,) bezeichnet c_w(I, X) die Menge aller f ∈ B(I, X) f¨ur die einx_f ∈X existiert, sodass lim^w_i∈If(i) =x_f, das heißt lim_i∈Iφ(f(i)) =φ(x_f) f¨ur alleφ∈X⁰. 4.5 Lemma. cw(I, X) ist ein abgeschlossener Unterraum von B(I, X). Au- ßerdem ist Lw : cw(I, X) → X, f 7→ lim^w_i∈If(i) eine lineare Abbildung mit kLwk= 1.

Beweis. Konstante Funktionen sind incw(I, X) enthalten, womitcw(I, X) nicht leer ist. Da f¨ur schwach konvergente Netze (f(i))i∈I, (g(i))i∈I und komplexe Zahlenλ

limi∈Iφ[f(i) +λg(i)] = lim

i∈Iφ(f(i)) +λlim

i∈Iφ(g(i)) f¨ur alle φ∈X⁰ gilt, ist cw(I, X) ein Unterraum vonB(I, X). Daraus folgt außerdem auch die Linearit¨at vonLw.

F¨ur f ∈cw(I, X) giltf(i)∈B^X_kfk

∞(0) f¨ur allei∈I. Nachdem diese Menge konvex und abgeschlossen in der Normtopologie ist, ist sie laut [2, Satz 5.3.8]

auch abgeschlossen in der schwachen Topologie. Damit istLw(f) = lim^w_i∈If(i) ebenfalls in B^X_kfk

∞(0) enthalten und infolge gilt kL_w(f)k ≤ kfk_∞, wobei f¨ur konstante Funktionen Gleichheit gilt.

Ist (fn)_n∈Neine Folge aus cw(I, X), die gegen einf ∈ B(I, X) konvergiert, so giltkLw(fn)−Lw(fm)k ≤ kfn−fmk_∞. Daher ist (Lw(fn))_n∈Neine Cauchy Folge in X und infolge konvergent gegen ein x0 ∈X. Mit (fn)_n∈N konvergiert auch (φ◦fn)_n∈N f¨ur alle φ∈X⁰ gleichm¨aßig. Wegen der Stetigkeit von φund Satz 2.9 gilt

limi∈Iφ(f(i)) = lim

i∈I lim

n∈N

φ(fn(i)) = lim

n∈N

limi∈Iφ(fn(i)) = lim

n∈N

φ(Lw(fn)) =φ(x0)

f¨ur alleφ∈X⁰. Also istf ∈c_w(I, X) mitL_w(f) =x₀.

q 4.6 Definition. Analog zuc(I,(Ai,j), X) l¨asst sich f¨ur schwache Konvergenz

cw(I,(Ai,j), X) :=B(I,(Ai,j), X)∩cw(I, X) definieren.

Der Raumcw(I,(Ai,j), X) ist selbst als Schnitt zweier abgeschlossener Un- terr¨aume ein abgeschlossener Unterraum

4.7 Satz. Sei (ei)i∈N eine schwache Schauderbasis eines Banachraums X, (Pn)n∈N die dazugeh¨origen Projektionen und f¨ur n ≤m sei Pn,m : ranPm → ranPn die Einschr¨ankungPn|ranPm.

Dann istL : c_w(N,(P_n,m), X) → X, f 7→ lim^w_n∈Nf(n) eine in beide Rich- tungen beschr¨ankte lineare Bijektion.

Beweis. Die Injektivit¨at vonL_wkann analog zu der Injektivit¨at vonLim Beweis von Satz 2.13 gezeigt werden.

F¨ur x ∈ X ist (P_nx)_n∈N als schwach konvergente Folge laut Lemma 4.3 beschr¨ankt. Daher liegtf := (Pnx)_n∈N in cw(N,(Pn,m), X), wobeiLw(f) =x.

Also istLw surjektiv.

Nun istLwals bijektive beschr¨ankte lineare Abbildung wegen des Satzes der offenen Abbildung [2, Satz 4.3.1] ein Hom¨oomorphismus.

q 4.8 Korollar. Ist(ei)_i∈N eine schwache Schauderbasis eines Banachraums X, so ist(ei)i∈N eine Schauderbasis vonX.

Beweis. Die Projektionenfolge (Pn)n∈Nist gleichm¨aßig beschr¨ankt durch L⁻¹_w

. Der Beweis daf¨ur verl¨auft exakt wie jener in Korollar 2.14.

F¨ur jedes x ∈ span{ei|i ∈ N} konvergiert P_nx ^n→∞→ x nicht nur in der schwachen Topologie sondern auch in der Normtopologie, da die Folge ab einem hinreichend großen Index n₀ konstant ist. Nachdem span{ei|i ∈ N} konvex ist, stimmt der Normabschluss mit dem schwachen Abschluss, welcher X ist, uberein.¨

Proposition 2.7 besagt, dass (ei)_i∈Nbereits eine Schauderbasis f¨urX ist.

q

5 Duale Schauderbasis

5.1 Definition. IstX ein Banachraum und (ei)_i∈Neine Schauderbasis vonX, dann wird die dazu gegebenen Folge von Koeffizientenabbildungen (e⁰_i)i∈N aus X⁰ (Korollar 2.14)duale Schauderbasis genannt.

5.2 Bemerkung. Die duale Schauderbasis (e⁰_i)i∈N ist im Allgemeinen keine Schauderbasis von X⁰.

5.3 Bemerkung.Nachdeme⁰_i(e_j) = 0 f¨uri6=j, gilt f¨ur alle Koeffizienten (a_i)_i∈N e⁰_i(e_i) = 16= 0 = X

k∈N\{i}

a_ke⁰_k(e_i).

Daher ist jedesφ∈cls{e⁰_k|k∈N\{i}}ausgewertet an e_i gleich 0, wohingegen e⁰_i(e_i) = 1. Das implizierte⁰_i∈/ cls{e⁰_k|k∈N\{i}}, womit die duale Schauderba- sis nicht nur linear unabh¨angig, sondern auchunendlich linear unabh¨angig ist, was genaue⁰_i∈/cls{e⁰_k|k∈N\{i}}f¨ur allei∈Nbedeuten soll.

5.4 Satz.Sei(e_i)_i∈Neine Schauderbasis eines BanachraumesX,(e⁰_i)_i∈Ndessen duale Schauderbasis und(P_n)_n∈N die dazugeh¨origen Projektionen. Dann gilt:

(i) F¨ur die Konjugierte Abbildung P_n⁰ : X⁰ → X⁰ von Pn gilt, P_n⁰x⁰=Pn

i=1x⁰(ei)e⁰_i.

(ii) lim^w_n∈N^∗ P_n⁰x⁰=x⁰ f¨ur allex⁰∈X⁰.

(iii) (e⁰_i)_i∈N ist eine Schauderbasis f¨urcls{e⁰_i|i∈N} ⊆X⁰. Beweis.

(i) Wegen der Linearit¨at einesx⁰ ∈X⁰ gilt f¨ur allex∈X hx, P_n⁰x⁰i=hPnx, x⁰i=

n

X

i=1

e⁰_i(x)hei, x⁰i=

n

X

i=1

x⁰(ei)hx, e⁰_ii

=D x,

n

X

i=1

x⁰(ei)e⁰_iE .

(ii) Bezeichnetι:X →X⁰⁰ die kanonische Einbettung, so erh¨alt man ι(x)(P_n⁰x⁰) =

n

X

i=1

x⁰(ei)e⁰_i(x) =x⁰Xⁿ

i=1

e⁰_i(x)ei

.

Somit l¨asst sich der Grenzwert f¨ur n→ ∞, wegen der Stetigkeit von x⁰ wie folgt berechnen:

n∈limN

ι(x)(P_n⁰x⁰) = lim

n∈N

x⁰Xⁿ

i=1

e⁰_i(x)ei

=x⁰(x) =ι(x)(x⁰).

(iii) Da die duale Schauderbasis linear unabh¨angig ist (vgl. Bemerkung 5.3), gilt dim ranP_n⁰ = n. Nachdem wegen [2, Satz 6.1.2] kP_n⁰k = kPnk gilt, ist auch (P_n⁰)_n∈N gleichm¨aßig beschr¨ankt durch bc(ei). F¨ur ein x⁰ aus span{e⁰_i|i ∈ N} konvergiert Pnx⁰ sogar in der Norm gegen x⁰. Da span{e⁰_i|i∈N} =S

n∈NranP_n⁰ dicht in cls{e⁰_i|i∈N} liegt, ist aufgrund von Proposition 2.7 (e⁰_i)_i∈Neine Schauderbasis von cls{e⁰_i|i∈N}.

q 5.5 Definition.Sei (ei)i∈Neine Schauderbasis vonX und (e⁰_i)i∈Ndessen duale Schauderbasis.

• (e_i)_i∈N wirdschrumpfend genannt, falls cls{e⁰_i|i∈N}=X⁰.

• (ei)_i∈Nwirdbeschr¨ankt vollst¨andiggenannt, falls die ReiheP∞

i=1aieischon dann konvergiert, wenn sup_n∈NkPn

i=1aieik<∞.

5.6 Bemerkung.Ist eine Schauderbasis (e_i)_i∈N eines BanachraumsX so bedeu- tet, wegen Satz 2.13 beschr¨ankt vollst¨andig nichts anderes als

c(N,(Pn,m), X) =B(N,(Pn,m), X).

5.7 Satz.F¨ur eine schrumpfende Schauderbasis(e_i)_i∈Neines Banachraums X ist T : X⁰⁰ → B(N,(Pn,m), X) mit x⁰⁰ 7→

Pn

i=1x⁰⁰(e⁰_i)ei

n∈N eine in beide Richtungen beschr¨ankte lineare Bijektion.

Ist(ei)_i∈Nzus¨atzlich monoton, d.h.bc(ei) = 1, so istT sogar eine Isometrie.

Beweis. Da (ei)i∈N schrumpfend ist, ist die duale Schauderbasis (e⁰_i)i∈N ei- ne Schauderbasis von X⁰. Daher kann Satz 5.4 (i) auf (e⁰_i)i∈N mit der dualen Schauderbasis (ι(ei))i∈Nangewandt werden. Insbesondere sind die entsprechen- den Projektionen gegeben durch:

P_n⁰⁰: X⁰⁰ → X⁰⁰ x⁰⁰ 7→ Pn

i=1x⁰⁰(e⁰_i)ι(e_i) . Nachdemι:X→X⁰⁰ eine lineare Isometrie ist, folgt

kT x⁰⁰k_∞=

Xⁿ

i=1

x⁰⁰(e⁰_i)e_i

n∈N

_∞=

Xⁿ

i=1

x⁰⁰(e⁰_i)ι(e_i)

n∈N

_∞= sup

n∈N

kP_n⁰⁰x⁰⁰k.

Aus kP_n⁰⁰k =kP_n⁰k=kP_nk ≤bc(e_i) (vgl. [2, Satz 6.1.2]) erh¨alt man kT x⁰⁰k_∞≤bc(ei)kx⁰⁰k.

Gilt T x⁰⁰ = T y⁰⁰, so folgt x⁰⁰(e⁰_i) = y⁰⁰(e⁰_i) f¨ur alle i ∈ N. Weil die e⁰_i eine Schauderbasis f¨urX⁰ bilden, gilt daher auchy⁰⁰=x⁰⁰. Somit istT injektiv.

Ist andererseitsf ∈ B(N,(Pn,m), X), so giltf(n) =Pn

i=1aiei f¨ur eine ein- deutige Folge (ai)_i∈N. Nachdem auch ι◦f =

Pn

i=1aiι(ei)

n∈N

in X⁰⁰ be- schr¨ankt ist, hat diese Folge bez¨uglich der w^∗-Topologie vonX⁰⁰, aufgefasst als Dualraum von X⁰, einen H¨aufungspunkt x⁰⁰. Das heißt es existiert eine gerich- tete Menge (J,) und eine Funktionn:J →N, sodass

Pn(j)

i=1 a_iι(e_i)

j∈J ein Teilnetz vonι◦f ist und

x⁰⁰(φ) = lim

j∈J n(j)

X

i=1

a_iι(e_i)(φ) f¨ur alle φ∈X⁰

gilt. Wertet man x⁰⁰ an jedem Vektor der dualen Schauderbasis aus, so erh¨alt man, wegene⁰_i(e_j) =δ_i,j

x⁰⁰(e⁰_k) = lim

j∈J n(j)

X

i=1

a_ie⁰_k(e_i) =a_k. Also giltT(x⁰⁰) =f, womitT surjektiv ist.

Daher istT eine bijektive beschr¨ankte lineare Abbildung zwischen zwei Ba- nachr¨aumen. Außerdem folgt aus den ¨Uberlegungen zur Surjektivit¨at von T, dass

T⁻¹f

≤ kfk_∞, da abgeschlossene Normkugeln auch in derw^∗-Topologie abgeschlossen sind. Also gilt

T⁻¹

≤1, womitT⁻¹ beschr¨ankt ist.

Wenn (e_i)_i∈Nmonoton ist, so giltbc(e_i) = 1, und folglich kx⁰⁰k ≤ kT x⁰⁰k_∞≤ kx⁰⁰k.

Also istT eine Isometrie.

q 5.8 Satz. Ein Banachraum X mit einer Schauderbasis (ei)i∈N ist genau dann reflexiv, wenn (e_i)_i∈N schrumpfend und beschr¨ankt vollst¨andig ist.

Beweis. Ist (ei)_i∈N schrumpfend so ist T aus Satz 5.7 eine in beide Richtun- gen beschr¨ankte lineare Bijektion vonX⁰⁰aufB(N,(Pn,m), X). Nachdem (ei)_i∈N auch beschr¨ankt vollst¨andig ist, folgt wegen Bemerkung 5.6, dassT bereits auf c(N,(Pn,m), X) abbildet. Das heißt,L◦T :X⁰⁰→X (Laus Satz 2.13) ist wohl- definiert und ebenfalls eine eine beide Richtungen beschr¨ankte lineare Bijektion.

Somit existiert die Umgekehrabbildung und f¨ur diese gilt (T⁻¹◦L⁻¹)x=T⁻¹Xⁿ

i=1

e⁰_i(x)ei

n∈N=T⁻¹Xⁿ

i=1

ι(x)(e⁰_i)ei

n∈N=ι(x).

Damit istι:X →X⁰⁰ bijektiv.

Nun seiX umgekehrt reflexiv. Aus Satz 5.4 folgt, dass lim^w_n∈^∗_NP_n⁰x⁰ =x⁰ f¨ur beliebiges x⁰ ∈ X⁰. Wegen X⁰⁰ =ι(X) stimmt die schwache Topologie mit der w^∗-Topologie ¨uberein. Also ist die duale Schauderbasis eine schwache Schauder- basis vonX⁰ und wegen Korollar 4.8, sogar eine Schauderbasis vonX⁰. Also ist (ei)i∈N schrumpfend. F¨ur jedesx⁰⁰∈X⁰⁰ existiert einx∈X, sodassι(x) =x⁰⁰. Nun gilt

T x⁰⁰=T ι(x) =Xⁿ

i=1

e⁰_i(x)ei

n∈N=L⁻¹x.

Nachdem sowohlT als auchLbijektiv sind, folgt daraus

B(N,(Pn,m), X) =T X⁰⁰=L⁻¹X =c(N,(Pn,m), X).

Somit ist (e_i)_i∈Nbeschr¨ankt vollst¨andig.

q

6 Beispiele

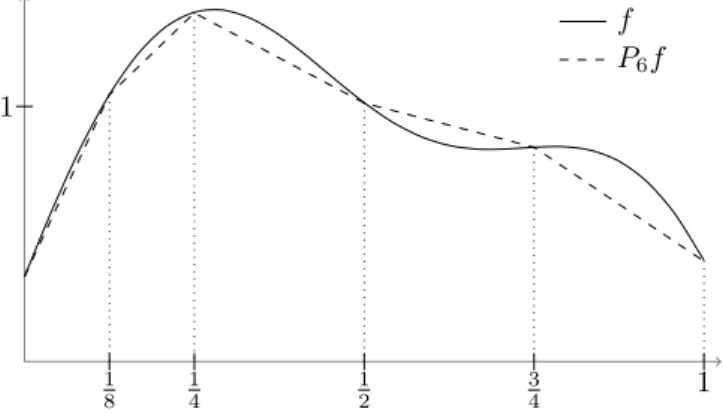
6.1 Beispiel. Um eine Schauderbasis f¨urC([0,1],K) zu erhalten, w¨ahle man zun¨achst eine Folge (ti)_i∈N, sodass t1 = 0, t2 = 1 und {ti|i ∈ N} dicht in [0,1] ist. Weiters definiere man P1f =f(0) und Pnf als eine st¨uckweise linea- re Funktion mit Knoten (ti)ⁿ_i=1, sodass Pnf(ti) = f(ti) f¨ur i ≤ n. Dann gilt kPnfk_∞ ≤ kfk_∞ f¨ur allen ∈N, wobei bei konstanten Funktionen Gleichheit herrscht. Somit sind die P_n gleichm¨aßig mit 1 beschr¨ankt. Außerdem gilt

PnPmf =PmPnf =P_min{n,m}f (3)

f¨ur alle f ∈C([0,1],K), womit es sich bei den (P_n)_n∈N um Projektionen han- delt. Um nachzuweisen, dass C([0,1],K) eine Schauderbasis hat, wird Satz 2.4 bem¨uht. Mit (3) ist Bedingung (ii) bereits erf¨ullt.

1

1

1 2 1

4

3 4 1

8

f P6f

Abbildung 1: Funktion und ihre Projektion

NachdemC¹([0,1],K) dicht inC([0,1],K) liegt und die (Pn)_n∈Ngleichm¨aßig beschr¨ankt sind, reicht es, um Bedingung (iii) nachzuweisen, wegen Lemma 2.5 zu zeigen, dass limn∈NPnf =f f¨ur allef ∈C¹([0,1],K).

F¨ur festesf erh¨alt man f¨ur jede ProjektionPndie Steigungen der st¨uckwei- sen linearen Teile durch

sn,i:= Pnf(t_π(i))−Pnf(t_π(i+1))

t_π(i)−t_π(i+1) = f(t_π(i))−f(t_π(i+1))

t_π(i)−t_π(i+1) i∈N<n, wobei π die Permutation ist, die (ti)ⁿ_i=1 der Gr¨oße nach ordnet, das heißt t_π(i) < t_π(i+1). Pnf ist f¨ur jedes n ∈ N eine lipschitzstetige Funktionen mit Lipschitzkonstantesn:= max_i∈N<n|sn,i|. Wegen des Mittelwertsatzes der Diffe- rentialrechnung folgt sn≤ kRef⁰k_∞+kImf⁰k_∞:=C, womit (Pnf)_n∈N gleich- gradig lipschitzstetig ist. Nachdem (ti)i∈N dicht in [0,1] ist, gibt es f¨ur jedes > 0 ein k ∈ N, sodass es f¨ur jedes x ∈ [0,1] ein tx,k ∈ {ti|i ∈ N≤k} mit

|x−tx,k|< gibt. Nun gilt

|Pnf(x)−f(x)|=|Pnf(x)−Pnf(tx,k) +Pnf(tx,k)−f(tx,k) +f(tx,k)−f(x)|

≤ |Pnf(x)−Pnf(tx,k)|+|Pnf(tx,k)−f(tx,k)|+|f(x)−f(tx,k)|

≤2C|x−tx,k|+|Pnf(tx,k)−f(tx,k)|.

W¨ahlek∈Nnun so groß, dass |x−tx,k| ≤ _2C . Nachdem Pnf(ti)−f(ti) = 0 f¨urn≥i, folgt

kPnf−fk ≤ f¨urn≥k,

womit nach Lemma 2.5 die Bedingung (iii), limn∈NPnf = f f¨ur alle f ∈ C([0,1],K), erf¨ullt ist.

F¨ur Bedingung (i) muss man dim ranPn =n zeigen, daf¨ur betrachte man folgende lineare Funktion

ψn : ranPn → Kⁿ f 7→ f(ti)ⁿ

i=1

.