Skript Vorlesung zur Statistischen Mechanik

Vorlesung zur Statistischen Mechanik

Fachbereich Physik an der Universitat Konstanz

gelesen von Prof. Dr. Matthias Fuchs

bearbeitet von Ulrike Ritzmann und Greta Huber

Stand: 8. Marz 2010

Dieses Skript ist eine Mitschrift der Vorlesung Statistische Mechanik an der Universitat Konstanz (Winter- semester 2009/2010) gelesen von Prof. M. Fuchs. Es basiert auf einem Skript der gleichen Vorlesung aus dem Wintersemster 2005/2006 ebenfalls von Prof. M. Fuchs, das von Thomas Lauermann und Raphael Straub geschrieben worden ist, und im Wintersemester 2007/2008 von Thomas Wiedenmann und Marcel Wunram uberarbeitet worden ist. Die Autoren erheben keinen Anspruch auf Vollstandigkeit und Richtigkeit.

Lob, Kritik und Anregung bitte per Mail an:

gretahuber@gmx.de

1 Vorbetrachtungen 5

1.1 Wahrscheinlichkeitstheorie . . . 5

1.1.1 Denitionen . . . 5

1.1.2 Variablentransformationen . . . 9

1.1.3 Normal- oder Gauss-Verteilung . . . 12

1.1.4 Bedingte Wahrscheinlichkeiten und wichtige Formeln . . . 12

1.1.5 (stochastisch) unabhangige Zufallsvariablen . . . 14

1.1.6 Der Zentrale Grenzwertsatz (Law of large numbers) . . . 14

1.2 Quantenstatistik. . . 18

1.2.0 Wiederholung der Quantenmechanik vieler Freiheitsgrade . . . 18

1.2.1 statistischer Dichteoperator; reine Zustande und Gemische . . . . 20

1.2.2 Subsysteme und reduzierte Dichteoperatoren . . . 25

1.2.3 Von-Neumann-Gleichung . . . 29

1.3 Klassische Statistik . . . 30

1.3.1 Der Phasenraum, Phasenraumverteilungsfunktion . . . 30

1.3.2 Liouville-Theorem und Liouville-Gleichung . . . 31

1.4 Wichtige Gesamtheiten (Ensemble) . . . 33

1.4.1 Das Beispiel paramagnetischer Salze . . . 33

1.4.2 Der kanonische Dichteoperator %. . . 33

1.4.3 Fortsetzung: Curie-Paramagnetismus . . . 36

1.4.4 Das Mikrokanonische klassische monoatomare ideale Gas. . . 47

1.4.5 Mikrokanonischer Dichteoperator / Wahrscheinlichkeitsdichte . . 48

1.4.6 Fortsetzung: ideales Gas . . . 48

1.5 Schwankungen makroskopischer additiver (extensiver) Groen . . . 53

1.5.1 Zusammenfassung der einfachen Beispiele . . . 56

2 Konzepte & Postulate der Statistischen Mechanik 61 2.1 Systeme & Thermisches Gleichgewicht. . . 61

2.1.1 Systeme . . . 61

2.1.2 Thermisches Gleichgewicht . . . 63

2.1.3 Postulat: 'gleiche apriori Wahrscheinlichkeit' (Laplace) . . . 64

2.1.4 BoltzmannEntropie S . . . 67

2.1.5 Mikrokanonische Gesamtheit . . . 69

2.1.6 Kanonische Gesamtheit. . . 70

2.2 Extremalprinzipien . . . 80

2.2.1 Informationsentropie S⁰ und Gibbssche Entropieformel . . . 81

2.2.2 Kleinsche Ungleichung . . . 83

2.2.3 Extremalprinzipien der Entropie und derGibbsschen Potentiale . 85 2.2.4 Mikrokanonische Gesamtheit . . . 86

2.2.5 Kanonische Gesamtheit. . . 86

2.2.6 Grokanonische Gesamtheit . . . 88

2.2.7 Partielle Gleichgewichte in der verallgemeinerten Grokanonischen Gesamtheit . . . 93

2.2.8 Zeitabhangigkeit der Entropien . . . 95

3 Thermodynamik 97 3.1 Nullter Hauptsatz, thermisches Gleichgewicht & Temperatur . . . 97

3.2 Erster Hauptsatz, Arbeit & Warme. . . 98

3.3 Zweiter Hauptsatz, Entropie & Irreversibilitat . . . 101

3.4 Dritter Hauptsatz & absoluter Temperatur-Nullpunkt . . . 106

3.5 Thermodynamischer Grenzfall . . . 108

4 (Ideale) Quantengase 113 4.0 Erinnerung an die Zustandssumme des harmonischen Oszillators . . . 113

4.1 Teilchen-Ununterscheidbarkeit und Quantenstatistik . . . 115

4.1.1 DasPauli-Prinzip . . . 116

4.1.2 Besetzungszahlen n & Grokanonische Gesamtheit . . . 118

4.1.3 Die Fermi-Dirac- & Bose-Einstein-Besetzungsfunktionen . . 122

4.2 Fast Entartetes idealesFermi-Gas. . . 124

4.3 Bose-Gase & Bose-Einstein-Kondensation . . . 128

4.3.1 Das chemische Potential nicht-erhaltener Teilchen . . . 129

4.3.2 Photonen und elektromagnetische Strahlung . . . 129

4.3.3 Bose-Einstein-Kondensation . . . 131

5 Systeme wechselwirkender Teilchen und Phasenubergange 139 5.1 Uberblick . . . 139

5.2 Exkurs: Strukturfunktionen . . . 147

5.3 Perturbative Naherungsverfahren . . . 156

5.3.1 Virial-Entwicklung. . . 157

5.4 Selbstkonsistente Variationsverfahren. . . 160

5.4.1 Molekularfeld-Theorie (MFT) . . . 160

5.4.2 Curie-Wei MFT des Ising-Modells. . . 162

5.5 Isingartige Phasenubergange . . . 171

5.5.1 Existenz geordneter Phasen . . . 171

5.5.2 Spontane Symmetriebrechung . . . 171

5.5.3 Universalitat. . . 172

A Literaturverzeichnis 175

Das Thema der statistischen Physik ist das Verstandnis der Materie, bestehend aus vielen (10²³) Teilchen, ausgehend von den Teilchen-Wechselwirkungen.

1.1 Wahrscheinlichkeitstheorie

1.1.1 Denitionen

[A] Eindimensionale Wahrscheinlichkeitsdichte Denition:

Eine Groe ist eine (reelle) Zufallsgroe, wenn die Wahrscheinlichkeit, dass (reelle) Werte x im Bereich x bis x + dx annimmt, gegeben ist durch P (x) dx.

Wobei die Wahrscheinlichkeitsdichte P (x) folgende Voraussetzungen erfullt:

i) P (x) 0 (Positivitat) ii) R

dxP (x) = 1 (Normierung)¹ Bemerkung:

Die Werte x heien Ereignisse aus der Ereignismenge.

Die obige Denition gilt fur kontinuierliche Wahrscheinlichkeitsdichte. Wenn nur diskrete Werte xn annehmen kann, ersetzt man

P (x) !

N

X

n=1

Pn(x xn) mit Dirac--Ma. Auch hier ist i) P_n 0 und ii) P_N

n=1P_n = 1. P_n ist die Wahr- scheinlichkeit, dass den Wert xn annimmt.

P(x) = R_x

1 dx⁰P (x⁰): kumulierte Wahrscheinlichkeitsverteilungsfunktion.

Beispiele:

diskret: N Munzwurfe

^= Haugkeit von Kopf, xn= 1n mit n = 0;1;2; : : : ;N P_n =

1 2

n1 2

N n N!

(N n)!n!

P_n ist die Binomialverteilung mit Binomialkoezient ^N_n

, Zahl der n-elementigen Unter- menge der N-elementigen Menge. Dann Multiplikation der unabhangigen Wahrscheinlich- keiten, dass n mal Kopf und (N n) mal Zahl geworfen wird.

1Dabei geht das Integral immer uber den gesamt moglichen Wertebereich. Wenn keine Grenzen angegeben sind, dann istR1

1 dx gemeint.

kontinuierlich: Planck'sches Strahlungsgesetz des schwarzen Strahlers

P (;T ) d = 8h c³

³

e^kBTh 1d : Frequenz

P (;T ) d = c ²P

= c ;T

d : Wellenlange

Es genugt = ^c zu ersetzen bei einer Variablentransformation einer Funktion. Bei einer Wahrscheinlichkeitsdichte tritt weiter der Vorfaktor

^d_d auf.

[B] Mehrdimensionale Wahrscheinlichkeitsdichte Denition:

N Groen i, i = 1 : : : N bilden einen (reellen) N-dimensionalen Zufallsvektor , wenn die Wahrscheinlichkeit dafur, dass Werte im Bereich [x;x + dx] (genauer: _i Werte in [xi;xi+ dxi]) annimmt, gegeben ist durch PN(x) dx1 dxN = PN(x) d^Nx (N-dimensionales Volumenelement), wobei die gemeinsame Wahrscheinlichkeitsdichte erfullen muss:

i) P_N(x) 0 (Positivitat) ii) R

d^NxP_N(x) = 1 (Normierung)² Beispiel:

Maxwell-Boltzmann-Verteilung der Geschwindigkeiten im idealen Gases v = (v_x;v_y;v_z) P₃(v) d³v / 1

T¹³e ^2kBTmv2 d³v [C] Denitionen wichtiger Groen:

Mittelung: h: : :i =Z

d^Nx : : : P_N(x)

Mittelwert: hi =Z

d^NxxP_N(x) = Varianz:^{3 2}:= ²: = h( )²i =

N

X

i=1

Z

d^Nx x_{i i}2P_N(x)

=

N

X

i=1

Z

d^Nx

x_i² 2xii + i2

PN(x)

= hi 2hihi + ²

= h²i hi² ) ² 0

P (x) dx ist die Wahrscheinlichkeit fur Werte in [x;x + dx] anzunehmen. Diese ist messbar durch die relative Haugkeit:

Zahl Messungen von x in [x;x + dx]

Gesamtzahl der Messungen = W = P (x) dx

2wobeiR

d^Nx = R¹

1 dx₁ R¹

1 dx₂ ¹R

1 dx_N

3oder auch totales Schwankungsquadrat

Abbildung 1.1: Verteilung von Zufallszahlen von x mit charakteristischem Mittelwert und der Standardabweichung

fur viele identisch wiederholte Messungen.

Einzel-Varianz: _i²= h(i i)²i (1.1)

(relative) Streuung:

jj ( : Standardabweichung) (1.2) Korrelation: Kij = h i i

j j

i (1.3)

=Z

d^Nx xi i

xj j

PN(x) = Kji

Bemerkung:

Die Korrelation ist eine symmetrische Matrix und hat somit (vgl. lineare Algebra) reelle Eigenwerte. Ihre Eigenvektoren bilden ein Orthogonalsystem. Dies bedeutet wiederum, dass lineare Transformationen der i auf _i⁰ =P

i Ajii existieren, so dass die Matrix:

K⁰ = A^TK A diagonal ist.

K ist positiv denit, d.h. fur einen beliebigen Vektor a 2 R^N ist folgendes erfullt:

0

N

X

ij=1

aiKijaj

Beweis:

Es muss auf jeden Fall gelten:

X

ij

aih i i

j j

i aj = hA²i 0

wobei A = A() = P^N

i=1a_{i i i} .

Durch geschickte Wahl von A kann man daraus folgern:

i) Wir wahlen zunachst ai = ii0 d.h. der Vektor a ist auer an der i0-ten Kompo- nente (wo er 1 ist) Null. Dann folgt trivialerweise:

K_i0i0 = h _{i0 i0}2i = ²_i0 0

ii) Sind die Komponenten i₁ und i₀ von a Eins und alle anderen Null, d.h. a_i = ii0 ii1, so folgt:

K_i0i0 + K_i1i1 2K_i0i1 0

Dies bedeutet, dass die Kreuzkorrelationen kleiner sind, als die Selbstkorrelatio- nen:

jK_i0i1j 1

2 K_i0i0 + K_i1i1

Aus den obigen Uberlegungen ergibt sich auch der Zusammenhang mit der Varianz als Summe der Selbstkorrelationen zu:

² =

N

X

i=1

Kii = SpK

Die charakteristische Funktion ist fur k 2 R^N deniert uber:

'(k) = he^iki = Z

d^Nxe^ikxPN(x)

'(k) ist Erwartungswert der Phase e^ik mit k 2 R^N festem Vektor. Sie ist also die Fourier- Transformierte von PN(x). Im Folgenden wollen wir zur Vereinfachung diese charakteristi- sche Funktion im Eindimensionalen betrachten.

'(k) generiert die Momente, wobei das m-te Moment lautet:

h^mi = Z

dxx^mP (x) =

i @

@k _m

'(k)

k=0 m = 1;2; : : : Falls die Momente existieren, d.h. jh^mij 1, gilt:

'(k) = he^iki =

1

X

m=0

1

m!(ik)^mh^mi (1.4)

'(k) bestimmt die sogenannten Kumulanten uber:

'(k) = exp



 X1 m=1

(ik)^m m! h^mic

| {z }



 (1.5)

Dabei ist die m-te Kumulante:

h^mic =

i @

@k m

ln '(k) k=0

Diese ist eine (geschickte) Kombination aller Momente h^m0i mit Ordnung m⁰ < m. Fur die ersten Kumulanten gilt:

h⁽⁰⁾i_c = 0 h⁽¹⁾i_c = hi =

h⁽²⁾i_c = h²i hi² = ²

h⁽³⁾ic = h³i 3h²ihi + 2hi³ ...

Die erste Kumulante ist also der Mittelwert, die zweite die Varianz.

Beweis:

Durch Taylorreihenentwicklung um k = 0 '(k) = 1 + ikhi 1

2k²h²i i

6k³h³i + :::

'(k) = exp

ikh¹i_c k²

2 h²i_c i

6h³i_c + : : :

= 1 + ikh¹ic 1

2k² h²ic + h¹i²_c i

6k³ h³ic+ 3h²ich¹ic + h¹i³_c

+ O(k⁴) Vergleichen wir nun die k-Ordnungen:

h¹i_c = hi

h²ic = h²i hi²= ²

h³ic = h³i + 3hi²hi 3h²ihi h³i

Kumulanten charakterisieren Wahrscheinlichkeitsdichten praziser als Momente.

1.1.2 Variablentransformationen

Sei die Zufallsvariable (m-dimensional) eine Funktion der N-dimensionalen Zufallsva- riablen , = f_y() = y(), dann ist die Wahrscheinlichkeit, dass Werte im Intervall [y; y + dy] annimmt, gegeben durch

Pm(y) d^my = Z

d^NxPN(x) Integral uber Bereich, sodass y f(x) y + dy

Aquivalente Formulierung mit dem Dirac-:

Pm(y) = h(y f())i = Z

d^Nx (y f(x))PN(x) Bemerkungen:

Bei diskreten Zufallsvariablen wird R

d^Nx zur Summe.

Fur m = N vereinfacht es sich zu P_N(y) =Z

d^Nx ^N(y y(x)) P_N(x)

Variablensubstitution x ! y⁰:

d^Nx =

@x

@y⁰ d^Ny⁰ (Jacobi-Determinante)

somit folgt:

PN(y) =

@x

@y

PN(x(y)) 1. Beispiel:

Planck'sche Strahlung

P (;T ) = Z ₁

0 dP (;T )

c

⁰=^c

= Z ₀

1 d⁰ c ⁰²Pc

⁰ = ;T

( ⁰)

! P (;T ) = c ²P

= c ;T Also gilt die Beziehung:

P (;T ) d =

d d

P (;T )

=^c d

Abbildung 1.2: links: Planck-Verteilungsfunktion bei 5800 Kelvin unterteilt in gleiche 100nm Wellenlangen-Intervalle; rechts: die gleiche Funktion und die glei- chen Intervalle transformiert in Frequenz-Intervalle; entnommen aus [Bal]

2. Beispiel:

Wir betrachten die Summe = f (;) = + zweier Zufallsvariablen mit gemeinsamer Wahrscheinlichkeitsdichte P2(x;y)

P(z) = h(z ( + ))i =Z

dx dy P₂(x;y) (z x y)

=Z

dx P₂(x;z y)

was zu einer einfachen Beziehung der charakteristischen Funktion fuhrt:

'(k) = he^iki = Z

dz e^ikzP(z)

= Z

dx dy dz e^ikzP2(x;y)(z x y)

=Z

dx dy e^ik(x+y)P₂(x;y) Beispiel: Begegnungwahrscheinlichkeit

Person A und Person B kommen zwischen 12 und 13 Uhr in den Horsaal und bleiben je 20 Minuten. Wie gro ist die Wahrscheinlichkeit, dass sie sich begegnen?

Die gemeinsame Wahrscheinlichkeit der Ankunft von A in [y; y + dy] und der Ankunft vom B in [y; y + dy] ist

P2(x;y) = dx 60

dy 60

Die Wahrscheinlichkeit des Treens ist die kumulierte Wahrscheinlichkeit, dass die Zeit- dierenz z = jx yj der Ankunftszeiten weniger als 20 Minuten ist:

p =Probfz = jx yj 20g Also

P (z) =Z ₆₀

0 dx dy (z jx yj)P₂(x;y) p =Z ₂₀

0 dz P (z)

= Z ₆₀

0 dx dy Z ₂₀

0 (z jx yj) 1

60²

=Z ₆₀

0 dx dy (20 jx yj)

=relative Fl¨ache des roten Streifens jx yj < 20 = (60² 40²)=60² = 5 9

Abbildung 1.3: Graphische Darstellung der Begegnungswahrscheinlichkeit

1.1.3 Normal- oder Gauss-Verteilung

Die wichtigste Wahrscheinlichkeitsdichte lautet (hier zur Vereinfachung im eindimensiona- len):

P (x) = p 1

2²e ^{(x 22)2}

mit den zwei Parametern hxi = (Mittelwert) und ² = h(x )²i (Varianz) und der charakteristischen Funktion:

'(k) = exp

ik ² 2 k²

Der Bedeutung dieser Funktion kommt in x1.1.6

Die Gau-Wahrscheinlichkeitsdichte ist eindeutig durch erste Kumulante (= ) und zweite Kumulante (= ²) festgelegt. Alle weiteren Kumulanten sind Null:

h^m3ic = 0

Abbildung 1.4: Gauverteilung

1.1.4 Bedingte Wahrscheinlichkeiten und wichtige Formeln

Zur Vereinfachung sei N = 2 bis auf weiteres.

[A] Denition

Zwei Zufallsvariablen und mit gemeinsamer Wahrscheinlichkeitsdichte P2(x;y) seien gegeben. Unter der Bedingung, dass den Wert y (angenommen) hat, ist

P (xjy) dx

! die bedingte Wahrscheinlichkeit, dass Werte in [x;x + dx] annimmt. Dabei muss die bedingte Wahrscheinlichkeitsdichte wiederum erfullen:

i) P (xjy) 0 ii) R

dxP (xjy) = 1

fur alle y Bemerkung:

P (xjy) ist Wahrscheinlichkeitsdichte in fur jedes y

Achtung: Jede Wahrscheinlichkeitsdichte ist abhangig von Bedingungen ("fairer Wurfel\).

[B] Rechenregeln:

Die "marginale Wahrscheinlichkeitsdichte\, dass Werte in [x;x + dx] annimmt, un- abhangig davon, welchen Wert y annimmt, lautet:

P1(x) = Z

dyP2(x;y) (1.6)

Additionssatz Das Integral geht uber alle moglichen Werte von y.

P2(x;y) dx dy = (P1(y) dy)(P (xjy) dx)

Die gemeinsame Wahrscheinlichkeit P2(x;y) dx dy ist gleich der marginalen Wahrschein- lichkeit, dass Werte in [y;y + dy] annimmt (also P₁(y) dy), egal welche Werte hat, multipliziert mit der bedingten Wahrscheinlichkeit, dass Werte in [x;x + dx] annimmt, gegeben, dass Wert y hat.

) P₂(x;y) = P (xjy)P₁(y) (1.7)

Symmetrieaus

= P (yjx)P1(x) Multiplikationssatz

Aus Additionssatz und Multiplikationssatz folgt die "Formel der totalen Wahrscheinlich- keit\

P₁(x) =Z

dyP₂(x;y) P1(x) =Z

dyP (xjy)P1(y)

Dabei geht das Integral uber alle moglichen Werte y gewichtet mit marginaler Wahrschein- lichkeit bei y zu sein, egal wo ist, multipliziert mit Bedingung fur gegebenen y.

Ansatzpunkt der Quantenmechanik nach Feynman

Formel von Bayes zur Uberprufung der Wahrscheinlichkeit von Hypothesen:

P2(x;y) = P (xjy)P1(y) = P (yjx)P1(x) ) P (xjy) = P (yjx)P1(x)

P1(y)

Add.-Satz= P (yjx)P1(x) R dxP (yjx)P1(x) Bemerkung:

Zur Erlauterung von P1(x) = R

dyP (xjy)P1(y) betrachten wir Abbildung 1.5. Dort sind zwei Verteilungen abgebildet. Von jedem Punkt der linken Verteilung gibt es eine Uber- gangswahrscheinlichkeit zur rechten Verteilung.

Abbildung 1.5: "Zwei Hunde mit Flohen\

1.1.5 (stochastisch) unabhangige Zufallsvariablen

Denition:

Es gebe zwei Untermengen von Zufallszahlen f₁; : : : ;_rg und f_r+1; : : : ;_Ng mit

1 r N. Sie heien (stochastisch) unabhangig, wenn die gemeinsame Wahrscheinlich- keitsdichte separiert ist (ein Produkt ist).

PN(x1: : : xN) = Pr(x1: : : xr)PN r(xr+1: : : xN)

Es folgt dann, dass die bedingte Wahrscheinlichkeitsdichte gleich den marginalen werden.

P (x1: : : xrjxr+1: : : xN) = Pr(x1: : : xr) P (xx+1: : : xNjx1: : : xr) = PN r(xr+1: : : xN) Beweis:

Mult.-Satz ) PN(x) = P (x1: : : xrjxr+1: : : xN)PN r(xr+1: : : xN)

Durch Vergleich mit der Denition von "unabhangig\ und Division durch P^{N r} folgt die Behauptung.

Bemerkung:

Wenn Werte von ₁ bis _r nicht von denen von _r+1 bis _N abhangen, ist die Bedin- gung keine Einschrankung.

1.1.6 Der Zentrale Grenzwertsatz (Law of large numbers)

Betrachtet sei die Summe _N =P_N

i=1_i von N unabhangigen Zufallsvariablen ₁, ... , _N (d.h. PN(x) = P (x1) : : : P (xN)) mit endlichen Mittelwerten und endlichen Varianzen, d.h.

jh_iij = _i

< 1

und h(i _i)²i = _i² < 1

(d.h. sowohl < i > als auch _i² existieren und sind betragsmaig kleiner als 1). Die Wahrscheinlichkeitsdichte von N fur groe N wird eine Gauverteilung.:

P_N(z) = 1

p2²_N exp

(z _N)² 2²_N

mit dem Mittelwert

_N =

N

X

i=1

_i und der Varianz

²_N =

N

X

i=1

_i²

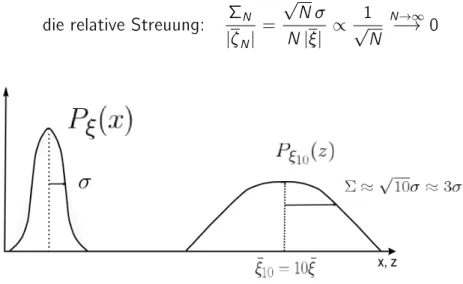
Fur (zur Vereinfachung) gleichverteilte _i, also _i = und ²_i = ², nden wir also eine sehr enge Verteilung mit verschwindender relativer Streuung, weil Gleichverteilung _N = N und ²_N = N² bedeutet, und die relative Streuung mit wachsendem N immer geringer wird:

die relative Streuung: N

j_Nj = pN

N jj / p1 N

N!1! 0

Abbildung 1.6: Betrachtet wird eine Verteilung P und P10 und man erkennt zunachst, dass die Verteilung P₁₀ deutlich breiter ist

Abbildung 1.7: Durch Reskalierung wird die Verteilung P10 schmaler.

Beweis:

Fur (zur Vereinfachung) gleichverteilte, unabhangige _i (mit _i = und _i²= ²) betrach- ten wir

N = p1 N

N

X

i=1

(i ) mit unabhangigen PN, also:

P_N(x) = P (x₁)P (x₂) : : : P (x_N)

_N hat die Wahrscheinlichkeitsdichte:

P_N(y) =Z

d^Nx P_N(x) y p1 N

N

X

i=1

(x_i )

!

wobei der Mittelwert

=Z

dx x P₁(x) ist und die Varianz

²=Z

dx(x )²P₁(x) Die charakteristische Funktion erfullt also

'N(k) = Z

dy e^ikyPN(y)

=Z dy Z

d^NxP_N(x)e^iky y p1 N

N

X

i=1

(x_i )

!

= Z

dx1: : : dxN P (x1) : : : P (xN) exp

"

pik N

N

X

i=1

(xi )

#

=







e^pikN Z

dx e^pikNxP1(x)

| {z }









N

mit charakt. Fkt. von : = '(pk N)

=

e ^pikN'

pk N

_N

Unter der Annahme, dass jh^m3i_cj < 1 gilt, verwenden wir nun die Kumulanten-Entwicklung von '

pk N

:

' pk

N

= exp pik

N k²

2N² ik³

6N³²h³i_c + : : :

so folgt (der Term mit hebt sich weg):

'(k) = exp k²

2 ²+ O

h³ic

N¹²

N!1! e ^k222

Mit Fourier-Rucktransformation erhalten wir:

PN(y) =Z dk

2 e ^ikye

pk22 2

| {z }

'(k)

= p 1

2² e ^22y2 Die Wahrscheinlichkeitsdichte von N = N +p

NN folgt gema Variablentransformation

PN(z) = dy

dzPN(y = p1

N(z N )) = p 1

2N² e ^{(z N 2N2)}

Bemerkung:

Der Beweis wurde hier nur unter den Voraussetzungen der Gleichverteilung der i und der Endlichkeit der Kumulanten gefuhrt. Er kann auf den allgemeinen Fall ausgeweitet werden, dann mussen jedoch weitere Bedingungen an das Wohlverhalten der _i gestellt werden.

Bemerkung:

Die Voraussetzungen waren: Unabhangige i und endliche Mittelwerte bzw. Varian- zen, was zu einer Gaussverteilung mit _N / N und ²_N / N fuhrt; d.h. dass 2 Kumulanten also die Wahrscheinlichkeitsdichte P festlegen.

Der zentrale Grenzwertsatz ist wichtig fur die statistische Mechanik und die Thermo- dynamik, wo N im Bereich 10²³ liegt, da die dort auftretenden Mengen- (oder exten- sive) Groen solche additiven Groen sind. Wir haben also viele kleine unabhangige Beitrage zu einer extensiven Groe.

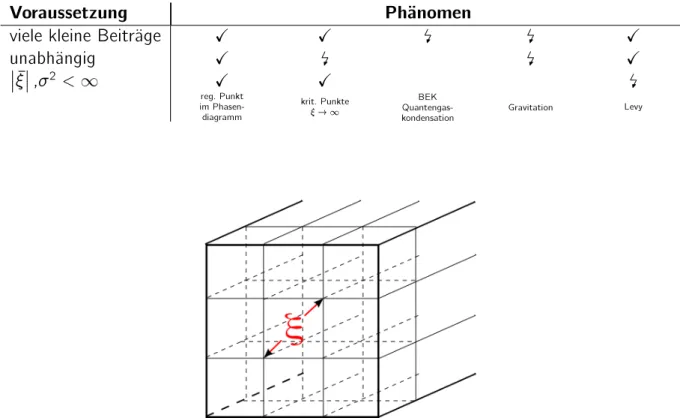
Voraussetzung Phanomen

viele kleine Beitrage X X X

unabhangig X X

;² < 1 X X

reg. Punkt im Phasen- diagramm

krit. Punkte ! 1

Quantengas-BEK

kondensation Gravitation Levy

Abbildung 1.8: Subvolumen eines makroskopischen Korpers, welches unabhangig von den anderen Subvolumina ist; ist die Korrelationslange

Bemerkung:

Korrelationslange : Unterteilung in stochastisch unabhangiger Subvolumina mit Volumen / ³. ist dabei der Durchmesser der unabhangigen Teilvolumen.

Ein regularer Punkt eines Materials im Phasendiagramm hat < 1 ( 10nm typisch).

Ein kritischer Punkt hingegen hat ! 1 (kritischer Phasenubergangspunkt).

1.2 Quantenstatistik

1.2.0 Wiederholung der Quantenmechanik vieler Freiheitsgrade

Mogliche Zustande j i eines quantenmechanischen Systems von f Freiheitsgraden sind Elemente aus einem Hilbertraum H, also j i 2 H und sie sollen normiert sein:

h j i = 1 Der Hilbertraum H besitzt eine Orthonormalbasis

fjn₁; ::: n_fig = fjnig mit

hnjn⁰i = _nn0

und j i =X

n c_njni

Die Zeitabhangigkeit ist gegeben durch die Schr¨odinger-Gleichung fur den unitaren Zeitevolutionsoperator U:

i~ @

@tU(t;t0) = H(t)U(t;t0) mit U(t = t₀;t₀) = 1

wobei H(t) = H(t)^y der Hamilton-Operator ist.

In der Vorlesung IK IV wurden bereits die beiden Betrachtungsweisen Schr¨odinger- und Heisenberg-Bild eingefuhrt:

Ist ein Operator nicht von sich aus schon zeitabhangig, so bekommt er im Schr¨odinger- Bild keine Zeitabhangigkeit hinzu. Die Zeitabhangigkeit steckt hier in der Wellenfunktion:

j (t)i = j (t)i_S = U(t;t₀)j (t₀)i A_S(t) = A_S = A

ImHeisenberg-Bild dagegen tragt der Operator die ganze Zeitabhangigkeit und die Wel- lenfunktion ist zeitlich konstant:

j (t)i_H = j (t₀)i

A_H(t) = U ¹(t;t₀) A_S(t)U(t;t₀)

Zum Beweis betrachtet man die Ableitung des Heisenberg-Operators und erhalt:

d

dtAH(t) = i

~(HAH AHH) + ( @

@tA)H = i

~ [H;A] + ( @

@tA)H

) AH(t) = e^iHt=~Ase ^iHt=~

wobei wir _@t^@A

H = 0 angenommen haben.

Beispiele:

Ein freies Teilchen in einer Box mit dem Volumen V = L³ mit der periodischen Randbedingung fur seine Wellenfunktion:

(r + L^e) = (r)

Seine Hamilton-Funktion bei drei Freiheitsgraden lautet:

H = p² 2m zu der Orthonormalbasis







jki ; k = 2 L



 nx

n_y nz



 ; n_i = 0; 1; 2; : : :





 Seine Eigenwerte lauten dann:

k = ~²k² 2m N freie nicht wechselwirkende Teilchen in einer Box:

Fur die Hamilton-Funktion gilt dann:

H =

N

X

i=1

1 2mp²_i Fur die Orthnormalbasis ergibt sich dann:

fjk1; : : : ;kNi ; mit den k von obeng

Fur das Wasserstoatom gilt mit den Indizes e fur Elektron und p fur Proton:

H = p²_p

2mp + p²_e 2me

c jre rpj mit der Orthonormalbasis

fjPn;l;mig wobei P der Schwerpunktsimpuls ist.

Zwei nichtwechselwirkende Spins besitzen im externen Magnetfeld die Hamilton- Funktion:

H = ~

2(₁+ ₂) B(t) mit der Orthonormalbasis

fj ""i = j "i1j "i2 ; j ##i = j #i1j #i2; j "#i = j "i1j #i2 ; j #"i = j #i1j "i2g

1.2.1 statistischer Dichteoperator; reine Zustande und Gemische

A) Erwartungswerte

Der hermitesche Operator A auf H hat den Erwartungswert h jAj i = P

nn⁰c_n0c_n hn⁰jAjni im reinen Zustand j i, fur den gilt:

j i =X

n c_n jni 2 H

Dabei sind die c_n seine Entwicklungskoezienten und fur diese gilt:

c_n = hnj i

In einem reinen Zustand lautet der Erwartungswert in Matrixdarstellung:

h jAj i =X nn⁰

c_nhnjAjn⁰ic_n0

mit dem Dichteoperator eines reinen Zustands:

% := j ih j schreibt man:

h jAj i = SpA%

Zum Beweis muss man die Spur von A% in Matrix-Darstellung in der Orthonormalbasis fjnig ausrechnen:

Sp (A% ) =X n⁰

hn⁰jA% jn⁰i

Durch das Einfugen der dyadischen Eins zwischen dem Operator A und dem Dichteoperator

% erhalt man:

Sp (A% ) =X nn⁰

hn⁰jAjni

cn z }| { hnj i

c

n⁰ z }| { h jn⁰i

=X

nn⁰

c_nc_n0 hn⁰jAjni

=X

n⁰

hn⁰jc_n0jAX n c_njni

= h jAj i

B) Spur und Spurrechenregeln (zur Vereinfachung sei H endlich dimensional) Die Spur eines Operators ist deniert als:

SpA :=X

n hnjAjni mit der Orthonormalbasisfjnigi

Die Spur entspricht also der Summe der Diagonalterme von A.

Es gelten die folgenden Rechenregeln:

a) Die Spur ist invariant unter zyklischer Vertauschung:

Sp (AB) =X nn⁰

hnjAjn⁰ihn⁰jBjni =X nn⁰

hn⁰jBjnihnjAjn⁰i = Sp (BA) Sp (ABC) = Sp (CAB) = Sp (BCA)

b) Invarianz unter Basiswechsel:

Geht man zu einer neuen Orthonormalbasis fj ~mig mit j ~mi = P

n U_mn jni uber, wobei U der unitare Transformationsoperator U^y = U ¹ (d.h. U^yU =1) ist, so folgt mit der Tatsache, dass ~A = UAU ¹(vgl. U^yUAU ¹

| {z }

= ~A

U = A) sowie durch zweimaliges Einfuhren der dyadischen Eins: 1 =P

mj ~mihmj:

SpA =X

n hnjAjni =X

n hnjU^y A Ujni~

= X

n ~m ~m⁰

hnjU^yj ~mi

| {z }

h ~mj ~Aj ~m⁰i

| {z }

h ~m⁰jUjni = F

Der Term wird nun hinter die beiden anderen gestellt, so dass nach vorne rutscht.

MitP

n h ~m⁰jUjnihnjU^yj ~mi = _mm0 folgt weiter:

F =X

~ m

h ~mj ~Aj ~mi

c) Spur und Eigenwerte:

Die Spur eines diagonalisierbaren Operators A ist die Summe seiner Eigenwerte ai. Ein hermitescher Operator ist diagonalisierbar mit einer unitaren Transformation und die Spur des Operators ergibt sich dann aus der Summe seiner Eigenwerte:

SpA =X

i

a_i

C) Denition: Der Dichteoperator eines reinen Zustands % erfullt:

% = %^y (hermitesch )

% ist positiv, d.h. h'j%j'i 0 8j'i 2 H Sp% = 1 (Norm)

Sp%²= 1 (rein)

Bemerkung: % = j ih j ist rein.

Beweis:

Man kann leicht nachweisen, dass die oberen vier Eigenschaften erfullt sind:

Die Matrix (% )_nn0 = hnj ih jn⁰i ist hermitesch, weil:

(%^y)_nn0 = %_n0n = hn⁰j ih jni = (% )_nn0

Auerdem ist:

h'j% j'i = jh'j ij² 0 sowie:

Sp% =X

n hnj ih jni = h jX n jnihnj

| {z }

=1

j i = h j i = 1

und:

Sp%² = Spj i h j i

| {z }

=1

h j = Sp% = 1 D) Dichteoperator eines Gemisches

Ein quantenmechanisches System liege mit der Wahrscheinlichkeit ~pi in verschiedenen (reinen) nicht interferenzfahigen Zustanden j _ii vor.

In einem solchen Gemisch lautet der Mittelwert eines Operators A:

hAi :=

I

X

i=1

~pi h ijAj ii

Er setzt sich also zusammen aus dem statistischen Mittelwert und dem quantenmechani- schen Erwartungswert von A im Zustand j _ii.

Als Wahrscheinlichkeit muss ~p_i die folgenden Bedingungen erfullen:

0 ~p_i 1 P^I

i=1~pi = 1 Bemerkung:

Die Kreuzterme h ijAj i⁰i (mit i 6= i⁰) fehlen, da die Wahrscheinlichkeit ~pi fur das Vorliegen von Mikrozustanden j ii aus (Probenpraparation) Wechselwirkung mit der Umgebung resultiert.

Beispiele:

Systeme, die mit einem Warmebad wechselwirken unpolarisierter Lichtstrahl

N Teilchen in einer Box, die wechselwirken (stoen) und eine Maxwell-Boltzmann- Verteilung der Geschwindigkeiten haben

Mit dem Dichteoperator

% :=

I

X

i=1

~p_ij _iih _ij (1.8)

lautet der Mittelwert:

hAi = Sp%A Beweis:

hAi =X

m hmj%Ajmi =X m; i

hmj~p_ij _iih _ijAjmi

=X

m; i

~p_ihmj

| {z }

=~picm⁽ⁱ⁾

iiX m⁰

c_m0hm⁰jAjmi

= X

mm⁰ X

i

c_m⁽ⁱ⁾₀ c_m ~pi

=X

i

~pih ijAj ii

In der Summe liegt der Unterschied zum reinen Zustand (in der Matrix-Darstellung von %).

Dargestellt in ONB hat % folgende Matrixelemente:

hnj%jn⁰i =X

i

~p_i c_n⁽ⁱ⁾

h|{z}nj ii

c_n⁽ⁱ⁾₀

Denition:

Ein (statistischer) Dichteoperator % auf H erfullt die folgenden Eigenschaften:

% = %^y (hermitesch )

% ist positiv, d.h. h'j%j'i 0 8j'i 2 H Sp% = 1 (Norm)

Der statistische Mittelwert eines beliebigen Operators A lautet dann im Zustand %:

hAi = Sp%A Bemerkung:

Zur Vereinfachung wird angenommen, dass H nicht unendlich-dimensional sei.

% = P

i ~p_ij _iih _ij sei der Dichteoperator und dessen Aufenthaltswahrscheinlichkeit lautet:

hxj%jxi =

I

X

i=1

~pijhxj iij²

E) Eigenschaften von %

a) Eigenwerte und Eigenzustande Die dyadische Zerlegung % = P

n=1pnjnihnj existiert mit %jni = pnjni (Eigenwertglei- chung) sowie hnjn⁰i = _nn⁰ (orthonormal). Die Eigenwerte p_n geben eine (diskrete) Wahrscheinlichkeit an, dass der Eigenzustand fjnig im Gemisch vorliegt, somit muss fur diese gelten:

0 pn 1 und X

n=1

pn= 1 Bemerkung:

% ist diagonal in den Eigenzustanden jni (aber nicht notwendigerweise in den j ii, weil h _ij _ji 6= 0 moglich ist). Die Eigenzustande fjnig, wobei n fur mehrere Quantenindizies stehen kann, sind Vielteilchen-Zustande mit Entwicklung:

jni =X

n c_n;njni in alten ONB fjnig von H

Beispiel: % = _Z¹e ^H ist der Dichteoperator im kanonischen Ensemble mit = _kT¹ und Z als Normierungszahl.

Beweis:

%⁺ = % (hermitesch) ! kann diagonalisiert werden. Die Tatsache, dass % hermitesch ist, liefert % = P

n=1p_n jnihnj mit orthonormierter Eigenbasis von %. Weil laut Vor- aussetzung h'j%j'i = Ppnh'jnihnj'i = P

n pnjh'jnij² 0 8j'i 2 H gilt, muss pn 0 sein. Auerdem muss die Spur des Dichteoperators gleich Eins sein und wegen 1 = Sp% =P

nhnj%jni = Pp_njhnjnij²=P

np_n folgt somit p_n 1.

b) Reine Zustande Satz:

Gehort % zu einem reinen Zustand (also Sp%² = 1), dann sind folgende Aussagen

aquivalent:

i) %²= % (d.h. % ist ein Projektor) ii) pi0 = 1 und pi = 0 sonst

iii) % hat den Rang 1 Beweis:

Die Aussagen i)-iii) sind aquivalent, aus % = j ioih i0j folgt sofort, dass Sp%² = 1 gilt.

Ist nun anders herum Sp%² = 1, so hat %² die Eigenwerte p²_i pi fur pi 1 Somit ist aber 1 =P

i p²_i P

i p_i = 1, was nur mit "=\ erfullt sein kann und damit ist gezeigt, dass pi0 = 1 und pi = 0 sonst gelten muss.

Bemerkung:

Ein Mikrozustand ist also ein Makrozustand, der nur ein ji₀i enthalt. Der reine Dichte- operator ist die Projektion an ji0i welcher mit der Wahrscheinlichkeit pi0 = 1 auftrit.

Ein Gemisch (Makrozustand) ist die Summe vieler reiner Zustande mit einer Wahr- scheinlichkeit pi 6= 0.

1.2.2 Subsysteme und reduzierte Dichteoperatoren

H sei ein f -dimensionaler Produkt-Hilbert-Raum: H = H1 H2 zweier Subsysteme, wobei H₁ r-dimensional und H₂ (f r)-dimensional sei.

fjnig = fjn1n2: : : nfig

Spannen nun die jn₁i₁ den H₁ und die jn₂i₂ den H₂ auf, so bilden die Produktzustande:

fjnig = fjn1i1 jn2i2g mit n1=





 n11

n...1r







und n2=





 n2r+1

n..._2f







eine Orthonormalbasis zu H.

Denition:

Der reduzierte Dichteoperator %1 auf H1:

%₁= Sp₂f%g =X n2

2hn₂j % jn₂i₂ (Absummieren von H₂ gewichtet auf H₁)

[A] Subsysteme und reduzierte Dichteoperatoren

% gehore (zur Vereinfachung) zu einem reinen Zustand j i in H, so gilt mit j i =P

nc_njni =P

n1;n2c_n1c_n2jn₁i jn₂i:

% = j ih j =X nn⁰

c_nc_n0jn⁰i hnj

= X

n1n⁰₁n2n⁰₂

c_n1n2c_n⁰_1n⁰₂ jn⁰₁i1jn⁰₂i2 1hn₁j2hn⁰₂j (*)

mit n jc_nj²= 1. Damit folgt der reduzierte Dichteoperator:

%1= Sp₂f%g = Sp₂j i h j =X n2

2hn2j i h j n2i2

= X

n2;n⁰2;n⁰⁰2;n⁰1;n⁰⁰1

c_n0₁;n⁰2c_n00₁;n⁰⁰22hn2jn⁰⁰2i2

| {z }

n2;n⁰⁰2

2hn⁰j n2

| {z }

n2;n⁰2

i2jn⁰⁰1i_{1 1}hn⁰1j

= X

n⁰1;n⁰⁰1

X n2

c_n0₁;n2c_n00₁;n2

!

jn⁰⁰1i_{1 1}hn⁰1j Behauptung:

i) %1 ist (i.A. nicht reiner) Dichteoperator auf H1

ii) Der Mittelwert hA1i = Sp%A1 eines beliebigen Operators A1, der nur auf H1 wirkt, kann mit %₁ alleine bestimmt werden:

hA₁i = Sp(A₁12)% = Sp₁(A₁%) Beweis:

i) z.z.:1h'1j % j'1i₁ 0 8 j'1i₁ 2 H1 mit j'1i =P

n1d_n1jn1i₁

1h'j % j'i₁ = X n1;n⁰1

d_n1X n2

c_n1;n2c_n0

1n2d_n0

1 =X

n2

jb_n2j² 0 mit b_n2 =X

n1

dn1c_n;n2 ii)

hA₁i = Sp(A₁12)% = X n1;n⁰1;n2;n⁰2

c_n0₁;n2 1hn₁j A₁jn⁰₁i₁ c_{n1;n2 2}hn₂j12jn⁰₂i₂

= X

n1;n⁰1

1hn₁j A₁jn⁰₁i₁ X n2;n⁰2

c_n1;n2c_n0

1;n2 2hn₂j12jn⁰₂i₂ Weiterhin gilt:

hA₁i = Sp%A₁= X n1n2n⁰1n⁰2

1hn₁j₂hn₂j % jn⁰₂i₂jn⁰₁i_{1 1}hn⁰₁j A₁jn₁i_{1 1}hn⁰₂j1jn₂i₂

| {z }

=n2n⁰2

= X

n1;n2

hn₁j A jn⁰₁iX

c_n1;n2c_n0₁n₂ Beide Ausdrucke sind identisch.

Bemerkung:

Fur einen beliebigen Operator A, der nur auf Subsystem H₁ wirkt, kann Mittelwert ohne Wissen uber Subsystem 2 bestimmt werden, falls %1 bekannt ist.

Allerdings enthalt %1 = Sp₂f%g nur reduzierte Informationen, woraus i.A. % des Gesamtsystems nicht wieder hergestellt werden kann.

[B] Unabhangigkeit Denition:

Zwei Subsysteme eines quantenmechanischen Systems heien unabhangig, wenn % = %1

%₂ gilt (d.h. wenn der Dichteoperator des gesamten Systems sich aus dem Tensorprodukt der reduzierten Dichteoperators der beiden Subsysteme zusammen setzt.)

Das bedeutet fur die Matrixdarstellung von %:

hnj%jn⁰i =1hn1j2hn2j%1 %2jn⁰₁i1 jn⁰₂i2

= ₁hn₁j%₁jn⁰₁i₁

| {z } Matrixelement inH1

₂hn₂j%₂jn⁰₂i₂

| {z } Matrixelement inH2

Mit j i =P

nc_njni folgt fur %:

% = j i h j =



 X n1;n⁰1

c_n⁽¹⁾₁ c_n0

1jn⁰1i_{1 1}hn1j





| {z }

=%1=j i₁₁h j



 X n2;n⁰2

c_n⁽²⁾₂ c_n0

2jn⁰2i_{2 2}hn2j





| {z }

=%2=j i₂₂h j

Satz:

Der reduzierte Dichteoperator %₁ gehort zu einem reinen Zustand, wenn das Subsystem 1 vom Rest (hier Subsystem 2) unabhangig ist.

Bemerkung:

Wechselwirkungen zwischen dem Subsystem zwingen aber (fast immer), dass der redu- zierte Dichteoperator %₁ zu einem Gemisch gehort.

Beweis:

Zu zeigen ist die Behauptung

Sp₁ %²₁= 1 ) % = %1 %2

Ein beliebiger Dichteoperator auf H lautet in der Eigenbasis (mit den Eigenwerten p_i):

% =X

i

pi jnihnj wobei jni =P

n c_n⁽ⁱ⁾jni die Orthonormalbasis von H ist. Somit kann % mit jni = jn1i2 jn2i2

% geschrieben werden als:

% =X

inn⁰ p_i

c_n⁽ⁱ⁾₀ c_n⁽ⁱ⁾

jnihn⁰j Geht man damit in die Denition des reduzierten Dichteoperators:

%1= Sp₂% =X n2

hn2j2 % jn2i2

so erhalt man fur %₁:

%₁= X

in1n⁰1

p_i jn₁i₁hn⁰₁j₁ X n2

c_n⁽ⁱ⁾_1n2 c_n⁽ⁱ⁾_1n2 Da %1 rein sein soll, muss naturlich auch gelten: %1= j i1h j1.

Man kommt nun im Beweis weiter voran, wenn man die Orthonormalbasis in H so wahlt, dass i1= jn⁽⁰⁾₁ i1 ist, dann mussen namlich alle anderen Summanden verschwinden:

%₁= jn⁰₁i₁hn⁰₁j₁ 0 =X

in2

pi

c_n⁽ⁱ⁾₀

1n2

c_n⁽ⁱ⁾_1n2 fur n16= n⁽⁰⁾₁ 6= n⁰1

Bei der speziellen Wahl von n1= n⁰1 6= n⁰₁ sieht man:

X

in2

Pijc_n⁽ⁱ⁾_1n2j² = 0

was bedeutet, dass c_n1n2 = 0 fur alle n₂und n₁ 6= n⁰₁. Damit erhalt der Dichteoperator die folgende Darstellung:

% =X

i

X n2n⁰2

p_i c_n⁽ⁱ⁾₀

1n⁰2

c_n⁽ⁱ⁾0

1n2 jn⁰₁i₁jn₂i₂hn⁰₁j₁hn⁰₂j₂

=: jn⁰₁i1hn⁰₁j1

| {z }

reiner Zustand auf H1

%2=: %1 %2

[C] Beispiele

Beispiel: Zwei Teilchen in einer Box:

a) 2 nichtwechselwirkende Teilchen

Die Orthonormalbasis ist gegeben durch fjk1k2ig = fjk1i jk2ig mit folgender Wellen- funktion:

hr₁j k₁i = p1 re^ikr

Ein Operator, der nur auf H₁ wirkt: z.B. T₁ = _2m¹ p²₁= _2m^~2k²₁: kinetische Energie von Teilchen 1.

Operator der auf H wirkt, z.B. H = T₁+ T₂

Allgemein sind j 1i₁ und j 2i₂ Wellenpakte und % = j 1i_{1 1}h 1j j 2i_{2 2}h 2j un- abhangig.

b) 2 wechselwirkende Teilchen

H = p²₁ 2m + p²₂

2m + V (r₁;r₂)

Um % als Produkt schreiben zu konnen werden Schwerpunktkoordinaten eingefuhrt:

MR = m₁r₁+ m₂r₂ mit M = m₁+ m₂ r = r₁ r₂

1 = 1

m1 + 1 m2

Daraus folgt fur den Hamilton-Operator:

H = 1 2MpR2

| {z }

H1

+ 1

2pr2+ V (r) H2

| {z } Die allgemeine Wellenfunktion nimmt dann folgende Gestalt an:

j i = ji_r X K

ckjKi_R mit hR jKi = p1 re^iKR

Obwohl E = konst:, ergibt sich ein Gemisch in der relativen Bewegung, wenn das Wellenpaket der Schwerpunktbewegung in H2 verschmiert.

1.2.3 Von-Neumann-Gleichung

Die Zeitentwicklung eines reinen Dichteoperators % = j ih j folgt aus derSchr¨odinger- Gleichung

@

@th (t)j = i

~h (t)jH(t) zu

i~ @

@t%(t) = i~ @

@tj (t)ih (t)j

@

@t h (t)j = i

~ h (t)j H⁺(t)

= H(t)%(t) %(t)H(t) H⁺= H

= [H;%]

In wurde die Produktregel verwendet.

Werden im Gemisch % =P

i ~pi j iih ij die ~pi als konstant (zeitunabhangig) angenommen, so gilt dort ebenfalls:

@

@t%(t) = i

~[H(t);%(t)]

von-Neumann-Gleichung Bemerkung:

Wenn % = %(H) ) _@t^@% = 0 (! Erhaltungsgroe) weil eine Funktion des Hamil- tonoperators mit diesem kommutiert.

d

dt%(H) = i

h[H;%(H)] = 0

Im Heisenberg-Bild gilt dd^tAH(t) = _~ⁱ[H;AH] mit umgekehrten Vorzeichen. Dies ist eine Andeutung darauf, dass % kein gewohnlicher (Heisenberg) Operator ist. Ei- gentlich ist der Dichteoperator eine Abbildung, die allen Operatoren ihren Mittelwert zuordnet, und davon abhangt in welchem quantenmechanischen Mikrozustand das System ist.

1.3 Klassische Statistik

1.3.1 Der Phasenraum, Phasenraumverteilungsfunktion

Dem klassischen Makrozustand eines N-Teilchen-Systems wird eine Phasenraumvertei- lungsfunktion d.h. eine Wahrscheinlichkeitsdichte

% (r1; :::; rN; p1; :::;pN) = % (frg;fpg) = % ( N) Phasenraumpunkt im 6N-dimensionalen Phasenraum zugeordnet, so dass

%( N) d n

mit

d N = 1 N! 1

h^3N

N

Y

i=1

d³ri d³pi

(dem normierten Phasenraumvolumenelement) die Wahrscheinlichkeit ist, dass das System den Mikrozustand im Phasenraumvolumenelement Q_N

i=1 d³rid³pi um den Punkt N = fr;pg annimmt. Der Vorfaktor _h¹3N folgt aus der Quantenmechanik, und der Vorfaktor _N!¹ aus der Vertauschbarkeit der Teilchen).

Der Mittelwert einer beliebigen Funktion A( _N) im Phasenraum lautet:

hAi = Z

d N %( N) A( N) = 1 N!

1 h^3N

Z Y

d³r d³p % (fr;pg) A (fr;pg) = Sp%A

Bemerkung:

Ein Mikrozustand liegt vor, wenn alle Orte und Impulse bekannt sind:

%mikro= h^3NN!

N

Y

i=1

(r_i r_i(t))(p_i p_i(t))

wobei die ri(t) und pi(t) der Trajektorie des i-ten Teilchens entsprechen. Das N! ist ein Permutationsfaktor, dass das i-te Teilchen im Phasenraum r_i, p_i annimmt. r_i und p_i sind