Statistik II f¨ur Betriebswirte Vorlesung 14

Statistik II f¨ ur Betriebswirte Vorlesung 14

Dr. Andreas W¨unsche

TU Bergakademie Freiberg Institut f¨ur Stochastik

27. Januar 2020

8.2 Mehrstufige Stichprobenpl¨ ane

I Um die Anzahl der zu pr¨ufenden Teile zu verringern, k¨onnen mehrstufige Stichprobenpl¨aneverwendet werden.

I Dabei werden (in Abh¨angigkeit der Ergebnisse der einzelnen Stichproben) mehrere Stichproben nacheinander gezogen.

I F¨ur jede der m¨oglichen Stichproben (außer der letzten) gibt es 3 Entscheidungsm¨oglichkeiten:

I Annahme des Postens (und keine weitere Ziehung einer Stichprobe);

I Ablehnung des Postens (und keine weitere Ziehung einer Stichprobe);

I Ziehung einer weiteren Stichprobe (f¨allt bei der letzten weg).

I Diese Stichproben haben im Allgemeinen einenkleineren Umfang im Vergleich zu einstufigen Pl¨anen, so dass sich auch insgesamt eine geringere Anzahl von zu pr¨ufenden Teilen ergibt.

I Diese Stichprobenpl¨ane sind im Allgemeinen komplizierter und k¨onnen auch organisatorisch ung¨unstiger sein, deshalb nutzt man praktisch meistens nurzweistufige Stichprobenpl¨ane.

8.2.1 Zweistufige (oder doppelte) Stichprobenpl¨ ane

I Zun¨achst: Stichprobe vom Umfang n1 aus dem Los und Bestimmung der Anzahl x1 der Ausschussst¨ucke darin.

I Entscheidung mit Annahmezahl c1 undAblehnezahl c2>c1:

I falls x1≤c1 gilt, nimmt man den Posten an;

I falls x1>c2 gilt, lehnt man den Posten ab;

I falls c1<x1≤c2 gilt, zieht man eine weitere Stichprobe, diesmal vom Umfang n2 und bestimmt die Anzahl der Ausschussteile x2 in dieser zweiten Stichprobe.

I Entscheidung mit Annahmezahl c₃:

I falls x1+x2≤c3 gilt, nimmt man den Posten an;

I falls jedoch x1+x2>c3 gilt, lehnt man den Posten ab.

I Damit m¨ussen f¨ur einen zweistufigen Stichprobenplan 5 Parameter durch ¨ahnliche ¨Uberlegungen wie beim einstufigen Stichprobenplan bestimmt werden: die Stichprobenumf¨ange n₁,n₂ und die

Annahme- bzw. Ablehnezahlen c₁,c₂,c₃.

OC-Funktion f¨ ur den zweistufigen Stichprobenplan

I X1,X2: Anzahl der Ausschussteile in Stichprobe 1 bzw. 2 ; N: Anzahl der Teile im Posten;

M: Anzahl der Ausschussteile im Posten (unbekannt), p = M N ; P_p: Wahrscheinlichkeit, falls p die tats¨achliche Ausschussquote ist .

I Annahmewahrscheinlichkeit des Loses:

L(p) =P_p({X₁≤c₁} ∪[{c₁<X₁ ≤c₂} ∩ {X₁+X₂ ≤c₃}])

=P_p(X₁ ≤c₁) +

c2

X

x1=c1+1

P_p(X₁+X₂≤c₃|X₁=x₁)P_p(X₁ =x₁)

=

c1

X

x1=0

Pp(X1 =x1)

+

c2

X

x1=c1+1

Pp(X2 ≤c3−x1|X₁=x1)Pp(X1 =x1).

Exakte Formel f¨ ur die OC-Funktion

L(p) =

c1

X

x1=0

P_p(X₁ =x₁)

+

c2

X

x1=c1+1 c3−x₁

X

x2=0

Pp(X2=x2|X₁=x1)Pp(X1 =x1).

Da X1 und X2 (bedingt) hypergeometrisch verteilt sind, gilt somit

L(p) =

c1

X

x1=0 M x1

N−M n1−x₁

N n1

+

c2

X

x1=c1+1 c3−x1

X

x2=0 M−x₁

x2

N−n₁−(M−x₁) n2−x₂

_M

x1

N−M n1−x₁

N−n₁ n2

_N

n1

.

N¨ aherungsformeln f¨ ur die OC-Funktion

I Binomialapproximation

p= M N

:

L(p)≈

c1

X

x1=0

n₁ x₁

p^x1(1−p)^n1−x1

+

c2

X

x1=c1+1 c3−x₁

X

x2=0

n1

x1

n2

x2

p^x1+x2(1−p)^{n1+n2−x1−x2}.

I Poissonapproximation (λ1 =n1p, λ2=n2p) : L(p)≈

c1

X

x1=0

(n₁p)^x1 x₁! e^−n1p +

c2

X

x1=c1+1 c3−x₁

X

x2=0

n^x₁¹·n^x₂²

x1!·x2!p^x1+x2e^−(n1+n2)p.

Bestimmung des Stichprobenplanes

I Durch Vorgabe von zwei Punkten der OC-Funktion sind die f¨unf Kenngr¨oßen n₁,n₂,c₁,c₂,c₃ nicht eindeutig bestimmbar.

I Diese Freiheit kann genutzt werden, um z.B. relativ einfache Stichprobenpl¨ane aufzustellen. H¨aufig werden genutzt:

I c₂=c₃,

I c₂= 3c₁ oder c₂= 5c₁ und

I n₂=n₁ oder n₂= 2n₁.

I Sinnvolle Bedingungen an die Kenngr¨oßen sind weiterhin:

I 0≤c₁<c₂≤n₁, damit tats¨achlich eine Zweistufigkeit vorliegt;

I c₁<c₃<c₂+n₂, damit eine 2. Stichprobe n¨otig wird, falls keine Annahme- oder Ablehneentscheidung im 1. Schritt erfolgt;

I c1

n1

< c3

n1+n2

, der f¨ur die Annahme erlaubte H¨ochstausschussanteil der 1. Stichprobe ist kleiner als der der Gesamtprobe;

I c3+ 1

n₁+n₂ <c2+ 1

n₁ , der Mindestausschussanteil zur Ablehnung ist in der 1. Stichprobe gr¨oßer als der in der Gesamtprobe.

Stichprobenumfang f¨ ur den zweistufigen Stichprobenplan

I Der Stichprobenumfang Ns ist jetzt zuf¨allig:

N_s =

n₁, falls X₁ ≤c₁ oder X₁ ≥c₂+ 1 ; n₁+n₂, falls c₁<X₁≤c₂.

I Zum Vergleich mit einstufigen Stichprobenpl¨anen nutzt man den erwarteten Stichprobenumfang(”ASN”, ”average sample number”, dieser h¨angt von der tats¨achlichen Ausschussquote p ab)

E_pN_s =n₁+n₂P_p(c₁ <X₁≤c₂)

=n1+n2 c2

X

x1=c1+1 M x1

_N−M

n1−x1

N n1

≈n₁+n₂

c2

X

x1=c1+1

n₁ x1

p^x1(1−p)^n1−x1, letztere Formel im Fall einer Binomialapproximation.

Vergleich mit einstufigen Stichprobenpl¨ anen

Beispiel 8.2:

Erwarteter Stichprobenumfang falls n1=n2 = 50 , c1= 0,c2 =c3 = 2 (Binomialapproximation)

I Um festzustellen, ob sich die Zweistufigkeit gegen¨uber der Einstufigkeit lohnt, vergleicht manEpNs mit dem

Stichprobenumfangn eines einstufigen Tests mit n¨aherungsweise gleicher OC-Funktion.

I Als Kenngr¨oße kann man dazu die sogenannteinverse Zweckdienlichkeit eff = max_pE_pN_s

n nutzen.

Beispiel 8.2 (N ≥ 1000 ⇒ Binomialapproximation)

I Zweistufiger Plan: n1 =n2= 50 , c1 = 0,c2=c3 = 2 (rot);

Einstufiger Plan: n= 94 , c = 3 (blau).

I

OC-Funktionen Erwarteter Stichprobenumfang

I Der Maximalwert von E_pN_s liegt bei ≈80 (f¨ur p = 0.0283 ist EpNs = 79.696)

⇒ eff ≈ 80

94 = 0.851 (≈ 85% des einstufigen Aufwandes) .

8.2.2 Sequentielle Stichprobenpl¨ ane

I Sequentielle Stichprobenpl¨ane kann man als Verallgemeinerung von mehrfachen Stichprobenpl¨anen ansehen. Bei ihnen wird jeweils ein Element aus dem Posten zuf¨allig ausgew¨ahlt und gepr¨uft und dann auf Basis der bislang vorliegenden Information entschieden, ob

I der Posten angenommen wird, oder

I der Posten abgelehnt wird, oder

I ein weiteres Element gezogen und gepr¨uft wird.

I Die mathematische Modellierung dieser Situation erfordert

weiterf¨uhrende Begriffe und die Berechnungen werden schwieriger.

I Im Folgenden bezeichnen

I k die Anzahl der schon gepr¨uften St¨ucke,

I Xk die zuf¨allige Anzahl der Ausschussst¨ucke unter den ersten k gepr¨uften.

Der sequentielle (Likelihood-Quotienten-)Test

I Gute Eigenschaften hat der folgende sequentielle (Likelihood-Quotienten-)Test:

I X_k ≤c_s·k−a Annahme des Postens,

I Xk ≥cs·k+b Ablehnung des Postens,

I cs·k−a<Xk <cs·k+b Fortsetzung der Pr¨ufung.

Dabei sind (als Funktionen von k) c_s·k−a dieAnnahmegerade und cs·k+b dieAblehnungsgerade.

I Die Forderungen L(pα)≈1−α und L(pβ)≈β werden n¨aherungsweise erf¨ullt durch (bei Binomialapproximation):

a= ln

1−α β

d , b = ln

1−β α

d , cs = ln

1−pα

1−p_β

d

mit d = ln

p_β(1−pα) p_α(1−p_β)

.

Beispiel 8.3

I Sequentieller Stichprobenplan mit:

Annahmegrenze p_α= 0.02 mit Produzentenrisiko α= 0.1 , Ablehngrenze p_β = 0.05 mit Konsumentenrisiko β= 0.1 .

I d = ln

0.05·0.98 0.02·0.95

= 0.9474 , a=b= ln ^0.9_0.1

d = 2.319 , cs = ln ^0.98_0.95

d = 0.03282 .

I Pr¨ufverfahren:

k Anzahl der bisher gepr¨uften St¨ucke,

xk Anzahl der bisher gefundenen Ausschussst¨ucke.

I xk ≤csk−a= 0.03282·k−2.319 , Annahme des Postens;

I x_k ≥c_sk+b= 0.03282·k+ 2.319 , Ablehnung des Postens;

I c_sk−a= 0.03282k−2.319<x_k <0.03282k+ 2.319 =c_sk+b, Fortsetzung der Pr¨ufung.

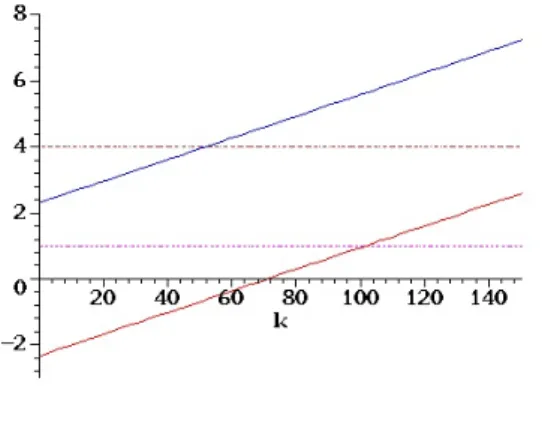
Grafik zum Beispiel 8.3

I Wenn z.B. bei k ≤51 bereits xk = 4 , dann Ablehnung des Postens.

I Wenn z.B. bei k ≥102 immer noch xk = 1 , dann Annahme des Postens.

Erwarteter Stichprobenumfang

I Der Stichprobenumfang N_s ist auch in diesem Fall eine Zufallsgr¨oße.

I F¨ur den erwarteten (oder durchschnittlichen Stichprobenumfang ASN) ergibt sich ungef¨ahr

E_pN_s =

( b−(a+b)L(p)

p−cs , f¨ur p 6=c_s;

ab

cs(1−cs), f¨ur p =cs.

(L(p) ist der Wert der OC-Funktion f¨ur diesen Stichprobenplan, falls der tats¨achliche Ausschussanteil des Postens p ist.)

I Im Allgemeinen ist der erwartete Stichprobenumfang eines sequentiellen Stichprobenplanes wesentlich kleiner als der eines vergleichbaren einfachen Stichprobenplanes.

I Die konkreten Stichprobenumf¨ange k¨onnen aber bei sequentiellen Stichprobenpl¨anen starken Schwankungen unterliegen, wodurch sich z.B. organisatorische Probleme ergeben k¨onnen.

Erwarteter Stichprobenumfang im Beispiel 8.3

EpNs ≈























b−(a+b)·1 0−cs = _c^a

s ≈ 70.7, f¨urp = 0 ;

b−(a+b)·(1−α)

pα−cs ≈ 144.8, f¨urp =p_α= 0.02 ;

ab

cs(1−cs) ≈ 169.5, f¨urp =cs = 0.03282 ;

b−(a+b)·β

pβ−cs ≈ 108.0, f¨urp =p_β = 0.05 ;

b−(a+b)·0 1−c_s = _1−c^b

s ≈ 2.4, f¨urp = 1.

I Im Vergleich dazu hat ein einfacher Stichprobenplan mit etwa den gleichen G¨uteeigenschaften einen vom Ausschussanteil p

unabh¨angigen Stichprobenumfang n = 232 (f¨ur N= 10000) bei einer Annahmezahl von c = 7 (berechnet mit Statgraphics, also der hypergeometrischen Verteilung).

Beispiel 8.3 mit Statgraphics

Describe → Numeric Data→ Sequential Sampling Beschreiben→ Numerische Daten→ Sequentielle Tests

Als n¨achstes muss ein Datensatz (Data Datenvariable ) ausgew¨ahlt werden. Dann stehen verschiedene sequentielle Tests zu Auswahl.

Test Performance

p Prob(accept null) Average sample number

Null hyp. 0,02 0,9000 144,76

0,023 0,8333 157,47

0,026 0,7454 166,95

0,029 0,6412 171,57

0,032 0,5301 170,64

0,035 0,4225 164,66

0,038 0,3268 154,99

0,041 0,2472 143,30

0,044 0,1842 131,00

0,047 0,1360 119,05

Alt. hyp. 0,05 0,1000 107,98

Sample size for fixed test n = 258

Dr. Andreas W¨unsche Statistik II f¨ur Betriebswirte Vorlesung 14 Version: 21. Januar 2020 17

Analysis Summary im Beispiel 8.3 mit Statgraphics Sequential Sampling

Data variable: X

Count 500

Average 0,024

Median 0,0

Standard deviation 0,153202

Minimum 0,0

Maximum 1,0

Stnd. skewness 56,9537 Stnd. kurtosis 169,214

Hypothesis Test

Null hypothesis p = 0,02 alpha risk = 0,1 Alternative hypothesis p = 0,05 beta risk = 0,1 Decision: accept null hypothesis at sample 102

Decision Numbers

Acceptance Rejection Sample Cumulative sum Number Number

1 1,0 -2,28644 2,35208

2 1,0 -2,25363 2,3849

3 1,0 -2,22081 2,41771

4 1,0 -2,18799 2,45053

. . .

100 1,0 0,962478 5,601

101 1,0 0,995296 5,63382

102 1,0 1,02811 5,66664

103 1,0 1,06093 5,69945

Dr. Andreas W¨unsche Statistik II f¨ur Betriebswirte Vorlesung 14 Version: 21. Januar 2020 18

Seqentieller Test mit Statgraphics

Werte der OC- und ASN-Funktion mit Statgraphics

Test Performance

p Prob(accept null) Average sample number

Null hyp. 0,02 0,9000 144,76

0,023 0,8333 157,47

0,026 0,7454 166,95

0,029 0,6412 171,57

0,032 0,5301 170,64

0,035 0,4225 164,66

0,038 0,3268 154,99

0,041 0,2472 143,30

0,044 0,1842 131,00

0,047 0,1360 119,05

Alt. hyp. 0,05 0,1000 107,98

Sample size for fixed test n = 258

OC-Funktion im Beispiel 8.3 mit Statgraphics

Dr. Andreas W¨unsche Statistik II f¨ur Betriebswirte Vorlesung 14 Version: 21. Januar 2020 21

ASN-Funktion im Beispiel 8.3 mit Statgraphics

Weitere Bemerkungen zu Stichprobenpl¨ anen

I Bei den einstufigen Verfahren l¨asst sich der Pr¨ufaufwand

gegebenenfalls etwas reduzieren, wenn die Kontrolle abgebrochen wird, sobald die Anzahl der schlechten St¨ucke die Annahmezahl

¨

uberschreitet.

I Entsprechend l¨asst sich auch bei zwei- oder mehrstufigen Verfahren gegebenenfalls etwas Pr¨ufarbeit einsparen.

I Sequentielle Verfahren werden inzwischen auch in vielen anderen Gebieten der Technik, Medizin, Naturwissenschaften usw.

angewendet, wo es darauf ankommt, den durchschnittlichen Stichprobenumfang m¨oglichst gering zu halten und

Wahrscheinlichkeiten f¨ur Fehler erster und zweiter Art unter Kontrolle zu halten.

Stichprobenpl¨ ane f¨ ur quantitative Merkmale

I Bisher wurden attributive Stichprobenpl¨anebehandelt, bei denen nur festgestellt wird, ob die ¨uberpr¨uften St¨ucke brauchbar oder unbrauchbar sind.

I Trifft man die Entscheidung

”gut“ oder

”schlecht“ aber aufgrund eines quantitativen Merkmals, wie L¨ange, Gewicht, Lebensdauer etc., dann lassen sich auchStichprobenpl¨ane f¨ur quantitative Merkmale (Stichprobenpl¨ane f¨ur die Variablenpr¨ufung) verwenden.

I Diese nutzen Informationen ¨uber den Verteilungstyp des Merkmals aus und k¨onnen dadurch mit wesentlich geringeren

Stichprobenumf¨angen auskommen. Allerdings kann der Pr¨ufaufwand f¨ur die einzelne Messung gr¨oßer sein.

I Konkrete Beispiele f¨ur derartige Pr¨ufpl¨ane findet man in der Fachliteratur.