Statistik I f¨ur Betriebswirte Vorlesung 3

Statistik I f¨ ur Betriebswirte Vorlesung 3

Dr. Andreas W¨ unsche

TU Bergakademie Freiberg Institut f¨ur Stochastik

15. April 2019

Verteilungsfunktion einer Zufallsgr¨ oße

I

Die Verteilungen von diskreten oder stetigen Zufallsgr¨ oßen (oder anderen Typen) k¨ onnen vollst¨ andig durch die Verteilungsfunktion der jeweiligen Zufallsgr¨ oße beschrieben werden.

I

Definition: Die Funktion F

einer reellen Variablen mit reellen Funktionswerten, die durch

F

(x) = P (X < x) = P (−∞ < X < x), x

, definiert wird, heißt Verteilungsfunktion der Zufallsgr¨ oße

. Der Funktionswert ist f¨ ur jede reelle Zahl x die Wahrscheinlichkeit daf¨ ur, dass die Zufallsgr¨ oße X einen Wert annimmt, der kleiner als x ist.

I

Bemerkung: Mitunter wird die Verteilungsfunktion einer

Zufallsgr¨ oße X auch durch F

(x) = P (X

x ), x

, definiert,

Verteilungsfunktion einer diskreten Zufallsgr¨ oße

I

F¨ ur diskrete Zufallsgr¨ oßen X mit endlich oder auch unendlich vielen m¨ oglichen Werten x

ist die Verteilungsfunktion eine Treppen- funktion mit Spr¨ ungen der H¨ ohe p

= P (X = x

) an den Werten x

.

I

Beispiel 1.1: X Augenzahl beim W¨ urfeln mit einem gerechten

W¨ urfel: Verteilungsfunktion F

.

Verteilungsfunktion einer stetigen Zufallsgr¨ oße

I

F¨ ur stetige Zufallsgr¨ oßen ist die Verteilungsfunktion eine in allen Punkten stetige Funktion.

I

F

(x) =

−∞

f

(t)

x

und f

(x) = F

(x) in den Werten x, in denen die Ableitung existiert.

I

Beispiel 1.2: Zufallsgr¨ oße X auf [0, 1] gleichverteilt: Verteilungs-

funktion F

.

Allgemeine Eigenschaften von Verteilungsfunktionen

I

Eine Verteilungsfunktion F

ist monoton nicht fallend.

I

Es gilt lim

x→−∞

F

(x) = 0 .

I

Es gilt lim

x→+∞

F

(x) = 1 .

I

Es gilt f¨ ur beliebige reelle Zahlen a < b :

P (a

X < b) = F

(b)

F

(a) .

I

Spezialf¨ alle:

a =

: P (X < b) = F

(b) , b =

: P (a

X ) = 1

F

(a) .

I

F¨ ur eine stetige Zufallsgr¨ oße X gelten

P(a

X < b) = P (a < X < b) = P (a < X

b) = P (a

X

b) .

Quantile einer stetigen Zufallsgr¨ oße

I

Die reelle Zahl x

mit 0 < q < 1 heißt

der stetigen Zufallsgr¨ oße X , wenn die Werte von X mit einer Wahrscheinlichkeit q links von x

liegen, d.h. x

ist eine L¨ osung der Gleichung

P (X < x

) = F

(x

) = q =

x

= F

(q) .

I

q−Quantile k¨ onnen auch f¨ ur diskrete und andere Zufallsgr¨ oßen betrachtet werden.

I

Wichtige Quantile sind:

I das 0.5–Quantil, es heißtMedian vonX;

I das 0.25– bzw. 0.75–Quantil, dies sind die sogenannten Viertelquantile (Quartile) vonX;

I dieα−, (1−α)−, 1−α

2

−Quantile f¨ur kleine Werteα,

sie spielen bei statistischen Fragen eine große Rolle.

Exponentialverteilung

Eine Zufallsgr¨ oße X heißt exponentialverteilt mit Parameter

0, falls f¨ ur die Verteilungsfunktion F

bzw. die Verteilungsdichte f

gilt:

F

(x) =

0 , x

0 ,

1

exp(−λx) , x > 0 , f

(x) =

0 , x

0 ,

λ exp(−λx) , x > 0 .

Verteilungsfunktion (λ = 1) Dichtefunktion (λ = 1)

Quantile f¨ ur Exponentialverteilung

I

Es sei X exponentialverteilt mit Parameter λ = 1, d.h.

F

(x) = P (X < x) =

0, x

0, 1

exp(−x), x > 0.

I

Dann gilt f¨ ur das q−Quantil x

(mit 0 < q < 1) :

F

(x

) = 1

exp(−x

) = q, also x

=

ln (1

q) .

I

q x

0.25 0.288 0.5 0.693 0.75 1.386 0.95 2.996

Verteilungsfunktion Dichtefunktion

1.5.2 Charakteristische Gr¨ oßen von Verteilungen

I

Die Gesamtinformation, die mit einer Wahrscheinlichkeitsverteilung gegeben wird (oder gegeben werden muss), ist h¨ aufig zu

umfangreich, deshalb nutzt man abgeleitete Kenngr¨ oßen, die in praktischen Situationen gut zu nutzen sind. Dabei kann man bei den Kenngr¨ oßen im Allgemeinen Lageparameter und Streuungsparameter unterscheiden.

I

Die am h¨ aufigsten genutzte Kenngr¨ oße ist der Erwartungswert

einer Zufallsgr¨ oße X (auch Mittelwert der Zufallsgr¨ oße genannt). Er ist ein Lageparameter, eine (nichtzuf¨ allige) reelle Zahl und

beschreibt den Schwerpunkt der Wahrscheinlichkeitsmasse.

Erwartungswert einer Zufallsgr¨ oße I

I

Definition: F¨ ur eine diskrete Zufallsgr¨ oße X mit m¨ oglichen Werten x

, x

, . . . und zugeh¨ origen Wahrscheinlichkeiten p

= P (X = x

), p

= P (X = x

), . . . wird der Erwartungswert definiert durch

EX =

i

x

p

.

F¨ ur eine stetige Zufallsgr¨ oße X mit Dichtefunktion f

wird der Erwartungswert definiert durch

EX =

−∞

x

f

(x)

.

Erwartungswert einer Zufallsgr¨ oße II

Beispiele 1.1 und 1.2:

X Augenzahl beim W¨ urfeln X gleichverteilt auf [0, 1]

Einzelwahrscheinlichkeiten Dichtefunktion

und Erwartungswert und Erwartungswert

Erwartungswert einer Zufallsgr¨ oße III

I

Es gelten folgende Rechenregeln f¨ ur Erwartungswerte:

Sind X und Y Zufallsgr¨ oßen und a und b reelle Zahlen, dann gelten E(a + b

X ) = a + b

EX ;

E(X + Y ) = EX + EY .

Dies sind die Linearit¨ atseigenschaften der Erwartungswertbildung.

I

Nicht jede Zufallsgr¨ oße besitzt einen Erwartungswert.

I

Ist g :

eine (z.B. stetige) Funktion und X eine Zufallsgr¨ oße, dann kann man den Erwartungswert der Zufallsgr¨ oße Y = g (X ) wie folgt berechnen:

EY = Eg (X ) =

i

g (x

)p

f¨ ur eine diskrete ZG X ;

EY = Eg (X ) =

g (x)f

(x)

f¨ ur eine stetige ZG X .

Varianz einer Zufallsgr¨ oße

I

Die wichtigste Kenngr¨ oße f¨ ur die Variabilit¨ at von Zufallsgr¨ oßen ist die Varianz der Zufallsgr¨ oße, auch Streuung oder Dispersion genannt. Sie gibt die erwartete quadratische Abweichung der Zufallsgr¨ oße von ihrem Erwartungswert an.

I

Definition: Die Varianz

der Zufallsgr¨ oße X ist die nichtnegative reelle Zahl (falls sie existiert)

VarX = E (X

EX )

=









 P

i

(x

EX )

p

, diskrete ZG;

∞

R

−∞

(x

EX )

f

(x)

, stetige ZG.

I

Die Varianz l¨ asst sich meistens bequemer mit Hilfe der Formel VarX = E X

−

(EX )

Standardabweichung einer Zufallsgr¨ oße und Eigenschaften

I

Definition: Die Standardabweichung

der Zufallsgr¨ oße X ist die positive Quadratwurzel aus der Varianz der Zufallsgr¨ oße:

σ

=

√

VarX .

I

Ist a eine reelle Zahl und X eine Zufallsgr¨ oße, dann gelten

I Var(aX) =a²VarX,

I Var(a+X) =VarX,

I σ_(aX)=|a|σX,

I σ_(a+X) =σX.

I

Es gilt genau dann VarX = σ

= 0, wenn es eine reelle Zahl x

gibt, so dass P(X = x

) = 1 gilt.

Berechnung der Varianzen in den Beispielen 1.1 und 1.2

I

X Augenzahl beim W¨ urfeln mit einem gerechten W¨ urfel.

EX

= 1

6 + 2

6 + 3

6 + 4

6 + 5

6 + 6

6 = 91 6 VarX = 91

6

7

2

= 35

12 = 2.917.

I

X gleichm¨ aßig verteilt auf dem Intervall [0, 1].

EX

=

0

x

1

= 1 3 VarX = 1

3

1

2

= 1

12 = 0.0833.

Standardisierung und Variationskoeffizient

I

Definition: F¨ ur eine Zufallsgr¨ oße X mit endlicher Varianz wird die Standardisierung definiert durch

Z = X

EX

σ

.

Dies ist eine mit X zusammenh¨ angende Zufallsgr¨ oße, die den Erwartungswert 0 und eine Varianz von 1 besitzt.

I

Definition: F¨ ur eine Zufallsgr¨ oße X mit endlicher Varianz und EX

Variationskoeffizient

definiert durch

V

= σ

EX .

Mit ihm wird die Streuung der m¨ oglichen Werte zum mittleren Wert

(Erwartungswert) in Beziehung gesetzt, dadurch hilft er beim

Vergleich der m¨ oglichen zuf¨ alligen Schwankungen der Werte von

Kovarianz und Unkorreliertheit zweier Zufallsgr¨ oßen

I

F¨ ur zwei Zufallsgr¨ oßen X und Y mit endlicher Varianz heißt die reelle Zahl

Cov (X , Y ) = E ((X

EX )(Y

EY )) = E(XY )

EX

EY die Kovarianz der beiden Zufallsgr¨ oßen. Sie ist ein Maß f¨ ur die St¨ arke eines linearen Zusammenhangs zwischen X und Y .

I

Der Korrelationskoeffizient der Zufallsgr¨ oßen X und Y ist dann

%

= Corr (X , Y ) = Cov (X , Y )

σ

σ

.

Dieser Wert liegt immer zwischen -1 und 1 . Im Fall

= 1 besteht ein vollst¨ andiger linearer Zusammenhang zwischen beiden Gr¨ oßen.

I

Zwei Zufallsgr¨ oßen X und Y heißen unkorreliert, falls

Unabh¨ angigkeit von Zufallsgr¨ oßen und Varianz einer Summe von unabh¨ angigen Zufallsgr¨ oßen

I

Definition: Zwei Zufallsgr¨ oßen X und Y heißen stochastisch unabh¨ angig, falls f¨ ur beliebige reelle Zahlen x, y gilt:

P ({X < x} ∩ {Y < y}) = P (X < x )

P (Y < y ) .

I

Sind zwei Zufallsgr¨ oßen X und Y mit endlichen Erwartungswerten stochastisch unabh¨ angig, dann gilt E(X

Y ) = EX

EY . Damit sind X und Y auch unkorreliert.

I

Satz: Sind zwei Zufallsgr¨ oßen X und Y stochastisch unabh¨ angig (oder unkorreliert), dann gilt f¨ ur deren Summe:

Var(X + Y ) = VarX + VarY .

Diese Eigenschaft gilt aber nicht im Allgemeinen !

Tschebyschew-Ungleichung

I

Man kann mit Hilfe von Erwartungswerten und Varianzen auch Wahrscheinlichkeiten absch¨ atzen. Dabei finden die folgenden Ungleichungen ¨ ofters Verwendung.

I

Satz:

F¨ ur eine Zufallsgr¨ oße X mit E|X

<

gilt f¨ ur beliebige c > 0 P (|X

c )

E|X

c . Ist die Varianz der Zufallsgr¨ oße X endlich, d.h.

VarX = E(X

EX )

<

, dann gilt auch

P (|X

EX

c )

VarX

c

.

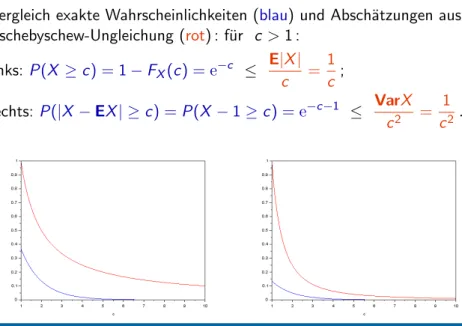
Illustration Tschebyschew-Ungleichung f¨ ur eine Exponentialverteilung mit Parameter λ = 1

Vergleich exakte Wahrscheinlichkeiten (blau) und Absch¨ atzungen aus Tschebyschew-Ungleichung (rot) : f¨ ur c > 1 :

links:

(X

) = 1

(c ) =

c

;

rechts:

(|X

1

) =

c²

.